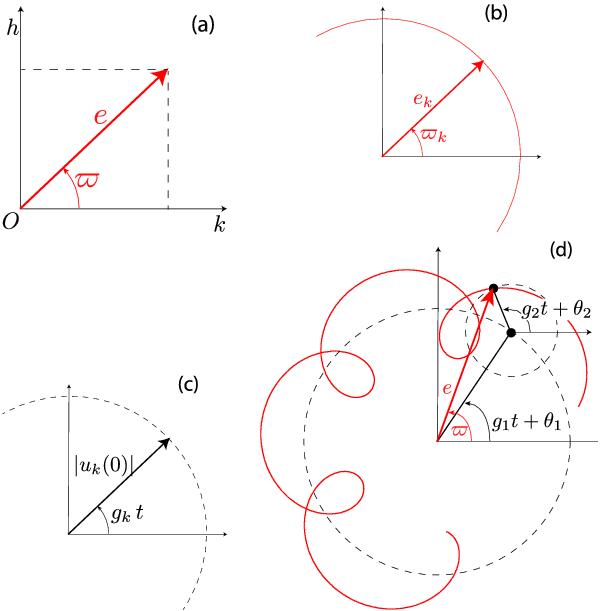
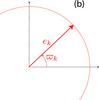
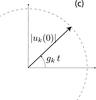
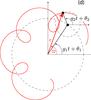
a) The complex variable z = eexp(iϖ) provides the orientation and eccentricity of the orbit in the plane. Alternatively, one can use the rectangular real coordinates k = ecosϖ, h = esinϖ, as in Murray & Dermott (1999). b) If the Lagrange-Laplace matrix A were diagonal, the eccentricity of all planets would be constant with uniform precession. c) As A is not diagonal, one needs to make a linear transformation to transform z_k into proper modes u_k. The proper modes amplitude are then constant and u_k precess uniformly with frequency g_k. d) The full solution z_j = e_jexp(ϖ_j) are linear combinations of the proper modes u_k. In the figure, with two proper modes (i.e. two planets and n = 2). The red curve represents the evolution of the eccentricity and longitude of perihelia of Jupiter over 200 000 years under the perturbation of Saturn.