EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A43 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A43
Number of page(s) 7
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201015940
Published online 30 January 2012

© ESO, 2012

1. Introduction

The discovery of strong gravitational lensing in Q0957+561 (Walsh et al. 1979) opened up a vast possibility of using strong-lens systems in the study of cosmology and astrophysics. Up to now, strong lensing has developed into an important astrophysical tool for probing both cosmology (Fukugita et al. 1992; Kochanek 1993; Zhu 2000a,b; Chae et al. 2002; Chae 2003; Chae et al. 2004; Mitchell et al. 2005; York et al. 2005; Zhu & Mauro 2008a; Zhu et al. 2008b) and galaxy structures, formations, and evolutions (Zhu & Wu 1997; Mao & Schneider 1998; Jin et al. 2000; Keeton 2001; Kochanek & White 2001; Chae & Mao 2003; Ofek et al. 2003; Rusin & Kochanek 2005; Chae 2005; Chae et al. 2006; Koopmans et al. 2006; Treu et al. 2006). Now several hundred strong lens systems produced by massive galaxies have been discovered, but only  ~90 galactic-scale strong lenses with known redshift of the source and the image separation can form well-defined samples that are useful for statistical analyses.

These well-defined strong lenses are particularly useful not only for constraining the statistical properties of galaxies such as optical region velocity dispersions (Chae 2005; Chae et al. 2006) and galaxy evolutions (Chae & Mao 2003; Ofek et al. 2003), but also for constraining cosmological parameters such as the present matter density Ωm and the equation of state of dark energy w (Chae 2003; Mitchell et al. 2005). For example, the CLASS statistical sample (Browne et al. 2003; Chae 2003) containing 13 lenses that strictly satisfy the well-defined selection criteria was first extensively used by Chae et al. (2002) and Chae (2003), who found Ωm ≈ 0.3 in a flat cosmology with non-evolving galaxy populations. Then this CLASS sample was reanalyzed with the velocity dispersion function (VDF) of early-type galaxies derived from the SDSS Data Release 1 (DR1 Sheth et al. 2003) galaxies (Mitchell et al. 2005).

In our paper, we summarize a complete lens-redshift sample from various imaging surveys including the Cosmic Lens ALL-Sky Survey (CLASS; Browne et al. 2003; Myers et al. 2003), the JVAS, the Sloan Digital Sky Survey (SDSS; Oguri et al. 2006), the PMN-NVSS Extragalactic Lens Survey (PANELS; Winn et al. 2001) and the Snapshot survey, which accumulates 29 galactic-scale lenses so far to form a well-defined radio-selected lens sample. Newly measured J1620+1203 (Kayo et al. 2010) from SDSS is also included.

An important point is the measurement of the velocity dispersion function (VDF) of galaxies. Chae (2005) found that the Sheth et al. (2003) VDF of early-type galaxies underestimated their abundance based on the Wilkinson Microwave Anisotropy Probe (WMAP) 1st year cosmology (Spergel et al. 2003). Then, with a new method of classifying galaxies (Park & Choi 2005), Choi et al. (2007) made a new VDF measurement of early-type galaxies based on the much larger SDSS Data Release 5 (DR5; Adelman-McCarthy et al. 2007). The Choi et al. (2007) VDF has a much higher comoving number density of early-type galaxies and a different shape for the lower velocity part compared with the (Spergel et al. 2003) VDF. Recently, Chae (2007) have determined the VDF of the late-type population using the Tully-Fisher relation and a SIE galaxy model that matches that of Sheth et al. (2003) relatively well. These authors also considered the scatter of the Tully-Fisher relation. More recently, Chae (2010) introduced a correction term for high-velocity dispersions and used the Monte Carlo method to separately generate the early-type and late-type galaxies and to derive a total VDF for the entire population of galaxies (see also in Bernardi et al. 2010). However, the simulated data points for the total population of galaxies are not fitted well by the VDF of the morphologically-typed galaxy populations, which might be the true nature of the total VDF and may be caused by the errors in the adopted correlations between luminosity and velocity especially at low velocities (Chae 2010).

Moreover, strong lensing has also been extensively applied to constrain dark energy, one of the most important questions of the modern cosmology ever since the observations of type Ia supernovae (SNe Ia), which first indicated an accelerating expansion of the universe at the present stage (Riess et al. 1998). Up to now, diverse analyses have revealed that our universe is spatially flat and consists of 70 percent dark energy with negative pressure, the remaining 30 percent are dust matter (cold dark matter plus baryons) and negligible radiation. Among diverse dark-energy models, the most simple candidate for the uniformly distributed dark energy is considered to be in the form of vacuum energy density or cosmological constant (Λ). However, the cosmological constant is always entangled with (i) a fine-tuning problem (the present amount of dark energy is too small compared with the fundamental scale) and (ii) a coincidence problem (dark-energy density is comparable to the critical density today). Alternatively, there are other choices, for example, an X-matter component, which is characterized by an equation of state p = wρ, where  −1 ≤ w ≤ 0 (Zhu 1998; Peebles & Ratra 2003). The goal of this work is to use the lens-redshift test combined with the revised VDF of all-type galaxies based on the SDSS DR5 data to constrain two cosmological models.

This paper is organized as follows. In Sect. 2 we briefly describe the analysis method including assumptions about the lens population. We then present the lens-redshift data from various surveys in Sect. 3. We introduce two prevalent cosmologies and show the results of constraining cosmological parameters using the MCMC method in Sect. 4. Finally, we conclude and make a discussion in Sect. 5.

2. Lens-redshift test

The statistical lensing model used in this paper incorporates the (differential) lensing probabilities of specific image multiplicities for the multiply-imaged sources using the SIE lens model. The primary assumption we make is that the distribution of early-type galaxies in luminosity is given by the Schechter (1976) form 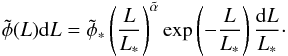(1)Considering a power-law relation between luminosity (L) and velocity dispersion (σ), i.e. 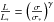, we can describe the distribution of galaxies in velocity dispersion in the form of the modified Schechter function φ(σ) (Sheth et al. 2003; Mitchell et al. 2005) (2)where \begin{lxirformule}$\phi_*$\end{lxirformule} is the integrated number density of galaxies, σ ∗  is the characteristic velocity dispersion, with the following relations: 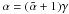, β = γ, and .

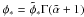Following Eq. (2), the particular differential probability that a source at redshift zs be multiply imaged by a distribution of galaxies at redshift zl with a image separation Δθ can be written as (3)Meanwhile, Δθ ∗  is the characteristic image separation given by 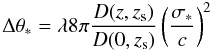(4)where D(z1,z2) is the angular-diameter distance between redshifts z1 and z2. On the hypothesis that galaxies are not biased toward oblate or prolate shape, we choose the dynamical normalization factor λ ≈ 1 for the singular isothermal ellipsoid (SIE) model (Chae 2003, 2005). Though isothermal mass model would, in general, be too simplified to accurately model individual lenses (Chae et al. 2002), it is accurate enough as first-order approximations to the mean properties of galaxies for the analyses of statistical lensing (Kochanek 1993; Mao & Kochanek 1994; Rix et al. 1994; Kochanek 1996; King et al. 1997; Fassnacht & Cohen 1998; Rusin & Kochanek 2005).

Following Chae (2003), the likelihood ℒ of the observed image separations for NL multiply-imaged sources reads 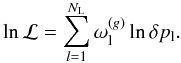(5)Here δpl is the particular differential probability for the l-th multiply-imaged source. 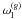(g = e, s) is the weight factor given to the early-type or the late-type populations, which satisfies 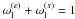. If the lensing galaxy type is unknown, we use (g = e, s) (Chae 2003). Accordingly, a “χ2” is defined as 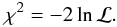(6)Notice that the χ2 here is free of the dimensionless Hubble constant h, which makes it an individual cosmological probe besides SNeIa, CMB, BAO etc. The “best-fit” model parameters are determined by minimizing the χ2 (Eq. (6)) and confidence limits on the model parameters are obtained by using the usual Δχ2 ( ≡ 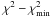) static, where 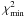is the global minimum χ2 for the best-fit parameters. Our calculating method is based on the publicly available package CosmoMC (Lewis & Bridle 2002).

On the side of the measurement of VDF, the first direct measurement of the VDF of early-type galaxies was the SDSS DR1 (Sheth et al. 2003): (7)then Choi et al. (2007) obtained a new VDF based on the much larger SDSS DR5: (8)Obviously, the revised DR5 VDF, which has been proved to provide an efficient way to constrain dark-energy models combined with gravitational lensing statistics (Zhu & Mauro 2008a), is quite different from the DR1 VDF in the characteristic velocity dispersion at 1σ. While early-type galaxies dominate strong lensing, late-type galaxies cannot be neglected. However, for the late-type galaxy population, the direct measurement of the VDF is complicated by the significant rotations of the disks. Chae (2007) estimated all parameters of Eq. (2) for the late-type population with the Tully-Fisher relation and SIE galaxy model: (9)which matches relatively well that of Sheth et al. (2003) who determined 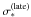using a Tully-Fisher relation taking into account the scatter of the Tully-Fisher relation.

Currently, it is found that simple evolutions do not significantly affect the lensing statistics if all galaxies are early-type (Mao & Kochanek 1994; Rix et al. 1994; Mitchell et al. 2005; Capelo & Natarajan 2007). Many previous studies on lensing statistics without evolutions of the velocity function have also derived appealing results that agree with the galaxy number counts (Im et al. 2002) and the redshift distribution of lens galaxies (Chae 2003; Ofek et al. 2003). However, in this paper, we consider galaxy evolutions both for early-type and late-type galaxies with a recent semi-analytical model of galaxy formation (Kang et al. 2005; Chae et al. 2006). Specially, the evolutions of both the number density σ ∗  and the characteristic velocity dispersion φ ∗  are 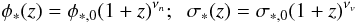(10)with the best-fit parameters of Kang et al. (2005): (νn,νv) = ( − 0.229, − 0.01) for early-type and (νn,νv) = (1.24, − 0.186) for late-type galaxies.

3. Lens-redshift data

Large systematic surveys of gravitationally lensed quasars provide a large statistical lens sample appropriate for studying cosmology. In this section, we summarize a sample from CLASS, SDSS observations, and recent large-scale observations of galaxies, which will be used as the input for the statistical lensing model described in Sect. 2. Two main sources of the lens redshift data are the Cosmic Lens All-Sky Survey and the Sloan Digital Sky Survey Quasar Lens Search.

3.1. CLASS

As the largest completed galactic mass scale gravitational lens search project, the Cosmic Lens All-Sky Survey, along with its predecessor project, the Jodrell-Bank-VLA Astrometric Survey (JVAS) has confirmed 22 multiply-imaged systems out of a total of 16521 radio sources (Browne et al. 2003). Out of the entire CLASS sample including the JVAS sources, a subsample of 8958 sources containing 13 multiply-imaged systems constitutes a statistical sample that satisfies well-defined observational selection criteria (Browne et al. 2003), which can be used for the statistical analysis of gravitational lensing in this paper. In this work we need galactic-scale strong lens samples that satisfy well-defined observational selection criteria. With the well-defined selection criteria from Browne et al. (2003); Chae (2003), two out of the four multiply-imaged sources in the JVAS, 0414+054 and 1030+074, are excluded from the final CLASS statistical sample because 0414+054 has a spectral index that is too steep and 1030+074 has two images whose fainter-to-brighter image flux-density ratio is less than 0.1. Meanwhile, we stress that the measured lens redshifts, source redshifts, image separations, image multiplicities and the lensing galaxy types (if determined) as shown in Table 1 are all needed through the likelihood function defined in Sect. 2 to constrain cosmological parameters. With this criterion, the CLASS sources B0850+054, B0445+123, B0631+519, B1938+666 are clearly excluded because of their unknown source redshifts, while for B0739+366 and J2004.1349, redshifts for source and lens are unavailable1. Moreover, the measured image separations of 1359+154, 1608+656 and 2114+022 are not used because the observed angular sizes are caused by multiple galaxies within their critical radii.

3.2. SDSS

The Sloan Digital Sky Survey Quasar Lens Search (SQLS; Oguri et al. 2006) is a photometric and spectroscopic survey that covers nearly a quarter of the entire sky (York et al. 2000) and therefore provides a large statistical lens sample apposite for cosmology study and research. We tried to find suitable lens samples from the optical quasar catalog of the Sloan Digital Sky Survey (SDSS; York et al. 2000). The first complete lens sample from Data Release 3 selected from 22 683 low-redshift (0.6 < z < 2.2) is provided in Inada et al. (2008). It consists of 11 lensed quasars satisfying the following well-defined selection criteria: 1) the image separation is between 1′′ and 20′′ with quasars brighter than i = 19.1; 2) the flux ratio of faint to bright images is greater than 10-0.5 for double lenses. We applied an additional cut to select an appropriate subsample: the lensing galaxy should be fainter than the quasar components, because a lens galaxy that is too bright will strongly affect the colors of the quasars (Richards et al. 2002). Four lensed quasars, Q0957+561, SDSS J1004+4112, SDSS J1332+0347, and SDSS J1524+4409 are removed with this cut. As in the CLASS, two more quasars, SDSS J1001+5027 and SDSS J1021+4913 are excluded because they have no redshift available. However, we successfully added four lens-redshift data including SDSS J1620+1203, one of the eight newly discovered and confirmed two-image lensed quasars by SDSS Quasar Lens Search (Kayo et al. 2010).

In Table 1 we summarize 29 strongly-lensed sources (redshifts both for sources and lenses as well as the largest image separations and galaxy types) from the CLASS (JVAS), the SDSS, the PANELS, and the Snapshot, which constitute a well-defined combined statistical sample for model constraints.

Table 1

Summary of strongly-lensed sources.

4. Dark-energy models and constraint results

Below we choose two popular dark-energy models and examine whether they are consistent with the lens-redshift data listed above.

  • 1.

    Cosmologically constant model.

  • 2.

    Dark energy with a constant equation of state.

The two models are currently viable candidates to explain the observed cosmic acceleration. On the one hand, given the current status of cosmological observations, there is no strong reason to go beyond the simple, standard cosmological model with a cosmological constant. On the other hand, to allow for deviations from the simple w =  −1 case, it is interesting to explore dark energy with a constant equation of state model to make a comparison. Unless stated otherwise, throughout the paper we calculate the best-fit values and vary the parameters within their 2σ uncertainties for either class of model. Next, we shall outline the basic equations describing the evolution of the cosmic expansion in both dark-energy models and calculate the best-fit parameters.

4.1. Constraint on the standard cosmological model (ΛCDM)

4.1.1. Constraint from the lens-redshift data

In the simplest scenario, the dark energy is simply a cosmological constant, Λ, i.e., a component with constant equation of state w = p/ρ =  −1. If flatness of the FRW metric is assumed, the Hubble parameter according to the Friedmann equation is 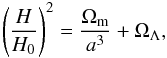(11)where Ωm and ΩΛ parameterize the density of matter and cosmological constant, respectively. Moreover, in the zero-curvature case (Ω = Ωm + ΩΛ = 1), this model has only one independent parameter θ = ΩΛ.

We plot the likelihood distribution function for this model in Fig. 1. The best-fit value of the parameter is 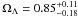. Obviously, the lens-redshift data only give a relatively weak constraint on the model parameter ΩΛ, though the universally recognized value of ΩΛ = 0.75 is still included at 68.3% CL (1σ). To make a comparison, it is necessary to refer to the previous results: the current best-fit value from cosmological observations is ΩΛ = 0.73 ± 0.04 in the flat case (Davis et al. 2007), which is in relatively stringent accordance with our result. Moreover, Komatsu et al. (2009) gave the best-fit parameter Ωm = 0.274 for the flat Λ CDM model from the WMAP 5-year results with the BAO and SN Union data. We find that the constraint result from the lens-redshift data is marginally consistent with the previous works above.

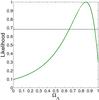thumbnail Fig. 1

Likelihood distribution function for the Λ CDM model constrained by the lens-redshift data.

4.1.2. Joint analysis with BAO and CMB

For the BAO data, the parameter 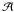is used, which is independent of cosmological models and for a flat universe can be expressed as (12)where zBAO = 0.35 and 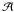is 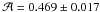from the SDSS (Eisenstein et al. 2005).

For the CMB data, the shift parameter ℛ is used, which may provide an effective way to constrain the parameters of dark energy models owning to its large redshift distribution. Derived from the CMB data, ℛ takes the form 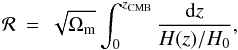(13)where zCMB = 1090 (Komatsu et al. 2009) is the redshift of recombination and the 5-year WMAP data give ℛ = 1.710 ± 0.019 (Komatsu et al. 2009).

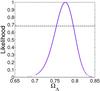thumbnail Fig. 2

Likelihood distribution function for the Λ CDM model constrained by the lens-redshift data combined with CMB.

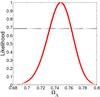thumbnail Fig. 3

Likelihood distribution function for the Λ CDM model constrained by the lens-redshift data combined with CMB and BAO.

In Figs. 2 and 3 we show the result by combining the lens redshift data with CMB and CMB+BAO, respectively. The best-fit parameter is 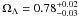and 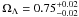, a relatively satisfactory result consistent with that of Li et al. (2010). Compared with Fig. 1, apparently, ΩΛ is more tightly constrained with the joint data sets.

4.2. Dark energy with a constant equation of state (w)

4.2.1. Constraint from the lens-redshift data

If we allow for a deviation from the simple w =  −1, a component with a arbitrary, constant value for the equation of state could be introduced. The accelerated expansion can be obtained when w <  −1/3. In a zero-curvature universe, the Hubble parameter for this generic dark energy component with density Ωx then becomes 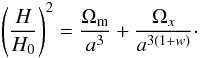(14)Obviously, when flatness is assumed (Ω = Ωm + ΩΛ = 1), it is a two-parameter model with the model parameters θ =  { Ωx,   w } .

thumbnail Fig. 4

w model constrained by the lens-redshift data: likelihood contours at 68.3% and 95.4% CL in the Ωx − w plane.

For the lens-redshift data only, the best-fit values of the parameters are Ωx = 0.78,w =  −1.15. Figure 4 shows the confidence limits in the Ωx − w plane. On the one hand, we have w <  −0.52 at 68.3% CL, which is quite different from the result of Chae (2007); on the other hand, Einstein’s cosmological constant (w =  −1) is still favored within 1σ error region. Therefore, it seems that the present lens-redshift data do not necessarily favor the phantom DE model with w <  −1 (Caldwell 2002, 2003). However, it is still interesting to see whether this remains so with future lager and better lens-redshift data.

4.2.2. Joint analysis with BAO and CMB

In Figs. 5 and 6 we plot the likelihood contours with the joint data by combining the lens-redshift data with CMB and CMB+BAO in the Ωx − w plane. The best-fit parameters are 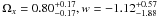and 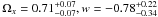. Notice that both Ωx and w are more stringently constrained with the joint observational data. Meanwhile, the currently preferred values of w in this model still include the cosmological constant case: w =  −1.01 ± 0.15 (Davis et al. 2007). Therefore, when the equation of state does not depend on the redshift, the dark energy is consistent with a flat cosmological constant model within 1σ error region.

thumbnail Fig. 5

w model constrained by the lens-redshift data combined with CMB: likelihood contours at 68.3% and 95.4% CL in the Ωx − w plane.

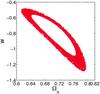thumbnail Fig. 6

w model constrained by the lens-redshift data combined with CMB and BAO: likelihood contours at 68.3% and 95.4% CL in the Ωx − w plane.

5. Conclusion and discussion

Recent new observations, such as SNeIa, Wilkinson Microwave Anisotropy Probe (WMAP) (Komatsu et al. 2009) and baryon acoustic oscillations (BAO) (Percival et al. 2009), the time drift of subtended angles (Zhang & Zhu 2009), the updated Gamma-ray bursts (GRB) (e.g., Gao et al. 2012; Liang et al. 2011) have provided many robust tools to study the dynamical behavior of the universe. However, it is still important to use other different probes to set bounds on cosmological parameters.

In this work, we have followed this direction and used the distribution of gravitationally-lensed image separations observed in the Cosmic Lens All-Sky Survey (CLASS), the PMN-NVSS Extragalactic Lens Survey (PANELS), the Sloan Digital Sky Survey (SDSS) and other surveys to constrain cosmological models with the new measurements of the velocity dispersion function of galaxies based on the SDSS DR5 data and recent semi-analytical modeling of galaxy formation. Two dark-energy models (ΛCDM and constant w) were considered under a flat universe assumption.

For the zero-curvature Λ CDM model, although the lens-redshift data can not tightly constrain the model parameter 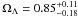, a stringent constraint can be obtained by combining the lens-redshift data with the comic macrowave background data 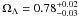and the baryonic acoustic oscillation peak data 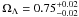. Furthermore, we consider a flat cosmology with a constant w dark energy. For the lens-redshift data, we have w <  −0.52 at 68.3% CL, a result different from that of Chae (2007) with w <  −1.2 (68.3% CL), therefore, these strong lensing data do not necessarily favor a super-negative equation of state for dark energy. However, Einstein cosmological constant (w =  −1) is still included within 1σ error region. Likewise, adding CMB and CMB+BAO does lead to further improvements in parameter constraints with 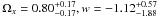and 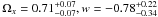, respectively. Therefore, it indicates that the cosmological constant model is still the best one to explain these lens-redshift data, a conclusion in accordance with the previous works (Davis et al. 2007) and the results from the WMAP and the large-scale structures in the SDSS luminous red galaxies (Spergel et al. 2003; Tegmark et al. 2004; Eisenstein et al. 2005).

However, we also notice that firstly, the implementation of singular isothermal ellipsoid model (SIE) may be a source of systematic errors. For example, a lens ellipticity of 0.4 can lead to a difference of ΔΩm ≈  −0.05 compared with the spherical case due to the variation of magnification bias and cross section (Huterer et al. 2005). Secondly, for the source of the lens redshift data, in this paper we simply discarded lens systems that do not have measured lens or source redshifts. This could as well possibly bring biases and will be considered in our future work. Thirdly, though the lens redshift test applied in this paper is free from the magnification bias arising from the uncertain source counts, it may also lose the statistical power of absolute lensing probabilities (or “lensing rates”). Lastly, though we used the VDF of galaxies based on a much larger SDSS Data Release in the strong-lensing statistics, the accuracy of measurements on relevant parameters of VDF may also make a difference. Hopefully, large new samples of strong lenses will be expected to be obtained in future wide-field imaging surveys such as the Large Synoptic Survey Telescope (LSST; Ivezić et al. 2000) etc. Meanwhile, within a few decades, next generation observation tools such as the Square Kilometre Array (e.g., Blake et al. 2004) will also improve the precision of lensing statistics by several orders of magnitude. Therefore, the lens-redshift test can play an important role in uncovering the physical processes of galaxy formation and universe evolution with much larger and better lens-redshift data.

Summarizing, from the above discussion we may safely arrive at a conclusion that the results from the observational lens-redshift data agree relatively well, and furthermore, the lens-redshift test can be seen as a future supplement to other cosmological probes.

1

We discard lens systems that do not have measured lens or source redshifts, which may possibly cause biases. For many multiply-imaged sources without measured source redshifts, a possible strategy is to take zs = 2, which is the mean source redshift for the multiply-imaged sources with measured source redshifts. However, in order to ensure the accuracy of constraint, we choose to abandon such a choice in our paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under the Distinguished Young Scholar Grant 10825313 and Grant 11073005, the Ministry of Science and Technology national basic science Program (Project 973) under Grant No. 2012CB821804, the Fundamental Research Funds for the Central Universities and Scientific Research Foundation of Beijing Normal University.

References

  1. Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bernardi, M., Shankar, F., Hyde, J. B., et al. 2010, MNRAS, 404, 2087 [NASA ADS] [Google Scholar]
  3. Blake, C. A., Abdalla, F. B., Bridle, S. L., & Rawlings, S. 2004, NewAR, 48, 1063 [Google Scholar]
  4. Browne, I. W. A., Wilkinson, P. N., Jackson, N. J. F., et al. 2003, MNRAS, 341, 13 [NASA ADS] [CrossRef] [Google Scholar]
  5. Caldwell, R. R. 2002, PLB, 545, 23 [Google Scholar]
  6. Caldwell, R. R., Kamionkowski, M., & Weinberg, N. N. 2003, PRL, 91, 071301 [Google Scholar]
  7. Capelo, P. R., & Natarajan, P. 2007, NJPh, 9, 445 [NASA ADS] [Google Scholar]
  8. Chae, K.-H. 2003, MNRAS, 346, 746 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chae, K.-H. 2005, ApJ, 630, 764 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chae, K.-H. 2007, ApJ, 658, L71 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chae, K.-H. 2010, MNRAS, 402, 2031 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chae, K.-H., & Mao, S. D. 2003, ApJ, 599, L61 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chae, K.-H., Biggs, A. D., Blandford, R. D., et al. 2002, PRL, 89, 151301 [Google Scholar]
  14. Chae, K.-H., Chen, G., Ratra, B., & Lee, D.-W. 2004, ApJ, 607, L71 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chae, K.-H., Mao, S. D., & Kang, X. 2006, MNRAS, 373, 1369 [NASA ADS] [CrossRef] [Google Scholar]
  16. Choi, Y.-Y., Park, C., & Vogeley, M. S. 2007, ApJ, 884, 897 [Google Scholar]
  17. Davis, T. M., Mörtsell, E., Sollerman, J., et al. 2007, ApJ, 666, 716 [NASA ADS] [CrossRef] [Google Scholar]
  18. Eigenbrod, A., Courbin, F., Dye, S., et al. 2006a, A&A, 451, 74 [Google Scholar]
  19. Eigenbrod, A., Courbin, F., Meylan, G., Vuissoz, C., & Magain, P. 2006b, A&A, 451, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Eigenbrod, A., Courbin, F., & Meylan, G. 2007, A&A, 465, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
  22. Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fassnacht, C. D., & Cohen, J. G. 1998, AJ, 115, 377 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fukugita, M., Futamase, T., Kasai, M., & Turner, E. L. 1992, ApJ, 393, 3 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gao, H., Liang, N., & Zhu, Z.-H. 2012, Int. J. Mod. Phys. D, in press [arXiv:1003.5755] [Google Scholar]
  26. Huterer, D., Keeton, C. R., & Ma, C.-P. 2005, ApJ, 624, 34 [NASA ADS] [CrossRef] [Google Scholar]
  27. Im, M., Simard, L., Faber, S. M., et al. 2002, ApJ, 571, 136 [NASA ADS] [CrossRef] [Google Scholar]
  28. Inada, N., Becker, R. H., Burles, S., et al. 2003, AJ, 126, 666 [NASA ADS] [CrossRef] [Google Scholar]
  29. Inada, N., Burles, S., Gregg, M. D., et al. 2005, AJ, 130, 1967 [NASA ADS] [CrossRef] [Google Scholar]
  30. Inada, N., Oguri, M., Becker, R. H., et al. 2008, AJ, 135, 496 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Ivezić, Z., Tyson, J. A., Acosta, E., et al. 2008, for the LSST Collaboration [arXiv:0805.2366] [Google Scholar]
  32. Jin, K.-J., Zhang, Y.-Z., & Zhu, Z.-H. 2000, PLA, 264, 335 [CrossRef] [Google Scholar]
  33. Kang, X., Jing, Y. P., Mo, H. J., & Börner, G. 2005, ApJ, 631, 21 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kayo, I., Inada, N., Oguri, M., et al. 2010, AJ, 139, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Keeton, C. R. 2001, ApJ, 561, 46 [NASA ADS] [CrossRef] [Google Scholar]
  36. King, L. J., Browne, I. W. A., Muxlowm, T. W. B., et al. 1997, MNRAS, 289, 450 [NASA ADS] [Google Scholar]
  37. Kochanek, C. S. 1993, ApJ, 419, 12 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kochanek, C. S. 1996, ApJ, 466, 638 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kochanek, C. S., & White, M. 2001, ApJ, 559, 531 [NASA ADS] [CrossRef] [Google Scholar]
  40. Komatsu, E., Dunkley, J., Nolta, M. R., et al., WMAP Collaboration 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
  41. Koopmans, L. V. E., Treu, T., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 649, 599 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lewis, A., & Bridle, S. 2002, PRD, 66, 103, 511 [Google Scholar]
  43. Li, M., Li, X.-D., & Zhang, X. 2010, Sci. China Phys. Mech. Astron., 53, 1631 [NASA ADS] [CrossRef] [Google Scholar]
  44. Liang, N., Wu, P.-X., & Zhu, Z.-H. 2011, RAA, 11, 1019 [NASA ADS] [Google Scholar]
  45. Lubin, L. M., Fassnacht, C. D., Readhead, A. C. S., Blandford, R. D., & Kundic, T. 2000, AJ, 119, 451 [NASA ADS] [CrossRef] [Google Scholar]
  46. Mao, S. D., & Kochanek, C. S. 1994, MNRAS, 268, 569 [NASA ADS] [Google Scholar]
  47. Mao, S. D., & Schneider, P. 1998, MNRAS, 295, 587 [NASA ADS] [CrossRef] [Google Scholar]
  48. McKean, J. P., Koopmans, L. V. E., Flack, C. E., et al. 2007, MNRAS, 378, 109 [NASA ADS] [CrossRef] [Google Scholar]
  49. Mitchell, J. L., Keeton, C. R., Frieman, J. A., & Sheth, R. K. 2005, ApJ, 622, 81 [NASA ADS] [CrossRef] [Google Scholar]
  50. Morokuma, T., Inada, N., Oguri, M., et al. 2007, AJ, 133, 214 [NASA ADS] [CrossRef] [Google Scholar]
  51. Myers, S. T., Jackson, N. J., Browne, I. W. A., et al. 2003, MNRAS, 341, 1 [NASA ADS] [CrossRef] [Google Scholar]
  52. Ofek, E. O., Rix, H.-W., & Maoz, D. 2003, MNRAS, 343, 639 [NASA ADS] [CrossRef] [Google Scholar]
  53. Oguri, M., Inada, N., Castander, F. J., et al. 2004, PASJ, 56, 399 [NASA ADS] [Google Scholar]
  54. Oguri, M., Inada, N., Pindor, B., et al. 2006, AJ, 132, 999 [NASA ADS] [CrossRef] [Google Scholar]
  55. Oguri, M., Inada, N., Clocchiatti, A., et al. 2008, AJ, 135, 520 [NASA ADS] [CrossRef] [Google Scholar]
  56. Oscoz, A., Serra-Ricart, M., Mediavilla, E., Buitrago, J., & Goicoechea, L. J. 1997, ApJ, 491, L7 [NASA ADS] [CrossRef] [Google Scholar]
  57. Park, C., & Choi, Y.-Y. 2005, ApJ, 635, L29 [NASA ADS] [CrossRef] [Google Scholar]
  58. Peebles, P. J. E., & Ratra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  59. Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  60. Richards, G. T., Fan, X., Newberg, H., et al. 2002, AJ, 123, 2945 [NASA ADS] [CrossRef] [Google Scholar]
  61. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  62. Rix, H.-W., Mao, D., Turner, E. L., & Fukugita, M. 1994, ApJ, 435, 49 [NASA ADS] [CrossRef] [Google Scholar]
  63. Rusin, D., & Kochanek, C. S. 2005, ApJ, 623, 666 [NASA ADS] [CrossRef] [Google Scholar]
  64. Sheth, R. K., Bernardi, M., Schechter, P. L., et al. 2003, ApJ, 594, 225 [NASA ADS] [CrossRef] [Google Scholar]
  65. Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
  66. Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
  67. Surpi, G., & Blandford, R. D. 2003, ApJ, 584, 100 [NASA ADS] [CrossRef] [Google Scholar]
  68. Tegmark, M. E., Gaafar, M., Abdel Gawad, M. M. H., El-Muraikhi, M., & Ragab, I. M. 2004, PRD, 69, 103 [Google Scholar]
  69. Treu, T., Koopmans, L. V. E., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 640, 662 [NASA ADS] [CrossRef] [Google Scholar]
  70. Walsh, D., Carswell, R. F., & Weymann, R. J. 1979, Nature, 279, 381 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  71. Winn, J. N., Hewitt, J. N., & Schechter, P. L. 2001, in Gravitational Lensing: Recent Progress and Future Goals, ed. T. G. Brainerd, & C. S. Kochanek (San Francisco: ASP), ASP Conf. Proc., 237, 61 [Google Scholar]
  72. York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 157 [Google Scholar]
  73. York, T., Jackson, N., Browne, I. W. A., Wucknitz, O., & Skelton, J. E. 2005, MNRAS, 357, 124 [NASA ADS] [CrossRef] [Google Scholar]
  74. Young, P., Gunn, J. E., Oke, J. B., Westphal, J. A., & Kristian, J. 1981, ApJ, 244, 736 [NASA ADS] [CrossRef] [Google Scholar]
  75. Zhang, H.-B., & Zhu, Z.-H. 2009 [arXiv:0911.1859v1] [Google Scholar]
  76. Zhu, Z.-H. 1998, A&A, 338, 777 [NASA ADS] [Google Scholar]
  77. Zhu, Z.-H. 2000a, Mod. Phys. Lett. A, 15, 1023 [NASA ADS] [CrossRef] [Google Scholar]
  78. Zhu, Z.-H. 2000b, Int. J. Mod. Phys. D, 9, 591 [NASA ADS] [Google Scholar]
  79. Zhu, Z.-H., & Mauro Sereno 2008, A&A, 487, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Zhu, Z.-H., & Wu, X.-P. 1997, A&A, 324, 483 [NASA ADS] [Google Scholar]
  81. Zhu, Z.-H., Hu, M., Alcaniz, J. S., & Liu, Y.-X. 2008, A&A, 483, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Summary of strongly-lensed sources.

In the text

All Figures

thumbnail Fig. 1

Likelihood distribution function for the Λ CDM model constrained by the lens-redshift data.
In the text
thumbnail Fig. 2

Likelihood distribution function for the Λ CDM model constrained by the lens-redshift data combined with CMB.
In the text
thumbnail Fig. 3

Likelihood distribution function for the Λ CDM model constrained by the lens-redshift data combined with CMB and BAO.
In the text
thumbnail Fig. 4

w model constrained by the lens-redshift data: likelihood contours at 68.3% and 95.4% CL in the Ωx − w plane.
In the text
thumbnail Fig. 5

w model constrained by the lens-redshift data combined with CMB: likelihood contours at 68.3% and 95.4% CL in the Ωx − w plane.
In the text
thumbnail Fig. 6

w model constrained by the lens-redshift data combined with CMB and BAO: likelihood contours at 68.3% and 95.4% CL in the Ωx − w plane.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.