| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 6 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201118400 | |
| Published online | 23 December 2011 | |
Transmission spectrum of Venus as a transiting exoplanet⋆,⋆⋆
1 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, Grenoble, France
e-mail: david.ehrenreich@obs.ujf-grenoble.fr
2 Institut d’Astrophysique de Paris, Université Pierre & Marie Curie, CNRS UMR 7095, Paris, France
3 LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris-Diderot, Meudon, France
4 NASA Langley Research Center, Science Directorate, Chemistry and Dynamics Branch, Hampton, Virginia, USA
5 Laboratoire Cassiopée, UMR 6202, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, Nice, France
6 Observatoire de Haute-Provence, CNRS/OAMP, Saint-Michel l’ Observatoire, France
Received: 4 November 2011
Accepted: 1 December 2011
On 5–6 June 2012, Venus will be transiting the Sun for the last time before 2117. This event is an unique opportunity to assess the feasibility of the atmospheric characterisation of Earth-size exoplanets near the habitable zone with the transmission spectroscopy technique and provide an invaluable proxy for the atmosphere of such a planet. In this letter, we provide a theoretical transmission spectrum of the atmosphere of Venus that could be tested with spectroscopic observations during the 2012 transit. This is done using radiative transfer across Venus’ atmosphere, with inputs from in-situ missions such as Venus Express and theoretical models. The transmission spectrum covers a range of 0.1–5 μm and probes the limb between 70 and 150 km in altitude. It is dominated in UV by carbon dioxide absorption producing a broad transit signal of ~20 ppm as seen from Earth, and from 0.2 to 2.7 μm by Mie extinction (~5 ppm at 0.8 μm) caused by droplets of sulfuric acid composing an upper haze layer above the main deck of clouds. These features are not expected for a terrestrial exoplanet and could help discriminating an Earth-like habitable world from a cytherean planet.
Key words: radiative transfer / planets and satellites: atmospheres / astrobiology / planetary systems / scattering / planets and satellites: individual: Venus
Appendix A is available in electronic form at http://www.aanda.org
Full Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/537/L2
© ESO, 2012
1. Introduction
On 5–6 June 2012, Venus will be transiting the Sun as seen from the Earth, for the last time until 2117. This rare astronomical event was previously observed and reported in the literature six times only. The first detection of the atmosphere of Venus (the cytherean atmosphere) is traditionally attributed to Lomonosov, who observed the 26 May 1761 transit from the observatory of Saint-Petersburg (Marov 2005). Today, modern approaches are used to detect the atmospheres of transiting exoplanets. Several studies using the transmission spectroscopy technique have provided significant insights into the atmospheric composition, structure, and dynamics of hot giant exoplanets (e.g., Charbonneau et al. 2002; Vidal-Madjar et al. 2003, 2011; Snellen et al. 2010) This technique is now attempted on Neptune-mass exoplanets (Stevenson et al. 2010; Knutson et al. 2011) and on “super-earths” (1–10 M⊕; Bean et al. 2010, 2011; Désert et al. 2011). The next step, characterising the atmospheres of Earth-mass planets with transmission spectroscopy, is extremely challenging because of the small spatial extent of these gas envelopes: photometric precisions of the order of 0.1 ppm should be reached for that purpose (Ehrenreich et al. 2006; Kaltenegger & Traub 2009). The class of Earth-mass planets includes telluric – rocky – planets such as the Earth, Venus, or CoRoT-7b (Léger et al. 2011) and so-called “ocean-planets” (Léger et al. 2004), possibly such as GJ 1214b (Charbonneau et al. 2009). Among planets in this mass range, the atmospheres of telluric exoplanets are the most challenging to characterise because these dense planets have small atmospheric scale heights, and thus compact atmospheres (Ehrenreich et al. 2006).
In this context, Venus can provide an essential proxy for a telluric exoplanet. Obtaining its transmission spectrum during a transit across the Sun will serve both as a comparison basis for transiting Earth-mass exoplanets to be observed in the future, and a proof of feasibility that such observations can effectively probe the atmospheres of exoplanets in this mass range. In addition, transit observations of Venus can bring precious information about how the atmosphere of a non-habitable world – observed as an exoplanet – differ from that of a habitable planet, the Earth, also observed as an exoplanet in transit during Lunar eclipses (Vidal-Madjar et al. 2010). The previous transit of Venus in 2004 was the first to be scrutinised with modern instrumentation, from space (Schneider et al. 2006; Pasachoff et al. 2011) and from the ground (Hedelt et al. 2011; Tanga et al. 2011). This letter aims at providing a theoretical transmission spectrum of the atmosphere of Venus, from the ultraviolet to the infrared, as it could be observed during the transit of June 2012.
2. Model
2.1. Atmosphere
Transmission spectroscopy probes the atmospheric limb of the transiting planet. In the following, we consider an unidimensional atmospheric model, only varying with respect to the altitude and ignoring latitudinal and longitudinal variations in atmospheric structure and composition. Although latitudinal variation observations are well documented (e.g., in the atmospheric density and temperature, cloud top altitude, etc.), this simplification is correct considering the geometry of the experiment and the lack of spatial resolution: the latitudinal variations are averaged in the transmission spectrum of the whole limb.
 |
Fig. 1 Atmospheric profiles used in the model. Left: pressure-temperature. Right: gas mixing ratios (thin lines) and haze densities for mode-1 (thick violet line) and mode-2 (thick blue line) particles from Venus Express data (Wilquet et al. 2009). |
We consider an altitude range comprising the troposphere (0–60 km), the mesosphere (60–100 km), and the upper atmosphere (>100 km) of Venus, up to 400 km in altitude. Pätzold et al. (2007) measure the mesospheric temperature profile T(z) with radio sounding from the VeRa instrument on Venus Express. We use their profile assuming an upper boundary temperature of 200 K at 100 km. The tropospheric temperature profile is extrapolated from the tropopause (220 K at 61 km) down to the surface assuming a constant temperature lapse rate of +8.5 K km-1, yielding a surface temperature of 740 K. Above 100 km, the temperature profile corresponds to the neutral component of the ionosphere and follow those used by Gronoff et al. (2008), initially calculated by Hedin et al. (1983). The pressure profile p(z) is calculated across the whole altitude range (0–400 km) assuming the atmosphere behaves as a perfect gas at hydrostatic equilibrium, p(z) = p0exp[− dz/H(z)], where p0 = 93 bar is the surface pressure and H(z) = kBT(z)/ [μ(z)g(z)] is the atmospheric scale height, with g(z) the acceleration of gravity, kB the Boltzmann constant, and μ(z) the mean atmospheric molar mass.
Atoms and molecules – The mean molar mass variations with altitude are small from the ground up to ~120 km, where carbon dioxide dominates the atmospheric composition (volume mixing ratio XCO2 = 96.5%). Above this altitude, XCO2 follows the model of Gronoff et al. (2008). In addition to CO2, we are considering molecular nitrogen (XN2 = 3.5%), molecular and atomic oxygen (O2 and O i), carbon monoxide (CO), water (H2O), and sulfur dioxide (SO2). The mixing ratio profiles for CO, SO2, and H2O are extrapolated from the values from Cotton et al. (2011), de Bergh et al. (2006), and Titov et al. (2009), respectively. Mixing ratios of O2 and O i are considered to be non-zero only in the upper atmosphere, where these species are produced; there, their mixing ratio profiles follow those calculated by Gronoff et al. (2008). We finally include mesospheric ozone (O3) following its recent detection by Montmessin et al. (2011).
Clouds and haze – The thick deck of clouds extending across the troposphere and a part of the mesosphere (45–70 km) is treated as an achromatic optically thick layer. This assumption is justified by the effective Mie scattering from particles with a broad (multimodal) size distribution composing the main deck of clouds (Wilquet et al. 2009), over the considered wavelength range (0.1–5 μm). Practically, this means that no signatures can be detected below the top of the cloud deck, set at an altitude of 70 km (Ignatiev et al. 2009; Pasachoff et al. 2011). We distinguish, however, this main cloud deck from the upper haze (70–90 km). While both are mainly composed of sulfuric acid (H2SO4) aerosol particles, the particle size distribution is different in these layers, yielding different scattering properties. In the upper haze, particles are smaller than in the cloud deck, with typical radii from 0.1 to 0.3 μm, as expected from pure “mode-1” particles (Knollenberg & Hunten 1980; Esposito et al. 1997). Following Wilquet et al. (2009) and references therein, we consider an upper haze consisting of concentrated (75%) aqueous and spherical droplets of H2SO4. The size distribution of mode-1 droplets is described by a log-normal distribution with parameters rg = 0.2 μm and σg = 0.2. Wilquet et al. (2009) also present the first evidence for a bimodal distribution of aerosol particles in the upper haze of Venus, similar to the two modes in the upper clouds, at the latitudes probed by Venus Express: “mode-2” particles, with 0.4 ≲ rg ≲ 1.0 μm. In the following, we consider that mode-2 particle sizes follow a log-normal distribution with rg = 0.6 μm and σg = 1.5. The vertical density profiles of upper haze mode-1 and mode-2 particles are constrained from data from the UV channel of the SPICAV instrument and the SOIR instrument, respectively, on board Venus Express during orbit n. 485 (Wilquet et al. 2009,see their Fig. 9).
Radiative transfer – The radiative transfer model is based on Ehrenreich et al. (2006). It is an unidimensional, single-scattering code calculating the atmospheric opacities along line of sights crossing the limb of Venus. The opacities are then integrated over the whole limb to give a wavelength-dependent effective surface of absorption. The ratio of this surface to the surface of the Sun is the depth of the transit, as measured for exoplanets. In this frame, the transit depth can be converted into a radius ratio and, knowing both the radii of Venus and the Sun, to the effective height h of absorbing species in the cytherean atmosphere, as defined in Sect. 3. During the transit on 5–6 June 2012, Venus will be approximately three times closer to the Earth than the Sun. Consequently, the angular diameters of Venus and the Sun will be 57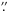 8 and 31
8 and 31 51, respectively, and the transit depth measured from Earth will be the ratio between these solid angles, δ♀ = 934 ppm. If Venus were a real exoplanet transiting a Sun-like star, the transit depth δ would be 75.7 ppm. We thus define a “geometric” factor γ = δ♀/δ = 12.3.
51, respectively, and the transit depth measured from Earth will be the ratio between these solid angles, δ♀ = 934 ppm. If Venus were a real exoplanet transiting a Sun-like star, the transit depth δ would be 75.7 ppm. We thus define a “geometric” factor γ = δ♀/δ = 12.3.
Photoabsorption – The model computes opacities from photoabsorption cross-sections of the atmospheric components. These cross-sections give rise to the spectroscopic signatures that will be sought for during the transit. Infrared molecular cross-sections are calculated from the HITRAN 2004 line list (Rothman et al. 2005) following Rothman et al. (1998,Sect. A.2.4) but using Voigt functions instead of Lorentzian line profiles. The UV cross-sections of CO2, O2, SO2, and O3 are taken from the AMOP2 and AMP3 data repositories. The photoabsorption cross sections are plotted in Fig. 2a.
Scattering – Important additional absorption is caused by diffusion processes: Rayleigh scattering from atmospheric CO2 and, to a lesser extent, N2, CO, and H2O, emerging above the main cloud deck at 70 km, and Mie scattering caused by H2SO4 droplets in the upper haze (70–90 km). Rayleigh diffusion, which efficiency increases toward the blue following λ-4, results from the scattering of light by particles with sizes r much smaller than the wavelength (x = 2πr/λ ≪ 1), typically, molecules composing the atmospheric gases. In the case of Venus, the diffusion is mainly caused by CO2: the scattering cross section is 8/3x4(n2 − 1)2/(n2 + 1)2 (see, e.g., Lecavelier des Etangs et al. 2008a), where n is the refractive index of the gas. For CO2, we use the formula of Sneep & Ubachs (2005) to calculate n as a function of wavelength. The upper haze is composed by particles with sizes larger than the wavelength (4 ≲ x ≲ 300). Consequently, the calculation of the extinction (scattering + absorption) cross section by the bimodal distribution of upper haze particles is based on Mie theory. The complex refractive index of H2SO4 droplets is taken from Hummel et al. (1988). Below 3 μm, the imaginary part of the refractive index is negligible and the scattering dominates the Mie extinction. The absorption cross section, linked to the imaginary part of the refractive index, becomes non-negligible above ~3 μm, whereas the scattering cross section drops. The extinction cross section is the sum of the scattering and absorption. It is calculated for log-normal particle size distributions with the set of light scattering routines available at the University of Oxford Physics Department4 and plotted as a function of wavelength for hazes with different particle size distributions in Fig. 2a.
3. Results and discussion
The transmission spectrum of Venus is shown with a resolution of 1 nm in Fig. 2b, as relative absorption Δδ♀(λ) = δ♀(λ) − δ♀(λmin), where δ♀(λ) = { [R♀ + h(λ)] /R⊙ } 2 and λmin is defined as the wavelength where the transit depth is minimal; it is 1.67, 2.50, and 2.65 μm for the haze-free, mode-1 haze, and modes-1+2 haze models, respectively. The effective height of absorption h(λ) has the same meaning as in Kaltenegger & Traub (2009) and is plotted in Fig. 2c. It can be retrieved on-line (Table A.1). The amplitude of the spectrum reaches ~25 ppm for the prominent CO2 UV bands below 0.2 μm. From 0.2 μm and above, the spectrum is dominated by Mie scattering (<2.7 μm) and absorption (>2.7 μm) by upper haze particles, which can significantly impact on the amplitude of the absorption from the other spectral features, such as the CO2 transitions around 2 μm or the Hartley UV band of O3, depending on the assumed particle size distribution. The maximum amplitude of this effect (between UV and IR) is ~6 to 8 ppm for mode-1 and modes-1+2 haze models, respectively. In the infrared, the most noticeable feature is the ν3 vibrational band of CO2 at ~ 4.3 μm (~15 ppm). For a real exoplanet transit, these absorption would be a factor 12.3 smaller because there is no parallax effect – the distance to the exoplanet equals the distance to the transited star.
 |
Fig. 2 a) Absorption cross sections of the considered atmospheric gases, Rayleigh scattering cross section of CO2 (dashed red line), and Mie extinction cross sections for mode-1 (thick blue line) and mode-2 (thick violet line) haze particles. b) Transit spectrum of Venus transiting in front of the Sun, as seen from Earth, in relative absorption and c) effective height of absorption. The different transit spectra shown are models with no upper haze (black), mode-1 upper haze (red), and modes-1+2 upper haze (green). The top of the main cloud deck is set at 70 km. The transit spectrum of the Earth calculated by Kaltenegger & Traub (2009) is overplotted (blue) and shifted by + 100 km for clarity. |
In terms of effective height of absorption h(λ) (Fig. 2c), the cytherean limb could be probed from 70 to 150 km, i.e., from the top of the cloud deck up to above the mesopause, in case the upper haze is only composed by mode-1 particles. If larger mode-2 particles are involved, it won’t be possible to probe the limb below ~80 km, reached at 2.65 μm.
In fact, the lowest altitude that it is possible to reach with transmission spectroscopy is set by the dominant diffusion regime, Rayleigh or Mie. In the case of Venus, the most remarkable and extended spectral signature is that of Mie scattering by the upper haze. This situation contrasts with the Earth, whose transmission spectrum is dominated at short wavelengths by Rayleigh scattering from N2 and the broad Chappuis band of O3, as modelled by Ehrenreich et al. (2006). This first basic modelling has been refined in the case of the Earth by Kaltenegger & Traub (2009), whose spectrum is reproduced in Fig. 2c.
In an atmosphere where Rayleigh scattering is the dominant diffusion process, it is fairly straightforward to assume that, eventhough there is no spectral identification from spectral lines, the main carrier of the Rayleigh scattering is the most abundant atmospheric gas. That would be H2 for a giant exoplanet (Lecavelier des Etangs et al. 2008b) or N2 and CO2, for the Earth (or Titan) and Venus, respectively. Because the atmospheric scale height can be calculated from the Rayleigh scattering signature, if the temperature is measured or modelled independently, this signature provides an estimation of the atmospheric mean molecular mass and thus some information on the atmospheric composition. The situation is, however, more complex when Mie scattering is involved because it cannot be simply attributed to the dominant atmospheric species, as illustrated in the case of the hot jupiter HD 189733b, which transmission spectrum appears dominated by diffusion from the visible to the near-infrared (Pont et al. 2008; Sing et al. 2011). Lecavelier des Etangs et al. (2008a) assess the possibility of Mie scattering by a haze layer and propose enstatite particles (MgSiO3) as scattering carriers, since their refractive index is compatible with the observed wavelength range of the Rayleigh signature. In this case, however, the identification is tentative mainly because we have no real proxies of such a planet in the Solar System.
There are a couple of other remarkable molecular signatures besides CO2 ones. In spite of a low mixing ratio (10-7 to 10-6) and a localised vertical distribution (~90–100 km; Montmessin et al. 2011), the Hartley band of O3 emerges from the Mie scattering. This somewhat surprising spectral feature is actually enhanced by the “ideal” location of the ozone layer, just above the upper haze. However, this relies on the assumption that the O3 distribution is constant with latitude all around Venus, which should be regarded with extreme caution. In the range 200–240 nm, the intense absorption system 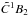 –
–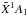 of SO2 (Freeman et al. 1984) dominates the spectrum.
of SO2 (Freeman et al. 1984) dominates the spectrum.
Although O i becomes the main component in the upper atmosphere above 150 km, the column density is too low at these altitudes and the 131-nm line too thin to produce significant absorption along the line of sight. The upper atmosphere of a planet similar to Venus, whose lower atmosphere is dominated by CO2, is too cold (~200 K), and the scale height too small, to give rise to detectable signatures from exospheric atoms. This contrasts with the warmer (~1000 K) upper atmosphere of the Earth, where high-altitude atomic species should be easier to detect than on Venus. In fact, on Venus infrared emissions from CO2 molecules (quenched at low altitudes) are the main source of atmospheric cooling above the mesosphere. It would be difficult to detect atmospheric signatures from an Earth-size exoplanet with a small thermospheric scale height. If the precision of the measurements is high enough, a lack of detection could then be attributed to the presence of an efficient upper atmosphere cooler (very likely CO2). In such a planet, the greenhouse effect would drastically change the surface temperature and the criteria used to decide if it lies in the habitable zone.
The only spectroscopic data against which we could validate the present model are the near-infrared observations of the 2004 Venus transit by Hedelt et al. (2011). These authors observed the transit with an instrument designed to measure the solar photosphere, the Vacuum Tower Telescope (VTT) in Tenerife. Out of spatially resolved, dispersed images, Hedelt et al. (2011) obtain high-resolution (R ~ 200 000) transmission spectra over narrow wavelength ranges. A direct comparison with our model is uneasy because the observations are spatially resolved over only a small fraction of the solar disc and of Venus’ limb. We use a correction factor equal to the ratio of the solar surface covered by the spectrograph slit to the surface of the whole Sun (~87 000), allowing us to roughly compare our model to Hedelt et al. (2011)’s observations in the spectral region 1597.5–1598.3 nm (see Fig. A.1). Given the uncertainties in the data and in the rescaling factor used, there is a fair agreement between our model and their data.
Transmission spectroscopy is a powerful tool to probe the atmospheres of transiting exoplanets. Current challenges involve identifying the scatterers responsible for hot jupiter spectra (Sing et al. 2011), understanding the “flat” spectra of super-earths (Bean et al. 2011), and determining the observational differences between habitable and hostile worlds. Mie scattering by clouds or hazes is likely to play a central role in these problems.
The June 2012 transit will be a unique occasion to collect non-spatially resolved transmission spectra of a planet that was long-believed to be the Earth’s twin sister. Enshrouded by clouds and hazes, Venus still hides numerous mysteries in spite of its proximity, such as the nature of “absorber X” detected by the Vega entry probes (Bertaux et al. 1996). A spatially unresolved and multi-wavelength coverage of the spectral region impacted by Mie scattering, sulfur dioxide, carbon dioxide, and absorber X could give access to these components, validating and bringing new constraints to the model presented here.
The TESS and Plato missions from NASA and ESA, respectively, are designed to detect “Earth’s twins” transiting bright stars before and beyond the end of the decade. Their transmission spectra could be obtained with the James Webb Space Telescope. The next transit of Venus will provide key diagnostic tools to discriminate between Earth-like and Venus-like atmospheres of exoplanets transiting their stars.
Online material
Appendix A
 |
Fig. A.1 Upper-haze free (black line), mode-1, and modes-1+2 upper-haze models (red and green lines, respectively) compared to the high-resolution limb transmission spectrum observed by Hedelt et al. (2011) (dark grey line). All spectral lines are CO2 transitions, including isotopes 12C16O2, 13C16O2, and 16O12C18O. |
Acknowledgments
We thank the referee W. Traub for a prompt and thoughtful report, J. Pasachoff for discussions around this work, and V. Wilquet for inputs on the particle size distribution of the upper haze.
References
- Bean, J. L., Kempton, E. M.-R., & Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bean, J. L., Désert, J.-M., Kabath, P., et al. 2011, ApJ, 743, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bertaux, J.-L., Widemann, T., Hauchecorne, A., Moroz, V. I., & Ekonomov, A. P. 1996, J. Geophys. Res., 101, 12709 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cotton, D. V., Bailey, J., Crisp, D., & Meadows, V. S. 2011, Icarus, accepted [arXiv:1105.4406] [Google Scholar]
- de Bergh, C., Moroz, V. I., Taylor, F. W., et al. 2006, Planet. Space Sci., 54, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Bean, J., Kempton, E. M.-R., et al. 2011, ApJ, 731, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., Tinetti, G., Lecavelier des Etangs, A., Vidal-Madjar, A., & Selsis, F. 2006, A&A, 448, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esposito, L. W., Bertaux, J.-L., Krasnopolsky, V., Moroz, V. I., & Zasova, L. V. 1997, in Venus II: Geology, Geophysics, Atmosphere, and Solar Wind Environment, ed. S. W. Bougher, D. M. Hunten, & R. J. Phillips, 415 [Google Scholar]
- Freeman, D. E., Yoshino, K., Esmond, J. R., & Parkinson, W. H. 1984, Planet. Space Sci., 32, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Gronoff, G., Lilensten, J., Simon, C., et al. 2008, A&A, 482, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hedelt, P., Alonso, R., Brown, T., et al. 2011, A&A, 533, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hedin, A. E., Niemann, H. B., Kasprzak, W. T., & Seiff, A. 1983, J. Geophys. Res., 88, 73 [Google Scholar]
- Hummel, J. R., Shettle, E. P., & Longtin, D. R. 1988, A new background stratospheric aerosol model for use in atmospheric radiation models, AFGL-TR-88-0166, Air Force Geophys. Lab., Hanscom Air Force Base, Mass. [Google Scholar]
- Ignatiev, N. I., Titov, D. V., Piccioni, G., et al. 2009, J. Geophys. Res., 114 [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Knollenberg, R. G., & Hunten, D. M. 1980, J. Geophys. Res., 85, 8039 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Madhusudhan, N., Cowan, N. B., et al. 2011, ApJ, 735, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008a, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Vidal-Madjar, A., Désert, J.-M., & Sing, D. 2008b, A&A, 485, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Léger, A., Selsis, F., Sotin, C., et al. 2004, Icarus, 169, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Grasset, O., Fegley, B., et al. 2011, Icarus, 213, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Marov, M. Y. 2005, Transits of Venus: New Views of the Solar System and Galaxy, 209 [Google Scholar]
- Montmessin, F., Bertaux, J.-L., Lefèvre, F., et al. 2011, Icarus, 216, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Pasachoff, J. M., Schneider, G., & Widemann, T. 2011, AJ, 141, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Pätzold, M., Häusler, B., Bird, M. K., et al. 2007, Nature, 450, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Knutson, H., Gilliland, R. L., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Rinsland, C. P., Goldman, A., et al. 1998, JQSRT, 60, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spect. Rad. Trans., 96, 139 [Google Scholar]
- Schneider, G., Pasachoff, J. M., & Willson, R. C. 2006, ApJ, 641, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Pont, F., Aigrain, S., et al. 2011, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Sneep, M., & Ubachs, W. 2005, J. Quant. Spect. Rad. Trans., 92, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stevenson, K. B., Harrington, J., Nymeyer, S., et al. 2010, Nature, 464, 1161 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tanga, P., Widemann, T., Sicardy, B., et al. 2011, Icarus, accepted [Google Scholar]
- Titov, D. V., Svedhem, H., Taylor, F. W., et al. 2009, Sol. Syst. Res., 43, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vidal-Madjar, A., Arnold, L., Ehrenreich, D., et al. 2010, A&A, 523, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Sing, D. K., Lecavelier des Etangs, A., et al. 2011, A&A, 527, A110 [Google Scholar]
- Wilquet, V., Fedorova, A., Montmessin, F., et al. 2009, J. Geophys. Res., 114 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Atmospheric profiles used in the model. Left: pressure-temperature. Right: gas mixing ratios (thin lines) and haze densities for mode-1 (thick violet line) and mode-2 (thick blue line) particles from Venus Express data (Wilquet et al. 2009). |
| In the text | |
 |
Fig. 2 a) Absorption cross sections of the considered atmospheric gases, Rayleigh scattering cross section of CO2 (dashed red line), and Mie extinction cross sections for mode-1 (thick blue line) and mode-2 (thick violet line) haze particles. b) Transit spectrum of Venus transiting in front of the Sun, as seen from Earth, in relative absorption and c) effective height of absorption. The different transit spectra shown are models with no upper haze (black), mode-1 upper haze (red), and modes-1+2 upper haze (green). The top of the main cloud deck is set at 70 km. The transit spectrum of the Earth calculated by Kaltenegger & Traub (2009) is overplotted (blue) and shifted by + 100 km for clarity. |
| In the text | |
 |
Fig. A.1 Upper-haze free (black line), mode-1, and modes-1+2 upper-haze models (red and green lines, respectively) compared to the high-resolution limb transmission spectrum observed by Hedelt et al. (2011) (dark grey line). All spectral lines are CO2 transitions, including isotopes 12C16O2, 13C16O2, and 16O12C18O. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


