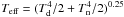| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117975 | |
| Published online | 17 January 2012 | |
Day and night side core cooling of a strongly irradiated giant planet
1
Astronomical Institute, Slovak Academy of Sciences,
05960
Tatranská Lomnica, Slovak
Republic
e-mail: budaj@ta3.sk
2
Steward Observatory and Dept. of Astronomy, University of
Arizona, 933 North Cherry
Avenues, Tucson
AZ
85721-0065,
USA
e-mail: hubeny@as.arizona.edu
3
Dept. of Astrophysical Sciences, Princeton, USA
e-mail: burrows@astro.princeton.edu
Received: 30 August 2011
Accepted: 9 November 2011
Context. The internal heat loss, or cooling, of a planet determines its structure and evolution.
Aims. We study the effects of irradiation, metallicity of the atmosphere, heat redistribution, stratospheres, and the depth where the heat redistribution takes place on the atmospheric structure, the core entropy, and subsequently on the cooling of the interior of the planet.
Methods. We address in a consistent fashion the coupling between the day and the night sides of a planet by means of model atmosphere calculations with heat redistribution. We assume that strong convection leads to the same entropy on the day and night sides and that gravity is the same on both hemispheres.
Results. We argue that the core cooling rates from the two hemispheres of a strongly irradiated planet may not be the same and that the difference depends on several important parameters. If the day-night heat redistribution is very efficient or if it takes place at the large optical depth, then the day-side and the night-side cooling may be comparable. However, if the day-night heat transport is not efficient or if it takes place at a shallow optical depth then there can be a large difference between the day- and the night-side cooling and the night side will cool more efficiently. If stellar irradiation becomes stronger, e.g. owing to stellar evolution or migration, cooling from both the day and the night sides is reduced. Enhanced metallicity of the atmosphere would act as an added “blanket" and reduces both the day- and the night-side cooling. However, a stratosphere on the planetary day side can enhance day-side cooling since its opacity acts as a “sunshade” that screens the stellar irradiation. These effects may also influence the well-known gravity darkening and bolometric albedo effects in interacting binaries, especially for strongly irradiated cold components.
Key words: convection / radiative transfer / planets and satellites: atmospheres / planets and satellites: interiors / planets and satellites: physical evolution / binaries: eclipsing
© ESO, 2012
1. Introduction
During its evolution, a planet derives heat from both its gravitational energy and other possible extra heat sources. In particular, tidal heating (Jackson et al. 2008; Liu et al. 2008) or ohmic heating (Batygin et al. 2011; Perna et al. 2010) may be quite important for some close-in extrasolar planets. Also, a small fraction of received stellar irradiation may be transported to deeper layers (Guillot & Showman 2002). This energy is radiated from the planet via its atmosphere, which acts as a valve that regulates cooling. A close-in planet is subject to strong stellar irradiation that is many orders of magnitude stronger than the internal heat loss of the planet. Subsequently, the structure of the atmosphere and the emergent spectrum are governed by the stellar irradiation.
Incoming stellar radiation does not penetrate very deeply into the interior of a planet and is effectively reradiated. Consequently, for any given assumed chemical composition, the structure of the planet itself is governed by its internal heat content, together with possible, additional energy sources. This has direct observational consequences. As a planet evolves, its interior cools and its radius shrinks, even if the planet is exposed to enhanced stellar irradiation due to stellar evolution or the planet’s migration. Planet cooling, however, can be significantly affected by stellar irradiation, which can keep the planet inflated for a longer period of time (Guillot et al. 1996).
Throughout this paper, we concentrate solely on close-in planets for which the spin and orbital periods are forced to be equal. Consequently, the planet surface is naturally divided between a day side that permanently faces the star and a night side that experiences no direct stellar irradiation. The irradiation energy is scattered, absorbed, and reradiated on the day side of the planet. Moreover, a fraction of the total incoming stellar energy is carried to the night side of the planet, where it can be reradiated. This complex radiative and hydrodynamical mechanism determines the properties of the atmosphere, and, thus, also planet cooling. Generally, the planet core may cool at a very different rate on the day and on the night sides. The magnitude of cooling depends mainly on the magnitude of the stellar irradiation, the amount of the day-night heat redistribution, the depth where this day-night heat redistribution takes place, and the atmospheric structure and opacities. Previous evolutionary studies (Laughlin et al. 2005; Burrows et al. 2007a; Fortney et al. 2007; Liu et al. 2008) have implicitly assumed full heat redistribution, i.e. that the night-side atmosphere is identical with the one on the day side and that the core heat loss from the night side is equal to that from the day side. The effect of the irradiation and the day-night heat redistribution was achieved by simply reducing the irradiating stellar flux by a factor of two prior to its encounter with the atmosphere of the planet (e.g., Sudarsky et al. 2003). Recently, Guillot (2010) and Heng et al. (2012) have constructed analytical gray irradiated atmosphere models to study planet cooling.
Irradiation effects have also been studied in the field of interacting binaries. Irradiated models of the atmosphere have been constructed by Rucinski (1970, 1973). Rucinski (1969) and Vaz & Norlund (1985) estimated the bolometric albedo for irradiated stars having deep adiabatic convective envelopes, assuming constant entropy.
The aim of this paper is to assess, in a systematic way, differences between the day and the night side core cooling rates, and to study the effects of the strength of stellar irradiation, atmospheric metallicity, the efficiency of day-night heat redistribution, and the depth where this redistribution takes place. We use a state-of-the-art model atmosphere code, where the day-night heat redistribution is treated in a parametric way. We illustrate the effects on the prototype of a close-in extrasolar planet: HD 209458b. In Sect. 2, we describe the calculations and in Sects. 3–7 we study the effects of the various parameters that are important for the day- and night-side core cooling rates.
2. Modeling procedure
As is well known from planetary evolution models, the interior of the planet is fully convective (e.g., Hubbard et al. 2002), and that the convection is very nearly adiabatic. We make the realistic assumption that the entropy in the convection zone is constant everywhere in the planet. Specifically, the entropies at the base of the convection zone at the day and night sides are equal. Moreover, we assume that the planet is spherical, so that the gravitational accelerations on the day and the night sides are equal. This is also a reasonable assumption for our purpose. Budaj (2011) calculated shapes and variations in the effective gravity over the surface of all currently known transiting exoplanets. He found that largest departures from the spherical symmetry are expected for WASP-12b and WASP-19b, of about 12–15%, respectively which translates into the variations of the gravity over the surface of about 25–32%. The gravity difference between the substellar and antistellar points were less than 2%. For convenience, we assume that the thickness of the atmosphere is small compared to the planetary radius, so that the gravity is a constant.
The entropy of the planetary core is thus determined by the entropy at the base of the convection zone, which in turn is determined by the magnitude of stellar irradiation, radiation transport in the atmosphere, and other details of the atmospheric physics. Therefore, sophisticated evolutionary models have to take into account proper boundary conditions, in particular the values of the entropy and the radiation cooling, using detailed atmospheric models, as was done e.g. in Burrows et al. (2003), Burrows et al. (2007a), Fortney et al. (2007), and Liu et al. (2008).
The amount of radiation cooling from the day and the night sides is calculated in the following way: From the definition of the effective temperature, the total energy flux incoming at a unit surface area at the lower base of an atmosphere is given by 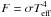 . Since no energy is being lost in the atmosphere, this quantity also represents the total radiation flux escaping from the unit surface at the upper boundary of the atmosphere. Therefore, it provides a quantitative measure of the radiation heat loss through the planet’s atmosphere, and, thus, from the whole planet. For usual atmospheric models, the effective temperature, together with surface gravity (and overall chemical composition) are taken as fundamental parameters, while from the point of view of interior and evolutionary models, the primary parameter is the core entropy.
. Since no energy is being lost in the atmosphere, this quantity also represents the total radiation flux escaping from the unit surface at the upper boundary of the atmosphere. Therefore, it provides a quantitative measure of the radiation heat loss through the planet’s atmosphere, and, thus, from the whole planet. For usual atmospheric models, the effective temperature, together with surface gravity (and overall chemical composition) are taken as fundamental parameters, while from the point of view of interior and evolutionary models, the primary parameter is the core entropy.
We divide the whole planetary surface into two parts, and treat the overall planetary atmosphere as composed of two distinct atmospheres – an averaged day-side atmosphere and an averaged night-side atmosphere. The effective temperature on the day side is called Td, and on the night side Tn. To avoid confusion with other possible meanings of the term “effective temperature” used for instance in planetary science, we will call Td and Tn “intrinsic effective temperatures”. Obviously, these effective temperatures should not be confused with brightness temperatures or an actual atmospheric temperature, which is a function of depth in the atmosphere and strongly depends on the irradiation.
As mentioned above, to compute the total heat loss consistently, the model atmospheres for the day and the night side must have the same entropy at the convective base. To this end, we calculate a grid of models with/without the irradiation corresponding to the day/night side of the planet for a range of day- and night-side intrinsic effective temperatures and surface gravities (log g). Each model has a certain entropy in the convection zone. In the next step we match the entropy and gravity of the day and night sides, which results in different effective temperatures (Td ≠ Tn) for the day and night sides. Notice that we can obtain a unique match because entropy is a monotonic function of the intrinsic effective temperature. Since Td and Tn represent the total radiation flux on the day and night sides, they represent the day and the night side internal heat loss, or, equivalently, the cooling of the interior. The total internal heat loss (cooling), Lcool, from the planet is then given by 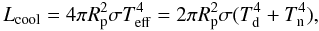 (1)where Rp is the radius of the planet, σ is the Stefan-Boltzmann constant, and Teff is the composite intrinsic effective temperature.
(1)where Rp is the radius of the planet, σ is the Stefan-Boltzmann constant, and Teff is the composite intrinsic effective temperature.
The individual model atmospheres are computed using the code CoolTlusty designed to model atmospheres of irradiated giant planets and brown dwarfs. This code is a version of the stellar atmosphere code Tlusty (Hubeny 1988; Hubeny & Lanz 1995); modifications for CoolTlusty are described in Hubeny et al. (2003) and Sudarsky et al. (2003). The code solves the hydrostatic and the radiative+convective equilibrium equations, assumes LTE, and can take into account clouds and departures from local chemical equilibrium (Hubeny & Burrows 2007). The computed models represent separately averaged-day and averaged-night side atmospheres. The upper boundary is set to the pressure 10-5 bars and extends deeply into the convection zone. At a specified depth range, we allow for an energy removal on the day side, and an energy deposition on the night side of the planet, using the procedure described in Burrows et al. (2008). The amount of the heat redistribution between the day and night sides is parametrized by the Pn parameter, which is defined as the fraction of the incoming stellar irradiation that is transferred from the day side to the night side and radiated from there (Burrows et al. 2006).
We consider here the well-known planet HD 209458b. If not stated otherwise, we assume solar chemical composition of the planetary atmosphere, energy removal/deposition at 0.03–0.3 bar, and Pn = 0.3. TiO and VO opacity is not considered. Opacities are taken from Sharp & Burrows (2007), assuming chemical-equilibrium compositions with rainout but no cloud opacity. Kurucz (1993) spectrum of the parent star HD 209458 is used as the source of irradiation. Parameters of the star and planet are taken from Henry et al. (2000), Charbonneau et al. (2000), and Knutson et al. (2007). We assume Teff = 6000 K, R = 1.13 R⊙ for the star, and a semi-major axis of the planet’s orbit a = 0.045 AU. The models were calculated for a grid of effective temperatures ranging from 50 K up to 300 K and gravities from 2.4 up to 3.6 (cgs).
We plot in Fig. 1 the entropy (per baryon, divided by the Boltzmann constant k) as a function of temperature and pressure (Saumon et al. 1995). The crucial point is that the entropy increases with temperature and decreases with pressure. In Fig. 2 we plot the temperature - pressure (T − P) profiles as a function of the intrinsic effective temperature all else being equal. We assumed Pn = 0.5 and irradiated day side of the planet. This temperature affects mainly the deeper layers and shifts the location of the top of the convection zone. The higher the intrinsic effective temperature the lower the pressure at the convection boundary and, given the relation from Fig. 1, the higher the core entropy. This monotonically changes the entropy in the convection zone. It means that we can use this intrinsic effective temperature to adjust the entropy in the convection zone on the day and night sides.
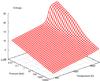 |
Fig. 1 Entropy (per baryon and divided by k) as a function of pressure and temperature. Entropy decreases with pressure and increases with temperature. |
 |
Fig. 2 The effect of the intrinsic effective temperature on the T − P profile of the atmosphere on the day side. D-stands for day, numbers give the effective temperature in K and the core entropy, respectively. Circles mark the top of the convection zone. Notice that for higher effective temperatures the convection zone starts at lower pressures (densities) but at about the same temperatures. Consequently, given the relation from Fig. 1, models with higher intrinsic effective temperature have higher core entropy. |
 |
Fig. 3 Left: the effect of the planet-star distance (a magnitude of irradiation) on the T − P profile of the atmosphere. Red lines represent the day side, blue lines represent the night side. Circles mark the top of the convection zone. D-stands for day, N-stands for night, numbers give the planet-star distance in AU and the core entropy, respectively. Notice that entropy on both day and night sides increases with increasing irradiation (shorter distance). Right: the effect of the planet-star distance or irradiation on the day-night side cooling of the planet. The cooling is expressed as the intrinsic effective temperature in K as a function of the core entropy for several surface gravities. The day-side is solid, and night-side is dashed. The models are calculated for two planet-star distances 0.045 (green) and 0.0225 AU (red). The cooling from the day side decreases with the stellar irradiation (shorter distance). The cooling from the night side behaves in a similar way. Consequently, the total heat loss is lower at a higher irradiation. |
3. The effect of the stellar irradiation on day-night side cooling
Planets are generally exposed to very different intensities of stellar irradiation. Solar-type stars on the main sequence increase in luminosity in the course of their evolution. Planets migrate as a result of their interaction with the protoplanetary disk or with their host stars. Therefore, we first explore the effects of irradiation on the day- and night-side cooling.
Stellar irradiation considerably modifies the day side T − P profile of the atmosphere. It flattens the temperature gradient and creates a noticeable plateau (Sudarsky et al. 2003; Hubeny et al. 2003). Because of day to night side heat transport, this plateau has a signature on the night side T − P profile as well (Burrows et al. 2008). To study the effect of irradiation on the core heat loss we calculate a set of day- and night-side atmosphere models at two different planet-star distances, one corresponding to the nominal distance a = 0.045 AU, and the other two times closer: a = 0.0225 AU, which approximately corresponds to a 4 fold increase in stellar irradiation. We set Pn = 0.3; and assume that the incoming irradiation energy is removed at the depth region between 0.03 and 0.3 bar on the day side, and is deposited on the night side at the same range of pressures.
T − P profiles for a model with Teff = 100 K and log 10g = 3 are shown in Fig. 3 (left). Notice that the position of the top of the convection zone varies; this is exactly the location of the point that determines the entropy in the convection zone. The location of this point closely correlates with the temperature of the plateau. On the day side, the temperature plateau and the top of the convection zone are hotter for higher irradiation. Given the dependence from Fig. 1 the core entropy is also higher for higher irradiation (closer distance). This means that one has to lower the day side internal effective temperature (keeping g constant) to obtain the same entropy as on the night side. Consequently, this means that we obtain less cooling from the day side. The night side behaves similarly, since its T − P profiles reflect that of the day side.
Figure 3 (right) illustrates the intrinsic effective temperature, and thus core cooling, as a function of entropy for several gravities. Notice that both the day- and the night-side core cooling rates decrease with increasing irradiation. Night side cooling is more efficient. This means that for a higher irradiation flux the total heat loss from both the day and the night side is lower (Fig. 4 left). This somewhat counterintuitive behavior is understood by noticing that the irradiation heats the atmosphere, flattens the temperature gradient, and thus creates a “barrier” that inhibits the heat loss from the interior (Burrows et al. 2000).
In conclusion, if the star is brighter or the planet-star separation is lower, the total heat loss from a planet is reduced.
 |
Fig. 4 The combined night and day side cooling as a function of the surface gravity and core entropy. It is expressed as the intrinsic effective temperature |
 |
Fig. 5 Left: the effect of varying the metallicity on the T − P profile of the atmosphere. The curves are labeled by the value of the metallicity in the atmosphere (1 or 3 × solar) and the core entropy, respectively. Notice that entropy on both day and night sides increases with increasing metallicity. Right: the effect of varying the metallicity of the planetary atmosphere on the day-night side cooling. Models are calculated for two metallicities: solar and 3 × solar metallicity. The cooling from both the day and the night side decreases with the metallicity. Consequently, the total heat loss decreases with increasing metallicity. |
 |
Fig. 6 Left: the effect of the Pn parameter (day-night heat transfer efficiency) on the T − P profile of the atmosphere. The curves are labeled with the values of the Pn parameter and the core entropy, respectively. Notice that the entropy on the day side decreases with increased efficiency of heat redistribution. Entropy on the night side behaves in the opposite way and increases with increasing heat redistribution, or Pn value. Right: the effect of the Pn parameter on the day-night side cooling. The models are calculated for three different values of Pn = 0.1,0.3,0.5. Cooling from the night side decreases with the efficiency of heat redistribution (Pn). Cooling from the day side behaves in the opposite way and increases with increasing Pn. However, the night side is more sensitive to the Pn parameter, so it governs total core heat loss, which decreases with increasing Pn. The difference between night and the day side cooling is largest for the smallest values of Pn. |
4. The effect of atmospheric metallicity
In this section we investigate the effect of enhanced metallicity (and, therefore, opacity) on the cooling of the planetary interior. Burrows et al. (2007a) have already demonstrated that an enhanced opacity in the planetary atmosphere due to higher metallicity reduces the escape of internal heat. They considered Pn = 0.5, and assumed that the night side cools at the same rate as the day side.
To study the effects of metallicity on the day- and night-side cooling rates we calculate a set of day and night atmosphere models for two different metallicities. One corresponds to solar metallicity, and the other is enhanced by 0.5 dex, i.e. a factor of about 3. We assume Pn = 0.3; the incoming irradiation energy is removed at depths between 0.03 and 0.3 bar on the day side, and is deposited on the night side in the same pressure region.
Figure 5 (left) illustrates the effect of metallicity on the T − P profiles, for a model with Teff = 100 K and log 10g = 3. The day-side temperature plateau level is not very sensitive to metallicity. However, for the lower metallicity the plateau extends much deeper into the interior, where pressure and density are higher. This is easily understood by noticing that lower metallicity results in a lower opacity; consequently the atmosphere is more transparent and the effect of irradiation is felt at deeper layers. Pressure at the top of the convection zone is lower for higher metallicity. Consequently, given the relation from Fig. 1, entropy is higher (at a particular gravity and intrinsic effective temperature) for models with higher metallicity. This means that one has to lower the intrinsic effective temperature (i.e., lower the cooling) to fit the same entropy. The night side behaves analogously. Consequently, the total core cooling rate is also reduced for higher metallicity models, as expected. Figure 5 (right) depicts this cooling as a function of entropy for several gravities. This demonstrates that the above mentioned behavior holds for the whole grid of models with a range of entropies and gravities. Figure 4 (right) depicts the total combined day+night cooling for the whole grid of models.
In conclusion, increased metallicity (opacity) acts as a blanket that inhibits heat loss, and, thus, keeps the planet warm for a longer period of time.
5. The effect of the Pn parameter
The Pn parameter is an empirical parameter that specifies the portion of irradiated energy received by the day side that is transported to the night side (Burrows et al. 2006), and thus measures the efficiency of day-night heat transfer. Pn = 0 means that there is no heat flow from the day to the night side, while Pn = 0.5 means that half of the energy received by the day side is carried to the night side and re-radiated from there.
The value of Pn can be constrained by secondary eclipse observations. It turned out that its value may differ from planet to planet. Harrington et al. (2006) favor a small amount of the heat redistribution for υ And. Cowan et al. (2007) estimated that Pn ≤ 0.30 (1σ) for HD 179949b, while Pn ≥ 0.32 (1σ) for HD 209458b. Burrows et al. (2008) estimated heat redistribution efficiencies for six transiting hot Jupiters. Cowan & Agol (2011) studied Bond albedos and heat redistribution of a sample of 24 exoplanets. Smith et al. (2011) found low heat redistribution for WASP-33b. Anderson et al. (2010), Gibson et al. (2010) and Budaj (2011) found low heat redistribution for WASP-19b.
To investigate the effect of day-night heat transfer on day and night side core cooling we calculate a set of day and night side atmosphere models for different values (0.1, 0.2, 0.3, 0.4, 0.5) of the Pn parameter. We assume that the incoming irradiation energy is removed between 0.03 and 0.3 bar on the day side, and is deposited on the night side in the same pressure region.
Figure 6 (left) illustrates the T − P profiles for a model with Teff = 100 K and log 10g = 3. On the day side the temperatures on the plateau and at the top of the convection zone decrease with increasing Pn. Subsequently (see Fig. 1), the entropy in the convection zone on the day side decreases with increasing Pn, all else being equal. This means that cooling (that is, Td) must increase for higher Pn values (at the same entropy and gravity), thus, day side heat loss is higher. On the other hand, the plateau temperature and the entropy on the night side increase with increasing Pn. This means that for higher Pn (at the same entropy and gravity) Tn must be lower, and, thus, the losses from the night side are lower. Figure 6 (right) depicts cooling as a function of entropy for several gravities, and shows that the same trend is valid for the whole grid of models. Notice that the difference between night and day cooling Tn − Td is higher for low heat redistribution, and decreases with more efficient day-night heat transport.
In this case, the day and the night sides behave in opposite ways. However, the night side is more sensitive to heat transfer and the total (day plus night side) heat loss decreases with increasing heat transfer. This is shown in the Fig. 7 (left). This behavior can be understood in the following way. On the night side, a higher Pn value means more energy deposited at a certain depth. This has a similar effect on the T − P profiles as stronger irradiation and the outcome is the same – a reduced heat loss. The day side with an energy removal behaves in the opposite way.
 |
Fig. 7 The combined night and day side cooling as a function of the surface gravity and core entropy. It is expressed as the intrinsic effective temperature |
 |
Fig. 8 Left: the effect of a stratospheric absorber on the T − P profile of the day-side atmosphere. The curves are labeled with the values of the extra opacity, κ = 0.,0.02,0.05 cm2g-1, and the core entropy, respectively. Notice that the entropy on the day side decreases with increasing the extra opacity. There is no stratosphere on the night side, so only one model is plotted. Right: the effect of the extra opacity in the upper atmosphere of the day side on the day-night side cooling. The models are calculated for three different values of the extra opacity, κ = 0.,0.02,0.05 cm2 g-1. Cooling from the day side increases with the value of the extra opacity. Cooling from the night side core is the same since only the day side exhibits a stratosphere. The difference between the night and the day side cooling is largest for lower values of the extra opacity, and the total core heat loss increases with increasing extra opacity. |
6. The effect of extra opacity in the upper atmosphere of the day side of the planet
Hubeny et al. (2003) first pointed out that highly irradiated cold atmospheres with an efficient opacity source in the optical could exist in two distinct configurations; one with a temperature monotonically decreasing outward, and one exhibiting a temperature increase toward a surface. They also showed that a strong temperature inversion at the top of the atmosphere would have a significant effect on the emergent spectrum. Early spectrophotometric observations of the secondary eclipses indeed gave a strong indication of a temperature inversion on the day side of some close-in planets (Burrows et al. 2007b; Fortney et al. 2008). Some attributed the opacity that leads to such a temperature inversion to TiO and VO. However, there is uncertainty as to whether TiO and VO can indeed be supported in the upper atmosphere, that is whether one can find an efficient mechanism that would prevent TiO and VO from settling downward in the atmosphere to colder regions where they would be rained out (the so-called cold trap effect – Spiegel et al. 2009). Therefore, given the uncertainty about the actual opacity source that is responsible for the creation of the “stratosphere”, we use the term “extra” opacity and parametrized its value and the wavelength range in which it operates (Burrows et al. 2008).
Here, we investigate how such an extra opacity on the day side can affect the day-night side core cooling of the planet. We calculate a grid of day- and night-side atmosphere models with an extra absorber with various opacities, κ = 0.,0.02,0.05 g cm -2 corresponding to optical depths of 0, 0.5, 1.4. The extra absorption is gray, operating only in the optical region for wavelengths between 0.3 and 1 micron, and placed only in the upper atmosphere of the day side. The efficiency of heat redistribution is set to Pn = 0.3, and we assume that the incoming stellar energy is removed at the depth region between 0.03 and 0.3 bar at the day side, and is deposited on the night side over the same pressure region.
Figure 8 (left) shows the effect of the absorber on the T − P profile for a model with Teff = 100 K and log 10g = 3. The day-side plateau and temperature at the top of the convection zone decrease with increasing extra opacity. Consequently (see Fig. 1), the core entropy decreases with increasing extra opacity, and, thus, the heat loss from the day side must be higher if the entropy is to be constant. At first glance this might seem strange because it is just the opposite of the effect of increasing the metallicity (see Sect. 4). The explanation is that a higher metallicity leads to a higher opacity throughout the whole atmosphere, and, thus, it acts as a blanket that reduces the heat loss from the day side. In contrast, a higher extra stratospheric opacity works differently. It acts more like a “shield” that prevents the energy flux from the star from penetrating deeper into the planet atmosphere because part of the irradiation energy is now deposited high in the atmosphere.
This “shield” becomes hotter with increasing extra opacity, but the layers below become cooler since they are optically thin at other wavelengths. Speaking figuratively, the overall effect resembles a breeze that carries heat out and creates a cool and comfortable area under a hot sunshade on a sunny beach. Thus, the behaviour of the temperature plateau is analogous to the situation studied in Sect. 3 when the planet was farther away from the star, which results in higher day side cooling for higher extra opacity. Figure 8 (right) illustrates the cooling effect as a function of the entropy for several gravities and shows that this result holds for the whole grid of models. Figure 9 shows the total combined day+night cooling which increases with increasing extra opacity.
 |
Fig. 9 The combined night and day side cooling as a function of the surface gravity and core entropy. It is expressed as the intrinsic effective temperature |
7. The effect of the depth of day-night heat transport region
In the above mentioned calculations, we kept the region of day-night heat redistribution constant in pressure and equal for both the day and night sides for the whole grid of models, while either the planet-star separation, metallicity, Pn, or extra opacity were varied. However, the optical depth at a certain pressure level is a strong function of gravity. The actual day-night heat redistribution may take place within a certain range of optical depths, rather than in a constant pressure range. This is why we calculate a set of models where, on the day side, we adjust the region of the day-night heat redistribution so that the Rosseland optical depth of the region is constant. We study three cases, and place the energy sink on the day side at τRoss = 0.06 − 1, 0.2 − 3, and 0.6–9. On the night side, the energy is deposited at the same pressures (corresponding to the above mentioned optical depths) as the energy is being removed on the day side. In all models, we assume Pn = 0.3.
Figure 10 (left) illustrates the effect of varying the depth of the heat redistribution region on the T − P profiles. On the day side, the plateau and temperature at the top of the convection zone decrease with increasing optical depth. Consequently, (see Fig. 1) the core entropy decreases with increasing optical depth. This means that heat loss is higher at the same entropy and gravity. On the night side the plateau temperature and entropy increase with increasing optical depth, which means that the heat loss is lower (at the same entropy and gravity) for higher optical depth. This is shown in Fig. 10 (right), where we plot the cooling rate as a function of entropy for several gravities. The night side is more sensitive to the optical depth, and the total heat loss decreases with increasing depth of the day-night heat redistribution region (see Fig. 7 right). This behavior is very similar to the dependence of the heat loss on the Pn parameter. This is not surprising, since the effect of increasing the depth of heat redistribution on the model atmosphere is analogous to the effect of an increase of the heat redistribution efficiency. Moreover, in reality these two effects are probably correlated, in the sense that if heat redistribution takes place at deeper layers it is likely to be more efficient, and, thus, to be described by a higher Pn value, which has the same effect on day-night side cooling. Consequently, their mutual correlation could make the effect stronger.
In all the above calculations we assumed that the heat redistribution region on the night side corresponds to the same pressure range as on the day side. Based on these calculations one can speculate what will happen if this is not the case. The 3D models of Dobbs-Dixon & Lin (2008) and Showman et al. (2008) indicate that this problem is very complex. The eastward and westward flows can circumnavigate the planet at different latitudes, and one can sink below the other depending on the cooling they experience. If energy is deposited on the night side at lower pressures than those at which energy is being removed on the day side then we would observe an enhanced amount of core cooling from the night side. On the other hand, if energy is deposited at higher pressures on the night side than energy is removed from on the day side, night-side cooling could be significantly reduced.
 |
Fig. 10 Left: the effect of the depth of the day-night heat transport region on the T − P profile of the atmosphere. The curves are labeled with the values of the Rosseland optical depth of the bottom of the day-night heat transfer region, and the core entropy, respectively. Notice that the entropy on the day side decreases with increasing optical depth. The entropy on the night side behaves in the opposite way, and increases with the optical depth of the heat redistribution region. Right: the effect of the depth of the day-night heat transport on the day-night side cooling. The day-side (solid) and the night-side (dashed) cooling of the planet for three different values of the day-side Rosseland optical depth at the bottom of the heat redistribution region τross = 1,3,9. On the day side, the heat loss increases with increasing optical depth. On the night side, the heat loss decreases with increasing optical depth and this trend tends to dominate the opposite trend on the day side. As a result the night-to-day difference in heat loss is lower for larger optical depth and the total heat loss decreases with increasing the optical depth. |
8. Conclusions
We have studied the effects of several mechanisms on day- and night-side core cooling of strongly irradiated planets. The main conclusions are:
-
We have demonstrated that the cooling of a strongly irradiated giant planet is different on the day and the night sides.
-
An increased amount of planet irradiation leads to reduced day and night side cooling, and thus to reduced total core heat loss.
-
An increased metallicity throughout the atmosphere leads to reduced day and night side cooling, and thus to reduced total core heat loss.
-
An increased efficiency of the day-night heat redistribution reduces heat loss from the night side, while increasing heat loss from the day side. The night side is more sensitive to this effect, and as a result the total heat loss is reduced.
-
A possible extra opacity in the stratosphere on the day side of the planet acts as a sunshade that partly blocks the irradiation from the star. Consequently, it increases the day side cooling as well as the total heat loss.
-
If day-night heat redistribution takes place at larger optical depths it increases day side core cooling, while night side core cooling is suppressed. The total heat loss is also reduced.
-
Night side cooling is generally more efficient than the day side cooling. However, this does not rule out the possibility that there is a combination of parameters where the opposite conclusion applies.
These effects may influence the evolution of strongly irradiated substellar-mass objects. If a particular effect results in enhanced core cooling this leads to faster shrinking and lower radii and vice versa. These effects will also compete with gravity darkening and bolometric albedos in interacting binaries (von Zeipel 1924; Lucy 1967; Rucinski 1969; Vaz & Norlund 1985; Claret 1998), especially for strongly irradiated cold components. As a result one might observe a sort of “day side darkening” or “night side brightening” in the intrinsic flux coming from the interior of an irradiated object.
Acknowledgments
The work of J.B. has been supported by the VEGA grants of the Slovak Academy of Sciences Nos. 2/0074/09, 2/0078/10, 2/0094/11. I.H. wishes to thank the Slovak Academic Information Agency SAIA for a support during his stay at the Astronomical Institute of SAV where the work was completed. We also thank an anonymous referee for his/her comments and suggestions on the manuscript. We also thank Prof. Saumon and an anonymous referee for their comments and suggestions on the manuscript.
References
- Anderson, D. R., Gillon, M., Maxted, P. F. L., et al. 2010, A&A, 513, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batygin, K., Stevenson, D. J., & Bodenheimer, P. H. 2011, ApJ, 738, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Charbonneau, D., Gilliland, R. L., Noyes, R. W., & Burrows, A. 2001, ApJ, 552, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Budaj, J. 2011, AJ, 141, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Guillot, T., Hubbard, W. B., et al. 2000, ApJ, 534, L97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burrows, A., Sudarsky, D., & Hubbard, W. B. 2003, ApJ, 594, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Sudarsky, D., & Hubeny, I. 2006, ApJ, 650, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., & Hubbard, W. B. 2007a, ApJ, 661, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., Knutson, H. A., & Charbonneau, D. 2007b, ApJ, 668, L171 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Burrows, A., Budaj, J., & Hubeny, I. 2008, ApJ, 678, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Claret, A. 1998, A&AS, 131, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., Agol, E., & Charbonneau, D. 2007, MNRAS, 379, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs-Dixon, I., & Lin, D. N. C. 2008, ApJ, 673, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aiprain, S,Pollacco, D. L., et al. 2010, MNRAS, 404, L114 [NASA ADS] [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Burrows, A., Hubbard, W. B., Lunine, J. I., & Saumon, D. I. 1996, ApJ, 459, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, J., Hansen, B. M., Luszcz, S. H., et al. 2006, Science, 314, 623 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Heng, K., Hayek, W., Pont, F., & Sing, D. K. 2012, MNRAS, 420, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, G. W., Marcy, G. W., Butler, R. P., & Vogt, S. 2000, ApJ, 529, L41 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hubbard, W. B., Burrows, A., & Lunine, J. I. 2002, ARA&A, 40, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1988, Computer Phys. Comm., 52, 103 [Google Scholar]
- Hubeny, I., & Burrows, A. 2007, ApJ, 669, 1248 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Hubeny, I., Burrows, A., & Sudarsky, D. 2003, ApJ, 594, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, B., Greenberg, R., & Barnes, R. 2008, ApJ, 681, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Noyes, R. W., Brown, T. M., & Gilliland, R. L. 2007, ApJ, 655, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz R. L. 1993, CD-ROM 13, ATLAS 9 Stellar Atmosphere programs and 2 km s-1 Grid (Cambridge: SAO) [Google Scholar]
- Laughlin, G., Wolf, A., Vanmunster, T., et al. 2005, ApJ, 621, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X., Burrows, A., & Ibgui, L. 2008, ApJ, 687, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1967, Z. Astrophys., 65, 89 [Google Scholar]
- Perna, R., Menou, K., & Rauscher, E. 2010, ApJ, 724, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Rucinski, S. M. 1969, Acta Astron., 19, 245 [Google Scholar]
- Rucinski, S. M. 1970, Acta Astron., 20, 327 [Google Scholar]
- Rucinski, S. M. 1973, Acta Astron., 23, 301 [NASA ADS] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saumon, D., Chabrier, G., & Van Horn, H. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Sharp, C., & Burrows, A. 2007, ApJS, 168, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Cooper, C. S., Fortney, J. J., & Marley, M. S. 2008, ApJ, 682, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, A. M. S., Anderson, D. R., Skillen, I., Collier Cameron, A., & Smalley, B. 2011, MNRAS, accepted [Google Scholar]
- Spiegel, D. S., Silverio, K., & Burrows, A. 2009, ApJ, 699, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Sudarsky, D., Burrows, A., & Hubeny, I. 2003, ApJ, 588, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Vaz, L. P. R., & Norlund, A. 1985, A&A, 147, 28 [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Entropy (per baryon and divided by k) as a function of pressure and temperature. Entropy decreases with pressure and increases with temperature. |
| In the text | |
 |
Fig. 2 The effect of the intrinsic effective temperature on the T − P profile of the atmosphere on the day side. D-stands for day, numbers give the effective temperature in K and the core entropy, respectively. Circles mark the top of the convection zone. Notice that for higher effective temperatures the convection zone starts at lower pressures (densities) but at about the same temperatures. Consequently, given the relation from Fig. 1, models with higher intrinsic effective temperature have higher core entropy. |
| In the text | |
 |
Fig. 3 Left: the effect of the planet-star distance (a magnitude of irradiation) on the T − P profile of the atmosphere. Red lines represent the day side, blue lines represent the night side. Circles mark the top of the convection zone. D-stands for day, N-stands for night, numbers give the planet-star distance in AU and the core entropy, respectively. Notice that entropy on both day and night sides increases with increasing irradiation (shorter distance). Right: the effect of the planet-star distance or irradiation on the day-night side cooling of the planet. The cooling is expressed as the intrinsic effective temperature in K as a function of the core entropy for several surface gravities. The day-side is solid, and night-side is dashed. The models are calculated for two planet-star distances 0.045 (green) and 0.0225 AU (red). The cooling from the day side decreases with the stellar irradiation (shorter distance). The cooling from the night side behaves in a similar way. Consequently, the total heat loss is lower at a higher irradiation. |
| In the text | |
 |
Fig. 4 The combined night and day side cooling as a function of the surface gravity and core entropy. It is expressed as the intrinsic effective temperature |
| In the text | |
 |
Fig. 5 Left: the effect of varying the metallicity on the T − P profile of the atmosphere. The curves are labeled by the value of the metallicity in the atmosphere (1 or 3 × solar) and the core entropy, respectively. Notice that entropy on both day and night sides increases with increasing metallicity. Right: the effect of varying the metallicity of the planetary atmosphere on the day-night side cooling. Models are calculated for two metallicities: solar and 3 × solar metallicity. The cooling from both the day and the night side decreases with the metallicity. Consequently, the total heat loss decreases with increasing metallicity. |
| In the text | |
 |
Fig. 6 Left: the effect of the Pn parameter (day-night heat transfer efficiency) on the T − P profile of the atmosphere. The curves are labeled with the values of the Pn parameter and the core entropy, respectively. Notice that the entropy on the day side decreases with increased efficiency of heat redistribution. Entropy on the night side behaves in the opposite way and increases with increasing heat redistribution, or Pn value. Right: the effect of the Pn parameter on the day-night side cooling. The models are calculated for three different values of Pn = 0.1,0.3,0.5. Cooling from the night side decreases with the efficiency of heat redistribution (Pn). Cooling from the day side behaves in the opposite way and increases with increasing Pn. However, the night side is more sensitive to the Pn parameter, so it governs total core heat loss, which decreases with increasing Pn. The difference between night and the day side cooling is largest for the smallest values of Pn. |
| In the text | |
 |
Fig. 7 The combined night and day side cooling as a function of the surface gravity and core entropy. It is expressed as the intrinsic effective temperature |
| In the text | |
 |
Fig. 8 Left: the effect of a stratospheric absorber on the T − P profile of the day-side atmosphere. The curves are labeled with the values of the extra opacity, κ = 0.,0.02,0.05 cm2g-1, and the core entropy, respectively. Notice that the entropy on the day side decreases with increasing the extra opacity. There is no stratosphere on the night side, so only one model is plotted. Right: the effect of the extra opacity in the upper atmosphere of the day side on the day-night side cooling. The models are calculated for three different values of the extra opacity, κ = 0.,0.02,0.05 cm2 g-1. Cooling from the day side increases with the value of the extra opacity. Cooling from the night side core is the same since only the day side exhibits a stratosphere. The difference between the night and the day side cooling is largest for lower values of the extra opacity, and the total core heat loss increases with increasing extra opacity. |
| In the text | |
 |
Fig. 9 The combined night and day side cooling as a function of the surface gravity and core entropy. It is expressed as the intrinsic effective temperature |
| In the text | |
 |
Fig. 10 Left: the effect of the depth of the day-night heat transport region on the T − P profile of the atmosphere. The curves are labeled with the values of the Rosseland optical depth of the bottom of the day-night heat transfer region, and the core entropy, respectively. Notice that the entropy on the day side decreases with increasing optical depth. The entropy on the night side behaves in the opposite way, and increases with the optical depth of the heat redistribution region. Right: the effect of the depth of the day-night heat transport on the day-night side cooling. The day-side (solid) and the night-side (dashed) cooling of the planet for three different values of the day-side Rosseland optical depth at the bottom of the heat redistribution region τross = 1,3,9. On the day side, the heat loss increases with increasing optical depth. On the night side, the heat loss decreases with increasing optical depth and this trend tends to dominate the opposite trend on the day side. As a result the night-to-day difference in heat loss is lower for larger optical depth and the total heat loss decreases with increasing the optical depth. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.