| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201117926 | |
| Published online | 21 December 2011 | |
Atomic data for the X-ray lines of Fe viii and Fe ix⋆
1 DAMTP, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
e-mail: b.o-dwyer@damtp.cam.ac.uk
2 Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
3 Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
Received: 22 August 2011
Accepted: 19 September 2011
The distorted wave extension of the autostructure code has been used to calculate energy levels, radiative transition probabilities and collisional excitation rates of Fe viii and Fe ix up to n = 6 for Fe ix and n = 7 for Fe viii. We have compared some of the data with previous calculations, finding overall agreement for radiative transition rates, but interesting differences for some collisional data. We have merged our data for the higher energy levels with published R-matrix collisional excitation rates for the lower ones to calculate spectral line intensities and compare them with observations. In particular, we have focused on the transitions from high energy levels of Fe viii & Fe ix which are present in the 93–95 Å region. A few new identifications are tentatively provided. We find that Fe ix 5f–3d and Fe viii 7f–3d transitions only comprise a small fraction of the observed lines in the 93–95 Å region for quiet Sun conditions, and thus their contribution to the Solar Dynamics Observatory (SDO) Atmospheric Imaging Assembly (AIA) 94 Å band is expected to be small.
Key words: atomic data / line: identification / techniques: spectroscopic
A complete list of calculated energies, radiative data and thermally averaged collision strengths is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/537/A22
© ESO, 2012
1. Introduction
The 50–170 Å spectral region is dominated by a forest of transitions, many of which are from n = 4,5,6 and 7 states of highly ionised iron ions, and for which little atomic data are available (see Fawcett et al. 1968; Jordan 1968). This spectral region has been observed with various solar instruments on-board sounding rockets, and more recently with Chandra LETG (see Brinkman et al. 2000) and the Solar Dynamics Observatory (SDO). SDO has been providing new extreme-ultraviolet (EUV) observations of the Sun, at unprecedented cadence. One of the instruments, the Atmospheric Imaging Assembly (AIA, see Lemen et al. 2011) has been providing narrow-band EUV images at various wavelengths, centred at 94, 131, 171, 193, 211, and 335 Å. The relevant atomic data for the spectral lines contributing to some of these bands are relatively well understood, however a significant amount of data is still lacking. See O’Dwyer et al. (2010) and Del Zanna et al. (2011) for details.
This work is in part motivated by the desire to determine the contribution of transitions from high energy levels of Fe viii & Fe ix to the SDO AIA 94 Å band. The work of Aschwanden & Boerner (2011) has hinted at the presence of missing flux at lower temperatures in the response curve for the 94 Å band. Fe viii 7f–3d transitions at 93.469 and 93.616 Å have been identified by Ramonas & Ryabtsev (1980). Approximate excitation data for these transitions were estimated by Czyzak & Krueger (1966), and a proper scattering calculation was needed. The presence of Fe ix 5f–3d transitions in the 94 Å region has been proposed by Lepson et al. (2002), but appropriate calculations have been missing.
In this work, we have therefore carried out calculations for Fe viii and Fe ix using a new distorted wave (DW) development of the autostructure code, described in Badnell (2011) and outlined below. We have used this new code to obtain collisional and radiative data for levels up to n = 6 for Fe ix and n = 7 for Fe viii. We have merged the data for the higher energy levels with those of the lower R-matrix ones (n = 3), previously available, to build an atomic model and calculate spectral line intensities, to compare with observations. Recently, Foster & Testa (2011) have also carried out atomic calculations for the Fe ix 5f − 3d transitions using the Flexible Atomic Code (FAC, see Gu 2003). Towards the end of the paper, we briefly compare our results with theirs.
The discussion in this paper focuses on transitions from n = 4 − 7 configurations observed in the Soft X-rays, from 50 to 170 Å. These atomic data are needed, because there are a large number of lines (many of which are still unidentified) in this wavelength range. This spectral range is also routinely observed now by the SDO Extreme ultraviolet Variability Experiment (EVE). EVE includes two spectrographs and multiple photometers for measuring the solar EUV irradiance from 1 to 1220 Å (Woods et al. 2010). The EUV spectra are from two Multiple EUV Grating Spectrographs (MEGS) in the 50–380 Å and 350–1050 Å spectral ranges, with ≃ 1 Å spectral resolution.
The paper is organised as follows. In Sect. 2, we give details of the methods used for the atomic structure and electron scattering calculations. The Fe ix and Fe viii calculations are discussed in Sects. 3 and 4, respectively. Comparisons are made with the results of previous publications. In Sect. 5 we benchmark the atomic data we have calculated for Fe viii and Fe ix against solar and laboratory spectra. Our conclusions are given in Sect. 6.
2. Method
The atomic structure calculations were carried out using the program autostructure (Badnell 1997) which constructs target wavefunctions using radial wavefunctions calculated in a scaled Thomas-Fermi-Dirac statistical model potential. The scaling parameters were determined by minimising the sum of the energies of all the target terms, computed in LS-coupling, i.e. neglecting all relativistic effects.
The Breit-Pauli distorted wave calculations were carried-out using the autostructure code. Full details of this recent development of the code are found in Badnell (2011). Although it bears some superficial similarities with the historic UCL-DW code (Eissner 1998) due to their common superstructure heritage (Eissner et al. 1974), it is an independent implementation which differs fundamentally from the UCL-DW code in a number of important ways. We note salient points of the implementation. It places no restrictions of the atomic structure. Two-body fine-structure can be included if desired, for example. The continuum distorted waves are calculated using the same form for the distorting potential as specified for the target, but now for the (N + 1)-electron problem. Non-relativistic or kappa-averaged relativistic orbitals can be used. Unlike the bound-free problem (e.g. autoionization) the continuum orbitals are not orthogonalized to the bound orbitals, nor are the “zero” overlaps neglected. Rather, the appropriate exchange overlap integrals are determined. The electrostatic and, optionally, two-body non-fine-structure (N + 1)-electron interaction Hamiltonian for the collision problem is determined in an unmixed LS-coupling representation. It is then transformed to an LSJ representation. The two-body fine-structure collisional interaction can be added, optionally, at this stage. The full (N + 1)-electron interaction Hamiltonian is transformed to a full Breit-Pauli jK-coupling representation (i.e. including both configuration and fine-structure target mixing) in the same manner as is done for the (inner-region) Breit-Pauli R-matrix.
Collision strengths are calculated at the same set of final scattered energies for all transitions. Zero gives all threshold transitions, for example. A small continuum interpolation basis is used to enable the interaction Hamiltonian to be evaluated at the appropriate initial scattering energy for each transition. “Top-up” in the contribution of high partial waves is done using the same Breit-Pauli methods and subroutines implemented in the R-matrix outer-region code STGF. The implementation is designed for efficiency in determining collision strengths from a low-lying set of (user specifiable) “metastable” levels to all possible “spectroscopic” excited states. “Correlation” levels/terms/configurations can be flagged for efficiency so that they contribute only to the target description. The final deliverable is a (type-5) adf04 file (Summers 2006) which contains energy levels, radiative rates, ordinary collision strengths (as a function of final scattered energy) and infinite energy Born limits (and line strengths). These ordinary collision strengths can then be convoluted with any desired electron energy distribution. A utility code (adf04_om2ups.f) is provided which converts this file to the more familiar (type-3) adf04 file which contains Maxwell-averaged effective collision strengths.
We note that resonances are omitted in the first instance. Since resonances in electron-impact excitation are just the complement of dielectronic recombination then their contribution can be determined independently, if desired. Alternatively, our approach lends itself to complementing the results of an R-matrix calculation, as herein, since resonances are more prominent in low-lying transitions. There is also compatibility in atomic structure which aids merging of the two datasets. Starting with the R-matrix target structure, which may be much larger than that for which collision data is calculated, additional orbitals and configurations included in the DW calculation should not perturb the original structure too much. If it does then the original R-matrix structure is questionable.
In addition to the original tests and comparisons (Badnell 2011) some further comparisons of collision strengths from the autostructure DW code have been made with both FAC and (background) R-matrix collision strengths, and which emphasise the importance of the atomic structure in such – see Liang & Badnell (2011) and Liang et al. (2011).
3. Fe ix
A significant number of transitions from n = 4,5 levels for this ion remain unidentified. Kruger et al. (1937) identified the two strong decays from the 4s levels to the ground state. Alexander et al. (1965) later identified four decays from the 4d and 5s levels. Wagner & House (1971) were the first to identify 12 transitions from the 3p5 3d–3p5 4f array, in the 111.69–116.81 Å spectral range. We adopt the measurements from Fawcett et al. (1972) who revised the Wagner & House (1971) wavelengths. Young (2009) identified three lines from the 3s2 3p4 3d2 configuration and one from the 3s2 3p5 4p configuration. Young & Landi (2009) identified some more transitions from the 3s2 3p4 3d2 configuration. Landi & Young (2009) identified two more transitions from the 3s2 3p5 4p configuration.
Lines from Fe ix have been observed in the extreme ultraviolet with an electron beam ion trap (EBIT) by Beiersdorfer et al. (1999) and Lepson et al. (2002). Lepson et al. (2002) suggested that a few weak lines observed around 94 Å arise from 5f − 3d transitions, however a firm identification was not provided.
Radiative data for this ion have been calculated by a number of authors. Aggarwal et al. (2006) calculated radiative data with the General purpose Relativistic Atomic Structure Package (GRASP) for transitions between some n = 3 and the 3s2 3p5 4l configurations.
Verma et al. (2006) produced a large-scale structure calculation using Hibbert’s CIV3 Program and semi-empirical corrections to obtain a good match in level energies for those known. They included some n = 3,4,5 configurations, but not the 3s2 3p5 5f. The configuration 3s2 3p3 3d3, which is important for configuration interaction, was omitted from their calculations.
FAC atomic structure calculations were carried out by Landi & Young (2009) up to n = 4.
In terms of electron excitation data, the most accurate calculation so far is from Storey et al. (2002). These data are included in CHIANTI v.6 (Dere et al. 2009). Storey et al. (2002) performed an R-matrix calculation, producing collisional excitations rates among the lowest 140 energy levels, in six configurations, which include levels from the 3s2 3p5 4s and 3s2 3p5 4p configurations. His target had 12 configurations, of which 6 were included as correlation configurations.
Electron configuration basis for the DW calculation and orbital scaling parameters for Fe ix.
Level energies for Fe ix.
We have run several structure calculations with various configurations (12, 27, 45 and 67 configuration calculations). The 12 configuration target is identical to that of Storey et al. (2002). Our final choice for the scattering calculation is the largest run, where the target wavefunctions are expanded in the 67 configuration basis listed in Table 1. Those configurations listed above the horizontal line in Table 1 are spectroscopic configurations. Those below this line are present solely for correlation purposes. The Thomas-Fermi-Dirac scaling parameters are also given in Table 1.
In Table 2 we list the calculated and, where available, experimental energies for a sample of levels of the target. A complete list of the calculated energies of all 379 levels of the target is available at the CDS.
Table 3 contains a comparison of transition probabilities for a sample of the stronger transitions. Transition probabilities are provided for our 27, 45 and 67 configuration targets as well as those calculated by Storey et al. (2002) (in agreement with our 12 configuration calculation), Landi (2011, priv. comm.) corresponding to those of Landi & Young (2009) and Verma et al. (2006). Overall agreement (to within a relative 20%) is found, with the exception of the 3p61S0–3p5 5s 1P1 and 3p61S0–3p5 5s 3P1 transitions for which there are substantial differences. As Verma et al. pointed out, the 3s2 3p5 5s 1P1 and 3P1 are highly mixed, and these levels also mix with the 3s 3p6 4p 1P1 level.
Transition probabilities for Fe ix.
In our largest structure run, 67 configurations, level 263 (5s 1P1) is composed of 38% (5s 1P1), 32% (5s 3P1) and 10% (3s 3p6 4p 1P1), while level 265 (5s 3P1) is composed of 55% (5s 3P1), and 41% (5s 1P1). Our predicted energy difference between the two 5s levels (13690 cm-1) is close to the observed one (14 530 cm-1). For our smaller structure calculations the mixing is: for 27 configurations, 3s2 3p5 5s 1P1 is 52% (5s 1P1) plus 45% (5s 3P1); for 45 configurations, 3s2 3p5 5s 1P1 is 55% (5s 1P1) plus 44% (5s 3P1). This change is mainly due to the position of the 3s 3p6 4p 1P1 level. Verma et al. quote mixing values for 3s2 3p5 5s 1P1 as 55% (5s 1P1) plus 31% (5s 3P1), but they also mention that the 3s 3p6 4p 1P1 level is coupled with the 3s2 3p5 5s 3P1 level, and that they have carried out some semi-empirical adjustments to the Hamiltonian. Our ab-initio model predicts the decay from the 5s 1P1 level to be about twice as strong the decay from the 5s 3P1. Both Alexander et al. (1965) and Lepson et al. (2002) indicate a ratio of two between these two lines, in agreement with our prediction. We cannot understand why the transition probability given by Verma et al. (their Table 5, our Table 3) for the transition 5s 1P1 to the ground level is signifcantly less than that for 5s 3P1 to the ground level. This seems most unusual, even if the mixing with the 3s 3p6 4p 1P1 level is more significant than we have calculated.
List of the strongest Fe ix lines in the 50–130 Å range.
For our largest structure calculation, 67 configurations, the level 3s2 3p5 4s 1P1 is composed of 66% (4s 1P1) plus 30% (4s 3P1). These values are close to those of Verma, 61% (4s 1P1) plus 36% (4s 3P1). Our transition probabilities for 4s transitions to the ground (Table 3) are in reasonable agreement with Verma et al., in contrast to those for 5s to the ground.
An R-matrix calculation including all of the excited levels for n = 5 & 6 would be quite demanding. We have instead used the distorted wave autostructure code to calculate collision strengths for the high lying levels of Fe ix. These calculations do not include low-energy resonance effects, which could be significant for some transitions. As a result we use the collision strengths from the R-matrix calculation of Storey et al. (2002) for lower levels where available.
Levels up to level 79 contain some metastable levels. For the 79 energetically lowest levels collision strengths are calculated between themselves and up to all excited states. Collisional transitions between excited states higher than level 79 are omitted. Radiative data is calculated for all transitions.
Table 4 contains predicted intensities for the strongest Fe ix lines in the 50–170 Å range. The relative intensities (photons) Int = NjAji/Ne are normalised to the strongest transition and were calculated at electron densities of 108 and 1012 cm-3 and log T[K] = 5.85, typical of the quiet solar corona, and of high-density laboratory plasmas. Weighted oscillator strengths gf and A-values (s-1) are shown. Also included are the calculated and, where available, experimental wavelengths for these lines. The strongest lines are the decays from the 3s2 3p5 4s,d to the ground state, and the 3d–4f transitions.
One issue of concern is the reliability of DW results for transitions to the n = 4,5 levels. A comparison between the R-matrix and DW results for the 3p–4s transitions shows that resonances attached to higher-lying levels are significant. This is caused by the the fact that the 3s2 3p5 4s levels are relatively low-lying, and the background collision strength is small, hence the contribution from resonances can have an important effect.
 |
Fig. 1 Top: collision strength for the 3s2 3p61S0–3s2 3p5 4s 1P1 transition of Fe ix. Squares with dashed line from present results. Histogram from Storey et al. (2002). Bottom: thermally averaged collision strength for the 3s2 3p61S0–3s2 3p5 4s 1P1 transition. Solid line with squares from present results. Diamonds from Storey et al. (2002). |
For example, the collision strength for the 3s2 3p61S0–3s2 3p5 4s 1P1 transition is shown in Fig. 1 (top). Good agreement in the background values is found with the R-matrix results from Storey et al. (2002), however the large contributions from the resonances near threshold do affect the thermally-averaged collision strength (shown in Fig. 1, below), with a significant increase (by a factor of two near peak Fe ix abundance in equilibrium). Further investigation indicates that the main contribution comes from the 3s2 3p5 4p 1S0 level.
 |
Fig. 2 Top: collision strength for the 3s2 3p61S0–3s2 3p5 4p 1S0 transition of Fe ix. Squares with dashed line from present results. Histogram from Storey et al. (2002). Bottom: thermally averaged collision strength for the 3s2 3p61S0–3s2 3p5 4p 1S0 transition. Solid line with squares from present results. Diamonds from Storey et al. (2002). |
Figure 2 shows the collision strength for the strong 3s2 3p61S0–3s2 3p5 4p 1S0 transition. Again, good agreement in the background values is found, as expected. The R-matrix result does not contain resonances because the 3s2 3p5 4p 1S0 level was the highest one included in the Storey et al. (2002) calculation. It is interesting to note the large collision strength for this forbidden transition between configurations with the same parity. This was a somewhat unexpected result. The 3s2 3p5 4p 1S0 level decays via a strong dipole-allowed transition to the 3s2 3p5 3d 1P1. An estimate of the wavelength for this transition with our 67 configuration calculation provides a value very close to that suggested by Young (2009), who identified this transition with a line in the Hinode EIS spectrum, at 197.862 Å. The observed intensity of this line, relative to that of other Fe ix transitions, is in good agreement with that predicted using the Storey et al. (2002) calculation, hence indirectly confirming the large collision strength from the ground state to the 3s2 3p5 4p 1S0 level.
We have run various checks by looking at the collision strengths near thresholds for all transitions to levels with n ≥ 4, and we believe that significant enhancements due to resonances such as those occurring to the 3s2 3p5 4s levels should not be present. However, a further in-depth analysis, which is beyond the scope of this paper, is in progress.
4. Fe viii
The identification of Fe viii lines is reviewed in Del Zanna (2009). It started with Kruger & Weissberg (1937), who identified the main decays of the 4f, 5f, 6f and 7f levels. That study was followed by the fundamental laboratory work of Fawcett and co-workers on the ZETA spectrum (see Gabriel & Fawcett 1965), where a number of identifications for the EUV lines were provided. The main source of accurate wavelengths and further identifications came from the excellent work of Ramonas & Ryabtsev (1980).
Several atomic structure calculations exist in the literature. The latest ones are from Zeng et al. (2003), and Del Zanna (2009). Zeng et al. (2003) performed large-scale multi-configuration Hartree-Fock (MCHF) calculations for Fe viii, to show the importance of including core-valence electron correlations. Del Zanna (2009) used autostructure and searched a “benchmark” configuration basis which reproduced well the positioning of a few key low n = 3,4 mixed levels. The additional n > 4 configurations were added to obtain a good target for these levels.
The latest electron scattering calculation for this ion is the R-matrix calculation by Griffin et al. (2000). It included the 33 terms and the 77 levels of the configurations 3s2 3p6 3d, 3s2 3p5 3d2, 3s2 3p5 3d 4s, 3s2 3p6 4s, 3s2 3p6 4p, 3s2 3p6 4d and 3s2 3p6 4f in the close-coupling expansion. The Griffin et al. (2000) data have been benchmarked by Del Zanna (2009) using Hinode EUV Imaging Spectrometer (EIS, see Culhane et al. 2007) observations, measurements found in the literature, and laboratory plates from B.C. Fawcett (see Del Zanna et al. 2004, for details on the benchmark method). The benchmark work showed that significant discrepancies (60% or so) between Hinode EIS observed intensities and those predicted with the Griffin et al. (2000) data exist for some lines. It was shown with the run of a large-scale autostructure “benchmark” calculation that this was due to missing configuration interaction (CI). The effects are subtle for some strong transitions arising from very mixed levels, and were also noted by Griffin et al. (2000).
In order to improve the Griffin et al. (2000) data, the collision strengths of the dipole-allowed transitions were scaled by Del Zanna (2009) according to the ratio of the gf values (and energies) in the Griffin et al. (2000) and the “benchmark” calculation. These data are included in CHIANTI v.7 and are adopted here.
The structure calculation by Del Zanna et al. (2004) was optimised for transitions between the n = 3 configurations. We have extended the structure (and scattering) calculations to levels up to n = 7.
Electron configuration basis for the DW calculation and orbital scaling parameters for Fe viii.
An R-matrix calculation including all of the excited levels for n = 5, 6 & 7 would be quite demanding. Instead we use the distorted wave autostructure code to calculate collision strengths between levels of Fe viii included in our structure calculations. Levels up to level 40 contain some metastable levels. For the 40 energetically lowest levels collision strengths are calculated between themselves and to all excited states. Collisional transitions between excited states higher than level 40 are omitted. Radiative data is calculated for all transitions.
The target wavefunctions are expanded in the 23 configuration basis listed in Table 5. The configuration 3s2 3p4 3d2 4f is present solely for correlation purposes. The resulting scaling parameters are also given in Table 5.
In Table 6 we list the calculated and, where available, experimental energies for a sample of levels of the target. A complete list of the calculated energies of all 104 levels of the target is available at the CDS.
Table 7 contains predicted intensities for the strongest Fe viii lines in the 50–170 Å range. The relative intensities (photons) Int = NjAji/Ne are normalised to the strongest transition and were calculated at electron densities of 108 and 1012 cm-3 and log T[K] = 5.6. Weighted oscillator strengths gf and A-values (s-1) are shown. Aslo included are the calculated and, where available, experimental wavelengths for these lines.
Thermally averaged collision strength for the 3s2 3p6 3d 2D5/2–3s2 3p6 4f 2F7/2 transition of Fe viii is plotted as a function of temperature in Fig. 3. The corresponding thermally averaged collision strength from the R-matrix calculation of Griffin et al. (2000), adjusted by Del Zanna, is found to be in very good agreement.
Level energies for Fe viii.
 |
Fig. 3 Thermally averaged collision strength for the 3s2 3p6 3d 2D5/2–3s2 3p6 4f 2F7/2 transition of Fe viii. Solid line from present results. Diamonds from the R-matrix calculation of Griffin et al. (2000), adjusted by Del Zanna (2009). |
List of strongest Fe viii lines in the 50–170 Å range.
5. Benchmarking the atomic data
There is relatively little experimental data that we can use to benchmark the atomic data we have calculated. Most solar spectra have a relatively low resolution or are not calibrated. In terms of spectral resolution, the best soft X-ray solar spectrum is from Behring et al. (1972). They published a line list based on a LASP rocket flight that observed the entire Sun in the 60–385 Å region with very high-resolution (0.06 Å). A list of those lines observed in quiet conditions are included in Table 8. In terms of both spectral resolution and flux calibration, the best soft X-ray spectra of the quiet Sun are from Manson (1972). Manson (1972) provided an excellent list of lines observed in quiet and active conditions. The list of lines observed in quiet conditions are included in Table 8.
In terms of laboratory spectra, we use here the flux-calibrated theta-pinch spectra of Datla et al. (1975), and the EBIT measurements of Lepson et al. (2002). Lepson et al. provided some estimates of the line intensities. We are not sure about the actual flux calibration, so only lines not too far in wavelength are considered here.
List of lines in the soft X-rays from quiet Sun observations.
5.1. Fe ix
The strongest line in the soft X-ray spectra is the 3p–4s 1S0–1P1 103.566 Å line, which we use as a reference. First, we note that the use of the R-matrix data in the Fe ix model ion means that the predicted intensity of this line is about twice that which is obtained when only DW data are used. The relative intensity of this line with e.g. the 3d–4f transitions suggests that we have about the correct theoretical intensity. The decay from the 4s 3P1 105.208 Å is predicted to have half the intensity of the 103.566 Å line at coronal densities, but actually in the solar spectrum the ratio is 0.7. This could be due to a blend, considering that at high densities the ratio increases to 0.6, closer to that which is observed (0.75, Lepson et al. 2002). The alternative is that level mixing is not accurate, although all of the different structure runs provide similar values for the radiative data.
Our ion model predicts several 3d–4f transitions to be strong. Some of them have not been previously identified. We tentatively identify two of them, observed both in solar and laboratory spectra. We assign them the 133.923 and 136.572 Å, and notice that identification of these lines with 3d–4f transitions was already suggested by Lepson et al. (2002) and also by Foster & Testa (2011). In addition, we identify the 116.803 Å as a self-blend. The decays from the 4d levels were identified by Alexander et al. (1965).
After the 3p–4d lines, we predict that the strongest transition array is the 3d–5f one. By comparing EBIT results with calculations using the Hebrew University Lawrence Livermore Atomic Code (HULLAC, Bar-Shalom et al. 2001) Lepson et al. (2002) suggested that there are a number of 5f–3d transitions around 90 Å, in particular three 5f–3d transitions at 91.98, 93.59 and 94.07 Å.
Relative intensities for Fe ix lines.
At low coronal densities, we find that only one line should be observable in the solar spectra, the 5–302 3p5 3d 3F4–3p5 5f 3G5. At high densities, there are a number of transitions which might become observable. We have searched for a correspondence between our theoretical energy splittings among the 5f levels and the difference in wavelengths provided by Lepson et al., and found a few possible coincidences. A tentative identification for these lines is provided in Table 9.
The strongest 3d–5f line would be at 91.98 Å and further blended with two other transitions. The predicted ratio of this line with our reference 3p–4s 103.566 Å line is in excellent agreement with the measurement from Lepson et al. (2002), as Table 9 shows. This is very encouraging. Two other coincidences have been found. Two self-blends contributing to the lines observed at 93.59 and 94.07 Å by Lepson et al. In these cases, the predicted intensities are only half of what was observed. In the solar case, the strongest 91.98 Å line provides only 1/3 of the observed intensity (assuming that our reference line, the 3p–4s 103.566 Å is not in itself blended in the solar spectrum). The other 3d–5f lines provide very little flux to the observed solar lines. This is not surprising, considering that most lines are noted as blended by Manson. Also, this of course does not mean that in particular conditions, where strong transition-region emission is present, these lines could not be providing a significant contribution to the 94 Å AIA channel.
We searched for a possible identification of the lines from the 3d–6f transition array, considering that at least one should be observable in the EBIT spectra, but could not find any suitable candidate. Further work is needed to identify these lines, as well as other ones such as the 3d–5p.
It is interesting to note that many of the strongest lines, even at relatively low densities (quiet Sun corona), are decays to metastable levels. Indeed, many of the transitions, including the strongest of the 3d–5f, are from levels which become mainly populated through excitation from a metastable one, and not from the ground state. For example, the intensity of the 3p5 3d 3F4–3p5 5f 3G5 line becomes four times weaker if only the excitation from the ground state is included in the model.
We have compared our results for Fe ix with those presented by Foster & Testa (2011) at the same density and temperature values and have found that their results are in reasonable agreement with ours.
We compare the intensities of the 3d–4f lines using the intensities listed in Datla et al. (1975, first case), which included corrections due to optical depth effects. The plasma source was measured to have Ne = 1016.07 cm-3 and log Te[K] = 6.04. We make use of the “emissivity ratio” technique (see Del Zanna et al. 2004, for details), whereby the observed intensity of a line is divided by its emissivity:
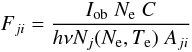 (1)calculated at a fixed electron density Ne (in this case 1016.07 cm-3) and plotted as a function of the temperature Te. Iob is the observed intensity in the line, h is Planck’s constant, ν is the frequency of the line and Nj is the number density of the upper level j of the emitting ion. The scaling constant C is chosen so the curves are close to unity. The emissivity ratios (see Fig. 4) show good agreement to within ± 30%, with one exception, between theory and experiment for the 3s2 3p6–3d, 3s2 3p6–4s, and 3d–4f transitions, thus giving us confidence in the reliability of the present calculations for the 4f levels.
(1)calculated at a fixed electron density Ne (in this case 1016.07 cm-3) and plotted as a function of the temperature Te. Iob is the observed intensity in the line, h is Planck’s constant, ν is the frequency of the line and Nj is the number density of the upper level j of the emitting ion. The scaling constant C is chosen so the curves are close to unity. The emissivity ratios (see Fig. 4) show good agreement to within ± 30%, with one exception, between theory and experiment for the 3s2 3p6–3d, 3s2 3p6–4s, and 3d–4f transitions, thus giving us confidence in the reliability of the present calculations for the 4f levels.
5.2. Fe viii
 |
Fig. 4 The emissivity ratio curves from the calibrated theta-pinch laboratory spectra of Datla et al. (1975). Iob indicates the measured line intensity. Dashed lines at ± 30% have been added to give an indication of the agreement. |
Relative intensities for Fe viii lines.
We compare the intensities of the 3d–4f, 3d–5f lines using the intensities listed in Datla et al. (1975, second case). The level populations are in the high density limit and therefore have no relative sensitivity to changes in electron density. As the relative variation in temperature is greater than that in density the emissivity ratio has been plotted as function of the temperature and not of the density. The emissivity ratios show very good agreement between theory and experiment to within ± 20% for the 3d–3d, 3d–4f, and 3d–5f transitions, thus giving us confidence in the reliability of the present calculations for the 5f levels (see Fig. 5). The contribution of missing resonances in the collision strengths for levels n ≥ 5 is in fact not expected to be large.
We then consider the 3d–5f, 3d–6f, 3d–7f transitions. Table 10 shows the relative intensities, predicted and observed. We find an excellent agreement between the relative ratios as observed in the laboratory by Ramonas & Ryabtsev (1980), which is very encouraging. We find some differences with the corresponding intensities predicted using the excitation data from Czyzak & Krueger (1966).
 |
Fig. 5 The emissivity ratio curves from the calibrated theta-pinch laboratory spectra of Datla et al. (1975). Iob indicates the measured line intensity. Dashed lines at ± 20% have been added to give an indication of the agreement. |
The two Fe viii 3p6 3d 2D3/2–3p6 7f 2F5/2 (93.56 Å) and 3p6 3d 2D5/2–3p6 7f 2F7/2 (93.72 Å) transitions are within the SDO AIA 94 Å filter, together with the above Fe ix lines, and both the Fe xviii (93.923 Å) transition from 2s 2p61S1/2–2s2 2p53P3/2 and the Fe x (94.012 Å) 3s2 3p4 4s 2D5/2–3s2 3p52P3/2. Del Zanna et al. (2011) used the approximate excitation data from Czyzak & Krueger (1966), included in CHIANTI v6.0, to show that in particular conditions (at the footpoints of 1 MK loops) these 7f–3d lines are expected to provide a considerable contribution to the photons recorded in this band, so we can confirm here that to be the case. However, as Table 10 shows, there is plenty of unidentified flux in quiet Sun conditions, i.e. the 7f–3d transitions only provide a small fraction of the observed lines contributing to the 94 Å AIA channel.
6. Conclusions
The new atomic calculations presented here provide a significant advance over previous work. We have extended existing calculations of energy levels, radiative transition rates and collisional excitation rates up to n = 6 for Fe ix and n = 7 for Fe viii. The new data allow the calculation of line intensities. We have provided several new identifications, but many other lines are still unknown.
This paper is just a first step into the complex area of identifying and providing atomic data for lines in the crowded 50–170 Å spectral region. Jordan (1968) used collisional excitation rates estimated by one of us (PJS) to suggest that e.g. for Fe ix transitions from 3p5 4l (l = s, p, d, f) to either the ground state or the 3p5 3d would contribute significantly to the observed lines. A large number of lines present in this region have yet to be identified, however we do find for some transitions a relatively good agreement with observations.
Based on our calculations the predicted contribution of Fe ix 5f − 3d and Fe viii 7f–3d transitions is only a small fraction of the observed lines in the 93–95 Å region for quiet Sun conditions. As a result the contribution of these lines to the SDO/AIA 94 Å filter is predicted to be small.
Acknowledgments
The authors thank Dr. Adam Foster & Dr. Paola Testa for providing their Fe ix atomic data for comparison with our own. The authors acknowledge the support of STFC. B.O.D. was supported by funding from
the Gates Cambridge Trust. CHIANTI is a collaborative project involving researchers, at the Universities of: Cambridge (UK), George Mason (USA), and Michigan (USA). This work was carried out as part of the UK APAP project.
References
- Aggarwal, K. M., Keenan, F. P., Kato, T., & Murakami, I. 2006, A&A, 460, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, E., Feldman, U., & Fraenkel, B. S. 1965, J. Opt. Soc. Am., 55, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Boerner, P. 2011, ApJ, in press [Google Scholar]
- Badnell, N. R. 1997, J. Phys. B: At. Mol. Opt. Phys., 30, 1 [Google Scholar]
- Badnell, N. R. 2011, Comp. Phys. Commun., 182, 1528 [Google Scholar]
- Bar-Shalom, A., Klapisch, M., & Oreg, J. 2001, J. Quant. Spec. Radiat. Transf., 71, 169 [Google Scholar]
- Behring, W. E., Cohen, L., & Feldman, U. 1972, ApJ, 175, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Beiersdorfer, P., Lepson, J. K., Brown, G. V., et al. 1999, ApJ, 519, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkman, A. C., Gunsing, C. J. T., Kaastra, J. S., et al. 2000, ApJ, 530, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 60 [Google Scholar]
- Czyzak, S. J., & Krueger, T. K. 1966, ApJ, 144, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Datla, R. U., Blaha, M., & Kunze, H.-J. 1975, Phys. Rev. A, 12, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G. 2009, A&A, 508, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Berrington, K. A., & Mason, H. E. 2004, A&A, 422, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., O’Dwyer, B., & Mason, H. E. 2011, A&A, accepted [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eissner, W. 1998, Comp. Phys. Commun., 114, 295 [Google Scholar]
- Eissner, W., Jones, M., & Nussbaumer, H. 1974, Comp. Phys. Commun., 8, 270 [Google Scholar]
- Fawcett, B. C., Peacock, N. J., & Cowan, R. D. 1968, J. Phys. B: At. Mol. Phys., 1, 295 [Google Scholar]
- Fawcett, B. C., Kononov, E. Y., Hayes, R. W., & Cowan, R. D. 1972, J. Phys. B: At. Mol. Phys., 5, 1255 [Google Scholar]
- Foster, A. R., & Testa, P. 2011, ApJ, 740, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, A. H., & Fawcett, B. C. 1965, Nature, 206, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, D. C., Pindzola, M. S., & Badnell, N. R. 2000, A&AS, 142, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gu, M. F. 2003, ApJ, 582, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Jordan, C. 1968, J. Phys. B: At. Mol. Phys., 1, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Kruger, P. G., & Weissberg, S. G. 1937, Phys. Rev., 52, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Kruger, P. G., Weissberg, S. G., & Phillips, L. W. 1937, Phys. Rev., 51, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., & Young, P. R. 2009, ApJ, 707, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J., Title, A., Akin, D., et al. 2011, Sol. Phys., submitted [Google Scholar]
- Lepson, J. K., Beiersdorfer, P., Brown, G. V., et al. 2002, ApJ, 578, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, G. Y., & Badnell, N. R. 2011, A&A, 528, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, G. Y., Badnell, N. R., Zhao, G., Zhong, J. Y., & Wang, F. L. 2011, A&A, 533, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manson, J. E. 1972, Sol. Phys., 27, 107 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dwyer, B., Del Zanna, G., Mason, H. E., Weber, M. A., & Tripathi, D. 2010, A&A, 521, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramonas, A. A., & Ryabtsev, A. N. 1980, Optics and Spectroscopy, 48, 348 [NASA ADS] [Google Scholar]
- Storey, P. J., Zeippen, C. J., & Le Dourneuf, M. 2002, A&A, 394, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Summers, H. P. 2006, The ADAS User Manual v2.6, http://www.adas.ac.uk/manual.php [Google Scholar]
- Verma, N., Jha, A. K. S., & Mohan, M. 2006, ApJS, 164, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, W. J., & House, L. L. 1971, ApJ, 166, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., Eparvier, F. G., Hock, R., et al. 2010, Sol. Phys., DOI: 10.1007/S11207-009-9487-6 [Google Scholar]
- Young, P. R. 2009, ApJ, 691, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., & Landi, E. 2009, ApJ, 707, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, J., Jin, F., Zhao, G., & Yuan, J. 2003, J. Phys. B: At. Mol. Opt. Phys., 36, 3457 [Google Scholar]
All Tables
Electron configuration basis for the DW calculation and orbital scaling parameters for Fe ix.
Electron configuration basis for the DW calculation and orbital scaling parameters for Fe viii.
All Figures
 |
Fig. 1 Top: collision strength for the 3s2 3p61S0–3s2 3p5 4s 1P1 transition of Fe ix. Squares with dashed line from present results. Histogram from Storey et al. (2002). Bottom: thermally averaged collision strength for the 3s2 3p61S0–3s2 3p5 4s 1P1 transition. Solid line with squares from present results. Diamonds from Storey et al. (2002). |
| In the text | |
 |
Fig. 2 Top: collision strength for the 3s2 3p61S0–3s2 3p5 4p 1S0 transition of Fe ix. Squares with dashed line from present results. Histogram from Storey et al. (2002). Bottom: thermally averaged collision strength for the 3s2 3p61S0–3s2 3p5 4p 1S0 transition. Solid line with squares from present results. Diamonds from Storey et al. (2002). |
| In the text | |
 |
Fig. 3 Thermally averaged collision strength for the 3s2 3p6 3d 2D5/2–3s2 3p6 4f 2F7/2 transition of Fe viii. Solid line from present results. Diamonds from the R-matrix calculation of Griffin et al. (2000), adjusted by Del Zanna (2009). |
| In the text | |
 |
Fig. 4 The emissivity ratio curves from the calibrated theta-pinch laboratory spectra of Datla et al. (1975). Iob indicates the measured line intensity. Dashed lines at ± 30% have been added to give an indication of the agreement. |
| In the text | |
 |
Fig. 5 The emissivity ratio curves from the calibrated theta-pinch laboratory spectra of Datla et al. (1975). Iob indicates the measured line intensity. Dashed lines at ± 20% have been added to give an indication of the agreement. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


