| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117870 | |
| Published online | 21 December 2011 | |
Spectro-polarimetry of the bright side of Saturn’s moon Iapetus⋆
1 Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
e-mail: ejeta@mps.mpg.de
2 Institut für Geophysik und extratrrestishe Physik, TU Braunschweig, Germany
3 Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland, UK
4 INAF – Oss. Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received: 10 August 2011
Accepted: 18 October 2011
Context. Measurements of the polarized reflected sunlight from atmosphereless solar system bodies, over a range of phase angles, provide information about the surface structure and composition.
Aims. With this work, we provide analysis of the polarimetric observations of the bright side of Iapetus at five different phase angles, and over the full useful wavelength range (400–800 nm), so as to assess the light scattering behaviour of a typical surface water ice.
Methods. Using FORS2 of the ESO VLT, we have performed linear spectro-polarimetric observations of Iapetus’ bright side from 2009 to 2011 at five different phase angles, in the range from 0.80−5.20°, along with circular spectro-polarimetric observations at one phase angle.
Results. By measuring, with high accuracy (~0.1% per spectral bin for each Stokes parameter), the spectral polarization of the bright trailing hemisphere of Saturn’s moon Iapetus, we have identified the polarimetric characteristics of water ice, and found that its linear degree of negative polarization decreases with increasing phase angle of observation (varying from −0.9% to −0.3%), with a clear dependence on wavelengths of observation.
Key words: polarization / techniques: polarimetric
© ESO, 2012
1. Introduction
Iapetus has a radius of 718 km and orbits Saturn every 79.33 earth days at a distance of 3 560 840 km; it has an average bulk density of 1.150 ± 0.004 g/cm3 (http://ssd.jpl.nasa.gov) that might imply that it is made mostly of ices. Tidal interactions with Saturn have synchronized the rotation of Iapetus with its orbital period, and as a result, the moon always keeps the same face to Saturn and always leads with the same face in its orbital motion. Iapetus has a striking property that its leading and trailing hemispheres represent a contrast in surface albedo amounting to a factor of ~10 (Squyres & Sagan 1983). The leading hemisphere is much darker than its trailing hemisphere, with an albedo of 0.04 and 0.39, respectively (Spencer & Denk 2010). There are several hypothesis as to how this global albedo dichotomy has originated. Spencer & Denk (2010) have developed the idea put forward pre-cassini mission by Mendis & Auxford (1974), suggesting that exogenic deposition of dark material, possibly from Saturn’s outer retrograde satellites, has resulted in darkening of the leading hemisphere thereby raising its temperature and water ice sublimation rates.
2. Observations and data reduction
Linear spectro-polarimetric observations of the bright side of Iapetus have been obtained at five different epochs, using the FORS2 instrument of the European Southern Observatory (ESO) Very Large Telescope (VLT), from April 2009 to March 2011. FORS is the visual and near UV FOcal Reducer and low dispersion Spectrograph of the ESO VLT (Appenzeller et al. 1998). FORS2, installed on Unit Telescope 1 (Antu), is the version of FORS in operation since April 2009, and it offers many observing modes, including imaging polarimetry (IPOL) and multi-object spectro-polarimetry (PMOS). In addition to the linear polarization, we have also performed circular polarization observations of the same side of Iapetus at one phase angle. Our observing cadence of Iapetus’ bright side polarimetry followed from the scientific requirement to measure separately its bright hemisphere (to avoid contamination from the dark side), which is only possible close to its western elongation during its orbit around Saturn. Hence, all our observations were performed according to the observing blocks prepared considering a 12 days wide window centered at the date of maximum elongation, when a rather exclusive viewing geometry of the bright hemisphere of the moon is guaranteed. During the entire observation epochs, we used the same instrument set up (grism 300V, filter GC 435, and a 1′′ slit width), with a λ/2 retarder waveplate (for linear polarization) or λ/4 (for circular polarization) and a Wollaston prism inserted in the FORS2 optical path. The Wollaston splits up the incoming beam into two rays that are characterized by orthogonal polarization states with respect to the orientation (principal plane) of the Wollaston. The two signals from the Wollaston beams do not overlap as a special aperture masks are employed for this purpose.
Each epoch of linear polarimetric observations of Iapetus’ bright hemisphere were performed at all position angles of the λ/2 retarder waveplate (with respect to the principal plane of the Wollaston prism) from 0° to 337.5°, in 22.5° steps; and at λ/4 retarder wave plate position angles of 315°, 45°,135°, 225° for the circular polarization. FORS instrument is proved to be affected by a cross-talk problem from linear to circular polarization (Bagnulo et al. 2009). To strongly reduce this linear to circular cross talk, we measured a unique circular polarization signal as an average of the values obtained at instrument position angles that differ by 90°, as suggested by Bagnulo et al. (2009), to which we refer for further technical details. For the data reduction, we mainly used ESO FORS pipeline tool (see Izzo et al. 2010) but independent manual reduction with MIDAS and IRAF packages were also used as a cross-check. We applied bias-subtraction to the frames using a master bias obtained from a series of five frames taken closer in time to the observations, then divided by a flat-field obtained by combining five lamp frames. In fact, by performing the data reduction with and without flat-fielding, we have verified that the flat fielding does not change the value of the Stokes profiles, as we measure polarization from the normalized flux difference. For each frame observed at various retarder wave plate positions α, we rebinned spectral points to 10 pixels bin, a value we considered as the best compromise between spectral resolution loss and increase of signal to noise ratio, and then we extracted the parallel and the perpendicular beams (f ∥ and f ⊥ , respectively). The extraction radius we used is 6 pixels (rebinned); but we have also performed the extraction for larger radii (8 pixels and 10 pixels) and confirmed that the results are practically the same. We then performed independent wavelength calibration for the two beams of each of the frames using an arc lamp frame reduced in the same way as the science frames.
 |
Fig. 1 Spectro-polarimetry of the non-polarized standard star HD 97689 observed with FORS2 during night 2010-05-04. The measured reduced Stokes PQ and PU profiles, both with a value of ~ 0.1% are indicated in solid blue lines, with the statistical error bars in red. In both panels, the black dotted lines show the total flux (in arbitrary units), and is not corrected for the instrument + telescope transmission functions. |
 |
Fig. 2 Same as Fig. 1, for the non polarized standard star WD 1620391 observed with FORS2 during nights 2010-07-25 (upper panel) and 2011-03-28 (lower panel). In the upper panels, it can be seen that the polarization value is ~0.1% both in Stokes PQ and PU, while it is less in the case of lower panel, ~0.05%. |
2.1. Method of performing spectro-polarimetry
We measured the reduced Stokes Q , U, and V parameters (normalized by intensity) by combining fluxes of the pararallel and the perpendicular beams, employing the technique called the difference method, implemented in Bagnulo et al. (2009), as: ![\begin{equation} P_{X}=\frac{1}{2N}\sum_{j\,=\,1}^{N}\left [ \left ( \frac{f^{\parallel}-f^{\perp}}{f^{\parallel}+f^{\perp}}\right )_{\alpha_{j}}- \left (\frac{f^{\parallel}-f^{\perp}}{f^{\parallel}+f^{\perp}}\right )_{\alpha_{j}+\Delta P}\right], \end{equation}](/articles/aa/full_html/2012/01/aa17870-11/aa17870-11-eq25.png) (1)where N is the number of pairs of exposures for each Stokes parameters (in our case, 4 for the linear polarization, and 2 for the circular polarizatiin), and
(1)where N is the number of pairs of exposures for each Stokes parameters (in our case, 4 for the linear polarization, and 2 for the circular polarizatiin), and
-
for X = Q, ΔP = 45°, and αj belongs to the set {0°, 90°, 180°, 270°};
-
for X = U, ΔP = 45°, and αj belongs to the set {22.5°, 112.5°, 202.5°, 292.5°};
-
for X = V, ΔP = 90°, and αj belongs to the set { − 45°, 135°},
where Q/I = PQ, U/I = PU, and V/I = PV.
Assuming the flux and the standard deviation in each beam to be approximately equal to f and σ, respectively (see e.g., Bagnulo et al. 2009) the statistical error can be given as: 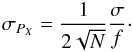 (2)
(2)
2.2. Analysis of standard stars for linear polarization
 |
Fig. 3 Spectro-polarimetry of the standard star for linear polarization CD-28 13479 (=Hiltner 652) observed during the night 2009-04-04. In the PQ and PU panels, the blue solid lines represent the PQ and PU values after taking into account the combined correction due to the chromatism of the retarder waveplate and the Wollaston prism (i.e., wavelength dependent deviations of the position angle of the fast axis of the retarder waveplate and of the Wollaston prism from their respective nominal values), and the instrumental polarization; all discussed in the text. The error bars of each spectral point are represented in red. The PL panel shows the total fraction of linear polarization, and the bottom right panel shows the position angle of the observed polarization (blue solid lines). These observed values have to be corrected for the FORS2 instrument offset of the respective epoch to be fully consistent with their expected values, measured with FORS1. All dotted black lines show Stokes I expressed in arbitrary units. |
As part of calibration of our measurements, we have carefully analysed spectro-polarimetric observations of standard stars for linear polarization (both the non-polarized ones and those with well known higher polarization values), observed with the same instrument setup, and the same night as our target. Figures 1 and 2 show the measured reduced Stokes PQ and PU profiles of two non-polarized standard stars observed during the same night as our target. From Fig. 1, it is evident that there is a polarization value of ~0.10% both in PQ and PU for the standard star HD 97689 (observed during the night 2010-05-04). This value, obtained after applying correction for the instrument offset during the respective epoch of the observation (discussed below), accounts for an instrumental contribution to the observed polarization in PQ. Figure 2 shows the reduced Stokes PQ and PU profiles of the standard star WD 1620391 observed during the nights 2010-07-25 and 2011-03-28. In the upper panels (corresponding to the epoch 2010-07-25), it can be seen that there is a polarization value of ~0.10% both in PQ and PU, while in the lower panels (for the epoch 2011-03-28) the respective values are a bit lower (~0.05%).
From the observations of the polarized standard stars, observed during the same night as our target, we discovered also that the measured position angles of these stars during some of our observation epochs are different from their corresponding expected values measured using FORS1 by Fossati et al. (2007). This observed offsets clearly demonstrate that the polarimetric optics of the instrument were not correctly aligned during some of our observing epochs. Hence, we have calculated the FORS2 instrument offsets during some epochs of our observation, and the values are depicted in Table 1. Figure 3 shows such a particular case of our spectro-polarimetric measurements of the standard star for linear polarization CD-28 13479 (Hiltner 652) that was obtained during the night 2009-04-04 with grism 300V and filter GC 435, adopting a 0.4′′ slit width. The blue solid lines in the left panels are the measured PQ and PU values (in %) obtained after correcting for the respective instrumental polarization, and the combined wavelength dependent effect for imperfections of the alignment of the fast axis of the retarder wave plate, and of the principal plane of the Wollaston prism. The solid lines in the right panels show the fraction of linear polarization (upper panel), and the position angle (bottom panel) corresponding to the PQ and PU values represented in the left panels. According to Fossati et al. (2007), this star has a fraction of linear polarization (wavelength dependent) of 5.7% in the B band, 6.3% in the V band, 6.1% in the R band, and a position angle of about 179.5°. Hence, for the measured values of the Stokes profiles, the fraction of linear polarization, and the position angle of polarization of this star to be fully consistent with their respective values given by Fossati et al. (2007), they have to be corrected for the FORS2 instrument offset of the respective night (see Table 1).
ESO VLT FORS2 instrument offset during different observation periods.
2.3. Results for Iapetus
Equation (2) above conveys that the error bar for PX is equal to the inverse of the S/N of the flux accumulated in both beams (f ∥ + f ⊥ ) from all exposures obtained at all retarder wave plate positions. The signal-to-noise ratio we achieved during our observation varies from ~830–1250 (on both beams at all positions of the retarder waveplate), which is high enough to obtain polarization measurements with uncertainty levels of ~0.1% per spectral bin (see e.g., Bagnulo et al. 2006a,b).
 |
Fig. 4 Linear polarization of the bright side of Iapetus versus wavelength, observed with FORS2 at the ESO VLT in April 2009 at phase angle 2.90°. In the |
As a validation of the reliability of our measurement uncertainities,we have also systematically calculated the null profiles, i.e., the difference between Stokes profiles obtained from different pairs of exposures, using the relation: ![\begin{equation} N_{X}=\frac{1}{2N} \sum_{j\,=\,1}^{N}(-1)^{(j-1)} \left [\left( \frac{f^{\parallel}-f^{\perp}} {f^{\parallel}+f^{\perp}} \right )_{\alpha_{j}} - \left ( \frac{f^{\parallel}-f^{\perp} } {f^{\parallel}+f^{\perp}} \right )_{\alpha_{j}+ \Delta P}\right], \end{equation}](/articles/aa/full_html/2012/01/aa17870-11/aa17870-11-eq64.png) (3)where ΔP is the difference in the position of the retarder waveplate between two consecutive exposures, and is equal to 45° for the linear polarization measurements, and 90° in the case of circular polarization measurements. These expressions are valid only for an even number of pairs of exposures at different position angles, and could be calculated only for the scientific observations of Iapetus, but not for the polarimetric standard stars discussed above, that were observed only at two position angles of the retarder wave plate for each Stokes parameter. The null profiles should have a Gaussian distribution centered about 0 with the same σ given by Eq. (3). For further technical details of null parameters, we refer the reader to Bagnulo et al. (2009).
(3)where ΔP is the difference in the position of the retarder waveplate between two consecutive exposures, and is equal to 45° for the linear polarization measurements, and 90° in the case of circular polarization measurements. These expressions are valid only for an even number of pairs of exposures at different position angles, and could be calculated only for the scientific observations of Iapetus, but not for the polarimetric standard stars discussed above, that were observed only at two position angles of the retarder wave plate for each Stokes parameter. The null profiles should have a Gaussian distribution centered about 0 with the same σ given by Eq. (3). For further technical details of null parameters, we refer the reader to Bagnulo et al. (2009).
Adopting the perpendicular to the great circle passing through Iapetus and the Sun as the reference direction, as it was the case in Bagnulo et al. (2006a) and Landi Degl’lnnocenti et al. (2007), our measurements are transformed from the instrument reference system (the north celestial pole) to the reference system with the x-axis (the reference direction) perpendicular to the scattering plane, according to the relation: ![\begin{equation} \begin{aligned} P'_{Q} &=(P_{Q}-q_{\rm ins})\cos(2\Theta)+ P_{U}\sin(2\Theta),\\[2mm] P'_{U} &=-(P_{Q}-q_{\rm ins})\sin(2\Theta)+ P_{U}\cos(2\Theta),\\[2mm] P'_{V}&=P_{V} \end{aligned} \end{equation}](/articles/aa/full_html/2012/01/aa17870-11/aa17870-11-eq68.png) (4)with
(4)with 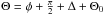 , where Θ0 is the FORS2 instrument offset angle during each epoch of our observation as indicated in Table 1, and φ is the angle between the celestial meridian passing through Iapetus and the great circle passing through the Sun and Iapetus (increased by 90°, so as to have the reference direction perpendicular to the scattering plane). Using Eq. (10) of Landi Degl’lnnocenti et al. (2007), for the nights 2009-04-04, 2010-02-22, 2010-05-04, and 2010-07-25 of our observations, we calculated φ values (at the middle of the series of exposures) of −62.95°, −70.94°, −64.08°, and −67.92°, respectively. The quantity Δ is a combined value for deviations of the fast axis of the retarder waveplate and of the principal plane of the Wollaston prism from their nominal values (both wavelength dependent, (see e.g., Bagnulo et al. 2009), and is tabulated in the ESO instrument webpage1. The quantity qins is a constant polarization value we set to ~0.1% (as discussed above), and accounts for an instrumental contribution to the observed polarization in PQ (in the instrument reference system) that seems to affect spectro-polarimetric observations (Fossati et al. 2007). Without adding it to PQ, we would measure an offset in the PU profile from zero by a (small) constant value, which is in fact consistent with what was observed with FORS1 by Fossati et al. (2007). In Eq. (4) above, the prime index (′) is used to refer to the profiles measured in the reference system associated to the scattering plane.
, where Θ0 is the FORS2 instrument offset angle during each epoch of our observation as indicated in Table 1, and φ is the angle between the celestial meridian passing through Iapetus and the great circle passing through the Sun and Iapetus (increased by 90°, so as to have the reference direction perpendicular to the scattering plane). Using Eq. (10) of Landi Degl’lnnocenti et al. (2007), for the nights 2009-04-04, 2010-02-22, 2010-05-04, and 2010-07-25 of our observations, we calculated φ values (at the middle of the series of exposures) of −62.95°, −70.94°, −64.08°, and −67.92°, respectively. The quantity Δ is a combined value for deviations of the fast axis of the retarder waveplate and of the principal plane of the Wollaston prism from their nominal values (both wavelength dependent, (see e.g., Bagnulo et al. 2009), and is tabulated in the ESO instrument webpage1. The quantity qins is a constant polarization value we set to ~0.1% (as discussed above), and accounts for an instrumental contribution to the observed polarization in PQ (in the instrument reference system) that seems to affect spectro-polarimetric observations (Fossati et al. 2007). Without adding it to PQ, we would measure an offset in the PU profile from zero by a (small) constant value, which is in fact consistent with what was observed with FORS1 by Fossati et al. (2007). In Eq. (4) above, the prime index (′) is used to refer to the profiles measured in the reference system associated to the scattering plane.
 |
Fig. 5 Circular polarization of the bright side of Iapetus versus wavelength, obtained with FORS2 at the ESO VLT during the night 2011-03-28 at a phase angle of 0.77°. The blue dashed curve shows the Stokes |
Figure 4 shows linear spectro-polarimetric measurement of Iapetus’ bright side at a single observing epoch. In the left panels, The red lines in the left panels represent the measured 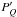 and
and 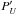 values (in %) after applying the transformation relation given in Eq. (4). The respective null profiles, NU (offseted to + 0.25% for display purposes), and NQ are are shown as blue solid lines, superposed to the statistical error bars reporeted in light blue. This allows one to immediately visualize the points of the null profiles that are different from zero by a quantity higher than the error bar, and thus, to evaluate the reliability of the corresponding points of the Stokes profiles. The right panels of Fig. 4, show the total fraction of linear polarization (top panel), and the observed position angle. As clearly demonstrated in Fig. 4, when
values (in %) after applying the transformation relation given in Eq. (4). The respective null profiles, NU (offseted to + 0.25% for display purposes), and NQ are are shown as blue solid lines, superposed to the statistical error bars reporeted in light blue. This allows one to immediately visualize the points of the null profiles that are different from zero by a quantity higher than the error bar, and thus, to evaluate the reliability of the corresponding points of the Stokes profiles. The right panels of Fig. 4, show the total fraction of linear polarization (top panel), and the observed position angle. As clearly demonstrated in Fig. 4, when 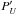 equals zero, the position angle of the polarization plane, computed using Eq. (6) of Bagnulo et al. (2006a), and measured from the axis perpendicular to the scattering plane, equals 90°.
equals zero, the position angle of the polarization plane, computed using Eq. (6) of Bagnulo et al. (2006a), and measured from the axis perpendicular to the scattering plane, equals 90°.
Results of polarimetric observations of the bright side of Iapetus.
 |
Fig. 6
|
To compare our linear spectro-polarimetric measurements of Iapetus with the imaging polarimetry of other objects, we convolved the obtained polarized spectra with the transmission function of the BVRI Bessel filters applying the convolution relation given by Eq. (12) of Fossati et al. (2007), and the results are depicted in Fig. 6.
Figure 5 shows measurement of our circular polarization at a single phase angle. The red solid line represents the average 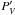 profile (in %) obtained from instrument position angles that differ by 90°. The blue dashed line represents measurement at 0° instrument position angle, while the dotted green line is the measurement at 90° instrument position angle on the sky. The average null profile is found to be scattered around zero within the corresponding error bars of the average Stokes
profile (in %) obtained from instrument position angles that differ by 90°. The blue dashed line represents measurement at 0° instrument position angle, while the dotted green line is the measurement at 90° instrument position angle on the sky. The average null profile is found to be scattered around zero within the corresponding error bars of the average Stokes 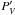 profile, thereby confirming the reliability of our measurement.
profile, thereby confirming the reliability of our measurement.
3. Discussions
Our linear spectro-polarimetric measurements of Iapetus’ bright side against their respective phase angles of observations are given in Fig. 6. The measurements show that the linear degree of Iapetus’ bright side polarization changes with increasing phase angle, from ~−0.90% at 0.77° to ~−0.30% at 5.20°. The polarization of Iapetus’ bright side at 1.0° phase angle obtained by Rosenbush et al. (2002) was ~−0.8%, and the value measured at phase angles between 5.0 and 6.0° was ~−0.2% (see Zellner 1972; Rosenbush et al. 2002; Veverka 1977). The later polarization value is believed to be typical for E-type asteroids 44 Nysa (Rosenbush et al. 2009) and 64 Angelina (Rosenbush et al. 2005), and also for the Galilean satellites, Europa and Ganymede (Rosenbush et al. 1997a), at similar phase angles. Thus, our measurements (at similar phase angles), confirm the same notion as depicted in Table 2. It is worth noting, in particular, that the largest linear polarization at all wavelengths we obtained is at the smallest phase angle 0.77°. The coherent backscattering model (Mishchenko et al. 2000) suggests that polarizations as large as -2.8% can occur near 1.0° phase angle, and such trends of dramatic change in polarization have been observed for some of the Galilean satellites at phase angles of about 0.6 − 0.7° (see Rosenbush et al. 1997a). Hence, our measurement at the 0.77° phase angle is well consistent with such polarization trend.
As for the wavelength dependence of polarization, the variation of Iapetus’ bright side polarization with wavelength is in general less pronounced (see Table 2). Rosenbush et al. (1997a) have also reported that the spectral dependence of polarization of Io, Europa and Ganymede in the BVR filters is weak, and hence, our measurements confirm that such a small wavelength dependence of polarization might be typical for some satellites. However, it is not obvious at present to judge if it offers any significant constraints on the nature of the scattering surface, although Belskaya et al. (2009) have pointed out that, in the case of asteroids, the variation in the observed wavelength dependence of polarization seems to be attributed mainly to the surface composition.
It has been revealed that the larger TNOs like Pluto and Eris display shallow polarimetric phase functions, almost constant over the observed phase angle range (Bagnulo et al. 2008), and possibly indicative for surfaces dominated by large (compared to wavelength) inhomogeneous particles (Belskaya et al. 2008), while the smaller ones show rather steep negative polarization phase functions most likely produced by a mixture of at least two different types of smaller (10–100 μm size) grains of single scattering albedo (Boehnhardt et al. 2004; Bagnulo et al. 2006a).
Comparison of our measurements with those of TNOs (Boehnhardt et al. 2004; Bagnulo et al. 2006a, 2008; Belskaya et al. 2008), within the same phase-angle range, has shown that the polarization of Iapetus’ bright hemisphere seems to be slightly deeper than that of the larger TNOs, and it tends to have a similar value as that of smaller ones particularly around a phase angle of ~1.0°. Larger TNOs are believed to have surfaces dominated by either methane ice or water ice (see, e.g., Barucci et al. 2008; Brown 2008), and hence, the fact that Iapetus’ polarization is deeper than that of these objects clearly demonstrates that polarization is strongly sensitive to a variety of the scattering surface parameters such as particle size, composition, shape (structure), surface texture, refractive indices, etc., apart from surface reflectance of objects, and it is almost impossible to interpret such differences uniquely. Compared to polarimetric measurements Centaurs (Bagnulo et al. 2006a; Belskaya et al. 2010), Iapetus’ polarization is shallower than that of any of the three Centaurs (Chiron, Pholus, and Chariklo), in agreement with the fact that darker surfaces exhibit deeper linear degree of negative polarization than the brighter ones, since these objects are of lower albedo than the trailing hemisphere of Iapetus.
Comparison of our measurements with that of the nucleus of comet 2P/Encke (Boehnhardt et al. 2008) and the main belt object 133P/Elst-Pizarro (Bagnulo et al. 2010) around similar phase angle range of observations, shows that Iapetus has a completely different polarimetric behaviour since the polarimetric phase function of the nucleus of comet 2P/Encke was found to be different from any of other solar system objects, while that of 133P/Elst-Pizarro resembles more likely that of F-type asteroids than icy bodies.
Our measurements of circular polarization of Iapetus’ bright side (see Fig. 5) had the goal to test whether optically active, possibly organic surface material is present on the bright hemisphere that is believed to induce circular polarization of a few percent due to its chiralic character (Sterzik et al. 2010, Rosenbush et al. 2007). Our observed circular polarization depends on the instrument position angle, and in particular it changes in sign when the instrument is rotated by 90°(see Fig. 5). As discussed by Bagnulo et al. (2009), this is attributed to an instrumental effect, and most likely it is a symptom of cross-talk from linear to circular polarization. If we assume that the only instrumental effect is pure cross-talk from linear to circular polarization, then the average of the 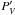 profiles observed at the two instrument position angles (solid red line in Fig. 5) should be intrinsic to the source. In a strict sense, this value is a non-zero, as in particular can be seen clearly around shorter wavelengths. Hence, given the fact that circular polarization is typically small (see, e.g., Rosenbush et al. 1997b), such a small non-zero value of our circular polarization is not unexpected. However, we must also remark that the FORS instrument lacks a sufficiently accurate characterisation to validate a detection of circular polarization at the level of a few units in 10-4 in the continuum, even using our specific observing technique.
profiles observed at the two instrument position angles (solid red line in Fig. 5) should be intrinsic to the source. In a strict sense, this value is a non-zero, as in particular can be seen clearly around shorter wavelengths. Hence, given the fact that circular polarization is typically small (see, e.g., Rosenbush et al. 1997b), such a small non-zero value of our circular polarization is not unexpected. However, we must also remark that the FORS instrument lacks a sufficiently accurate characterisation to validate a detection of circular polarization at the level of a few units in 10-4 in the continuum, even using our specific observing technique.
4. Conclusions
We have measured the spectral polarization of the bright side of Iapetus with an accuracy better than ~0.1%. The linear degree of negative polarization decreases with increasing phase angle from −0.9% at 0.77° to −0.3% at 5.2°. The magnitude of the polarization increases monotonically with wavelength across the wavelength range. The fact that our polarimetric phase function of Iapetus is fully in agreement with previous measurements (Zellner 1972; Rosenbush et al. 2002; Veverka 1977), and with other high albedo objects (icy Galilean satellites, E-type asteroids, etc.), it offers an additional line of evidence for the light scattering behaviour of small solar system bodies that have high surface albedo and (or) that have surfaces rich in water ice. To confirm the notion of Rosenbush et al. (2002) that Iapetus’ bright hemisphere displays two branches of negative polarization, one called the polarization opposition effect (occurring at very small phase angles), and the other one called the normal branch of negative polarization (at relatively higher phase angles), measurements at low phase angles would be highly needed. Apart from being a test for optically active (chiral) organic molecules, circular polarization is also believed to be sensitive to the shape, structure and composition of the scattering surfaces (Rosenbush et al. 2007), and thus, our measurement of circular polarization of Iapetus’ bright hemisphere combined with its linear polarization measurements would allow one to translate this polarimetric characteristic of typical water ice to the light scattering behaviour of other solar system bodies of dominant water ice surface constitution.
Acknowledgments
The authors sincerely thank Dr. Jay Goguen (the referee) for the help in his useful and detailed report to significantly improve the quality of this paper. C. Ejeta acknowledges the PhD studentiship supported by the Helmholtz Association through the research alliance “Planetary Evolution and Life”, and he thanks Armagh observatory for the kind hospitality during his research visits.
References
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Bagnulo, S., Boehnhardt, H., Muinonen, K., et al. 2006a, A&A, 450, 1239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Mason, E., et al. 2006b, A&A, 450, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Belskaya, I., Muinonen, K., et al. 2008, A&A, 491, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landolfi, M., Landstreet, J. D., et al. 2009, PASP, 121, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Tozzi, G. P., Boehnhardt, H., Vincent, J.-B., & Muinonen, K. 2010, A&A, 514, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barucci, M. A., Brown, M. E., Emery, J. P., & Merlin, F. 2008, in The Solar System Beyond Neptune, ed. A. Barucci, H. Boehnhard, P. Cruiksank, & A. Morbidelli (Tucson: University of Arizona Press), 143 [Google Scholar]
- Belskaya, I., Bagnulo, S., Muinonen, K., et al. 2008, A&A, 479, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belskaya, I. N., Levasseur-Regourd, A.-C., Cellino, A., et al. 2009, Icarus, 199, 97 [Google Scholar]
- Belskaya, I. N., Bagnulo, S., Barucci, M. A., et al. 2010, Icarus, 210, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Boehnhardt, H., Bagnulo, S., Muinonen, K., et al. 2004, A&A, 415, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boehnhardt, H., Tozzi, G. P., Bagnulo, S., et al. 2008, A&A, 489, 1337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, M. E. 2008, The Largest Kuiper Belt Objects, ed. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, A. Morbidelli, & R. Dotson, 335 [Google Scholar]
- Fossati, L., Bagnulo, S., Mason, E., & Landi Degl’lnnocenti, E. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 503 [Google Scholar]
- Izzo, C., de Bilbao, L., Larsen, J., et al. 2010, in SPIE Conf. Ser., 7737 [Google Scholar]
- Landi Degl’lnnocenti, E., Bagnulo, S., & Fossati, L. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 495 [Google Scholar]
- Mishchenko, M., Luck, J.-M., & Nieuwenhuizen, T. 2000, J. opt. soc. Am. A, 17, 888 [Google Scholar]
- Rosenbush, V., Kiselev, N., Avramchuk, V., & Mishchenko, M. 2002, in Optics of Cosmic Dust, ed. G. Videen, & M. Kocifaj, 191 [Google Scholar]
- Rosenbush, V. K., Avramchuk, V. V., Rosenbush, A. E., & Mishchenko, M. I. 1997a, ApJ, 487, 402 [Google Scholar]
- Rosenbush, V. K., Shakhovskoj, N. M., & Rosenbush, A. E. 1997b, Earth Moon and Planets, 78, 381 [Google Scholar]
- Rosenbush, V. K., Kiselev, N. N., Shevchenko, V. G., et al. 2005, Icarus, 178, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V., Kolokolova, L., Lazarian, A., Shakhovskoy, N., & Kiselev, N. 2007, Icarus, 186, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., Shevchenko, V. G., Kiselev, N. N., et al. 2009, Icarus, 201, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., & Denk, T. 2010, Science, 327, 432 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Squyres, S. W., & Sagan, C. 1983, Nature, 303, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Veverka, J. 1977, in Planetary Satellites, ed. J. A. Burns, IAU Colloq. 28, 210 [Google Scholar]
- Zellner, B. 1972, ApJ, 174, L107 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spectro-polarimetry of the non-polarized standard star HD 97689 observed with FORS2 during night 2010-05-04. The measured reduced Stokes PQ and PU profiles, both with a value of ~ 0.1% are indicated in solid blue lines, with the statistical error bars in red. In both panels, the black dotted lines show the total flux (in arbitrary units), and is not corrected for the instrument + telescope transmission functions. |
| In the text | |
 |
Fig. 2 Same as Fig. 1, for the non polarized standard star WD 1620391 observed with FORS2 during nights 2010-07-25 (upper panel) and 2011-03-28 (lower panel). In the upper panels, it can be seen that the polarization value is ~0.1% both in Stokes PQ and PU, while it is less in the case of lower panel, ~0.05%. |
| In the text | |
 |
Fig. 3 Spectro-polarimetry of the standard star for linear polarization CD-28 13479 (=Hiltner 652) observed during the night 2009-04-04. In the PQ and PU panels, the blue solid lines represent the PQ and PU values after taking into account the combined correction due to the chromatism of the retarder waveplate and the Wollaston prism (i.e., wavelength dependent deviations of the position angle of the fast axis of the retarder waveplate and of the Wollaston prism from their respective nominal values), and the instrumental polarization; all discussed in the text. The error bars of each spectral point are represented in red. The PL panel shows the total fraction of linear polarization, and the bottom right panel shows the position angle of the observed polarization (blue solid lines). These observed values have to be corrected for the FORS2 instrument offset of the respective epoch to be fully consistent with their expected values, measured with FORS1. All dotted black lines show Stokes I expressed in arbitrary units. |
| In the text | |
 |
Fig. 4 Linear polarization of the bright side of Iapetus versus wavelength, observed with FORS2 at the ESO VLT in April 2009 at phase angle 2.90°. In the |
| In the text | |
 |
Fig. 5 Circular polarization of the bright side of Iapetus versus wavelength, obtained with FORS2 at the ESO VLT during the night 2011-03-28 at a phase angle of 0.77°. The blue dashed curve shows the Stokes |
| In the text | |
 |
Fig. 6
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


