| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117503 | |
| Published online | 13 January 2012 | |
Solar wind bulk velocity fluctuations acting as velocity space diffusion on comoving ions
1 Argelander Institut für Astronomie der Universität Bonn, Abteilung f. Astrophysik und Extraterrestrische Forschung, Auf dem Huegel 71, 53121 Bonn, Germany
2 Lebedev Physical Institute, Leninskii Prospect 53, 117924 Moscow, Russia
Received: 17 June 2011
Accepted: 30 October 2011
From most in-situ plasma observations made in the outer heliosphere it became evident that above the injection border of pick-up ions (≃1 keV), an extended suprathermal ion tail is found which in most cases can be fitted by a power law with velocity power indices of (−6) ≤ γv ≤ (−4). As has been shown by theory such energetic ion tails cannot be explained by Fermi-2 type velocity diffusion, since in the outer heliosphere both Alfvenic and magnetoacoustic turbulences become too weak. Here we come to a new solution of this unsolved problem by studying the action of solar wind bulk velocity fluctuations on ions co-moving with the wind. As we show the passage of such fluctuations results in energization of each individual ion and systematic evolution of the ion distribution function towards suprathermal tails. From the basic knowledge that we can obtain on this process we can calculate the velocity divergence of the ion phasespace flow and thus can derive a velocity diffusion operator. As we can show here this operator leads to a velocity diffusion coefficient proportional to the square of the ion velocity and, when employed in the phasespace transport equation, together with terms for convective changes, cooling processes and pick-up ion injection, interestingly enough, permits to find solutions for suprathermal power law tails with power indices of γv ≃ −5 as very often observed.
Key words: magnetohydrodynamics (MHD) / shock waves / plasmas / solar wind
© ESO, 2012
1. Introduction
Many independent in-situ spacecraft observations in the inner and outer heliosphere show ion distribution functions which in specific energy ranges are power laws. Most interesting, since unexplained up to now are suprathermal ions in the energy region above the pick-up ion (PUI) injection border, say between 1 to 10 keV. In this region power laws with power indices γv ≃ −5 have been found (see Gloeckler 2003; Fisk & Gloeckler 2006; Dayeh et al. 2009; Hill et al. 2009). Velocity space diffusion in form of Fermi-2 acceleration by nonlinear ion interactions with counterstreaming Alfvenic or magnetosonic, convected turbulences has been shown as being too ineffective to energize freshly injected PUIs (see Fahr et al. 2009). Even a consistent description of turbulence generation by freshly injected PUIs and energization of PUIs by nonlinear interaction with this turbulence cannot produce these tails as shown by Chalov et al. (2004, 2006). Therefore some alternative ideas have more recently come up that perhaps could bring a solution here. One is connected with the injection of low-energy anomalous cosmic rays into the PUI regime at higher energies of about 100 keV (Fahr et al. 2009), another with the hope for a stationary equilibrium of an ion plasma interacting with compressive turbulence in a thermally isolated system (Fisk & Gloeckler 2007, 2008), and a third one with the study of ion energization due to travelling shocks passing over a background ion population (Zhang 2010; Fahr & Siewert 2011).
In the following we shall make use of this latter idea and shall formulate a general description of these bulk velocity jumps for application in the more conventional framework of diffusive theory, obtaining a new type of velocity space diffusion. We are not yet aiming to explain specific phenomena such as v-5 ion power tails in the heliosphere, which however might emerge from our theory as a by-result.
2. Theoretical approach
In the recent paper by (Fahr & Siewert 2011), kinetic relations of ions at repeated passages over solar wind bulk velocity jumps had been derived. Under the conservation of two characteristic ion invariants specific relations between the ion velocity components upstream and downstream of this bulk velocity structure were obtained, which not only permit to determine the unique positions in velocity space to which upstream ions are translocated when passing from upstream to downstream, but in addition fulfilling the continuity of differential phasespace flux according to Liouville’s theorem. This also allowed to obtain the associated velocity distribution function, expressed as a function of the upstream distribution. Without going into too many details, the theory behind the following kinetic considerations is based on the assumption that the magnetic moment is conserved when ions cross a shock-like structure, which is valid as long as the magnetic field which causes the individual ions to gyrate does not undergo rapid reorientation processes (as pointed out by Fahr & Siewert 2010). An approach like this is required since conventional MHD is unable to describe the behaviour of the distribution function at a shock wave, which appears as a discontinuity in the solutions of the MHD equations. Full diffusive theory, on the other hand, is likewise unable to predict the behaviour of the distribution function in the absence of additional explicit model assumptions on the microphysics of the shock transition layer. Therefore, we have developed a semikinetic model, which allows to merge kinetic and MHD aspects of shock waves, with additional modeling input based on the conservation of classical invariants (Siewert & Fahr 2008).
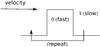 |
Fig. 1 A geometrical representation of the “double-hump” shock structure, where two inverse shock transitions follow upon each other, which ultimately returns ions back to the initial upstream flow configuration. |
Here, we begin by taking their results and consider the effect on ion speeds of a second passage of a reverse bulk velocity jump over such an ion ensemble (i.e. one single double-hump structure, see Fig. 1). At the first travelling jump, the plasma bulk velocity is reduced from U1 to U2 = U1/sfs, while at the second jump the bulk velocity is increased again to U1 = U2/ssf, where sfs = 1/ssf are the shock-associated compression ratios. The total velocity gain after passage of this double-hump structure and subsequent re-isotropisation of the ion population by pitchangle scattering is then defined by means of Eqs. (25) and (26) of Fahr & Siewert (2011) and is given by:
 (1)where the above expression contains the two following shock-associated functions
(1)where the above expression contains the two following shock-associated functions
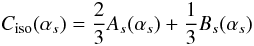 (2)with
(2)with  (3)and
(3)and 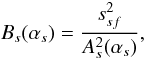 (4)and the corresponding relations for the opposite direction are obtained by ssf → sfs and αs → αf.
(4)and the corresponding relations for the opposite direction are obtained by ssf → sfs and αs → αf.
Hereby the tilt angles between the co-convected frozen-in field and the shock surface normal are denoted by αs (slow side) and αf (fast side), respectively (see Fig. 2). As an abbreviation we may for practical reasons use here the notation 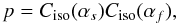 (5)and thus we obtain the energy gain per mass as given by
(5)and thus we obtain the energy gain per mass as given by 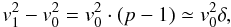 (6)with δ = p − 1 ≪ 1. To give an idea how extended is the validity range of this approach, one obtains
(6)with δ = p − 1 ≪ 1. To give an idea how extended is the validity range of this approach, one obtains 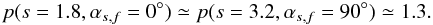 (7)This is motivated by the energy-driving mechanism behind this process (i.e.bulk velocity fluctuations with ΔU/U ≪ 1; ssf = 1 + ϵ; ϵ ≪ 1), i.e. where the velocity gains after individual double jump passings are small. After some elementary arithmetics, it follows that
(7)This is motivated by the energy-driving mechanism behind this process (i.e.bulk velocity fluctuations with ΔU/U ≪ 1; ssf = 1 + ϵ; ϵ ≪ 1), i.e. where the velocity gains after individual double jump passings are small. After some elementary arithmetics, it follows that 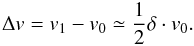 (8)The corresponding change in the velocity distribution function f(v) per double-hump passage can be derived starting from Eq. (35) of Fahr & Siewert (2011):
(8)The corresponding change in the velocity distribution function f(v) per double-hump passage can be derived starting from Eq. (35) of Fahr & Siewert (2011):
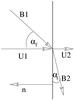 |
Fig. 2 The geometrical configuration at the shock. |
 (9)Then, using again the condition that δ ≪ 1, one derives from the above Eq. (9), neglecting terms nonlinear in δ, the following approximate relation
(9)Then, using again the condition that δ ≪ 1, one derives from the above Eq. (9), neglecting terms nonlinear in δ, the following approximate relation 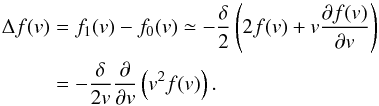 (10)Then, combining Eqs. (8) and (10) and replacing small differences by differentials, we find
(10)Then, combining Eqs. (8) and (10) and replacing small differences by differentials, we find ![\begin{equation} \frac{\Delta f(v)}{\Delta v} \approx \frac{\partial f(v)}{\partial v} = -\frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ v^{2}f(v)\right]. \end{equation}](/articles/aa/full_html/2012/01/aa17503-11/aa17503-11-eq32.png) (11)To derive the full phasespace transport equation, we now derive the velocity space divergence of the differential velocity space flux. For ions distributed according to f(v) and undergoing bulk velocity fluctuations, this flux is given by
(11)To derive the full phasespace transport equation, we now derive the velocity space divergence of the differential velocity space flux. For ions distributed according to f(v) and undergoing bulk velocity fluctuations, this flux is given by  (12)where τs is the time period characterizing the shock occurence rate, i.e. the average time between two velocity changes by Δv caused by bulk velocity jumps. Here one can adopt this period to be given in the selfsuggesting form by τs = L/ΔU, where L is the mean radial distance between consecutive travelling shocks, and ΔU = U0 − U1 is the mean speed of the travelling bulk velocity structure in the solar rest frame. Then the jump-induced velocity space divergence of the differential flux is given by
(12)where τs is the time period characterizing the shock occurence rate, i.e. the average time between two velocity changes by Δv caused by bulk velocity jumps. Here one can adopt this period to be given in the selfsuggesting form by τs = L/ΔU, where L is the mean radial distance between consecutive travelling shocks, and ΔU = U0 − U1 is the mean speed of the travelling bulk velocity structure in the solar rest frame. Then the jump-induced velocity space divergence of the differential flux is given by ![\begin{equation} \mathrm{div}_{\vec{v}} F(v) = \frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ v^{2}\left[\frac{\Delta U\delta }{2L}\frac{\partial }{\partial v}\left( v^{2}f(v)\right) \right]\right], \end{equation}](/articles/aa/full_html/2012/01/aa17503-11/aa17503-11-eq39.png) (13)where we have used the divergence operator in spherical coordinates for an angle-isotropic distribution function. This expression provides one term of the phasespace transport equation for pick-up ions. Introducing the additional terms for pick-up ion injection, convective changes of the ion distribution function in configuration space, and ion cooling at convection with the bulk solar wind in spherically symmetric flows, we finally find for the pitchangle-isotropic distribution function the following complete phasespace transport equation (for comparison see Fahr & Fichtner 2011)
(13)where we have used the divergence operator in spherical coordinates for an angle-isotropic distribution function. This expression provides one term of the phasespace transport equation for pick-up ions. Introducing the additional terms for pick-up ion injection, convective changes of the ion distribution function in configuration space, and ion cooling at convection with the bulk solar wind in spherically symmetric flows, we finally find for the pitchangle-isotropic distribution function the following complete phasespace transport equation (for comparison see Fahr & Fichtner 2011) ![\begin{equation} \begin{split} \frac{\partial f(v)}{\partial t} =& -\frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ \left(\frac{\Delta U\delta }{2L}\right)v^{2}\frac{\partial }{\partial v}\left(v^{2}f(v)\right) \right] \\ &-\bar{U}\frac{\partial f(v)}{\partial r} +\frac{1}{v^{2}}\frac{\partial }{\partial v}\left(\frac{v^{3}\bar{U}}{r}f\right) +S(r,v,t). \end{split} \label{eq-transport} \end{equation}](/articles/aa/full_html/2012/01/aa17503-11/aa17503-11-eq40.png) (14)Here the first term on the right hand side (RHS) replaces the unspecified velocity-diffusion term used by Fahr & Fichtner (2011), the second term describes the standard convective change of f, the third term the magnetic ion cooling of ions comoving with the bulk, and the fourth term, S(r,v,t), is the pick-up ion injection function. The velocity
(14)Here the first term on the right hand side (RHS) replaces the unspecified velocity-diffusion term used by Fahr & Fichtner (2011), the second term describes the standard convective change of f, the third term the magnetic ion cooling of ions comoving with the bulk, and the fourth term, S(r,v,t), is the pick-up ion injection function. The velocity 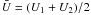 , in case of equally extended fast and slow bulk flow trains, is the average bulk speed by which ions are transported radially outwards to larger solar distances.
, in case of equally extended fast and slow bulk flow trains, is the average bulk speed by which ions are transported radially outwards to larger solar distances.
2.1. The steady state solution
The above equation possesses a steady-state solution (i.e. 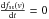 ), in the absence of source or sink terms (i.e. in regions where S(r,v ≶ U,t) = 0). As one can easily verify, this “saturated” solution of Eq. (14) for the velocity distribution function takes a power law form, fss(v) ~ v − k, with k = 3, i.e. just the specific form of an equilibrium distribution which was also obtained in recent papers by Zhang (2010) and Fahr & Siewert (2011). However, this study also includes the cooling term, which is not considered by the aforementioned papers. This means that cooling processes can be compensated by adequate energization through bulk velocity fluctuations, keeping the above derived power law form of a distribution function stable as soon as it has developed in the plasma.
), in the absence of source or sink terms (i.e. in regions where S(r,v ≶ U,t) = 0). As one can easily verify, this “saturated” solution of Eq. (14) for the velocity distribution function takes a power law form, fss(v) ~ v − k, with k = 3, i.e. just the specific form of an equilibrium distribution which was also obtained in recent papers by Zhang (2010) and Fahr & Siewert (2011). However, this study also includes the cooling term, which is not considered by the aforementioned papers. This means that cooling processes can be compensated by adequate energization through bulk velocity fluctuations, keeping the above derived power law form of a distribution function stable as soon as it has developed in the plasma.
2.2. A more general formulation in terms of diffusion
This rather stiff and flat steady-state ion distribution fss obviously is not reflected in heliospheric space data (where power laws with significantly different indices are observed), meaning that saturation between cooling and heating in the above required form is not fully established in the inner heliosphere. Therefore we now want to study a more general solution resulting from that off-equilibrium condition, which is described by the complete phasespace transport equation as used by Fahr & Fichtner (2011) in the form 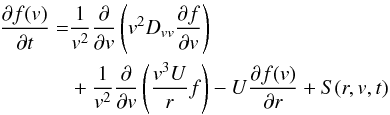 (15)here, the first term on the RHS of Eq. (15) was thought (without giving details) to describe Fermi-2 acceleration due to quasilinear particle interactions with Alfven turbulence (see Schlickeiser 1989) which, at larger distances (r ≥ 5 AU), is however considered to be too ineffective compared to the other terms (see Fisk & Gloeckler 2008; Fahr et al. 2009).
(15)here, the first term on the RHS of Eq. (15) was thought (without giving details) to describe Fermi-2 acceleration due to quasilinear particle interactions with Alfven turbulence (see Schlickeiser 1989) which, at larger distances (r ≥ 5 AU), is however considered to be too ineffective compared to the other terms (see Fisk & Gloeckler 2008; Fahr et al. 2009).
Instead of this conventional, ineffective diffusion term, we now derive a new diffusion term, based on the bulk velocity formalism described above. Comparing Eqs. (15) with (14), one immediately sees that we may identify a new diffusion operator by evaluating the first term in Eq. (14),
![\begin{equation} \begin{split} & \frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ \frac{\Delta U\delta }{2L}v^{2}\frac{\partial }{\partial v}\left( v^{2}f(v)\right) \right]= \\ & \qquad\,\,\frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ \frac{\Delta U\delta }{2L}v^{4}\frac{\partial f(v)}{\partial v}\right] +\frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ \frac{\Delta U\delta }{L}v^{3}f(v)\right], \end{split} \end{equation}](/articles/aa/full_html/2012/01/aa17503-11/aa17503-11-eq51.png) (16)which can be identified as a sum of a pure diffusion-type term ( ∝
(16)which can be identified as a sum of a pure diffusion-type term ( ∝ 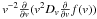 ) and a heating term ( ∝
) and a heating term ( ∝ 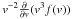 ). This now brings us to the following modified transport equation for pick-up ions undergoing bulk velocity fluctuations:
). This now brings us to the following modified transport equation for pick-up ions undergoing bulk velocity fluctuations: ![\begin{equation} \begin{split} \frac{\partial f(v)}{\partial t} =\,& \frac{-1}{v^{2}}\frac{\partial}{\partial v}\left[ v^2 D_{vv}^{\Delta U}(v)\frac{\partial f(v)}{\partial v}\right] +S(r,v,t) \\ &+ \frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ \left(\frac{\bar{U}}{r}-\frac{\Delta U\delta }{L}\right)v^{3}f(v)\right] -\bar{U}\frac{\partial f(v)}{\partial r}, \end{split} \label{eq-diff-1} \end{equation}](/articles/aa/full_html/2012/01/aa17503-11/aa17503-11-eq55.png) (17)with a new diffusion coefficient defined by
(17)with a new diffusion coefficient defined by  (18)which is connected with a specific velocity dependence of the form
(18)which is connected with a specific velocity dependence of the form 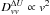 , and which has just the same principle form as one of the alternative models used in a comparative study carried out in a most recent paper by Fahr & Fichtner (2011). This specific model was derived for an idealistic steady state equilibrium between turbulence driving by pick-up ions and pick-up ion energization by velocity diffusion, suggesting that this mechanism might result in the generation of the velocity fluctuations introduced as motivation earlier in this study (see their Eq. (24) for PUI-interaction with selfgenerated turbulence).
, and which has just the same principle form as one of the alternative models used in a comparative study carried out in a most recent paper by Fahr & Fichtner (2011). This specific model was derived for an idealistic steady state equilibrium between turbulence driving by pick-up ions and pick-up ion energization by velocity diffusion, suggesting that this mechanism might result in the generation of the velocity fluctuations introduced as motivation earlier in this study (see their Eq. (24) for PUI-interaction with selfgenerated turbulence).
It is furthermore of interest that the influence of bulk velocity fluctuations not only leads to the above mentioned velocity diffusion, but also automatically provides an additional term similar to the cooling term derived by Fahr & Fichtner (2011). In the above Eq. (15), the first two terms are contracted into one, resulting in the interesting form ![\begin{equation} \left| \frac{\partial f}{\partial t}\right| _{\rm cool} = \left(\frac{\bar{U}}{r}-\frac{\Delta U\delta }{L}\right)\frac{1}{v^{2}}\frac{\partial }{\partial v}\left[ v^{3}f(v)\right], \label{eq-heat-cool} \end{equation}](/articles/aa/full_html/2012/01/aa17503-11/aa17503-11-eq58.png) (19)where the first term represents the conventional contribution to the cooling, while the second one originates from the influence of bulk velocity fluctuations with a sign opposite to the first one, i.e. describing a heating process. While the conventional cooling fades off with 1/r, the “heating term” is constant in magnitude. Therefore, the “effective” cooling becomes weaker with increasing solar distance.
(19)where the first term represents the conventional contribution to the cooling, while the second one originates from the influence of bulk velocity fluctuations with a sign opposite to the first one, i.e. describing a heating process. While the conventional cooling fades off with 1/r, the “heating term” is constant in magnitude. Therefore, the “effective” cooling becomes weaker with increasing solar distance.
 |
Fig. 3 The relevant factor of the cooling amplitude (ϵcool) as a function of solar distance, using Uslow = 400 km s-1, sfs = 1.4 and L = 2 AU. |
Of special interest are situations where the cooling becomes ineffective, or may even transform into an effective heating process. First, we note that for a power law distribution v − k, one “turnover point”, i.e. a point where Eq. (19) switches signs, defined by 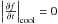 , is characterised by k = 3, with softer (k > 3) distribution functions resulting in a cooling-dominated system, while harder (k < 3) distribution functions result in the cooling process turning over into heating. However, according to all existing models and observations (see e.g. Gloeckler 2003), the solar wind distribution function is uniformly softer than the turnover index (with realistic power indices found in the interval 4 ≤ k ≤ 6), exclusively resulting in a cooling-dominated system.
, is characterised by k = 3, with softer (k > 3) distribution functions resulting in a cooling-dominated system, while harder (k < 3) distribution functions result in the cooling process turning over into heating. However, according to all existing models and observations (see e.g. Gloeckler 2003), the solar wind distribution function is uniformly softer than the turnover index (with realistic power indices found in the interval 4 ≤ k ≤ 6), exclusively resulting in a cooling-dominated system.
Another possibility for the cooling to become ineffective is to assume that the difference between heating and cooling amplitudes changes sign. Defining the relevant factor of the cooling amplitude 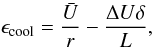 (20)we see that the “turnover distance” (ϵcool(rto) = 0) is therefore given by
(20)we see that the “turnover distance” (ϵcool(rto) = 0) is therefore given by 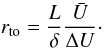 (21)This equation is a quantitative formulation of the earlier result that cooling is decreasingly efficient at large solar distances, now compensated by the opposite-sign contribution due the bulk velocity fluctuations mechanism. To study the behaviour of this resulting equation, we present Eq. (20) in Fig. 3 for a set of typical solar wind parameters extracted from Richardson et al. (1995). This figure proves that the cooling process may indeed flip its sign, resulting in a heating process within o(100) AU, and that, depending on the magnetic field orientation, this process may appear in the inner heliosphere.
(21)This equation is a quantitative formulation of the earlier result that cooling is decreasingly efficient at large solar distances, now compensated by the opposite-sign contribution due the bulk velocity fluctuations mechanism. To study the behaviour of this resulting equation, we present Eq. (20) in Fig. 3 for a set of typical solar wind parameters extracted from Richardson et al. (1995). This figure proves that the cooling process may indeed flip its sign, resulting in a heating process within o(100) AU, and that, depending on the magnetic field orientation, this process may appear in the inner heliosphere.
 |
Fig. 4 The turnover distance rto according to Eq. (21), with rto restricted to realistic termination shock distances (also covering the heliotail distance). |
Finally, we study the behaviour of the fluctuation-induced heating process under varying solar wind parameters. In Fig. 4, we present the turnover point (i.e. the root) of Eq. (21) as a function of the parameters s (i.e. the strength of the fluctuations) and L (i.e. a measure for the average distance between velocity jump structures). We see that heating starts to dominate the system for increasingly shorter distances with an increase of the compression parameter s. In addition to this, we see that the magnetic field orientation similarly has a strong influence on the distances where the cooling processes is overcompensated by the heating due to multiple consecutive shock transitions, with parallel shocks being clearly favored in terms of a close heating process.
3. Conclusions
We have studied the action of solar wind bulk velocity fluctuations stochastically passing over ions that are co-convected with the wind while keeping pitch-angle isotropic distribution functions. As we could show a statistically relevant set of bulk velocity fluctuations acts on these ions, when judged in terms of a phasespace transport equation, like the sum of two terms, namely a conventional velocity diffusion term with a velocity diffusion coefficient 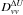 proportional to the square of the ion velocity and a heating term describing an energy gain whenever ions are distributed according to power laws steeper than a velocity-power index of κv = (−3). The latter, however, is always fulfilled in a spherically diverging solar wind in which ion spectra tend towards, but never reach from below power spectra with spectral indices of (−3).
proportional to the square of the ion velocity and a heating term describing an energy gain whenever ions are distributed according to power laws steeper than a velocity-power index of κv = (−3). The latter, however, is always fulfilled in a spherically diverging solar wind in which ion spectra tend towards, but never reach from below power spectra with spectral indices of (−3).
As turns out from our studies here, the diffusion coefficient 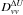 induced by stochastic bulk velocity fluctuations is constant in its magnitude with solar distance and thus its relevance is very different from diffusion coefficients connected with nonlinear wave-particle interactions falling off with distance, since the wave amplitudes are rapidly decreasing (for estimates see Fahr et al. 2009). Thus at larger distances when the relevance of cooling disappears compared to diffusion, then the ion spectra should clearly tend towards ( − 3)-power spectra, as can be seen from Eq. (17). More quantitative results can only be obtained from the solution of a corresponding phasespace transport equation in the form developed by Fahr & Fichtner (2011). At this state of our present work we are not yet able to present solutions of the full phasespace transport Eq. (17) including the newly developed energy diffusion process induced by bulk velocity jumps, but in the nearest future we intend to deliver such solutions of this partial differential equation of second order. Here we shall instead only briefly discuss some interesting new aspects of this new energy-diffusion process in contrast to conventional nonlinear wave-particle diffusion processes as studied since Isenberg (1987). While Isenberg (1987) considers solar wind convected MHD turbulences of Alfvenic type with turbulence amplitudes falling off inversely proportional with the solar distance, in our case here the relevant driving amplitude is the solar wind bulk velocity fluctuation ΔU which can be assumed to be constant in magnitude with distance (see Richardson et al. 2008).
induced by stochastic bulk velocity fluctuations is constant in its magnitude with solar distance and thus its relevance is very different from diffusion coefficients connected with nonlinear wave-particle interactions falling off with distance, since the wave amplitudes are rapidly decreasing (for estimates see Fahr et al. 2009). Thus at larger distances when the relevance of cooling disappears compared to diffusion, then the ion spectra should clearly tend towards ( − 3)-power spectra, as can be seen from Eq. (17). More quantitative results can only be obtained from the solution of a corresponding phasespace transport equation in the form developed by Fahr & Fichtner (2011). At this state of our present work we are not yet able to present solutions of the full phasespace transport Eq. (17) including the newly developed energy diffusion process induced by bulk velocity jumps, but in the nearest future we intend to deliver such solutions of this partial differential equation of second order. Here we shall instead only briefly discuss some interesting new aspects of this new energy-diffusion process in contrast to conventional nonlinear wave-particle diffusion processes as studied since Isenberg (1987). While Isenberg (1987) considers solar wind convected MHD turbulences of Alfvenic type with turbulence amplitudes falling off inversely proportional with the solar distance, in our case here the relevant driving amplitude is the solar wind bulk velocity fluctuation ΔU which can be assumed to be constant in magnitude with distance (see Richardson et al. 2008).
While the wave-induced velocity diffusion coefficient used by Isenberg and successors (Isenberg 1987) falls off in its magnitude with (1/r) and shows a velocity dependence by (vγ − 1) = (v2/3), in our derivation here we find a constant magnitude of the diffusion coefficient and velocity dependence by (v2). This already qualitatively demonstrates that this new type of diffusion, compared to the wave-induced one, keeps a constant efficiency with solar distance and tends to increase comparatively faster with ion velocity. The effect of the latter virtue has recently been studied by Fahr & Fichtner (2011), who have compared solutions of ion distributions resulting under the action of different velocity-dependences of the diffusion coefficient. As shown by them, especially the v2-dependence of the diffusion coefficient at solar distances between 4 and 8 AU practically leads to (−5)-velocity power laws for the resulting ion distribution and thus comes very close to what is observed (see Gloeckler 2003).
In fact, Fisk & Gloeckler (2006, 2007, 2008) have demonstrated that, under specific assumptions for the compressive plasma turbulence, ( − 5)-power laws emerge in energy regions above 100 keV. The formalism presented here allows to describe power law distributions with comparable indices in energy regions below this boundary, perhaps serving as a complementing mechanism which allows to extend power laws to much smaller energies (where no experimental data is available), and maybe also to conserve the original power index far away from the regions where the tails are produced.
On the other hand, as we could show in Fig. 3, the new type of diffusion studied here inherently also contains a term acting similar to the normal cooling term (see Eq. (17)), but has an opposite sign for distribution functions falling off steeper than with (v-3). This means that power laws with spectral indices close to γ = (−5), which are established at medium solar distances of 6 to 8 AU, automatically lead to the situation that the usual omnipresent cooling then is more and more compensated by a heating, so that at distances beyond 40 AU (see Fig. 3), there are regions with no cooling at all. In these regions, however, as manifest from Eq. (17), the ion distribution function needs to tend to a power law with a velocity index of γ = (−3). In the nearest future, however, we shall aim at deriving continuous solutions from solving the full transport Eq. (17).
The theoretical approach used in this paper is based on the assumption of a stochasticity of bulk velocity actions on ions at their passage from small to large solar distances. That means, the average ion described by the distribution function derived in this paper should have seen a statistic sample of consecutive bulk velocity fluctuations. This requires that the jump repetition time period τs ≃ L/ΔU should be small compared to the total ion passage time τr = r/U meaning that L/ΔU ≪ r/U. This latter condition can, however, only be fulfilled at solar distances larger than a critical distance rc with r ≥ rc = LU/ΔU.
Acknowledgments
This work was partially supported by DFG project Si-1550/2-1, DFG/RFBR grant 436 RUS 113/110/0-4 and by the program “Plasma processes in the solar system” of the Russian Academy of Sciences.
References
- Chalov, S. V., Alexashov, D. B., & Fahr, H. J. 2004, A&A, 416, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chalov, S. V., Alexashov, D. B., & Fahr, H.-J. 2006, Astrophys. Space Sci. Trans., 2, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dayeh, M. A., Desai, M. I., Dwyer, J. R., et al. 2009, ApJ, 693, 1588 [Google Scholar]
- Fahr, H.-J., & Fichtner, H. 2011, A&A, 533, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H.-J., & Siewert, M. 2010, Astrophys. Space Sci. Trans., 7, 1 [NASA ADS] [Google Scholar]
- Fahr, H.-J., & Siewert, M. 2011, A&A, 527, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H., Chashei, I. V., & Verscharen, D. 2009, A&A, 505, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2006, ApJ, 640, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2007, PNAS, 104, 5749 [NASA ADS] [CrossRef] [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2008, ApJ, 686, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Gloeckler, G. 2003, in Solar Wind Ten, ed. M. Velli, R. Bruno, F. Malara, & B. Bucci, AIP Conf. Ser., 679, 583 [Google Scholar]
- Hill, M. E., Schwadron, N. A., Hamilton, D. C., Di Fabio, R. D., & Squier, R. K. 2009, ApJ, 699, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Isenberg, P. A. 1987, J. Geophys. Res., 92, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. D., Paularena, K. I., Lazarus, A. J., & Belcher, J. W. 1995, Geophys. Res. Lett., 22, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. D., Liu, Y., Wang, C., & McComas, D. J. 2008, A&A, 491, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlickeiser, R. 1989, ApJ, 336, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Siewert, M., & Fahr, H.-J. 2008, A&A, 485, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, M. 2010, J. Geophys. Res., 115, A12102 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 A geometrical representation of the “double-hump” shock structure, where two inverse shock transitions follow upon each other, which ultimately returns ions back to the initial upstream flow configuration. |
| In the text | |
 |
Fig. 2 The geometrical configuration at the shock. |
| In the text | |
 |
Fig. 3 The relevant factor of the cooling amplitude (ϵcool) as a function of solar distance, using Uslow = 400 km s-1, sfs = 1.4 and L = 2 AU. |
| In the text | |
 |
Fig. 4 The turnover distance rto according to Eq. (21), with rto restricted to realistic termination shock distances (also covering the heliotail distance). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


