| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116706 | |
| Published online | 12 January 2012 | |
Research Note
Implications of the radio spectral index transition in LS I +61°303 for its INTEGRAL data analysis
Max Planck Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: lzimmerm@mpifr-bonn.mpg.de; mmassi@mpifr-bonn.mpg.de
Received: 13 February 2011
Accepted: 17 November 2011
Context. The TeV emitting X-ray binary LS I +61°303 has two radio periodicities that correspond to a large periodic outburst with the same period as the orbit, 26.5 days (phase Φ), and a second periodicity of 1667 days (phase Θ), which modulates the orbital phase and amplitude of the large outburst. Analyses of the radio spectral index revealed in LS I +61°303 the presence of the critical transition typical for microquasars from optically thick emission (related to a steady jet) to an optically thin outburst (related to a transient jet), and found that it occurs at Φcrit, which is modulated by Θ: Φcrit = f(Θ).
Aims. We examine the possible implications of averaging high energy data over large Θ and Φ intervals in the light of puzzling published INTEGRAL results, which differ for different averaging of the data.
Methods. In microquasars, a simultaneous transition between two X-ray states occurs at the switch from optically thick radio emission to an optically thin radio outburst, from the low/hard to the steep power-law state. Assuming that the same transition occurs in LS I +61°303 at Φcrit, we can show qualitatively the effect of averaging high energy data on Θ, by analysing the effects of averaging radio spectral index data across the same Θ interval. We then model the two X-ray states, low/hard and steep power-law state, and show quantitatively how their mixing can affect the results.
Results. When folded over too large a Θ interval, spectral data from INTEGRAL can yield a false picture of the emission behaviour of the source along the orbit because it may be mixing two spectral states. Furthermore, averaging the data along the orbit may result in a dominant low/hard spectral state, which, for insufficiently extended sampling, might appear without a cut-off.
Conclusions. The INTEGRAL results can be interpreted as two X-ray states that alternate with each other along the orbit. The implications of this analysis for HE/VHE data from LS I +61°303 and a possible connection between HE/VHE emission and the steep power-law state are discussed.
Key words: radio continuum: stars / X-rays: binaries / gamma-rays: stars / X-rays: individuals: LS I +61°303
© ESO, 2012
1. Introduction
The clear periodicity of the X-ray binary LS I +61°303, formed by a compact object and a rapidly rotating B0 V star, is amongst its most peculiar characteristics. The orbital period of P = 26.496 days (phase Φ with Φperiastron = 0.23 − 0.28, Aragona et al. 2009; Casares et al. 2005) modulates the radio flux resulting in a large outburst towards apastron, whereas a superorbital period of 1667 days (phase Θ) modulates both the amplitude and the orbital phase of the large radio outburst (Gregory et al. 1999; Gregory 2002). Two models exist for this system: the two-peak microquasar model (Marti & Paredes 1995; Bosch-Ramon et al. 2006; Romero et al. 2007) and the pulsar model (Maraschi & Treves 1981; Dubus 2006). The name of the first model was coined because of the highly eccentric orbit in LS I +61°303, for which two ejections are expected along the orbit: one around periastron and a second one shifted about ΔΦ ~ 0.3 towards apastron. In the radio regime, the first model interprets the often observed one-sided radio morphology and as well the observed switch to a double-sided morphology, as that of a precessing microquasar with a small and variable angle between the jet and the line of sight (Massi et al. 2004; Massi & Zimmermann 2010). The second model interprets the one-sided structures as a cometary tail of the pulsar (Dhawan et al. 2006).
Massi & Kaufman Bernadó (2009) analyzed the dependence of the radio spectral index α with flux density S ∝ να, on both periods Θ and Φ. The analysis uses 6.7 years (1994 − 2000) of NASA/NRAO GBI data from LS I +61°303 at two frequencies, ν1 = 2.2 GHz and ν2 = 8.3 GHz. The analysis had two main findings. The first was that in LS I +61°303 the optically thin outburst occurs after an interval of optically thick emission. In microquasars, the optically thin outburst is due to a transient jet consisting of shocks propagating in a pre-existing optically thick emitting steady jet (Fender et al. 2004; Massi 2011a). The second remarkable finding resulting from the radio spectral index analysis of Massi & Kaufman Bernadó (2009) was that in LS I +61°303 this switch from one kind of a jet (steady jet) to the other one (transient jet) occurs twice along the orbit at the orbital phases predicted by the two-peak microquasar model. One sees a spectral transition, optically thick/optically thin emission, first around periastron at Φcrit,1 = 0.33 ± 0.13 and then again towards apastron at Φcrit,2 = 0.7 ± 0.13. Owing to the qualitative and quantitative agreement between radio data and the two peak microquasar model, the microquasar scenario is assumed here as a working hypothesis to explain the puzzling results obtained from INTEGRAL observations. We use the well-established relationship for microquasars between radio and X-ray states (Fender et al. 2004).
The two radio states, the steady jet (α ≥ 0) and the transient jet (α < 0), should be directly linked to two spectrally distinct X-ray states in the unified model of X-ray states with radio jets: the low/hard X-ray state and the steep power-law state (Fender et al. 2004). The X-ray states are clearly distinguishable by their energy spectra (Grove et al. 1998; Fender et al. 2004; McClintock & Remillard 2006). A steady jet (α ≥ 0) occurs in the low/hard X-ray state and its X-ray spectrum is characterized by a power-law with photon index Γ ≈ 1.5 − 1.8 and a cut-off at high energies. The high energy cut-off is different for different sources, with some showing a folding energy Ef ≈ 115 keV (Grove et al. 1998) and others, as GX 339-4, a folding energy Ef of only 66 keV (Caballero-García et al. 2009). In particular for LS I +61°303, the very low X-ray luminosity, the observed optical modulation correlated with the radio outburst (see Massi & Kaufman Bernadó 2009), and the softening associated to a decrease in X-ray flux (Sidoli et al. 2006), which is consistent with accreting systems in quiescence (Corbel et al. 2006, 2008), all point towards the source exhibiting a very low hard, nearly quiescent, X-ray state. Finally, the transient jet (α < 0) is associated with the steep power-law X-ray state with a black-body component (with kT ~ 1 keV) and a power-law with a photon index of Γ ≳ 2.4 and no cut-off, thereby intrinsically allowing also for high energy emission.
Data from LS I +61°303 taken with the International Gamma-ray Astrophysics Laboratory (INTEGRAL/ISGRI 20 − 500 keV, LS I +61°303 is detectable in the 20 − 150 keV range), however, yielded surprising results, finding e.g. along most of the orbit a photon index only compatible with a low hard state, but without a cut-off. The photon index of the hard X-ray spectrum, furthermore, depended on how much data was averaged together and whether it was also averaged over the orbital period (Chernyakova et al. 2006; Zhang et al. 2010). Here, we aim to explain these results by using the relationship between radio and X-ray states that allows us to predict the kind of emission expected at soft gamma-rays based on the radio emission, or viceversa. In particular, in LS I +61°303, the Θ and Φ periodicities allow us to test this relationship by using GBI data, even if no simultaneous observations are available (as is the case for INTEGRAL). From the radio spectral transitions seen in the GBI data one can infer which spectral transition is expected in X-rays and when. The combination of radio spectral index data from different Θ intervals can then help us to understand what happens when INTEGRAL data is averaged over large parts of Θ.
2. INTEGRAL observations versus Θ and Φ
In Fig. 1, INTEGRAL observations published to date are displayed in terms of the Θ intervals in which they were carried out (Zhang et al. 2010) and denoted as I1−I3 (see also Fig. 1 in Zimmermann et al. 2011). Any spectral analysis should consider Θ, because within the energy range covered by INTEGRAL data, two states, the low hard and the steep power-law state, can be detected, when they occur.
Radio spectral index curves showing Φcrit,2, the transition for the large radio outburst towards apastron, for Θ = 0.0−0.1 and 0.7−0.8 are shown in Fig. 2. The orbital occurrence at phase Φcrit,2 of the transition from α ≥ 0 to α < 0 lies for Θ = 0.0−0.1 around Φcrit ≈ 0.73−0.77, and for Θ = 0.7−0.8 it occurs around Φcrit ≈ 0.63−0.67. Owing to the connection between radio and X-ray states, it now becomes evident from Fig. 2 that, if the energy range of an instrument covers both the low hard and the steep power-law state, folding over the orbital period data of different Θs might result in the mixture of different states. The orbital phase of the transition from optically thick emission to an optically thin outburst does not remain the same over the 1667 d period and the unified X-ray state model with radio jets assumes a physical connection between the radio spectral transition and the X-ray states (Fender et al. 2004). The folded data no longer provides any accurate information about the orbital occurrence of the spectral transition. As we show here, the information about one state could even be lost completely, if e.g. the sampling for one Θ interval is finer, which leads to the suppression of information from the other interval, and/or data from several different Θ-intervals, and not only the two intervals shown in Fig. 2, are mixed up.
 |
Fig. 1 Published high energy observations of LS I +61°303 by INTEGRAL (I1 − I3) shown in the context of the 1667 day radio period (Θ). The underlying light curve gives 6.7 yr radio Green Bank Interferometer data at 8.3 GHz folded with Θ. |
 |
Fig. 2 Radio spectral index for two different Θ intervals. The vertical lines mark the Φ interval where Chernyakova et al. (2006) determined a photon index compatible with a steep power-law state (see Sect. 2). |
Folding all data or parts of I1 − I3 together in terms of orbital phase increases the sampling and the significance of the signal. In doing so, several authors established that the emission in the interval 10−100 keV is clearly modulated by the orbital phase (Chernyakova et al. 2006; Hermsen & Kuiper 2007; Zhang et al. 2010). Moreover, Chernyakova et al. (2006), who used data from almost all of I3 (covering Θ = 0.57−0.99) and a few data points from the beginning of I1 (covering Θ = 0.0−0.06), have found that whereas along most of the orbit the photon index Γ was ≈ 1.4−1.7 (i.e. low hard state), it changed to 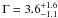 (i.e. compatible with a steep power-law state) in the orbital phase interval Φ = 0.6−0.8. This result is consistent with the radio spectral index analysis of Massi & Kaufman Bernadó (2009), giving for the same Θ-intervals of I3 the transition to an optically thin outburst (a transient jet) after Φ = 0.6 ± 0.1. In Fig. 2, one sees that for Θ = 0.7−0.8 (which is part of I3) the optically thin emission dominates in the interval Φ = 0.6−0.8. Following the radio spectral index though, folding over too much of a Θ cycle could imply that, although the resulting light curves can establish the overall periodicity of the source at these energies, it mixes different spectral states. The analysis of Zhang et al. (2010), who used I1 − I3 together (following the same data reduction method as Chernyakova et al. 2006), thereby covering both the minimum and the maximum amplitude interval of Θ, give a hard photon index of Γ ≈ 1.4−1.9 along the whole orbit (average: 1.7), no longer finding evidence of a very soft spectrum (Γ ≥ 2.4) in the interval Φ = 0.6−0.8.
(i.e. compatible with a steep power-law state) in the orbital phase interval Φ = 0.6−0.8. This result is consistent with the radio spectral index analysis of Massi & Kaufman Bernadó (2009), giving for the same Θ-intervals of I3 the transition to an optically thin outburst (a transient jet) after Φ = 0.6 ± 0.1. In Fig. 2, one sees that for Θ = 0.7−0.8 (which is part of I3) the optically thin emission dominates in the interval Φ = 0.6−0.8. Following the radio spectral index though, folding over too much of a Θ cycle could imply that, although the resulting light curves can establish the overall periodicity of the source at these energies, it mixes different spectral states. The analysis of Zhang et al. (2010), who used I1 − I3 together (following the same data reduction method as Chernyakova et al. 2006), thereby covering both the minimum and the maximum amplitude interval of Θ, give a hard photon index of Γ ≈ 1.4−1.9 along the whole orbit (average: 1.7), no longer finding evidence of a very soft spectrum (Γ ≥ 2.4) in the interval Φ = 0.6−0.8.
How can these results be interpreted in terms of the radio spectral index analysis from above? By examining Fig. 2, we can see, how by folding together data of two Θ intervals, optically thin and thick emission can be mixed, because the orbital occurrences of Φcrit,2, and therefore of the transition between optically thin/thick emission, differ for the Θ intervals. The optically thin emission then no longer dominates the orbital interval Φ = 0.6−0.8. When averaging over the intervals I1−I3, optically thick and thin emission get mixed together in the Φ interval of interest. Therefore, the measured photon index must not be directly interpreted as a continuous low/hard state of the source, because it represents the combination of different states. Moreover, we note that this mixing also occurs, when only one Θ interval is selected and the data is averaged over the whole orbit. As one sees in Fig. 2, optically thick and thin emission occur alternately during the orbit. When averaging the spectrum across the whole orbit, Chernyakova et al. (2006) find again an average photon index of Γ ≈ 1.6 but no cut-off at high energies. An example of the effect of this mixing of X-ray states is shown in Fig. 3; here we show one spectrum for a low/hard state (open squares) and one spectrum for a steep power-law state (open triangles) and the spectrum for the low/hard state is 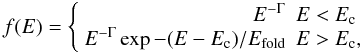 (1)where Ec is the cut-off energy and Efold the folding energy, which is in Grove et al. (1998) assumed to be approximately twice Ec. We use as an example the source GRS 1716-249 with Efold = 115 ± 8 keV, because this source, analysed by Grove et al. (1998) in both spectral states, results in a steep power-law state of significantly lower luminosity. This might also hold for LS I +61°303, as suggested by the results of Chernyakova et al. (2006) (i.e. dominance of the low hard state when mixing the data). In Fig. 3, we superimpose an average of the two curves (filled circles). The four vertical lines indicate the four points of the averaged (over both Φ and Θ) spectra derived by Chernyakova et al. (2006). The fit to these points resulted in a photon index Γ consistent with a low hard state, but no cut-off at high energies was found. This example shows how an average could yield a curve, where the photon index of the power-law below the cut-off energy (Ec ≈ 115/2 keV) is consistent with a low/hard state although the steep power-law is part of the data. In addition, we see in this example for GRS 1716-249 that only the last point, among the four ones by Chernyakova et al. (2006), samples the average curve after the cut-off and lies, with around 84 keV, still quite close to the cut-off energy (Ec ≈ 115/2 keV). It would be difficult under this condition to detect the cut-off. For GRS 1716-249, Grove et al. indeed established that there is exponential decay with Efold = 115 ± 8 keV for very well-sampled data up to 300 keV. However, if the cut-off in LS I +61°303 were to occur well before the assumed one, the contribution of the steep power-law would strongly bias the analysis of the averaged data.
(1)where Ec is the cut-off energy and Efold the folding energy, which is in Grove et al. (1998) assumed to be approximately twice Ec. We use as an example the source GRS 1716-249 with Efold = 115 ± 8 keV, because this source, analysed by Grove et al. (1998) in both spectral states, results in a steep power-law state of significantly lower luminosity. This might also hold for LS I +61°303, as suggested by the results of Chernyakova et al. (2006) (i.e. dominance of the low hard state when mixing the data). In Fig. 3, we superimpose an average of the two curves (filled circles). The four vertical lines indicate the four points of the averaged (over both Φ and Θ) spectra derived by Chernyakova et al. (2006). The fit to these points resulted in a photon index Γ consistent with a low hard state, but no cut-off at high energies was found. This example shows how an average could yield a curve, where the photon index of the power-law below the cut-off energy (Ec ≈ 115/2 keV) is consistent with a low/hard state although the steep power-law is part of the data. In addition, we see in this example for GRS 1716-249 that only the last point, among the four ones by Chernyakova et al. (2006), samples the average curve after the cut-off and lies, with around 84 keV, still quite close to the cut-off energy (Ec ≈ 115/2 keV). It would be difficult under this condition to detect the cut-off. For GRS 1716-249, Grove et al. indeed established that there is exponential decay with Efold = 115 ± 8 keV for very well-sampled data up to 300 keV. However, if the cut-off in LS I +61°303 were to occur well before the assumed one, the contribution of the steep power-law would strongly bias the analysis of the averaged data.
 |
Fig. 3 Model spectra for the low/hard state (power-law plus cut-off, open squares), the steep power-law state (open triangles) together with a black-body disk component with kT ~ 1 keV and the average of the two states (filled circles). |
3. Conclusions and discussion
We have investigated the implications of the radio spectral index transition, Φcrit = f(Θ), in LS I +61°303 for the analysis of INTEGRAL data. In microquasars, this transition is directly linked to the transition between two spectrally distinct high energy states that cover the energy range from X-rays to gamma-rays (Grove et al. 1998), but which in this paper are simply referred to as X-ray states: the low hard X-ray state and the steep power-law X-ray state. For the energy range covered by INTEGRAL data, both states can be detected, when they occur. From our analysis, we conclude that:
-
Folding data over too large Θ intervals could mix up data from different states so that the resulting spectra can no longer be unambiguously interpreted and mimic a persistent low hard state.
-
For data from the energy range accessible to INTEGRAL, even if the data were not folded on Θ, averaging across Φ will destroy any information about the different states.
-
We have pointed out that the lack of a cut-off in the power-law for data averaged all over the orbit, means that if LS I +61°303 has a cut-off well below ~115/2 keV, the contribution of the steep power-law will strongly bias the analysis of the spectrum of the averaged data. However, we have shown that a higher cut-off requires highly sensitive sampling, extending well beyond the used range of up to 100 keV.
The INTEGRAL results are then explainable with two X-ray states alternating along the orbit in parallel to, as expected in the microquasar scenario, the two radio states. What does this imply for the analysis of the HE/VHE data? For VHE, when LS I +61°303 is detected by MAGIC or VERITAS, its spectrum is always closely fitted with a photon index of ≳ 2.4 (Albert et al. 2009; Acciari et al. 2011; MAGIC Collaboration et al. 2012), which is the same as expected for the steep power-law. In this context, the observations of Anderhub et al. (2009) are of special interest. They have observed simultaneously X-ray and VHE emission from LS I +61°303 and found a correlation. Massi & Zimmermann (2010) noticed that for these observations the two fluxes result in 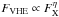 with η = 0.99, which is in agreement with the correlation observed in blazars (Katarzyǹski & Walczewska 2010). Here the X-ray emission is due to synchrotron, and VHE is synchrotron self-Compton (SSC) (Katarzyński et al. 2005). For LS I +61°303, several authors have explained the X-ray excess around apastron with synchrotron emission and the VHE with either external inverse Compton (EIC) or SSC emission (Gupta & Boettcher 2006; Zabalza et al. 2011). Zabalza et al. (2011) demonstrated that the X-ray/VHE correlation observed by Anderhub et al. (2009) is compatible with a one-zone leptonic particle population producing the emission. Their models use the observed X-ray photon index (1.55−1.67) and can reproduce the observed lightcurves quite well. Interestingly, this X-ray photon index is comparable to the one expected for the low hard state and could be mistaken as such. The soft X-ray synchrotron emission during the steep power-law state can then explain two findings. First, the VHE emission by invoking EIC or SSC and, second, the absence of an accretion disk black-body component in the soft X-rays (0.1−10 keV) expected during the steep power-law state, if the synchrotron X-ray component outshines the disk. Owing to the lack of simultaneous hard X-ray/TeV observations of LS I +61°303, it remains open, if the jet component extends into the hard X-ray regime.
with η = 0.99, which is in agreement with the correlation observed in blazars (Katarzyǹski & Walczewska 2010). Here the X-ray emission is due to synchrotron, and VHE is synchrotron self-Compton (SSC) (Katarzyński et al. 2005). For LS I +61°303, several authors have explained the X-ray excess around apastron with synchrotron emission and the VHE with either external inverse Compton (EIC) or SSC emission (Gupta & Boettcher 2006; Zabalza et al. 2011). Zabalza et al. (2011) demonstrated that the X-ray/VHE correlation observed by Anderhub et al. (2009) is compatible with a one-zone leptonic particle population producing the emission. Their models use the observed X-ray photon index (1.55−1.67) and can reproduce the observed lightcurves quite well. Interestingly, this X-ray photon index is comparable to the one expected for the low hard state and could be mistaken as such. The soft X-ray synchrotron emission during the steep power-law state can then explain two findings. First, the VHE emission by invoking EIC or SSC and, second, the absence of an accretion disk black-body component in the soft X-rays (0.1−10 keV) expected during the steep power-law state, if the synchrotron X-ray component outshines the disk. Owing to the lack of simultaneous hard X-ray/TeV observations of LS I +61°303, it remains open, if the jet component extends into the hard X-ray regime.
For the high energy emission in the GeV range, detected e.g. with Fermi-LAT, the picture is more diverse. Zabalza et al. (2011) note that in their one-zone population model, a broken power-law electron energy distribution is needed to explain the GeV component as observed with Fermi-LAT. The steep power-law might not then be the only emission process, also because GeV emission is detected all along the orbit. Electrons from the steady jet can always upscatter stellar UV photons to GeV energies (i.e. EIC see Bosch-Ramon et al. 2006). Nevertheless, more energetic particles from the transient jet could in addition produce as well GeV emission via EIC and SSC. Intriguingly, the spectrum measured by Fermi-LAT shows, in addition to a power-law with a cut-off around 6 GeV, upper limits possibly compatible with the spectrum measured with MAGIC and VERITAS (see e.g. Fig. 2 in Hadasch 2011).
In any case, owing to the connection between the radio and the HE/VHE emission, the analysis performed here for INTEGRAL can and should in principle be extended to other high energy instruments, if the Θ coverage is good enough. In particular, the flux evolutions recently detected at HE/VHE imply that this data should be analysed on as short a Θ interval as possible. As discussed in Massi & Kaufman Bernadó (2009), the two peak shape of the α versus Φ curve varies with Θ. It is most pronounced in Θ = 0.0−0.1 and 0.9−1.0, appreciable at Θ = 0.2−0.3 and 0.7−0.9, and absent at Θ = 0.3−0.6 (see Fig. 5 in Massi & Kaufman Bernadó 2009). In addition, the distance of the two peaks varies with Θ. These variations in the accretion curve are predicted by the two-peak microquasar model of Marti & Paredes (1995) by incorporating variable wind velocities of the Be star (see their Fig. 6). A reflection of this behaviour at other wavelengths owing to the related emission processes is expected. As a matter of fact, there is an interesting increase in the overall flux level observed with Fermi-LAT after March 2009 (Θ ≈ 0.92) together with a broadening of the peak shape (Hadasch 2011). The flux variations observed with Fermi-LAT to date are therefore consistent with α varying with Θ. Similarly, strong variations are observed at very high energies. The source went from being detected around apastron with VERITAS and MAGIC (VERITAS: Θ = 0.38, 0.4−0.47; MAGIC: Θ = 0.17−0.25, 0.37−0.44, 0.59−0.6) to becoming quiescent during 2008−2010. No detection was reported by VERITAS for Θ = 0.83−0.08, but weak detection was detected by MAGIC for Θ = 0.05−0.11 around apastron. The source was again detected by VERITAS in October 2010 corresponding to Θ = 0.26, but this time around periastron (Albert et al. 2009; Acciari et al. 2011; MAGIC Collaboration et al. 2012). Nonetheless, at the moment the insufficient Θ coverage of these instruments does not allow a closer comparison. Nevertheless, the observations clearly indicate that for the analysis of these data, Θ should be considered to avoid any mixing of signal from the outbursts.
Acknowledgments
The work of L. Zimmermann is partly supported by the German Excellence Initiative via the Bonn Cologne Graduate School. We thank Lars Fuhrmann, Victoria Grinberg and the anonymous referee for comments and fruitful discussions. The Green Bank Interferometer is a facility of the National Science Foundation operated by the NRAO in support of NASA High Energy Astrophysics programs.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 701, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2011, ApJ, 738, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2009, ApJ, 693, 303 [NASA ADS] [CrossRef] [Google Scholar]
- MAGIC Collaboration, Aleksić, J., Alvarez, E. A., et al. 2012, ApJ, accepted [arXiv:1111.6572] [Google Scholar]
- Anderhub, H., Antonelli, L. A., Antoranz, P., et al. 2009, ApJ, 706, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Aragona, C., McSwain, M. V., Grundstrom, E. D., et al. 2009, ApJ, 698, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Paredes, J. M., Romero, G. E., & Ribó, M. 2006, A&A, 459, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caballero-García, M. D., Miller, J. M., Trigo, M. D., et al. 2009, ApJ, 692, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Ribas, I., Paredes, J. M., Martí, J., & Allen de Prieto, C. 2005, MNRAS, 360, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Chernyakova, M., Neronov, A., & Walter, R. 2006, MNRAS, 372, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Connors, T. W., Johnston, S., Manchester, R. N., & McConnell, D. 2002, MNRAS, 336, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Corbel, S., Tomsick, J. A., & Kaaret, P. 2006, ApJ, 636, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Corbel, S., Koerding, E., & Kaaret, P. 2008, MNRAS, 389, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, V., Mioduszewski, A., & Rupen, M. 2006, Proceedings of the VI Microquasar Workshop, 52.1 [Google Scholar]
- Dubus, G. 2006, A&A, 456, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2002, ApJ, 575, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., Peracaula, M., & Taylor, A. R. 1999, ApJ, 520, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Grove, J. E., Johnson, W. N., Kroeger, R. A., et al. 1998, ApJ, 500, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S., & Boettcher, M. 2006, ApJ, 650, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Hadasch, D. 2011, for the Fermi-LAT collaboration [arXiv:1111.0350] [Google Scholar]
- Hermsen, W., & Kuiper, L. 2007, in First GLAST Symposium [Google Scholar]
- Katarzyǹski, K., & Walczewska, K. 2010, A&A, 510, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katarzyński, K., Ghisellini, G., Tavecchio, F., et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maraschi, L., & Treves, A. 1981, MNRAS, 194, 1P [NASA ADS] [CrossRef] [Google Scholar]
- Marti, J., & Paredes, J. M. 1995, A&A, 298, 151 [NASA ADS] [Google Scholar]
- Massi, M. 2011a, Mem. Soc. Astron. It., 82, 24 [Google Scholar]
- Massi, M. 2011b, Mem. Soc. Astron. It., 82, 77 [NASA ADS] [Google Scholar]
- Massi, M., & Kaufman Bernadó, M. 2009, ApJ, 702, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Massi, M., & Zimmermann, L. 2010, A&A, 515, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Ribó, M., Paredes, J. M., et al. 2004, A&A, 414, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2006, Compact Stellar X-ray Sources (Cambridge University Press), 157 [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sidoli, L., Pellizzoni, A., Vercellone, S., et al. 2006, A&A, 459, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zabalza, V., Paredes, J. M., & Bosch-Ramon, V. 2011, A&A, 527, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, S., Torres, D. F., Li, J., et al. 2010, MNRAS, 408, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Zimmermann, L., Grinberg, V., Massi, M., & Wilms, J. 2011, The X-ray Universe, 308 [Google Scholar]
All Figures
 |
Fig. 1 Published high energy observations of LS I +61°303 by INTEGRAL (I1 − I3) shown in the context of the 1667 day radio period (Θ). The underlying light curve gives 6.7 yr radio Green Bank Interferometer data at 8.3 GHz folded with Θ. |
| In the text | |
 |
Fig. 2 Radio spectral index for two different Θ intervals. The vertical lines mark the Φ interval where Chernyakova et al. (2006) determined a photon index compatible with a steep power-law state (see Sect. 2). |
| In the text | |
 |
Fig. 3 Model spectra for the low/hard state (power-law plus cut-off, open squares), the steep power-law state (open triangles) together with a black-body disk component with kT ~ 1 keV and the average of the two states (filled circles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


