| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201118059 | |
| Published online | 09 December 2011 | |
Radiative transition rates for the forbidden lines in Fe II⋆
School of Mathematics and Physics, Queen’s University Belfast, Belfast BT7 1NN, Northern Ireland, UK
e-mail: a.hibbert@qub.ac.uk
Received: 9 September 2011
Accepted: 6 October 2011
Aims. We report electric quadrupole and magnetic dipole transitions among the levels belonging to 3d64s, 3d7 and 3d54s2 configurations of Fe II in a large scale configuration interaction (CI) calculation.
Methods. The CIV3 code developed by Hibbert and coworkers is used to determine configuration interaction wave functions for these levels: for the optimisation of two different sets of orbitals based on alternative choices of the 3d function, for creating and diagonalising the Hamiltonian matrices and finally for calculating transition probabilities.
Results. Where possible, we have used experimental energies, not only for transition energies but also to enhance the accuracy of our ab initio CI expansions. We compare our results with those of other authors, and discuss differences between them. The good agreement between our results obtained for the same transitions but with different d-functions indicates that we have treated the state dependence of the d-functions sufficiently well. Most of our results are available in electronic form as an appendix to the paper.
Conclusions. Our analysis of our own results and those of others suggests that many of our transition rates are more accurate than the rather conservative 20−30% we have stated in the text, though in a small proportion of transitions, we could not justify an accuracy greater than this.
Key words: methods: numerical / atomic data
Tables 5–9 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/536/A74
© ESO, 2011
1. Introduction
The spectra of many astronomical objects are rich in Fe II lines, both allowed and forbidden. The analysis of those spectra, for example through the the construction of synthetic spectra, requires a knowledge of the oscillator strengths or transition rates of those lines (see, for example, Brandt et al. 1999; Verner et al. 2002; Verner et al. 2009; Castelli et al. 2009; Castelli & Kurucz 2010). In such cases, the data for many lines must be determined. The Fe II data for a smaller number of lines are needed for the determination of the Fe abundance of (inter alia) H II regions (Rodriguez 2002), for the study of mass loss in supernovae (Smith & Hartigan 2006), or the determination of the dominant excitation mechanisms in active galactic nuclei (Rodriguez-Ardila et al. 2004).
Spectra containing specifically forbidden [Fe II] lines have been studied for many years, dating back to Merrill (1928), and have in more recent years been a focus of specific attention through an analysis of data from space-based observatories such as from the Space Telescope Imaging Spectrograph (STIS) on the Hubble Space Telescope (Gull et al. 1999; Hartman et al. 2003). Again, the analysis requires both radiative and collisional atomic data.
Generally, though, the volume of atomic data required means that the data has to be produced using theoretical methods. However, there are several potential sources of inaccuracy in theoretical data, and it is helpful when such data can be compared either with laboratory data (for example, Verner et al. 2002; Hartman et al. 2003), or data derived from observations (for example, Smith & Hartigan 2006). Such comparisons are important, but are often not definitive in deciding which data are the most accurate, since laboratory determinations are not always direct measurements themselves, and the analysis of observational data usually contains some built-in suppositions of astrophysical modelling with the result that conflicting results occur even in a single observational approach or when applied to different astronomical objects (see for example, Dennefeld 1982, 1986).
In two recent papers (Deb & Hibbert 2010a,b) we have discussed a similar variation between different theoretical determinations of data for [Fe II] lines, and have been able to point to possible causes of discrepancies amongst them, as well as to disagreements with observationally derived data. It is relatively easy to calculate oscillator strengths of transitions, even in Fe II, by using simple wave functions. But the results may not be of sufficient accuracy for astrophysical modelling purposes. Using more elaborate wave functions, for example, by using a configuration interaction wave function with many configuration state functions (CSFs), will give better accuracy, but no calculation is exact for a system such as Fe II, and so approximations of varying types are made. Unfortunately there is no monotonic convergence of oscillator strengths as the wave functions are improved – a more elaborate set of wave functions will not necessarily lead to more accurate oscillator strengths. When the goal is the calculation of data for a few transitions between energetically low-lying states, it may be possible to achieve a measure of convergence. But in most cases, many transitions have to be calculated simultaneously (for example, when transitions are between higher-lying states, wave functions for the lower-lying states must also be included in the calculation, to a reasonable degree of accuracy). Then for a calculation within (computer-)constrained resources, the wave functions cannot be as extensive as if just a few transitions were under consideration. The determination of the atomic data therefore requires a strategy aimed at optimising the accuracy, and different strategies have led to different, sometimes very different, results.
In this paper we will focus on the “forbidden” electric quadrupole (E2) and magnetic dipole (M1) transitions in Fe II. We will present our results of oscillator strengths of transitions among levels of the 3d64s, 3d7 and 3d54s2 configurations. We have already published oscillator strengths of a few such transitions (Deb & Hibbert 2010a,b) with the aim of discussing a number of particular astrophysical issues. We also discussed the accuracy of our work compared with that of the few other sets of [Fe II] data which already exist in the literature, and argued for our own results to be preferred. In this paper, we present our full set of results (mostly accessible electronically), and attempt to set some bounds of accuracy on these data.
2. Theoretical method
We use the general configuration interaction program CIV3 (Hibbert 1975; Glass & Hibbert 1978; Hibbert et al. 1991). The configuration interaction (CI) wavefunction in intermediate (LSJ) coupling take the form 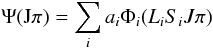 (1)where Φi represents a CSF with varying Li and Si but with a common J and parity π, while ai is the CI expansion (mixing) coefficient. The CSFs are constructed from one-electron orbitals whose radial parts are expressed as analytic sums of basis functions given by
(1)where Φi represents a CSF with varying Li and Si but with a common J and parity π, while ai is the CI expansion (mixing) coefficient. The CSFs are constructed from one-electron orbitals whose radial parts are expressed as analytic sums of basis functions given by 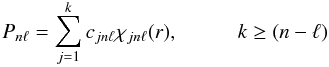 (2)where χjnℓ are taken to be normalised Slater-type orbitals (STOs) and are given by
(2)where χjnℓ are taken to be normalised Slater-type orbitals (STOs) and are given by ![\begin{equation} \chi_{jn\ell}=\left[\frac{(2\xi_{jn\ell})^{2I_{jn\ell}+1}}{(2I_{jn\ell})!}\right]^{1/2} r^{I_{jn\ell}} \exp(-\xi_{jn\ell}r). \end{equation}](/articles/aa/full_html/2011/12/aa18059-11/aa18059-11-eq16.png) (3)The parameters ξjnℓ and cjnℓ are determined variationally by minimising one or other of the energy eigenvalues of the Hamiltonian matrix, and the radial functions are subject to the orthonormality conditions
(3)The parameters ξjnℓ and cjnℓ are determined variationally by minimising one or other of the energy eigenvalues of the Hamiltonian matrix, and the radial functions are subject to the orthonormality conditions 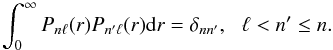 (4)All optimisations of orbitals were carried out in LS coupling. In previous work on E1 transitions (for example Corrégé & Hibbert 2005), we chose the orbitals up to 4s from ground 3d64s state, as given in the Hartree-Fock tabulations of Clementi & Roetti (1974), and then optimised the remaining radial functions on energies of states with 3d6 or 3d5 cores. In the present work, some of the main E2 or M1 transitions involve the 3d7 states. So, while we retained the 1s, 2s, 2p, 3s, 3p, 4s orbitals of this previous work, we chose the 3d function to be that given by Clementi & Roetti (1974) for the 3d74F state. The basis functions for the remaining d-functions were still those of the earlier work, but the 4d, 5d, 6d functions were re-orthogonalised to the new 3d, and to each other. The parameters of the radial functions not given in Clementi & Roetti (1974) are shown in Table 1.
(4)All optimisations of orbitals were carried out in LS coupling. In previous work on E1 transitions (for example Corrégé & Hibbert 2005), we chose the orbitals up to 4s from ground 3d64s state, as given in the Hartree-Fock tabulations of Clementi & Roetti (1974), and then optimised the remaining radial functions on energies of states with 3d6 or 3d5 cores. In the present work, some of the main E2 or M1 transitions involve the 3d7 states. So, while we retained the 1s, 2s, 2p, 3s, 3p, 4s orbitals of this previous work, we chose the 3d function to be that given by Clementi & Roetti (1974) for the 3d74F state. The basis functions for the remaining d-functions were still those of the earlier work, but the 4d, 5d, 6d functions were re-orthogonalised to the new 3d, and to each other. The parameters of the radial functions not given in Clementi & Roetti (1974) are shown in Table 1.
In our LSJ calculation the nonrelativistic Hamiltonian is supplemented by the following relativistic operators associated with Breit-Pauli approximation: mass correction, Darwin and a modified form of spin-orbit operator. The one-electron modified form of spin-orbit operator proposed by Hibbert & Bailie (1992) is of the form 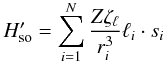 (5)where Z is the nuclear charge and ζℓ are parameters which depend only on ℓ-value of the interacting electrons. These parameters are chosen to reproduce the values of the full spin-orbit plus spin-other-orbit matrix elements between the main CSFs. This method reduces the computation time significantly while retaining all the important relativistic effects. This simplification changes the energy values by at most a few cm-1.
(5)where Z is the nuclear charge and ζℓ are parameters which depend only on ℓ-value of the interacting electrons. These parameters are chosen to reproduce the values of the full spin-orbit plus spin-other-orbit matrix elements between the main CSFs. This method reduces the computation time significantly while retaining all the important relativistic effects. This simplification changes the energy values by at most a few cm-1.
The choice of configurations has been undertaken in two stages:
-
1.
all possible CSFs obtained by allowing single and doublereplacements, to all possible orbitals, from the 3d and 4s subshellsof the main configurations 3d64s, 3d7, 3d54s2, but keeping subshells up to 3p closed;
-
opening of the 3s and 3p subshells by incorporating the following correlation effects:
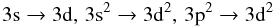 in all the main configurations.
in all the main configurations.
This leads to very large numbers of CSFs for any J-value. Yet many of those CSFs have tiny CI coefficients and so contribute very little to the energy calculation or to oscillator strengths. Therefore, with the configurations chosen as above, we adopted a three stage process:
-
1.
the non-relativistic Hamiltonian matrix was diagonalised foreach LS symmetry. CSFs were then deleted if their CI coefficientsai satisfied |ai| < 0.001 for each of the eigenvectors corresponding to real states used in this calculation;
-
2.
the sets of remaining CSFs were combined for each J-value and the corresponding Breit-Pauli Hamiltonian diagonalised;
-
3.
small corrections were added to the diagonal elements of the Hamiltonian matrix so that the energy eigenvalues matched experimental energy differences (our “fine-tuning” process, see for example Hibbert 1996).
Finally, we note that we have repeated these calculations using our earlier set of radial functions (Corrégé & Hibbert 2005). These differ in the optimisation of the d-functions. For most of our transitions, the A-values obtained with the two sets of functions agree to within about 20%, with many agreeing to within 10%, giving us some measure of confidence that the state-dependence of the d-functions has been accounted for by the inclusion of the 4d, 5d, 6d functions.
Orbital parameters for Fe II.
3. Results and discussion
We have evaluated transition rates for all M1 and E2 transitions between the 100 even parity levels of 3d64s, 3d7 and 3d54s2, as listed in the NIST tables (Ralchenko et al. 2011), using both the radial functions displayed in Table 1 (set 1) and also with the radial functions we have used in previous calculations (set 2) of E1 transitions (Corrégé & Hibbert 2005). The NIST tables omit certain of the higher levels of these configurations. Using the latter set of radial functions, we have estimated the energy positions of these levels and have evaluated transition rates involving these levels also.
A number of other sets of calculations have been undertaken in recent years, using different methods. Early semi-empirical calculations of Garstang (1962) expressed the various matrix elements in terms of adjustable parameters. He noted and used the fact that (particularly) the 3d orbital function needed to be different for different levels and for different configurations, so that the E2 radial integrals were configuration-dependent. Nussbaumer & Storey (1980, 1988) used the SUPERSTRUCTURE code of Eissner et al. (1974), with radial functions determined as eigenfunctions of scaled Thomas-Fermi potentials, with the scaling factors determined from a least-squares fit to known energy levels. The same code has been used by Quinet et al. (1996), but with a larger configuration basis set, and they also used (in parallel) the HFR code of Cowan (1981). The HFR code forms the basis of many of the calculations included in the databases of Kurucz (1988) as well as in the work of Fawcett (1988).
In two recent papers, we have discussed the accuracy of some of our transition rates, in comparison with those of other researchers, and the causes of discrepancies between different sets of calculations. In calculations of M1 transitions within a multiplet, particularly in the lower-lying ones, most calculations agree, as shown in Deb & Hibbert (2010a). This is expected because the states involved are spectroscopically almost pure and the dipole matrix elements do not involve the radial functions. But for transitions between levels from different LS terms, calculations even of M1 transition rates can give rise to different results when using different methods (Deb & Hibbert 2010b). This is because, although again the radial functions are not involved in the dipole integrals, the rates are strongly dependent on the mixing between different LS levels (of the same J), and the radial functions are involved in the calculation of the CI mixing coefficients. For E2 transitions, again the differences between calculations are often due to the differing values of the mixing coefficients, but also to the different values determined for the multipole radial integrals. In our own work, we have used two different radial function sets, as indicated above, in order to estimate how inaccurate our results might be because of this state-dependent effect.
E2 transitions: a6S2–a6DJ.
Comparison of A-values of transitions among low-lying levels.
E2 and M1 A-values (in s-1) among levels of 3d64s, 3d7 and 3d54s2 configurations of Fe II.
In order to illustrate the range of results obtained using different methods, and also to compare with the rather limited range of experimental data, we have shown in Table 2 transition rates (in s-1) for the five transitions which contribute to the calculation of the lifetime τ (in seconds) of the 3d54s2 a6S2 level. There is generally good agreement between the sets of calculated results, with the branching fractions agreeing to within one or two units in the third significant figure. Also there is very good agreement (within the limits of experimental uncertainty) with the laboratory measurements of Rostohar et al. (2001). We do not show the corresponding results of Garstang (1962), which are around 40% lower, but even then the branching fractions agree very well. For these transitions the key, determining, factor is the quadrupole radial integral, the other factors being related to angular momenta. CI mixing is relatively limited in effect.
A second set of examples, for which CI mixing is more important, is displayed in Table 3. The lines of the multiplet 3d64s a6D → 3d7 a4P are driven by the mixing between 6D, 4D and 4P (depending on the particular J-values). Our values differ from the SST and HFR results of Quinet et al. (1996) by up to 40%, and rather more from the earlier SST values of Nussbaumer et al. (1988) which used a smaller set of configurations in the HFR model. For the lines of this multiplet which are dominated by an E2 transition, our values obtained with our two different sets of radial functions are in good agreement, whereas for the transitions dominated by M1, the use of set 1 (specifically optimised for transitions of this type) gives rather larger values than are obtained with set 2.
However, for the other transitions dominated by M1, 3d7 a4F → 3d7 a2G, the two sets of radial functions give A-values in close agreement, but which contrast somewhat with the SST and HFR results of Quinet et al. (1996), which agree among themselves.
The other two multiplets, 3d7 a4F → 3d64s a4D and 3d7 a4F → 3d7 a4P, are mostly dominated by the E2 multipole and for them, our two sets of radial functions give closely agreeing A-values. For a few lines, the M1 contribution is not negligible, and in the case of the 3d7 a4F1.5 → 3d7 a4P2.5 line, the two operators give almost equal contributions. Table 4 of Nussbaumer et al. (1988) mentions only E2 for this transition, and our E2 value for this line is in good agreement with the total given by Nussbaumer et al. (1988) or by Quinet et al. (1996).
Recently, Quinet (private communication) has undertaken a new HFR calculation with a more extended set of configurations. We note that his new calculations come closer to our own. In the case of the 3d7 a4F → 3d7 a2G multiplet, his new values are roughly halfway between the earlier results and ours, while in the case of the 3d64s a6D → 3d7 a4P multiplet, where our values with the two sets of radial functions differ by about 25%, his new values lie between our two values in almost all the lines of this multiplet.
While this converging of results using different methods or sets of radial functions gives us increasing confidence in the accuracy of our results, in a few lines the different methods do still give very different results, even to several orders of magnitude. However, these situations are rather special, arising because of severe CI cancellation, and consequently the A-value obtained with at least one of the methods is very small. Two examples, of E2 transitions, will suffice to demonstrate the difficulty in obtaining accurate results in these (albeit small number of) situations:
-
3d64s6D4.5 → 3d74P2.5. This line is part of the first multiplet in Table 3, although we did not list it there because no other published results were available for comparison. However, Quinet’s new calculation still gives a value around two orders of magnitude smaller than our value which is 3.05E-6 (with the radial functions of set 1) or 2.62E-6 (with the radial functions of set 2). It is convenient to look at the contribution to the multipole matrix element from individual configurations in the form of ⟨ φ1|Op|φ2 ⟩ , where Op is the E2 operator but includes the square root of the various overall factors, such as the energy factor. Then to obtain the A-value, one simply has to add these contributions and square the result. In this case, the spins of the two states are different, so the transition is driven by the admixture of 4F in 6D and 6D and 6S in 4P. Here the dominant contributions to these interactions are as follows (powers of 10 in parentheses):
⟨3d64s 6D | Op | 3d64s 6D⟩ –1.043 (–3) ⟨3d64s 6D | Op | 3d64s 6S⟩ –1.498 (–3) ⟨3d74F | Op | 3d74P⟩ –5.321 (–3) ⟨3d6(3F1)4s 4F | Op | 3d74P⟩ –2.639 (–3) ⟨3d6(3F2)4s 4F | Op | 3d74P⟩ 9.177 (–3) Total –1.324 (–3) Square root of A-value –1.746 (–3). The remaining 0.422 (–3) comes from a myriad of other interactions, many of which are of this order, so again there is substantial cancellation. The (3F1) and (3F2) symmetries of 3d6 refer to two 3F cores, with different seniority numbers. There are two real states with these as the dominant configurations, lying higher than 3d7. There is a similar situation regarding the 4P states, but the 3d64s 4P states do not seem to have a large contribution to the total. The total of the five contributions in the above table is 7 times smaller than the largest of the individual contributions. The contributions are critically dependent on rather small CI coefficients in the wave functions for the two levels. It is a similar situation to the calculation of intercombination lines in E1 transitions. If, for example, the single positive contribution were to increase by 5% while the negative contributions were to decrease by 5%, the difference would change from − 1.324 ( − 3) to − 0.340 ( − 3) and the A-value would reduce by a factor of 15. Such is the sensitivity of the calculation to small changes in these contributions, brought about by small proportionate changes in the already small mixing coefficients. Our method of fine-tuning to give the mixing coefficients as accurately as our model will allow, together with the fact that our two sets of radial functions give A-values which differ by only about 15%, encourages us to believe that, while there is indeed strong CI mixing, our results are reasonably accurate.
-
3d72H4.5 → 3d6(3F2)4s 2F2.5. Our A-values for this line are 8.32E-5 (using the radial functions of set 1) or 6.13E-5 (with set 2 functions). Quinet’s new result (priv. comm.) is about three orders of magnitude smaller, so there is an even greater proportionate difference here. This line suffers from rather similar cancellation effects, even though a 2H → 2F transition should be more straightforward, not needing to depend of the mixing of states of different LS to “drive” it. This time the contributions one would expect to dominate again cancel:
⟨3d72H | Op | 3d72F⟩ 0.01351 ⟨3d72H | Op | 3d6(3F1)4s 2F⟩ 0.01996 ⟨3d72H | Op | 3d6(1F)4s 2F⟩ –0.00103 ⟨3d72H | Op | 3d6(3F2)4s 2F⟩ –0.03124 Total 0.00120 so that the actual value is determined by other small contributions, also of the order of 0.001, the total being 0.0091. Even then, some of these other contributions cancel. Again, with the total being smaller than individual contributions by a factor of 25, it is not difficult to see how small changes in the CI coefficients can lead to a significant change in the total of these contributions and result in changes by orders of magnitude in the A-values. We note that our two values, obtained with different radial functions and therefore with differing fine-tuning being necessary, differ by only around 35%, not by orders of magnitude.
4. Description of the electronic tables
We present in Table 4 a complete list of E2 and M1 transition rates among the 100 fine-structure levels of 3d64s, 3d7 and 3d54s2 configurations which are listed in the NIST tabulation. The complete table is available only by email from the second author. However, a one-page sample of this table is presented below. In all, there are 3628 transitions listed. Table 4 is arranged in ascending energy order of the lower level. The wavelengths are given in vacuo for λ < 2000 Å (=0.2 μ) and in air for λ > 2000 Å. However, while this is useful for a visual reading of the data, it is not easily machine readable. Hence we have constructed the same data in different layouts, in ascii format, which are available at the CDS
First, we give in Table 5 the 100 levels given in the NIST tables: Col. 1 gives an index number for each level, Col. 2 gives the usual level labels in spectroscopic form, Col. 3 gives their LS character while Col. 4 gives their J-values; Col. 5 gives their energies (in cm-1) relative to the ground level, as given by Ralchenko et al. (2011) where possible, otherwise by our calculations involving these levels – these will not be as accurate as those for the NIST-tabulated levels and should be treated with caution. The same data as in the full Table 4 (but in ascii format) is presented in Table 6, that is, in order of increasing energy for the lower level: Col. 1 gives the index number (as defined in Table 5) for the lower level, Col. 2 gives the index number of the upper level, Col. 3 gives the wavelength (in air for wavelengths greater than 2000 Å), Col. 4 gives the A-value of the E2 transition, Col. 5 the A-value for the M1 transition and Col. 6 the sum of the two. Table 7 gives the same data, but in order of upper level, while Table 8 gives the same data but in descending order of wavelength. Finally, in Table 9 and in the same format as Table 6, we give transition rates of transitions involving those levels which are not in the NIST tabulations. These rates will probably not be as reliable as those in Tables 5−8. They are presented for completeness.
5. Conclusions
We have completed a series of calculations of E2 and M1 transitions among the 100 fine-structure levels of 3d64s, 3d7 and 3d54s2 configurations. Extensive CI is used, including configurations which allow for correlation within the 3s and 3p subshells. Experimental energies have been used, not only for transition energies, but also (through our fine-tuning process) to enhance the accuracy of the CI mixing coefficients in the wave functions, thereby improving the accuracy of the transition rates. We have used the 3d orbital function which is the most appropriate for many of the transitions reported here, but we also found that, by including three other d-functions to act as correctors, our transition rates were largely independent of the choice of the 3d function.
But it is difficult to place uncertainty bounds on our calculated rates. Many of the rates are of order 10-3–10-4. Transitions within a multiplet are probably correct to within about 5% while most of those where the main configurations satisfy the usual angular momentum selection rules should be reliable to within 20 − 30%, or better (and often much better). But others are “driven” by coupling with other configurations, and the accuracy of the transition rates is dependent on the accuracy of the mixing. Our fine-tuning process is designed to represent that mixing as accurately as possible, and in many cases an accuracy of say 20 − 50% can still be achieved. But there are also transitions where there is very considerable cancellation in the multipole integral due to CI mixing, and in this case small changes in the CI mixings can lead to substantial changes in the transition rates, as we have seen. But even then, those transition rates obtained with our two sets of orbital radial functions lead to quite similar results, again to within 50% and often much closer than that. So while we could not demonstrate high accuracy for such transitions, we still believe that our rates would be within a factor of two accuracy, and again are frequently much better than this.
Acknowledgments
The authors would like to thank PPARC/STFC, UK for support under Rolling Grant PP/D00103X/1 and also ST/G001626/1. We also wish to thank Dr Pascal Quinet and Dr Achim Tappe for helpful communications.
References
- Brandt, J. C., Heap, S. R., Beaver, E. A., et al. 1999, AJ, 117, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2010, A&A, 520, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., Kurucz, R. L., & Hubrig, S. 2009, A&A, 508, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clementi, E., & Roetti, C. 1974, At. Data Nucl. Data Tables, 14, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Corrégé, G., & Hibbert, A. 2005, ApJ, 627, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley, California: University of California Press) [Google Scholar]
- Deb, N. C., & Hibbert, A. 2010a, A&A, 524, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deb, N. C., & Hibbert, A. 2010b, ApJ, 711, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Dennefeld, M. 1982, A&A, 112, 215 [NASA ADS] [Google Scholar]
- Dennefeld, M. 1986, A&A, 157, 267 [NASA ADS] [Google Scholar]
- Eissner, W., Jones, M., & Nussbaumer, H. 1974, Comp. Phys. Commun., 8, 270 [Google Scholar]
- Fawcett, B. C. 1988, At. Data Nucl. Data Tables, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Garstang, R. H. 1962, MNRAS, 124, 321 [NASA ADS] [Google Scholar]
- Glass, R., & Hibbert, A. 1978, Comp. Phys. Commun., 16, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Gull, T. R., Ishibashi, K., Davidson, K., & the Cycle 7 STIS Go Team 1999, in Eta Carinae at The Millennium, ASP Conf. Ser., 179, 144 [Google Scholar]
- Hartman, H., Derkatch, A., Donnelly, M. P., et al. 2003, A&A, 397, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hibbert, A. 1975, Comp. Phys. Commun., 9, 141 [Google Scholar]
- Hibbert, A. 1996, Phys. Scripta T, 65, 104 [Google Scholar]
- Hibbert, A., & Bailie, A. C. 1992, Phys. Scr., 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbert, A., Glass, R., & Fischer, C. F. 1991, Comp. Phys. Commun., 64, 455 [Google Scholar]
- Kurucz, R. L. 1988, Trans. IAU, 28, 168 [Google Scholar]
- Merrill, P. W. 1928, ApJ, 67, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Nussbaumer, H., & Storey, P. J. 1980, A&A, 89, 308 [NASA ADS] [Google Scholar]
- Nussbaumer, H., & Storey, P. J. 1988, A&A, 193, 327 [NASA ADS] [Google Scholar]
- Nussbaumer, H., Pettini, M., & Storey, P. J. 1981, A&A, 102, 351 [NASA ADS] [Google Scholar]
- Quinet, P., Le Dourneuf, M., & Zeippen, C. J. 1996, A&AS, 120, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ralchenko, Yu., Kramida, A. E., Reader, J., & NIST ASD Team 2011, NIST Atomic Spectra Database (version 4.1.0), http://physics.nist.gov/asd3 [2011, August 24], National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- Rodriguez, M. 2002, A&A, 389, 556 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez-Ardila, A., Pastoriza, M. G., Viegas, S., et al. 2004, A&A, 425, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rostohar, D., Derkatch, A., Hartman, H., et al. 2001, Phys. Rev. Lett., 86, 1446 [Google Scholar]
- Smith, N., & Hartigan, P. 2006, ApJ, 638, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, E., Gull, T. R., Bruhweiler, F., et al. 2002, ApJ, 581, 1154 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, E., Bruhweiler, F., Johansson, S., et al. 2009, Phys. Scripta T, 134, 014006 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
E2 and M1 A-values (in s-1) among levels of 3d64s, 3d7 and 3d54s2 configurations of Fe II.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


