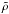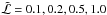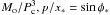Mass loss, destruction and detection of Sun-grazing and -impacting cometary nuclei

J. C. Brown; H. E. Potts; L. J. Porter; G. Le Chat

doi:10.1051/0004-6361/201015660

Home

All issues

Volume 535 (November 2011)

A&A, 535 (2011) A71

Full HTML

Free Access

Issue		A&A Volume 535, November 2011


Article Number		A71
Number of page(s)		12
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/201015660
Published online		10 November 2011

A&A 535, A71 (2011)

Mass loss, destruction and detection of Sun-grazing and -impacting cometary nuclei^⋆

J. C. Brown¹^,4^,5, H. E. Potts¹, L. J. Porter¹^,2 and G. Le Chat¹^,3

¹ School of Physics and Astronomy, University of Glasgow, G12 8QQ, UK
e-mail: john.brown@glasgow.ac.uk
² Max-Planck-Institut für Astrophysik, 85748 Garching, Germany
³ LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Diderot, 92190 Meudon, France
⁴ NCAR High Altitude Observatory, Boulder, CO 80303, USA
⁵ Astrophysics Research Group. Trinity College, Dublin (TCD), Ireland

Received: 30 August 2010
Accepted: 12 October 2011

Abstract

Context. Sun-grazing comets almost never re-emerge, but their sublimative destruction near the sun has only recently been observed directly, while chromospheric impacts have not yet been seen, nor impact theory developed.

Aims. We seek simple analytic models of comet destruction processes near the sun, to enable estimation of observable signature dependence on original incident mass M_o and perihelion distance q.

Methods. Simple analytic solutions are found for M(r) versus q and distance r for insolation sublimation and, for the first time, for impact ablation and explosion.

Results. Sun-grazers are found to fall into three (M_o,q) regimes: sublimation-, ablation-, and explosion-dominated. Most sun-grazers have M_o too small (<10¹¹ g) or q too large (>1.01R_⊙) to reach atmospheric densities (n > 2.5 × 10¹¹/cm³) where ablation exceeds sublimation. Our analytic results for sublimation are similar to numerical models. For q < 1.01R_⊙,M_o > 10¹¹ g, ablation initially dominates but results are sensitive to nucleus strength P_c = 10⁶P₆ dyne/cm² and entry angle φ to the vertical. Nuclei with M_o ≼ 10¹⁰(P₆secφ)³ g are fully ablated before exploding, though the hot wake itself explodes. For most sun-impactors secφ ≫ 1 (since q ~ r_∗), so for q very close to r_∗ the ablation regime applies to moderate 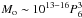$M_{o} ~ 10^{13 - 16} P_{6}^{3}$ $\hbox{$M_{\rm o} \sim 10^{13-16}P_6^3$}$ g impactors unless P₆ ≼ 0.1. For higher masses, or smaller q, nuclei reach densities n > 2.5 × 10¹⁴P₆/cm³ where ram pressure causes catastrophic explosion.

Conclusions. Analytic descriptions define (M_o,q) regimes where sublimation, ablation and explosion dominate sun-grazer/-impactor destruction. For q ≺ 1.01R_⊙,M_o ≽ 10¹¹ g nuclei are destroyed by ablation or explosion (depending on M_ocos³φ/P_c) in the chromosphere, producing flare-like events with cometary abundance spectra. For all plausible M_o,q and physical parameters, nuclei are destroyed above the photosphere.

Key words: Sun: flares / comets: general / Sun: general

^⋆

This paper is dedicated to the memories of: Brian G. Marsden, world expert on minor bodies of the solar system and an irreplaceable friend and colleague; Gerald S. Hawkins who introduced me to the joys of this field in my (J.C.B.’s) first real (radar meteor) research experience at HSRAO/CfA in the summer of 1967.

© ESO, 2011

1. Introduction

Close sun-grazing comets are discovered almost daily by white light coronagraphs (e.g., SoHO LASCO). Most are small and fully sublimated by insolation at a few solar radii R_⊙ while almost none have re-emerged (Marsden 2005). The majority have perihelion distances q well above R_⊙ but some have q ≈ or ≺ R_⊙ (e.g., Marsden 2005 and http://www.minorplanetcenter.org/mpec/RecentMPECs.html.) The death of a comet at r ~ R_⊙ has been seen directly only very recently (Schrijver et al. 2011) using the SDO AIA XUV instrument. This recorded sublimative destruction of Comet C/2011 N3 as it crossed the solar disk very near perihelion q = 1.139R_⊙. The next challenge in studying the demise of close sun-grazers will be to catch one of the even rarer cases of chromospheric impact (q < 1.01R_⊙, M_o > 10¹¹ g). As anticipated by Weissman (1983) and shown below, these undergo explosive destruction in the dense chromosphere. Understanding the destruction processes, and their radiation signatures, are essential steps in searching for and modeling these.

The processes leading to sublimation of the icy conglomerate mix (Whipple 1950) of cometary nuclei, and in some cases their splitting and fragmentation, were considered by Huebner (1967), Weissman & Kieffer (1981), Weissman (1983), Iseli et al. (2002), Sekanina (2003) and others. These models essentially solve for the insolative sublimation mass loss rates of icy-conglomerate mixes (the dust being carried away in the flow of these evolved components). They variously allow for the complicating factors of rotation, albedo, insulating surface dust layers, radiative cooling, interior thermal conduction, and fragmentation by tidal, thermal and volatile explosion effects. Huebner (1967) and Iseli et al. (2002), for example, found that, for high sublimation rates near the sun, these effects were secondary, the mass loss being reasonably approximated by a pure sublimation description: mass loss rate = heating rate/latent heat. Using SoHO data, Sekanina (2003) addressed in detail how mass loss rates and fragmentation relate to cometary light curves via atomic line emission (e.g., by sodium) and by dust scattering of sunlight, though emphasising that most of the mass remains in a primary fragment. None of these studies considered ablation or ram-pressure driven explosion due to solar atmospheric impact (which we show below are negligible till r ≼ 1.01R_⊙) though Weissman (1983) had remarked “ultimate destruction of the nucleus [of sun-impacting comets] likely results from the shock of hitting the denser regions of the solar atmosphere”. It is well known in the planetary physics community that ablation and explosion are central processes in comet-planetary atmosphere impacts (e.g., Carslon et al. 1997).

Here we revisit the theory of sun-grazer sublimation then develop the first estimates of the much higher rates of mass loss by ablation for the rarer cases which reach ≼ 1.01R_⊙. This regime (Sects. 3.4, 6.1, 6.2) resembles that of comet-planetary impacts though with some differences. One is that almost all sun-grazing comets belong to secondary comet groups (mostly Kreutz) formed from primordial comets. A significant number of the latter must have q < R_⊙ (Hughes 2001) and large enough mass (M_o ≽ 10¹¹ g – see Sect. 5, Eq. (27)) to survive sublimation down to the intense ablation/explosion regime. However only a small fraction of group comets (Biesecker et al. 2003; Knight et al. 2010) come that close or are that massive, larger sun-grazers mostly having q ≽ 1.5R_⊙. Comet C/2010 E6 (STEREO) discussed by Raftery et al. (2010) came close, having q ≈ 1.02R_⊙ while the destruction of Comet C/2011 N3 seen by SDO (Schrijver et al. 2011) on the solar disk was solely by sublimation as it had q ≈ 1.14R_⊙. Most of the few group comets reaching the ablation/explosion regimes will have small mass and very shallow incidence angles (since q ≈ R_⊙) with implications for the relative importance of ablation and explosion. By analogy with models of planetary atmospheric impacts (e.g., Carlson et al. 1997), chromospheric impactors are expected to lose mass, momentum and kinetic energy very rapidly, the soaring temperature and pressure leading to destructive detonation of the nucleus and its wake. This “air burst” should be followed by explosive expansion of the resulting “fireball” of cometary and solar atmospheric material. The total masses and energies of these explosive chromospheric events are in roughly the same range as those of solar magnetic flares so they could be termed “cometary flares”.

Section 2 discusses relevant nucleus parameter values while Sect. 3 estimates the relative importance and time/distance-scales of nucleus mass loss, explosion, and deceleration processes. We then consider in some detail approximate analytic treatment of mass loss (Sect. 4) purely by sublimation (Sect. 5) and by ablation and explosion (Sect. 6).

2. Comet nucleus parameters

2.1. Masses and densities

In the past there was wide range of opinions over the masses M_o and mean mass densities ρ of the icy-conglomerate mix thought to comprise comet nuclei, and on how these quantities varied between different comets (Whipple 1950). We simply take the incident mass M_o to be a parameter ranging from the faintest comets detected almost daily to the largest super-massive comets. Concerning the density ρ, MacLow & Zahnle (1994) said “the density of comets is the stuff of speculation [probably] 0.3–1.0 g/cm³ but with extreme claims of 0.01–5”. In his sublimation modeling Sekanina (2003) used ρ = 0.15 g/cm³. More recently, however, Weissman & Lowry (2008) critically discussed results from a range of methods and data, including Deep Impact. All results have a considerable error range, but they conclude that ρ = 0.6 ± 0.2 g/cm³ is the most likely range for the comets they studied (cf., Richardson et al. 2007). Here we therefore also take ρ as a parameter, and express it relative to that of (water) ice ρ_ice = 0.9 g/cm³ via the dimensionless scaling parameter 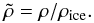$\begin{matrix} ˜ \\ ρ \end{matrix} = ρ / ρ_{ice} .$ $\begin{equation} \label{deftilderho} \tilde{\rho}=\rho/\rho_{\rm ice}. \end{equation}$ (1)In discussing results we mainly use a mean value 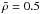$\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5$ $\hbox{$\tilde{\rho}=0.5$}$ (ρ ≈ 0.45 g/cm³) though showing how results, such as for M_o, can be scaled for other values (see Eq. (20) and Fig. 1).

2.2. Latent heat of sublimation

The major nucleus parameter determining its rate of mass loss for power input $\hbox{${\cal P}$}$ (erg/s) is the mean latent heat ℒ (erg/g) of sublimation/ablation for the cometary ice-conglomerate mix. The value for water ice is about 2.6 × 10¹⁰ erg/g. This is of order the relevant value when the mass lost is in the form of water vapor whose pressure sweeps dust and other non-volatiles away with it. However, in situations of intense ablation and explosion, all components are eventually vaporized and the relevant value is the weighted mean over all mass components, including volatile and refractory ones. Sekanina (2003) finds values for what he terms “effective latent heat of erosion” to be around 0.3 of the water ice value. However Huebner et al.’s (2006) mass composition [Silicates:organics:carbonaceous:ices] = [0.26:0.23:0.086: 0.426] suggests refractory silicates to be the most important non-ice component. Mendis (1975) give ℒ = 2.30 × 10¹⁰ erg/g for silicates, which is close to that of water ice, while organics will lower the mean slightly. Chyba et al. (1993) adopted 2.3 × 10¹⁰ erg/g for comets, 5 × 10¹⁰ erg/g for carbonaceous and 8 × 10¹⁰ erg/g for stone/iron bodies and just 10¹¹ erg/g even for solid iron. 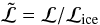Here we use the water ice value for ℒ as a reasonable first approximation, but include a dimensionless scaling parameter $\begin{matrix} ˜ \\ ℒ \end{matrix} = ℒ / ℒ_{ice}$ $\begin{equation} \label{deftildecalL} \tilde{{\cal L}}={\cal L}/{\cal L}_{\rm ice} \end{equation}$ (2)to allow application to other ℒ values though adopting 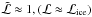$\begin{matrix} _{˜} \\ ℒ \end{matrix} \approx 1, (ℒ \approx ℒ_{ice})$ $\hbox{$\tilde{{\cal L}} \approx 1,\linebreak ({\cal L}\approx {\cal L}_{\rm ice})$}$ , in most numerical evaluations. To convert to other values see Fig. 1 and Eq. (20).

2.3. Physical strength and sound speed

The effects on the nucleus of the pressure associated with the processes driving sublimation/ablation depend on how strong the nucleus material is and how fast pressure waves propagate through its volume. In the initial stages the relevant strength is that of the loose low density ice-conglomerate mix, estimated by Zahnle & MacLow (1994) to be a pressure ( ≈ energy density) of P_c ≈ 10⁶ dyne/cm²( ≡ erg/cm³) while values discussed by Chyba et al. (1993) range from 10⁸ dyne/cm² for very solid asteroid-like bodies to 10⁵ dyne/cm² for fluffy snowy structures. The last value is also that estimated by Richardson et al. (2007) for Comet 9P/Tempel 1 using Deep Impact data, while tidal disruption data suggest the possibility of even lower values for some comets. Here we allow consideration of a range of values by parametrically setting P = 10⁶P₆ dyne/cm² and specifically discuss the range P₆ = 0.1 − 1. For the sound speed, Zahnle & MacLow (1994) suggest c_s ≈ 1 − 3 × 10⁵ cm/s for the initial state nucleus material. Values for a range of more or less solid materials do not differ greatly.

2.4. Nucleus shape and “size”

For a given density the mass loss, deceleration and explosion rates for a nucleus depend on its volume V and effective area A which depend on its size scale “a” and shape. Since nuclei have irregular and uncertain shapes, as evidenced by images and light curves, rather than treat precisely the hypothetical case of a sphere, we will use A ≈ a²,V ≈ a³ for an effective mean size a. This formulation gives A and V correctly to within 10% for the case of a sphere of radius b if we adopt a ≈ 1.67b. We use this later when referring to spherical cases for illustration (Sects. 5.2.2 and 5.3).

3. Rough comparison of nucleus mass loss, deceleration and explosion processes

3.1. “Evaporative” mass loss versus deceleration

Whether mass loss from the nucleus is by sublimation or by ablation, the total energy needed to vaporize the whole nucleus is ℰ_vap = M_oℒ while the energy needed to stop it is 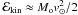$ℰ_{kin} \approx M_{o} v_{⊙}^{2} / 2$ $\hbox{${\cal E}_{\rm kin}\approx M_{\rm o}v_\odot^2/2$}$ . The ratio is tiny, 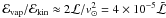$ℰ_{vap} / ℰ_{kin} \approx 2 ℒ / v_{⊙}^{2} = 4 \times 10^{-5} \begin{matrix} _{˜} \\ ℒ \end{matrix}$ $\hbox{${\cal E}_{\rm vap}/{\cal E}_{\rm kin} \approx 2{\cal L}/v_\odot^2= 4\times 10^{-5}\tilde{\cal L}$}$ for the solar escape speed 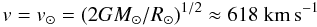$v = v_{⊙} = (2 G M_{⊙} / R_{⊙})^{1 / 2} \approx 618 km s^{-1}$ $\begin{equation} \label{defvodot} v=v_\odot=(2GM_\odot/R_\odot)^{1/2}\approx 618~{\rm km\,s^{-1}} \end{equation}$ (3)with G,M_⊙,R_⊙ the gravitational constant, solar mass, and solar radius respectively. Thus total vaporization can occur well before the nucleus decelerates significantly, though ram pressure can result in explosive destruction dominating. Equivalently, to conserve momentum in slowing down, the nucleus must encounter an atmospheric mass comparable to M_o. In doing so it absorbs far more energy than needed to vaporize it. The mass per unit area (g cm^-2) of a comet nucleus is 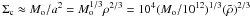$Σ_{c} \approx M_{o} / a^{2} = M_{o}^{1 / 3} ρ^{2 / 3} = 10^{4} (M_{o} / 10^{12})^{1 / 3} (\begin{matrix} _{˜} \\ ρ \end{matrix})^{2 / 3}$ $\hbox{$\Sigma_{\rm c}\approx M_{\rm o}/a^2=M_{\rm o}^{1/3}\rho^{2/3}=10^4(M_{\rm o}/10^{12})^{1/3}(\tilde{\rho})^{2/3}$}$ g cm^-2 while that of the sun’s atmosphere even down to the photosphere is only Σ_⊙ ≈ 1 g cm^-2. Consequently, unless they explode, increasing the deceleration, only objects of <10³ g or so would be much decelerated by the mass of the sun’s atmosphere down to the photosphere though, in practice, they would be vaporized earlier by sublimation and/or ablation. Note also that, at infall speed v_⊙, in the frame of the nucleus a solar atmospheric proton has kinetic energy ~2 keV which is enough to knock off about 4000 water molecules, or about 10⁵ times its own mass.

This situation of initial ablative mass loss without significant deceleration is paralleled by the dynamics in planetary atmospheres of meteors – e.g., McKinley (1961), Kaiser (1962) – and at least of the initial (high altitude) stages of comet-planet impacts – e.g., Shoemaker Levy 9 with Jupiter – cf. Sect. 6.

In the sublimation regime the radiation has negligible effect on the nucleus speed, even though it delivers a large amount of energy. Specifically the ratio of the radiation pressure force F_rad to the gravitational is (ignoring the correction factor 1.0–2.0 for albedo) 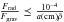$\frac{F_{rad}}{F_{grav}} ≼ \frac{10^{-4}}{a (cm) \begin{matrix} _{˜} \\ ρ \end{matrix}}$ $\hbox{$\frac{F_{\rm rad}}{F_{\rm grav}}\preceq \frac{{10^{-4}}}{a({\rm cm})\tilde{\rho}}$}$ . The radiation pressure F_rad/c ≃ 2 dyne/cm² is also tiny compared to the nucleus strength P_c so causes no direct explosion effect. It is also straightforward to show that, during perihelion passage, the rocket effect of mass loss leaving the nucleus anisotropically has negligible effect on v during vaporization. This is because the very high nucleus ρ value implies very low mass loss speed u and hence momentum flux. Consequently, the velocity of the nucleus during its vaporization is well approximated by that of a gravitational parabolic orbit, viz., in orbital plane polar coordinate (r,θ) and for perihelion distance q 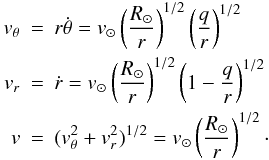$\begin{matrix} v_{θ} & = & r θ̇ = v_{⊙} {(\frac{R_{⊙}}{r})}^{1 / 2} {(\frac{q}{r})}^{1 / 2} \\ v_{r} & = & ṙ = v_{⊙} {(\frac{R_{⊙}}{r})}^{1 / 2} {(1 - \frac{q}{r})}^{1 / 2} \\ v & = & (v_{θ}^{2} + v_{r}^{2})^{1 / 2} = v_{⊙} {(\frac{R_{⊙}}{r})}^{1 / 2} \cdot \end{matrix}$ $\begin{eqnarray} \label{veloccomps} v_\theta &=& r\dot{\theta}= v_\odot \left(\frac{R_\odot}{r}\right)^{1/2}\left(\frac{q}{r}\right)^{1/2}\nonumber\\ v_r&=&\dot{r}= v_\odot \left(\frac{R_\odot}{r}\right)^{1/2}\left(1-\frac{q}{r}\right)^{1/2}\nonumber\\ v&=&(v_\theta^2+v_r^2)^{1/2}= v_\odot\left(\frac{R_\odot}{r}\right)^{1/2}\cdot \end{eqnarray}$ (4)

3.2. Deceleration of sublimated/ablated mass

While, throughout the total vaporization lifetime of the nucleus, its velocity is well described by Eqs. (4), this is not true of the material it loses. Small particles leaving the nucleus do not obey Eqs. (4), non-gravitational accelerations on them being very important. These include F_rad on sub-micron particles and atmospheric drag on atoms and ions. The Coulomb collisional stopping column density for a proton of speed v_⊙ ≈ 618 km s^-1 (~2 keV) in a hydrogen plasma is around 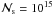$\hbox{${\cal N}_{\rm s}=10^{15}$}$ cm^-2 (Emslie 1978). Thus the stopping distance at number density n is 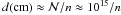$\hbox{$d ({\rm cm}) \approx {\cal N}/n\approx 10^{15}/n$}$ , i.e. just 1 km in the corona and 0.1 mm in the photosphere. So ablated dust and ions stop abruptly and form an exploding wake as they blend with and heat the atmosphere, creating large local enhancements of heavy element abundances.

3.3. Insolation sublimation case q ≽ r_∗, M_o ≼ 10¹¹ g

Very near the sun, the timescale for sublimation of the whole mass is 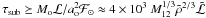$τ_{sub} ≽ M_{o} ℒ / a_{o}^{2} ℱ_{⊙} \approx 4 \times 10^{3} M_{12}^{1 / 3} {ρ^{2 / 3}}_{˜} \begin{matrix} _{˜} \\ ℒ \end{matrix}$ $\hbox{$\tau_{\rm sub}\succeq M_{\rm o}{\cal L}/a_{\rm o}^2{\cal F}_\odot \approx 4\times 10^3~M_{12}^{1/3}\tilde{\rho}^{2/3}\tilde{{\cal L}}$}$ s, where ℱ_⊙ = 6 × 10¹⁰ erg/cm²/s is the bolometric photospheric energy flux and M₁₂ = M_o/10¹² g. The corresponding distance scale is roughly 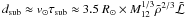$d_{sub} \approx v_{⊙} τ_{sub} \approx 3.5 R_{⊙} \times M_{12}^{1 / 3} {ρ^{2 / 3}}_{˜} \begin{matrix} _{˜} \\ ℒ \end{matrix}$ $\hbox{$d_{\rm sub}\approx v_\odot\tau_{\rm sub}\approx 3.5~R_\odot\times M_{12}^{1/3}\tilde{\rho}^{2/3}\tilde{{\cal L}}$}$ cm as first seen directly by Schrijver et al. (2011). Total sublimation occurs in a close perihelion passage roughly for d_sub ≼ R_⊙ which is the case for masses 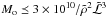$M_{o} ≼ 3 \times 10^{10} / {ρ^{2}}_{˜} \begin{matrix} _{˜} \\ ℒ^{3} \end{matrix}$ $\hbox{$M_{\rm o}\preceq 3\times 10^{10}/ \tilde{\rho}^2\tilde{{\cal L}}^3$}$ g or about 10¹¹ g for 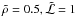$\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\hbox{$\tilde{\rho}= 0.5,\tilde{{\cal L}}=1$}$ . This shows the majority of close sun-grazers (q ≽ 1.01R_⊙) to have M_o ≼ 10¹¹ g as they never re-emerge.

3.4. Impact ablation and ram pressure explosion cases

3.4.1. Background

The problems of comet, asteroid, and even large meteoroid impact with planetary atmospheres closely parallel those of a solar impact, though the parameter regimes are rather different, and there is no planetary equivalent of insolation. Unlike the solar case, planetary impacts have been addressed in detail, early work including that of Revelle (1979) and others. Progress was greatly accelerated in anticipation, and in the aftermath, of the collisions of fragments of Comet Shoemaker-Levy 9 with Jupiter in July 1994. Many authors (e.g., Chyba et al. 1993; Chevalier & Sarazin 1994; Zahnle & MacLow 1994) developed semi-analytic and numerical models to predict what should be expected of these impacts. Others, notably MacLow & Zahnle (1994), Field & Ferrara (1995) and Carlson et al. (1995, 1997), developed models further by drawing on actual event data. In particular the Carlson et al. (1995, 1997) “heuristic model” combined data analysis, numerical simulations, and observational inputs. They identified and addressed both the “bolide initial phase” (which we have called the detonation or airburst) and the subsequent “fireball” exploding out and up from the nucleus and its wake. Detailed observations of the G-fragment impact were synthesised with their numerical simulations of the fireball (e.g., their Fig. 7). Chyba et al. (1993), Zahnle & MacLow (1994) and MacLow & Zahnle (1994) showed that the airburst phase is dominated by ablation only in the upper atmosphere, and below that by catastrophic pressure-driven disruption. In the Jupiter case, the latter is true for all impacting masses except those very much smaller than that ( ≈ 10¹⁵ g) of the Shoemaker-Levy 9 fragments in 1994. We summarize here the essence of the arguments leading to these conclusions so that we can adapt them to the somewhat different conditions of solar impacts.

3.4.2. Rough comparison of the importance of impact processes

The relative importance of ablation, explosion and deceleration in the initial destruction of the nucleus depends on atmospheric scale height H as well as on the nucleus mass, speed and entry angle. They can be expressed in terms of the atmospheric column densities 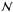$\hbox{$\cal N$}$ (cm^-2) = ^∫_snds traversed along the path s of the nucleus after which each process is complete. (The vertical column density 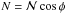$\hbox{$N={\cal N}\cos \phi$}$ for constant path angle φ to the vertical.) First, to deliver enough energy to ablate the whole mass (without expansion) requires an encounter with column density 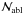$\hbox{${\cal N}_{\rm abl}$}$ such that 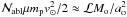$𝒩_{abl} μ m_{p} v_{⊙}^{2} / 2 \approx ℒ M_{o} / a_{o}^{2}$ $\hbox{${\cal N}_{\rm abl}\mu { m}_{\rm p} v_\odot^2/2 \approx {\cal L}M_{\rm o}/a_{\rm o}^2$}$ where m_p is the proton mass and μ the mean mass present per H (atoms and ions) in units of m_p. This implies 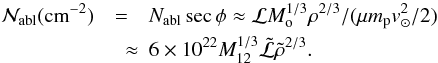$\begin{matrix} 𝒩_{abl} ({cm}^{-2}) & = & N_{abl} \sec φ \approx ℒ M_{o}^{1 / 3} ρ^{2 / 3} / (μ m_{p} v_{⊙}^{2} / 2) \\ \approx & 6 \times 10^{22} M_{12}^{1 / 3} \begin{matrix} ˜ \\ ℒ \end{matrix} {ρ^{2 / 3}}_{˜} . \end{matrix}$ $\begin{eqnarray} \label{Nabl} {\cal N}_{\rm abl} ({\rm cm}^{-2})&=&N_{\rm abl}\sec \phi\approx {\cal L}M_{\rm o}^{1/3}\rho^{2/3}/(\mu {m}_{\rm p} v_\odot^2/2) \nonumber\\ &\quad \approx& 6\times 10^{22}M_{12}^{1/3}\tilde{{\cal L}}\tilde{\rho}^{2/3}. \end{eqnarray}$ (5)Total deceleration of the nucleus (without expansion) requires 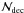$\hbox{${\cal N}_{\rm dec}$}$ such that 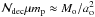$𝒩_{dec} μ m_{p} \approx M_{o} / a_{o}^{2}$ $\hbox{${\cal N}_{\rm dec}\mu {m}_{\rm p} \approx M_{\rm o}/a_{\rm o}^2$}$ implying 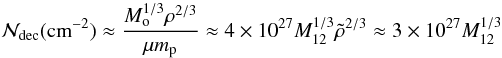$𝒩_{dec} ({cm}^{-2}) \approx \frac{M_{o}^{1 / 3} ρ^{2 / 3}}{μ m_{p}} \approx 4 \times 10^{27} M_{12}^{1 / 3} {ρ^{2 / 3}}_{˜} \approx 3 \times 10^{27} M_{12}^{1 / 3}$ $\begin{equation} \label{Ndec} {\cal N}_{\rm dec} ({\rm cm}^{-2})\approx \frac{M_{\rm o}^{1/3}\rho^{2/3}}{\mu {m}_{\rm p}}\approx 4\times 10^{27}M_{12}^{1/3}\tilde{\rho}^{2/3}\approx 3\times 10^{27}M_{12}^{1/3} \end{equation}$ (6)which is ≫ 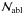$\hbox{$ {\cal N}_{\rm abl}$}$ . For internal strength (energy density) P_c = 10⁶P₆ dyne/cm², nuclei will undergo hydrodynamic flow once they reach the depth where atmospheric ram pressure 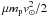$μ m_{p} v_{⊙}^{2} / 2$ $\hbox{$\mu {m}_{\rm p} v_\odot^2/2$}$ approaches the value P_c. This implies an atmospheric proton density 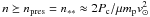$n ≽ n_{pres} = n_{* *} \approx 2 P_{c} / μ m_{p} v_{⊙}^{2}$ $\hbox{$n \succeq n_{\rm pres}=n_{**}\approx 2 P_{\rm c}/\mu {m}_{\rm p} v_\odot^2$}$ . The corresponding column density 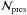$\hbox{${\cal N}_{\rm pres}$}$ along the path for atmospheric scale height H = 10⁸H₈ cm is 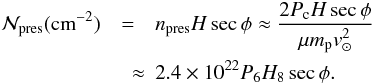$\begin{matrix} 𝒩_{pres} ({cm}^{-2}) & = & n_{pres} H \sec φ \approx \frac{2 P_{c} H \sec φ}{μ m_{p} v_{⊙}^{2}} \\ \approx & 2.4 \times 10^{22} P_{6} H_{8} \sec φ . \end{matrix}$ $\begin{eqnarray} \label{Npres} {\cal N}_{\rm pres} ({\rm cm}^{-2})&=&n_{\rm pres}H\sec\phi\approx \frac{2P_{\rm c}H \sec \phi}{\mu {m}_{\rm p} v_\odot^2} \nonumber\\ &\quad \approx & 2.4 \times 10^{22} P_6 H_8 \sec \phi. \end{eqnarray}$ (7)The ratio of critical 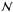$\hbox{$\cal N$}$ for ablation end to ram pressure onset is (Eqs. (5, 7)) 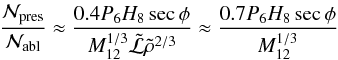$\frac{𝒩_{pres}}{𝒩_{abl}} \approx \frac{0.4 P_{6} H_{8} \sec φ}{M_{12}^{1 / 3} \begin{matrix} ˜ \\ ℒ \end{matrix} {ρ^{2 / 3}}_{˜}} \approx \frac{0.7 P_{6} H_{8} \sec φ}{M_{12}^{1 / 3}}$ $\begin{equation} \label{NablovrNPres} \frac{{\cal N}_{\rm pres}}{{\cal N}_{\rm abl}}\approx \frac{0.4P_6 H_8\sec\phi}{M_{12}^{1/3}\tilde{{\cal L}}\tilde{\rho}^{2/3}} \approx \frac{0.7P_6 H_8\sec\phi}{M_{12}^{1/3}} \end{equation}$ (8)where the last expression is for 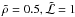$\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\hbox{$\tilde{\rho}=0.5,\tilde{{\cal L}}=1$}$ . There is thus a maximum mass 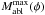$M_{abl}^{\max} (φ)$ $\hbox{$M_{\rm abl}^{\rm max}(\phi)$}$ above which destruction of the nucleus is driven by explosion rather than ablation, namely (setting ratio (8) to unity) $\begin{matrix} M_{abl}^{\max} (φ_{*}) & = & M_{* *} \sec^{3} φ \approx 6 \times 10^{10} {[\frac{P_{6} H_{8} \sec φ}{\begin{matrix} ˜ \\ ℒ \end{matrix} {ρ^{2 / 3}}_{˜}}]}^{3} g \\ \approx & 2.4 \times 10^{11} [P_{6} H_{8} \sec φ]^{3} g \end{matrix}$ $\begin{eqnarray} \label{MAblmax} M_{\rm abl}^{\rm max}(\phi_*) & =& M_{**}\sec^3\phi\approx 6\times 10^{10}\left[\frac{P_6 H_8\sec\phi}{\tilde{{\cal L}}\tilde{\rho}^{2/3}}\right]^3 {\rm g} \nonumber\\ &\quad \approx& 2.4\times 10^{11}[P_6 H_8\sec\phi]^3{\rm g} \end{eqnarray}$ (9)the last value again for $\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\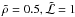hbox{$\tilde{\rho}=0.5,\tilde{{\cal L}}=1$}$ . (Note – In the rest of this paper we use subscripts _∗ and _∗∗ respectively for values of quantities at the points where ablation first exceeds sublimation, and _∗∗ where explosion first becomes dominant.)

Thus although ram pressure sets in at a lower n for the sun than for Jupiter (because v is higher) the same v dependence occurs in the ablation expression so the ratio (8) just scales as 1/H and reaches unity only at a higher n in the solar case. 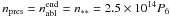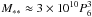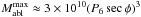For solar H₈ ~ 0.5 we find $n_{pres} = n_{abl}^{end} = n_{* *} = 2.5 \times 10^{14} P_{6}$ $\hbox{$n_{\rm pres}=n_{\rm abl}^{\rm end} = n_{**}=2.5\times 10^{14}P_6$}$ cm^-3 while $M_{* *} \approx 3 \times 10^{10} P_{6}^{3}$ $\hbox{$M_{**}\approx 3 \times 10^{10}P_6^3$}$ g and $M_{abl}^{\max} \approx 3 \times 10^{10} (P_{6} \sec φ)^{3}$ $\hbox{$M_{\rm abl}^{\rm max}\approx 3\times 10^{10}(P_6\sec\phi)^3$}$ g. In the case of impacts with Jupiter H₈ ~ 0.01 − 0.1 so, for relatively steep impacts (secφ ≼ 2), Eqs. (8, 9) show that ram pressure will cause explosion before ablation is complete for 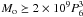$M_{o} ≽ 2 \times 10^{9} P_{6}^{3}$ $\hbox{$M_{\rm o}\succeq 2\times 10^9P_6^3$}$ g. Thus, as argued by Chyba et al. (1993), Zahnle & MacLow (1994) and Carlson et al. (1997), for steep planetary impacts the ablation process is secondary to pressure-driven explosion except for small masses (or extremely shallow entry) and during the initial entry phase. In the case of solar chromospheric impacts, however, H₈ = 0.5 is larger so that the maximum ablation-dominated mass (after sublimation losses) is around 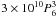$3 \times 10^{10} P_{6}^{3}$ $\hbox{$3\times 10^{10}P_6^3$}$ g for steep entry. However, most sun-impactors have q ≈ R_⊙ and secφ ≫ 10. Thus the maximum ablation-dominated mass for these is ≫ 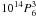$10^{14} P_{6}^{3}$ $\hbox{$ 10^{14}P_6^3$}$ g as discussed further in Sect. 6.1.

In the planetary impact literature two factors are discussed which act to limit ablation and we show briefly here why they are less relevant to the solar case. The first is possible overestimation of the drag coefficient – we have taken the nucleus effective area to equal its geometrical area, which is an overestimation for fluid flow round an obstacle. However, for the solar case the nucleus speed is so high and the atmospheric density so low that we can reasonably use a kinetic description and treat the particles as impacting the nucleus directly rather than flowing around it. We note, however, that our kinetic approach may break down toward the lower chromosphere relevant to very heavy nuclei and steeper incidence angles. There the high density results in a shorter collisional mean free path and more fluid like behavior with only indirect ablation via the radiation from a stand-off shock. This can decrease the drag coefficient considerably so that our ablation and deceleration rates are overestimates there. Secondly, it has been argued in the planetary case (e.g., Zahnle & MacLow 1994) that ablation is limited by the loss of energy needed to ionize hydrogen. However, the solar atmosphere is around 100 times hotter than Jupiter’s atmosphere and is already substantially ionized at least in the upper chromopshere. Further, solar impacting protons have keV kinetic energies – far higher than H ionization energy (13.6 eV) and than the 10 eV value for Jupiter so direct impact ionization is very effective in the sun but not Jupiter. Again, however, heavier and steeper entry nuclei reaching the deep chromosphere are in a cooler medium of lower ionization so energy lost to ionization may become significant and our ablation rate an overestimate.

4. Theory of nucleus sublimation/ablation

4.1. General formulation

Having discussed orders of magnitude we now want to model the evolution of evaporative mass loss along the comet path. We take the nucleus to have constant ρ and to shrink due to mass loss, neglecting for now any pressure driven explosion or distortion which we address later. The changing M(r) and a(r) are then functions of distance r from the solar centre. 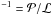We treat mass loss (by sublimation or ablation) via the simple approximation that a heating/energy deposition rate of $\hbox{$\cal P$}$ erg s^-1 results in mass loss rate Ṁ g s $\hbox{$^{-1}= {\cal P}/ {\cal L}$}$ with the relevant ρ,ℒ values averages over the icy conglomerate components (Sects. 2.1 and 2.2.) For the sublimation case the dominant power required for loss of mass from the nucleus is that for sublimation of the ices only, the solid dust particles released escaping with the vapor outflow. That is, fairly near the sun at least, the power going into sublimation is larger than that going into further heating offset by cooling – e.g., Weissman (1993), Sekanina (2003). (Far from the sun our neglect of cooling etc will overestimate the mass loss rate). For the ablation case, heating is intense and vaporizes all components, including the most non-volatile ones but (Sect. 2.3), the overall ℒ is similar to ℒ_ice. We further assume that all mass lost clears the nucleus quickly enough for incident energy fluxes to act directly on it – i.e. the mass loss does not obstruct the mass loss driver. To justify this, we note that latent heat ℒ is equivalent to a speed ~2ℒ^1/2 ~ 2.3 × 10⁵ cm/s. If vaporized material outflow occurs at this speed then, on the timescale H/v_⊙cosφ ~ 10 s relevant to ablation, it clears nuclei of a_o ≼ 2.3 × 10⁶ or M_o ≼ 10¹⁹ g so our assumption is justified except for very large masses. These are in any case destroyed by explosion rather than ablation. In the case of sublimation the mass loss rate is much lower (Sect. 3.3) so the approximation is very good.

Then, for an incident energy flux ℱ (erg cm^-2 s^-1), 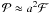$\hbox{${\cal P} \approx a^2 {\cal F}$}$ and, with a² = (M/ρ)^2/3, and constant ρ and shape, we get 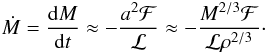$Ṁ = \frac{d M}{d t} \approx - \frac{a^{2} ℱ}{ℒ} \approx - \frac{M^{2 / 3} ℱ}{ℒ ρ^{2 / 3}} \cdot$ $\begin{equation} \label{dM/dt} \dot M = \frac{{\rm d}M}{{\rm d}t}\approx -\frac{a^2{\cal F}}{{\cal L}}\approx -\frac{M^{2/3}\cal F}{{\cal L} \rho^{2/3}}\cdot \end{equation}$ (10)Note that we consider only mass loss in the one hemisphere (cross section ≈ a²) containing flux ℱ since rotation times are long (Samarachinha et al. 2004) compared to the short near-sun mass-loss time scale. Using Eq. (4) to express dt = −dr/v_r we can eliminate t from Eq. (10) and express it as a differential equation for the fractional mass m = M(r)/M_o remaining as a function of r, viz. 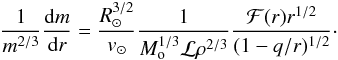$\frac{1}{m^{2 / 3}} \frac{d m}{d r} = \frac{R_{⊙}^{3 / 2}}{v_{⊙}} \frac{1}{M_{o}^{1 / 3} ℒ ρ^{2 / 3}} \frac{ℱ (r) r^{1 / 2}}{(1 - q / r)^{1 / 2}} \cdot$ $\begin{equation} \label{dm/dx} \frac{1}{m^{2/3}}\frac{{\rm d}m}{{\rm d}r}=\frac{R_\odot^{3/2}}{v_\odot}\frac{1}{M_{\rm o}^{1/3}{\cal L }\rho^{2/3}}\frac{{\cal F}(r)r^{1/2}}{(1-q/r)^{1/2}}\cdot \end{equation}$ (11)This can be integrated for any specified form of ℱ(r) with boundary condition m(r → ∞) = 1. We have formulated the problem in terms of r dependence since this allows analytic treatment. Conversion to the time domain can be done numerically via Barker’s equation (cf. results in Porter 2007, 2008).

4.2. Heating energy flux terms and regimes

(a) Absorbed insolation energy flux for albedo ≪ 1 is 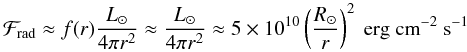$ℱ_{rad} \approx f (r) \frac{L_{⊙}}{4 π r^{2}} \approx \frac{L_{⊙}}{4 π r^{2}} \approx 5 \times 10^{10} {(\frac{R_{⊙}}{r})}^{2} {erg cm}^{-2} s^{-1}$ $\begin{equation} \label{Frad} {{\cal F}_{\rm rad}} \approx f(r)\frac{L_\odot}{ 4\pi r^2}\approx \frac{L_\odot}{ 4\pi r^2}\approx 5\times 10^{10}\left(\frac{R_\odot}{r}\right)^2~{\rm erg~ cm}^{-2}~{\rm s}^{-1} \end{equation}$ (12)where f(r) is the factor by which the heating rate at r exceeds our estimate in Eq. (12) where we use the approximation of near radial insolation. As r → R_⊙ non-radial insolation from the finite solar disk increases and for a sphere just above the photosphere the maximum is f(R_⊙) = 2 ( = 4 below the photosphere) but this can increase the mass required to survive insolation 8-fold. f(r) declines above r = R_⊙, is shape dependent, and partly offset by the cooling processes we have neglected but our use of f ~ 1 must be borne in mind in considering our results.
(b) Ablation energy flux Impacting solar protons have a collisional mean free path (mfp) in nucleus material (n ≈ 10²³ cm^-3) of order 10^-6 cm (cf. Brown 1972; Emslie 1978) while in the atmosphere at n > n_∗ = 2.5 × 10¹¹, the mfp is ~ 4 × 10⁵ cm, much bigger than most nuclei. Furthermore, the nucleus speed is highly supersonic (~Mach 50 in the chromosphere). Thus the bombarding atmospheric protons have neither enough time nor undergo enough collisions to behave as a fluid. We therefore treat the problem as one of surface ablation by this particle kinetic flux rather than as a fluid flow. The particle bombardment energy flux is then 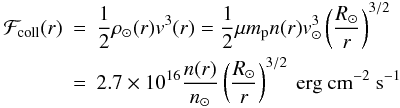$\begin{matrix} ℱ_{coll} (r) & = & \frac{1}{2} ρ_{⊙} (r) v^{3} (r) = \frac{1}{2} μ m_{p} n (r) v_{⊙}^{3} {(\frac{R_{⊙}}{r})}^{3 / 2} \\ = & 2.7 \times 10^{16} \frac{n (r)}{n_{⊙}} {(\frac{R_{⊙}}{r})}^{3 / 2} {erg cm}^{-2} s^{-1} \end{matrix}$ $\begin{eqnarray} \label{Fcoll} {{\cal F}_{\rm coll}}(r) & = & \frac{1}{2}\rho_\odot(r)v^3(r) =\frac{1}{2}\mu {m}_{\rm p} n(r)v_\odot^3\left(\frac{R_\odot}{r}\right)^{3/2}\nonumber\\ &= &2.7\times 10^{16} \frac{n(r)}{n_\odot}\left(\frac{R_\odot}{r}\right)^{3/2}~{\rm erg~cm}^{-2}~{\rm s}^{-1} \end{eqnarray}$ (13)(cf. meteor mass loss in the earth’s atmosphere – e.g., Kaiser 1962, Chap. 8). Here n(r) is the total (atom + ion) number density (cm^-3) of hydrogen, m_p the proton mass and μ ≈ 1.3 the mean total mass present (including helium etc) per hydrogen (so that ρ_⊙ = μnm_p) while n_⊙ ≈ 10¹⁷ cm^-3 is the value of n at the photosphere (r = R_⊙) which we take as reference point.
Ratio of ablation to sublimation energy fluxes is 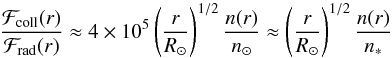$\frac{ℱ_{coll} (r)}{ℱ_{rad} (r)} \approx 4 \times 10^{5} {(\frac{r}{R_{⊙}})}^{1 / 2} \frac{n (r)}{n_{⊙}} \approx {(\frac{r}{R_{⊙}})}^{1 / 2} \frac{n (r)}{n_{*}}$ $\begin{equation} \label{FcollovrFrad} \frac{{\cal F}_{\rm coll}(r)}{{\cal F}_{\rm rad}(r)} \approx 4 \times 10^5\left(\frac{r}{R_\odot}\right)^{1/2}\frac{n(r)}{n_\odot}\approx \left(\frac{r}{R_\odot}\right)^{1/2}\frac{n(r)}{n_*} \end{equation}$ (14)where n_∗ = n(r_∗) ≈ 2.5 × 10¹¹cm^-3 is the n value at r = r_∗ = 1.01R_⊙ where ℱ_rad,ℱ_coll are equal. At the photosphere (n = n_⊙ = 10¹⁷ cm^-3), ℱ_coll ≈ 10⁵ℱ_rad which is equivalent to a black body energy flux at T ≽ 100000 K!

From Eq. (14) we see that sublimation dominates over ablation only at distances where n(r) ≺ n_∗ ≈ 2.5 × 10¹¹ cm^-3 where they are equal. This value n = n_∗ is in the (upper) chromosphere where the density rises very steeply with depth with a fairly constant temperature (of order 10 000 K) and hence mean exponential density scale height H ≈ 5 × 10⁷ cm ≈ 7 × 10^-4R_⊙, viz. 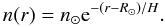$n (r) = n_{⊙} e^{- (r - R_{⊙}) / H} .$ $\begin{equation} \label{densityexponential} n(r)=n_\odot {\rm e}^{-(r-R_\odot)/H}. \end{equation}$ (15)In this approximation, the values r = r_∗,n = n_∗ occur at a height z above the photosphere of z = z_∗ = r_∗ − R_⊙ ≈ Hln(4 × 10⁵) ≈ 6500 km ≈ 0.01R_⊙. Since h = H/R_⊙ ≈ 7 × 10^-4, over a very small r range (a few H) the dominant energy flux changes rapidly from radiative at z − z_∗ ≫ H to collisions at z − z_∗ ≪ − H, a z range ≪ R_⊙. At several H above z_∗ ablation becomes negligible compared with sublimation so use of analytic expression (15) for n(r) at all heights, results in negligible error in the total energy flux. Over the very narrow range of 1.005 < r/R_⊙ < 1.015 around r = r_∗, ℱ_rad(r) ∝ r^-2 increases by 1% while ℱ_coll(r) falls × 10⁶. Throughout the present paper, for simplicity we approximate H by a height-independent mean value though H changes slowly with depth since the temperature and hydrogen ionization vary. The variation in H is around a factor of 4 over the entire range r_∗ → R_⊙ (and far less over the much smaller range of r which proves to be important) while n(r) increases by a factor 10⁶. A detailed model of n(r) over a large range of r was developed by Porter (2007, 2008) and should be used in more precise analysis. In addition chromospheric n structure varies on small horizontal scales about the mean stratified form n(r) so that fluctuating mass loss rate is expected along the path.

From the above discussion, the total energy flux ℱ(r) is reasonably well approximated by 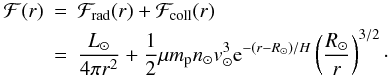$\begin{matrix} ℱ (r) & = & ℱ_{rad} (r) + ℱ_{coll} (r) \\ = & \frac{L_{⊙}}{4 π r^{2}} + \frac{1}{2} μ m_{p} n_{⊙} v_{⊙}^{3} e^{- (r - R_{⊙}) / H} {(\frac{R_{⊙}}{r})}^{3 / 2} \cdot \end{matrix}$ $\begin{eqnarray} \label{Ftot} {\cal F}(r) & = & {\cal F}_{\rm rad}(r) + {\cal F}_{\rm coll}(r)\nonumber\\ & = & \frac{L_\odot}{4 \pi r^2}+ \frac{1}{2}\mu {m}_{\rm p} n_\odot v_\odot^3 {\rm e}^{-(r-R_\odot)/H}\left(\frac{R_\odot}{r}\right)^{3/2}\cdot \end{eqnarray}$ (16)If we define dimensionless variables x = r/R_⊙,m(x) = M(r)/M_o,p = q/R_⊙,h = H/R_⊙, and use Eq. (16) for ℱ(r), differential Eq. (10) becomes, with (incoming) boundary condition m(r → ∞₋) = 1 $\frac{1}{m^{2 / 3}} \frac{d m}{d x} = α [\frac{1}{x (x - p)^{1 / 2}} + β \frac{e^{- (x - 1) / h}}{x^{1 / 2} (x - p)^{1 / 2}}]$ $\begin{equation} \label{dmdx} \frac{1}{m^{2/3}}\frac{{\rm d}m}{{\rm d}x}=\alpha\left[\frac{1}{x(x-p)^{1/2}} +\beta\frac{{\rm e}^{-(x-1)/h}}{x^{1/2}(x-p)^{1/2}}\right] \end{equation}$ (17)where the dimensionless parameters α, β are $α = \frac{L_{⊙}}{4 π ℒ ρ^{2 / 3} v_{⊙} R_{⊙} M_{o}^{1 / 3}} = \frac{0.27}{ℳ_{12}^{1 / 3}} \approx \frac{0.43}{M_{12}^{1 / 3}}$ $\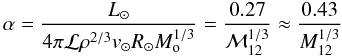begin{equation} \label{alphadef} \alpha =\frac{L_\odot}{4\pi{\cal L}\rho^{2/3}v_\odot R_\odot M_{\rm o}^{1/3}}=\frac{0.27}{{\cal M}_{12}^{1/3}}\approx \frac{0.43}{ M_{12}^{1/3}} \end{equation}$ (18)where ℳ₁₂ = ℳ_o/10¹²g,M₁₂ = M_o/10¹²g, 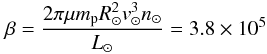$β = \frac{2 πμ m_{p} R_{⊙}^{2} v_{⊙}^{3} n_{⊙}}{L_{⊙}} = 3.8 \times 10^{5}$ $\begin{equation} \label{betadef} \beta= \frac{2\pi\mu {m}_{\rm p} R_\odot^2 v_\odot^3n_\odot}{L_\odot}=3.8\times 10^5 \end{equation}$ (19)and we define an effective mass 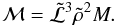$ℳ = {ℒ^{3}}_{˜} {ρ^{2}}_{˜} M .$ $\begin{equation} \label{effectivemass} {\cal M} =\tilde{{\cal L}}^3\tilde{\rho}^2 M. \end{equation}$ (20)In Fig. 1 we show the dependence of M_o/ℳ_o on 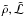$\begin{matrix} _{˜} \\ ρ \end{matrix}, \begin{matrix} _{˜} \\ ℒ \end{matrix}$ $\hbox{$\tilde{\rho}, \tilde{{\cal L}}$}$ . ℳ is the mass of water ice which would sublimate at the same rate (g/s) as the actual nucleus mass M with its specific values of 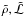$\begin{matrix} _{˜} \\ ρ \end{matrix}, \begin{matrix} _{˜} \\ ℒ \end{matrix}$ $\hbox{$\tilde{\rho},\tilde{{\cal L}}$}$ . Note also, for dimensional clarity, that M₁₂ and ℳ₁₂ in all equations here are dimensionless, the dimensional scaling unit 10¹² g being included as a factor in the (overall dimensionless) numerical value of α.

In cases where the sole processes acting on the nucleus were sublimation and ablation (i.e. hydrodynamic explosion effects were small prior to total vaporisation) the pure sublimation/ablation solution m(x) = M(r)/M_o of Eq. (17) is, on the inbound trajectory (∞₋ > x > p), $\begin{matrix} m (x) & = & m_{-} (x) \\ = & {[1 - \frac{α}{3} (\int_{x}^{\infty} \frac{d x}{x (x - p)^{1 / 2}} + β \int_{x}^{\infty} \frac{e^{- (x - 1) / h} d x}{x^{1 / 2} (x - p)^{1 / 2}})]}^{3} \\ = & {[1 - \frac{α}{3} (\frac{2}{p^{1 / 2}} \sin^{-1} {(\frac{p}{x})}^{1 / 2} + β \int_{x}^{\infty} \frac{e^{- (x - 1) / h} d x}{x^{1 / 2} (x - p)^{1 / 2}})]}^{3} \end{matrix}$ $\begin{eqnarray} \label{m-(x)general} m(x)&=& m_-(x)\nonumber \\ &=& \left[1-\frac{\alpha}{3} \left(\int_x^\infty\frac{{\rm d}x}{x(x-p)^{1/2}}+ \beta\int_x^\infty\frac{{\rm e}^{-(x-1)/h}{\rm d}x}{x^{1/2}(x-p)^{1/2}}\right)\right]^3\nonumber\\ &=& \left[1-\frac{\alpha}{3} \left(\frac{2}{p^{1/2}}\sin^{-1}\left(\frac{p}{x}\right)^{1/2}+ \beta\int_x^\infty\frac{{\rm e}^{-(x-1)/h}{\rm d}x}{x^{1/2}(x-p)^{1/2}}\right)\right]^3 \end{eqnarray}$ (21)while on the outbound trajectory (q < x < ∞₊) it is (with $^{\int} . d x = {^{\int}}_{q}^{\infty} . d x + {^{\int}}_{q}^{x} . 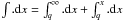d x$ $\hbox{$\int.{\rm d}x = \int_q^\infty.{\rm d}x+\int_q^x.{\rm d}x$}$ ) $\begin{matrix} m (x) & = & m_{+} (x) \\ = & [1 - \frac{α}{3} \times (\frac{2}{p^{1 / 2}} \times [π - \sin^{-1} (\frac{p}{x})^{1 / 2}] \\ + & β \times (2 \int_{p}^{\infty} \frac{e^{- (x - 1) / h} d x}{x^{1 / 2} (x - p)^{1 / 2}} - \int_{x}^{\infty} \frac{e^{- (x - 1) / h} d x}{x^{1 / 2} (x - p)^{1 / 2}}))]^{3} . \end{matrix}$ $\begin{eqnarray} \label{m+(x)general} m(x)&=& m_+(x) \nonumber \\ & =& \Biggl[1\!-\!\frac{\alpha}{3}\times \Biggl(\frac{2}{p^{1/2}}\!\times\! \bigg[\pi-\sin^{-1}\Bigl(\frac{p}{x}\Bigr)^{1/2}\bigg] \nonumber\\ & + & \beta \times \Bigl(2\int_{\rm p}^\infty\!\frac{{\rm e}^{-(x\!-\!1)/h}{\rm d}x}{x^{1/2}(x\!-\!p)^{1/2}}\!-\! \int_x^\infty\!\frac{{\rm e}^{-(x-1)/h}{\rm d}x}{x^{1/2}(x-p)^{1/2}}\Big)\Biggr)\Biggr]^3.\ \end{eqnarray}$ (22)Since L_⊙, R_⊙, v_⊙, n_⊙,H are all known, for specified ρ,ℒ,P_c, this solution m(x) depends solely on the the parameters q and ℳ_o and we will see below that the combination ℳ_oq^3/2 appears frequently in the solution. Equations (21, 22) for m(x) allow derivation of any property of M(r). For example the mass loss rate Ṁ = M_om′(x)ẋ where ẋ = ṙ/R_⊙ = (v_⊙/R_⊙)(1/p/x)^1/2/x^1/2 by Eqs. (4). 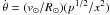Very near the sun x → 1 and is not a convenient variable since 1 − p/x → 0,m′(x) → ∞ and rates should be expressed via the θ coordinate with $\hbox{$\dot{\theta} = (v_\odot/R_\odot)(p^{1/2}/x^2)$}$ .

From the discussion above it is apparent that comets with q − R_⊙ ≽ 0.01R_⊙ never enter the ablation regime so can be treated neglecting the ablation terms. On the other hand comets with q − R_⊙ ≼ 0.01R_⊙, and of large enough ℳ_o to survive sublimation, encounter the ablation regime. If, further, they are of large enough ℳ_o to survive to r = r_∗ = 1.01R_⊙ with only a small mass loss fraction Δm = 1 − m(x_∗ = r_∗/R_⊙) ≪ 1 then their m(x) can be well approximated by including only the ablation terms and neglecting the preceding sublimation Δm. These sublimation and ablation dominated regimes are treated analytically in Sects. 5 and 6.1 while the role of ram pressure driven explosion, vital in the destruction of larger masses or steep entry angle, is discussed in Sect. 6.2.

5. Sublimation dominated mass loss solutions

(ℳ_o ≼ 10¹¹ g or q − r_∗ ≫ H ≈ 0.01R_⊙)

5.1. Sublimation dominated solution for m(x)

Fig. 1

Conversion factor M_o/ℳ_o from ice equivalent mass ℳ_o to real mass M_o versus $\begin{matrix} ˜ \\ ρ \end{matrix}$ $\hbox{$\tilde{\rho}$}$ for $\begin{matrix} _{˜} \\ ℒ \end{matrix} = 0.1, 0.2, 0.5, 1.0$ $\hbox{$\tilde{{\cal L}}= 0.1, 0.2, 0.5, 1.0$}$ – Eq. (20). For our canonical values $\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\hbox{$\tilde{\rho}=0.5, \tilde{{\cal L}}=1$}$ , the true mass M_o = 4 × ℳ_o since comet nuclei are less dense than ice so easier to evaporate. This figure is available in colour in electronic form.

In this case solution (21, 22) for m(x) along the incident and outgoing paths become $\begin{matrix} m_{-}^{rad} (x) & = & {[1 - \frac{2 α}{3 p^{1 / 2}} \sin^{-1} {(\frac{p}{x})}^{1 / 2}]}^{3} \\ \to & {[1 - \frac{2 α}{3 x^{1 / 2}}]}^{3} as p \to 0 \\ m_{+}^{rad} (x) & = & {[1 - \frac{2 α}{3 p^{1 / 2}} (π - \sin^{-1} {(\frac{p}{x})}^{1 / 2})]}^{3} \end{matrix}$ $\begin{eqnarray} \label{m(x)rad} m^{\rm rad}_-(x)&=&\left[1-\frac{2\alpha}{3p^{1/2}}\sin^{-1}\left(\frac{p}{x}\right)^{1/2}\right]^3\nonumber\\ &\rightarrow &\left[1-\frac{2\alpha}{3x^{1/2}} \right]^3~{\rm as}~ p\rightarrow 0 \nonumber \\ m^{\rm rad}_+(x)&=& \left[1-\frac{2\alpha}{3p^{1/2}} \left(\pi - \sin^{-1}\left(\frac{p}{x}\right)^{1/2}\right)\right]^3 \end{eqnarray}$ (23)which is plotted in Fig. 2 in terms of m(x/p) for various values of the parameter ℳ_op^3/2. In the following subsections we discuss features of this solution which are of particular interest.

Fig. 2

m(x) versus x/p for various ℳ_op^3/2 showing cases of survival of sublimation through an orbit, and of terminal mass loss before and after perihelion. This figure can be used for any values of M_o,p,ρ,ℒ because of the scaling and combination of variables used. This figure is available in colour in electronic form.

5.2. Sublimation solution properties

5.2.1. Fractional mass lost by perihelion/after one orbit

By Eq. (23) with x = p = q/R_⊙, the fractional masses m surviving, and Δm lost by sublimation to perihelion are $\begin{matrix} m_{q}^{rad} & = & 1 - Δ m_{q}^{rad} = {[1 - \frac{πα}{3 p^{1 / 2}}]}^{3} \\ \approx & {[1 - \frac{0.27}{p^{1 / 2} ℳ_{12}^{1 / 3}}]}^{3} \approx {[1 - \frac{0.43}{p^{1 / 2} M_{12}^{1 / 3}}]}^{3} \end{matrix}$ $\begin{eqnarray} \label{mq} m^{\rm rad}_q &=&1-\Delta m^{\rm rad}_q =\left[1-\frac{\pi\alpha}{3p^{1/2}}\right]^3 \nonumber \\ &\quad \approx&\left[1-\frac{0.27}{p^{1/2}{\cal M}_{12}^{1/3}}\right]^3 \approx\left[1-\frac{0.43}{p^{1/2}M_{12}^{1/3}}\right]^3 \end{eqnarray}$ (24)while after one orbit they are, by Eq. (23) for m₊(x → ∞) $\begin{matrix} m_{orbit}^{rad} & = & 1 - Δ m_{orbit}^{rad} = {[1 - \frac{2 πα}{3 p^{1 / 2}}]}^{3} \\ \approx & {[1 - \frac{0.56}{p^{1 / 2} ℳ_{12}^{1 / 3}}]}^{3} \approx {[1 - \frac{0.86}{p^{1 / 2} M_{12}^{1 / 3}}]}^{3} \end{matrix}$ $\begin{eqnarray} \label{morbit} m^{\rm rad}_{\rm orbit}&=&1-\Delta m^{\rm rad}_{\rm orbit} = \left[1-\frac {2\pi\alpha}{3p^{1/2}}\right]^3 \nonumber \\ &\quad \approx & \left[1-\frac{0.56}{p^{1/2}{\cal M}_{12}^{1/3}}\right]^3\approx\left[1-\frac{0.86}{p^{1/2}M_{12}^{1/3}}\right]^3 \end{eqnarray}$ (25)the last forms being for our canonical $\begin{matrix} _{˜} \\ ρ \end{matrix}, \begin{matrix} _{˜} \\ ℒ \end{matrix}$ $\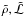hbox{$\tilde{\rho},\tilde{{\cal L}}$}$ values. (These expressions are valid for p > π²α²/9,4π²α²/9 respectively.) Note that Δm = ΔM/M_o = Δℳ/ℳ_o, and that the minimum initial mass needed to just survive sublimation through one orbit is 8 times that needed to just survive to perihelion (the corresponding minimum a_o values being in the ratio 2:1). We can rewrite Eq. (24) as $p^{3 / 2} ℳ_{12} = \frac{0.022}{[1 - (1 - Δ m_{q}^{rad})^{1 / 3}]^{3}}$ $\begin{equation} \label{MovsDeltamq} p^{3/2}{\cal M}_{12}=\frac{0.022}{[1-(1-\Delta m_q^{\rm rad})^{1/3}]^3} \end{equation}$ (26)which lets us evaluate the initial ℳ_o ≈ 0.25M_o which will lose a fraction Δm by perihelion – see Fig. 3.

Fig. 3

Value of ℳ_op^3/2 which has undergone fractional sublimation mass loss Δm_q by perihelion – Eq. (26). The figure can be used for any values of M_o,p,ρ,ℒ because of the scaling and combination of variables used. This figure is available in colour in electronic form.

5.2.2. Minimum initial masses and radii surviving sublimation to perihelion and through one orbit

Equations (24, 25) imply the following for the minimum initial masses needed to just survive sublimation to perihelion and through one complete orbit. $\begin{matrix} M_{ominq}^{rad} (q) & = & \frac{ℳ_{ominq}^{rad}}{\begin{matrix} ˜ \\ ℒ^{3} \end{matrix} {ρ^{2}}_{˜}} = \frac{M_{ominorbit}^{rad} (q)}{8} = {[\frac{L_{⊙}}{12 ℒ ρ^{2 / 3} v_{⊙} R_{⊙} p^{1 / 2}}]}^{3} \\ \approx & \frac{2.2 \times 10^{10} g}{\begin{matrix} ˜ \\ ℒ^{3} \end{matrix} {ρ^{2}}_{˜} p^{3 / 2}} \approx \frac{8.8 \times 10^{10} g}{p^{3 / 2}} \end{matrix}$ $\begin{eqnarray} \label{Mominq} M^{\rm rad}_{\rm ominq}(q)&=& \frac{{\cal M}_{\rm ominq}^{\rm rad}}{\tilde{{\cal L}}^3\tilde{\rho}^2} =\frac{M^{\rm rad}_{\rm ominorbit}(q)}{8} = \left[\frac{L_\odot}{12{\cal L}\rho^{2/3}v_\odot R_\odot p^{1/2}}\right]^3 \nonumber \\ &\quad \approx& \frac{2.2\times 10^{10}\,{\rm g}}{\tilde{{\cal L}}^3\tilde{\rho}^2p^{3/2}}\approx \frac{8.8\times 10^{10}\,{\rm g}}{p^{3/2}} \end{eqnarray}$ (27)the corresponding minimum initial sizes being $a_{ominorbit}^{rad} = 2 a_{ominq}^{rad} \approx \frac{2.7 \times 10^{3} cm}{\begin{matrix} ˜ \\ ℒ \end{matrix} \begin{matrix} ˜ \\ ρ \end{matrix} p^{1 / 2}} \approx \frac{5.4 \times 10^{3} cm}{p^{1 / 2}} \cdot$ $\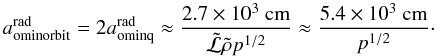begin{equation} \label{aomin} a_{\rm ominorbit}^{\rm rad}=2a_{\rm ominq}^{\rm rad}\approx \frac{2.7\times 10^3~{\rm cm}}{\tilde{{\cal L}}\tilde{\rho}p^{1/2}}\approx \frac{5.4\times 10^3~{\rm cm}}{p^{1/2}}\cdot \end{equation}$ (28)According to Sect. 2.4 for the case of a sphere this corresponds to radius b_ominorbit ≈ a_ominorbit/1.67 ≈ 3.2 × 10³/p^1/2 cm. Consequently (for 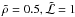$\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\hbox{$\tilde{\rho}=0.5,\tilde{{\cal L}}=1$}$ ) any M_o ≼ 10¹¹ g with p ≈ 1 will be totally sublimated before reaching the ablation zone while M_o ≽ 10¹¹ g with p ≼ 1.01 will undergo ablation and be totally dominated by it or by explosion, according to the conditions discussed in Sects. 3.4 and 6.1–6.2.

Equations (27, 28) can be generalised to find the mass ℳ_o which is totally sublimated at any point x₊ or x₋ by setting m = 0 and solving for ℳ_o. Thus observation of such x_end values allows nucleus mass estimation as indeed does any measurement of mass loss or mass loss rate at specific x. Note that specifying m at x does not define ℳ_o uniquely unless one know if it is x₊ or x₋. A small ℳ_o has the same m at inbound point x as a corresponding large ℳ_o has when outbound at x.

From all of the above it is apparent (cf. Sect. 3.3) that, near the sun, mass loss by sublimation, and the subsequent deposition of kinetic energy and abundance-anomalous matter in the corona occur over distance scales of order R_⊙ and timescales of order R_⊙/v_⊙. So even total destruction of the nucleus is a slow extended “fizzle”, not an explosion (cf. observations by Schrijver 2011 for a case with p ~ 1.14). This contrasts sharply with low altitude ablation/explosion over a few scale heights H ≈ 10^-3R_⊙ directly powered by nucleus kinetic energy – Sect. 6.

5.3. Comparison with numerical models

In order to see whether our simple analytic expressions above give reasonable approximations to mass loss, at least for q ≼ a few R_⊙, we can compare them with those from numerical models incorporating effects we have neglected, such as the early numerical thermal modeling by Weissman & Keiffer (1982) and Weissman (1983). Weissman (1983) (his Fig. 2) predicts for water ice spheres the change Δa resulting from sublimation through infall to q = R_⊙ to be Δa ≈ 2 × 10³ cm for zero albedo. This can be compared with our expression (28) with p = 1 namely, (with 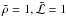$\begin{matrix} _{˜} \\ ρ \end{matrix} = 1, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\hbox{$\tilde{\rho}=1, \tilde{{\cal L}}= 1$}$ for water ice) a_omin ≈ 2.7 × 10³ cm. Converting this to the equivalent radius for the case of a sphere (Sect. 2.4) gives 1.6 × 10³ cm in good (20%) agreement with Weissman, given our approximations (e.g., radial insolation and no cooling processes). This gives us confidence in applying our analytic approach to get estimates for the ablation regime (Sect. 6).

6. Ablation and explosion of Sun-impactors

6.1. Ablation dominated solution when ram pressure can be neglected – M_o(1-q/r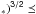 ${}_{})^{3 / 2} ≼$ $\hbox{$_)^{\sf 3/2}\preceq$}$ M_∗∗ ≈ 10¹⁰g, r_∗–q ≽ H

For nuclei with q ≼ r_∗ and with original M_o large enough ≽ 10¹¹ g to survive sublimation down to r < r_∗ the residual mass 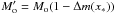$M_{o}^{'} = M_{o} (1 - Δ m (x_{*}))$ $\hbox{$M'_{\rm o}=M_{\rm o}(1-\Delta m(x_*))$}$ has (cf. Sect. 5.2.1) essentially the same velocity as if it had arrived at r_∗ without any sublimation. Because of the very rapid large switch from the sublimation to the ablation regime, its subsequent mass loss can thus be treated using only the ablation term in our m(x) expression (21) for a mass 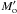$M_{o}^{'}$ $\hbox{$M'_{\rm o}$}$ falling from infinity. For simplicity here we will only consider M_o large enough that Δm(x_∗) ≪ 1 and simply equate 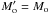$M_{o}^{'} = M_{o}$ $\hbox{$M'_{\rm o}=M_{\rm o}$}$ . Consequently our results for masses in the transition range around 10¹¹ g are approximate. In this section we further restrict ourselves to impactors having small enough M_o and/or shallow enough incidence that atmospheric ablative mass loss is complete before ram pressure driven explosion is significant (exploding impactors are discussed in Sect. 6.2). The inbound evolution of m(x) = M(r)/M_o by ablation alone can then be well described by using only the ablation terms in Eq. (21). That is $m_{-}^{coll} (x) = m_{coll} (x) = {[1 - \frac{αβ}{3} \int_{x}^{\infty} \frac{e^{- (x - 1) / h} d x}{x^{1 / 2} (x - p)^{1 / 2}}]}^{3} \cdot$ $\begin{equation} \label{mcoll-(x)} m^{\rm coll}_-(x)=m_{\rm coll}(x)=\left[1-\frac{\alpha\beta}{3} \int_x^\infty\frac{{\rm e}^{-(x-1)/h}{\rm d}x}{x^{1/2}(x-p)^{1/2}}\right]^3\cdot \end{equation}$ (29)The integral in Eq. (29) has in general no standard closed analytic form but, since h ≪ 1, a good analytic approximation is readily obtained for almost all p. Expression (29) is only physically relevant down to where ablation is complete – viz ^∫.dx ≤ 3/αβ – which always occurs close to x = x_∗ ≈ 1.01 since h ≪ 1. Below x = x_∗ the integrand increases exponentially with depth so is maximal at the x limit of the integral. Consequently, (unlike the exponential numerator) the integrand denominator can be well approximated by setting x_∗(x_∗ − p)^1/2 ≈ (1 − p/x_∗)^1/2 (Rare cases where | x_∗ − p | ≼ h need a more refined treatment, and inclusion of both ablation and sublimation). Solution (29) can then be integrated to give $m (x) = m_{coll} (x) \approx {[1 - Γ \frac{e^{- (x - 1) / h}}{(1 - p / x_{*})^{1 / 2}}]}^{3}$ $\begin{equation} \label{m(x)coll} m(x)=m_{\rm coll}(x)\approx \left[1-\Gamma \frac{{\rm e}^{-(x-1)/h}}{(1-p/x_*)^{1/2}}\right]^3 \end{equation}$ (30)where $Γ = \frac{αβh}{3} = \frac{μ n_{⊙} m_{p} v_{⊙}^{2} H}{6 ℒ ρ^{2 / 3} M_{o}^{1 / 3}} \approx \frac{30}{(ℳ_{o} / 10^{12})^{1 / 3}}$ $\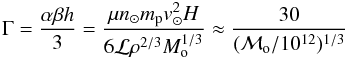begin{equation} \label{Gammadef} \Gamma = \frac{\alpha\beta h}{3}=\frac{\mu n_\odot m_{\rm p}v_\odot^2H}{6{\cal L}\rho^{2/3}M_{\rm o}^{1/3}}\approx \frac{30}{({\cal M}_{\rm o}/10^{12})^{1/3}} \end{equation}$ (31)from which it follows that the nucleus will be totally ablated by the height $\begin{matrix} z_{abl}^{end} (km) & = & H \ln \frac{Γ}{(1 - p / x_{*})^{1 / 2}} \\ = & 2000 + 1100 \times [\frac{1}{2} \log_{10} (1 - p / x_{*}) - \frac{1}{3} \log_{10} M_{12}] \end{matrix}$ $\begin{eqnarray} \label{zablend} z_{\rm abl}^{\rm end}({\rm km})&=& H\ln \frac{\Gamma}{(1-p/x_*)^{1/2}} \nonumber \\ &=& 2000 \!+\!1100\!\times\!\left[\frac{1}{2}\log_{10}(1\!\!-p/x_*)\!-\!\frac{1}{3}\log_{10} M_{12}\right] \end{eqnarray}$ (32)with corresponding atmospheric density 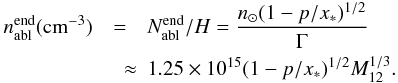$\begin{matrix} n_{abl}^{end} ({cm}^{-3}) & = & N_{abl}^{end} / H = \frac{n_{⊙} (1 - p / x_{*})^{1 / 2}}{Γ} \\ \approx & 1.25 \times 10^{15} (1 - p / x_{*})^{1 / 2} M_{12}^{1 / 3} . \end{matrix}$ $\begin{eqnarray} \label{nablend} n_{\rm abl}^{\rm end}({\rm cm}^{-3})&=&N_{\rm abl}^{\rm end}/H =\frac{n_\odot(1-p/x_*)^{1/2}}{\Gamma} \nonumber \\ &\quad \approx& 1.25\times 10^{15}(1-p/x_*)^{1/2}M_{12}^{1/3}. \end{eqnarray}$ (33)Equation (32) shows that, even neglecting explosion, all nuclei are destroyed over a few scale heights vertically. Such short paths suggest that the ablation path may be approximated as rectilinear, starting around the point where n ≈ n_∗ at angle φ ≈ φ_∗ to the vertical, and of nearly constant speed v_⊙. From Eq. (4) we find that 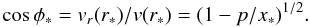$\cos φ_{*} = v_{r} (r_{*}) / v (r_{*}) = (1 - p / x_{*})^{1 / 2} .$ $\begin{equation} \label{cosphistar} \cos\phi_* =v_r(r_*)/v(r_*)=(1-p/x_*)^{1/2}. \end{equation}$ (34)If one re-derives and solves the equation for dm/dx for a rectilinear path one arrives at exactly the same expressions as found in Eqs. (32, 33) given the relation (34) of φ_∗ to p/x_∗ so our algebraic approximation there is equivalent to the geometric one of a rectilinear path.

From Eq. (8) it then follows that ram pressure driven explosion is small throughout the total ablation phase (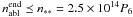 $n_{abl}^{end} ≼ n_{* *} = 2.5 \times 10^{14} P_{6}$ $\hbox{$n_{\rm abl}^{\rm end} \preceq n_{**}=2.5\times 10^{14}P_6$}$ ) cm^-3 only for masses smaller than $\begin{matrix} M_{o} ≼ M_{abl}^{\max} (φ) & = & {[\frac{P_{c} H}{\begin{matrix} ˜ \\ ℒ \end{matrix} {ρ^{2 / 3}}_{˜}}]}^{3} (1 - p / x_{*})^{- 3 / 2} = M_{* *} \sec^{3} φ_{*} \\ \approx & \frac{10^{10} P_{6}^{3}}{(1 - p / x_{*})^{3 / 2}} \approx 10^{10} P_{6}^{3} \sec^{3} φ_{*} g \end{matrix}$ $\begin{eqnarray} \label{Momaxofphi} M_{\rm o} \preceq M_{\rm abl}^{\rm max}(\phi)& =& \left[\frac{P_{\rm c} H}{\tilde{{\cal L}} \tilde{\rho}^{2/3}}\right]^3(1-p/x_*)^{-3/2}=M_{**}\sec^3\phi_* \nonumber \\ &\quad \approx& \frac{ 10^{10}P_6^3}{(1-p/x_*)^{3/2}}\approx 10^{10}P_6^3 \sec^3\phi_*~~{\rm g} \end{eqnarray}$ (35)where we have used H₈ ≈ 0.5 and $\begin{matrix} _{˜} \\ ℒ \end{matrix} = 1, \begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5$ $\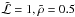hbox{$\tilde{{\cal L}}=1, \tilde{\rho}= 0.5$}$ . Here M_∗∗ is the maximum vertical entry mass which is totally ablated by depth n = n_∗∗. These values of 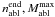$n_{abl}^{end}, M_{abl}^{\max}$ $\hbox{$n_{\rm abl}^{\rm end}, M_{\rm abl}^{\max}$}$ differ by factors of a few from the estimates in Sect. 3.4.2 due to the more accurate treatment of ablation. Since x_∗ = 1.01, for the range 1 < p < 1.0099, the final sec³φ_∗ factor is in the range 10³−10⁶ and the mass above which explosion becomes dominant for such grazing impactors is in the range 3 × 10¹³⁻¹⁶ g for P₆ = 1 and 3 × 10^10 − 13 g for P₆ = 0.1. This solar limit is much larger than for the conditions of the Shoemaker-Levy 9 Jupiter impacts (with fragment masses estimated to be around 10¹⁵ g) because of Jupiter’s smaller H and steep angle of those impacts (~45°) which result in a much larger density n and hence ram pressure at a specified 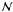$\hbox{${\cal N}$}$ (Sect. 3.4.2). This modifies somewhat the relative importance and regimes of ablation and explosion in nucleus destruction in the solar case, as we discuss below after discussing the explosion regime.

6.2. Explosive end point for nuclei of high M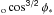 ${}_{o}\cos^{3 / 2} φ_{}$ $\hbox{$_{\rm o}\cos^{\sf 3/2}\phi_$}$

For nuclei of 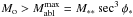$M_{o} > M_{abl}^{\max} = M_{* *} \sec^{3} φ_{*}$ $\hbox{$M_{\rm o}>M_{\rm abl}^{\rm max}=M_{**}\sec^3\phi_*$}$ , mass loss and destruction of the nucleus become dominated by expansion due to the action of the exponentially growing ram pressure. This is compounded by breakup of the nucleus and flow via hydrodynamic instabilities – see Chyba et al. (1993), Field & Ferrara (1994), MacLow & Zahnle (1994), Zahnle & MacLow (1994) and Carlson et al. (1997). Modeling this intense localised explosion and the subsequent fireball expansion in the solar case is beyond the scope of the present exploratory paper and should be addressed using modified versions of the numerical simulations conducted for planetary cases. Here we simply make an estimate of how much the end depth is reduced by explosion and by the enhanced deceleration and ablation arising from the growing area, based on the analytic approximation given by the above authors. The explosive lateral expansion of nuclei can be approximated as incompressible longitudinal shortening combined with lateral expansion with lateral size a_⊥ increasing as (MacLow & Zahnle 1994 Eq. (2)) 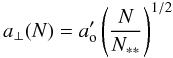$a_{⊥} (N) = a_{o}^{'} {(\frac{N}{N_{* *}})}^{1 / 2}$ $\begin{equation} \label{explradius} a_\perp(N)= a'_{\rm o}\left(\frac{N}{N_{**}}\right)^{1/2} \end{equation}$ (36)where 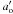$a_{o}^{'}$ $\hbox{$a'_{\rm o}$}$ is the size when pure ablation ends at N = N_∗ ∗ given by (Eq. (30)) 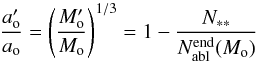$\frac{a_{o}^{'}}{a_{o}} = {(\frac{M_{o}^{'}}{M_{o}})}^{1 / 3} = 1 - \frac{N_{* *}}{N_{abl}^{end} (M_{o})}$ $\begin{equation} \label{aone} \frac{a'_{\rm o}}{a_{\rm o}}= \left(\frac{M'_{\rm o}}{M_{\rm o}}\right)^{1/3}= 1-\frac{N_{**}}{N_{\rm abl}^{\rm end}(M_{\rm o})} \end{equation}$ (37)with 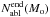$N_{abl}^{end} (M_{o})$ $\hbox{$N_{\rm abl}^{\rm end}(M_{\rm o})$}$ (Eq. (33)) the depth (hypothetical for 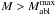$M > M_{abl}^{\max}$ $\hbox{$M>M_{\rm abl}^{\rm max}$}$ ) at which ablation would be complete in the absence of explosion. Determination of the final destruction depth in the explosion regime requires numerical simulation but as an upper limit we can evaluate the depth at which ablation across the exploding area alone would destroy the nucleus. The relevant rate is 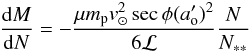$\frac{d M}{d N} = - \frac{μ m_{p} v_{⊙}^{2} \sec φ (a_{o}^{'})^{2}}{6 ℒ} \frac{N}{N_{* *}}$ $\begin{equation} \label{dMdNexp} \frac{{\rm d}M}{{\rm d}N} = - \frac{\mu {m}_{\rm p} v_\odot^2 \sec\phi (a'_{\rm o})^2}{6{\cal L}}\frac{N}{N_{**}} \end{equation}$ (38)with solution $M (N) = M_{o}^{'} [1 - \frac{μ m_{p} v_{⊙}^{2} \sec φ (a_{o}^{'})^{2}}{12 ℒ M_{* *}} ({(\frac{N}{N_{* *}})}^{2} - 1)]$ $\begin{equation} \label{Mexp(N)} M(N)=M'_{\rm o}\left[1-\frac{\mu {m}_{\rm p} v_\odot^2\sec\phi (a'_{\rm o})^2}{12{\cal L}M_{**}} \left( \left(\frac{N}{N_{**}}\right)^2-1\right)\right] \end{equation}$ (39)with resulting end depth ( $N_{end}^{\exp} = H n_{end}^{\exp}$ $\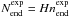hbox{$N_{\rm end}^{\exp}=Hn_{\rm end}^{\exp}$}$ ) $\begin{matrix} N_{end}^{\exp} & = & N_{* *} {[1 + \frac{12 ℒ ρ^{2 / 3} \cos φ M_{o}^{1 / 3}}{μ m_{p} v_{⊙}^{2} N_{* *}} (1 - \frac{N_{* *}}{N_{end}^{abl} (M_{o})})]}^{1 / 2} \\ = & N_{* *} {[\frac{N_{end}^{abl} (M_{o})}{N_{* *}} - 1]}^{1 / 2}, M_{o} ≽ M_{abl}^{\max} . \end{matrix}$ $\begin{eqnarray} \label{Nexpend} N_{\rm end}^{\exp}&=&N_{**}\left[1+\frac{12{\cal L}\rho^{2/3}\cos\phi M_{\rm o}^{1/3}}{\mu {m}_{\rm p} v_\odot^2N_{**}}\left(1-\frac{N_{**}}{N_{\rm end}^{\rm abl}(M_{\rm o})}\right)\right]^{1/2}\nonumber\\ &=&N_{**}\left[\frac{N_{\rm end}^{\rm abl}(M_{\rm o})}{N_{**}}-1\right]^{1/2},~ M_{\rm o} \succeq M_{\rm abl}^{\max}. \end{eqnarray}$ (40)Combining Eqs. (33) and (40) we show in Fig. 4 the estimated density n_end = N_end/H and height z_end = Hln(n_⊙/n) at which destruction ends as a function of M_o(cosφ/0.01)³ for values of P₆ = 0.1,1. P_∞ is also shown to make clear how explosion shortens the path relative to ablation alone. The x-axis values are the actual M_o values for cosφ = 0.01 which maximises the ablation regime. For photospheric p = 1,cosφ = 0.1 the mass values are 1000 times smaller. Thus as one decreases P₆ and as p/x_∗ becomes progressively smaller than unity, the mass regime of ablation dominated destruction becomes smaller and smaller. We conclude that for grazing solar impacts, for P_c ≽ 10⁵ dyne/cm² our ablation-dominated treatment is appropriate for masses well above the sublimation survival limit only when the entry angle is very shallow (i.e. q is very near to r_∗ = 1.01R_⊙). For larger M_o or lower P_c or lower p (less shallow entry), ram pressure driven explosion of the nucleus becomes wholly dominant. For solid objects with P₆ ≫ 1 the ablation regime is much larger.

Fig. 4

Estimate of the heights z_end and densities n_end at which nuclei are destroyed as a function of M_ocos³φ_∗ for specified P₆. Note that results are very sensitive to cosφ_∗ and to P₆. To the left of the knee ablation vaporizes the nucleus before ram pressure exceeds the strength of nucleus material. To the right ram pressure drives destructive explosion of the nucleus. It is clear that a very large range of masses is destroyed within a few scale heights in the chromosphere and that for all plausible masses and parameters, all nuclei are destroyed above the photosphere. This figure is available in colour in electronic form.

6.3. Energy deposition profiles of Sun-impacting comets

To calculate observable diagnostic signatures of the destruction of comets near the sun requires modeling the primary energy deposition profile then calculating the thermal, hydrodynamic, and radiative response of the solar atmosphere – the evolution of the fireball which follows the primary airburst. For the impact case, doing this numerically along somewhat similar lines to planetary impact work by e.g., Carlson et al. (1995, 1997) and other work cited in Sects. 3.4.1 and 6.2 should be done but is beyond the scope of the present paper. Here we simply take a first step by estimating the height distribution of the nucleus kinetic energy deposition for the ablation dominated case, touching briefly on the explosion domain.

The height distribution dℰ/dr (erg/cm) of kinetic energy deposited along the ablation path can be approximated by ${[\frac{dℰ}{d r}]}_{abl} \approx \frac{1}{2} v^{2} (r) M_{o} \frac{d m}{d r} = \frac{M_{o} v_{⊙}^{2}}{2 R_{⊙} x} \frac{d m}{d x} \approx \frac{M_{o} v_{⊙}^{2}}{2 R_{⊙}} \frac{d m}{d x}$ $\begin{equation} \label{heatingperunitht} \left[\frac{{\rm d}{\cal E}}{{\rm d}r}\right]_{\rm abl}\approx \frac{1}{2}v^2(r)M_{\rm o}\frac{{\rm d}m}{{\rm d}r}=\frac{M_{\rm o}v_\odot^2}{2~R_\odot x}\frac{{\rm d}m}{{\rm d}x}\approx \frac{M_{\rm o}v_\odot^2}{2R_\odot }\frac{{\rm d}m}{{\rm d}x} \end{equation}$ (41)since x is very close to unity and v very close to v_⊙ over the few scale heights involved.

Using Eq. (30) to find dm/dx leads to the conclusion that dℰ/dr is very sharply peaked in height z (Δz ≈ H) with a maximum of 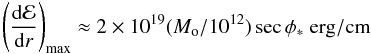${(\frac{dℰ}{d r})}_{\max} \approx 2 \times 10^{19} (M_{o} / 10^{12}) \sec φ_{*} erg / cm$ $\begin{equation} \label{dEcaldrmax} \left(\frac{{\rm d}{\cal E}}{{\rm d}r}\right)_{\max}\approx 2\times 10^{19}(M_{\rm o}/10^{12})\sec\phi_*~{\rm erg/cm} \end{equation}$ (42)at $n_{\max} ({cm}^{-3}) \approx 2 \times 10^{14} (1 - p / x_{*})^{1 / 2} (M_{o} / 10^{12})^{1 / 3} .$ $\begin{equation} \label{nmax} n_{\max}({\rm cm}^{-3})\approx 2\times 10^{14}(1-p/x_*)^{1/2}( M_{\rm o}/10^{12})^{1/3}. \end{equation}$ (43)In the rare cases of steep entry/higher masses we have seen in Sect. 6.2 that the onset of explosion causes rapid deceleration and disintegration of the nucleus. This will result in even higher volumetric heating rates than in the case of pure ablation, though numerical simulations are needed to quantify this. Such atmospheric power input is similar to that in solar magnetic flares (10^27 − 30 erg/s over loop lengths ~10⁹ cm).

7. Discussion and conclusions

7.1. Summary of nucleus destruction regimes

We have shown there to be three regimes of nucleus destruction, depending on the values of M_o,q for given values of 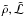$\begin{matrix} _{˜} \\ ρ \end{matrix}, \begin{matrix} _{˜} \\ ℒ \end{matrix}$ $\hbox{$\tilde{\rho}, \tilde{{\cal L}}$}$ (for which we use here 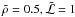$\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\hbox{$\tilde{\rho}=0.5, \tilde{{\cal L}}=1$}$ ), namely

(a) Sublimation dominated (Sect. 5.2.2,Eq. (27)) Nuclei of p ≽ x_∗,M_o ≼ M_∗∗(p) given by 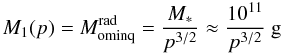$M_{1} (p) = M_{ominq}^{rad} = \frac{M_{*}}{p^{3 / 2}} \approx \frac{10^{11}}{p^{3 / 2}} g$ $\begin{equation} \label{M1ofp} M_1(p) =M_{\rm ominq}^{\rm rad}=\frac{M_{*}}{p^{3/2}}\approx \frac{10^{11}}{p^{3/2}}~{\rm g} \end{equation}$ (44)are completely sublimated before they reach perihelion, (or r_∗). This is by far the commonest regime for group comets.
(b) Ablation dominated (Sects. 3.4.2, 6.1) Since n = n_∗∗ = 2.5 × 10¹⁴P₆ at x_∗∗, where atmospheric ram pressure starts to exceeds nucleus strength, nuclei with x_∗∗ < p < x_∗ and M₁(p) < M_o < M₂(p) (i.e. of sufficiently low mass or shallow entry angle) lose all their mass to ablation before explosion with 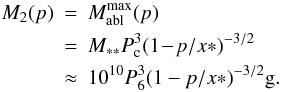$\begin{matrix} M_{2} (p) & = & M_{abl}^{\max} (p) \\ = & M_{* *} P_{c}^{3} (1 - p / x *)^{- 3 / 2} \\ \approx & 10^{10} P_{6}^{3} (1 - p / x *)^{- 3 / 2} g . \end{matrix}$ $\begin{eqnarray} \label{M2ofp} M_2(p) &=& M_{\rm abl}^{\max}(p)\nonumber \\ &=&M_{**}P_{\rm c}^3(1\!-\!p/x*)^{-3/2}\nonumber \\ &\approx& 10^{10}P_6^3(1-p/x*)^{-3/2}{\rm g}. \end{eqnarray}$ (45)Since most larger sun-grazers have p > x_∗, these are rarer than comets in the sublimation regime.
(c) Explosion dominated (Sect. 6.2) Nuclei with p < x_∗ ∗ and M_o > M₂(p) (ie of sufficiently high mass or steep entry) undergo ram pressure driven explosion. These are also rare compared to sublimative destruction.

These domains in the plane of (p/x_∗,M_o) are summarized Fig. 5 with the M_o axis scaled with respect 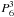$P_{6}^{3}$ $\hbox{$P_6^3$}$ . P₆ = 1 represents relatively strongly bound nuclei. For P_c ~ 10⁵ dyne/cm² the ablation regime becomes confined to about M_o ≽ 10¹¹g,0.99 ≼ p/x_∗ ≼ 1. Though this is very narrow in p space, how common ablation domination is compared to explosion domination depends on the distribution of p/x_∗ ∗ and is very sensitive to the value of P_c. For very weakly bound bodies (P₆ ≪ 0.1) ablation would only dominate briefly prior to explosion totally dominating. Solid stony or iron bodies with P₆ ≽ 10 would, unless extremely massive, be wholly in the ablative destruction regime.

Fig. 5

Domains of destruction of comet nuclei in the plane ( $M_{o} / P_{c}^{3},p / x_{*} = \sin φ_{*}$ $\hbox{$M_{\rm o}/P_{\rm c}^3,p/x_*=\sin \phi_*$}$ ) for entry angle φ_∗ = arcsin(p/x_∗) to the vertical at r = r_∗. Note the change from linear to log scale on the p/x_∗ axis across the point p/x_∗ = 1 so as to display the very rapid variation in the range p/x_∗ ≤ 1. The axes are scaled with respect to P₆ as discussed in Sect. 2.2. For P₆ = 0.1 the ablation regime becomes a slender strip at 0.99 ≼ p/x_∗ ≼ 1.

7.2. Visibility of Sun-grazer destruction by sublimation

It was shown in Sect. 3.3 that destruction by sublimation of low mass nuclei even very near the sun occurs over scales ~R_⊙ in space and ~10³⁻⁴ s in time, making them hard to observe against solar atmospheric emission and scattering. However, the abrupt collisional stopping of sublimated material in the wake could raise its initial temperature by up to around 10⁷ K which may make it visible in the XUV by charge exchange or thermal line emission if it does not cool too quickly by radiation, conduction or expansion and if its emission measure ^∫_Vn²dV is high enough. (The first observation, in XUV, of such an event was made by Schrijver et al. 2011, using SDO AIA during the revision stage of this paper.) A 10¹² g mass totally sublimated over a 0.5R_⊙ path into a conical wake of half angle say 10^-2 radians would have an emission measure of order 3 × 10⁴⁴ cm^-3 and a mean density of ~5 × 10⁸ cm^-3 in a solar plasma environment of roughly similar density.

7.3. Signatures of Sun-impactor destruction

7.3.1. Mass, energy and temperature of the fireball

The kinetic energy initially released in the lower solar atmosphere by sun impacting cometary nuclei with M_o = 10¹¹ − 10¹⁹ g is 5 × (10²⁶ − 10³⁴) erg, similar to the range of the magnetic energy release from “nano” – flares to “super” – flares. If 50% of ℰ_kin went into heating the comet material the temperature attainable would be 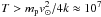$T > m_{p} v_{⊙}^{2} / 4 k \approx 10^{7}$ $\hbox{$T>m_{\rm p}v_\odot^2/4k\approx 10^7$}$ K where k is Boltzmann’s constant. This is of order the solar escape temperature since it is generated by infall of matter effectively from ∞.

Flare masses ejected are of the order of 10^12 − 16 g, also comparable with those of larger impacting cometary nuclei. Thus a comet impact in the dense chromosphere should produce phenomena somewhat resembling a solar (magnetic) flare, though the initial comet volume is much smaller, its density much higher, and the heating rise time faster ( ≼ 10 s). Because of the initially small size scale and high density and pressure we might expect rapid initial cooling (seconds) by radiation, expansion and conduction, followed by a radiative/conductive decay phase more like that of solar flares (~10^2 − 3 s) as the fireball expands outward and upward, sweeping solar plasma with it (cf. the Carlson et al. 1997 study of the Jupiter impact fireball).

7.3.2. Cometary flare size, emission measure and optical depth

If optically thin, the radiative output of a hot plasma of volume V depends on its temperature and its emission measure EM = ^∫_Vn²dV ≈ a³(M_o/μ_cm_p)² ≈ 10⁴⁸(M_o/10¹²)²/(a/10⁸)³/μ_c cm^-3 for a nucleus of mass M_o when it has expanded to size a. (Here μ_c is the mean comet mass per particle in units of m_p). Explosion of a nucleus occurs over a few scale heights ≈ 10⁸ cm vertically, traversed in ~ 10 s at speed v_⊙cosφ. If the lateral expansion speed of the hot wake were similar then the lateral dimension of the exploding wake would also be a few scale heights. Its optical depth for a process with absorption cross-section σ would then be τ ≈ σM_o/m_pa² = (M_o/10¹²)(σ/10^-20)/μ_c/(a/10⁸)². Thus when a nucleus of, say, M_o = 10¹² g (a_o ~ 10⁴ cm) becomes optically thin (a = 10⁶ cm) for σ = 10^-20 cm², it would have an EM ≈ 10⁴⁸ cm^-3 for that emission. This EM is only for the cometary material itself, but the EM of the heated atmosphere may also be important since an atmospheric mass ≽ M_o is involved in decelerating it. Since H ~ 1 arcsec we may expect to see initially a source of a few arcsec expanding at about 0.1 arcsec per sec at chromospheric altitudes and atmospheric density ≃ 10^13 − 16 cm^-3 depending on M_o as per Fig. 4. XUV line spectra should exhibit highly non-solar abundances (e.g., O:H ratio) as should any matter ejected into space (cf. Iseli et al. 2002). There may also be a variety of nonthermal radio and other signatures (e.g., charge exchange – e.g., Lisse et al. 1996 – and impact polarized spectrum lines – e.g., Fletcher & Brown 1992, 1995) arising from plasma phenomena driven by the highly supersonic expansion, such as shock and/or turbulent acceleration of electrons and ions and charge separation currents as the ablated matter decelerates in the atmosphere – cf., review by Pégauriér (2007) of fusion pellet ablation physics.

7.3.3. Cometary sunquakes and other solar disturbances

The phenomenon of flare induced sunquakes – waves in the photosphere – discovered by Kosovichev & Zharkova (1998) and now widely studied (e.g,. Kosovichev 2006) should also result from the momentum impulse delivered by a cometary impact. All such impacts, however small the comet mass, involve a huge kinetic energy density (ram pressure) 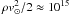$ρ v_{⊙}^{2} / 2 \approx 10^{15}$ $\hbox{$\rho v_\odot^2/2\approx 10^{15}$}$ erg/cm³. This is ~10¹⁰ times the thermal energy density (pressure) of the photosphere or the magnetic energy density in a sunspot, being the energy density of a 40 MG magnetic field! Even when the kinetic energy is converted by ablation and ram pressure to heat and kinetic energy of explosion, it is initially spread over only a few scale heights. Hence the explosive airburst energy density of a comet like a Shoemaker-Levy 9 (10¹⁵ g) is about 10⁶ erg/cm³ equivalent to that of a 5 kG field and still more than the thermal energy density of the photosphere. Thus, while the total energy of most impacting sun-grazers is small compared to that of large flares and CMEs their energy density is so high that local disruption of magnetic fields and triggering of larger scale events are not impossible.

7.4. Conclusions

Our simple analytic treatment of comet nucleus sublimation gives results for mass loss in reasonable agreement with previous numerical simulations . We have proved that nuclei reaching p = q/R_⊙r_∗/R_⊙ ≈ 1.01 undergo intense bombardment by solar atmospheric ions (energy 2 keV per nucleon) the rate increasing exponentially with depth on a scale of around 500 km. It follows that, above depth r_∗ where n = n_∗ = 2.5 × 10¹¹/cm³, evaporative destruction is essentially by sublimation only. On the other hand, the behavior of any nucleus surviving sublimation to below this height is dominated by atmospheric collisional effects - ablation and ram pressure driven explosion. This creates an exploding air burst followed by a fireball spreading and rising through the atmosphere similarly to the Shoemaker Levy 9 impacts on Jupiter (e.g., Carlson et al. 1997).

Because of the exponential distribution of atmospheric density and the small atmospheric scale height H (compared to R_⊙) the terminal heights of these cometary flares is only logarithmically sensitive to the incoming cometary mass (and to the density and latent heat of the nucleus). It only ranges from the upper chromosphere for small to moderate comet masses with typically shallow entry angles to the low chromosphere for very massive steep entry comets.

The ablated matter (atoms and small particles) decelerates very quickly in collisions with the atmosphere, depositing its kinetic energy and momentum over a few scale heights in tens of seconds, heating the debris and local solar plasma to X-ray emitting temperatures similar to solar flares and with comparable plasma masses and emission measures. Observing such very small impulsive but very luminous “cometary flares” poses a fascinating challenge but will enable new diagnostics of cometary element abundances from the highly non-solar flash emission spectra. In addition the downward momentum impulse should generate cometary sunquakes as observable ripples in the photosphere akin to those found in conventional magnetically-energized solar flares. In the case of impacts by the most massive comets (10²⁰ g or so) the cometary flare energy release (2 × 10³⁵ erg) is much larger than that of the largest solar flares ever observed. An impact of this magnitude would have very significant terrestrial effects.

Acknowledgments

We wish to thank referee Paul Weissman for his very detailed reports. These helped us improve the clarity and terminology of the paper and to fill a serious gap in our original discussion of the physics, namely the role of atmospheric ram pressure in destruction of impacting comets, well known to be important for planetary impacts. The paper has also benefited from discussions with K. Battams, R. Galloway, H. S. Hudson, D. W. Hughes, S. W. McIntosh, C. Schrijver, P. St. Hilaire, and the late B. G. Marsden, to all of whom we are very grateful. We gratefully acknowledge financial support from the UK STFC and RSE Cormack Bequest and from NCAR and TCD.

References

Biesecker, D. A., Lamy, P., St. Cyr, O. C., Llebaria, A., & Howard, R. A. 2002, Icarus, 157, 323 [NASA ADS] [CrossRef] [Google Scholar]
Brown, J. C. 1972, Sol. Phys., 26, 441 [NASA ADS] [CrossRef] [Google Scholar]
Carlson, R. W., Weissman, P. R., Segura, M., et al. 1995, Geophys. Res. Lett., 22, 1557 [NASA ADS] [CrossRef] [Google Scholar]
Carlson, R. W., Drossant, P., Encrenaz, Th., et al. 1997, Icarus, 128, 251 [NASA ADS] [CrossRef] [Google Scholar]
Chevalier, R. A., & Sarazin, C. L. 1994, ApJ, 429, 863 [NASA ADS] [CrossRef] [Google Scholar]
Chyba, C. F., Thomas, P. J., & Zahnle, K. J. 1993, Nature, 361, 40 [NASA ADS] [CrossRef] [Google Scholar]
Emslie, A. G. 1978, ApJ, 224, 241 [NASA ADS] [CrossRef] [Google Scholar]
Field, G. B., & Ferrara, A. 1995, ApJ, 438, 957 [NASA ADS] [CrossRef] [Google Scholar]
Fletcher, L., & Brown, J. C. 1992, A&A, 259, L43 [NASA ADS] [Google Scholar]
Fletcher, L., & Brown, J. C. 1995, A&A, 294, 260 [NASA ADS] [Google Scholar]
Huebner, W. F. 1967, Z. Astrophys., 65, 185 [NASA ADS] [Google Scholar]
Huebner, W. F., Benkhoff, J., Capria, M.-T., et al. 2006, Heat and Gas Diffusion in Comet Nuclei, ISSI Scientific Report SR-004, Bern [Google Scholar]
Hughes, D. W. 2001, MNRAS, 326, 515 [Google Scholar]
Iseli, M., Kuppers, M., Benz, W., & Bochsler, P. 2002, Icarus, 350 [Google Scholar]
Kaiser, T. R. 1962, Meteor science and engineering (London: McGraw-Hill) [Google Scholar]
Knight, M. M., A’Hearn, M. F., Biesecker, D. A., et al. 2010, ApJ, 139, 926 [Google Scholar]
Kosovichev, A. G. 2006, Sol. Phys., 238, 1 [NASA ADS] [CrossRef] [Google Scholar]
Kosovichev, A. G., & Zharkova, V. V. 1998, Nature, 393, 317 [NASA ADS] [CrossRef] [Google Scholar]
Le Chat, G. 2006, Internal Report, University of Glasgow [Google Scholar]
Lisse, C. M., Dennerl, J., Englhauser, M., et al. 1996, Science, 274, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
MacLow, M.-M., & Zahnle, K. 1994, ApJ, 434, L33 [NASA ADS] [CrossRef] [Google Scholar]
McKinley, D. W. R. 1961, Meteor Science and Engineering (New York: McGraw-Hill) [Google Scholar]
Marsden, B. G. 2005, ARA&A, 43, 75 [NASA ADS] [CrossRef] [Google Scholar]
Mendis, D. A., & Wickramasinghe, N. C. 1975, Ap&SS, 37, L13 [NASA ADS] [CrossRef] [Google Scholar]
Pégouriéz, B. 2007, Plasma Phys. Control. Fusion, 49, R87 [CrossRef] [Google Scholar]
Petrov, C. I., & Stulov, V. P. 1975, Kosmicheskie Issledonvaniya, 13, 587 [NASA ADS] [Google Scholar]
Porter, L. J. 2007, RSE Cormack Project Report, Glasgow University [Google Scholar]
Porter, L. J. 2008, MSci Project Report, Glasgow University [Google Scholar]
Raftery, C. L., Martinez-Oliveros, J. C., Saint-Hilaire, P., & Krucker, S. 2010, AAS Meeting, 216, 407.23 [Google Scholar]
Revelle, D. O. 1979, J. Atmosph. Terrest. Phys., 41, 453 [Google Scholar]
Richardson, J. E., Melosh, H. J., Lisse, C. M., & Carcich, B. 2007, Icarus, 191, 176 [NASA ADS] [CrossRef] [Google Scholar]
Schrijver, C., Brown, J. C., Battams, K., et al. 2011, Science, submitted [Google Scholar]
Sekanina, Z. 2003, ApJ, 597, 1237 [NASA ADS] [CrossRef] [Google Scholar]
Samarashinha, N. H., Mueller, B. E. A., Belton, M. J. S., & Jorda, L. 2004, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 281 [Google Scholar]
Weissman, P. R. 1983, Icarus, 55, 448 [NASA ADS] [CrossRef] [Google Scholar]
Weissman, P. R., & Lowry, S. C. 2008, MPS, 43, 1033 [Google Scholar]
Whipple, F. 1950, ApJ, 55, 83 [Google Scholar]
Zahnle, K., & MacLow, M.-M. 1994, Icarus, 108, 1 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

Fig. 1

Conversion factor M_o/ℳ_o from ice equivalent mass ℳ_o to real mass M_o versus $\begin{matrix} ˜ \\ ρ \end{matrix}$ $\hbox{$\tilde{\rho}$}$ for $\begin{matrix} _{˜} \\ ℒ \end{matrix} = 0.1, 0.2, 0.5, 1.0$ $\hbox{$\tilde{{\cal L}}= 0.1, 0.2, 0.5, 1.0$}$ – Eq. (20). For our canonical values $\begin{matrix} _{˜} \\ ρ \end{matrix} = 0.5, \begin{matrix} _{˜} \\ ℒ \end{matrix} = 1$ $\hbox{$\tilde{\rho}=0.5, \tilde{{\cal L}}=1$}$ , the true mass M_o = 4 × ℳ_o since comet nuclei are less dense than ice so easier to evaporate. This figure is available in colour in electronic form.

In the text

	Fig. 2 m(x) versus x/p for various ℳ_op^3/2 showing cases of survival of sublimation through an orbit, and of terminal mass loss before and after perihelion. This figure can be used for any values of M_o,p,ρ,ℒ because of the scaling and combination of variables used. This figure is available in colour in electronic form.
In the text

	Fig. 3 Value of ℳ_op^3/2 which has undergone fractional sublimation mass loss Δm_q by perihelion – Eq. (26). The figure can be used for any values of M_o,p,ρ,ℒ because of the scaling and combination of variables used. This figure is available in colour in electronic form.
In the text

Fig. 4

Estimate of the heights z_end and densities n_end at which nuclei are destroyed as a function of M_ocos³φ_∗ for specified P₆. Note that results are very sensitive to cosφ_∗ and to P₆. To the left of the knee ablation vaporizes the nucleus before ram pressure exceeds the strength of nucleus material. To the right ram pressure drives destructive explosion of the nucleus. It is clear that a very large range of masses is destroyed within a few scale heights in the chromosphere and that for all plausible masses and parameters, all nuclei are destroyed above the photosphere. This figure is available in colour in electronic form.

In the text

Fig. 5

Domains of destruction of comet nuclei in the plane ( $M_{o} / P_{c}^{3},p / x_{*} = \sin φ_{*}$ $\hbox{$M_{\rm o}/P_{\rm c}^3,p/x_*=\sin \phi_*$}$ ) for entry angle φ_∗ = arcsin(p/x_∗) to the vertical at r = r_∗. Note the change from linear to log scale on the p/x_∗ axis across the point p/x_∗ = 1 so as to display the very rapid variation in the range p/x_∗ ≤ 1. The axes are scaled with respect to P₆ as discussed in Sect. 2.2. For P₆ = 0.1 the ablation regime becomes a slender strip at 0.99 ≼ p/x_∗ ≼ 1.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Biesecker, D. A., Lamy, P., St. Cyr, O. C., Llebaria, A., & Howard, R. A. 2002, Icarus, 157, 323 [NASA ADS] [CrossRef] [Google Scholar]

[2] Brown, J. C. 1972, Sol. Phys., 26, 441 [NASA ADS] [CrossRef] [Google Scholar]

[3] Carlson, R. W., Weissman, P. R., Segura, M., et al. 1995, Geophys. Res. Lett., 22, 1557 [NASA ADS] [CrossRef] [Google Scholar]

[4] Carlson, R. W., Drossant, P., Encrenaz, Th., et al. 1997, Icarus, 128, 251 [NASA ADS] [CrossRef] [Google Scholar]

[5] Chevalier, R. A., & Sarazin, C. L. 1994, ApJ, 429, 863 [NASA ADS] [CrossRef] [Google Scholar]

[6] Chyba, C. F., Thomas, P. J., & Zahnle, K. J. 1993, Nature, 361, 40 [NASA ADS] [CrossRef] [Google Scholar]

[7] Emslie, A. G. 1978, ApJ, 224, 241 [NASA ADS] [CrossRef] [Google Scholar]

[8] Field, G. B., & Ferrara, A. 1995, ApJ, 438, 957 [NASA ADS] [CrossRef] [Google Scholar]

[9] Fletcher, L., & Brown, J. C. 1992, A&A, 259, L43 [NASA ADS] [Google Scholar]

[10] Fletcher, L., & Brown, J. C. 1995, A&A, 294, 260 [NASA ADS] [Google Scholar]

[11] Huebner, W. F. 1967, Z. Astrophys., 65, 185 [NASA ADS] [Google Scholar]

[12] Huebner, W. F., Benkhoff, J., Capria, M.-T., et al. 2006, Heat and Gas Diffusion in Comet Nuclei, ISSI Scientific Report SR-004, Bern [Google Scholar]

[13] Hughes, D. W. 2001, MNRAS, 326, 515 [Google Scholar]

[14] Iseli, M., Kuppers, M., Benz, W., & Bochsler, P. 2002, Icarus, 350 [Google Scholar]

[15] Kaiser, T. R. 1962, Meteor science and engineering (London: McGraw-Hill) [Google Scholar]

[16] Knight, M. M., A’Hearn, M. F., Biesecker, D. A., et al. 2010, ApJ, 139, 926 [Google Scholar]

[17] Kosovichev, A. G. 2006, Sol. Phys., 238, 1 [NASA ADS] [CrossRef] [Google Scholar]

[18] Kosovichev, A. G., & Zharkova, V. V. 1998, Nature, 393, 317 [NASA ADS] [CrossRef] [Google Scholar]

[19] Le Chat, G. 2006, Internal Report, University of Glasgow [Google Scholar]

[20] Lisse, C. M., Dennerl, J., Englhauser, M., et al. 1996, Science, 274, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[21] MacLow, M.-M., & Zahnle, K. 1994, ApJ, 434, L33 [NASA ADS] [CrossRef] [Google Scholar]

[22] McKinley, D. W. R. 1961, Meteor Science and Engineering (New York: McGraw-Hill) [Google Scholar]

[23] Marsden, B. G. 2005, ARA&A, 43, 75 [NASA ADS] [CrossRef] [Google Scholar]

[24] Mendis, D. A., & Wickramasinghe, N. C. 1975, Ap&SS, 37, L13 [NASA ADS] [CrossRef] [Google Scholar]

[25] Pégouriéz, B. 2007, Plasma Phys. Control. Fusion, 49, R87 [CrossRef] [Google Scholar]

[26] Petrov, C. I., & Stulov, V. P. 1975, Kosmicheskie Issledonvaniya, 13, 587 [NASA ADS] [Google Scholar]

[27] Porter, L. J. 2007, RSE Cormack Project Report, Glasgow University [Google Scholar]

[28] Porter, L. J. 2008, MSci Project Report, Glasgow University [Google Scholar]

[29] Raftery, C. L., Martinez-Oliveros, J. C., Saint-Hilaire, P., & Krucker, S. 2010, AAS Meeting, 216, 407.23 [Google Scholar]

[30] Revelle, D. O. 1979, J. Atmosph. Terrest. Phys., 41, 453 [Google Scholar]

[31] Richardson, J. E., Melosh, H. J., Lisse, C. M., & Carcich, B. 2007, Icarus, 191, 176 [NASA ADS] [CrossRef] [Google Scholar]

[32] Schrijver, C., Brown, J. C., Battams, K., et al. 2011, Science, submitted [Google Scholar]

[33] Sekanina, Z. 2003, ApJ, 597, 1237 [NASA ADS] [CrossRef] [Google Scholar]

[34] Samarashinha, N. H., Mueller, B. E. A., Belton, M. J. S., & Jorda, L. 2004, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 281 [Google Scholar]

[35] Weissman, P. R. 1983, Icarus, 55, 448 [NASA ADS] [CrossRef] [Google Scholar]

[36] Weissman, P. R., & Lowry, S. C. 2008, MPS, 43, 1033 [Google Scholar]

[37] Whipple, F. 1950, ApJ, 55, 83 [Google Scholar]

[38] Zahnle, K., & MacLow, M.-M. 1994, Icarus, 108, 1 [NASA ADS] [CrossRef] [Google Scholar]

Mass loss, destruction and detection of Sun-grazing and -impacting cometary nuclei⋆

1. Introduction

2. Comet nucleus parameters

2.1. Masses and densities

2.2. Latent heat of sublimation

2.3. Physical strength and sound speed

2.4. Nucleus shape and “size”

3. Rough comparison of nucleus mass loss, deceleration and explosion processes

3.1. “Evaporative” mass loss versus deceleration

3.2. Deceleration of sublimated/ablated mass

3.3. Insolation sublimation case q ≽ r∗, Mo ≼ 1011 g

3.4. Impact ablation and ram pressure explosion cases

3.4.1. Background

3.4.2. Rough comparison of the importance of impact processes

4. Theory of nucleus sublimation/ablation

4.1. General formulation

4.2. Heating energy flux terms and regimes

5. Sublimation dominated mass loss solutions

5.1. Sublimation dominated solution for m(x)

5.2. Sublimation solution properties

5.2.1. Fractional mass lost by perihelion/after one orbit

5.2.2. Minimum initial masses and radii surviving sublimation to perihelion and through one orbit

5.3. Comparison with numerical models

6. Ablation and explosion of Sun-impactors

6.1. Ablation dominated solution when ram pressure can be neglected – Mo(1-q/r)3/2∗≼ M∗∗ ≈ 1010g, r∗–q ≽ H

6.2. Explosive end point for nuclei of high Mcos3/2oφ∗

6.3. Energy deposition profiles of Sun-impacting comets

7. Discussion and conclusions

7.1. Summary of nucleus destruction regimes

7.2. Visibility of Sun-grazer destruction by sublimation

7.3. Signatures of Sun-impactor destruction

7.3.1. Mass, energy and temperature of the fireball

7.3.2. Cometary flare size, emission measure and optical depth

7.3.3. Cometary sunquakes and other solar disturbances

7.4. Conclusions

Acknowledgments

References

All Figures

Mass loss, destruction and detection of Sun-grazing and -impacting cometary nuclei^⋆

3.3. Insolation sublimation case q ≽ r_∗, M_o ≼ 10¹¹ g

6.1. Ablation dominated solution when ram pressure can be neglected – M_o(1-q/r ${}_{})^{3 / 2} ≼$ $\hbox{$_)^{\sf 3/2}\preceq$}$ M_∗∗ ≈ 10¹⁰g, r_∗–q ≽ H

6.2. Explosive end point for nuclei of high M ${}_{o}\cos^{3 / 2} φ_{}$ $\hbox{$_{\rm o}\cos^{\sf 3/2}\phi_$}$