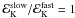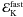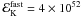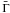| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117404 | |
| Published online | 14 October 2011 | |
Was the “naked burst” GRB 050421 really naked?
Institut d’Astrophysique de Paris, UMR 7095 Université Pierre et Marie Curie-Paris 6 – CNRS, 98 bis boulevard Arago, 75014 Paris, France
e-mail: hascoet@iap.fr; mochko@iap.fr
Received: 3 June 2011
Accepted: 24 August 2011
Context. A few long gamma-ray bursts such as GRB 050421 show no afterglow emission beyond the usual initial steep decay phase. It has been suggested that these events correspond to “naked” bursts that occur in a very low density environment. We reconsider this possibility in the context of various scenarios for the origin of the afterglow.
Aims. In the standard model where the afterglow results from the forward shock as well as in the alternative model where the afterglow comes from the reverse shock, we aim to obtain constraints on the density of the environment, the microphysics parameters, or the Lorentz factor of the ejecta, which are imposed by the absence of a detected afterglow.
Methods. For the two models we compute the afterglow evolution for different values of the external density (uniform or wind medium) and various burst parameters. We then compare our results to the Swift data of GRB 050421, which is the best example of a long burst without afterglow.
Results. In the standard model we show that consistency with the data imposes that the external density does not exceed 10-5 cm-3 or that the microphysics parameters are very small with ϵe ≲ 10-2 and ϵB ≲ 10-4. If the afterglow is caused by the reverse shock, we find that its contribution can be strongly reduced if the central source has mainly emitted fast-moving material (with less than 10–30% of the kinetic energy at Γ < 100) and was located in a dense environment.
Conclusions. The two considered scenarios therefore lead to opposite constraints on the circumburst medium. The high-density environment, favored by the reverse shock model, better corresponds to what is expected if the burst progenitor was a massive star.
Key words: radiation mechanisms: non-thermal / gamma-ray burst: general / gamma-ray burst: individual: GRB 050421 / shock waves
© ESO, 2011
1. Introduction
In the pre-Swift era afterglow observations typically started a few hours after the trigger, so that the very early evolution immediately following the prompt phase remained a “terra incognita”. The situation dramatically changed with Swift (Gehrels et al. 2004) which is capable to slew in one minute and point its X-ray and optical telescopes (XRT, Burrows et al. 2005, and UVOT, Roming et al. 2005) to the source. Swift has revealed several unexpected features in the early afterglow of gamma-ray bursts (Nousek et al. 2006; O’Brien et al. 2006; Zhang et al. 2007). The prompt phase ends with a steep decay of the X-ray flux, FX ∝ t − α with 2 ≲ α ≲ 5. The afterglow continues with a plateau where the index α lies between 0 and 1. At 0.1–1 day it recovers the more standard value α ~ 1−1.5, which was known before Swift. Finally, at later times it sometimes further steepens as a result of a jet break. Flares with short rise and decay times can be superimposed on this global evolution (Chincarini et al. 2007; Falcone et al. 2007). These different components are not always present. Flares are observed in about 50% of the bursts. The plateau is sometimes absent and the afterglow then follows a single power-law already from the beginning of the XRT observations (the most extreme case being GRB 061007 which maintained a constant slope α = 1.6 from 100 s, to more than 10 days after trigger; Schady et al. 2007).
GRB 050421 was even more peculiar because it only showed the initial steep decay phase and a few flares at 100–150 s but no plateau and no standard afterglow at later times. This behavior had been predicted by Kumar & Panaitescu (2000) for a burst occurring in an extremely low density environment. In such a “naked” burst one only sees the high latitude emission once the on-axis prompt emission has stopped. Radiation from an annulus making an angle θ with the line of sight arrives with a delay to the observer and benefits less from the Doppler boost of the relativistic motion. The predicted flux at a given frequency then decays steeply as Fν(t) ∝ t − αν − β with α = 2 + β and 0 ≲ β ≲ 2.
In their detailed study of GRB 050421 Godet et al. (2006) found that this event fits well with these theoretical predictions and concluded that it was a good naked burst candidate. However, the authors did not provide any estimate of the maximum external density that could still be compatible with the data.
A very low density environment has been frequently invoked to explain why a fraction of the short burst population has very dim afterglows (see Nakar 2007, and references therein). If short bursts result from the merging of two compact objects, the kick received when the neutron star or black hole components formed in supernova explosions allows the system to reach the low-density outskirts of the host galaxy before coalescence occurs. But GRB 050421 lasted about 10 s and may be associated to the long burst population (except if it was located at a high redshift, z > 4; Xiao & Schaefer 2011). Long bursts are expected to form during the collapse and explosion of rapidly rotating Wolf-Rayet stars (Woosley 1993). The typical environment of the burst should then first consist of the wind from the star, followed by a wind termination shock and several shells, successively containing the shocked wind and the remnants of previous mass loss episodes (van Marle et al. 2005; Eldridge et al. 2006). This may seem to contradict afterglow modeling, which generally favors a uniform external medium, even for long bursts. One should keep in mind, however, that this conclusion relies on several uncertain assumptions such as the constancy of the microphysics redistribution parameters ϵe and ϵB, while the presence of a wind is a conspicuous feature in observed Wolf-Rayet stars.
Apart from GRB 050421, at least three other, possibly long bursts (GRB 070531, GRB 080727A and GRB 081016B) showed no afterglow after the steep decay phase (Vetere et al. 2008). GRB 070531 lasted 44 s and had a FRED shape. GRB 080727A and GRB 081016BA had respective durations t90 = 4.9 and 2.6 s. Because their redshift is not known, it is not clear if they belong to the short or long burst populations.
In this work we concentrate on GRB 050421, which has the best data. Our aim is to perform afterglow calculations to obtain for different scenarios the limits on the external density that are compatible with the absence of an afterglow. For a given density we also constrain the microphysics parameters ϵe and ϵB and the distribution of the Lorentz factor in the ejecta. The paper is organized as follows: we briefly summarize the observational data on GRB 050421 in Sect. 2 and estimate the isotropic kinetic energy released by this burst. We consider in Sect. 3 several possible origins for the afterglow. First, the standard case, where it is made by the forward shock propagating in the external medium, then the alternative model where it comes from the reverse shock that sweeps back into the ejecta, and finally a few more exotic possibilities. Our results are discussed in Sect. 4, which is also the conclusion.
2. GRB 050421: a burst with no afterglow
2.1. Summary of the observational data
GRB 050421 belongs to the 10% faintest bursts of the Swift sample. Its fluence in the 15–150 keV energy range integrated over t90 = 10 s was S15 − 150 = 1.1 ± 0.7 × 10-7 erg cm-2. The light curve during t90 approximately had a FRED shape. It was followed by a weak tail and at least two flares at 110 and 154 s. Between 15 and 150 keV the prompt spectrum can be fitted by a single power-law Fν ∝ ν-0.7, which suggests that the peak energy Ep was higher than 150 keV (Godet et al. 2006). The XRT was able to follow the burst from about 100 s to 1000 s after trigger. Later, in an interval running from 5000 to 5 × 105 s, the source was not detected, leading to an upper limit1F0.3−10 keV < 8 × 10-14 erg cm-2 s-1. Any long-lasting afterglow component, if present, should therefore be very dim, lying after a few hours about five orders of magnitude below the flux recorded at 100 s.
Between 100 and 1000 s the flux exhibited a power law decline of index 3.1 ± 0.1 together with a hard-to-soft evolution, indicating that the peak energy of the spectrum was probably crossing the XRT band during the observations. This strongly suggests that what was observed was the high-latitude emission of the last shocked shells in the ejecta of GRB 050421 (Godet et al. 2006).
2.2. Constraining the isotropic kinetic energy of GRB 050421
The isotropic kinetic energy of the burst ejecta at the end of the prompt phase (after a fraction fγ of the initial amount has been converted to gamma-rays) is a key ingredient for any afterglow calculation. Unfortunately, the redshift of GRB 050421 is not known and, in a first step, we just estimate the total gamma-ray fluence Sγ from the fluence in the 15–150 keV band. We obtain Sγ = 4.5 × 10-7 erg cm-2 assuming that the spectrum is a Band function (Band et al. 1993) with α = −1.7, β = −2.5 and Ep = 350 keV. From the fluence we then obtain the total energy release in gamma rays as a function of redshift 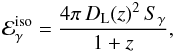 (1)where DL(z) is the luminosity distance. The kinetic energy
(1)where DL(z) is the luminosity distance. The kinetic energy 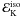 can now be estimated from the efficiency fγ
can now be estimated from the efficiency fγ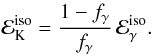 (2)In the case of internal shocks we have fγ ≃ ϵe × fdiss, where fdiss is the fraction of the kinetic energy dissipated by the shocks and ϵe the fraction transferred to electrons and eventually radiated (assuming fast cooling electrons). We take fdiss ~ 0.1, which is typical for internal shocks (Daigne & Mochkovitch 1998). To ensure a sufficient global efficiency, it is then necessary to have ϵe ~ 0.1–1. We adopt ϵe = 1/3, which leads to fγ ~ 3%. We also consider the possibility that the prompt emission may result from a more efficient process such as Comptonization at the photosphere (Rees & Mészáros 2005; Lazzati et al. 2009; Beloborodov 2010) or magnetic reconnection (Spruit et al. 2001; Drenkhan & Spruit 2002; Giannos & Spruit 2006; McKinney & Uzdensky 2011), for which we adopt a radiative efficiency of 30%. Our results for
(2)In the case of internal shocks we have fγ ≃ ϵe × fdiss, where fdiss is the fraction of the kinetic energy dissipated by the shocks and ϵe the fraction transferred to electrons and eventually radiated (assuming fast cooling electrons). We take fdiss ~ 0.1, which is typical for internal shocks (Daigne & Mochkovitch 1998). To ensure a sufficient global efficiency, it is then necessary to have ϵe ~ 0.1–1. We adopt ϵe = 1/3, which leads to fγ ~ 3%. We also consider the possibility that the prompt emission may result from a more efficient process such as Comptonization at the photosphere (Rees & Mészáros 2005; Lazzati et al. 2009; Beloborodov 2010) or magnetic reconnection (Spruit et al. 2001; Drenkhan & Spruit 2002; Giannos & Spruit 2006; McKinney & Uzdensky 2011), for which we adopt a radiative efficiency of 30%. Our results for 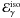 and
and 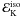 are summarized in Table 1 for different redshifts. They can vary by up to 50% if the parameters of the Band function (especially Ep) are changed. This uncertainty remains much smaller than the one resulting from the unknown distance and radiative efficiency of the burst.
are summarized in Table 1 for different redshifts. They can vary by up to 50% if the parameters of the Band function (especially Ep) are changed. This uncertainty remains much smaller than the one resulting from the unknown distance and radiative efficiency of the burst.
Isotropic gamma-ray and kinetic energies of GRB 050421 for different redshifts and H0 = 70 km s-1 Mpc-1, ΩM = 0.27 and ΩΛ = 0.73.
3. Explaining the lack of a regular afterglow
3.1. The forward shock case
In the standard model, where the afterglow is made by the forward shock, the predicted X-ray flux is much above the observational limit as long as the burst parameters keep “usual” values. This can be checked using the analytical formulae provided by Panaitescu & Kumar (2000). The relevant radiative regime corresponds to νX > νm (resp. νX > νc) for fast (resp. slow) cooling, where νm, νc and νX are the synchrotron, cooling, and typical X-ray frequencies respectively. The expression for the flux density is the same in the two cases and also for either a uniform external medium or a stellar wind (they differ only by constant factors on the order of 2 or less). We have ![\begin{equation} \begin{array}{l} F_{\rm X}(E) \simeq 0.3\, D_{28}^{-2}\,{\cal E}_{52}^{(p+2)/4}\,\epsilon_{\rm e,\,-1}^{p-1}\, \epsilon_{\rm B,\,-2}^{(p-2)/4}E_{\rm keV}^{-(p/2)}\,t^{-[(3p-2)/4]}\ \ {\rm Jy} , \end{array} \end{equation}](/articles/aa/full_html/2011/10/aa17404-11/aa17404-11-eq59.png) (3)where ϵe (in units of 10-1) and ϵB (in units of 10-2) are the microphysics redistribution parameters, ℰ52 is the isotropic kinetic energy in units of 1052 erg, D28 the luminosity distance in units of 1028 cm, EkeV the photon energy in keV and t the time in seconds (both EkeV and t are given here in the burst rest frame). This relation holds at times longer than the deceleration time. Assuming that this is the case for tobs > 1000 s, the data require F10 keV to be on the order of 2 × 10-9 Jy at 1000 s and smaller than 2 × 10-11 Jy at 5 × 104 s (Evans et al. 2007, 2010). For a reference case defined by z = 1, ℰK = 4 × 1052 erg, ϵe = 0.1, ϵB = 0.01 and p = 2.5 and using Eq. (3) with the rest frame values EkeV = 20 and t = 500 and 2.5 × 104 s, we obtain F10 keV = 1.6 × 10-6 and 7.3 × 10-9 Jy at observed times 1000 and 5 × 104 s respectively. The predicted X-ray afterglow is therefore much brighter than the observational limits. Changing the assumed redshift has little effect on this result because
(3)where ϵe (in units of 10-1) and ϵB (in units of 10-2) are the microphysics redistribution parameters, ℰ52 is the isotropic kinetic energy in units of 1052 erg, D28 the luminosity distance in units of 1028 cm, EkeV the photon energy in keV and t the time in seconds (both EkeV and t are given here in the burst rest frame). This relation holds at times longer than the deceleration time. Assuming that this is the case for tobs > 1000 s, the data require F10 keV to be on the order of 2 × 10-9 Jy at 1000 s and smaller than 2 × 10-11 Jy at 5 × 104 s (Evans et al. 2007, 2010). For a reference case defined by z = 1, ℰK = 4 × 1052 erg, ϵe = 0.1, ϵB = 0.01 and p = 2.5 and using Eq. (3) with the rest frame values EkeV = 20 and t = 500 and 2.5 × 104 s, we obtain F10 keV = 1.6 × 10-6 and 7.3 × 10-9 Jy at observed times 1000 and 5 × 104 s respectively. The predicted X-ray afterglow is therefore much brighter than the observational limits. Changing the assumed redshift has little effect on this result because 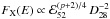 , which does not vary much with z for 2 < p < 3.
, which does not vary much with z for 2 < p < 3.
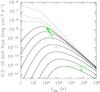 |
Fig. 1 Afterglow from the forward shock. The assumed redshift and burst energy are z = 1 and ℰK = 4 × 1052 erg and the average Lorentz factor of the ejecta is |
Another striking consequence of Eq. (3) is that the flux does not depend on the external density. This remains true as long as νX is higher than both νm and νc. Decreasing the density only increases the deceleration time and delays the rise of the afterglow but does not affect the flux level in the Blandford-McKee regime. It is only at very low density (n < 10-3 cm-3) when νc becomes higher than νX that the radiative regime changes and the flux begins to depend on density.
We have calculated the evolution of the X-ray flux (in the XRT band 0.3–10 keV) for the reference case, an average Lorentz factor in the ejecta2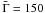 and different values of the density: from n = 1 to 10-6 cm-3 (uniform medium) and A∗ = 1 to 10-2 (stellar wind). We do not consider lower values of A∗, which would not be realistic for a massive star progenitor. Our results are shown in Fig. 1. It appears that the wind case is clearly excluded while a uniform density below 10-6 cm-3 is required, which would likely correspond to the intergalactic medium (IGM). But if GRB 050421 had a massive progenitor it should have normally occurred in a region of star formation, characterised by a dense environment. With the lower value of the kinetic energy ℰK = 4 × 1051 erg (for a higher efficiency of the prompt phase) the maximum allowed density is raised to about 10-5 cm-3 but still remains very low.
and different values of the density: from n = 1 to 10-6 cm-3 (uniform medium) and A∗ = 1 to 10-2 (stellar wind). We do not consider lower values of A∗, which would not be realistic for a massive star progenitor. Our results are shown in Fig. 1. It appears that the wind case is clearly excluded while a uniform density below 10-6 cm-3 is required, which would likely correspond to the intergalactic medium (IGM). But if GRB 050421 had a massive progenitor it should have normally occurred in a region of star formation, characterised by a dense environment. With the lower value of the kinetic energy ℰK = 4 × 1051 erg (for a higher efficiency of the prompt phase) the maximum allowed density is raised to about 10-5 cm-3 but still remains very low.
But these conclusions depend on our choice for the microphysics parameters. Assuming that 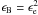 (which results from the acceleration process of electrons moving toward current filaments in the shocked material, Medvedev 2006), we find that more standard values of the density (n > 10-2 cm-3 or A∗ > 10-2) can be made consistent with the data as long as ϵe < 5 × 10-3. Starting from a lower density, n = 10-3 cm-3, typical of the hot interstellar medium and not too far from the transition to the radiative regime νm < νX < νc, the previous limit becomes ϵe < 2 × 10-2. Still with n = 10-3 cm-3 but with the lower kinetic energy ℰK = 4 1051 erg we finally obtain ϵe ≲ 4 × 10-2. Except maybe for this final case, such values of the microphysics parameters are lower than those usually inferred from multiwavelength fits of afterglow data (Panaitescu & Kumar 2001a,b; 2002) but it might be possible, for example, that below some threshold in density the transfer of shock-dissipated energy to electrons or/and magnetic field becomes less efficient, so that ϵe and/or ϵB drop suddenly.
(which results from the acceleration process of electrons moving toward current filaments in the shocked material, Medvedev 2006), we find that more standard values of the density (n > 10-2 cm-3 or A∗ > 10-2) can be made consistent with the data as long as ϵe < 5 × 10-3. Starting from a lower density, n = 10-3 cm-3, typical of the hot interstellar medium and not too far from the transition to the radiative regime νm < νX < νc, the previous limit becomes ϵe < 2 × 10-2. Still with n = 10-3 cm-3 but with the lower kinetic energy ℰK = 4 1051 erg we finally obtain ϵe ≲ 4 × 10-2. Except maybe for this final case, such values of the microphysics parameters are lower than those usually inferred from multiwavelength fits of afterglow data (Panaitescu & Kumar 2001a,b; 2002) but it might be possible, for example, that below some threshold in density the transfer of shock-dissipated energy to electrons or/and magnetic field becomes less efficient, so that ϵe and/or ϵB drop suddenly.
 |
Fig. 2 Afterglow from the reverse shock. Left panel: uniform medium of density n = 1000 cm-3. Right panel: wind medium with A∗ = 1. The four light curves correspond (from top to bottom) to |
3.2. The reverse shock case
In order to solve some of the problems raised by Swift observations of the early afterglow, Genet et al. (2007) and Uhm & Beloborodov (2007) have proposed a non-standard scenario where GRB afterglows are made by a long-lived reverse shock that propagates into the ejecta when it is decelerated by the external medium. In this scenario it is assumed that the forward shock is present but radiatively inefficient (if, for example, the magnetic field is too weak in the external medium) and that the reverse shock is long-lived because the central engine has produced an ejecta with a tail going down to very low Lorentz factors (possibly down to Γ ~ 1).
The reverse shock model offers an interesting alternative to explain the lack of an afterglow in objects like GRB 050421, which does not require to have a very low density environment. This model assumes that the central source mainly produced fast-moving material with a limited amount of energy in the tail at low Γ. As it sweeps back into the ejecta, the reverse shock encounters shells with a decreasing energy content and the observed flux exhibits a steep drop.
Moreover, because the total energy released by GRB 050421 was relatively modest and for a sufficiently high value of the external density, the reverse shock is relativistic and the emission takes place in the fast cooling regime. This is different from the situation considered by Sari & Piran (1999) to explain the early optical flash in GRB 990123, where slow cooling electrons were responsible for a flux decaying approximately as t-2. In the present case, a steeper slope can be obtained because the light curve is dominated by the high-latitude emission of the last shocked shells.
More precisely, we aim to quantify how much energy we can inject into material with a low Lorentz factor and still remain in agreement with the data. To model the source we consider that it has been active for 120/(1 + z) s but that more than 50% of the total energy has been released during the first 15/(1 + z) s. This may represent the fact that the main activity in GRB 050421 had a t90 of 10–15 s but was followed by a weaker emission with some flares, lasting for a total of about 100–150 s. We adopt a distribution of the Lorentz factor that varies between 100 and 400 with a typical variability timescale of 1 s, which is ended by a tail going from Γ = 100 to 2.
Because we implicitely suppose in this section that the prompt emission comes from internal shocks, we only consider the low-efficiency case for the prompt phase. We then inject a fixed kinetic energy 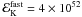 erg (for z = 1) into the fast-moving ejecta with Γ > 100 and a remaining
erg (for z = 1) into the fast-moving ejecta with Γ > 100 and a remaining 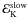 in the tail (Γ < 100). We do not try to fit the details of the prompt light curve (which is of poor quality owing to the weakness of the burst) with this distribution but simply to reproduce the general behavior of the prompt-to-early-afterglow transition.
in the tail (Γ < 100). We do not try to fit the details of the prompt light curve (which is of poor quality owing to the weakness of the burst) with this distribution but simply to reproduce the general behavior of the prompt-to-early-afterglow transition.
We computed the synchrotron emission from the internal and reverse shocks as explained in Daigne & Mochkovitch (1998) and Genet et al. (2007). Because these shocks all take place in the material ejected by the source and are mildly relativistic, we adopted similar values for the microphysics parameters: ϵe = ϵB = 1/3 and ζ (fraction of electrons that are accelerated) = 10-2, which were also used in the works cited above. They ensure a reasonable efficiency in the transfer of dissipated energy to electrons and allow the emission to take place in the gamma-ray range during the prompt phase.
The resulting flux in the XRT band is shown in Fig. 2 for four values of the ratio 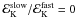 , 0.1, 0.3 and 1. The density in the burst environment is supposed to be high with n = 1000 cm-3 (uniform medium) or A∗ = 1 (stellar wind). The reverse shock is then relativistic and the emission takes place in the fast-cooling regime of the shock-accelerated electrons.
, 0.1, 0.3 and 1. The density in the burst environment is supposed to be high with n = 1000 cm-3 (uniform medium) or A∗ = 1 (stellar wind). The reverse shock is then relativistic and the emission takes place in the fast-cooling regime of the shock-accelerated electrons.
It can be seen in Fig. 2 that satisfactory solutions can be found for both a uniform and a wind external medium as long as the fraction of energy injected into material with Lorentz factors below 100 does not exceed about 10 and 30% in the uniform and wind medium, respectively3.
We checked how these results depend on our assumptions about the burst redshift and density of the environment. Increasing the redshift implies a higher injected energy and shorter intrinsic time scales. Going to values as high as z = 5 and keeping the same density (n = 1000 cm-3 or A∗ = 1) for the environment slightly delays the deceleration (in observer time), especially in the uniform density case. It is then more difficult to fit the data and it could become necessary to inject essentially the whole energy into material with Γ > 200. Similarly, reducing the density of the external medium from n = 1000 to 1 cm-3 (at a fixed z = 1) also delays the deceleration and leads to the same problem.
Therefore, GRB 050421 was not a naked burst in the context of the reverse shock scenario. On the contrary, it occurred in a dense environnement and was peculiar because it released a relatively modest amount of energy, mostly in high Lorentz factor material.
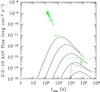 |
Fig. 3 Afterglow light curves for a sub-luminous burst (full lines) and an interrupted wind (dashed line). For the sub-luminous burst the injected kinetic energy is ℰK = 3.2 × 1048 erg at a redshift z = 0.01 and the four lines correspond (from top to bottom) to a density decreasing from 1 to 10-4 cm-3. The wind has A∗ = 1 but was interrupted 1000 years before the burst. |
3.3. Other possibilities
3.3.1. A sub-luminous burst
It is probable that a large number of sub-luminous bursts coexists with the classical population of cosmological GRBs. These objects are underrepresented in the observed sample because, contrary to the most powerful events they cannot be detected at far distances.
A prototype of these sub-luminous bursts was GRB 980425, which occurred at 34 Mpc and released an energy 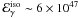 erg (Galama et al. 1998). Daigne & Mochkovitch (2007) argued that GRB 980425 was intrinsically faint (and not a normal event seen off-axis) and they have shown that it can be produced in a relativistic outflow with a moderate Lorentz factor Γ ~ 10–20. This scenario may work for GRB 050421 under the condition that the X-ray afterlow becomes dimmer when
erg (Galama et al. 1998). Daigne & Mochkovitch (2007) argued that GRB 980425 was intrinsically faint (and not a normal event seen off-axis) and they have shown that it can be produced in a relativistic outflow with a moderate Lorentz factor Γ ~ 10–20. This scenario may work for GRB 050421 under the condition that the X-ray afterlow becomes dimmer when 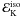 is decreased at constant burst fluence, i.e. if the X-ray flux
is decreased at constant burst fluence, i.e. if the X-ray flux 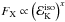 with x > 1. The analytic results of Panaitescu & Kumar (2000) show that the most favorable case (with x = (p + 3)/4) corresponds to the radiative regime νm < νX < νc, in a uniform external medium.
with x > 1. The analytic results of Panaitescu & Kumar (2000) show that the most favorable case (with x = (p + 3)/4) corresponds to the radiative regime νm < νX < νc, in a uniform external medium.
Assuming a redshift z = 0.01 for GRB 050421 we therefore considered an outflow with a Lorentz factor between 10 and 15, carrying a kinetic energy 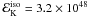 erg (see Table 1). The resulting afterglow light curves from the forward shock are shown in Fig. 3 for n = 1 to 10-4 cm-3, ϵe = 0.1 and ϵB = 0.01. A hot interstellar medium with n ≲ 10-3 cm-3 is almost consistent with the data. Because we have
erg (see Table 1). The resulting afterglow light curves from the forward shock are shown in Fig. 3 for n = 1 to 10-4 cm-3, ϵe = 0.1 and ϵB = 0.01. A hot interstellar medium with n ≲ 10-3 cm-3 is almost consistent with the data. Because we have 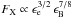 (for p = 2.5), in the considered regime only a modest reduction of either ϵe or ϵB would be enough to drive FX below the observational limits. A sub-luminous burst could therefore agree more easily with the data than a classical GRB without implying too low values of the density or microphysics parameters. But if GRB 050421 was indeed located at z ~ 0.01, one would expect to see a candidate host galaxy within one arc minute from the burst and to have detected an associated supernova. Contrary to GRB 980425, GRB 050421 fails to satisfy these two criteria.
(for p = 2.5), in the considered regime only a modest reduction of either ϵe or ϵB would be enough to drive FX below the observational limits. A sub-luminous burst could therefore agree more easily with the data than a classical GRB without implying too low values of the density or microphysics parameters. But if GRB 050421 was indeed located at z ~ 0.01, one would expect to see a candidate host galaxy within one arc minute from the burst and to have detected an associated supernova. Contrary to GRB 980425, GRB 050421 fails to satisfy these two criteria.
3.3.2. An interrupted wind
We finally consider a more exotic situation where the burst progenitor initially had a normal stellar wind with A∗ ~ 1, but we suppose that this wind was interrupted more than 1000 years before the explosion, creating a quasi-empty cavity around the star. Because there are no clear justifications for such a peculiar behavior we only briefly address this case. The density in the cavity should not exceed 10-5 cm-3 to ensure that there will be no afterglow signature before the ejecta hits the inner end of the wind, located at Rw = 3 v8 t3 pc where v8 and t3 are the wind velocity (in units of 108 cm s-1) and the time during which it has been inactive (in units of 103 years). When the ejecta finally reaches Rw, the wind has expanded to the point that the afterglow remains dimmer than the observational limit (see Fig. 3).
4. Discussion and conclusion
GRB 050421 was a very peculiar burst with no afterglow after an initial steep decay phase that went below the XRT detection limit at a few 103 s. This behavior corresponds to what is expected for a naked burst occurring in a very low density environment. We have reconsidered this interpretation in the context of the standard scenario, where the afterglow originates from the forward shock, but also within the alternative model where it is made by the reverse shock.
In the first case the density implied for the external medium is indeed very low. A wind environment with A∗ = 0.01 − 1, which would be typical of a Wolf-Rayet progenitor, is clearly excluded. The limit on the density for a uniform medium somewhat depends on the assumptions for the microphysics parameters ϵe and ϵB or the efficiency of the prompt mechanism, but always remains very low. For standard values, ϵe = 0.1 and ϵB = 0.01, we obtain n < 10-5 cm-3, lower than any reasonable ISM density and closer to a value representative of the IGM. Conversely, imposing a higher density on the burst environment requires a strong reduction of the microphysics parameters, below the values usually found in multiwavelength fits of afterglow data.
The fact that only very few long bursts similar to GRB 050421 have been observed would then be a consequence of the peculiar values required for the burst parameters, i.e. either an extremely low density environment, or very small ϵe or ϵB. These two conditions might indeed be related if below some threshold in density the transfer of shock-dissipated energy to electrons or/and the magnetic field becomes inefficient. Another possibility would be to suppose that GRB 050421 was a short burst and therefore located at z > 4−5. This could more easily account for the low density environment, but the burst should then have released an energy 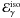 exceeding 1052 erg (see Table 1) corresponding to the very upper end of the observed range for short GRBs (Berger 2007).
exceeding 1052 erg (see Table 1) corresponding to the very upper end of the observed range for short GRBs (Berger 2007).
Still within the scenario where the afterglow comes from the forward shock we briefly considered two special cases: in the first one GRB 050421 was a nearby, sub-luminous burst and in the second it was surrounded, at the moment of the explosion, by a quasi-empty cavity created by a wind that was interrupted a few thousands years before the burst. Both can be made compatible with the XRT data but not with the absence of a host galaxy or supernova imprint in the first case, while the second case relies on a very ad hoc assumption that lacks clear justification.
In the alternative reverse shock scenario a long-lasting afterglow emission is produced when a tail of material with low Lorentz factor is present in the ejecta emitted by the central engine. We suggest that in some occasions this tail might be missing, which would simply explain the absence of an afterglow in objects like GRB 050421. Moreover, to ensure that the observed emission ends with the high-latitude emission of the last shocked shell, the radiating electrons must be in the fast-cooling regime, which is possible if the external medium has a high density. The situation is then just the reverse from the one found in the standard scenario: a dense burst environment is favored, as expected if the burst progenitor was a massive star.
Acknowledgments
We thank the anonymous referee for detailed and helpful comments and Paul O’Brien for kindly answering our questions regarding the XRT results. This work is partially supported by the French Space Agency (CNES). R.H.’s PhD work is funded by a Fondation CFM-JP Aguilar grant and Z.L.U. is supported by the grant “Research in Paris 2010/2011” of the City Hall of Paris.
References
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2010, MNRAS, 407, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2007, ApJ, 670, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Chincarini, G., Moretti, A., Romano, P., et al. 2007, ApJ, 671, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Daigne, F., & Mochkovitch, R. 1998, MNRAS, 296, 275 [Google Scholar]
- Daigne, F., & Mochkovitch, R. 2007, A&A, 465, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drenkhahn, G., & Spruit, H. C. 2002, A&A, 391, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eldridge, J. J., Genet, F., Daigne, F., et al. 2006, MNRAS, 367, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Willingale, R., Osborne, J. P., et al. 2010, A&A, 519, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcone, A. D., Morris, D., Racusin, J., et al. 2007, ApJ, 671, 1921 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Genet, F., Daigne, F., & Mochkovitch, R. 2007, MNRAS, 381, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Giannos, D., & Spruit, H. C. 2006, A&A, 450, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godet, O., Page, K. L., Osborne, J. P., et al. 2006, A&A, 452, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kumar, P., & Panaitescu, A. 2000, ApJ, 541, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., Morsony, B. J., & Begelman, M. C. 2009, ApJ, 700, L47 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., & Uzdensky, D. A. 2011, MNRAS, in press [arXiv:1011.1904] [Google Scholar]
- Medvedev, M. V. 2006, ApJ, 651, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E. 2007, PhR, 442, 166 [Google Scholar]
- Nousek, J. A., Kouveliotou, C., Grupe, D., et al. 2006, ApJ, 642, 389 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, P. T., Willingale, R., Osborne, J., et al. 2006, ApJ, 647, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2000, ApJ, 543, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2001a, ApJ, 554, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2001b, ApJ, 560, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2002, ApJ, 571, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Mészáros, P. 2005, ApJ, 628, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Piran, T. 1999, ApJ, 517, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Schady, P., de Pasquale, M., Page, M. J., et al. 2007, MNRAS, 380, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., Daigne, F., & Drenkhahn, G. 2001, A&A, 369, 694 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uhm, Z. L., & Beloborodov, A. M. 2007, ApJ, 665, L93 [NASA ADS] [CrossRef] [Google Scholar]
- van Marle, A. J., Langer, N., & García-Segura, G. 2005, A&A, 444, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vetere, L., Burrows, D. N., Gehrels, N., et al. 2008, GAMMA-RAY BURSTS 2007: Proceedings of the Santa Fe Conference, AIP Conf. Proc., 1000, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, L., & Schaefer, B. E. 2011, ApJ, 731, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Liang, E., Page, K. L., et al. 2007, ApJ, 655, 989 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Isotropic gamma-ray and kinetic energies of GRB 050421 for different redshifts and H0 = 70 km s-1 Mpc-1, ΩM = 0.27 and ΩΛ = 0.73.
All Figures
 |
Fig. 1 Afterglow from the forward shock. The assumed redshift and burst energy are z = 1 and ℰK = 4 × 1052 erg and the average Lorentz factor of the ejecta is |
| In the text | |
 |
Fig. 2 Afterglow from the reverse shock. Left panel: uniform medium of density n = 1000 cm-3. Right panel: wind medium with A∗ = 1. The four light curves correspond (from top to bottom) to |
| In the text | |
 |
Fig. 3 Afterglow light curves for a sub-luminous burst (full lines) and an interrupted wind (dashed line). For the sub-luminous burst the injected kinetic energy is ℰK = 3.2 × 1048 erg at a redshift z = 0.01 and the four lines correspond (from top to bottom) to a density decreasing from 1 to 10-4 cm-3. The wind has A∗ = 1 but was interrupted 1000 years before the burst. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.