EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 533 (September 2011) A&A, 533 (2011) A58 Full HTML
Free Access
Issue
A&A
Volume 533, September 2011
Article Number A58
Number of page(s) 2
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201117559
Published online 26 August 2011

© ESO, 2011

The standard ΛCDM cosmological model has been deduced from astronomical data that are generally interpreted within the Friedmann-Lemaître-Robertson-Walker framework for a homogeneous universe. The framework uses the Robertson-Walker metric with the proper time as a function of co-moving coordinates given by (1)The dimensionless scale parameter a(t) reflects the universal expansion relative to the present epoch, t0, a(t0) = 1. The spatial curvature parameter, K, can be positive or negative and is related to the curvature radius by . The metric allows one to calculate trajectories of test particles (e.g. photons) in terms of a(t) and K which are governed by the Friedmann equation: (2)for an energy density ρ(t).

Cosmological data analyzed in this framework imply a nearly flat (rc ≫ c/H0) model where the universal expansion is accelerating (). Both of these conclusions concern parameters of the Robertson-Walker metric so it is interesting to see to what extent they can be derived without assuming that a(t) is governed by the Friedmann equation, i.e., assuming homogeneity but not any particular gravitational dynamics. This is especially true given that the observed acceleration has encouraged speculation that gravity might be modified at cosmological scales.

By measuring directly the deceleration parameter, , data on moderate-redshift type Ia supernovae (SNIae) imply acceleration independent of the Friedmann equation (Shapiro & Turner 2006). Sutherland (2011) has recently proposed a Friedmann-free test for acceleration using baryon acoustic oscillation (BAO) effects in the matter correlation function.

Studying spatial curvature without using the Friedmann equation is a bit trickier. The very strong published limits on rc use the Friedmann equation evaluated at the present epoch which yields the geometry-density relation: (3)where H0 is the present value of the expansion rate and where ΩT is the present energy density in units of the critical density . Cosmic microwave background (CMB) data combined with BAO and SNIa data imply −0.0178 < (1 − ΩT) < 0.0063 (Komatsu et al. 2011) which gives 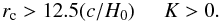(4)

In the cosmology of a homogeneous universe, the spatial curvature determines the relation between the present distance, d(z), to an object of redshift z and the luminosity and angular distances, dL(z) and dA(z). These two distances determine the flux, F, from objects of luminosity, L, and the angular size, Δθ, of an object of size R: In the absence of curvature, dL and dA are both proportional to d(z), with factors of proportionality (1 + z) for dL and (1 + z)-1 for dA. For universes with K > 0 (K < 0), dL and dA are less than (greater than) what would be expected from proportionality.

It is not easy to test this fundamental prediction. The basic problem is that while dA and dL can be determined directly by using standard candles and rulers, d(z) can only be calculated using knowledge of the expansion rate: (5)where the redshift is given by z(t) + 1 = 1/a(t). The limits of integration are given by the times of signal emission, t1, and reception, t0. The luminosity and angular distances depend on rc: (6)where S1(x) = sin(x) and S-1(x) = sinh(x) for K > 0 and K < 0. Equation (6) defines the relation between d(z) and dL,A(z) via the curvature radius rc. If d(z) were known, it would allow a determination of rc and a verification that it takes the value (3).

If a(t) and/or H(t) are not directly measured, d(z) can only be calculated by using the Friedmann equation in Eq. (5). This imposes the value of rc given by (3). As such, the fundamental relationship (6) cannot be tested in this way. Rather, the luminosity and angular distances are used to determine cosmological parameters (ΩM,ΩΛ,ΩT) that can then be used to calculate the distance d(z).

To avoid use of the Friedmann equation, one needs an independent measurement of H(z) to be injected into Eq. (5). Probably the best possibility is to use the radial BAO feature in the matter correlation function which gives directly H(z). Clarkson et al. (2008) noted that this could directly measure spatial curvature. Note that while the length of the BAO standard ruler depends on the Friedmann equation in the pre-recombination universe, the measurement of H(z) depends only on it being a co-moving ruler, i.e. that galaxies having nearly fixed co-moving coordinates. This is a non-trivial assumption but one that does not depend explicitly on the Friedmann equation.

In the absence of BAO measurements of H(z), we note that if galaxies were equipped with clocks that we could see and read, measuring distances would be trivial since an ensemble of such galaxies at different redshifts would yield z(t) from redshift and time measurements (Jimenez & Loeb 2002). Distances could then be calculated using Eq. (5) without imposing the Friedmann equation.

Stellar evolution in passive galaxies (those with negligible star formation) can be used as such a clock. The first steps in their use for cosmology have been performed by Simon et al. (2005), Figueroa et al. (2008) and Moresco et al. (2011). They derive expansion histories that are consistent with the standard flat ΛCDM cosmology (ΩΛ = 0.73 and ΩM = 0.27). The most precise results were obtained by Moresco et al. (2011) who observed the redshift evolution of the 4000 Å-spectral break in SDSS elliptical galaxies in the range 0.15 < z < 0.30. Stellar population evolution models then gave the elapsed time between z = 0.15 and z = 0.3 necessary for the spectral evolution. Using H(z) = ż/(1 + z), this gives the expansion rate for 0.15 < z < 0.30. They extrapolated this rate to zero redshift using the standard cosmology and found a value H0 = 72.6 ± 2.9(stat) ± 2.3(syst)   km   s-1   Mpc-1, that is in agreement with recent local measurements, H0 = (74.2 ± 3.6)   km   s-1   Mpc-1 (Riess et al. 2009). From our point of view, this means that at the 5% level the expansion rate in the range 0 < z < 0.3 follows the flat ΛCDM prediction.

Since the measured expansion rate follows the flat ΛCDM prediction, Eq. (5) implies that the distances d(z) to objects in this redshift range agree with the flat ΛCDM values. Furthermore, the mean luminosity distances in this redshift range from SNIa (Kessler et al. 2009) agree with those of the standard flat ΛCDM model to a precision of better than 5%. The agreement of both d(z) and dL(z) with the same flat model implies that spatial curvature effects must be small at z = 0.3.

To quantify the limit on rc, we invert (6), giving d(z) as a function of dL(z), and then take the derivative with respect to z. Using d′(z) = 1/H(z) and the fact that dL(z) is well described by a flat ΛCDM model, one finds (7)where Hflat and dflat are the expansion rate and distance for the flat ΛCDM model that gives the observed luminosity distance. For the measurement of H(z ~ 0.22) of Moresco et al. (2011), if we adopt a conservative limit (8)we find (9) (10)The work of Figueroa et al. (2008) provides H(z) up to z ~ 1.5, but at a precision of only  ~20%. Adopting (11)we find (12) (13)Here again, we use the fact that SNIa for 0.3 < z < 1.5 (Guy et al. 2010; Riess et al. 2007) give luminosity distances that are in agreement with flat ΛCDM. Baryon acoustic oscillations measurements (Eisenstein et al. 2005; Percival et al. 2010; Blake et al. 2011) imply the same for the distance combination dA(z)2c/H(z) (0.2 < z < 0.6 ).

The limits on rc obtained here are rather modest, implying only ΩT < 1.6 if one assumes the validity of the Friedmann equation. It will be possible to confirm and improve the limits in the future with BAO H(z) measurements (White et al. 2011; Slosar et al. 2011). We note that BAO has the advantage of not depending on stellar modeling. A particularly interesting challenge would be to perform a Friedmann-free CMB analysis with the hope of extending the limits to z = 1070. Unfortunately, unless our ideas of gravity are wrong at cosmological scales and the Friedmann equation does not apply, the present limits on ΩT mean that it will be very difficult to directly see cosmological curvature with these methods.

Acknowledgments

I thank Raul Jimenez, Jean-Baptiste Melin, Will Sutherland, and Jean-Philippe Uzan for stimulating discussions. I thank the referee for comments that improved the paper.

References

  1. Blake, C., Davis, T., Poole, G. B., et al. 2011, MNRAS, accepted [arXiv:1105:2862] [Google Scholar]
  2. Clarkson, C., Bassett, B., & Lu, T. H. 2008, Phys. Rev. Lett., 101, 011301 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  3. Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
  4. Figueroa, D.G., Verde, L., & Jimenez, R. 2008, JCAP, 10, 038 [NASA ADS] [Google Scholar]
  5. Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Jimenez, R., & Loeb, A. 2002, ApJ, 573, 37 [NASA ADS] [CrossRef] [Google Scholar]
  7. Kessler, R., Becker, A. C., Cinabro, D., et al. 2009, ApJ, 185, 32 [Google Scholar]
  8. Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJ, 180, 330 [Google Scholar]
  9. Moresco, M., Jimenez, R., Cimatti, A., & Pozzetti, L. 2011, JCAP, 3, 045 [Google Scholar]
  10. Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
  11. Riess, A.G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
  12. Riess, A.G., Macri, L., Casertano, S., et al. 2009, ApJ, 699, 539 [NASA ADS] [CrossRef] [Google Scholar]
  13. Shapiro, C., & Turner, M., 2006, ApJ, 649, 563 [Google Scholar]
  14. Slosar, A., Font-Ribera, A., Pieri, M., et al. 2011, JCAP, accepted [arXiv:1104.5244] [Google Scholar]
  15. Simon, J., Verde, L., & Jimenez, R. 2005, Phys. Rev. D, 71, 123001 [Google Scholar]
  16. Stern, D., Jimenez, R., Verde, L., et al. 2010, JCAP, 2, 008 [CrossRef] [Google Scholar]
  17. Sutherland, W. 2011, MNRAS, accepted [arXiv:1105.3838] [Google Scholar]
  18. White, M., Blanton, M., Bolton, A., et al. 2011, ApJ, 728, 126 [NASA ADS] [CrossRef] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.