| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201116519 | |
| Published online | 24 August 2011 | |
Nonradial and nonpolytropic astrophysical outflows
IX. Modeling T Tauri jets with a low mass-accretion rate
1
Laboratoire Univers et Théories, Observatoire de Paris, UMR 8102 du CNRS,
Université Paris Diderot,
92190
Meudon,
France
e-mail: christophe.sauty@obspm.fr
2
Centrum voor Plasma Astrofysica, Celestijnenlaan 200B bus
2400, 3001
Leuven,
Belgium
3
Centro de Astrofísica, Universidade do Porto,
Rua das Estrelas, 4150-762
Porto,
Portugal
4
Departamento de Física e Astronomia, Faculdade de Ciências,
Universidade Porto, Rua do Campo
Alegre, 687, 4169-007
Porto,
Portugal
5
IASA and Section of Astrophysics, Astronomy &
Mechanics, Department of Physics, University of Athens, Panepistimiopolis 157 84, Zografos, Greece
Received:
14
January
2011
Accepted:
3
May
2011
Context. A large sample of T Tauri stars exhibits optical jets, approximately half of which rotate slowly, only at ten per cent of their breakup velocity. The disk-locking mechanism has been shown to be inefficient to explain this observational fact.
Aims. We show that low mass accreting T Tauri stars may have a strong stellar jet component that can effectively brake the star to the observed rotation speed.
Methods. By means of a nonlinear separation of the variables in the full set of the MHD equations we construct semi-analytical solutions describing the dynamics and topology of the stellar component of the jet that emerges from the corona of the star.
Results. We analyze two typical solutions with the same mass loss rate but different magnetic lever arms and jet radii. The first solution with a long lever arm and a wide jet radius effectively brakes the star and can be applied to the visible jets of T Tauri stars such as RY Tau. The second solution with a shorter lever arm and a very narrow jet radius may explain why similar stars, either weak line T Tauri stars (WTTS) or classical T Tauri stars (CTTS) do not all have visible jets. For instance, RY Tau itself seems to have different phases that probably depend on the activity of the star.
Conclusions. First, stellar jets seem to be able to brake pre-main sequence stars with a low mass accreting rate. Second, jets may be visible only part time owing to changes in their boundary conditions. We also suggest a possible scenario for explaining the dichotomy between CTTS and WTTS, which rotate faster and do not have visible jets.
Key words: magnetohydrodynamics (MHD) / stars: pre-main sequence / stars: winds, outflows / ISM: jets and outflows / stars: mass-loss / stars: rotation
© ESO, 2011
1. Introduction
1.1. The angular momentum problem, observational facts
Observations of star-forming regions show that several T Tauri stars are associated with well collimated jets. These jets are made of strongly accelerated plasma that travels at a few hundred km s-1 (Bally 2009) and is magnetically collimated at large distances (Dougados et al. 2000). The jets are usually associated with classical T Tauri stars (CTTS), which are low mass stars ≤ 2 M⊙ in their late stages of pre-main sequence evolution, showing strong evidence of the presence of a surrounding accretion disk. The outflow is usually thought to be ejected from the Keplerian disk (e.g. Cabrit & André1991). However, a significant part of the jet, if not all, may be ejected by the star itself, at least for the lower mass accreting T Tauri stars.
Observations also reveal that approximately half of the T Tauri stars rotate slowly, at about 10% or less of their breakup speed (Matt et al. 2010). This indicates that a very efficient mechanism is at work to remove the angular momentum in these stars; the nature of this mechanism is still controversial.
Kundurthy et al. (2006), see also Edwards et al. (1993), claimed that CTTS are slow rotators with circumstellar disks, while WTTS are fast rotators without accretion disks. However, the association of CTTS with slow rotators and WTTS with fast ones is not as yet observationally confirmed. Moreover, Stassun et al. (1999, 2001) and Rebull et al. (2004) could not find a strong correlation of fast rotators with stars that have dispersed their disks. Conversely, new results (Rebull et al.2006; Herbst et al.2007; Cieza & Baliber2007) found a bimodal distribution where stars with disks rotate slower than stars without disks. However, the two distributions clearly overlap. The prevailing theory has been that magnetic interaction between the star and its circumstellar disk regulates the stellar rotation periods. Attempts to observationally confirm this conjecture have produced mixed results. Hence, from the observational point of view, the presence of an accretion disk may not be enough to explain stellar angular momentum removal.
In order to understand slow stellar rotators, Schatzman (1962) suggested that the magnetic braking of a stellar wind would be sufficient even with a low mass loss rate, and this has been explored by several authors (e.g. Weber & Davis1967; Mestel1968a,b). Following this track, it is essential to address stellar wind models in detail, with and without the presence of an accretion disk, to see how efficient the wind is in extracting angular momentum from the star. Moreover, recent observations confirm that stellar winds are present in at least 60% of CTTS (Kwan et al. 2007), as was already suggested by various authors (e.g. Edwards et al.2003).
Decampli (1981) showed that thermal stellar winds cannot support jets with a high mass loss rate, simply because this would require too high temperatures to be physical. For low mass loss rates, less than 10-9 M⊙/yr, he showed that a thermally driven or line-driven radiative wind can support the formation of the jet. For a higher mass loss rate, such a driving is still possible provided that there is an extra supply of pressure from Alfvén waves. If the temperature of the wind is around one million degrees, the pressure can drive the jet up to 300 km s-1. However, the pressure may exceed the thermal pressure by a large amount if it includes ram pressure or turbulent magnetic pressure. The situation is similar to the well known case of the solar wind, where to obtain wind speeds of several hundred km s-1 with a temperature of a few million degrees one requires extra pressure from either turbulence or kinetic effects. These effects yield an effective temperature of around ten million degrees (see Aibéo et al.2007, and references therein).
Ignoring the important question regarding the nature of the pressure and following the early study of Decampli (1981), most authors disregarded stellar wind models up to now. This explains why disk wind models have been extensively studied.
1.2. Disk wind theory
In disk wind models, the main source of acceleration is the magneto-centrifugal driving, as proposed originally by Blandford & Payne (1982), who presented the first MHD radial self-similar solutions extending the earlier hydrodynamical solutions of Bardeen & Berger (1978) for galactic winds. Since then, their original model has been improved in various ways (e.g., Li et al.1992; Contopoulos1994; Vlahakis & Tsinganos1998; Vlahakis et al.2000). In particular Ferreira (1997) has shown that a consistent treatment of the connection with the disk is possible. From the theoretical point of view however, self-similar disk wind models are not consistently describing the inner part of the jet close to its axis (Gracia et al. 2006). The solution has to be cut at the inner and outer edges of the disk. From the observational point of view, cold disk winds turned out to be too rapid and too light (Garcia et al.2001b). This last point can be overcome with warm disk solutions and explains the high speed, dense powerful jets of early T Tauri stars like DG Tau, as well as their rotation (Ferreira et al.2006). DG Tau is probably one of the most powerful sources with an accretion rate of 10-6 M⊙/yr and a corresponding mass loss rate that is about 10% of this value (Hartigan et al. 1995). In this case, disk wind solutions seem more adapted. Recent observations suggest that DG Tau is variable on short timescales with an accretion rate dropping down to 10-7 M⊙/yr (Beck et al. 2010).
Simultaneously, several numerical simulations have investigated the jet launching of these disk winds (e.g., Ouyed & Pudritz1997; Ustyugova et al.2000; Krasnopolsky et al.2003; Casse & Keppens2004). By investigating various boundary conditions and initial configurations, they confirmed that disk winds could indeed be accelerated and collimated by their own magnetic field. More recently several authors (Matsakos et al.2008; Stute et al.2008; Matsakos et al.2009) have shown that analytical solutions such as the radially self-similar ones are structurally stable. This result indicates that these solutions are good complementary tools to numerical simulations.
According to theoretical arguments (Pudritz & Norman 1986) and numerical simulations (e.g. Meliani et al.2006), disk winds can remove most of the angular momentum of the accreting plasma. However, disk winds need the presence of an inner stellar jet component to be globally consistent.
From the theoretical point of view, it was initially proposed that fieldlines of the stellar magnetosphere anchored into the disk could efficiently brake the central star, in the so-called disk-locking mechanism proposed by Choi & Herbst (1996). In principle a fieldline rooted into the star will slow down (respectively speed up) the central star rotation, if it connects to a region of the disk rotating at lower rotational speed (respectively higher speed) after (respectively before) the corotation radius. Using a simple analytical model based on the Ghosh & Lamb mechanism (1979a,b), Matt & Pudritz (2005) showed however that the disk-locking efficiency is reduced because it leads to an opening of the fieldlines that disconnects the disk from the star. Instead they proposed that angular momentum can be lost via accretion-powered stellar winds provided the mass loss rate is 1 to 10% of the accretion rate as usually inferred from observations (Calvet 1998). Their results were confirmed via numerical simulations (Matt & Pudritz2008a,b; Matt et al.2010). Küker et al. (2003), using similar simulations, concluded that even when the disk-magnetosphere connection is not disrupted, the magnetic field could slow down the central object but the dominant disk torque still spins up the star. As mentionned by Romanova et al. (2009), these conclusions are not definitive because long-term simulations are required to establish the validity of this result. Ultimately the authors insist on the essential role of the axial jet. Zanni & Ferreira (2009) performed various additional simulations where the disk-locking is not disrupted by the building of large toroidal field. However, even in this situation, the magnetic accretion torque is not sufficient to cause an efficient spin-down of the star.
1.3. Stellar jet theory
As a conclusion of the precedent subsection, the presence of a pure stellar wind in addition to a possible outer disk wind is required to effectively remove the excess of stellar angular momentum.
Besides, more evolved T Tauri stars like RY Tau seem to have weaker jets with accretion rates on the order of only a few 10-8 M⊙/yr, which may be an indication that disk winds are not always absolutely necessary for the weaker and more evolved jets. We see that with a mass loss rate of only 10% of this value, these jets are more difficult to analyze. From spectroscopic observations of RY Tau, Gómez de Castro & Verdugo (2001, 2007) suspected the presence of a small-scale pure stellar jet because the UV emission lines originate in a region that is too small to be produced by a disk wind. New observations (St-Onge & Bastien2008; Agra-Amboage et al.2009) clearly show a microjet in this faint object. It is interesting to investigate if these (micro-)jets can be modeled through stellar winds or a combination of a stellar wind and a sub Keplerian disk wind.
This combination of a two-component outflow is under numerical investigation (Matt et al.2003; Koide2003; Küker et al.2003; Matsakos et al.2008). Recent simulations (Meliani et al.2006; Romanova et al.2009; Matsakos et al.2009; Fendt2009) also show the interplay of mixing between the two components. Several authors, e.g. Küker et al. (2003), Romanova et al. (2009) and Fendt (2009), have shown in their numerical simulations that the disk-magnetosphere connection produces strong intermittent outflows, the results of flares and reconnection. This is somewhat similar to coronal mass ejections in the solar wind and in microquasars. Though important to model, those outflows are not necessarily more important on the long-term duration compared to the continuous underlying steady flow, as suggested by Romanova et al. (2009). Moreover, Matsakos et al. (2009) have shown that the variability of the source does not destroy the continuous steady jet. Indeed, they use the first solution presented in this paper, as initial condition for the inner spine jet of their simulations, but use a polytropic equation of state. In their previous paper (Matsakos et al. 2008) they have shown that changing from non polytropic to polytropic would reduce the size of the radius of the jet, without drastically affecting the outflow behavior, however.
However, numerical simulations are usually time-consuming to such an extent that they cannot explore a wide range of parameters. Moreover, they do not really start ejecting mass directly from the star but rather at a given height between the sonic and the Alfvén surfaces. Therefore, it is of absolute interest to model the stellar jet that originates in the central star.
All these problems can be overcome by studying MHD solutions obtained via a nonlinear separation of the variables. These so-called self-similar solutions contain as special cases all known MHD outflow solutions (e.g., Vlahakis & Tsinganos 1998; Sauty et al.2002, hereafter STT02). As shown in Sauty & Tsinganos (1994, hereafter ST94), these self-similar models can be seen as a combination of stellar wind and X-wind models. Conversely to formal X-winds (Shu et al.1994; Shang et al.2002), they do not require that all fieldlines emerge from a single point of the disk in the form of a fan. Instead there is a smooth transition between the stellar wind and the disk jet. They are also shown to be structurally stable (Matsakos et al.2008; 2009). This was far from obvious because the heating function is not polytropic as usually in most analytical solutions. In a series of papers – Sauty et al. (1999, hereafter STT99), STT02, and Sauty et al. (2004, hereafter STT04) – we have systematically explored the full parameter space of this problem. In ST94 we have shown that the double disk and star component was promising. However, the solutions presented there had mass loss rates that were too low. Here we present solutions where the stellar jet is both under-dense and under-pressured compared to the disk wind in the launching region. These solutions have the advantage to adapt themselves not only to CTTS, which are connected with the surrounding accretion disk, but also to WTTS where there iseither no accretion disk or no connection with the disk itself (Walter et al. 1988; Bertout 1989). Although winds from WTTS are difficult to measure, mass loss rates between 10-11 and 10-10 M⊙/yr have been obtained by André et al. (1992). Winds of WTTS might be similar to the solar wind in terms of collimation (see Aibéo et al.2007, and references therein). However, these young stars have higher mass loss rates and rotational speeds than our sun and might as well have strongly collimated jetsindependently of the presence of an accretion disk. Their rotation periods range from 0.6 to 24 days with peaks near two and eight days (Herbst et al. 2007) while the solar rotational period is 24.5 day. Thus, WTTS may well produce self-collimated jets that nevertheless are so weak that they cannot be detected.
We will use the ST94 meridionally self-similar model to examine the contribution of the stellar component to the overall jet and how efficiently it brakes the star. We first explore how the model parameters can be constrained from the observations of CTTS jets (Sect. 3). Then, we focus our attention on two different classes of solutions (Sects. 4 and 5) and explore the efficiency of these winds to spin down the central object. In the final section (Sect. 6) we discuss how these two classes of solutions may explain the dichotomy between CTTS and WTTS and how they can be adapted to also model multiphases of T Tauri faint jets, such as in RY Tau.
2. Meridional self-similar solutions
We summarize the main assumptions of our meridionally (θ−) self-similar treatment of the MHD equations in Appendix A. More details can be found in STT94, STT99 and STT02.
2.1. Parameters and variables
Using spherical coordinates (r,θ,ϕ), all quantities are normalized to
the Alfvén surface along the rotation axis, which is by assumption a sphere of radius
r = r∗. The dimensionless radial distance
is denoted by R = r/r∗,
while B∗, V∗
and ρ∗ are the poloidal magnetic field, velocity and
density along the polar axis at the Alfvén radius r∗, with
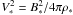 .
.
The original system of MHD equations reduces to two coupled partial differential equations for the density and the magnetic flux. Then, the momentum conservation law provides three ordinary differential equations, which together with Eq. (A.12) can be solved for the four variables M2(R), F(R), Π(R) and G(R), which are the square of the poloidal Alfvén Mach number, the expansion factor, the dimensionless pressure, and the dimensionless cross section radius, respectively.
The model is controlled by the following four parameters.
-
The parameter δ governs the non spherically symmetric distribution of the density. For δ > 0 (δ < 0) the density increases (decreases) by moving away from the polar axis.
-
The parameter κ controls the non spherically symmetric distribution of the pressure. For κ > 0 (κ < 0) the gas pressure increases (decreases) by moving away from the polar axis.
-
The parameter λ is related to the rotation of the poloidal streamlines at R = 1 (i.e., at the Alfvén surface).
-
The parameter ν is defined by the gravitational field whose acceleration can be written as
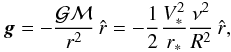 (1)where ℳ is
the central gravitating mass. This extra parameter ν is the ratio
of the escape velocity to the poloidal flow velocity on the polar axis at
R = 1 (i.e., at the Alfvén surface),
(1)where ℳ is
the central gravitating mass. This extra parameter ν is the ratio
of the escape velocity to the poloidal flow velocity on the polar axis at
R = 1 (i.e., at the Alfvén surface), 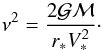 (2)
(2)
2.2. Collimation efficiency of the magnetic rotator
By integrating the momentum equations along a fieldline, we obtain the conserved total
energy flux density per unit of mass flux density. This is equal to the sum of the kinetic
and gravitational energies together with the enthalpy and net heating along a specific
streamline. In the framework of the present meridionally self-similar model, the variation
of the energy from one line to the other gives an extra parameter (STT99): ![\begin{eqnarray} \epsilon &=& {M^4\over (GR)^2}\left[ {F^2\over 4} - 1 \right] - \kappa {M^4\over G^4} - {(\delta\,- \kappa) \nu^2 \over R} \nonumber\\[1.5mm] \label{EnEps} && + {\lambda^2 \over G^2} \left({M^2-G^2 \over 1-M^2}\right)^2 + 2\lambda^2{1-G^2 \over 1-M^2}, \label{epsilon} \end{eqnarray}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq36.png) (3)which
is a constant onall streamlines (ST94).
(3)which
is a constant onall streamlines (ST94).
Physically, ϵ is related to thevariation across the fieldlines of the specific energy that is left available to collimate the outflow once the thermal content converted into kinetic energy and into balancing gravity has been subtracted (STT99).
We can express ϵ/2λ2 in terms of the
conditions at the source boundary ro (see STT99 for details),
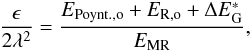 (4)where
EMR is the energy of the magnetic rotator (see Eq. (2.5a) in
STT99), EPoynt.,o is the Poynting energy
and ER,o is the rotational energy at the base.
(4)where
EMR is the energy of the magnetic rotator (see Eq. (2.5a) in
STT99), EPoynt.,o is the Poynting energy
and ER,o is the rotational energy at the base.
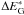 is the
excess or deficit of the gravitational energy (per unit mass) that is not compensated by
the thermal driving, on a nonpolar streamline compared to the polar one,
is the
excess or deficit of the gravitational energy (per unit mass) that is not compensated by
the thermal driving, on a nonpolar streamline compared to the polar one,
![\begin{equation} \Delta E_{\rm G}^* = - {{\cal G}{\cal M} \over r_{\rm o}} \left[ 1-{T_{\rm o}(\alpha)\over T_{\rm o}({\rm{pole}})} \right] = -{{\cal G}{\cal M} \over r_{\rm o}} {(\delta - \kappa)\alpha \over 1 + \delta \alpha }\cdot \end{equation}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq45.png) (5)For
ϵ > 0 collimation is mainly provided by magnetic terms, while for
ϵ < 0 the outflow can be confined only by thermal pressure,
which is not possible for overpressured flows. Accordingly, in STT99 we classified flows
with positive or negative ϵ as efficient or inefficient magnetic
rotators, respectively (EMR or IMR).
(5)For
ϵ > 0 collimation is mainly provided by magnetic terms, while for
ϵ < 0 the outflow can be confined only by thermal pressure,
which is not possible for overpressured flows. Accordingly, in STT99 we classified flows
with positive or negative ϵ as efficient or inefficient magnetic
rotators, respectively (EMR or IMR).
Considering the fairly large opening of stellar jets, we expect to find values of ϵ close to zero. We have shown in STT99 that this corresponds to large asymptotic jet radius of magnetically confined outflows.
3. Constraining the model parameters from the observations
3.1. Stellar constraints
Though their jets are fainter than those of class I and early CTTS, low mass accreting classical T Tauri stars exhibit jets as many other class II objects. They have well measured mass, radius and rotation frequency (Hartigan et al. 1995; Bouvier et al. 1997; Herbst & Mundt 2005; Marilli et al. 2007). We suspected that one good such example of a faint jet in an evolved CTTS would be, among others, the RY Tau jet (Gómez de Castro & Verdugo2001). This has been recently observed and extensively studied (St-Onge & Bastien2008; Agra-Amboage et al.2009). Classical T Tauri stars are low mass stars between 0.5 and 2 solar masses, with typical radius ranging from 2 to 3 solar radii (Bertout1989; Mora et al.2001). They are typical precursors of solar-type stars. Rotational speeds are usually assumed to be around one tenth of their breakup speed, namely typically around 15 km s-1 for CTTS and around 20 km s-1 for WTTS (Bouvier et al.1993), but with large variations and uncertainties. In particular, there is a large discrepancy between spectroscopic measurements of projected rotational velocities and periods measured using photometry.
3.2. Jet constraints
For some CTTS we have measurements of various physical quantities in the optical jet itself (Hartigan et al. 1995; Lavalley-Fouquet et al. 1999; Cabrit 2007; St-Onge & Bastien 2008; Agra-Amboage et al. 2009). Observations give mass loss rates from 10-7 down to 10-10 M⊙/yr. On the other hand, low mass accreting stars are also associated with low mass loss rates, close to the minimum value. The averaged asymptotic speeds are on the order of 100 km s-1 to 300 km s-1 (Bally 2009). Microjets are hardly resolved transversely. Thus, this speed might be a mixing of the high- and low-velocity components similarly to what is observed in DG Tau (Anderson et al.2003). For the high-velocity component we can easily take a higher value and assume 400 km s-1 along the polar axis, where we expect to find this maximum value. This remains of course arbitrary but is consistent with the model developed here. In that respect, more precise measurements from observations are also needed to assess the velocity profile in the jet (Günther et al.2009).
We assume that the jet carries a typical mass loss rate of a few times 10-9 M⊙/yr. Following Gómez de Castro & Verdugo (2001), we took 3.1 × 10-9 M⊙/yr for the mass loss rate of RY Tau. Electronic densities can be directly measured only in shocks. Typically they are around 104 cm-3. However, the inferred electronic density is not unambiguously determined.
First the jet radius may be much smaller than the shock radius, as shown in many numerical simulations (e.g. Matsakos et al.2009). As mentioned in the introduction, Matsakos et al. (2009) used as initial condition our solution for the inner spine jet but with different thermodynamics. Switching to a polytropic equation of state reduces the radius of this inner part of the outflow by a significant factor, as shown in Matsakos et al. (2008). Even with such a small radius of the spine jet, the long term variability of the stellar mass loss rate produces knots ten times larger than the jet radius, typically around 5 to 10 AU. We expect that keeping the turbulent heating along the flow would produce even larger knots.
Second, not all electrons are accelerated to sufficiently high energies. Large uncertainties may also arise because we do not precisely know the ionization fraction of the jet. Thus, densities and temperatures cannot be calculated precisely. The solutions presented in this paper can give a fairly accurate description of the outflow dynamics. In order to make a full synthetic emission map, further work is necessary starting from the dynamics given from these solutions, calculating the amount of mechanical heating and self-consistently deducing the emission lines by tuning the ionization fraction and the kinetic temperature. This has been done by Garcia et al. (2001a,b) for disk winds and will be similarly done for our solutions in a forthcoming study.
Finally, to have efficient magnetic braking, we looked for MHD solutions with long magnetic lever arms. We assume that a typical lever arm, the Alfvén cylindrical radius, is around 10 times the stellar radius, ϖa = 10 ϖo. For the meridionally self-similar model that we use this gives approximately r⋆ = 10 ro or Ro = 0.1.
As shown in Spruit (1997), if the accreting mass
rate is Ṁacc, the angular momentum is accreted at a rate
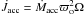 . Similarly, the angular
momentum loss rate in the wind is
. Similarly, the angular
momentum loss rate in the wind is 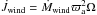 , because the plasma
corotates up to the Alfvén cylindrical radius ϖa. If the
entire angular momentum from the disk is removed by the wind, we can equal these
quantities
, because the plasma
corotates up to the Alfvén cylindrical radius ϖa. If the
entire angular momentum from the disk is removed by the wind, we can equal these
quantities 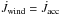 .
Combining the above we get
.
Combining the above we get 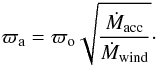 (6)If
ϖa = 10 ϖo, we deduce from the
above equation that the mass loss rate is only 1% of the mass accreting rate, which is a
fairly low value. The wind is probably more efficient than this 1% at extracting mass from
the disk. This means that even a relatively small wind outflow can remove angular momentum
from the disk very efficiently.
(6)If
ϖa = 10 ϖo, we deduce from the
above equation that the mass loss rate is only 1% of the mass accreting rate, which is a
fairly low value. The wind is probably more efficient than this 1% at extracting mass from
the disk. This means that even a relatively small wind outflow can remove angular momentum
from the disk very efficiently.
Alternatively, the wind can also remove angular momentum from the star if the magnetic
fieldlines and streamlines are anchored in the stellar photosphere instead of the disk. In
that case, we can calculate the braking time to remove the stellar angular momentum as
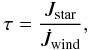 (7)where
(7)where
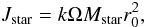 (8)and
(8)and 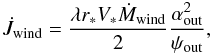 (9)with k
the dimensionless inertial constant of the star (Mestel1968a,b). For Eq. (9) we used Eq. (3.19b) of Sauty & Tsinganos (1994).
(9)with k
the dimensionless inertial constant of the star (Mestel1968a,b). For Eq. (9) we used Eq. (3.19b) of Sauty & Tsinganos (1994).
We use k = 0.06 as for the Sun (Schwartz & Schubert 1969), where 90% of its mass is within 50% of its radius (Cox 2000). For a T Tauri star with a bigger convective zone (Bouvier et al. 1997), k may be larger, up to 0.2. This maximum value is obtained for a fully convective star.
Substituting Ω from Sauty & Tsinganos
(1994) in Eq. (8), we obtain the
following expression for the braking time of the star 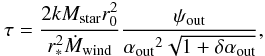 (10)with
(10)with ![\begin{equation} \psi_{\rm out} = \frac{2}{3\delta} \left[\left(1+\delta\alpha_{\rm out}\right)^{3/2}-1\right]. \label{psiout} \end{equation}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq74.png) (11)For instance, we know
that CTTS have lifetimes on the order of a million years, while WTTS last on this phase
around ten million years. The magnetic braking should accordingly be efficient in removing
most of the accreted and stellar angular momentum during this period, independent of the
uncertainty factor we have on.
(11)For instance, we know
that CTTS have lifetimes on the order of a million years, while WTTS last on this phase
around ten million years. The magnetic braking should accordingly be efficient in removing
most of the accreted and stellar angular momentum during this period, independent of the
uncertainty factor we have on.
3.3. Stellar parameters
To summarize, we will use a mass loss rate, stellar mass, radius and rotation given respectively by
-
Ṁwind = 3.1 × 10-9 M⊙/yr,
-
ℳ = 1.5 M⊙,
-
ro = 2.4 r⊙,
-
Ω = 5.99 × 10-6 rad/s or Vϕ,o = 10 km s-1.
These values are typical of CTTS and close to the ones of RY Tau that we will study in more detail, except for the rotation rate, which is much lower than the usual value. We argued, however, that the rotation rate of RY Tau is subject to caution because of the obscuration of the star by the disk, as discussed below. Instead, we prefer to keep a value close to that of most CTTS and remain more general.
Taking these constraints into consideration, we explored the parameter space and constructed various solutions using the procedure explained in STT02. Among the solutions adapted to T Tauri jets, we selected two different sets of model parameters that fit the RY Tau case particularly well. The first solution has a longer lever arm, corresponding to our initial guess, and a large opening angle for the jet. This should be close to the observed values for CTTS with a jet, such as the jet of RY Tau observed in February 2005 by St-Onge & Bastien (2008). In this solution, the jet is magnetically collimated into a cylindrical shape without any oscillation close to the star.
By a slight change of the pressure, we were able to get a second solution that is completely different from the previous one. Of course, a change in one of the parameters implies a search for a new set of the other parameters to keep the same observational constraints. In this second solution, the lever arm is reduced, as is the opening angle. The solution exhibits strong recollimation and oscillations. It may either reproduce WTTS or CTTS without jet such as RY Tau in 2001 when the jet was not visible. Instead, a UV shock was detected close to the star, possibly caused by the recollimation (Gómez de Castro & Verdugo 2001).
4. Nonoscillating collimated solution
4.1. Procedure
In STT99 and STT02, we have shown that exact MHD solutions corresponding to efficient magnetic rotators are usually collimated both by the magnetic field and by the external gas pressure. However, by decreasing the base pressure and keeping the other parameters fixed, we obtain a limiting solution where the asymptotic structure is collimated only by the magnetic hoop stress. From underpressured close to the star, the jet becomes overpressured at large distances. For even lower base pressures the wind is no longer collimated. We choose in this section a limiting solution that gives the widest possible opening of the jet. This can be done because the solution is an efficient magnetic rotator with a value of ϵ positive but close to zero (cf. STT99). In addition to the parameters defined in Sect. 3.3, to build our solutions we assumed that the jet speed at infinity along the polar axis is V∞ = 200 km s-1.
The process of obtaining a self-consistent solution is a long iterating one. As explained in STT02, we start our integration at the Alfvén point and integrate upstream and downstream, each time crossing the critical points and changing the parameters until we get as close as possible to the guessed values of the parameters.
 |
Fig. 1 Topolopy of the nonoscillating solution in the meridional plane. In a) zoom out showing the collimation. In b) zoom close to the star. All distances are given in astronomical units (AU). The solid (red) lines correspond to open fieldlines connected to the star. The dashed (green) lines correspond to closed stellar fieldlines and lines connected to the disk. All open lines are originating in a polar cap extending to a colatitude of 15 degrees. The dotted circle indicates the Alfvén surface. |
4.2. A model for low mass accreting T Tauri jets
Our iterative procedure converges on the following set of parameters
-
ϵ = 0.012,
-
δ = 0.0778,
-
κ = 0.021,
-
ν = 1.5,
-
λ = 0.775,
with a rotation frequency of
-
Ω = 5.15 × 10-6 rad/s, or, Vϕ,o = 8.6 km s-1.
This last value is in the lower range of the values measured for RY Tau. It corresponds to the value of a slowly rotating T Tauri star. From this point of view the example of RY Tau is an extreme one.
There is a large discrepancy for RY Tau between determinations of the spectroscopic projected rotational velocity and of the photometric rotational period. In this particular case a value of 52−55 km s-1 is inferred for Vsini (Petrov et al.1999; Mora et al.2001; Agra-Amboage et al.2009), where i is the angle between the line of sight and the stellar rotational axis. This value of Vsini is among the highest measured for CTTS. This specific determination of the projected rotational velocity seems to correspond to a special case of obscuration by the disk rather than a real rotational velocity, however. Thus, this value may not correspond to the rotation of the star itself. Bouvier et al. (1993, 1995) give a photometric period of 24 days corresponding to Vϕ,o = 5.1 km s-1, which is a lower limit. Flux measurements give a period from 5 to 66 days, closer to typical values for TTS (Petrov et al.1999). However, the variation is far from periodic and again one cannot exclude veiling from the disk. In other words, rotation measurements are extremely difficult to obtain for this object. We have tried to construct solutions with rotational values close to the canonical value of 15 km s-1, though within a factor of 2 or so, assuming that more precise observational data are needed.
The topology of the streamlines and magnetic fieldlines of the solution in the poloidal plane is displayed in Fig. 1. The stellar jet is surrounded by a diskwind and is self-collimated by its own magnetic field. It is produced in a fairly narrow coronal hole of half opening angle 15 degrees. The hole is surrounded by a large dead zone extending up to 8 stellar radii. This is comparable to the dipolar structure of 1.2 kG around BP Tau reconstructed from ESPaDOnS observations (Donati et al. 2008). We also plot in Fig. 2 the outflow speed along the polar axis and the one along the last open streamline connected to the star. The asymptotic speed along the polar axis is
-
V∞ = 393 km s-1,
which is higher by a factor of 2 than our initial guess. This may be quite large, but considering the uncertainties involved, it can be an acceptable value.
In Fig. 3 we plot the polar density (a), pressure (b) and temperature (c). The pressure is defined up to a constant Po, see Eq. (A.9). By varying this constant, we obtain the various curves of Figs. 3b and c. Adding different values of Po only affects the asymptotic part of the curves.
Note that the temperature in Fig. 3c has a maximum along the polar axis, reaching a value of one million degrees, which might be a rather high value. However, this effective temperature of the plasma is calculated from the equation of state of the gas using the total pressure plotted in Fig. 3b. This total pressure may include in addition to the kinetic pressure, ram pressure or Alfvén waves, etc. As we have shown in Aibéo et al. (2007), the effective temperature can be easily ten times higher than the kinetic one with a relative amplitude of the Alfvén waves δB/B less than unity. Note that Gómez de Castro & Verdugo (2007) inferred from UV lines high electronic temperatures associated with a wind close to 105 K consistent with this scenario and an effective temperature of one million degrees.
 |
Fig. 2 Plot of the poloidal velocity for the nonoscillating solution along the polar axis (solid line) and the last streamline connected to the star (dashed). By construction the poloidal velocity is zero on the last streamline where it reaches the equatorial plane. This creates the dip seen on the logarithmical scale. |
 |
Fig. 3 In a) we plot of the polar density, in b) the total pressure in dimensionless units along the polar axis, including nonkinetic terms such as turbulent magnetic or ram pressure. In c) we plot the polar effective temperature for the nonoscillating solution. The three additional asymptotic curves in c) correspond to three possible values of the temperature at infinity, obtained by adding non-zero values of the pressure at infinity, as shown in b). |
For this solution, the physical quantities at the Alfvén radius are
-
r⋆ = 9.29 ro = 0.104 AU,
-
V⋆ = 103 km s-1.
The last open streamline connected to the star corresponds to a value of the dimensionless magnetic flux of
-
αout = 0.989.
We assumed that the observed mass loss rate originates completely from the star. It means that the entire mass loss rate is contained within a flux tube with its last line connected to the star. This assumption yields a mass density, particle density and magnetic field at the Alfvén radius of
-
n⋆ = 3.05 × 109 cm-3
-
ρ⋆ = 2.48 × 10-15 g cm-3
-
B⋆ = 1.82 G,
respectively, where ρ⋆ is given by (see
Eqs. (3.14) and (3.15) in ST94) 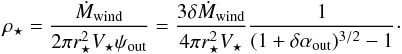 (12)We recall that
the mass loss rate of this solution is
Ṁwind = 3.1 × 10-9 M⊙/yr.
From these values at the Alfvén radius we obtain
(12)We recall that
the mass loss rate of this solution is
Ṁwind = 3.1 × 10-9 M⊙/yr.
From these values at the Alfvén radius we obtain
-
ρ∞ = 2.72 × 10-17 g cm-3, deduced from ρ⋆ and the Alfvén Mach number at infinity;
-
n∞ ≈ 107 cm-3 assuming the plasma is fully ionized;
-
Bo = 608 G;
-
B∞ = 76 mG;
-
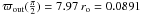 AU, which corresponds
to the cylindrical radius where the last line connected to the star reaches the
equatorial plane (see Fig. 1b);
AU, which corresponds
to the cylindrical radius where the last line connected to the star reaches the
equatorial plane (see Fig. 1b); -
ϖ∞,out = 42.8 ro = 0.478 AU,
which corresponds to the radius of the jet at large distances. The radii of bow shocks in jet simulations are much larger than the jet itself. They can easily be 10 times larger (e.g. Matsakos et al.2009). A jet with a radius of 1 AU may create shocks of width 10 AU. Thus the radius we have obtained in this solution is consistent with current observations, though for low mass accreting stars the jet radius cannot be resolved (St-Onge & Bastien 2008).
The star-braking time calculated from Eq. (10) for this solution is
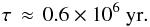 (13)This corresponds to the
typical life time of a CTTS (Bouvier et al. 1997).
If k equals 0.2 instead of 0.06, we obtain a star braking time of
2 million years. This does not drastically affect our final conclusion. This means that
the jet is efficiently removing angular momentum from the star. Thus we may explain the
low rotation frequency of those particular stars without invoking the disk locking
mechanism. This calculation relies on the steady solution we used. This does not prevent
the star from sudden violent outflows caused by reconnection as shown in various numerical
simulations. As we mentioned in the introduction, the presence of coronal mass ejections
(CMEs) does not affect the longterm evolution of the steady flow. It is interesting,
however, to note that the braking time obtained in the Küker et al. (2003) simulations is very similar, albeit with a different
process. The authors conclude that the accretion torque spins the star up because the
magnetic torque from the X-wind is too weak. We propose here alternatively that the
stellar jet could compensate for it.
(13)This corresponds to the
typical life time of a CTTS (Bouvier et al. 1997).
If k equals 0.2 instead of 0.06, we obtain a star braking time of
2 million years. This does not drastically affect our final conclusion. This means that
the jet is efficiently removing angular momentum from the star. Thus we may explain the
low rotation frequency of those particular stars without invoking the disk locking
mechanism. This calculation relies on the steady solution we used. This does not prevent
the star from sudden violent outflows caused by reconnection as shown in various numerical
simulations. As we mentioned in the introduction, the presence of coronal mass ejections
(CMEs) does not affect the longterm evolution of the steady flow. It is interesting,
however, to note that the braking time obtained in the Küker et al. (2003) simulations is very similar, albeit with a different
process. The authors conclude that the accretion torque spins the star up because the
magnetic torque from the X-wind is too weak. We propose here alternatively that the
stellar jet could compensate for it.
4.3. Higher mass accreting T Tauri jets
In brighter T Tauri jets, higher mass loss rates are usually observed. We may extend the same solution in cylindrical radius by including the disk-wind component. To obtain a jet mass loss rate of Ṁwind = 10-8 M⊙/yr, the solution should be extended to include the fieldline region connected to the disk up to αdisk,out = 3.07. Note that this value of Ṁwind is in the range of the mass loss rates, deduced for RY Tau seen in the optical by Agra-Amboage et al. (2009), typically 0.16 to 2.6 × 10-8 M⊙/yr.
The extended jet has a launching region of radius ϖdisk,out = 0.478 AU and an asymptotic cylindrical radius of ϖ∞,out = 0.890 AU. The extension of the launching region within the disk is quite large. Conversely the expansion of the disk outflow is too small. Indeed, we do not expect our model to be extended to this distance from the star. It does not apply to the Keplerian part of the accretion disk region. A more realistic disk wind model would naturally give a larger expansion factor of the jet and an asymptotic radius of a few tens of AU, as expected observationally.
We can also keep the same solution considering only the stellar wind component but
assuming a mass loss rate of
Ṁwind = 10-8 M⊙/yr.
Accordingly we recalculate the physical quantities. Increasing the mass loss rate by a
factor of 3 just increases the density by a factor of 3 and the magnetic field by a factor
of 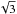 .
This does affect the velocity and the temperature within the jet. In this case the values
at the Alfvén radius are
.
This does affect the velocity and the temperature within the jet. In this case the values
at the Alfvén radius are
-
n∞ ≈ 3.2 × 107 cm-3 assuming the plasma is fully ionized;
-
Bo ≈ 1.1 kG;
-
B∞ ≈ 140 mG.
This adapts our solution to higher mass loss rates. In these cases however, the large
observed jet radii imply that there is a significant disk wind contribution. Note that
this high mass loss rate changes the braking time and reduces it by a factor of 3
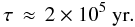 (14)It also increases the
dipolar magnetic field at the surface of the star up to 1.1 kG, which is still reasonable
(Donati et al. 2008). It does not change the
temperature profile of Fig. 3, but because the
density is significantly higher, this would probably lead to observational signatures in
X-rays.
(14)It also increases the
dipolar magnetic field at the surface of the star up to 1.1 kG, which is still reasonable
(Donati et al. 2008). It does not change the
temperature profile of Fig. 3, but because the
density is significantly higher, this would probably lead to observational signatures in
X-rays.
 |
Fig. 4 Topolopy of the streamlines and magnetic fieldlines of the oscillating solution in the meridional plane. In a) zoom out showing the recollimation. In b) zoom close to the star. All distances are given in astronomical units (AU). The solid (red) lines correspond to open fieldlines connected to the star. The dashed (green) lines correspond to lines connected to the disk. The dead zone here is reduced and all lines from the star are opened and not connected to the accretion disk. The solution recollimates at 38 stellar radii at a distance where the UV shock was observed for RY Tau from 1993 to 2001. The dotted circle indicates the Alfvén surface. |
5. A recollimating solution
5.1. Construction of the solution
By changing the initial pressure and the other parameters accordingly to keep the same stellar constraints, we obtain a second solution, which recollimates at about 38 stellar radii. The morphology of this solution is displayed in Fig. 4.
The model parameters are close to those corresponding to RY Tau again and the recollimation distance in that case corresponds to the distance of the shock seen in the UV by Ferro-Fontán & Gómez de Castro (2003). From the HST observations obtained in 1993, Gómez de Castro & Verdugo (2001) deduced the presence of a UV shock and suggested that it might correspond to the recollimation of the underlying jet. Following this track, we suggest that a shock could form in our solution at the position where the jet recollimates. Of course, a simple analytical model cannot describe the shock itself, this is beyond the scope of the present paper. We just note here that the outflow velocity at this point is super fast magnetosonic, and hence shocks can form without destroying the outflow. This has been shown numerically by Matsakos et al. (2009) for this solution.
St-Onge & Bastien (2008) observed episodic small scale outflows in 1998 and 2005 always along the same ejection axis. They proposed that these successive knots merge to form the large-scale jet. We suggest then that the two solutions may correspond to two different stages of the same object. The recollimating solution may correspond to the stage with a UV shock and the nonoscillating solution to another phase where the jet is visible.
 |
Fig. 5 Plot of the poloidal velocity for the oscillating solution along the polar axis (solid line) and the last streamline connected to the star (dashed). The jet decelerates after the recollimation distance. |
 |
Fig. 6 Plot of the polar density a), the dimensionless polar pressure b) and the polar temperature c) for the oscillating solution. The temperature is the effective one as in Fig. 3. The polar effective temperature is fairly constant along the jet, suggesting a uniform level of turbulence. The three extra asymptotic curves in c) correspond to three possible values of the temperature at infinity, obtained by subtracting non-zero values of the pressure at infinity, as shown in b). |
5.2. Physical discussion on the oscillating solution
After iterating, we found the following set of parameters
-
ϵ = −0.034;
-
δ = 0.075;
-
κ = 0.065;
-
ν = 5.8;
-
λ = 0.884.
Note that the value of ϵ is now slightly negative. This means that the magnetic rotator is important but less efficient in collimating. We know from previous study (STT99) that in that case the oscillations are more pronounced.
The corresponding rotation frequency, azimuthal velocity and asymptotic speed along the polar axis are
-
Ω = 4.68 × 10-6 rad/s;
-
Vϕ,o = 7.82 km s-1;
-
V∞ = 186 km s-1,
respectively. This last value is closer this time to our initial guess for RY Tau. We plot the polar velocity of this solution in Fig. 5, the corresponding polar density, pressure and temperature in Fig. 6. Similarly to Figs. 3b and c, changing the value of Po only affects the curves near their minimum but not close to the star.
For this solution, physical quantities at the Alfvén radius are:
-
r⋆ = 4.39 ro = 0.049 AU;
-
V⋆ = 38.75 km s-1.
We calculate the density again assuming that the observed mass loss rate of Ṁwind = 3.1 × 10-9 M⊙/yr entirely comes from the star. This means that the jet radius is defined as the last flux tube connected to the star that corresponds to a magnetic dimensionless flux
-
α(fmin) = αout = 0.361 (see Fig. 4).
It corresponds to a mass density, particle density and magnetic field at the Alfvén radius of, respectively,
-
n⋆ = 1.01 × 1011 cm-3 is we assume a fully ionized plasma as previously;
-
ρ⋆ = 8.19 × 10-14 g cm-3;
-
B⋆ = 3.94 G.
From this solution we obtain the following output values
-
Bo = 27.4 G;
-
B∞ = 6.28 G;
-
ϖ∞;out = 2.09 ro = 0.023 AU.
The asymptotic density is higher in this solution because we kept the same mass loss rate, but both the velocity and the jet radius are smaller. However, the stellar jet radius is so small in this case that even if it were drastically enlarged by a shock, say at most by a factor of ten, it would remain far below any possible detection.
This solution, as we mentioned, may describe RY Tau or any other CTTS during phases where the jet is not visible. We suggest that it may also be well adapted to WTTS where there is no obvious jet observed despite the similarity of the central star.
Moreover, the star braking time calculated from Eq. (10) is for this solution 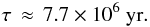 (15)This is longer than the
lifetime of CTTS, closer to the time spent by the star once the disk is dissipated. Thus
the magnetic braking is strongly reduced in this case and inefficient. If the accretion
rate remains identical, one would expect a spin-up of the star. But it is unclear in this
solution if the accretion rate is not also reduced because of the reduction of the large
dead zone of the first displayed solution (compare Fig. 1b and 4b).
(15)This is longer than the
lifetime of CTTS, closer to the time spent by the star once the disk is dissipated. Thus
the magnetic braking is strongly reduced in this case and inefficient. If the accretion
rate remains identical, one would expect a spin-up of the star. But it is unclear in this
solution if the accretion rate is not also reduced because of the reduction of the large
dead zone of the first displayed solution (compare Fig. 1b and 4b).
5.3. A possible application to the RY Tau jet
By analyzing high spatial resolution images of the classical T Tauri star RY Tauri in the Taurus-Auriga cloud taken with the Gemini North telescope, St-Onge & Bastien (2008) strongly suggested that the RY Tau jet is a pure stellar jet. They argue that the knots are intermittent microjets that merge on longer scales. In 2005, they deduced the tangential velocity of the brightest knot already seen by HST in 1998. Parallely, in 1993 and 2001, a UV shock was observed by Gómez de Castro & Verdugo (2001, 2007). They interpreted it as a signature of a stellar jet component.
In view of these observations, it is tempting to suggest that the two different MHD solutions discussed above may correspond to the two different stages of RY Tau. Thus, to explain the succession of knots seen close to the star, the first nonoscillating solution would be relevant for this stage. During this period, the stellar activity of the central star could be enhanced, producing a large visible stellar jet that efficiently brakes the central star.
On the other hand, during periods where the UV lines are detected, the outflow could be described by the second oscillating solution with an invisible jet, except for the recollimating region where the UV shock is observed. Moreover, the width of the stellar jet at the recollimating point is around 2 stellar radii, which corresponds to the width of the UV zone before the shock, as observed. This may take place during a short period, probably linked to a lack of magnetic activity, or even during stellar minimum.
The jet alternately takes the morphology of the two solutions depending on the activity of the star. A UV shock is formed during the low activity phase. Once the activity is high, the jet speed increases and blows away the UV shock.
Note that this multiphase behavior of the large scale jet has been found in time-dependent MHD simulations of a two-component MHD outflow, when the initial injection speed of the jet varies (Matsakos et al. 2009), a variability that may be caused by a magnetic activity cycle.
The density profiles of our two solutions are consistent with the densities given by Gómez de Castro & Verdugo (2007). They measure an electronic density of 1012 cm-3 in the SiIII UV line between 0.006 and 0.3 AU, and 1010 cm-3 in the CIII] UV semi-forbidden line between 0.05 and 1 AU. These two values are consistent with the densities of the second solution displayed in Fig. 6a. They also measure a density of 107 cm-3 in the [OII] forbidden UV line farther out between 4 and 100 AU. This last line is not formed in the UV shock region. The observed density corresponds to the asymptotic density of the first solution displayed in Fig. 3a.
6. Conclusions
We have used a simple semi-analytical MHD model (ST94) to show that the low rotational velocity of T Tauri stars can be understood by considering the effect of stellar jets to remove their angular momentum. In particular, we modeled stellar jets from CTTS with a mass loss rate consistent with observations. The solutions for collimated magnetized outflows are obtained via a nonlinear separation of the variables in the governing full set of the MHD equations. Two main results are obtained.
First, jets can efficiently brake the central star and remove the bulk of its angular momentum over a timescale of a million years, at least for low mass accreting stars. This corresponds to the typical lifetime of a star in the CTTS phase. Furthermore, with this mechanism the star can even slow down within 0.6 million years, if the disk does not transport angular momentum onto the star. This fairly short slow-down time shows the efficiency with which a magnetized outflow can remove angular momentum from a rapidly rotating young stellar object. This result strongly suggests that stellar jets may explain the low rotational speeds observed in those objects, independently of any disk locking. This mechanism could be complementary to other angular momentum removal mechanisms occurring at the X- wind emerging from the interaction zone between the disk and the magnetosphere. Our solution fairly well reproduces the mass loss rate, terminal speed and rotation rate of the jet. The effective plasma temperature in the jet is reasonable provided that non thermal processes, such as Alfvén waves, are at work in the plasma of the jets. These physical processes are likely to take place in the jets if one considers that the magnetic activity of CTTS is comparable to, or higher than, that of our own Sun.
Second, we also analyzed two interesting MHD solutions. The first corresponds to a gradually cylindrically collimated wide wind without oscillations in its width. The second is a narrower outflow that refocuses toward the jet axis and also oscillates in width. Note that these two very different solutions were obtained by a slight change of the parameters. It is a known result in nonlinear equations (e.g. Parker solutions, or, their MHD generalization). Correspondingly, we discussed the applicability of these two solutions in the context of the RY Tau jet, of which recent observations indicate that the plasma outflow from the rotating and magnetized star may have an intermittency exhibiting at least two phases. During one phase the cylindrical wind is relatively wide and nonoscillating. During the other phase the outflow is narrow and oscillates. Oscillations may produce radiative shocks seen in various emission lines, such as the observed UV lines of RY Tau. Matsakos et al. (2009) have shown that the self-similar solutions used in this paper will not be destroyed by the shock formation or the disk-wind interaction.
From a more general perspective, this dichotomic behavior can be seen in the two classes, CTTS and WTTS, which may both actually have jets, but these jets are visible only CTTS. The connection of CTTS with their disks through their magnetospheres may increase the width of their jets such as to make them visible. The mass loss rate measured in CTTS is thought to decrease as the star evolves toward the stage of WTTS. In this later stage, direct observations are more difficult and upper limits around 10-10 M⊙/yr can only be inferred. Weak T Tauri stars seem to have lost the gas component of their accretion disk or at least gas falling onto the star. Our second MHD solution suggests that even with the same mass loss rate, the jets of WTTS may be invisible with the present angular resolution because of their narrowness. The lack of accretion disk prevents the formation of disk winds and the possibility of higher mass loss rates. The lower jet width may be caused either by a lower stellar magnetic activity (see Vidotto et al.2009, 2010) or by a lack of magnetic connection into the disk. The magnetic braking time in this case would be on the order of 10 million years, which is indeed the time a T Tauri star is expected to spend in the weak-line stage.
Our modeling suggests that CTTS may produce visible jets in their active phase that would efficiently brake the star. Indeed, in the nonoscillating solution the magnetic field dominates the dynamics in the jet. Near the star, the magnetic field has a dipolar structure and the wind is more efficient in this case in extracting stellar angular momentum. On the other hand, WTTS may have jets as well, which are invisible because they are too narrow. These jets would be weaker because of the lack of direct connection with the accretion disk through a large dead zone.
Acknowledgments
The authors are grateful to J. F. Gameiro for his useful comments during the preparation of the manuscript and acknowledge support through the Marie Curie Research Training Network JETSET (Jet Simulations, Experiments and Theory) under contract MRTN-CT-2004-005592. Z.M. acknowledges financial support from the FWO, grant G.0277.08. J.J.G.L. acknowledges financial support from project PTDC/CTE-AST/65971/2006 from FCT, Portugal and the financial support and kind hospitality of the Observatory of Paris. V.C., N.G. and C.S. thank CAUP and the University of Athens for their kind hospitality.
References
- Agra-Amboage, V., Dougados, C., Cabrit, S., Garcia, P. J. V., & Ferruit, P. 2009, A&A, 493, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aibéo, A., Lima, J. J. G., & Sauty, C. 2007, A&A, 461, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, J. M., Li, Z.-Y., Krasnopolsky, R., & Blandford, R. D. 2003, ApJ, 590, L107 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Deeney, B. D., Phillips, R. B., & Lestrade, J.-F. 1992, ApJ, 401, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J. 2009, Protostellar Jets in Context, ed. K. Tsinganos, T. Ray, & M. Stute, ApS&S, 11 [Google Scholar]
- Bardeen, J. M., & Berger, B. K. 1978, ApJ, 221, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, T. L., Bary, J. S., & McGregor, P. J. 2010, ApJ, 722, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C. 1989, ARA&A, 27, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J., Cabrit, S., Fernandez, M., Martin, E. L., & Matthews, J. M. 1993, A&AS, 101, 485 [Google Scholar]
- Bouvier, J., Covino, E., Kovo, O., et al. 1995, A&A, 299, 89 [NASA ADS] [Google Scholar]
- Bouvier, J., Forestini, M., & Allain, S. 1997, A&A, 326, 1023 [NASA ADS] [Google Scholar]
- Cabrit, S. 2007, IAUS, 243, 203 [Google Scholar]
- Cabrit, S., & André, P. 1991, ApJ, 379, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N. 1998, AIPC, 431, 495 [NASA ADS] [Google Scholar]
- Casse, F., & Keppens, R. 2004, ApJ, 601, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, P. I., & Herbst, W. 1996, AJ, 111, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L., & Baliber, N. 2007, ApJ, 671, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J., & Bouvier, J. 2000, MNRAS, 319, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, J. 1994, ApJ, 432, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 2000, Allen’s astrophysical quantities, 4th ed. (Springer) [Google Scholar]
- Decampli, W. M. 1981, ApJ, 244, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Jardine, M. M., Gregory, S. G., et al. 2008, MNRAS, 386, 1234 [NASA ADS] [CrossRef] [Google Scholar]
- Dougados, C., Cabrit, S., Lavalley, C., & Ménard, F. 2000, A&A, 357, L61 [NASA ADS] [Google Scholar]
- Edwards, S., Strom, S. E., Hartigan, P., et al. 1993, AJ, 106, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, S., Fischer, W., Kwan, J., Hillenbrand, L., & Dupree, A. K. 2003, ApJ, 599, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Fendt, C. 2009, ApJ, 692, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 1997, A&A, 317, 340 [NASA ADS] [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferro-Fontán, C., & Gómez de Castro, A. I. 2003, MNRAS, 342, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, P. J. V., Ferreira, J., Cabrit, S., & Binette, L. 2001a, A&A, 377, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, P. J. V., Cabrit, S., Ferreira, J., & Binette, L. 2001b, A&A, 377, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979a, ApJ, 232, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979b, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez de Castro, A. I., & Verdugo, E. 2001, ApJ, 548, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez de Castro, A. I., & Verdugo, E. 2007, ApJ, 654, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Gracia, J., Vlahakis, N., & Tsinganos, K. 2001, MNRAS, 367, 201 [Google Scholar]
- Günther, H. M., Matt, S. P., & Li, Z.-Y. 2009, A&A, 493, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartigan, P., Edwards, S., & Ghandour, L. 1995, ApJ, 452, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., & Mundt, R. 2005, ApJ, 633, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Eislöffel, J., Mundt, R., & Scholz, A. 2007, Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 951, 297 [Google Scholar]
- Kopp, R. A., & Holzer, T. E. 1976, Sol. Phys., 49, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Koide, S. 2003, Phys. Rev. D, 67, 104010-1 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, R., Li, Z.-Y., & Blandford, R. D. 2003, ApJ, 595, 631 [Google Scholar]
- Küker, M., Henning, T., & Rüdiger, G. 2003, ApJ, 589, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Kundurthy, P., Meyer, M. R., Robberto, M., Beckwith, S. V. W., & Herbst, T. 2006, AJ, 132, 2469 [NASA ADS] [CrossRef] [Google Scholar]
- Kwan, J., Edwards, S., & Fisher, W. 2007, ApJ, 657, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalley-Fouquet, C., Cabrit, S., & Dougados, C. 2000, A&A, 356, L41 [NASA ADS] [Google Scholar]
- Li, Z.-Y., Chiueh, T., & Begelman, M. C. 1992, ApJ, 394, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, J. J. G., Priest, E. R., & Tsinganos, K. 2001, A&A, 371, 240 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marilli, E., Frasca, A., Covino, E., et al. 2007, A&A, 463, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsakos, T., Tsinganos, K., Vlahakis, N., et al. 2008, A&A, 477, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsakos, T., Massaglia, S., Trussoni, E., et al. 2009, A&A, 502, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2005, ApJ, 632, 135L [Google Scholar]
- Matt, S., & Pudritz, R. E. 2008a, ApJ, 678, 1109 [Google Scholar]
- Matt, S., & Pudritz, R. E. 2008b, ApJ, 681, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., Winglee, R., & Böhm, K.-H. 2003, MNRAS, 345, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., Pinzón, G., de la Reza, R., & Greene, T. P. 2010, ApJ, 714, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Meliani, Z., Casse, F., & Sauty, C. 2006, A&A, 460, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mestel, L. 1968a, MNRAS, 138, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1968b, MNRAS, 140, 177 [NASA ADS] [Google Scholar]
- Mora, A., Merín, B., Solano, E., et al. 2001, A&A, 378, 116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouyed, R., & Pudritz, R. E. 1997, ApJ, 482, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Petrov, P. P., Zajtseva, G. V., Efimov, Y. S., et al. 1999, A&A, 341, 553 [NASA ADS] [Google Scholar]
- Pudritz, R. E., & Norman, C. A. 1986, ApJ, 301, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Wolff, S. C., & Strom, S. E. 2004, AJ, 127, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Megeath, S. T., Hora, J. L., & Hartmann, L. 2006, ApJ, 646, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Wolff, S. C., & Strom, S. E. 2008, ASPC, 384, 327 [NASA ADS] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2009, MNRAS, 399, 1802 [NASA ADS] [CrossRef] [Google Scholar]
- Sauty, C., & Tsinganos, K. 1994, A&A, 287, 893 (ST94) [NASA ADS] [Google Scholar]
- Sauty, C., Tsinganos, K., & Trussoni, E. 1999, A&A, 348, 327 (STT99) [NASA ADS] [Google Scholar]
- Sauty, C., Trussoni, E., & Tsinganos, K. 2002, A&A, 389, 1068 (STT02) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sauty, C., Tsinganos, K., Trussoni, E., & Meliani, Z. 2003, Ap&SS, 287, 25 [Google Scholar]
- Sauty, C., Trussoni, E., & Tsinganos, K. 2004, A&A, 421, 797 (STT04) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schatzman, E. 1962, AnAp, 25, 18 [Google Scholar]
- Schwartz, K., & Schubert, G. 1969, ApS&S, 5, 444 [NASA ADS] [Google Scholar]
- Shang, H., Glassgold, A. E., Shu, F. H., & Lizano, S. 2002, ApJ, 564, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1997, LNP, 487, 67 [NASA ADS] [Google Scholar]
- Stassun, K. G., Mathieu, R. D., Mazeh, T., & Vrba, F. J. 1999, AJ, 117, 2941 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Mathieu, R. D., Vrba, F. J., Mazeh, T., & Henden, A. 2001, AJ, 121, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- St-Onge, G., & Bastien, P. 2008, ApJ, 674, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Stute, M., Tsinganos, K., Vlahakis, N., Matsakos, T., & Gracia, J. 2008, A&A, 491, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ustyugova, G. V., Lovelace, R. V. E., Romanova, M. M., Li, H., & Colgate, S. A. 2000, ApJ, 541, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Vidotto, A. A., Opher, M., Jatenco-Pereira, V., & Gombosi, T. I. 2009, ApJ, 699, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Vidotto, A. A., Opher, M., Jatenco-Pereira, V., & Gombosi, T. I. 2010, ApJ, 720, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahakis, N., & Tsinganos, K. 1998, MNRAS, 298, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahakis, N., Tsinganos, K., Sauty, C., & Trussoni, E. 2000, MNRAS, 318, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F. M., Brown, A., Mathieu, R. D., Myers, P. C., & Vrba, F. J. 1988, AJ, 96, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, E. J., & Davis, L. J. 1967, ApJ 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., & Ferreira, J. 2009, A&A, 508, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Governing equations for meridional self-similar outflows
The basic equations governing plasma outflows in the framework of an ideal MHD treatment
for steady, axisymmetric flows are the momentum, mass and magnetic flux conservation, the
frozen-in law for infinite conductivity, and the first law of thermodynamics. In
particular, the poloidal component of the magnetic field can be derived from the magnetic
flux in spherical coordinates (r,θ,ϕ), 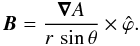 (A.1)We need to
specify the latidudinal dependences of the velocity, magnetic, density and pressure
fields, V, B,
P and ρ respectively. This can be resumed in the
following assumptions (for details see ST94, STT99 and STT02):
(A.1)We need to
specify the latidudinal dependences of the velocity, magnetic, density and pressure
fields, V, B,
P and ρ respectively. This can be resumed in the
following assumptions (for details see ST94, STT99 and STT02): ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{Br} &&B_r = B_{*} {1\over G^2(R)}\cos\theta, \\[1.5mm] && B_\theta = -B_{*} {1\over G^2(R)}{F(R)\over 2}\sin\theta, \\[1.5mm] \label{Bphi} && B_\varphi = - B_{*} {\lambda \over G^2(R)}{\displaystyle 1 - G^2(R) \over 1 - M^2(R) }{R\sin\theta}, \\[1.5mm] \label{Vr} && V_r = V_{*} {M^2(R)\over G^2(R)} { \cos\theta \over \sqrt{1+\delta \alpha(R,\theta)} },\;\;\;\;\;\; \\[1.5mm] && V_\theta = -V_{*} {M^2(R)\over G^2(R)}{F(R)\over 2}{ \sin\theta \over \sqrt{1+\delta \alpha(R,\theta)} }, \\[1.5mm] \label{Vphi} && V_\varphi = V_{*} {\lambda \over G^2(R)}{ G^2(R) - M^2(R) \over 1- M^2(R)}{R\sin\theta \over \sqrt{1+ \delta \alpha(R,\theta)}}\cdot \\[1.5mm] \label{density} \label{rho} && \rho(R,\alpha) = {{\rho_*} \over {M^2(R)}} (1 + \delta \alpha). \\[1.5mm] \label{pressure} && P(R,\alpha) = {1 \over 2} \rho_* V^2_* \Pi(R)[1+ \kappa \alpha] + P_{\rm o}. \end{eqnarray}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq154.png) We
used
We
used 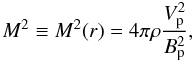 (A.10)the square of the
poloidal Alfvén number, which is a function of radial distance only.
(A.10)the square of the
poloidal Alfvén number, which is a function of radial distance only.
We defined the dimensionless magnetic flux function
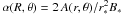 . This quantity is
related to G(R) through the following expression
. This quantity is
related to G(R) through the following expression
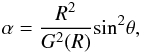 (A.11)where
G2(R) is the cross-sectional area of a flux
tube perpendicular to the symmetry axis in units of the corresponding area at the Alfvén
distance.
(A.11)where
G2(R) is the cross-sectional area of a flux
tube perpendicular to the symmetry axis in units of the corresponding area at the Alfvén
distance.
Finally, for homogeneity with the notations in ST94, STT99 and STT02, we also introduced
the function F(R), which is the logarithmic derivative
(with a minus sign) of the well known expansion factor used in solar wind theory (Kopp & Holzer1976): ![\appendix \setcounter{section}{1} \begin{equation} \label{F} F(R) = 2 \, \left[1 - {{\mathrm d}\!\ln G(R) \over {\mathrm d}\!\ln R} \right]\cdot \end{equation}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq161.png) (A.12)We recall that the value
of F defines the shape of the poloidal streamlines. For
F(R) = 0 the streamlines are radial, for
F(R) > 0 they are deflected to the polar axis
(F = 2 means cylindrical collimation), while for
F(R) < 0 they flare to the equatorial plane.
(A.12)We recall that the value
of F defines the shape of the poloidal streamlines. For
F(R) = 0 the streamlines are radial, for
F(R) > 0 they are deflected to the polar axis
(F = 2 means cylindrical collimation), while for
F(R) < 0 they flare to the equatorial plane.
Using these assumptions, the usual MHD equation system reduces to the three following
ordinary differential equations for Π(R),
M2(R)
and F(R), ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{Eq1} &&{\hbox {d} \Pi \over \hbox {d} R} = - {2 \over G^4 } \left[ {\hbox{d} M^2 \over \hbox{d} R} + {M^2 \over R^2} (F-2) \right] - {\nu^2 \over M^2 R^2 }, \\[1.5mm] \label{Eq2} && {\hbox {d} F(R) \over \hbox {d} R} = {{{\cal N}_F(R,G,F,M^2,\Pi; \kappa, \delta, \nu, \lambda)} \over \ {R \, {\cal D}(R,G,F,M^2; \kappa, \lambda)}}, \\[1.5mm] \label{Eq3} && {\hbox {d} M^2(R) \over \hbox {d} R}={{{\cal N}_M(R,G,F,M^2,\Pi; \kappa, \delta, \nu, \lambda)} \over \ {R \, {\cal D}(R,G,F,M^2; \kappa, \lambda)}}, \end{eqnarray}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq169.png) where
we defined
where
we defined ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{Eq4} && {\cal D} = \left(M^2-1\right)\left(1+\kappa {R^2\over G^2} \right) + {F^2\over 4} + R^2\lambda^2{N_B^2\over D^2}, \\[1.25mm] \label{Eq5} &&{\cal N}_F = - (\delta-\kappa)\nu^2 {R G^2\over 2 M^2}F + \left({2\kappa \Pi G^2 R^2} + (F+1)(F-2) \right)\nonumber\\[1.25mm] &&\qquad\ \ \times \left(1+\kappa {R^2\over G^2} - {F^2\over 4} - R^2\lambda^2{N_B^2\over D^3} \right) + {M^2F\over4}(F-2) \nonumber\\[1.25mm] &&\qquad\ \ \times \left(F+2+2\kappa{R^2\over G^2} + 2R^2\lambda^2{N_B^2\over D^3} \right)- \lambda^2 R^2 F(F-2){N_B\over D^2} \nonumber\\[1.25mm] &&\qquad\ \ + \lambda^2 R^2 \left(1 \!+\! \kappa {R^2\over G^2} \!-\! R^2\lambda^2{N_B^2\over D^3} \!-\! {F\over 2} \right) \left(4{N_B^2\over D^2} \!-\! {2\over M^2}{N_V^2\over D^2}\right), \\[1.25mm] \label{Eq6} && {\cal N}_M= (\delta-\kappa)\nu^2 {R G^2\over 2 M^2}\left(M^2-1\right) + \kappa \Pi R^2 G^2 M^2{F\over 2} -{M^4\over 4}(F-2)\nonumber\\[1.25mm] &&\qquad\ \ \times \left(4\kappa {R^2\over G^2} +F+4\right) + {M^2\over 8}(F-2)\left(8\kappa {R^2\over G^2} +F^2+4F+8\right) \nonumber\\[1.25mm] &&\qquad\ \ - \lambda^2 R^2 (F \!-\! 2){N_B\over D} \!+\! \lambda^2 R^2 \left(2M^2 \!+\! F \!-\! 2\right)\left({N_B^2\over D^2} \!-\! {1\over 2 M^2}{N_V^2\over D^2}\right),\nonumber \\ \end{eqnarray}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq170.png) with
with
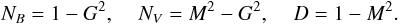 (A.19)The meaning of
the various parameters is discussed in Sect. 2.
(A.19)The meaning of
the various parameters is discussed in Sect. 2.
At the Alfvén radius, the slope of M2(R = 1)
is p = (2 − F∗)/τ,
where τ is a solution of the third-degree polynomial: ![\appendix \setcounter{section}{1} \begin{equation} \label{Eq8} \tau^3 + 2 \tau^2 + \left[ {{\kappa \Pi_*} \over {\lambda^2}} + {{F^2_* - 4} \over {4 \lambda^2}} - 1 \right] \tau + {{\left(F_*-2\right)F_*} \over {2 \lambda^2}} = 0, \end{equation}](/articles/aa/full_html/2011/09/aa16519-11/aa16519-11-eq175.png) (A.20)and the star indicates
values at R = 1 (for details see ST94).
(A.20)and the star indicates
values at R = 1 (for details see ST94).
All Figures
 |
Fig. 1 Topolopy of the nonoscillating solution in the meridional plane. In a) zoom out showing the collimation. In b) zoom close to the star. All distances are given in astronomical units (AU). The solid (red) lines correspond to open fieldlines connected to the star. The dashed (green) lines correspond to closed stellar fieldlines and lines connected to the disk. All open lines are originating in a polar cap extending to a colatitude of 15 degrees. The dotted circle indicates the Alfvén surface. |
| In the text | |
 |
Fig. 2 Plot of the poloidal velocity for the nonoscillating solution along the polar axis (solid line) and the last streamline connected to the star (dashed). By construction the poloidal velocity is zero on the last streamline where it reaches the equatorial plane. This creates the dip seen on the logarithmical scale. |
| In the text | |
 |
Fig. 3 In a) we plot of the polar density, in b) the total pressure in dimensionless units along the polar axis, including nonkinetic terms such as turbulent magnetic or ram pressure. In c) we plot the polar effective temperature for the nonoscillating solution. The three additional asymptotic curves in c) correspond to three possible values of the temperature at infinity, obtained by adding non-zero values of the pressure at infinity, as shown in b). |
| In the text | |
 |
Fig. 4 Topolopy of the streamlines and magnetic fieldlines of the oscillating solution in the meridional plane. In a) zoom out showing the recollimation. In b) zoom close to the star. All distances are given in astronomical units (AU). The solid (red) lines correspond to open fieldlines connected to the star. The dashed (green) lines correspond to lines connected to the disk. The dead zone here is reduced and all lines from the star are opened and not connected to the accretion disk. The solution recollimates at 38 stellar radii at a distance where the UV shock was observed for RY Tau from 1993 to 2001. The dotted circle indicates the Alfvén surface. |
| In the text | |
 |
Fig. 5 Plot of the poloidal velocity for the oscillating solution along the polar axis (solid line) and the last streamline connected to the star (dashed). The jet decelerates after the recollimation distance. |
| In the text | |
 |
Fig. 6 Plot of the polar density a), the dimensionless polar pressure b) and the polar temperature c) for the oscillating solution. The temperature is the effective one as in Fig. 3. The polar effective temperature is fairly constant along the jet, suggesting a uniform level of turbulence. The three extra asymptotic curves in c) correspond to three possible values of the temperature at infinity, obtained by subtracting non-zero values of the pressure at infinity, as shown in b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


