| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201016092 | |
| Published online | 19 August 2011 | |
Magnetic field evolution in interacting galaxies
Astronomical Observatory, Jagiellonian University,
ul. Orla 171
30-244,
Kraków
Poland
e-mail: drzazga@oa.uj.edu.pl
Received:
6
November
2010
Accepted:
10
June
2011
Aims. Violent gravitational interactions can change the morphologies of galaxies and, by means of merging, transform them into elliptical galaxies. We aim to investigate how they affect the evolution of galactic magnetic fields.
Methods. We selected 16 systems of interacting galaxies with available VLA archive radio data at 4.86 and 1.4 GHz and compared their radio emission and estimated magnetic field strengths with their star-forming activity, far-infrared emission, and the stage of tidal interaction.
Results. The estimated mean of total magnetic field strength for our sample of interacting galaxies is 14 ± 5 μG, which is larger than for the non-interacting objects. The field regularity (of 0.27 ± 0.09) is lower than in typical spirals and indicates enhanced production of random magnetic fields in the interacting objects. We find a general evolution of magnetic fields: for weak interactions the strength of magnetic field is almost constant (10−15 μG) as interaction advances, then it increases up to 2× , peaks at the nuclear coalescence (25 μG), and decreases again, down to 5−6 μG, for the post-merger remnants. The main production of magnetic fields in colliding galaxies thus terminates somewhere close to the nuclear coalescence, after which magnetic field diffuses. The magnetic field strength for whole galaxies is weakly affected by the star formation rate (SFR), while the dependence is higher for galactic centres. We show that the morphological distortions visible in the radio total and polarized emission do not depend statistically on the global or local SFRs, while they do increase (especially in the polarization) with the advance of interaction. The constructed radio-far-infrared relations for interacting and non-interacting galaxies display a similar balance between the generation of cosmic rays, magnetic fields, and the production of the thermal energy and dust radiation.
Conclusions. The regular magnetic fields are much more sensitive to morphological distortions induced by tidal interactions than are the random fields. As a result the polarized emission could be yet another indicator of an ongoing merging process. The found evolution of magnetic field with advancing interaction would definitely imply a stronger effect of magnetic fields on the galaxy surroundings in the earlier cosmological epochs. The process of strong gravitational interactions can efficiently magnetize the merger’s surroundings, having a similar magnetizing effect on intergalactic medium as supernova explosions or galactic winds. If interacting galaxies generate some ultra-high energy cosmic rays (UHECRs), the disk or magnetized outflows can deflect them (up to 23°), and make an association of the observed UHECRs with the sites of their origin very uncertain.
Key words: galaxies: general / galaxies: magnetic fields / galaxies: interactions / radio continuum: galaxies
© ESO, 2011
1. Introduction
Both observational evidence and theoretical considerations show that galaxy interactions are the most important processes during the formation and evolution of galaxies (Struck 1999). This is the case both locally in the nearby universe and, in particular, cosmologically at high redshifts, where galaxy encounters are expected to be more frequent. During such encounters, direct collisions between stars are highly unlikely, while collisions between the interstellar medium (ISM) of the two disks are inevitable and may trigger star formation. The interaction-induced starbursts, nuclear activity, feedback, gas infalls, and outflows, all play critical roles in shaping ISM and the surrounding intergalactic medium (IGM) (Smith et al. 2010).
Some low-speed collisions lead to merging of galaxies. Gas-rich mergers could reach the phase of a luminous infrared galaxy (LIRG), or even of an ultraluminous infrared galaxy (ULIRG) (Sanders & Mirabel 1996). Violent galaxy collisions are also suggested as a source of large-scale shocks and one of possible sources of ultra high energy cosmic rays (UHECR; e.g. Bhattacharjee & Sigl 2000). However, not all galaxy interactions will result in a merger, and it is equally important to study different types of galaxy interaction to understand their role in galaxy evolution.
There were several systematic attempts to study the effects of collisions on structures of galaxies and the properties of different ISM phases. An early work of Toomre & Toomre (1972) showed that numerical simulations quite readily reproduce the observed morphology of a wide range of interacting galaxies and explain the formation of bars, tidal arms, and bridges. Toomre (1977) compiled a sample of 11 ongoing merger systems at various stages of interaction, which became known as the Toomre sequence. The sequence itself and numerical simulations of its members explain how elliptical galaxies can be formed by the coalescence of spiral galaxies. The Toomre sequence was studied over the years in great detail in various wavelength bands in order to understand the evolving properties of interacting systems. It was shown that in moving along the sequence from early to late-stage mergers, a larger fraction of atomic gas appears outside the optical bodies (Hibbard & Gorkom 1996). In the final stages of nuclear coalescence, there is little H i within the remnant bodies, while the tidal material flows in and is able to trigger a nuclear starburst. In accordance with that, Hummel et al. (1990) found that the central sources of interacting galaxies are by a factor of five times brighter in the radio wavelengths than those in the isolated spirals.
The studies of broadband (V, I) and narrowband (Hα) images obtained with the Hubble Space Telescope (HST) by Laine et al. (2003) show surprisingly little evidence of any distinct trends in nuclear properties along the Toomre merger sequence. There is just a rise in the nuclear luminosity density in the most-evolved members of the sequence. However, the near-infrared (NIR) observations with the HST (Rossa et al. 2007), which are less affected by dust obscuration show a distinct trend for the nuclei in the sequence to become more luminous as the merger process advances. In a different way than the non-interacting objects, the Toomre-sequence galaxies also reveal newly formed stars that are more concentrated toward their centres. Rossa et al. also argue that if left to evolve and fade for several Gyr, the merger remnants would have the K-band luminosity profiles of normal elliptical galaxies.
More complicated evolution during the merging process was identified by Brassington et al. (2007) in the X-rays observed with Chandra. They studied a sample of nine interacting and post-merger objects. The original Toomre sequence was extended in this work to include very old (up to a 3 Gyr) merger-remnants. First, they find that unlike Hα and optical emission, the X-ray luminosity peaks about 300 Myr before the nuclear coalescence. The subsequent drop in X-ray emission is likely due to large-scale diffuse outflows coming out of the galactic disks and reducing the hot gas density. Second, about 1 Gyr after the coalescence the remnants are X-ray-fainter than typical elliptical galaxies, which are known to be generally strong X-ray emitters. Thirdly, the dynamically older mergers seem to rebuild the hot galactic halo and rise again the X-ray luminosity. This can be explained by an outflowing wind driven into the halo by a declining population of type Ia supernova (Brassington et al. 2007).
Although magnetic field constitute an important ingredient of the ISM, little is known about how galaxy interactions affect its strength and evolution, and how they respond to the evolution of other ISM phases presented above. The most detailed analysis of magnetic field in disks of interacting galaxies was done by Chyży & Beck (2004) for the Antennae galaxies. They show that the mean total magnetic field strength (about 20 μG) is significantly greater than in isolated grand-design spirals and may be due to the interaction-induced star formation. The field regularity (the ratio of regular to random field components) appeared to be lower than in undistorted galaxies, which can indicate enhanced turbulent motions in the merger system. A strong regular component (of 10 μG) was found to trace gas-shearing motions along the tidal tail. When and how the enhanced magnetic field arose and when it would disperse in this system are still not known.
The evolution of magnetic field in merging systems like the Antennae may look different from the evolution of the X-ray component revealed by Brassington et al. (2007). In general, the early-type galaxies are typically radio weak, and strong radio emission is only observed in ellipticals with an AGN activity. In such active galaxies, generation of strong magnetic fields, although possible in accretion disks, is not connected with any large-scale or small-scale galactic dynamo processes, which operate in typical spiral or irregular galaxies (Beck et al. 1996; Brandenburg & Subramanian 2005; Chyży et al. 2011). The first process requires a strong differential rotation with uniform sign of turbulence twisting, the second depends on the ISM turbulence, which likely declines in early-type galaxies owing to a weaker star formation.
The goal of this paper is to investigate the evolution of magnetic field during galaxy interactions. As magnetic fields are best studied from the synchrotron emission, we restrict our considerations to objects with available radio data. The polarized properties of radio emission also provides a unique diagnostic tool for recognizing gas flows and their distortions. In Sect. 2 we describe the selection criteria of the constructed sample of interacting galaxies and present the used (VLA1) radio data and the details of their reduction. The next section provides a brief description of each interacting system and its properties in radio total and polarized emission. We present estimations of equipartition magnetic field strength for all the galaxies and compare them with those for isolated spirals (Sect. 3.9).
The statistical analysis of all the galaxies begins from investigating the evolution of magnetic fields as the interaction and merging process advance (4.1). In Sect. 4.2 we examine the relation of magnetic fields to the star formation rate (SFR). An analysis of observed morphological asymmetries in total and polarized radio emission is provided in Sect. 4.3. The radio-far-infrared (FIR) diagram for interacting galaxies is presented in Sect. 4.4 and compared to the literature results. We also discuss the possible magnetization of IGM by magnetic fields of merger origin and the propagation effects of UHECRs in the vicinity of colliding galaxies (Sect. 4.5). We summarize our findings in Sect. 5.
Interacting systems and their members.
2. The sample and radio data reduction
Parameters of the reduced radio observations at 4.86 GHz.
To explore the evolution of magnetic field in interacting galaxies, we have compiled a sample of suitable objects. First, we chose objects of the best-known merging galaxy sequence of Toomre (1977) for which appropriate radio data are available. We restricted our search to the archive of the VLA, frequencies 4.86 and 1.4 GHz, and D, C, or BC configurations of the array to maximize the sensitivity for extended radio emission. There are 5 out of 11 merging systems with relevant radio data (see Table 1). Next, we selected six out of nine objects with available radio data from the X-ray merging sequence of Brassington et al. (2007) (Table 1). Furthermore, we performed a more general search for angularly-large interacting objects with the usable radio data. We looked for galaxies to fulfil the following criteria:
-
are RC3 galaxies (de Vaucouleurs et al. 1991)recognized as interacting objects according to Suraceet al. (2004);
-
are detected in the infrared (e.g. are included in the IRAS Bright Galaxies Sample: Sanders et al. 2003);
-
at least one object in the interacting system has an angular size larger than 2′ to study distribution of the radio emission, and are also smaller than 9′ to be within the primary beam of the VLA antenna;
-
declination >−40°;
-
total flux of at least one galaxy in the interacting system is larger than 80 mJy at 1.4 GHz (from the NVSS, Condon et al. 1998).
 |
Fig. 1 The total-power contours and B-vectors of polarized intensity of NGC 2207/IC 2163 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150) × 40.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 166.7 μJy/beam. The map resolution is 27′′ × 27′′ HPBW. |
We obtained 24 objects satisfying those requirements. For ten objects, which are members of seven interacting galaxy pairs, we found high-quality VLA archive radio polarimetric data at 4.86 GHz (see Table 1). We enriched this sample by a few important types of interacting objects: the polar-ring galaxy NGC 660, the weakly interacting spiral NGC 4254 in the Virgo Cluster (see Chyży et al. 2007b; Chyży 2008), and UGC 813/UGC 816 (see Sect. 3.6). In total, in our final sample we assembled 24 pre- and post-merger galaxies from 16 recognized interacting systems. Although they by no means constitute a complete sample of colliding galaxies, they do represent the different stages of tidal interaction and merging process, which is suitable for our study.
We reduced the original VLA radio data for the seven interacting systems listed in Table 2. Some of them were unpublished to date, some were published but without any analysis of polarization data, and for some objects we obtained the final images of better quality than those known from the literature (see the next section). Using the standard AIPS package and procedures, the instrumental polarization was corrected with phase calibrators, which were also applied in gain and phase calibration (Table 2). The flux density scale was established by the amplitude calibration sources and the data were self-calibrated in phase, except for NGC 5426/7. NGC 6907/8 data were also self-calibrated in amplitude. The combined maps in I, Q, and U Stokes parameters at both frequencies were then used in constructing the maps of polarized intensity, polarization position angle, and position angle of observed magnetic vectors (observed E-vectors rotated by 90° – the so-called B-vectors). The details of observations, obtained rms sensitivities of the radio maps at 4.86 GHz, and total and polarized radio fluxes are presented in Table 2.
Also at our disposal were reduced high-quality VLA radio polarization data at 4.86 GHz for the Antennae galaxies and for the Virgo Cluster member NGC 4254 from our previous publications (see for details Chyży & Beck 2004; Chyży et al. 2007b; Chyży 2008). For the seven other mergers we used the original images from the VLA archive. The details of those data and rms sensitivities in total radio emission are presented in Table 3. The short integration time prevented us from calibrating the polarized emission for these seven objects.
 |
Fig. 2 The contours of polarized intensity and B-vectors of polarization degree of NGC 2207/IC 2163 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12, 20, 35) × 21.2 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 10%. The map resolution is 27′′ × 27′′ HPBW. |
3. Results
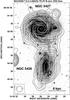 |
Fig. 3 The total power contours and B-vectors of polarized intensity of NGC 5426/NGC 5427 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250) × 23.3 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 83.3 μJy/beam. The map resolution is 22′′ × 22′′ HPBW. |
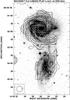 |
Fig. 4 The contours of polarized intensity and B-vectors of polarization degree of NGC 5426/NGC 5427 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12) × 14.9 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 17%. The map resolution is 22′′ × 22′′ HPBW. |
In this section we describe radio total and polarized emission of our interacting galaxies and compare them with morphological properties in other wavelengths. A detailed presentation of resolved systems is followed by concise descriptions of objects without well-resolved radio structures. Next, we estimate magnetic field strengths for all the objects investigated.
3.1. NGC 2207/IC 2163
In this pair of spiral galaxies, NGC 2207 appears in the foreground, obscuring the other one, IC 2163. According to the numerical simulations, 4 × 107 yr ago IC 2163 passed behind NGC 2207 from west to east at a distance of about 20 kpc (Elmegreen et al. 1995b). Seventeen young stellar clusters were discovered in both galaxies (Elmegreen et al. 2001), but the interaction has not yet led to a prominent starburst.
The radio emission at 4.86 GHz (Fig. 1) covers the optical extent of the system but displays a hole in the central part of NGC 2207 like in the map at 1.4 GHz (Condon 1983). The emission traces the optical western tidal tail of IC 2163 and peaks at the eastern edge of NGC 2207, where a gravitational instability region is suspected, producing a maximum in the infrared emission (Elmegreen et al. 2006). In this region, the total and polarized emission also have maxima, but not that degree of polarization, so there is no enhanced production of ordered magnetic field here, and the found radio properties of this region could result from a supply of relativistic electrons coming from the western tidal tail of the IC 2163. This idea is supported by accretion of gas from the IC 2163 onto the NGC 2207, as suggested by Elmegreen et al. (1995a). The H i velocity dispersion is quite high in a large area of the disk of NGC 2207 (40−50 km s-1). However, we do not see any correspondence of regions with enhanced velocity dispersion (cf. Elmegreen et al. 1995a) with observed distribution of total or polarized radio emission. Therefore, the tidally generated turbulence and/or stretching motions along the line of sight required to explain the observed pattern of velocity dispersion cannot significantly influence the magnetic field strength.
The regular magnetic field around the central part of NGC 2207 have an almost exclusively azimuthal direction (Fig. 2). Also HI gas forms a similar ring-like structure (Elmegreen et al. 1995a). However, in the southern part of the disk, the B-vectors have a larger pitch angle (45°) and go out of the disk. This may indicate an outflow of magnetized plasma along a tidal tail and conversion of random magnetic field to the regular component as in the eastern tail of the Antennae galaxies (Chyży & Beck 2004). With rising distance from the disk, the degree of polarization rises to 40%, and the magnetic field becomes more regular. In this region, the optical and infrared emission form long and narrow structures called “streamers” and have the same pitch angle as B-vectors (Fig. 2). In this part of NGC 2207, a large bubble of H i gas extends up to 30 kpc out of the disk to the south (Elmegreen et al. 1995a).
A similar behaviour of the magnetic field is also observed in the eastern part of IC 2163. The degree of polarization becomes larger with distance from the disk centre (reaching up to 30%), which can indicate stretching of field lines along the tidal tail (Fig. 2).
3.2. NGC 5426/7
Both galaxies in this binary system are spirals of the same Hubble class Sc, with similar sizes (≈20 kpc), and masses (3 × 1010 M⊙; Fuentes-Carrera et al. 2004). The evidence for weak gravitational interaction are the thin straight strands of the outer arms of NGC 5426 that overlap the southern spiral arms of NGC 5427 and the straight arm segment in the SW part of the spiral structure of NGC 5427 (Fig. 3). The velocity field of ionized gas in NGC 5427 is also slightly distorted (Fuentes-Carrera et al. 2004). Blackman (1982) found that 38% of the total optical flux of the system comes from two adjacent halves of both the disks. This suggests obscuration by dust in NGC 5426 that situates this galaxy in front of NGC 5427 (Fuentes-Carrera et al. 2004). All these features can be accounted for by an early phase of interaction that suggests a closer passage of galaxies in 5 × 107 yrs (Fuentes-Carrera et al. 2004).
This scenario of weak tidal interaction fully agrees with the radio polarimetric data at 4.86 GHz. The total radio intensity closely follows the optical morphology (Fig. 3). Both galaxies have coherent magnetic spiral patterns that closely follow the optical spiral arms. The absence of polarized emission in between the galaxies (Fig. 4) is probably due to beam depolarization of two structures of perpendicular B-vectors that overlap there.
In the most disturbed SW part of NGC 5427 there is no polarized emission, which makes this galaxy slightly asymmetric in the polarized intensity (Fig. 4). In the SE part of NGC 5427 the polarized emission occurs outside the density wave. To date, such outer magnetic arms have only been observed in the weakly interacting Virgo cluster spiral NGC 4254 (Chyży et al. 2007b).
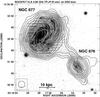 |
Fig. 5 The total power contours and B-vectors of polarized intensity of NGC 876/NGC 877 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250) × 16.5 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 83.3 μJy/beam. The map resolution is 18′′ × 18′′ HPBW. |
3.3. NGC 876/7
The larger component of this pair of galaxies – NGC 877 – is a late-type spiral with prominent and slightly disturbed optical spiral arms (Fig. 5). Bright Hα emitting regions are distributed along the arms but are not condensed in the central part of the disk (Hattori et al. 2004). The companion is a small, highly inclined galaxy (78°) at a projected separation of about 50 kpc.
The total radio emission at 4.86 GHz of both the galaxies corresponds well to optical and Hα disks and even reveals a bridge of low-surface brightness emission (at 180 μJy level) between the components (Fig. 5). The strong and elongated radio structure in the main body of NGC 877 is a galactic bar, from which regular magnetic fields stretch out to the N and S. The magnetic pattern is very coherent one and resembles those in grand-design spiral galaxies. The presence of tidally excited spiral arms in a system with a small companion is predicted by numerical simulations (Toomre 1981). This would explain the excess in infrared emission of NGC 877, which led to classifying this object as LIRG (Sanders et al. 2003). The smaller companion (NGC 876) has more concentrated radio emission, which may result from high inclination (78°) of this spiral. Surprisingly enough, it shows clear hints of the X-shape structure of B-vectors, often observed in the edge-on field galaxies (Fig. 5).
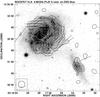 |
Fig. 6 The contours of polarized intensity and B-vectors of polarization degree of NGC 876/NGC 877 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8) × 14.0 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 14%. The map resolution is 18′′ × 18′′ HPBW. |
The distribution of the polarized emission of NGC 877 is asymmetrical (Fig. 6). The major part of this emission comes from the NW part of the disk, where the spiral arm is also better visible in the optical images. The optical morphology in the SE part of the disk is only slightly distorted but corresponds to a distinct magnetic spiral arm. A blob of polarized emission in the SE part of the disk coincides with an appendage in the near-infrared emission, which also accounts for asymmetrical appearance of this object at this band (Moriondo et al. 1999). The companion does not appear clearly asymmetrical in the polarized emission, indicating a weaker effect from interaction onto this object. The weak distortions of magnetic fields also indicate an early type of interaction of this system.
3.4. NGC 6907/8
NGC 6908 is a small lenticular galaxy superimposed on the NE arm of the dominant galaxy NGC 6907. It is most clearly seen in near-IR images (Madore et al. 2007). The spiral structure of NGC 6907 is distorted: its eastern arm is much longer and wraps around the entire galaxy (Fig. 7). The bulge of NGC 6907 has an elliptical shape, and is shifted off the base of the arms. The analysis of distortions in the HI velocity field suggests that the first collision between galaxies occurred 3.4 ± 0.6 × 107 yr ago, leaving behind a triangular HI gas stream to the NE from the current position of NGC 6908 (Scarano et al. 2008). Sanders et al. (2003) classifies NGC 6907 as LIRG.
In our maps at 4.86 GHz, the total radio emission is detected only from the larger galaxy and concentrates in its central part (Fig. 7). Two protrusions to N and S are likely some background objects. The polarized emission (Fig. 8) is more asymmetric and dominates outside the galactic bar in the SE part of the disk. The polarized data reveal a coherent spiral structure of magnetic B-vectors of small pitch angle (0°−30°), even in its eastern part, where the optical density waves are weak. In the eastern part of the disk the well-ordered magnetic fields seem to be pulled out and directed along the tidally stretched spiral arm.
 |
Fig. 7 The total power contours and B-vectors of polarized intensity of NGC 6907/NGC 6908 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250, 400) × 32.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 125.0 μJy/beam. The map resolution is 30′′ × 30′′ HPBW. |
 |
Fig. 8 The contours of polarized intensity and B-vectors of polarization degree of NGC 6907/NGC 6908 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12) × 23.3 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 8%. The map resolution is 30′′ × 30′′ HPBW. |
3.5. The Taffy
The unusual morphology of this pair of galaxies (UGC 12914 and UGC 12915), known as the Taffy system, comes from a recent (≈107 yr), nearly head-on encounter (Condon et al. 1993). Almost half of their radio emission at 1.49 GHz have been detected just from the bridge between the galaxies, which may be due to fresh relativistic CR electrons radiating in magnetic fields pulled out of the disks. In this system the H i gas is mostly distributed along the bridge (Condon et al. 1993), where a large amount of molecular gas and dust were also detected (Gao et al. 2003; Zhu et al. 2007).
Our re-reduced radio polarization data at 4.86 GHz (Fig. 9) show more details of the magnetic field structure than are presented in Condon et al. (1993). We have confirmed that the general orientation of magnetic field is along the line joining the galaxies, which is also a possible direction for passing the intruder galaxy UGC 12914. In addition, we found that in UGC 12915 the polarized emission is clearly visible on the interacting side of the disk, whereas the other side is almost completely devoid of polarized signal. Either the magnetic field was enhanced asymmetrically by the interaction or the magnetized ISM on the NE side of the disk was stripped away by ram pressure during the passage through UGC 12914. The UGC 12914 shows some patches of polarized signal on the disk side opposite the bridge, which are associated with ordered magnetic fields with large pitch angles of up to 90° (Fig. 9).
 |
Fig. 9 The total power contours and B-vectors of polarized intensity of the Taffy (UGC 12914/UGC 12915) at 4.86 GHz superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250, 400) × 17.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 71.4 μJy/beam. The map resolution is 16′′ × 16′′ HPBW. |
 |
Fig. 10 The total power contours and B-vectors of polarized intensity of the Taffy2 (UGC 813/UGC 816) at 4.86 GHz superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150) × 23.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 69.4 μJy/beam. The map resolution is 15′′ × 15′′ HPBW. |
 |
Fig. 11 a) The total power contours of NGC 660 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. A large warped ring in the NS direction is visible. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250, 400, 700, 1500, 4000) × 26.4 μJy/beam. b) The total power contours and B-vectors of polarized intensity of the disk of NGC 660 superimposed on DSS blue image. The contour levels are the same as for a). A vector of 10′′ length corresponds to the polarized intensity of 100.0 μJy/beam. c) The contours of polarized intensity and B-vectors of polarization degree of the disk of NGC 660 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12, 20, 35) × 13.4 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 11%. The maps resolution is 18′′ × 18′′ HPBW. |
3.6. The Taffy2
This pair of post-collision spiral galaxies (UGC 813 and UGC 816) is similar to the Taffy system and shows a radio bridge at 1.40 GHz (Condon et al. 2002). The suspected head-on collision was also a recent one that occurred about 5 × 107 yr ago. We call this system the Taffy2.
Our re-reduced data at 4.86 GHz show that, besides the radio bridge, the regular field is discerned in the barred disk of UGC 816 and resembles a typical spiral structure (Fig. 10). The configuration of B-vectors is not as clear in the second galaxy, which could be caused by its high inclination (72°). The orientation of magnetic field is almost perpendicular to the line joining the disks, which is somewhat puzzling, considering the opposite orientation of magnetic field in the Taffy system. The uncertainty of magnetic field orientations estimated from the signal-to-noise ratio of the polarized intensity is about 10°. On the other hand, the foreground rotation measure of the Milky Way is about 10 rad m-2 for the Taffy coordinates and about −50 rad m-2 for the Taffy2 (Johnston-Hollitt et al. 2004). Thus, the uncertainties of the magnetic field orientation due to the foreground RM are 2° and 11°. Therefore, neither uncertainties in determination of orientations of B-vectors nor the foreground RM could cause such large differences in the observed patterns of magnetic fields.
Following from this, magnetic field orientations perpendicular to the interaction axis in the Taffy2 shows that this system is less taffy-like than the Taffy one. This may indicate less violent interaction in Taffy2, hence weaker distortions of magnetic fields out of its galactic disks. The rough estimation of kinetic energy involved in gravitational interactions are 4.9−14.0 × 1057 erg and 3.2−4.6 × 1057 erg for Taffy and Taffy2 galaxies, respectively (Lisenfeld & Volk 2010). The Taffy2 thus indeed gives a hint of weaker interaction. Another possibility for different magnetic field orientations is a former collision in Taffy2 giving a longer time for galactic rotation to re-establish the global galactic magnetic field (especially in UGC 816, cf. Fig. 10). The differences in magnetic field configuration may also arise from projection effects, provided the magnetic field lines are not straight but are, e.g., helical in the bridges (M. Soida, priv. comm.). Detailed MHD simulations are needed to evaluate these possibilities.
3.7. NGC 660
NGC 660 is usually recognized as a polar-ring galaxy with a large warped ring of gas and stars (Fig. 11a). It was suggested that its morphology results from a central collision and subsequent merging of two spiral galaxies of similar masses that happened several Gyr ago (van Driel et al. 1995). However, numerical simulations can indicate another scenario where the tidal interactions between two objects without a final merger caused accretion of polar-ring material to NGC 660 from the donor galaxy (Bournaud & Combes 2003).
Our map of the total radio intensity at 4.86 GHz (Fig. 11b) displays a smooth emission from a disk with a strong central component. The
central source has a flux of 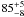 mJy,
which agrees with its total flux at 1.41 GHz and the spectral index
α = 0.6
(S ∝ ν−α) estimated by
Condon et al. (1982). Surprisingly enough, the
directions of B-vectors form an undistorted “X-like”
structure in the outer part of the disk and parallel to the disk in its inner part
(Fig. 11c). Such a configuration is typically
observed in normal late-type spiral galaxies seen edge-on (e.g. Braun et al. 2010). We suggest that in this case the second
evolutionary scenario with tidal accretion, rather than one involving a strong disk
deformation (expected for the merger), is more likely for this system. The convolution of
our maps to the larger beam of 1′ does not reveal any radio protrusion from the polar
ring. This could be expected, because in either evolutionary scenario, the life-time of
relativistic electrons at 4.86 GHz (about 108 yr) is much shorter than the
estimated age of the ring (about 109 yr; van Driel et al. 1995).
mJy,
which agrees with its total flux at 1.41 GHz and the spectral index
α = 0.6
(S ∝ ν−α) estimated by
Condon et al. (1982). Surprisingly enough, the
directions of B-vectors form an undistorted “X-like”
structure in the outer part of the disk and parallel to the disk in its inner part
(Fig. 11c). Such a configuration is typically
observed in normal late-type spiral galaxies seen edge-on (e.g. Braun et al. 2010). We suggest that in this case the second
evolutionary scenario with tidal accretion, rather than one involving a strong disk
deformation (expected for the merger), is more likely for this system. The convolution of
our maps to the larger beam of 1′ does not reveal any radio protrusion from the polar
ring. This could be expected, because in either evolutionary scenario, the life-time of
relativistic electrons at 4.86 GHz (about 108 yr) is much shorter than the
estimated age of the ring (about 109 yr; van Driel et al. 1995).
3.8. Other interacting and merging systems
NGC 4254 – This is a weakly interacting spiral galaxy in the Virgo cluster, which has recently experienced a gravitational encounter to have perturbed its spiral arms and triggered a burst of star formation (Chyży et al. 2007b). The galaxy shows a polarized emission throughout the disk, particularly strong in its southern ridge, shifted downstream of a density wave with up to 13 μG as a regular magnetic field component and 20 μG in the total field (Chyży 2008). In the ridge, the dynamo-induced magnetic fields are modified by stretching and shearing forces, which are likely triggered off by tidal forces, which produced an anisotropic component of regular field and enhanced the polarized emission.
NGC 4038/9 – This well-known interacting pair of almost identical spiral galaxies (“the Antennae”) is probably just prior to the second encounter, which will lead to their merging in 2 × 108 yr time (Mihos et al. 1993; Kotarba et al. 2010). The polarization properties of this system were studied in detail by Chyży & Beck (2004, see the Introduction). The strongest and almost random magnetic fields (30 μG) are located in the overlap region of both the galactic disks. In the NE tidal tail, away from star-forming regions, magnetic field is highly coherent with a strong regular component of 10 μG, tracing gas shearing motions along the tail. The radio spectrum is much steeper in this region, indicating ageing of the CR electron population as they propagate from their sources in the star-forming regions. This system was chosen by Toomre (1977) as the first step in his merging sequence.
NGC 6621 – This galaxy, together with NGC 6622, is included in the Toomre sequence as an intermediate-stage merger. At 1.49 GHz we see in our maps only the total power emission associated with the optically brightest part of the system.
NGC 520 – This system represents an intermediate stage of galaxy interactions according to Toomre (1977). The radio emission at 1.4 GHz is strong in the central part of the system and shows a protrusion to the NW along the optically bright ridge. According to Stanford & Barcells (1991), the system is at present 3 × 108 yr past the encounter and prior to the final coalescence.
NGC 3256 – A kinematic study of this ULIRG system (English et al. 2003) indicates that it is currently experiencing a starburst just prior to the merging. The two tidal tails visible in optical images probably formed about 5 × 108 yr ago and the coalescence is estimated to take place in ≈2 × 108 yr. The radio data at 4.86 GHz reveal only total emission peaked at the galactic centre, the site of intense infrared and X-ray emission (Brassington et al. 2007).
Arp 220 – This is the closest ULIRG, the merger at the point of coalescence (Brassington et al. 2007). The radio emission at 4.86 and 1.43 GHz is highly concentrated and coincident with the optical one.
NGC 7252 – This well-known merger, called “The Atoms for Peace”, shows remarkable optical loops and tidal tails surrounding it (Dopita et al. 2002). This is the last system within the Toomre (1977) sequence of interacting galaxies. The star formation is strongly concentrated towards the nucleus and has a counterpart in the radio emission at 4.86 GHz. According to Mihos et al. (1993), the SFR had dropped in this object by two thirds from the time of coalescence, estimated to occur ≈1 Gyr ago.
Arp 222 – A post-merger galaxy is at a slightly more advanced stage of evolution than NGC 7252 (Brassington et al. 2007). The protrusions and plums observed in optical and X-ray emission indicate that the system has not relaxed to an elliptical galaxy yet. Our analysis of available VLA radio data of this system at 1.49 GHz provides the total emission from the central part of the system.
NGC 1700 – A protoelliptical galaxy possesses a counter-rotating stellar core and other symptoms that it formed through merging of two spiral galaxies of similar mass (Brassington et al. 2007). The best age estimate for the coalescence event is about 3 Gyr (Brown et al. 2000). No radio emission of this galaxy was detected in the NVSS survey, so only the upper limit of radio emission at 1.4 GHz could be estimated (Table 3).
3.9. Magnetic field strength and regularity
The radio emission detected by us for interacting galaxies is composed of nonthermal (synchrotron) and thermal (free-free) radiation. The nonthermal emission and its polarized component can be used to obtain total and regular (ordered) magnetic field strengths (Beck & Krause 2005, see Appendix A for details). A typical equipartition energy condition between cosmic rays and magnetic fields can be applied, especially as spatial resolution of the the analysed radio observations are as large as hundreds of parsecs. For all galaxies the total and polarized radio intensities were integrated over the galactic disks as outlined by the optical emission visible in optical B-images. We assumed a typical unprojected pathlength through the synchrotron emitting region of 1 kpc. However, for NGC 1700, which is perfectly an edge-on object (Table 1) without detectable radio emission, we adopted the synchrotron pathlength L of 2 kpc (see Appendix A).
The nonthermal spectral indexes and thermal fractions for NGC 2207/IC 2163, NGC 660, NGC 4038/9, and NGC 4254 were taken from the separation of radio emission components by Niklas et al. (1997), Chyży & Beck (2004), and Chyży et al. (2007b). For other objects, a typical nonthermal spectral index of 0.8 was used (Niklas et al. 1997), and the radio thermal emission was estimated from the FIR data (Surace et al. 2004; Sanders et al. 2003; Brassington et al. 2007; Bushouse et al. 1988; Moshir et al. 1990) in the following way. First, we derived global SFRs from galactic infrared luminosities at 60 and 100 μm, according to the empirical SFR indicator derived by Kennicutt (1998). They range from less than 1 M⊙ yr-1 (NGC 5426, ARP 222, NGC 1700) up to 150 M⊙ yr-1 (ARP 220), with uncertainties less than 25%. Next, we converted the obtained SFRs to the predicted radio thermal emission, according to the modelling of free-free radiation by Caplan & Deharveng (1986), see also Chyży et al. (2007b). The estimated thermal fractions from this method are about 0.10 at 4.86 GHz with uncertainties of about 0.02. Synchrotron emission of galaxies was obtained by subtraction of their radio thermal components from the total radio emission.
Magnetic field strength and regularity for interacting galaxies.
As a consistency test of the applied approaches to calculating galactic magnetic field strengths, we compared the two methods of estimating of thermal emission: from the FIR SFR indicator and from the separation of thermal and non-thermal radio emission. For example for a weakly interacting galaxy NGC 4254 for which magnetic properties are well known (Chyży 2008), the first method gives Btot = 14 ± 4 μG, Breg = 6 ± 2 μG. From the second method we have Btot = 15 ± 4 μG, Breg = 7 ± 2 μG. Therefore, both methods give consistent results that are well within estimated uncertainties. We also note that the magnetic field strength only weakly depends on the thermal fraction (Eq. (A.1) in Appendix A).
The derived strengths of the total and regular magnetic fields for all our interacting galaxies are given in Table 4. The presented uncertainties include uncertainties of estimated non-thermal radio brightness, a factor of 2 uncertainties in adopted proton-to-electron density ratio and pathlength L, and the uncertainty of 0.1 of applied nonthermal spectral indexes. The mean values of total magnetic field strength Btot obtained for the interacting objects range from 5−6 μG for post-mergers Arp 222 and NGC 1700 to 25−27 μG for ongoing mergers NGC 3256 and Arp 220 (Table 4). This spread may result from the diversity in properties of individual galaxies, as well as from the particular stages of their gravitational interactions (see the next section). The averaged total magnetic field strength for the whole sample is 14 ± 5 μG. Excluding the two lowest values for the post-mergers (Arp 222 and NGC 1700), which much differ from the rest of the sample, the mean strength rises to 15 ± 4 μG. Both the means are more than the typical average total field strength of 9 μG estimated for 74 bright spiral galaxies (Niklas 1995, Beck & Krause 2005). As the previous studies of magnetic fields have involved all morphological types of galaxies, the cited mean is likely increased by including of interacting objects. For instance, the average strength of total magnetic field for typical large spirals in our neighbourhood (the Galaxy and M 31) is 5−7 μG, which is significantly lower than for the interacting objects in our sample.
We also calculated the strength of regular magnetic field Breg and the field regularity Breg/Bran, which is a useful measure of relative production of regular and random magnetic fields (Table 4). In contrast to the total magnetic field, the strength of regular component is similar to those in the non-interacting spirals, which leads to a mean of 2.5−3.5 μG. The enhanced total field with relatively normal regular component results in a small field regularity (0.27 ± 0.09) in the interacting objects.
The local magnetic fields are strongest in the centres of galaxies and reach 48 μG in Arp 220 and 53 μG in NGC 3256. Similar values were also observed in the centres of most starbursting galaxies, as in M 82 (Klein et al. 1988). The regular field peaks in the regions of weak total radio intensities, far off the regions of intense star formation. For example, in the bridges of Taffy and Taffy2 galaxies, Breg reaches 11 ± 3 μG. This value was obtained for the nonthermal spectral index of 1.3 ± 0.1 approximated from the spectral index maps of Condon et al. (1993, 2002). Furthermore, we adopted a synchrotron pathlength of about 15 kpc corresponding to the width of the observed radio bridges (cf. Figs. 9 and 10). A similar strength of regular field was observed at the base of the eastern tidal tail in the Antennae system (Chyży & Beck 2004). Because in all such regions the total field is also strong, i.e. 16 ± 4 μG in the bridges of the Taffy and Taffy2 systems, the magnetic field can affect the local gas dynamics. Actually, in the bridge of the Taffy system, the magnetic energy of 10.2 × 10-12 erg cm-3 is much larger than the energy of thermal gas, which is 1.4 × 10-12 erg cm-3 (as estimated from the radio thermal emission at 4.86 GHz, assuming 104 K gas temperature, and the volume filling factor of 0.5). The turbulent velocity of H i gas of about 30 km s-1 suggested by Condon et al. (1993) results in the turbulent energy of ISM of 6.6 × 10-12 erg cm-3, again lower than the magnetic energy. Although the kinetic energy of H i blobs orbiting the system is about two orders of magnitude higher, locally magnetic fields can still affect the gas phase, directing the gas motion along the magnetic field lines. Similar conclusions are valid for the bridge between the Taffy2 galaxies.
4. Statistical analysis
It is believed that gravitational interactions between galaxies can induce star formation (see Struck 2006, for a review). On the other hand, star-forming activity is one of the main factors in determining dynamo processes and regulating random and regular magnetic fields in galaxies (e.g. Chyży 2008). We have shown that the interacting galaxies reveal various radio structures and show a range of magnetic field strength (Table 4). Therefore, we investigate how, statistically, magnetic fields and radio morphologies are connected to the SFR in the interacting objects. Having optical sizes of galaxies (corrected for galactic extinction and inclination, from HyperLeda), we are able to build similar relations for the surface densities of the SFRs (ΣSFR).
In order to relate the properties of radio emission and magnetic fields to different stages of gravitational interactions we introduce “the interaction stage parameter”, IS, which is simply a number indicating the particular stage of interaction and galaxy morphological distortion. Toomre (1977) arranged 11 ongoing mergers according to the rising strength of observed and modelled tidal interactions (see Introduction). We assigned them consecutive IS values from 1 to 11 (Table 1). The values 1−9 correspond to pre-merger stages. IS = 1 describes systems after the first galaxy encounter and with significant disk distortions (e.g. the Antennae and Taffy systems). Galaxies with stronger interactions, evolving gradually to coalescence, are NGC 6621/2 (IS = 5), NGC 520 (IS = 7), and NGC 3256 (IS = 9), all displaying strong and concentrated radio emission associated with the optically brightest region in the system. The nuclear coalescence corresponds to IS = 10 (Arp 220), and the young merger remnant to IS = 11 (e.g. NGC 7252). We supplemented the Toomre sequence with weakly interacting galaxies from our sample: we assign IS = −1 to objects before the first encounter (e.g. NGC 876/7) and IS = 0 to galaxies close to the (first) encounter (e.g. NGC 6907/8) when the tidal tails are launched (Sect. 3; Table 1). The other side of the sequence we expand with age-advanced mergers but still not relaxed as for Arp 222 (IS = 12, cf. Brassington et al. 2007). Our last object NGC 1700 is a pre-elliptical system (IS = 13) that nevertheless shows evidence that it was formed from spiral galaxies (Brassington et al. (2007). It is clear that the attributed values of IS parameter may be affected by different interaction geometries or properties of individual galaxies. However, to the first approximation, they provide a rough indicator of the evolutionary stage and “strength” of galaxy interaction.
4.1. Evolution of magnetic fields
 |
Fig. 12 The evolution of magnetic field strength in interacting galaxies. Mean magnetic field strengths are given for the whole galaxies (circles), centres (squares), and off-centre regions (asterisks). Arrows indicate upper limits of the field strength. Two special stages of interaction are denoted: the first galaxy encounter and the coalescence of the merger nuclei. The error bar for NGC 520 is shown. |
We explore the evolution of magnetic fields through the interaction stages of galaxies using the introduced IS parameter (Fig. 12). For the weakly interacting galaxies, the strength of magnetic field is almost constant (10−15 μG). However, we show for the first time that there is a distinct trend toward the increasing strength of magnetic field as the interaction advances towards the nuclear coalescence (up to 25 μG for Arp 220; IS = 10). A completely opposite trend is found at the later stages, i.e. for post-mergers, for which the strength of magnetic field decreases in a systematic manner. Neither radio emission nor magnetic fields are detected for the last galaxy in our sequence, which is a proto-elliptical object (NGC 1700). Similar trends for the whole galaxies are observed when magnetic field strength is calculated only for the central regions of objects (of about 6.5 kpc size) or outside of them in the galactic disks (Fig. 12).
The diverse trend found in magnetic field evolution seems to be connected with the star-forming activity in the interacting systems. This view is supported by the results of Georgakakis et al. (2000), who show for a similar merger sequence that the FIR luminosity to molecular hydrogen mass ratio (the star formation efficiency) clearly increases close to the nuclear coalescence and declines again after merging. The strongly interacting and merging galaxies typically have star formation efficiency about an order of magnitude higher than that of the isolated and weakly interacting galaxies. Georgakakis et al. also show that, during the merging, the enhancement of star formation is moderate within the disk, while strong in the nucleus. In accordance with that, we observe that the major enhancement of magnetic energy in galaxies in our sample also occurs in galactic centres. The field strength increases here by more than 170%, whereas within the disk the rise is less than 100% (Fig. 12). A rise in nuclear luminosities has also been found in optical (Laine et al. 2003) and NIR observations with the HST (Rossa et al. 2007).
The H i study of the Toomre merging sequence by Hibbard & van Gorkom (1996) indicated that the hydrogen gas is pushed out from galactic disks into tidal features as the merging process advances. Such features are not traced by synchrotron emission on our radio continuum maps. Moreover, the large velocity dispersion estimated from H i measurements in weakly interacting galaxies (e.g. NGC 2207, Sect. 3.1), likely caused by tidally induced turbulence or large-scale gas motions, are not associated with the observed radio features. Therefore, the star-forming activity must be the main energy source for the radio (synchrotron) emission and magnetic fields in merging galaxies. The revealed evolution of magnetic fields agrees with the scenario of formation of ellipticals from mergers (Toomre & Toomre 1972), because there is no detection of synchrotron emission from the elliptical galaxies to date, apart from the AGN phenomena (Sect. 1).
The evolution of magnetic fields through the interaction stages differs significantly from what is observed in the X-rays. We do not find any enhancement of magnetic field long after the nuclear coalescence, which is observed in the X-ray emission in the merging sequence explored by Brassington et al. (2007). Therefore, it seems that unlike with X-rays, there is no process connected to type I supernova that could re-create the magnetic field in the merger remnants, as was proposed to account for the X-ray observations (Sect. 1). Magnetic fields and cosmic rays require powerful type II supernova explosions for their generation (Beck et al. 1996). Therefore, our findings suggest that the main production of magnetic fields in colliding galaxies must terminate close to the coalescence, after which magnetic field diffuses or is kept at the level of the turbulent energy of ISM. In either case, for the radio frequencies considered in this paper, the synchrotron emission should fade in proto-elliptical (merged) galaxies after about 108 yr if there are no sources of CR energization. The fading synchrotron emission in post-merger systems is too weak to be detected using the currently available radiointerferometric data. New radio instrumentation operating at extremely low frequencies such as LOFAR could possibly detect the faint synchrotron emission from the old population of CR electrons, revealing such “relic” magnetic fields.
4.2. Magnetic fields versus star formation rate
 |
Fig. 13 Total magnetic field strengths (circles) versus local SFRs for the whole interacting galaxies a), their centres b), and off-centre regions c). The random and regular components of magnetic fields are also provided (squares and asterisks, respectively). An expected evolutionary track of interacting systems is also indicated. |
In Fig. 13a we show total magnetic field strength related to the ΣSFR for 22 galaxies for which radio emission could be determined (except for NGC 6908 and NGC 6622, see Sect. 3). We also plotted mean magnetic field strengths in the galactic centres (Fig. 13b) and off-centre regions (Fig. 13c). We found that the statistical relation for the entire galaxies is weak (the Spearman correlation coefficient ρ = 0.49) with an index of fitted power law α = 0.20 ± 0.02. The dependence is stronger in galactic centres (0.27 ± 0.03) and weaker outside them (0.14 ± 0.03). We notice that, within a wide range of the ΣSFR of 10-3−10-2 M⊙ yr-1 kpc-2, the magnetic field strength is actually spread over 10−20 μG without any discernible tendency. In fact, the determined slopes are established mainly thanks to the galaxies of weakest and of strongest ΣSFR, which are all members of particularly strongly interacting systems (IS ≥ 9).
We also constructed diagrams similar to Fig. 13 but with the global value of SFR. The slopes and correlations are statistically similar (e.g. α = 0.21 ± 0.02, ρ = 0.63 for the entire galaxies). This therefore seems to be a general phenomenon that magnetic fields are only weakly dependent on galactic star-forming activity, showing a wide spread of estimated strengths. The wider the range of considered SFRs, the better defined and stronger the influence on magnetic fields. This result can explain the former findings of Hummel (1981) that the radio continuum properties of interacting galaxies differ from those for the isolated objects only in the central parts of galaxies, and not in their disks. His analysis ignores, however, all the advanced mergers that we included in our sample (NGC 3256, Arp 220, Arp 222, NGC 1700). Similarly, as shown by Kennicutt et al. (1987), only particularly strongly interacting galaxies show a distinct enhancement in star formation, as appraised from the Hα and FIR emission.
No mutual relation is found between B and SFR (Fig. 13), as observed for B and IS (Fig. 12). It is because both the advanced mergers and the weakly interacting galaxies have low SFRs, and they are undistinguishable in Fig. 13. Only when the magnetic field is set against the stage of interaction (Fig. 12), is the full evolution of B revealed. We plot in Fig. 13 an evolutionary track of exemplary interacting system as based on our results.
There is a hint of negative correlation between the regular component of magnetic field and the ΣSFR for entire galaxies, ρ = −0.55, and the power-law fit is −0.25 ± 0.07 (Fig. 13a). The same trend was more distinct for the magnetic field regularity of individual regions of the weakly interacting galaxy NGC 4254 (Chyży et al. 2007b). Magnetic field tangling in active star-forming regions and production of random magnetic fields by the local-scale dynamo process (Brandenburg & Subramanian 2005) result in a lower field regularity. This may also be the case over the galactic scales in the analysed interacting objects.
4.3. Asymmetries
Gravitational interactions are able to severely distort galactic disks (Sect. 1). Here, we investigate how they modify distributions of radio total and polarized emission at 4.86 GHz. First, we divided each galaxy into two parts by defining an axis in the N-S direction that crosses the galactic centre. We integrated the total radio intensities over the obtained galactic halves (T1, T2) and determined the ratio aT = T1/(T1 + T2), with a convention of aT ≥ 0.5. Next we rotated the radio map by 30° around the galactic optical centre and determined aT once again. The whole procedure was repeated with the step in the rotation of 30°, until the map involved all orientations (six positions). Finally, we determined the galaxy radio asymmetry AT as the highest of all aT values. We also calculated the difference φT between the original position angle of the major axis of the galaxy (Table 1) and the position angle of the major axis after rotation, which gave the asymmetry AT. A similar procedure was applied to the radio polarization map, which likewise yielded the polarization asymmetry AP and the offset angle of the polarization asymmetry axis φP. To estimate the accuracy of obtained values of asymmetry parameters, we rotated the axes which gave asymmetries AT and AP by ±15°. The uncertainties approximated as deviations from the original asymmetry parameters are small, typically less than 5%. All the above calculations were performed for those interacting galaxies for which total and polarized radio emissions were resolved and not too much affected by overlapping with a companion galaxy (Fig. 14).
 |
Fig. 14 Asymmetry parameters for total (AT; squares) and polarized radio emission (circles; AP) versus global SFR for interacting galaxies. The values of offset angles [φT](φP) for asymmetry axes in total and polarized emission are given in parentheses. Typical uncertainties of asymmetry parameters are less than 5%. |
The obtained wide range of values of offset angles (φT, φP, presented in Fig. 14) indicates that the asymmetries in total and polarized emission are not correlated with the apparent orientations of galactic disks. However, offset angles are within 60° from each other. The observed asymmetries are therefore not caused by projection effects and must be physically connected with galaxy morphologies as modified by the interaction process.
Among the analysed galaxies there is a trend that the asymmetry in distribution of polarized emission (mean of 0.75) is stronger than in the total radio intensity (mean of 0.64; Fig. 14). The ordered magnetic field is therefore much more sensitive to morphological distortions than the total field. Even in the weakly interacting galaxies (e.g. NGC 876/7), the polarized emission, as well as the orientation of magnetic field B-vectors (cf. Sect. 3), are sensitive to global galactic distortions and anomalous gas flows. We also notice that the higher the distortion in the total emission (AT), the greater is the difference between the asymmetry in total and polarized emission (AP).
There is no obvious dependence of the strength of asymmetries on global SFRs for galaxies (ρ = −0.35; −0.15 for total and polarized radio emission, see also Fig. 14). We also constructed a diagram similar to Fig. 14 but with the ΣSFR instead of global SFR. Also in this case the results are similar (ρ = −0.03, +0.12). It seems that differences in the gas content and mass of individual galaxies may blur the effect of possible enhancement of the SFR or ΣSFR by tidal interactions.
However, asymmetries are different before and after the first galactic encounter (Fig. 15). For all the weakly interacting objects (IS = −1; Table 1), the asymmetries are small with the mean values AT = 0.60 ± 0.03 and AP = 0.65 ± 0.07. For all the objects after the first encounter (IS = +1), the asymmetries are systematically stronger with their means AT = 0.68 ± 0.03 and AP = 0.87 ± 0.11. In polarization they attain the highest measured values (AP > 0.85 for Taffy, Taffy2, and NGC 4038). The exception from this behaviour is the galaxy NGC 6907 (IS = 0; Fig. 15), which is close to the moment of collision with NGC 6908 (Sect. 3). However, otherwise than in the other galaxy pairs, this system is likely a minor merger and apparently the low-mass intruder (NGC 6908) is not able to distort a much more massive galaxy. We thus conclude that the asymmetries visible in the radio emission in general only weakly depend on the global or local SFRs, while they increase (especially in the polarization) with advancing of interaction. As a result, the asymmetry in the radio polarized emission could be yet another indicator of an ongoing merging process.
 |
Fig. 15 Asymmetry parameters for total (AT; squares) and polarized radio emission (circles; AP) versus the interaction stage IS. Typical uncertainties of asymmetry parameters are less than 5%. |
4.4. Radio-infrared relation
The process of tidal interaction and induced star formation may cause an enhancement in the infrared luminosity. This may lead to formation of strong infrared emitters as LIRG or ULIRG objects that are believed to be associated with colliding galaxies (Sect. 1). In order to investigate whether radio emission also is correspondingly enhanced in such cases, we constructed a radio-FIR relation for our interacting systems and compared it to the one determined for a sample of normal galaxies of different Hubble types (Fig. 16). We used the radio surface brightness of interacting objects estimated from our maps at 4.86 GHz and the infrared surface brightness at 60 μm derived from Surace et al. (2004), Sanders et al. (2003), Bushouse et al. (1988), and Moshir et al. (1990). For galaxies with only 1.4 GHz flux available we scaled it to 4.86 GHz assuming a typical spectral index of 0.8. We did not include two of the weakest radio objects Arp 222 and NGC 1700 for which 60 μm infrared data are unavailable. Typical uncertainties of obtained values are indicated in Fig. 16 and were derived from uncertainties of radio fluxes (Tables 2 and 3) and 60 μm fluxes (given in the mentioned FIR catalogues). For the sample of normal galaxies radio data at 4.85 GHz were taken from Gioia et al. (1982) and Chyży et al. (2007a), whereas 60 μm data came from Helou & Walker (1995) and Moshir et al. (1990).
Our orthogonal fit to the radio-FIR relation for the sample of normal galaxies gives a power-law index of 0.98 ± 0.04. The interacting galaxies follow this relation (Fig. 16) and are located in the group of the strongest radio and FIR emitters. We note, however, that the brightest galaxy in our sample (Arp 220) is shifted slightly down from the main trend indicating possible flattening of the relation for relatively young mergers. A more numerous sample is needed to confirm this hint. Recently we have shown that low-mass dwarf galaxies, which are by orders of magnitude weaker optical and radio emitters than the interacting objects, also follow a similar power-law relation, with a slope of 0.91 ± 0.08 obtained for 2.64 GHz radio data (Chyży et al. 2011).
In fact, the tidally induced intense star formation and morphological distortion in the studied interacting galaxies do not seem to change processes responsible for radio-FIR correlation. This is quite interesting, as some of those systems are in the process of evolving and transformation towards S0 or elliptical merger remnants. The large-scale shocks, galactic large-scale, or small-scale dynamos, and processes mutually transforming magnetic field components (e.g. by compression and shearing, Sect. 4.2) therefore result in the production of magnetic energy and cosmic rays that are still well-balanced by production of thermal energy and dust radiation.
 |
Fig. 16 The radio–FIR correlation diagram for interacting (squares) and normal galaxies of different Hubble types (asterisks). The surface brightness at 4.86 GHz and at 60 μm (Jy/◻′) are used (see text for details). The solid line is an orthogonal fit to normal galaxies, and dashed lines represent simple X vs. Y and Y vs. X regressions. Error bars for interacting galaxies are marked. |
Interestingly enough, according to our study, the deviations of the Taffy and Taffy2 galaxies from the main trend of the radio-FIR relation at 4.86 GHz are small, 0.3 dex, and comparable to other objects from our sample (Fig. 16). However, according to Condon et al. (1993, 2002), these galaxies are twice as radio-loud as they ought to be if following the radio-FIR relation constructed at 1.4 GHz. The difference between 4.86 and 1.4 GHz is probably due to a more extended emission in the bridge at 1.4 GHz and the steep radio spectral index (up to 1.3−1.4). The reason for such strong radio emission at 1.4 GHz is not clear. According to Condon, the observed radio excess may come from the CRs electrons leaked from the galactic disks and trapped in enhanced (stretched) magnetic fields in the bridge between galaxies.
However, Lisenfeld & Voelk (2010) argue that in the Taffy systems, the kinetic energy of colliding gas probably brought about large-scale shock waves that accelerated CRs, as well as enhanced radio emission in the bridges. As this is not related to star formation, a deviation from the radio-FIR relation results. They assume in their modelling that the shocks in the Taffy disks correspond to the one in the middle-age supernova remnants and therefore could be described by the Sedov phase. However, according to our analysis of polarization data in the Taffy system (Sect. 1), the magnetic field in the bridge is well-ordered and aligned with the direction of gas flows between disks. Thus the field configuration clearly resembles a very young supernova with magnetic field vectors aligned with gaseous outflows, well before the Sedov phase. As a result, the configuration of ordered magnetic fields indicates that the physics involved in explaining the Taffy bridge might not be applicable here. Alternatively, we deal here with some other processes of field ordering and compression, which work differently than in the supernova remnant. Sensitive observations of gamma rays could independently assess the CR population, indicate their origin, and account for the strong radio emission in the bridge. In the Taffy2 system situation is different because magnetic field is not aligned with the bridge (Fig. 10). This may indicate a better correspondence with the Lisenfeld & Voelk model.
4.5. The impact of merger’s magnetic fields
Gravitational forces could play an important role in generation of magnetic field in the early-universe. If seed magnetic fields were produced by, e.g., Biermann battery or Weibel instability then small-scale dynamo during gravitational collapse of galaxies and accretion driven turbulence could strongly enhance the seed field (Schleicher et al. 2010). Further evolution of galaxies could build up stronger, galactic-scale magnetic fields by small and large scale dynamos as discussed by Arshakian et al. (2009). Gravitational forces during galaxy interactions and galaxy mergers could also play an important role in the magnetization of IGM. Although the strongly interacting objects represent just a small fraction of galaxies in the local Universe, <300 interacting objects within 50 Mpc distance according to the Vorontsov-Velyaminov et al. (2001) catalogue, they may have dominated the epoch of massive galaxy formation in the early Universe (Conselice 2006). Such galaxies are able to redistribute magnetic fields in IGM along tidal tails or bridges, as we in fact observe, e.g., in the Antennae and Taffy galaxies (Sect. 3). The lower limit on IGM magnetic fields of 5 × 10-15 μG was constrained by Tavecchio et al. (2010) based on analysis of TeV and GeV emission from blazars. Recent analysis of FERMI-LAT observations of blazars and the absence of their TEV envelopes can suggest that extragalactic magnetic fields must fill IGM with a large volume factor of ≈60% (Dolag et al. 2011). If such magnetic fields are not primordial, then they must have been redistributed from local sources, like colliding galaxies.
To address the idea of magnetization of IGM by interacting objects, we approximate the zone around these galaxies that might be filled with magnetic fields simply by the largest extent of their observed H i envelopes. The neutral hydrogen of colliding galaxies often reveals large protrusions that are not optically visible (Hibbard & van Gorkom 1996). If such gas is also accompanied by its partly ionized component, then the frozen magnetic field can be advected with gas flows and brought out from galactic disks. According to the collected literature data (Table 1), we find that such outflows are up to about 200 kpc in size for the most disrupted objects in our sample (e.g. Arp 220). This value is compatible with the results of numerical simulations of high-redshift mergers (Bournaud et al. 2011). The tidal interactions (estimated to operate within about 200 kpc) are therefore not sufficient to seed vast volumes of IGM with magnetic fields, as required by the Dolag et al. conclusion. Either unknown transport processes redistribute magnetic fields of distant mergers out of expected H i envelopes, or the proposed magnetization of space has a different origin. Even so, interactions can efficiently magnetize the merger surroundings. This could explain relatively strong magnetic fields (≈10 μG) found around host galaxies of quasars with Mg II absorption systems up to redshift z = 1.3 (Bernet et al. 2008). Chyży et al. (2011) suggest that massive galaxies in the redshift z = 3−5 could have magnetized IGM by supernova explosions and galactic winds to the extent of ≈200−500 kpc. The process of strong gravitational interactions and associated magnetized outflows thus exerts a similar impact on IGM. New observational methods, such as a rotation measure synthesis, applied to background sources shining through merger remnants, could reveal such magnetized cocoons around mergers. New instrumentation such as the EVLA, LOFAR, and SKA could be used for such detection experiments to confirm these predictions.
Deflection angle of UHECR in a colliding galaxy system.
A vital issue in high-energy astrophysics is to identify sites of origin of UHECRs. There may be problems arising from deflection of UHECR trajectories by intergalactic magnetic fields (Yoshiguchi et al. 2003; Neronov & Semikoz 2009; Ryu et al. 2010). Most interacting galaxies from our sample are within 100 Mpc distance and their spread-out magnetic fields could in principle affect propagation of UHECR on their path to the Earth. To estimate a deflection angle δ between the incoming direction of UHECR and the sky position of their sources, we follow the approach of Neronov & Semikoz (2009), assuming that UHECR protons with energy of 1020 eV propagate through a magnetized volume of pathlength LB. In the case of regular field, its strength Breg influences the deflection angle, while in the case of turbulent field, its strength Bran as well as its coherence length LBC have to be known. We divide our estimations into those for disks of interacting galaxies, for strongly magnetized outflows (as bridges or tidal tails), and for envelopes of merging galaxies filled with H i gas and spread out magnetic fields. We take LBC = 50 pc for galactic disks (a commonly adopted value) and the scaled values for the bridges and haloes (Table 5).
We obtained the largest deflections of 23° for the protrusions from colliding galaxies filled with the regular field such as in the Taffy system (Table 5). In the case of galactic disks with, e.g., regular magnetic fields stretched along spiral arms (like in the weakly interacting NGC 2207, Sect. 3) the deflection angle is also large (16°). The more disrupted (random) fields are here less important (δ ≈ 3°). The probability of an individual UHECR particle to cross the merger and deflect its way to the Earth is very low, <10-6, taking all 300 interacting galaxies into account within 50 Mpc distance, and 200 kpc size of their magnetized haloes. However, large-scale shocks in colliding galaxies and centres of merging systems were also proposed as possible sources of UHECRs (Bhattacharjee & Sigl 2000; Giller et al. 2003; Biermann et al. 2009). If interacting galaxies generate some UHECRs by large-scale shocks or AGNs within them, their magnetic fields would severely deflect their trajectories (up to ≈23°). Propagation of UHECRs through the disk or magnetized outflows (bridges, tidal tails) would make it very difficult to properly associate observed UHECRs with the sites of their origin.
We note that the magnetized halo around mergers, however large in extent, would only marginally impact the UHECR propagation (deflection up to about 1°), owing to dispersed, weak magnetic fields (Table 5). The propagation of protons through the Galaxy would also result in a small deflection of up to about 1° (for Bran ≈ 4 μG).
5. Summary and conclusions
We studied the influence of gravitational interactions on the distribution of radio emission and the properties of magnetic fields in galaxies. We perused archival radio data from the VLA at 4.86 GHz and 1.4 GHz for a sample of 24 galaxies in 16 interacting systems. Different stages of interaction were approximately described by the interaction stage (IS) parameter (Sect. 4). The main conclusions are as follows.
-
The estimated total magnetic field strengths are from5 μG (ARP 222) to 25−27 μG (NGC 3256, ARP 220), with a mean of 14 ± 5 μG, greater than for bright non-interacting galaxies. The mean field regularity of 0.27 ± 0.09 is less than for typical spirals, which indicates enhanced production of random magnetic fields in the interacting objects.
-
Detailed analysis of NGC 2207/IC 2163 reveals a region of enhanced radio total and polarized emission in the eastern part of NGC 2207, which can suggest a supply of CR electrons originating in IC 2163. Our studies of polarized properties of this system contradict the earlier hypothesis that the enhanced radio emission in this region is due to compression of magnetic fields (Elmegreen et al. 1995a).
-
The structure of magnetic field B-vectors in the polar-ring galaxy NGC 660 resembles an X-shape pattern, typical of late-type edge-on galaxies, which challenges some earlier suggestions that this is a post-merger system.
-
Even in weakly interacting galaxies, the polarized emission and the orientation of magnetic field B-vectors are very sensitive tools for revealing global galactic distortions (Taffy galaxies) or the direction of gas flow in tidally stretched spiral arms and tidal tails (NGC 2207, NCG 6907, NGC 4038).
-
We built a tentative scenario of magnetic field evolution in interacting galaxies. For weak interactions the strength of magnetic field is almost constant (10−15 μG), then it increases up to 2 × with advancing of interaction to later stages, and decreases again, down to the limiting value of 5−6 μG, for old post-mergers. We suggest that the main production of magnetic fields in colliding galaxies must terminate close to the nuclear coalescence, after which magnetic field diffuses or is kept at the level of turbulent energy of ISM. The revealed evolution of magnetic fields agrees with the scenario of formation of ellipticals from mergers (Toomre & Toomre 1972).
-
Magnetic field strength is weakly regulated by the galactic star-forming activity (e.g. SFR), showing a wide spread of estimated strength values (with a slope α = 0.21 ± 0.02 and correlation ρ = 0.63). The dependence is stronger in galactic centres and weaker outside. There is also a hint that the regular field is anticorrelated with SFR (ρ = −0.55).
-
Asymmetry in distribution of polarized emission is stronger (AP = 0.75) than in total radio intensity (AT = 0.64), which can indicate that the regular component of magnetic fields is much more sensitive to morphological distortions induced by tidal interactions than the random magnetic field. This means that, the asymmetry in the radio polarized emission could be yet another indicator of an ongoing merging process. The asymmetries visible in the radio emission do not statistically depend on the global or local SFRs, while they increase (especially in the polarization) with advancing interaction.
-
The constructed radio-FIR relation for interacting and non-interacting galaxies shows that the tidally induced intense star formation, morphological distortions, and processes mutually transforming magnetic field components (e.g. by compression and shearing) still lead to producing magnetic energy and cosmic rays that are balanced by the production of thermal energy and dust radiation. The interacting galaxies constitute the group of statistically strongest radio and FIR emitters. We also argued that the configuration of ordered magnetic fields in the bridge of the Taffy system indicates that the modelling of Lisenfeld & Voelk (2010), adopted to account for the strong radio emission in the bridge, might not be applicable here.
-
The process of strong gravitational interactions can efficiently magnetize the merger surroundings (likely up to about 200 kpc), exerting a similar impact on IGM to its magnetization by supernova explosions and galactic winds. However, tidal interactions are likely insufficient to fill IGM with magnetic fields with a large volume filling factor of ≈60% as recently suggested by Dolag et al. (2011). If interacting galaxies generate some UHECRs by large-scale shocks or AGNs, their propagation through the disk or magnetized outflows (bridges or tidal tails) can deflect them up to 23° and make association of observed UHECRs with the sites of their origin less obvious.
Among the interacting systems, those at the final stages of merging as well as the post-merging systems (as elliptical galaxies) are the least studied ones with respect to magnetic field evolution. After the interaction-induced starburst declines, the production of cosmic ray electrons ceases and cannot further enlighten magnetic fields (Sect. 4.1). Such fields may still exist in the mergers, before they disperse because of turbulent diffusivity, but could only be discovered by the Faraday rotation methods applied to the background sources. Thus there is a need for very high-resolution and sensitive radio spectropolarimetric data from interferometers, not yet available. Future EVLA, LOFAR and SKA instrumentation could reveal for the first time such fading or relic magnetic fields, if they are actually present in the post-merging systems.
Acknowledgments
We thank an anonymous referee for helpful comments and suggestions. This work was supported by the Polish Ministry of Science and Higher Education, grant 3033/B/H03/2008/35. We acknowledge the use of the HyperLeda (http://leda.univ-lyon1.fr) and NED (http://nedwww.ipac.caltech.edu) databases.
References
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., & Krause, M. 2005, AN, 326, 414 [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bernet, M. L., Miniati, F., Lilly, S. J., et al. 2008, Nature, 454, 302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bhattacharjee, P., & Sigl, G. 2000, Phys. Rep., 327, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, P. L., Becker, J. K., Caramete, L., et al. 2009, Nucl. Phys. B Proc. Suppl., 190, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Blackman, C. P. 1982, MNRAS, 200, 407 [NASA ADS] [Google Scholar]
- Bournaud, F., & Combes, F. 2003, A&A, 401, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Chapon, D., Teyssier, R., et al. 2011, ApJ, 730, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brassington, N. J., Ponman, T. J., & Read, A. M. 2007, MNRAS, 377, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, R., Heald, G., & Beck, R. 2010, A&A, 514, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, R. J. N., Forbes, D. A., Kissler-Patig, M., & Brodie, J. P. 2000, MNRAS, 317, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Bushouse, H. A., Lamb, S. A., & Werner, M. W. 1988, ApJ, 335, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Caplan, J., & Deharveng, L. 1986, A&A, 155, 297 [NASA ADS] [Google Scholar]
- Chyży, K. T. 2008, A&A, 482, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., & Beck, R. 2004, A&A, 417, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Bomans, D. J., Krause, M., et al. 2007a, A&A, 462, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Ehle, M., & Beck, R. 2007b, A&A, 474, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Weżgowiec, M., Beck, R., & Bomans, D. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J. 1983, ApJS, 53, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1987, ApJS, 65, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Condon, M. A., Gisler, G., & Puschell, J. J. 1982, ApJ, 252, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Helou, G., Sanders, D. B., & Soifer, B. T. 1993, AJ, 105, 1730 [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Helou, G., & Jarrett, T. H. 2002, AJ, 123, 1881 [Google Scholar]
- Conselice, C. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies (RC3) [Google Scholar]
- Dolag, K., Kachelriess, M., Ostapchenko, S., & Tomas, R. 2011, ApJ, 727, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Pereira, M., Kewley, L. J., et al. 2002, ApJS, 143, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Kaufman, M., Brinks, E., Elmegreen, B. G., & Sundin, M. 1995a, ApJ, 453, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Sundin, M., Kaufman, M., Brinks, E., & Elmegreen, D. M. 1995b, ApJ, 453, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Kaufman, M., Elmegreen, B. G., et al. 2001, AJ, 121, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Kaufman, M., et al. 2006, ApJ, 642, 158 [NASA ADS] [CrossRef] [Google Scholar]
- English, J., Norris, R. P., Freeman, K. C., & Booth, R. S. 2003, AJ, 125, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Fuentes-Carrera, I., Rosado, M., Amram, P., et al. 2004, A&A, 415, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, Y., Zhu, M., & Seaquist, E. R. 2003, AJ, 126, 2171 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Forbes, D. A., & Norris, R. P. 2000, MNRAS, 318, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Giller, M., Michalak, W., & Smialkowski, W. 2003, in 28th International Cosmic Ray Conference, 727 [Google Scholar]
- Gioia, I. M., Gregorini, L., & Klein, U. 1982, A&A, 116, 164 [NASA ADS] [Google Scholar]
- Hattori, T., Yoshida, M., Ohtani, H., et al. 2004, AJ, 127, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., & Walker, D. W. 1995, IRAS Small Scale Structure Catalog [Google Scholar]
- Hibbard, J. E., & van Gorkom, J. H. 1996, AJ, 111, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, E. 1981, A&A, 96, 111 [NASA ADS] [Google Scholar]
- Hummel, E., van der Hulst, J. M., Kennicutt, R. C., & Keel, W. C. 1990, A&A, 236, 333 [NASA ADS] [Google Scholar]
- Johnston-Hollitt, M., Hollitt, C. P., & Ekers, R. D. 2004, The Magnetized Interstellar Medium, ed. B. Uyaniker et al. (Katlenburg: Copernicus), 13 [Google Scholar]
- Kennicutt, R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt Jr., R. C., Keel, W. C., van der Hulst, J. M., Hummel, E., & Roettiger, K. A. 1987, AJ, 93, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, U., Wielebinski, R., & Morsi, H. W. 1988, A&A, 190, 41 [NASA ADS] [Google Scholar]
- Kotarba, H., Karl, S. J., Naab, T., et al. 2010, ApJ, 716, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Laine, S., van der Marel, R. P., Rossa, J., et al. 2003, ApJ, 126, 2717 [Google Scholar]
- Lisenfeld, U., & Voelk, H. J. 2010, A&A, 524, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madore, B. F., Gil de Paz, A., & Pevunova, O. 2007, AJ, 134, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. Ch., Bothun, G. D., & Richstone, D. O. 1993, ApJ, 418, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Moriondo, G., Baffa, C., Casertano, S., et al. 1999, A&AS, 137, 101 [Google Scholar]
- Moshir, M., Copan, G., Conrow, T., et al. 1990, IRAS Faint Source Catalogue, version 2.0, Vizier Online Data Catalog, 2156 [Google Scholar]
- Neronov, A., & Semikoz, D. V. 2009, Phys. Rev. D, 80, 123012 [NASA ADS] [CrossRef] [Google Scholar]
- Niklas, S. 1995, Ph.D. Thesis, University of Bonn [Google Scholar]
- Niklas, S., Klein, U., & Wielebinski, R. 1997, A&A, 322, 19 [NASA ADS] [Google Scholar]
- Rossa, J., Laine, S., van der Marel, R. P., et al. 2007, ApJ, 134, 2124 [Google Scholar]
- Ryu, D., Das, S., & Kang, A. 2010, ApJ, 710, 1422 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., et al. 2003, AJ, 126, 1607 [Google Scholar]
- Scarano, S., Madsen, F. R. H., Roy, N., & Lepine, J. R. D. 2008, MNRAS, 386, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., Banerjee, R., Sur, S., et al. 2010, A&A, 522, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Segalovitz, A., Shane, W. W., & de Bruyn, A. G. 1976, Nature, 264, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. J., Giroux, M. L., Struck, C., & Hancock, M. 2010, ApJ, 139, 1212 [Google Scholar]
- Stanford, S. A., & Balcells, M. 1991, ApJ, 370, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Struck, C. 1999, Phys. Rep., 321, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Struck, C. 2006, in Astrophysics Update, ed. J. W. Mason (Chichester: Springer, Praxis), 2, 115 [Google Scholar]
- Surace, J. A., Sanders, D. B., & Mazzarella, J. M. 2004, AJ, 127, 3235 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Foschini, L., et al. 2010, MNRAS, 406, L70 [NASA ADS] [Google Scholar]
- Toomre, A. 1977, in Evolution of Galaxies and Stellar Populations, Proceedings of a Conference at Yale University, May 19−21, ed. B. M. Tinsley, & R. B. Larson (New Haven: Yale University Observatory), 401 [Google Scholar]
- Toomre, A. 1981, in The structure and evolution of normal galaxies (Cambridge University Press), 111 [Google Scholar]
- Toomre, A., & Toomre, J. 1972, ApJ, 178, 623 [NASA ADS] [CrossRef] [Google Scholar]
- van Driel, W., Combes, F., & Casoli, F. 1995, AJ, 109, 942 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorontsov-Velyaminov, B. A., Noskova, R. I., & Arkhipova, V. P. 2001, Astron. Astrophys. Trans., 20, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshiguchi, H., Nagataki, S., & Sato, K. 2003, ApJ, 592, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, M., Gao, Y., Seaquist, E. R., et al. 2007, AJ, 134, 118 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Derivation of magnetic field strengths
The strength of the total Btot and
regular Breg magnetic field can be estimated using radio
polarimetric observations from the total synchrotron
intensity In and its degree of linear
polarization Pnth. After taking the
equipartition between the energy densities of the magnetic field and cosmic rays into
account, the total magnetic field is given by (Beck & Krause 2005) ![\appendix \setcounter{section}{1} \begin{equation} B_{\rm tot} = \left[\frac{4\pi(2\alpha_n+1)(K_0+1)I_{n}E_{\rm p}^{1-2\alpha_n}(\frac{\nu}{2c_1})^{\alpha_n}}{(2\alpha_n-1)c_2\alpha_nLc_3}\right]^{1\over{\alpha_n+3}} \label{e:B} \end{equation}](/articles/aa/full_html/2011/09/aa16092-10/aa16092-10-eq226.png) (A.1)where
K0 is the ratio of proton to electron number densities,
αn the mean synchrotron spectral index,
L the pathlength through the synchrotron emitting medium,
Ep the rest energy of the proton, and
(A.1)where
K0 is the ratio of proton to electron number densities,
αn the mean synchrotron spectral index,
L the pathlength through the synchrotron emitting medium,
Ep the rest energy of the proton, and
![\appendix \setcounter{section}{1} \begin{eqnarray} && c_1 = \frac{3e}{4\pi m_{\rm e}^3c^5} = 6.2648 \times 10^{18}~{\rm erg}^{-2}~{\rm s}^{-1}~{\rm G}^{-1}, \\ && c_2(\alpha_n) = {1\over4}c_3 \frac{(\alpha_n+{5\over3})}{(\alpha_n+1)} \Gamma\left[{(3\alpha_n+1)\over6}\right]\times\Gamma\left[{(3\alpha_n+5)\over6}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2011/09/aa16092-10/aa16092-10-eq231.png) \arraycolsep1.75ptConstants
c2 and c3 are geometrical
corrections that depend on magnetic field orientation. For a region where the field is
totally regular and has a constant inclination i with respect to the sky
plane,
c3 = (cosi)αn+1.
For a completely turbulent field,
c3 = (2/3)αn+1)/2.
If the synchrotron intensity is averaged over a large volume, such as the whole galaxy,
the value of c3 has to be replaced by its average over all
occurring values of i. For instance, the strength of the mean regular
magnetic field in the galactic disk can be obtained from the estimated nonthermal degree
of polarization (Segalovitz et al. 1976):
\arraycolsep1.75ptConstants
c2 and c3 are geometrical
corrections that depend on magnetic field orientation. For a region where the field is
totally regular and has a constant inclination i with respect to the sky
plane,
c3 = (cosi)αn+1.
For a completely turbulent field,
c3 = (2/3)αn+1)/2.
If the synchrotron intensity is averaged over a large volume, such as the whole galaxy,
the value of c3 has to be replaced by its average over all
occurring values of i. For instance, the strength of the mean regular
magnetic field in the galactic disk can be obtained from the estimated nonthermal degree
of polarization (Segalovitz et al. 1976):
![\appendix \setcounter{section}{1} \begin{equation} P_{n{\rm th}} = \left(\frac{3\gamma+3}{3\gamma+7}\right)\times \left[1+\frac{(1-q)\pi^{1\over2}\Gamma[(\gamma+5)/4]}{2q\Gamma[(\gamma+7)/4]F(i)}\right]^{-1}, \end{equation}](/articles/aa/full_html/2011/09/aa16092-10/aa16092-10-eq237.png) (A.4)where
(A.4)where
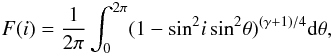 (A.5)q1/(1 + αn) = Breg/Bturb,
θ is the azimuthal angle, and Bturb the
turbulent component of the magnetic field.
(A.5)q1/(1 + αn) = Breg/Bturb,
θ is the azimuthal angle, and Bturb the
turbulent component of the magnetic field.
We assume K0 ≈ 100 in Eq. (A.1), which is consistent with acceleration of cosmic rays in supernova remnants and with the local Galactic cosmic ray data. For synchrotron sources, which have a volume filling factor the pathlength through the source L has to be replaced by L × f. However, the equipartition magnetic field strength only weakly depends on f e.g. its decrease from 1 to 0.8 results in the increase of field strength by less than 6%.
All Tables
All Figures
 |
Fig. 1 The total-power contours and B-vectors of polarized intensity of NGC 2207/IC 2163 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150) × 40.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 166.7 μJy/beam. The map resolution is 27′′ × 27′′ HPBW. |
| In the text | |
 |
Fig. 2 The contours of polarized intensity and B-vectors of polarization degree of NGC 2207/IC 2163 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12, 20, 35) × 21.2 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 10%. The map resolution is 27′′ × 27′′ HPBW. |
| In the text | |
 |
Fig. 3 The total power contours and B-vectors of polarized intensity of NGC 5426/NGC 5427 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250) × 23.3 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 83.3 μJy/beam. The map resolution is 22′′ × 22′′ HPBW. |
| In the text | |
 |
Fig. 4 The contours of polarized intensity and B-vectors of polarization degree of NGC 5426/NGC 5427 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12) × 14.9 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 17%. The map resolution is 22′′ × 22′′ HPBW. |
| In the text | |
 |
Fig. 5 The total power contours and B-vectors of polarized intensity of NGC 876/NGC 877 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250) × 16.5 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 83.3 μJy/beam. The map resolution is 18′′ × 18′′ HPBW. |
| In the text | |
 |
Fig. 6 The contours of polarized intensity and B-vectors of polarization degree of NGC 876/NGC 877 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8) × 14.0 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 14%. The map resolution is 18′′ × 18′′ HPBW. |
| In the text | |
 |
Fig. 7 The total power contours and B-vectors of polarized intensity of NGC 6907/NGC 6908 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250, 400) × 32.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 125.0 μJy/beam. The map resolution is 30′′ × 30′′ HPBW. |
| In the text | |
 |
Fig. 8 The contours of polarized intensity and B-vectors of polarization degree of NGC 6907/NGC 6908 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12) × 23.3 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 8%. The map resolution is 30′′ × 30′′ HPBW. |
| In the text | |
 |
Fig. 9 The total power contours and B-vectors of polarized intensity of the Taffy (UGC 12914/UGC 12915) at 4.86 GHz superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250, 400) × 17.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 71.4 μJy/beam. The map resolution is 16′′ × 16′′ HPBW. |
| In the text | |
 |
Fig. 10 The total power contours and B-vectors of polarized intensity of the Taffy2 (UGC 813/UGC 816) at 4.86 GHz superimposed on the DSS blue image. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150) × 23.0 μJy/beam. A vector of 10′′ length corresponds to the polarized intensity of 69.4 μJy/beam. The map resolution is 15′′ × 15′′ HPBW. |
| In the text | |
 |
Fig. 11 a) The total power contours of NGC 660 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. A large warped ring in the NS direction is visible. The contour levels are (−3, 3, 5, 8, 12, 20, 35, 80, 150, 250, 400, 700, 1500, 4000) × 26.4 μJy/beam. b) The total power contours and B-vectors of polarized intensity of the disk of NGC 660 superimposed on DSS blue image. The contour levels are the same as for a). A vector of 10′′ length corresponds to the polarized intensity of 100.0 μJy/beam. c) The contours of polarized intensity and B-vectors of polarization degree of the disk of NGC 660 at 4.86 GHz (natural weighting) superimposed on the DSS blue image. The contour levels are (3, 5, 8, 12, 20, 35) × 13.4 μJy/beam. A vector of 10′′ length corresponds to the polarization degree of 11%. The maps resolution is 18′′ × 18′′ HPBW. |
| In the text | |
 |
Fig. 12 The evolution of magnetic field strength in interacting galaxies. Mean magnetic field strengths are given for the whole galaxies (circles), centres (squares), and off-centre regions (asterisks). Arrows indicate upper limits of the field strength. Two special stages of interaction are denoted: the first galaxy encounter and the coalescence of the merger nuclei. The error bar for NGC 520 is shown. |
| In the text | |
 |
Fig. 13 Total magnetic field strengths (circles) versus local SFRs for the whole interacting galaxies a), their centres b), and off-centre regions c). The random and regular components of magnetic fields are also provided (squares and asterisks, respectively). An expected evolutionary track of interacting systems is also indicated. |
| In the text | |
 |
Fig. 14 Asymmetry parameters for total (AT; squares) and polarized radio emission (circles; AP) versus global SFR for interacting galaxies. The values of offset angles [φT](φP) for asymmetry axes in total and polarized emission are given in parentheses. Typical uncertainties of asymmetry parameters are less than 5%. |
| In the text | |
 |
Fig. 15 Asymmetry parameters for total (AT; squares) and polarized radio emission (circles; AP) versus the interaction stage IS. Typical uncertainties of asymmetry parameters are less than 5%. |
| In the text | |
 |
Fig. 16 The radio–FIR correlation diagram for interacting (squares) and normal galaxies of different Hubble types (asterisks). The surface brightness at 4.86 GHz and at 60 μm (Jy/◻′) are used (see text for details). The solid line is an orthogonal fit to normal galaxies, and dashed lines represent simple X vs. Y and Y vs. X regressions. Error bars for interacting galaxies are marked. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


