| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201117124 | |
| Published online | 22 July 2011 | |
Multiple flare-angle horn feeds for sub-mm astronomy and cosmic microwave background experiments
1 Department of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
e-mail: jxl@astro.ox.ac.uk
2 Physics Department, Mahidol University, Rama VI Road, Bangkok 10400, Thailand
3 Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire, OX11 OQX, UK
4 Observatoire de Paris, LERMA, 61 avenue de l’Observatoire, 75014 Paris, France
Received: 21 April 2011
Accepted: 14 June 2011
Context. The use of large-format focal plane imaging arrays employing multiple feed horns is becoming increasingly important for the next generation of single dish sub-mm telescopes and cosmology experiments. Such receivers are being commissioned on both general purpose, common user telescopes and telescopes specifically designed for mapping intensity and polarisation anisotropies in the cosmic microwave background (CMB). Telescopes are currently being constructed to map the CMB polarisation that employ hundreds of feeds and the cost of manufacturing these feeds has become a significant fraction of the total cost of the telescope.
Aims. We have developed and manufactured low-cost easy-to-machine smooth-walled horns that have a performance comparable to the more traditional corrugated feed horns that are often used in focal plane arrays. Our horns are much easier to fabricate than corrugated horns enabling the rapid construction of arrays with a large number of horns at a very low cost.
Methods. Our smooth walled horns use multiple changes in flare angle to excite higher order waveguide modes. They are designed using a genetic algorithm to optimise the positions and magnitudes of these flare angle discontinuities. We have developed a fully parallelised software suite for the optimisation of these horns. We have manufactured prototype horns by traditional electroforming and also by a new direct drilling technique and we have measured their beam patterns using a far-field antenna test range at 230 GHz.
Results. We present simulated and measured far-field beam patterns for one of our horn designs. They exhibit low sidelobe levels, good beam circularity and low cross-polarisation levels over a fractional bandwidth of 20%. These results offer experimental confirmation of our design technique, allowing us to proceed confidently in the optimisation of horns with a wider operational bandwidth. The results also show that the new manufacturing technique using drilling is successful, enabling the fabrication of large format arrays by repeatedly drilling into a single aluminium plate. This will enable the construction of focal plane arrays at a very low cost per horn.
Conclusions. We have developed a new type of high performance feed horn that is fast and easy to fabricate. Having demonstrated the efficacy of our horn designs experimentally, we are building and testing a prototype focal plane array of 37 hexagonally close packed horns. This prototype array will be an important step towards building a complete CMB mapping receiver using these feed horns.
Key words: instrumentation: detectors / instrumentation: photometers / instrumentation: spectrographs / instrumentation: polarimeters / submillimeter: general / cosmic background radiation
© ESO, 2011
1. Introduction
1.1. Astronomical motivation
Bolometric and heterodyne detectors are now approaching the background and quantum limits in sensitivity at sub-mm wavelengths and further gains in single dish telescope mapping speed therefore requires the integration of large numbers of detectors into the telescope focal plane. Such instruments, with many hundreds of detectors, are forming the next generation of both general purpose sub-mm instruments and cosmic microwave background mapping experiments. While “CCD-style” filled-aperture bolometer arrays, such as SCUBA-2 (Holland et al. 2006), are suitable for some mapping applications, heterodyne receivers (e.g., HARP-B Smith et al. 2008) and TES bolometer focal plane arrays for CMB mapping (e.g., Clover, North et al. 2008) continue to consist of close packed arrays of feed horns. Such feedhorn arrays are popular since they offer the high aperture efficiencies, low sidelobes, low stray light sensitivities and low cross-polarisations required for many astronomical applications. The problem of rapidly fabricating large numbers of high quality feeds at an acceptable cost is becoming increasingly difficult, and the cost of horn array fabrication is becoming a large fraction of the total instrument cost.
Some current and proposed sub-mm focal plane arrays for general astronomical applications and CMB mapping.
Table 1 describes some current and proposed mm and sub-mm wavelength focal plane arrays. Feedhorn arrays rather than filled-aperture bolometer arrays are seen to dominate both heterodyne receivers and CMB mapping experiments. For heterodyne receivers, arrays of feed horns are currently the only way to couple the astronomical and local oscillator signals efficiently into a waveguide and then to an SIS (superconductor-insulator-superconductor) or HEB (hot-electron-bolometer) mixer chip. For CMB mapping experiments, arrays of feed horns provide both the low sidelobe and low cross-polarisation levels that are essential scientific requirements. While filled-aperture bolometer arrays can provide higher mapping speeds with simpler observing modes, they are less sensitive for pointed observations and require more detectors in the focal plane to cover the same area of sky (Griffin et al. 2002). They are also much more vulnerable to stray radiation within the detector cryostat and so must be used with a very carefully designed optical system, typically consisting of a series of cooled aperture stops.
Common user submillimetre telescopes are increasingly falling into two scientifically complementary categories: (i) large aperture single dish telescopes equipped with focal plane array receivers that can rapidly map large areas of the sky, and (ii) interferometers that are best suited to mapping small areas of the sky with very high angular resolution. Typically, large area survey work (e.g., Wilson et al. 2009; Buckle et al. 2010) will be undertaken by the first type of telescope (e.g., JCMT, CCAT, APEX, LMT etc.) and individual objects will be further studied by using the large angular resolution of the second kind of telescope (e.g., ALMA, SMA etc.). Large format focal plane array receivers are essential for the first type of large single dish survey instrument, where the scientific output per unit integration time is, to a large extent, proportional to the number of detectors in the focal plane.
Focal plane arrays consisting of large numbers of feed horns are also required for the next generation of cosmic microwave background experiments. These will map the anisotropies in the polarisation of the CMB to a high sensitivity and with very low systematic errors. In particular, these experiments will search for primordial B-mode polarisation patterns that may be imprinted on the CMB by gravity waves produced during the period of cosmological inflation (Hu et al. 2003). Measurement of these B-modes will require receivers of exquisite sensitivity and a telescope whose beam pattern exhibits extremely low cross-polarisation and very low sidelobe levels. Focal plane arrays consisting of large numbers of feed horns are currently the only way of achieving these stringent optical requirements in a system that enables efficient scan mapping of large areas of the sky.
1.2. Submillimetre feed horns
Corrugated horns (Clarricoats 1984) are often used as sub-mm astronomical feeds, and have been used successfully in focal plane array receivers. These horns have azimuthal corrugations in their interior that present isotropic surface boundary conditions to the electric and magnetic fields resulting in the propagation of a so-called hybrid HE11 mode (Olver et al. 1994). Corrugated horns require several corrugations per wavelength, and each corrugation is close to a quarter wavelength deep away from the throat of the horn. While the radiation properties of these horns can be excellent over a wide bandwidth, they can be difficult and expensive to manufacture, particularly as the wavelength decreases into the THz regime. Typical fabrication methods include either electroforming or direct machining into a split block. For electroforming, an aluminium mandrel that is the shape of the required horn interior is turned on a lathe and then electroplated with a suitable metal (e.g., copper). The mandrel is then dissolved chemically to leave the finished horn. In split-block machining, the corrugated horn is fabricated directly in each half of a block of metal using a high precision milling machine. For either technique, a typical corrugated horn for wavelengths of around 1 mm will cost between 1000 and 2000 US dollars.
Given the time and expense of corrugated horn fabrication, there has been much interest in designing smooth-walled horns that have radiation characteristics comparable to corrugated horns (Granet et al. 2004). A simple horn design that gives good results is the Potter horn (Potter 1963; Pickett H. 1984). Here, a step or flare angle discontinuity near the throat of a smooth-walled conical horn excites the higher order TM11 mode at an amplitude of around 16% of the incident TE11 mode. The “dual-mode” then propagates through the rest of the horn whose length is chosen such that the two modes arrive at the horn aperture in phase. The result is a highly uniform field at the horn aperture resulting in sidelobe cancellation and low cross-polarisation in the far-field. While step discontinuities are most commonly used to excite the TM11 mode, a sudden change in the flare angle of the horn can also be used (Fig. 1a).
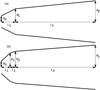 |
Fig. 1 A schematic diagram of a) 2-section and b) 3-section multiple flare angle horns. |
Step or flare-angle discontinuities near the throat of the horn will, unavoidably, excite other higher modes in addition to the desired TM11 mode. These higher order modes will affect the aperture field in a complicated, frequency dependent way, making the design of Potter horns that give good performance over a finite bandwidth more difficult. Fortunately, the effect of these modes on the far-field pattern of a particular horn can be predicted very accurately using the numerical modal-matching technique (Olver et al. 1994; Kittara 2002). Since modal matching can be used to calculate the far-field pattern for a Potter horn with a particular size and position of discontinuity, it is possible to use this technique in conjunction with suitable optimisation algorithms to determine the optimum horn profiles for good performance over a particular bandwidth. We have previously reported the successful use of a genetic algorithm and a downhill Simplex technique to design Potter horns with step and flare angle discontinuities (Kittara et al. 2007).
The horns described in this paper differ from Potter horns in that they feature multiple flare angle discontinuities near the throat of the horn. We used our genetic algorithm optimisation technique to optimise the sizes and positions of these multiple flare angle discontinuities (Kittara et al. 2008). We have found that increasing the number of flare angle discontinuities can significantly increase the bandwidth of these smooth walled horns compared to traditional Potter horns. We now have effective designs employing two (Fig. 1b) flare-angle discontinuities that give an expected bandwidth of around 20%. We are also currently optimising designs with three and four discontinuities with the hope of extending our bandwidths up to 50%.
In this paper we summarize our design process, present a horn design with a useful FWHM beamwidth of 14.6 degrees and describe our fabrication of these new smooth-walled horns using both traditional electroforming and a novel drilling technique. We then describe our first results in the experimental testing of these horns on a far-field antenna range. For the electroformed horns, these experimental results are shown to be in excellent agreement with expectations, verifying our design procedure. The experimentally measured beam patterns for the horns fabricated using the new drilling technique are also seen to be very good. This technique should enable the rapid low cost fabrication of focal plane arrays of many hundreds of horns by simply repeatedly drilling into a single plate of aluminium. Finally we present calculated and measured cross-coupling results from a 2-horn close packed array.
2. Feed horn design using a genetic algorithm
The horn designs presented in this paper were obtained using a genetic algorithm, the details of which have been previously reported by Kittara et al. (2007) and hence will be only briefly described here. Genetic algorithms employ a natural selection process similar to biological evolution to solve optimization problems (Haupt & Haupt 1998). We begin by encoding each of the parameters describing the geometry of a horn (i.e. R0,R1,R2,R3,L1,L2,L3 in Fig. 1b) to form a binary string known as a chromosome. Here the continuous numerical value of each parameter is represented by a binary integer, which is then further encoded using a Gray code, to ensure that each successive integer value differs only by a single bit. The collection of chromosomes, describing one particular horn geometry, is known as an individual. An initial population of individuals is formed where the parameters are chosen randomly between sensible upper and lower constraints e.g., such that R1 min < R1 < R1 max. In our case, these constraints are chosen such that the first two discontinuities are near the throat and are followed by a long, smooth phasing section. The fitness of each individual is now found by the evaluation of a cost function (described in detail below) that measures the quality of the individual’s far-field beam pattern. These beam patterns are calculated for each individual using the modal matching technique.
Once the cost function has been calculated, the individual horn designs with a high fitness (low cost function) are selected to form the parents that produce the next generation of individuals via a mating process. This mating process uses crossover and mutation to provide genetic diversity in the offspring population. In crossover, each parent chromosome is divided at the same random point along its length, and then the two offspring chromosomes are formed by swapping over each end of the two parent chromosomes and joining them back together. The Gray code encoding of the chromosomes described above ensures that this crossover will produce offspring chromosomes that are not too numerically dissimilar to the parent chromosomes. After the offspring are formed by crossover, the individual bits of each offspring chromosome may be flipped with some small probability, thus mimicking the random mutation in biological natural selection. After the new population of horn designs has been formed, the cost function for each individual design is re-evaluated, and the mating process is repeated to form a new generation. Thus the average fitness of the population of horns will tend to increase as the number of generations increases. After a sufficient number of generations the fittest individual horn design is selected, and further optimised using a Simplex minimisation technique.
Any optimisation algorithm requires a careful choice for the cost function that is to be minimised. We have chosen a cost function that maximises the far-field beam circularity and minimises the peak cross-polar level. Horns that exhibit good beam circularity and low cross-polarisation will also tend to exhibit low sidelobe levels and high beam efficiency, so we have not included the latter parameters explicitly in the cost function. Similarly, Potter horns tend to exhibit low return loss, so we have not explicitly optimised this parameter. We would like to emphasise that other cost functions can be chosen that incorporate these or other parameters depending on the horn design requirements. Our cost function, at single frequency f may be written as ![\begin{equation} \delta_f^2 = w_{\rm X} \Bigg[ \sum^{P=-30}_{P=-1} \Bigg( {{\sigma_P}\over{\sigma_p^{\rm{av}}}} \Bigg)^2 w_P \Bigg], \label{delta_f} \end{equation}](/articles/aa/full_html/2011/08/aa17124-11/aa17124-11-eq10.png) (1)where P is the power level in dB, wP = 10P/15 is the weighting function for the beam circularity, wX is the peak cross-polar power relative to main-beam peak power, σP is the difference between the E and H-plane beamwidths at power level P dB and
(1)where P is the power level in dB, wP = 10P/15 is the weighting function for the beam circularity, wX is the peak cross-polar power relative to main-beam peak power, σP is the difference between the E and H-plane beamwidths at power level P dB and  is the mean E and H-plane beamwidths at power level P dB. We calculate our final cost function across bandwidth σf = fU − fL centred at frequency f0 via
is the mean E and H-plane beamwidths at power level P dB. We calculate our final cost function across bandwidth σf = fU − fL centred at frequency f0 via 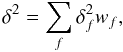 (2)where
(2)where 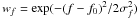 is the frequency dependent weighting factor.
is the frequency dependent weighting factor.
We have developed an efficient self-contained software package, hornsynth, to implement the horn design technique outlined above. Using this package we have successfully optimised horns consisting of two conical sections (Fig. 1a), three conical sections (Fig. 1b) and four conical sections. As the number of horn sections increases, the number of optimisation parameters, and hence the number of individuals required in the GA population, increases. For a 4-section horn, there are 7 free parameters (if we fix the initial waveguide and aperture radius) and hence we require at least 3N = 21 individuals in the population (Haupt & Haupt 1998). The most computationally expensive step in the design algorithm is the modal matching calculation of the beam pattern for each individual in the horn population, across the bandwidth of interest. Fortunately, genetic algorithms are readily parallelised – the beam pattern and cost function calculations for each individual in the population can be carried out simultaneously by distributing these tasks to separate CPUs on a Beowulf cluster. We have successfully parallelised the algorithm in this manner, using MPI messaging to pass cost function and parameter information between a master task, which handles the genetic portion of the algorithm, and multiple slave tasks, which calculate the beam patterns and resultant quality functions for each individual in the GA. By distributing the processing between 28 CPU cores, with one core per slave task and one core for the master task, we can perform a useful optimisation of a 4-section design using around 1000 GA generations.
Geometrical parameters for the 3-section 230 GHz horn design.
 |
Fig. 2 Theoretical beam patterns (E plane, H-plane and cross-polarisation) calculated using modal matching. |
3. A 230 GHz, 3-section design
In this section we describe a particular 3-section horn design optimised for a central frequency of 230 GHz. The geometry of the optimised horn is given in Table 2. The initial waveguide radius was fixed to 0.62 mm and the aperture radius was fixed to 3.652 mm to give a convenient FWHM beamwidth of around 14.6 degrees. The other 5 parameters of the horn design were left as variables to be determined using our GA software package.
Figure 2 shows the expected far-field beam patterns for this horn design. The patterns exhibit good beam circularity, low sidelobes and low cross-polarisation across a bandwidth of 20%. In order to verify experimentally the expected performance of our horn design, we had two prototype horns manufactured using conventional electroforming. Electroforming delivered a precise realisation of the horn geometry that enabled us to experimentally verify our design technique in the absence of significant manufacturing errors. This also enabled a useful comparison to be made with horns manufactured using the new direct drilling method described in Sect. 5.
4. Radiation patterns for electroformed prototype horns
The far-field radiation patterns of the prototype horns were measured directly in an anechoic chamber at the Rutherford Appleton Laboratory. We used an ABmm vector network analyzer (VNA) and a rotary scanner in an anechoic chamber to make a direct far-field measurement of the beam patterns of the prototype horns. Two identical prototype horns were used for transmission and reception, separated by 350 mm (~9 D2/λ), where D is the horn aperture diameter. The transmitter horn was rotated around its aperture using a stepper motor driven rotary table, under computer control. By using the VNA as a simple total power detector, we were able to achieve a measurement dynamic range of 60 dB. We removed the effect of stray reflections and standing waves by the careful positioning of Eccosorb RF absorber around the horns and their mounting brackets. The uniformity of our measured beam patterns show that this arrangement was successful in eliminating stray power pickup across the band centred at 230 GHz.
 |
Fig. 3 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns for the electroformed prototype horns. |
Figure 3 compares the theoretical H-plane and E-plane beam patterns calculated using modal matching and those obtained experimentally. We see a very good agreement with our predictions, confirming the excellent beam circularity and low sidelobe levels across the band. Figure 4 shows the measured co-polar and cross-polar levels for our horns. Again the result are very good, showing peak cross polar levels below –27 dB across the whole band of interest. These experimental results provide an excellent validation of this particular horn design, and show the effectiveness of our GA technique. We currently see good performance over a bandwidth of around 20% for these 3-section horns, and we expect to be able to extend this bandwidth by further optimisation of 4-section horns.
 |
Fig. 4 Experimental co-polar and cross-polar beam patterns for the electroformed prototype horns. |
5. Horn fabrication by drilling
The simple shape of the interiors of our smooth-walled horns is an attractive feature and lends itself well to fabrication techniques that are simpler and faster than electroforming. One technique that we have investigated is the fabrication of horns by direct machining using shaped drill bits (Leech et al. 2009, 2010). First we have manufactured a high speed steel machine tool whose cutting edge has the required shape of the interior of the horn (Fig. 5). We then use this cutting tool to drill the feed horn directly in a block of aluminium. The circular waveguide that feeds the horn is also manufactured by direct drilling. The process is very rapid and does not require the time consuming electroplating and dissolving stages used in electroforming. Once the machine tool and working metal plate have been properly aligned, one can quickly fabricate many feed horns by simply repeating the drilling process many times.
 |
Fig. 5 The machine tool used for the fabrication of the drilled horn prototype. |
 |
Fig. 6 A completed prototype drilled horn. |
 |
Fig. 7 The throat region of one half of the split drilled horn. For scale, the input waveguide on the left has a diameter of 1.24 mm. |
In order to test our new manufacturing technique, we fabricated three 230 GHz feed horns (Fig. 6), each with an identical design to the one described in Sect. 3. We split one of the horns using a milling machine to examine the machining quality along its interior (Fig. 7). The interior surface of both the horn and the input waveguide are seen to be very smooth, with a roughness of a few μm. We can also use Fig. 7 to estimate the accuracy of the alignment of the axes of the drilling tools used to cut the horn and the input waveguide. The overall accuracy of the alignment is seen to be good, although a close examination reveals a slight translational offset of around 50 μm. In order to excite the correct balance of higher order modes, it is important that the discontinuities near the throat have a high degree of sharpness. Figure 7 shows that the interior of the horn has taken the shape of the cutting tool very well and the machined discontinuities are very sharp, as desired.
 |
Fig. 8 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns, for the drilled horn, prototype No. 1. |
 |
Fig. 9 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns, for the drilled horn, prototype No. 2. |
 |
Fig. 10 Experimental co-polar and cross-polar beam patterns, measured for the drilled horn prototype No. 1. |
6. Radiation patterns for drilled prototype horns
The measured beam patterns for two drilled feed horns are shown in Figs. 8 − 10. The beam circularity is high and the sidelobe levels are low (below –25 dB across the band). One can also see that the measured patterns for each of the horns are virtually identical, showing that the horns made by drilling are highly repeatable – an important result for the fabrication of large arrays of many horns using this technique. There is a slight asymmetry in the sidelobe levels for each horn in the H-plane at 250 GHz. This may be caused by the small alignment mismatch of the horn throat and the input waveguide discussed above. Nevertheless, such machining imperfections do not have a significant effect on the overall quality of the patterns. The measured cross-polarisation of the horn (Fig. 10) remains low, at –20 dB or lower, across the band.
7. A 2-horn drilled array prototype
In order to investigate the suitability of our drilling technique for the manufacture of arrays of horns, we constructed a simple 2-horn array by drilling into a single block of aluminium (Fig. 11). The centres of the horns were separated by 8 mm, a packing density appropriate for large format focal plane arrays. We measured the beam patterns for each horn (Figs. 12, 13), and again found good agreement with the theoretical patterns calculated using modal matching. It should also be noted that the patterns measured for each horn are very similar to each other, again showing the reproducibility and consistency of the manufacturing technique.
 |
Fig. 11 A drilled 2-horn array prototype. |
 |
Fig. 12 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns for horn No. 1 of the 2-horn block. |
 |
Fig. 13 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns for horn No. 2 of the 2-horn block. |
We also used our 2-horn array to investigate the cross-coupling between two close packed horns. A low cross-coupling between horns is important for any horn design intended for use in close packed focal plane arrays. Historically, a variety of analytical and numerical approaches have been used to calculate the expected cross coupling between two horns (Olver et al. 1994), but we chose to perform the calculation using Ansoft’s HFSS, a full wave, finite element 3D electromagnetic simulation package. Such software packages are not generally used to design corrugated horns, since such horns depend on large numbers of corrugations per wavelength and thus require a very large amount of computer memory to mesh with sufficient accuracy. For the horns described here, which consist of a small number of flare angle discontinuities and long phasing sections, HFSS models can be sufficiently finely meshed with a moderate amounts of RAM (~8−16 GB). Figure 14 shows, for the 3-section horn described above, the good agreement between the beam patterns calculated using HFSS and the beam patterns calculated using traditional modal matching. While HFSS modelling requires much more memory and computing time than modal matching, it does not assume axial symmetry and hence will be useful in studying the effect of non-axisymmetric machining errors on horn performance.
 |
Fig. 14 A comparison of HFSS simulated H-plane beam patterns (green dashed line) and beam patterns calculated using modal matching (solid red line). |
We used HFSS to calculate the expected cross-coupling between our two horns and the experimentally measured the cross-coupling of the horns using a vector network analyser. The measurements were performed in an anechoic chamber, with a carbon loaded epoxy cone positioned in front of the two horn array as an absorber. Figure 15 shows the simulated and measured cross-coupling between the two horns across the 210 − 250 GHz operating bandwidth of the horns. The measured cross-coupling is seen to be below − 68 dB across the band, demonstrating that cross-coupling will not present a problem when these horns are close packed to form large format focal plane arrays. One should note that these experimentally determined cross-coupling measurements are in fact upper limits, due to the fact that there may be some residual reflection from our absorbing cone.
 |
Fig. 15 Measured and HFSS simulated cross-coupling between the two horns in the 2-horn prototype array. |
8. Conclusions and further work
We have developed a new technique for the design of smooth-walled multi-flare angle horns based on a genetic algorithm. These horns are much cheaper and easier to fabricate than corrugated horns and thus lend themselves more readily to the next generation of focal plane array sub-mm astronomical receivers. Our experimental results demonstrate the good agreement of our new designs with theoretical expectations obtained from modal matching, as well as the effectiveness of our new manufacturing technique using simple direct drilling. The measured beam patterns and cross-coupling from the horn prototype array show that these new horns will perform well in close packed large format focal plane arrays.
In order to further demonstrate the technology, we are currently constructing and testing a larger, 37 horn close packed focal plane prototype array. We have also made promising preliminary measurements for drilled horns designed for 700 GHz, demonstrating that we can routinely achieve the machining tolerances required to construct the much smaller horns required for wavelengths below ~1 mm.
Acknowledgments
The construction and testing of the horn array prototypes, and horn software development work was supported using an STFC follow-on fund grant and support from the Keck Institute for Space Studies, at the California Institute of Technology. The authors would like to thank Bertrand Thomas for his assistance in setting up and using the ABmm vector network analyser and 230 GHz antenna test range at the Rutherford Appleton Laboratories. We are now pursuing the commercialisation of this technology, both for sub-mm and longer wavelengths, in collaboration with ISIS Innovation Ltd, the technology transfer company of the University of Oxford.
References
- Ade, P. A. R., Savini, G., Sudiwala, R., et al. 2010, A&A, 520, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnold, K., Ade, P. A. R., Anthony, A. E., et al. 2010, in SPIE Conf. Ser. 7741 [Google Scholar]
- Buckle, J. V., Curtis, E. I., Roberts, J. F., et al. 2010, MNRAS, 401, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Cahill, G., O’Sullivan, C., Murphy, J. A., et al. 2004, in SPIE Conf. Ser. 5498, ed. C. M. Bradford, P. A. R. Ade, J. E. Aguirre, et al., 396 [Google Scholar]
- Clarricoats P. J. B. O. A. D. 1984, Corrugated horns for microwave antennas (Peter Peregrinus Ltd.) [Google Scholar]
- Crill, B. P., Ade, P. A. R., Artusa, D. R., et al. 2003, ApJS, 148, 527 [NASA ADS] [CrossRef] [Google Scholar]
- De Bernardis, P., Bucher, M., Burigana, C., & Piccirillo, L. 2009, Exp. Astron., 23, 5 [Google Scholar]
- Dowell, C. D., Allen, C. A., Babu, R. S., et al. 2003, in SPIE Conf. Ser. 4855, ed. T. G. Phillips, & J. Zmuidzinas, 73 [Google Scholar]
- Granet, C., James, G. L., Bolton, R., & Moorey, G. 2004, IEEE Trans. Antenna Propagat., 52, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Bock, J. J., & Gear, W. K. 2002, Appl. Opt., 41, 6543 [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Grimes, P. K., Ade, P. A. R., Audley, M. D., et al. 2009, in Twentieth International Symposium on Space Terahertz Technology, ed. E. Bryerton, A. Kerr, & A. Lichtenberger, 97 [Google Scholar]
- Groppi, C. E., Walker, C., Kulesa, C., et al. 2010, in Am. Astron. Soc. Meeting Abstracts, 215, 604.03 [Google Scholar]
- Haupt, R., & Haupt, S. 1998, Practical Genetic Algorithm. (Wiley-Interscience Publication) [Google Scholar]
- Holland, W. S., Robson, E. I., Gear, W. K., et al. 1999, MNRAS, 303, 659 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Holland, W., MacIntosh, M., Fairley, A., et al. 2006, in SPIE Conf. Ser., 6275 [Google Scholar]
- Hu, W., Hedman, M. M., & Zaldarriaga, M. 2003, Phys. Rev. D, 67, 043004 [NASA ADS] [CrossRef] [Google Scholar]
- Kittara, P. 2002, Ph.D. thesis, Cambridge University [Google Scholar]
- Kittara, P., Jiralucksanawong, A., Yassin, G., Wangsuya, S., & Leech, J. 2007, Int. J. Inf. Millim. Waves, 28 [Google Scholar]
- Kittara, P., Leech, J., Yassin, G., Jiralucksanawong, A., & Wangsuya, S. 2008, in Proc. 19th Int. Symposium Space Terahertz Technology, Gronigen, Netherlands [Google Scholar]
- Leech, J., Yassin, G., Tan, B. K., et al. 2009, in Proc. 20th Int. Symposium Space Terahertz Technology, Charlottesville, VA, USA [Google Scholar]
- Leech, J., Tan, B. K., Yassin, G., et al. 2010, in Proc. 21st Int. Symposium Space Terahertz Technology, Oxford, UK [Google Scholar]
- Mauskopf, P. D., Gerecht, E., & Rownd, B. K. 2000, in Imaging at Radio through Submillimeter Wavelengths, ed. J. G. Mangum, & S. J. E. Radford, ASP Conf. Ser., 217, 115 [Google Scholar]
- Narayanan, G. 2004, in Fifteenth International Symposium on Space Terahertz Technology, ed. G. Narayanan, 406 [Google Scholar]
- Niemack, M. D., Zhao, Y., Wollack, E., et al. 2008, J. Low Temp. Phys., 151, 690 [NASA ADS] [CrossRef] [Google Scholar]
- North, C. E., Johnson, B. R., Ade, P. A. R., et al. 2008, in Proc. XXXXIIIrd Rencontres de Moriond Cosmology [Google Scholar]
- Olver, A. D., Clarricoats, P. J. B., Kishk, A. A., & Shafai, L. 1994, Microwave horns and feeds (Bookcraft, Bath.) [Google Scholar]
- Pickett, H., Hardy, J. F. J. 1984, IEEE Trans. Microwave Theory Tech., MTT32, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Potter, P. 1963, Microwave J., 6, 71 [Google Scholar]
- Reichborn-Kjennerud, B., Aboobaker, A. M., Ade, P., et al. 2010, in SPIE Conf. Ser., 7741 [Google Scholar]
- Ruhl, J., Ade, P. A. R., Carlstrom, J. E., et al. 2004, in SPIE Conf. Ser. 5498, ed. C. M. Bradford, P. A. R. Ade, J. E. Aguirre, et al., 11 [Google Scholar]
- Runyan, M. C., Ade, P. A. R., Amiri, M., et al. 2010, in SPIE Conf. Ser., 7741 [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, H., Buckle, J., Hills, R., et al. 2008, in SPIE Conf. Ser. 7020 [Google Scholar]
- Staguhn, J. G., Benford, D. J., Allen, C. A., et al. 2008, in SPIE Conf. Ser. 7020 [Google Scholar]
- Wilson, C. D., Warren, B. E., Israel, F. P., et al. 2009, ApJ, 693, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, G. W., Austermann, J. E., Perera, T. A., et al. 2008, MNRAS, 386, 807 [Google Scholar]
- Yoon, K. W., Ade, P. A. R., Barkats, D., et al. 2006, in SPIE Conf. Ser. 6275 [Google Scholar]
All Tables
Some current and proposed sub-mm focal plane arrays for general astronomical applications and CMB mapping.
All Figures
 |
Fig. 1 A schematic diagram of a) 2-section and b) 3-section multiple flare angle horns. |
| In the text | |
 |
Fig. 2 Theoretical beam patterns (E plane, H-plane and cross-polarisation) calculated using modal matching. |
| In the text | |
 |
Fig. 3 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns for the electroformed prototype horns. |
| In the text | |
 |
Fig. 4 Experimental co-polar and cross-polar beam patterns for the electroformed prototype horns. |
| In the text | |
 |
Fig. 5 The machine tool used for the fabrication of the drilled horn prototype. |
| In the text | |
 |
Fig. 6 A completed prototype drilled horn. |
| In the text | |
 |
Fig. 7 The throat region of one half of the split drilled horn. For scale, the input waveguide on the left has a diameter of 1.24 mm. |
| In the text | |
 |
Fig. 8 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns, for the drilled horn, prototype No. 1. |
| In the text | |
 |
Fig. 9 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns, for the drilled horn, prototype No. 2. |
| In the text | |
 |
Fig. 10 Experimental co-polar and cross-polar beam patterns, measured for the drilled horn prototype No. 1. |
| In the text | |
 |
Fig. 11 A drilled 2-horn array prototype. |
| In the text | |
 |
Fig. 12 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns for horn No. 1 of the 2-horn block. |
| In the text | |
 |
Fig. 13 A comparison of the theoretical beam patterns calculated using modal matching and the experimentally measured beam patterns for horn No. 2 of the 2-horn block. |
| In the text | |
 |
Fig. 14 A comparison of HFSS simulated H-plane beam patterns (green dashed line) and beam patterns calculated using modal matching (solid red line). |
| In the text | |
 |
Fig. 15 Measured and HFSS simulated cross-coupling between the two horns in the 2-horn prototype array. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


