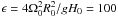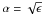| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 12 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201117122 | |
| Published online | 08 August 2011 | |
Rossby waves and polar spots in rapidly rotating stars: implications for stellar wind evolution
1
Space Research Institute, Austrian Academy of Sciences, Schmiedlstrasse 6, 8042 Graz, Austria
e-mail: teimuraz.zaqarashvili@oeaw.ac.at; maxim.khodachenko@oeaw.ac.at; helmut.lammer@oeaw.ac.at
2
Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
e-mail: ramon.oliver@uib.es; joseluis.ballester@uib.es
3
Departament de Matemàtiques i Informàtica, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
e-mail: marc.carbonell@uib.es;
4
Institut für Physik, IGAM, Karl-Franzens Universität Graz, Universitätsplatz 5, 8010 Graz, Austria
e-mail: martin.leitzinger@uni-graz.at; petra.odert@uni-graz.at
5 Abastumani Astrophysical Observatory at Ilia State University, University St. 2, Tbilisi, Georgia
Received: 21 April 2011
Accepted: 23 June 2011
Context. Rapidly rotating stars show short-period oscillations in magnetic activity and polar appearance of starspots.
Aims. The aim of this paper is to study large-scale shallow water waves in the tachoclines of rapidly rotating stars and their connection to the periodicity and the formation of starspots at high latitudes.
Methods. Shallow-water magnetohydrodynamic equations were used to study the dynamics of large-scale waves at the rapidly rotating stellar tachoclines in the presence of toroidal magnetic field. Dispersion relations and latitudinal distribution of wave modes were derived.
Results. We found that low-frequency magnetic Rossby waves tend to be located at poles, but high-frequency magnetic Poincaré waves are concentrated near the equator in rapidly rotating stars. These results have important implications for the evolution of the stellar wind in young Sun-like stars.
Conclusions. Unstable magnetic Rossby waves may lead to the local enhancement of magnetic flux at high latitudes of tachoclines in rapidly rotating stars. The enhanced magnetic flux may rise upwards owing to the magnetic buoyancy in the form of tubes and appear as starspots at polar regions. Magnetic Rossby waves may also cause observed short-term periodicity in the stellar magnetic activity.
Key words: stars: magnetic field / stars: activity / starspots / stars: oscillations / magnetohydrodynamics (MHD)
© ESO, 2011
1. Introduction
Rotation and convection lead to stellar dynamo activity, which results in the strong concentration of magnetic fields on the surface. These magnetic features are called starspots, and they represent the sunspot analog for other stars. Interested readers may find detailed information about starspots in two recent comprehensive reviews: Berdyugina (2005) and Strassmeier (2009). Hall (1972) explicitly postulated the starspot model as explaining the wave-like features in the light curves of rotating RS CVn stars. Doppler imaging technique showed spots on the RS CVn star HR 1099, and they exhibit a similarity in shape and location to X-ray images of solar coronal holes (Vogt & Penrod 1983). Later, Strassmeier (1990) observed a cool polar spot on the rapidly rotating G5 subgiant in the single-lined RS CVn binary HD 26337. The spot was rather long-lived, persisting for at least the nine years of observations.
Zeeman-Doppler imaging of the circularly polarized spectrum has led to the first magnetic maps of the active K1 subgiant in the RS CVn binary system HR 1099 = V711 Tau (K1IV+G5V) other than the Sun, which also showed the polar location of starspots (Donati et al. 1992). It was generally accepted that starspots on magnetically active, cool stars mainly appear near the poles. Schüssler & Solanki (1992) suggested that the preference for high latitudes is due to the rapid rotation to these stars, which in turn leads to a dominance of the Coriolis force over the buoyancy force in the dynamics of magnetic flux tubes. Later, Schüssler et al. (1996) carried out simulations on solar-type stars in an effort to predict the emergence latitude of magnetic flux tubes, after evolution from a toroidal magnetic field located at the base of the convection zone. They carried out simulations for stars of different ages and equatorial rotation velocities. The results predict high-latitude spots since, in a fast rotator, Coriolis forces acting on a rising magnetic flux tube cause movement parallel to the rotation axis.
On the other hand, Barnes et al. (1998) studied two rapidly rotating G dwarfs in the α Persei cluster, from spectra taken at the William Herschel Telescope. The image reconstructions demonstrate that both these stars have cool high-latitude regions or polar crowns and low-latitude features, contradicting the suggestion that only high-latitude spots should be present. The magnetic topology of AB Dor (young K0 dwarf) is also found to be very complex, with at least 12 different radial field regions of opposite polarities located all around the star (Donati et al. 1999; 2003). Significant azimuthal field fluxes are also detected in the form of one negative polarity region close to the equator, a series of positive polarity patches at intermediate latitudes and an almost complete ring of negative polarity encircling the rotational pole at high latitudes. Starspots on the young solar analog EK Dra (rotation period of 2.68 days) are observed to be formed everywhere, from the low latitudes up to polar regions (Strassmeier 2009). Therefore, the current view is that starspots appear at all latitudes in rapidly rotating stars.
The high-latitude sunspots could change the structure of coronal magnetic field as well as the formation of prominences, which may lead to the predominance of solar flares and coronal mass ejections (CMEs) near the polar regions. CMEs are believed to have tremendous influence on the atmosphere of exoplanets, leading to their erosion (Khodachenko et al. 2007). The polar CMEs may propagate significantly out off the ecliptic plane, which may cause more convenient conditions of planetary evolution; therefore, the detailed study of starspot distribution in rapidly rotating young solar analogs is very important for planetary evolution as well.
Observation of starspots at all latitudes complicates any explanation of their appearance. There are at least two suggested mechanisms of starspot formation in rapidly rotating stars. The first mechanism, which we already mentioned above, is that the magnetic tubes tend to move to the polar regions owing the Coriolis force acting during the rising across the convection zone (Schüssler & Solanki 1992; Schüssler et al. 1996; DeLuca et al. 1997; Granzer et al. 2000; Holzwarth et al. 2006; Isik et al. 2007). The second mechanism is the transport of photospheric magnetic flux towards the polar regions by meridional advection (Schrijver & Title 2001; Mackay et al. 2004). The first mechanism may explain the starspot appearance at high latitudes, but it may fail to explain the equatorial spots because the magnetic tubes should all tend to higher latitudes in rapid rotators. On the other hand, the second mechanism may explain the distribution of spots at all latitudes, but it requires a strong meridional flow in order to carry the magnetic flux towards the poles.
Another interesting observational indication is the cyclic behavior of stellar activity with shorter periods than the solar cycle (~11 yr). Massi et al. (1998, 2005) report short-term activity cycles on UX Arietis, which is a binary system formed by a spotted K0 IV primary and a G5 V secondary with an orbital period of 6.44 days. Short-period activity cycles have been observed on τ Bootis (Donati et al. 2008). Oláh et al. (2009) analyzed 20 active stars and came to the conclusion that stellar activity cycles are generally multiple and variable. Recently, Lanza et al. (2009) have observed a short-term cyclic oscillation of the total spotted area on the photosphere of CoRoT-Exo-2a, which is supposedly caused by Rossby waves. The rotation period of CoRoT-Exo-2a is 4.522 ± 0.024 days, while the total spotted area shows a cyclic oscillation with a period of 28.9 ± 4.3 days. Almost all observed periodicities are shorter than the solar cycles and are several times longer than the stellar rotation periods. It should be mentioned, however, that solar activity also undergoes intermediate periodicities in the range of several months (Rieger et al. 1984; Carbonell et al. 1990; Oliver et al. 1998) and ~ 2 years (Sakurai 1981; Gigolashvili et al. 1995; Vecchio et al. 2010). These periodicities are explained in terms of magnetic Rossby wave instability in the solar tachocline that is the joint effect of latitudinal differential rotation and toroidal magnetic field (Zaqarashvili et al. 2010a,b). The coincidence between the solar short term oscillations and the cyclic behavior of spotted stars indicate that magnetic Rossby waves can be important in rapidly rotating stars.
Here we study the behavior of magnetic shallow water waves in tachoclines of rapidly rotating stars and their role in the latitudinal distribution of starspots. The tachocline is the thin layer located between the external convection envelope and the internal radiative core (in the case of the Sun see Spiegel & Zahn 1992). Rossby waves are well studied in the geophysical context (Gill 1982); however, the presence of magnetic fields significantly modifies their dynamics (Zaqarashvili et al. 2007, 2009; Heng & Spitkovsky 2009; Mathis & de Brye 2011). We have used the shallow water magnetohydrodynamic (MHD) equations (Gilman 2000) to study the latitudinal structure of magnetic shallow water waves in tachoclines of rapidly rotating stars. We first write the governing equations of shallow water MHD in the rotating frame. Then, we derive the dispersion relations and latitudinal structure of magnetic shallow water waves in different configurations of toroidal magnetic field, which is followed by the discussion of the connection between the shallow water waves and the starspots at stellar photospheres.
Finally we discuss the implications of our findings in the context of the evolution of young stellar winds of Sun-like stars. There is observational evidence that zero-age-main-sequence solar-type stars rotate more than ten times faster than the present Sun (e.g., Güdel et al. 1997; Ribas et al. 2005; Lammer et al. 2011). As a consequence, young solar-type GV stars, including the early Sun, should have vigorous magnetic dynamos and correspondingly strong high-energy emissions. From the study of solar-type stars with different ages, Skumanich (1972), Simon et al. (1985) and others have shown that these young stars lose angular momentum with time via magnetized stellar winds, thus leading to a secular increase in their rotation period (Durney 1972). This rotation slowdown is well fitted by a power law roughly proportional to t1/2, where t is the stellar age in units of Gyr (e.g., Skumanich 1972; Soderblom 1982; Ayres 1997). As a response to slower rotation the solar dynamo strength diminishes with time, causing the Sun’s high-energy emissions also to undergo a significant decrease (Ribas et al. 2005). The fundamental question of whether the young fast-rotating Sun and similar stars have experienced some periods of stronger magnetic activity has a major impact on the evolution and plasma interaction of planetary atmospheres in the Solar System and beyond.
2. Governing equations
We use a spherical coordinate system (r,θ,φ) rotating with the stellar equator, where r is the radial coordinate, θ is the co-latitude, and φ the longitude. We consider an unperturbed toroidal magnetic field Bφ = B(θ)sinθ. Then, the linearized form of shallow-water MHD equations can be rewritten in the rotating frame as (Zaqarashvili et al. 2007, 2010a) ![\begin{eqnarray} \label{eq:21} && {{\partial {\hat u}_{\theta}}\over {\partial t}} - 2\Omega_0 \cos \theta {\hat u}_{\phi} +{{g}\over R_0}\sin \theta{{\partial h}\over {\partial \theta}}- {{B({\theta})}\over {{4\pi\rho R_0}}}{{\partial {\hat b}_{\theta}}\over {\partial \phi}}+ 2{{B({\theta})}\over {{4\pi\rho R_0 }}}{\cos \theta}{\hat b}_{\phi}=0, \\ \label{eq:22} && {{\partial {\hat u}_{\phi}}\over {\partial t}} + 2\Omega_0 \cos \theta {\hat u}_{\theta} +{{g}\over {R_0}}{{\partial h}\over {\partial \phi}}- {{{\hat b}_{\theta}\sin \theta}\over {{4\pi\rho R_0}}}{{\partial B({\theta})}\over {\partial \theta}}-{{B({\theta})}\over {{4\pi\rho R_0}}}{{\partial {\hat b}_{\phi}}\over {\partial \phi}}-{{2B({\theta})}\over {{4\pi\rho R_0 }}}{\cos \theta}{\hat b}_{\theta}=0,~~~~~~~~~~~~~~~~~~~ \\ \label{eq:23} && \sin^2 \theta{{\partial h}\over {\partial t}} + {{H_0}\over {R_0 }}\sin \theta{{\partial {\hat u}_{\theta}}\over {\partial \theta}} + {{H_0}\over {R_0}}{{\partial {\hat u}_{\phi}}\over {\partial \phi}}=0, \\ \label{eq:24} && {{\partial {\hat b}_{\theta}}\over {\partial t}}- {{B({\theta})}\over {{R_0}}}{{\partial {\hat u}_{\theta}}\over {\partial \phi}}=0, \\ && {{\partial {\hat b}_{\phi}}\over {\partial t}}+ {{1}\over {{R_0}}}\sin \theta{{\partial} \over {\partial \theta}}[{\hat u}_{\theta} B({\theta})]=0, \end{eqnarray}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq12.png) where ûθ = sinθuθ, ûφ = sinθuφ,
where ûθ = sinθuθ, ûφ = sinθuφ, 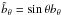 , and
, and 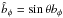 are the velocity and magnetic field perturbations, H0 is the tachocline thickness, h the perturbation of the thickness, ρ the density, R0 the distance from the stellar center to the tachocline, g the reduced gravity (due to subadiabatic temperature gradient; Gill 1982) and Ω0 the equatorial angular velocity. For a zero magnetic field, this system transforms into the HD shallow-water equations.
are the velocity and magnetic field perturbations, H0 is the tachocline thickness, h the perturbation of the thickness, ρ the density, R0 the distance from the stellar center to the tachocline, g the reduced gravity (due to subadiabatic temperature gradient; Gill 1982) and Ω0 the equatorial angular velocity. For a zero magnetic field, this system transforms into the HD shallow-water equations.
We now perform a Fourier analysis of the form exp( − iωt + isφ) and define 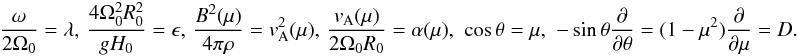 (6)After some algebra, we get a single equation (Zaqarashvili et al. 2009):
(6)After some algebra, we get a single equation (Zaqarashvili et al. 2009): ![\begin{eqnarray} (\lambda D \!+\!s \mu)\left \{{1\over {s^2 \!-\!\epsilon \lambda^2(1\!-\!\mu^2)}}\left [\lambda D \!-\! s \mu \!-\! {{\alpha^2}\over {\lambda^2}}s^2\lambda(D \!+\!2\mu)\right ]\right \}{\hat u}_{\theta}\!-\!(\lambda^2 -\mu^2){\hat u}_{\theta}\!+\!s^2\alpha^2{\hat u}_{\theta} \!+\! 2\alpha^2\mu D{\hat u}_{\theta} \!+\!\mu s {\alpha^2\over \lambda}(D\!+\!2\mu){\hat u}_{\theta}\!+\!\mu D(\alpha^2){\hat u}_{\theta}\!=\!0. \label{eq:general} \end{eqnarray}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq25.png) (7)This is the general equation for wave dynamics in a shallow-water MHD system. It contains various kind of waves (magneto-gravity, Rossby, Kelvin).
(7)This is the general equation for wave dynamics in a shallow-water MHD system. It contains various kind of waves (magneto-gravity, Rossby, Kelvin).
Equation (7) can be rewritten as ![\begin{eqnarray*} {{\partial }\over {\partial \mu}}\left (1-\mu^2 \right ){{\partial {{\hat u}_{\theta}}}\over {\partial \mu}} - \left [{{s+2\lambda}\over {\lambda^2-\alpha^2s^2}} \alpha^2 \lambda {\epsilon} \mu + {{2\lambda^2{\epsilon} \mu}\over {s^2 -\epsilon \lambda^2\left (1-\mu^2 \right )}} +{{2 \alpha s^2}\over {\lambda^2-\alpha^2s^2}}{{\partial \alpha}\over {\partial \mu}}\right ] \left (1-\mu^2 \right ){{\partial {\hat u}_{\theta}}\over {\partial \mu}} + \Big [ - {s^2\over {1-\mu^2}} + {\epsilon} \lambda^2 - {{s \lambda + 2\alpha^2s^2}\over {\lambda^2-\alpha^2s^2}} \end{eqnarray*}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq26.png)
![\begin{equation} \qquad -{{{\epsilon} \lambda^2 + 2{\epsilon} \alpha^2 s \lambda}\over {\lambda^2-\alpha^2s^2}}\mu^2 + {{2{\epsilon}\lambda^3 s + 4{\epsilon} \alpha^2 s^2 \lambda^2}\over {(\lambda^2-\alpha^2s^2)[s^2 -\epsilon \lambda^2\left (1-\mu^2 \right )]}}\mu^2-{{2 \alpha \epsilon \lambda^2 }\over {\lambda^2-\alpha^2s^2}}{{\partial \alpha}\over {\partial \mu}}\mu\left (1-\mu^2 \right ) - {{2 s^2 \alpha}\over {\lambda^2-\alpha^2s^2}}{{\partial \alpha}\over {\partial \mu}}\mu \Big ]{\hat u}_{\theta}=0. \label{eq:general1} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq27.png) (8)Now substitution of a new function
(8)Now substitution of a new function ![\begin{equation} {\hat u}_{\theta}= u_{\theta1}\exp{1\over 2} \int\left [{{s+2\lambda}\over {\lambda^2-\alpha^2s^2}} \alpha^2 \lambda {\epsilon} \mu + {{2\lambda^2{\epsilon} \mu}\over {s^2 -\epsilon \lambda^2\left (1-\mu^2 \right )}}+{{2 \alpha s^2}\over {\lambda^2-\alpha^2s^2}}{{\partial \alpha}\over {\partial \mu}}\right ] {\rm d}{\mu} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq28.png) (9)gives
(9)gives ![\begin{eqnarray*} {{\partial }\over {\partial \mu}}\left (1-\mu^2 \right ){{\partial {u_{\theta1}}}\over {\partial \mu}} + \left[ - {s^2\over {1-\mu^2}} + {\epsilon} \lambda^2 - {{s \lambda + 2\alpha^2s^2}\over {\lambda^2-\alpha^2s^2}} -{{{\epsilon} \lambda^2 + 2{\epsilon} \alpha^2 s \lambda}\over {\lambda^2-\alpha^2s^2}}\mu^2 + {{2{\epsilon} \lambda^3 s + 4{\epsilon} \alpha^2 s^2 \lambda^2}\over {(\lambda^2-\alpha^2s^2)[s^2 -\epsilon \lambda^2\left (1-\mu^2 \right )]}}\mu^2 -{{s+2 \lambda}\over {\lambda^2-\alpha^2s^2}}\epsilon \alpha^2 \lambda \mu^2 \right. \end{eqnarray*}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq29.png)
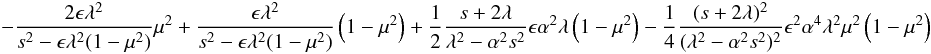
![\begin{eqnarray*} \qquad -{{(s+2\lambda)\epsilon^2 \alpha^2 \lambda^3}\over {(\lambda^2-\alpha^2s^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}}\mu^2 \left (1-\mu^2 \right ) -{{3\epsilon^2 \lambda^4}\over {[s^2 -\epsilon \lambda^2(1-\mu^2)]^2}}\mu^2 \left (1-\mu^2 \right )-{{2\epsilon \alpha \lambda^2 s^2}\over {(\lambda^2-\alpha^2s^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}}\mu {{\partial \alpha}\over {\partial \mu}}\left (1-\mu^2 \right ) \end{eqnarray*}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq31.png)
![\begin{equation} \qquad \left. +{{\epsilon \lambda -4s}\over {\lambda^2-\alpha^2s^2}}s \alpha {{\partial \alpha}\over {\partial \mu}} \mu \left (1-\mu^2 \right )+ {{s^2 \lambda^2}\over {\left (\lambda^2-\alpha^2s^2\right )^2}}\left ({{\partial \alpha}\over {\partial \mu}}\right )^2 \left (1-\mu^2 \right )+{{\alpha s^2}\over {\lambda^2-\alpha^2s^2}}{{\partial^2 \alpha}\over {\partial \mu^2}} \left (1-\mu^2 \right )\right]u_{\theta1} =0. \label{eq:working} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq32.png) (10)At this stage we should fix the magnetic field profile. We consider two different cases of the magnetic field
(10)At this stage we should fix the magnetic field profile. We consider two different cases of the magnetic field 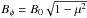 and
and 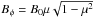 , where B0 is constant parameter. Here,
, where B0 is constant parameter. Here, 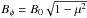 means that the resulting magnetic field is at its maximum at the equator and tends to zero at the poles. The magnetic field is opposite in the northern and southern hemispheres. Then,
means that the resulting magnetic field is at its maximum at the equator and tends to zero at the poles. The magnetic field is opposite in the northern and southern hemispheres. Then, 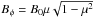 means that the magnetic field tends to zero at the solar equator and poles, reaching the maximum value at middle latitudes. This configuration is similar to the structure of the solar magnetic field, where the sunspots appear at middle latitudes (Gilman & Fox 1997). We now consider both cases separately.
means that the magnetic field tends to zero at the solar equator and poles, reaching the maximum value at middle latitudes. This configuration is similar to the structure of the solar magnetic field, where the sunspots appear at middle latitudes (Gilman & Fox 1997). We now consider both cases separately.
3. Uniform magnetic field (Bφ = B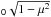 )
)
The equation 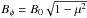 implies α = const. and Eq. (10) is rewritten as
implies α = const. and Eq. (10) is rewritten as ![\begin{equation} {{\partial }\over {\partial \mu}}\left (1-\mu^2 \right ){{\partial {u_{\theta1}}}\over {\partial \mu}} + \left [ - {s^2\over {1-\mu^2}} + B_1 + B_2\mu^2 + B_3\left (1-\mu^2 \right ) +B_4\mu^2\left (1-\mu^2 \right )\right ]u_{\theta1}=0, \label{eq:constant} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq40.png) (11)where
(11)where 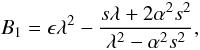 (12)
(12)![\begin{equation} B_2= -{{{\epsilon} \lambda^2 + 2{\epsilon} \alpha^2 s \lambda}\over {\lambda^2-\alpha^2s^2}} + {{2{\epsilon} \lambda^3 s + 4{\epsilon} \alpha^2 s^2 \lambda^2}\over {(\lambda^2-\alpha^2s^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}} -{{s+2 \lambda}\over {\lambda^2-\alpha^2s^2}}\epsilon \alpha^2 \lambda - {{{2 \epsilon} \lambda^2}\over {s^2 -\epsilon \lambda^2(1-\mu^2)}}, \label{eq:constant2} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq42.png) (13)
(13)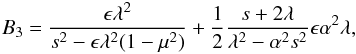 (14)
(14)![\begin{equation} B_4= - {1\over 4}{{(s+2\lambda)^2}\over {(\lambda^2-\alpha^2s^2)^2}}\epsilon^2 \alpha^4 \lambda^2 - {{(s+2\lambda)\epsilon^2 \alpha^2 \lambda^3}\over {(\lambda^2-\alpha^2s^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}} - {{3\epsilon^2 \lambda^4}\over {[s^2 -\epsilon \lambda^2(1-\mu^2)]^2}}\cdot \label{eq:constant4} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq44.png) (15)We now consider the approximation of rapidly rotating stars or a spherical shell with reduced gravity (such as in the overshoot region):
(15)We now consider the approximation of rapidly rotating stars or a spherical shell with reduced gravity (such as in the overshoot region): 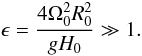 (16)In this case Eq. (11) is a spheroidal wave equation, but with a slightly complicated form (for example, the terms with μ4 arise). An analytical method for the solution of such equations was proposed by Longuet-Higgins (1965, 1968) for the Earth’s atmosphere. We closely follow this method. The equations contain two different branches of solutions: high and low frequency ones. The higher frequency branch is represented by magnetic Poincaré waves and the lower frequency one by magnetic Rossby waves. We study both cases separately.
(16)In this case Eq. (11) is a spheroidal wave equation, but with a slightly complicated form (for example, the terms with μ4 arise). An analytical method for the solution of such equations was proposed by Longuet-Higgins (1965, 1968) for the Earth’s atmosphere. We closely follow this method. The equations contain two different branches of solutions: high and low frequency ones. The higher frequency branch is represented by magnetic Poincaré waves and the lower frequency one by magnetic Rossby waves. We study both cases separately.
3.1. High-frequency waves
When ϵ ≫ 1, Eq. (11) is most easily satisfied if λ2, α2, and μ2 are small enough to compensate for the large ϵ. Let us introduce a new independent variable η = ϵ1/4μ and consider that λ ~ ϵ − 1/4L and α ~ ϵ − 1/2L, where L is near unity. Keeping only the terms ≥ ϵ1/4 in Eq. (11), we get ![\begin{equation} \left [{{\partial^2 }\over {\partial \eta^2}} + {A\over {\sqrt {\epsilon}}} - \eta^2 \right ]u_{\theta1}=0. \label{eq:weber} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq57.png) (17)where
(17)where 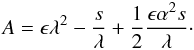 (18)This is the Weber (parabolic cylinder) equation, and the finite solutions at η → ± ∞ yield (Abramowitz & Stegun 1964)
(18)This is the Weber (parabolic cylinder) equation, and the finite solutions at η → ± ∞ yield (Abramowitz & Stegun 1964) 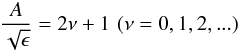 (19)and then
(19)and then 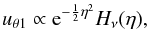 (20)where Hν(η) is the Hermite polynomial ν. The function uθ1 is exponentially small beyond the turning points
(20)where Hν(η) is the Hermite polynomial ν. The function uθ1 is exponentially small beyond the turning points 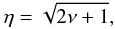 (21)that is to say,
(21)that is to say, 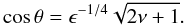 (22)Due to the large ϵ, the co-latitude θ satisfying this condition is close to 90°, therefore the solution is confined to the neighborhood of the equator.
(22)Due to the large ϵ, the co-latitude θ satisfying this condition is close to 90°, therefore the solution is confined to the neighborhood of the equator.
Equation (19) yields the wave dispersion relation as 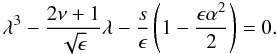 (23)For non-magnetic case, this equation transforms into Eq. (8.11) of Longuet-Higgins (1968).
(23)For non-magnetic case, this equation transforms into Eq. (8.11) of Longuet-Higgins (1968).
For high values of ϵ, the solutions of this cubic equation can be given as 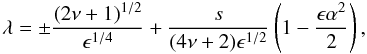 (24)
(24)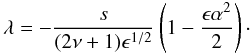 (25)The first solution represents the high-frequency branch of shallow-water equations, i.e. magnetic Poincaré waves (or magneto-gravity waves). For α = 0, expression (24) is the same as for the nonmagnetic case (Longuet-Higgins 1968). The dispersion relation yields λ ~ ϵ − 1/4, so it agrees with the approximation used in the derivation. On the other hand, expression (25) represents the magnetic Rossby waves, but it does not agree with the approximations as it yields λ ~ ϵ − 1/2. Therefore, the second solution does not describe the wave dynamics correctly.
(25)The first solution represents the high-frequency branch of shallow-water equations, i.e. magnetic Poincaré waves (or magneto-gravity waves). For α = 0, expression (24) is the same as for the nonmagnetic case (Longuet-Higgins 1968). The dispersion relation yields λ ~ ϵ − 1/4, so it agrees with the approximation used in the derivation. On the other hand, expression (25) represents the magnetic Rossby waves, but it does not agree with the approximations as it yields λ ~ ϵ − 1/2. Therefore, the second solution does not describe the wave dynamics correctly.
We solve the dispersion relation Eq. (23) numerically for different values of the ratio of Alfvén to surface speed α = vA/2Ω0R0 and the ratio of surface to internal gravity speed 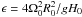 . Stability analysis of shallow-water MHD equations in the presence of latitudinal differential rotation shows that the s = 1 harmonic is the most unstable one in all considered cases (Gilman & Fox 1997; Zaqarashvili et al. 2010a,b). Therefore, in what follows, we always consider the s = 1 harmonics.
. Stability analysis of shallow-water MHD equations in the presence of latitudinal differential rotation shows that the s = 1 harmonic is the most unstable one in all considered cases (Gilman & Fox 1997; Zaqarashvili et al. 2010a,b). Therefore, in what follows, we always consider the s = 1 harmonics.
The normalized frequency λ = ω/2Ω0 vs. α and ϵ is shown in Fig. 1. The left hand panel shows the dependence of λ on α for s = 1 and ϵ = 100. We see that the frequency depends only slightly on α, i.e. on magnetic field strength. The right hand panel shows the dependence of λ on ϵ for s = 1 and α = 0.1. The dependence of the wave frequency on ϵ is more pronounced; higher ϵ yields smaller λ. The figure displays only those two solutions of the dispersion relation Eq. (23) that satisfy the condition λ ~ ϵ − 1/4. The third solution, which has lower frequency and does not satisfy λ ~ ϵ − 1/4, is not shown here.
The normalized frequency λ for four different values of ϵ (10, 100, 1000, 10 000) is shown in Fig. 2. The figure shows that the increase of ϵ leads to a significant decrease in the normalized frequency. For example, ϵ = 10 yields Tosc ≈ 0.8 Trot, while ϵ = 10 000 yields Tosc ≈ 5 Trot. Here Tosc is the oscillation period of s = 1, ν = 0 harmonics, and Trot is the stellar rotational period. This means that faster rotation leads to a longer oscillation period than the rotational period.
To check the analytical solutions, we solved Eq. (11) numerically for several frequencies, which were found from the dispersion relation Eq. (23). We searched the bounded solutions of Eq. (11) varying λ close to its analytical counterpart. The numerical solutions of Eq. (11) for three different values of λ are shown in Fig. 3. We see that all solutions are bounded and concentrated at low latitudes as suggested by the analytical solution. The frequencies for which the bounded solutions are calculated are in good coincidence with those obtained from the analytical dispersion relation Eq. (23). Therefore, the wave modes with frequency λ ~ ϵ − 1/4 are concentrated at low latitudes. These modes are magnetic Poincaré waves (Zaqarashvili et al. 2007).
 |
Fig. 1 Left: normalized frequency λ = ω/2Ω0 vs. ratio of Alfvén to surface speed α = vA/2Ω0R0. Here s = 1 (toroidal wave number) and |
 |
Fig. 2 Normalized frequency λ = ω/2Ω0 for four different values of ϵ (10, 100, 1000, 10 000). Here ϵ is shown on a logarithmic scale. The blue, red, and green asterisks correspond to the positive solutions of the dispersion relation Eq. (23) for the ν = 0, ν = 1, and ν = 2 harmonics (with s = 1), respectively. The dashed line corresponds to λ = ϵ − 1/4 slope. Here the ratio of Alfvén to surface speed α = vA/2Ω0R0 equals to ϵ − 1/2 as assumed in the derivation of Eq. (17). |
 |
Fig. 3 Numerical solutions of Eq. (11) for three different values of the normalized frequency λ = ω/2Ω0 (solid lines). μ = cosθ, where θ is the co-latitude, hence μ = 0 corresponds to the equator and μ = 1 corresponds to the northern pole. Left, middle and right panels correspond to the harmonics with ν = 2 (λ = 0.72012), ν = 1 (λ = 0.57518) and ν = 0 (λ = 0.36686), respectively. Dashed lines represent corresponding analytical solutions from Eq. (20). All solutions are concentrated at low latitudes. We take s = 1, ϵ = 100 and α = 0.1 during the simulations. |
3.2. Low-frequency waves
We now concentrate on lower frequency waves by considering λ = ϵ − 1/2L and α = ϵ − 1/2L, where L is close to unity. Then ϵλ2 ~ 1, which means that s2 − ϵλ2(1 − μ2) tends to zero for s = 1 and small μ. As a result, some terms in Eq. (11) tend to infinity. Therefore, Eq. (11) is most easily satisfied if 1 − μ2 is small instead of μ2. This means that the solutions are located near the poles not near the equator. We again follow the steps of Longuet-Higgins. Returning back to the variable θ, Eq. (11) is written ![\begin{equation} \sin \theta{{\partial }\over {\partial \theta}} \left (\sin \theta{\partial {u_{\theta1}}\over {\partial \theta}}\right ) + [ - s^2 + B_1\sin^2 \theta +B_2\cos^2 \theta \sin^2 \theta +B_3\sin^4 \theta + B_4\sin^4 \theta \cos^2 \theta ]u_{\theta1}=0. \label{eq:low-weber} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq104.png) (26)For small θ we have
(26)For small θ we have ![\begin{equation} {{\partial^2 {u_{\theta1}}}\over {\partial \theta^2}} + {1\over \theta}{{\partial {u_{\theta1}}}\over {\partial \theta}} + \left [ - {s^2\over \theta^2} + B_1 + B_2(1 - \theta^2) + B_3\theta^2 +B_4\theta^2(1-\theta^2)\right ]u_{\theta1}=0. \label{eq:low-weber-theta} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq105.png) (27)In order to estimate different terms in this equation, let us consider θ = ϵ − 1/4η, where η is near unity. Keeping only the terms ≥ ϵ1/2 we get from Eq. (27)
(27)In order to estimate different terms in this equation, let us consider θ = ϵ − 1/4η, where η is near unity. Keeping only the terms ≥ ϵ1/2 we get from Eq. (27) ![\begin{equation} {{\partial^2 {u_{\theta1}}}\over {\partial \theta^2}} + {1\over \theta}{{\partial {u_{\theta1}}}\over {\partial \theta}} + \left [ - {s^2\over \theta^2} + A_1 - A_2\theta^2\right ]u_{\theta1}=0, \label{eq:low-weber-theta1} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq109.png) (28)where
(28)where 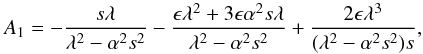 (29)
(29)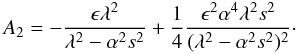 (30)Now if we consider mode frequencies in the range
(30)Now if we consider mode frequencies in the range 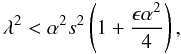 (31)but λ ≠ ± αs, then A2 is positive, and we can define a new variable
(31)but λ ≠ ± αs, then A2 is positive, and we can define a new variable 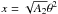 , which gives the equation
, which gives the equation ![\begin{equation} x{{\partial^2 {u_{\theta1}}}\over {\partial x^2}} +{{\partial {u_{\theta1}}}\over {\partial x}} + \left [-{x\over 4}+{{2n+s+1}\over 2} - {{s^2}\over {4 x}} \right ]u_{\theta1}=0, \label{eq:laguerre-constant} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq116.png) (32)where n is a nonnegative integer, and
(32)where n is a nonnegative integer, and 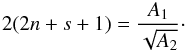 (33)This equation is self-adjoint and its solutions are sometimes called Laguerre functions
(33)This equation is self-adjoint and its solutions are sometimes called Laguerre functions 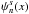 (see for example, Arfken & Weber 2005). These functions are bounded at x = 0 and x = ∞ and are linked to the associated Laguerre polynomials as
(see for example, Arfken & Weber 2005). These functions are bounded at x = 0 and x = ∞ and are linked to the associated Laguerre polynomials as 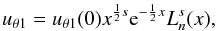 (34)where
(34)where 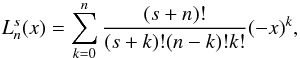 (35)so that s > − 1.
(35)so that s > − 1.
 |
Fig. 4 Left: normalized frequency λ = ω/2Ω0 vs. ratio of Alfvén to surface speed α = vA/2Ω0R0. Here s = 1 (toroidal wave number) and |
 |
Fig. 5 Normalized frequency λ = ω/2Ω0 for four different values of ϵ (10, 100, 1000, 10 000). Here λ and ϵ are shown on a logarithmic scale. The blue, red, green, and yellow asterisks (circles) correspond to the positive (negative) solutions of dispersion relation Eq. (36) for the n = 1, n = 2, n = 3, and n = 4 harmonics, respectively. Dashed lines correspond to λ = ϵ − 1/2 slope. Here the ratio of Alfvén to surface speed α = vA/2Ω0R0 equals ϵ − 1/2 as assumed in the derivation of Eq. (27). |
 |
Fig. 6 Upper panels: numerical solutions of Eq. (11) for two different values of ϵ and corresponding normalized frequency λ = ω/2Ω0. μ = cosθ, where θ is co-latitude, hence μ = 0 corresponds to the equator and μ = 1 corresponds to the northern pole. We take s = 1 and |
Then Eq. (33) gives the wave dispersion relation as 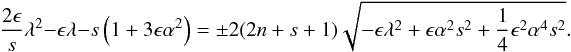 (36)The sign of λ2 − α2s2 and λ define the sign of the righthand side of Eq. (36):
(36)The sign of λ2 − α2s2 and λ define the sign of the righthand side of Eq. (36): 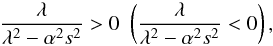 yields a + ( − ) sign. We solve the dispersion relation Eq. (36) numerically for different values of α and ϵ.
yields a + ( − ) sign. We solve the dispersion relation Eq. (36) numerically for different values of α and ϵ.
The normalized frequency λ vs. α and ϵ is shown in Fig. 4. The left hand panel shows the dependence of λ on α for s = 1 and ϵ = 100. We see that unlike the previous case here the frequency significantly depends on α, i.e., on magnetic field strength: higher α yields larger λ. The right hand panel shows the dependence of λ on ϵ for s = 1 and α = 0.1. The dependence of wave frequency on ϵ is less pronounced here.
The normalized frequency λ for four different values of ϵ (10, 100, 1000, 10 000) is displaced in Fig. 5. The figure shows that the increase of ϵ leads to a significant decrease in the normalized frequency. For example, ϵ = 10 yields Tosc ≈ 1.75 Trot, while ϵ = 10 000 yields Tosc ≈ 1000 Trot. Here Tosc is the oscillation period of the s = 1, n = 1 harmonics and Trot is the stellar rotational period. This means that faster rotation leads to a longer oscillation period with respect to the rotational period. However, the increase of ϵ leads to the deviation of λ from ϵ − 1/2, while the analytical solution is obtained in the approximation when λ is the same order of magnitude as ϵ − 1/2.
To check the analytical solutions, we solved Eq. (11) numerically for several frequencies, which were found from the dispersion relation Eq. (36). We searched the solutions of Eq. (11) fixing λ close to its analytical counterpart. The numerical solutions of Eq. (11) for two different values of ϵ and corresponding normalized frequency λ is displaced in Fig. 6 (upper panels). We see that all solutions are concentrated near the polar regions, as suggested by the analytical solution. The frequencies for which the solutions are calculated are in good coincidence with those obtained from the analytical dispersion relation Eq. (36). The lower panels of this figure display the corresponding analytical solutions plotted from Eq. (34). The figure shows that the analytical and numerical solutions show the same latitudinal behavior.
Therefore, the wave modes with low frequency, i.e. λ ~ ϵ − 1/2, are concentrated near the poles. These modes are magnetic Rossby waves (Zaqarashvili et al. 2007).
4. Non-uniform magnetic field (B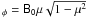 )
)
In this case, Eq. (10) is rewritten as ![\begin{equation} {{\partial }\over {\partial \mu}}\left (1-\mu^2 \right ){{\partial {u_{\theta1}}}\over {\partial \mu}} + \left [ - {s^2\over {1-\mu^2}} + B_1 + B_2\mu^2 + B_3\left (1-\mu^2 \right ) +B_4\mu^2\left (1-\mu^2 \right )+B_5 \mu^4+B_6\mu^4\left (1-\mu^2 \right )+B_7\mu^6\left (1-\mu^2 \right )\right ]u_{\theta1}=0, \label{eq:equation-mu} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq138.png) (37)where
(37)where ![\begin{eqnarray} && B_1={\epsilon} \lambda^2 - {{s \lambda}\over {\lambda^2-s^2\alpha_0^2\mu^2}}, \\ && B_2= -{{{\epsilon} \lambda^2}\over {\lambda^2-s^2\alpha_0^2\mu^2}} - {{2\alpha_0^2s^2}\over {\lambda^2-s^2\alpha_0^2\mu^2}}+ {{2{\epsilon} \lambda^3 s }\over {(\lambda^2-s^2\alpha_0^2\mu^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}}- {{{2 \epsilon} \lambda^2}\over {s^2 -\epsilon \lambda^2(1-\mu^2)}}, \\ && B_3={{{\epsilon} \lambda^2}\over {s^2 -\epsilon \lambda^2(1-\mu^2)}}+{{\lambda^2 \alpha_0^2 s^2}\over {(\lambda^2-s^2\alpha_0^2\mu^2)^2}}, \\ && B_4= - {{3\epsilon^2 \lambda^4}\over {[s^2 -\epsilon \lambda^2(1-\mu^2)]^2}} -{{2\epsilon \alpha_0^2 \lambda^2 s^2}\over {(\lambda^2-s^2\alpha_0^2\mu^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}}+{{\epsilon \lambda -4s}\over {\lambda^2-s^2\alpha_0^2\mu^2}}s \alpha_0^2+{1\over 2}{{s+2 \lambda}\over {\lambda^2-s^2\alpha_0^2\mu^2}}\epsilon \alpha_0^2 \lambda,~~~~~~~~~~~~~~~~~~~~ \\ && B_5=-{{2{\epsilon} \alpha_0^2s \lambda}\over {\lambda^2-s^2\alpha_0^2\mu^2}}+ {{4{\epsilon} \alpha_0^2 s^2 \lambda^2}\over {(\lambda^2-s^2\alpha_0^2\mu^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}} -{{s+2 \lambda}\over {\lambda^2-s^2\alpha_0^2\mu^2}}\epsilon \alpha_0^2 \lambda, \\ && B_6= -{{(s+2\lambda)\epsilon^2 \alpha_0^2 \lambda^3}\over {(\lambda^2-s^2\alpha_0^2\mu^2)[s^2 -\epsilon \lambda^2(1-\mu^2)]}}, \\ && B_7= -{1\over 4}{{(s+2\lambda)^2}\over {(\lambda^2-s^2\alpha_0^2\mu^2)^2}} \epsilon^2 \alpha_0^4\lambda^2. \end{eqnarray}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq139.png) We follow the steps of the previous section and introduce a new independent variable η = ϵ1/4μ, and also consider λ = ϵ − 1/4L and α = ϵ − 1/2L, where L is near unity. Keeping only the terms ≥ ϵ1/4 in Eq. (37) we get
We follow the steps of the previous section and introduce a new independent variable η = ϵ1/4μ, and also consider λ = ϵ − 1/4L and α = ϵ − 1/2L, where L is near unity. Keeping only the terms ≥ ϵ1/4 in Eq. (37) we get ![\begin{equation} \left [{{\partial^2 }\over {\partial \eta^2}} + {A\over {\sqrt {\epsilon}}} - \eta^2 \right ]u_{\theta1}=0, \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq141.png) (45)where
(45)where 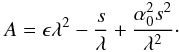 (46)This equation and the corresponding dispersion relation was already studied in detail by Zaqarashvili et al. (2009), so we do not repeat the calculations here. The solutions are concentrated near the equator as in the previous section. The resulting dispersion relation contains magnetic Poincaré and magnetic Rossby waves. The influence of the magnetic field on Poincaré waves is even less pronounced in this profile than in the previous section (compare Eq. (24) of the previous section to Eq. (11) in Zaqarashvili et al. 2009). The reason is that the magnetic field with this profile tends to zero near the equatorial regions, where the waves are concentrated. Therefore, it has almost no influence on the wave dynamics.
(46)This equation and the corresponding dispersion relation was already studied in detail by Zaqarashvili et al. (2009), so we do not repeat the calculations here. The solutions are concentrated near the equator as in the previous section. The resulting dispersion relation contains magnetic Poincaré and magnetic Rossby waves. The influence of the magnetic field on Poincaré waves is even less pronounced in this profile than in the previous section (compare Eq. (24) of the previous section to Eq. (11) in Zaqarashvili et al. 2009). The reason is that the magnetic field with this profile tends to zero near the equatorial regions, where the waves are concentrated. Therefore, it has almost no influence on the wave dynamics.
However, we now concentrate on lower frequency waves considering λ = ϵ − 1/2L and α0 = ϵ − 1/2L, where L is near unity. Then, some terms in Eq. (11) tend to infinity for s = 1 and small μ. Therefore, Eq. (11) is most easily satisfied if 1 − μ2 is small instead of μ2. This means that the solutions are located near the poles in this case. Returning back to the variable θ Eq. (37) is written 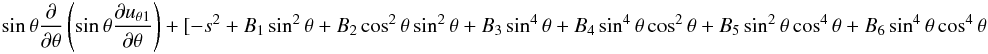
![\begin{equation} \qquad +B_7\sin^4 \theta \cos^6 \theta]u_{\theta1}=0. \label{eq:low-weber-mu} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq145.png) (47)For small θ we have
(47)For small θ we have ![\begin{equation} {{\partial^2 {u_{\theta1}}}\over {\partial \theta^2}} + {1\over \theta}{{\partial {u_{\theta1}}}\over {\partial \theta}} + \left [ - {s^2\over \theta^2} + B_1 + B_2(1 - \theta^2) + B_3\theta^2 + B_4\theta^2(1-\theta^2)+ B_5(1-\theta^2)^2+B_6\theta^2(1-\theta^2)^2+ B_7\theta^2(1-\theta^2)^3\right ]u_{\theta1}=0. \label{eq:low-weber-mu-theta} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq146.png) (48)To estimate different terms in this equation, let us consider θ = ϵ − 1/4η, where η is close to unity. Keeping only the terms ≥ ϵ1/2 we get from Eq. (48)
(48)To estimate different terms in this equation, let us consider θ = ϵ − 1/4η, where η is close to unity. Keeping only the terms ≥ ϵ1/2 we get from Eq. (48) ![\begin{equation} {{\partial^2 {u_{\theta1}}}\over {\partial \theta^2}} + {1\over \theta}{{\partial {u_{\theta1}}}\over {\partial \theta}} + \left [ - {s^2\over \theta^2} + A_1 - A_2\theta^2\right ]u_{\theta1}=0, \label{eq:low-weber-mu-theta1} \end{equation}](/articles/aa/full_html/2011/08/aa17122-11/aa17122-11-eq147.png) (49)where
(49)where 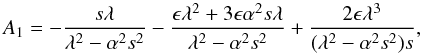 (50)
(50)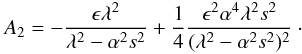 (51)One can find that Eq. (49) is the same as Eq. (28) therefore the dispersion relations and solutions are the same as in the previous section. This means that the magnetic field structure has no significant influence on the dynamics of magnetic Rossby waves. This is probably because the difference between the two profiles of the magnetic field is most important at the equator but much less important near the poles, where the eigenfunctions of magnetic Rossby waves are concentrated.
(51)One can find that Eq. (49) is the same as Eq. (28) therefore the dispersion relations and solutions are the same as in the previous section. This means that the magnetic field structure has no significant influence on the dynamics of magnetic Rossby waves. This is probably because the difference between the two profiles of the magnetic field is most important at the equator but much less important near the poles, where the eigenfunctions of magnetic Rossby waves are concentrated.
5. Discussion
Magnetic field and activity determine the structure of stellar chromosphere/corona and have a significant influence on the evolution of exoplanetary atmospheres (Khodachenko et al. 2007). Therefore, to study the stellar activity/magnetic field is crucial for recently discovered exoplanets. Magnetic activity is connected to starspots, which appear as strong concentrations of magnetic flux at stellar surfaces and thus are similar to sunspots. Emerged magnetic flux is probably connected to deeper regions, namely to the tachocline, which is a thin transition layer between the external convection envelope and the internal radiative core. The tachocline may prevent the spread of the solar angular momentum from the convection zone to the interior (Spiegel & Zahn 1992; Gough & McIntyre 1998), and it is probably the place where the large-scale magnetic field that governs the solar/stellar activity is generated/amplified. The magnetic flux rises upwards due to the magnetic buoyancy in the form of tubes and appears as spots at the surface.
Starspots on rapidly rotating stars are observed to be formed everywhere, from low latitudes up to polar regions (Strassmeier 2009). Enhanced Coriolis force in rapid rotators may push the rising magnetic flux tubes, which begin to rise in lower latitudes as in the solar case, towards higher latitudes to form polar spots (Schüssler & Solanki 1992; Schüssler et al. 1996; DeLuca et al. 1997; Granzer et al. 2000; Holzwarth et al. 2006; Isik et al. 2007). But rapidly rotating stars show low latitude spots as well, which is difficult to explain as all tubes should tend to higher latitudes. A meridional flow may also transport the photospheric magnetic flux towards the poles (Schrijver & Title 2001), but the flow should be significantly enhanced in rapid rotators compared to the Sun (Mackay et al. 2004).
Besides the longer periodicity caused by the α − ω or the α2 dynamo (~11 yr for the Sun), stellar magnetic activity also shows shorter periodicity (Massi et al. 1998, 2005; Donati et al. 2008; Lanza et al. 2009). Almost all observed periodicities are much shorter than the solar cycles but longer than the stellar rotation periods. This fact fits well with Rossby-type wave activity. There are observations of intermediate periodicity in solar activity (Rieger et al. 1984; Carbonell et al. 1990; Gigolashvili et al. 1995; Oliver et al. 1998; Vecchio et al. 2010), which were explained by the instability of magnetic Rossby waves (Zaqarashvili et al. 2010a,b). The rapid rotation may enhance the role of large-scale Rossby waves in the dynamics of stellar interior and atmospheres.
Here we study the linear dynamics of shallow water waves in rapidly rotating stellar tachoclines with toroidal magnetic field. The latitudinal differential rotation is not taken into account because it significantly complicates the solutions (Dzhalilov & Staude 2004; Mathis 2009; Zaqarashvili et al. 2010b). We derive analytical dispersion relations and find the dependence of the wave frequencies on various parameters, which are expressed by angular velocity, reduced gravity, and magnetic field strength. Then we plot the latitudinal structure of the first few harmonics. We find that high-frequency magnetic Poincaré waves are located mainly at low latitudes (Sect. 3.1; Fig. 3). In contrast, low-frequency magnetic Rossby waves are located near the poles in rapid rotators (Sect. 3.2; Fig. 6). Heng & Spitkovsky (2009) also find that the low-frequency waves, called magnetostrophic modes, reside near the poles. Actually, the magnetostrophic modes defined by Heng & Spitkovsky (2009) are the same wave modes as the magnetic Rossby waves defined here. The difference between these two considerations is the magnetic field structure. Heng & Spitkovsky (2009) used the radial magnetic field, which is valid for neutron star-related applications, while we use the toroidal magnetic field, which is applicable to stellar tachoclines. The latitudinal differential rotation and toroidal magnetic field may lead to the instability of magnetic Rossby waves, which may enhance the magnetic flux in the polar regions. Then the enhanced magnetic flux may rise upwards owing to the magnetic buoyancy and appear as polar spots (see Fig. 7).
 |
Fig. 7 Schematic picture of connection between Rossby waves and polar spots in rapidly rotating stars. Magnetic Rossby waves are concentrated near the polar regions in tachoclines of rapidly rotating stars. The erupted magnetic flux tubes lead to the appearance of polar spots at the stellar surfaces. |
The important parameter governing the dynamics of shallow water waves is ϵ and it should be estimated for rapidly rotating stars. The radius, density, and width of the stellar tachocline can be used from the solar values as R0 = 5 × 1010 cm, ρ = 0.2 g cm-3, and H0 = 0.01 R0 = 5 × 108 cm, respectively. The subadiabatic temperature gradient of the tachocline may significantly reduce the actual gravity. For example, the reduced gravity at the main, stably stratified part of the solar tachocline can be as low as 5 × 102 cm s-2 (Zaqarashvili et al. 2009). The typical value of the equatorial angular velocity of the solar tachocline is Ω⊙ = 2.7 × 10-6 s-1. We assume that κ is the ratio between angular velocities of a sample star and the Sun i.e. κ = Ω0/Ω⊙. Then we have 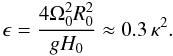 (52)Here κ is significantly larger than one for rapidly rotating stars. For example, the young solar analog EK Dra (rotation period of 2.68 days) yields κ ≈ 10, which leads to ϵ ≈ 30. More rapidly rotating stars will lead to larger ϵ. Therefore, the approximation of large ϵ is applicable for most rapid rotators. It should be mentioned that the reduced gravity g and the tachocline thickness H0 are very sensitive parameters (there are no exact values even in the case of Sun) and thus may vary significantly from star to star.
(52)Here κ is significantly larger than one for rapidly rotating stars. For example, the young solar analog EK Dra (rotation period of 2.68 days) yields κ ≈ 10, which leads to ϵ ≈ 30. More rapidly rotating stars will lead to larger ϵ. Therefore, the approximation of large ϵ is applicable for most rapid rotators. It should be mentioned that the reduced gravity g and the tachocline thickness H0 are very sensitive parameters (there are no exact values even in the case of Sun) and thus may vary significantly from star to star.
5.1. Polar spots, young stellar winds, and impact on early planetary environments
As pointed out in the introduction, young solar-like stars rotate much more faster than the present Sun. With enhanced high-energy emissions and frequent flares, young stars are also expected to have more powerful stellar winds (e.g. Wood et al. 2002; Güdel 2007). Wood et al. (2001, 2002) have applied a method to infer stellar wind characteristics from observations between the interaction of the fully ionized coronal stellar winds and the partially ionized local interstellar medium. Modeling the associated Lyman-α absorption features that are formed in the astrospheres of observed stellar sample stars have provided the first empirical estimate of coronal mass loss rates for GK main-sequence stars and indicated that the mass loss rates, so that the expected stellar winds appear to increase with stellar activity.
However, more recent observations by Wood et al. (2005) of the Lyman-α absorption signature of the astrosphere of about 0.55 Gyr old solar-like star ξ Boo indicate that there may possibly be a high-activity cut-off regarding the mass loss in a radiation activity relation derived in the form of a power law by Wood et al. (2002). The observations of ξ Boo indicate that the mass loss of that particular star is about 20 times less than the average stellar mass loss value inferred from stars with an age of about 3.9 Gyr.
From the findings of our study we would expect a rotation-related modification of the outflow region for young stellar winds, which may have affected the observation of Wood et al. (2002) in the equatorial plane. Polar starspots may completely change the structure of stellar winds in the rapidly rotating, young solar analogs. It is known that the dense slow solar wind is initiated above active regions with closed magnetic field lines at low latitudes, while the fast solar wind originates mostly in high-latitude coronal holes with opened field lines. The polar appearance of starspots may force the slow stellar wind to flow from the polar regions, so almost parallel to the rotation axis. Then this may change the current views about the magnetic braking of stellar rotation in the young age of their evolution.
Stellar magnetic activity has a tremendous influence on the planetary evolution. Coronal mass ejections in young, more active stars may lead to the erosion of atmospheres in exoplanets (Khodachenko et al. 2007; Lammer et al. 2007). On the other hand, the polar spots in young stars could change both the structure of coronal magnetic fields and the formation of prominences, which are the actual cause of CMEs. The polar location of prominences may trigger polar CMEs, which propagate significantly out of the ecliptic plane. Then the propagation of shocks and magnetic ropes/clouds out of the ecliptic plane may completely change the current picture of stellar–planetary interaction. The polar spots and related enhanced plasma flow out of the ecliptic plane during the fast-rotation period of the young Sun, or similar stars may lead to a longer stability of atmospheres related to planets that orbit in the ecliptic plane, and therefore to more convenient conditions of planetary evolution. Although our findings agree with the mass-loss observations of Wood et al. (2005), clearly more measurements are needed to better define the mass-loss, radiation activity relation of cool main-sequence stars, at high activity levels. More observations of G and K-type stars with X-ray surface fluxes greater than 106 erg cm-2 s-1 are needed to find out what is happening to stellar plasma outflow during high coronal activity periods. All these problems need to be studied in more detail in the future.
6. Conclusions
Large-scale magnetic Rossby waves may play a significant role in the dynamics of rapidly rotating stars. Here we have studied the shallow-water MHD waves in the tachoclines of rapid rotators. We considered a rotating spherical coordinate system and a toroidal magnetic field in the tachocline. We derived the dispersion relations for high (magnetic Poincaré waves) and low (magnetic Rossby waves) frequency spectra separately in the approximation of rapid rotation. We found that magnetic Rossby waves tend to locate mainly at the polar regions, while magnetic Poincaré waves are located at low latitudes. Magnetic Rossby waves may lead to the enhancement of magnetic flux at the polar regions and trigger its eruption towards the surface in the form of magnetic flux tubes. Then the magnetic tubes may form starspots at the polar region. Magnetic Rossby waves may cause the observed intermediate period oscillations in the magnetic activity of rapidly rotating stars, such as young solar proxies. The polar location of prominences during the fast-rotating period of the young star may trigger polar CMEs, which propagate significantly out of the ecliptic plane and completely change the current picture of the solar/stellar plasma interaction with young planetary environments.
Acknowledgments
The work was supported by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (projects P21197-N16 and P22950-N16). T.V.Z. acknowledges financial support from the Georgian National Science Foundation (under grant GNSF/ST09/4-310). R.O., M.C. and J.L.B. acknowledge financial support from grant AYA2006-07637 and Feder funds. The authors thank the referee, Dr. S. Mathis, for stimulating comments.
References
- Abramowitz, M., & Stegun, I. A. 1964, Handbook of Mathematical Functions (Washington, D.C.: National Bureau of Standards) [Google Scholar]
- Arfken, G. B., & Weber, H. J. 2005, Mathematical Methods for Physicists (Burlington: Elsevier Academic Press) [Google Scholar]
- Ayres, T. R. 1997, J. Geophys. Res., 102, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Collier Cameron, A., Unruh, Y. C., Donati, J. F., & Hussain, G. A. J. 1998, MNRAS, 299, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Living Rev. Sol. Phys., 2, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Carbonell, M., & Ballester, J. L. 1990, A&A, 238, 377 [NASA ADS] [Google Scholar]
- DeLuca, E., Fan, Y., & Saar, S. 1997, ApJ, 481, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., Brown, S. F., Semel, M., et al. 1992, A&A, 265, 682 [NASA ADS] [Google Scholar]
- Donati, J. F., Collier Cameron, A., Hussain, G. A. J., & Semel, M. 1999, MNRAS, 302, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., Collier Cameron, A., Semel, M., et al. 2003, MNRAS, 345, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., Moutou, C., Fares, R., et al. 2008, MNRAS, 385, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. 1972, in Solar Wind, ed. C. P. Sonett, P. J. Coleman, & J. M. Wilcox (Washington: NASA), 282 [Google Scholar]
- Dzhalilov, N. S., & Staude, J. 2004, A&A, 421, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gigolashvili, M. Sh., Japaridze, D. R., Pataraya, A. D., & Zaqarashvili, T. V. 1995, Sol. Phys., 156, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, A. E. 1982, Atmosphere-Ocean Dynamics (San Diego: Academic Press) [Google Scholar]
- Gilman, P. A. 2000, ApJ, 484, 439 [Google Scholar]
- Gilman, P. A., & Fox, P. A. 1997, ApJ, 484, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O., & McIntyre, M. E. 1998, Nature, 394, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Granzer, Th., Schüssler, M., Caligari, P., & Strassmeier, K. G. 2000, A&A, 355, 1087 [NASA ADS] [Google Scholar]
- Güdel, M., Guinan, E. F., & Skinner, S. L. 1997, ApJ, 483, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Khodachenko, M. L., Ribas, I., Lammer, H., et al. 2007, Astrobiology, 7, 167 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kulikov, Y. N., Lammer, H., Lichtenegger, H. I. M., et al. 2006, Planet. Space Sci., 54, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, D.S., 1972, PASP, 84, 498, 323 [Google Scholar]
- Heng, K., & Spitkovsky, A. 2009, ApJ, 703, 1819 [NASA ADS] [CrossRef] [Google Scholar]
- Holzwarth, V., Mackay, D. H., & Jardine, M. 2006, MNRAS, 369, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Isik, E., Schüssler, M., & Solanki, S. K. 2007, A&A, 464, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lammer, H., Lichtenegger, H. I. M., Kulikov, Y. N., et al. 2007, Astrobiol., 7, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Güdel, M., Kulikov, Y. N., et al. 2011, Earth Planet. Space, accepted [Google Scholar]
- Lanza, A. F., Pagano, L., Leto, G., et al. 2009, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longuet-Higgins, M. S. 1965, Proc. Roy. Soc. A, 284, 40 [Google Scholar]
- Longuet-Higgins, M. S. 1968, Proc. Roy. Soc. London A, 262, 511 [Google Scholar]
- Mackay, D. H., Jardine, M., Collier Cameron, A., Donati, J. F., & Hussain, G. A. J. 2004, MNRAS, 354, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Massi, M., Neidhöfer, J., Torricelli-Ciamponi, G., & Chiuderi-Drago, F. 1998, A&A, 332, 149 [NASA ADS] [Google Scholar]
- Massi, M., Neidhöfer, J., Carpentier, Y., & Ros, E. 2005, A&A, 435, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S. 2011, A&A, 506, 811 [Google Scholar]
- Mathis, S., & de Brye, N. 2011, A&A, 526, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, R., Ballester, J. L., & Baudin, F. 1998, Nature, 394, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Guinan, E. F., Güdel, M., & Audard, M. 2005, ApJ, 622, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Rieger, E., Share, G. H., Forrest, D. J., et al. 1984, Nature, 312, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Sakurai, K. 1981, Sol. Phys., 74, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, K. J., & Title, A. M. 2001, ApJ, 551, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., & Solanki, S. A. 1992, A&A, 264, 13 [Google Scholar]
- Schüssler, M., Caligari, P., Ferriz-Mas, A., Solanki, S. A., & Stix, M. 1996, A&A, 314, 503 [NASA ADS] [Google Scholar]
- Simon, T., Boesgaard, A. M., & Herbig, G. 1985, ApJ, 293, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R. 1982, ApJ, 263, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, E. A., & Zahn, J.-P. 1992, A&A, 265 [Google Scholar]
- Strassmeier, K. G. 1990, ApJ, 348, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Vecchio, A., Laurenza, M., Carbone, V., & Storini, M. 2010, ApJ, 709, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., & Penrod, G. D. 1983, PASP, 95, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Karovska, M., & Hack, W. 2001, ApJ, 556, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H.-R., Zank, G. P., & Linsky, J. L. 2002, ApJ, 574, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H.-R., Zank, G. P., Linsky, J. L., & Redfield, S. 2005, ApJ, 628, L143 [Google Scholar]
- Zaqarashvili, T. V., Oliver, R., Ballester, J. L., & Shergelashvili, B. M. 2007, A&A, 470, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Oliver, R. & Ballester, J. L. 2009, ApJ, 691, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., Carbonell, M., Oliver, R., & Ballester, J. L. 2010a, ApJ, 709, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., Carbonell, M., Oliver, R., & Ballester, J. L. 2010b, ApJ, 724, L95 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Left: normalized frequency λ = ω/2Ω0 vs. ratio of Alfvén to surface speed α = vA/2Ω0R0. Here s = 1 (toroidal wave number) and |
| In the text | |
 |
Fig. 2 Normalized frequency λ = ω/2Ω0 for four different values of ϵ (10, 100, 1000, 10 000). Here ϵ is shown on a logarithmic scale. The blue, red, and green asterisks correspond to the positive solutions of the dispersion relation Eq. (23) for the ν = 0, ν = 1, and ν = 2 harmonics (with s = 1), respectively. The dashed line corresponds to λ = ϵ − 1/4 slope. Here the ratio of Alfvén to surface speed α = vA/2Ω0R0 equals to ϵ − 1/2 as assumed in the derivation of Eq. (17). |
| In the text | |
 |
Fig. 3 Numerical solutions of Eq. (11) for three different values of the normalized frequency λ = ω/2Ω0 (solid lines). μ = cosθ, where θ is the co-latitude, hence μ = 0 corresponds to the equator and μ = 1 corresponds to the northern pole. Left, middle and right panels correspond to the harmonics with ν = 2 (λ = 0.72012), ν = 1 (λ = 0.57518) and ν = 0 (λ = 0.36686), respectively. Dashed lines represent corresponding analytical solutions from Eq. (20). All solutions are concentrated at low latitudes. We take s = 1, ϵ = 100 and α = 0.1 during the simulations. |
| In the text | |
 |
Fig. 4 Left: normalized frequency λ = ω/2Ω0 vs. ratio of Alfvén to surface speed α = vA/2Ω0R0. Here s = 1 (toroidal wave number) and |
| In the text | |
 |
Fig. 5 Normalized frequency λ = ω/2Ω0 for four different values of ϵ (10, 100, 1000, 10 000). Here λ and ϵ are shown on a logarithmic scale. The blue, red, green, and yellow asterisks (circles) correspond to the positive (negative) solutions of dispersion relation Eq. (36) for the n = 1, n = 2, n = 3, and n = 4 harmonics, respectively. Dashed lines correspond to λ = ϵ − 1/2 slope. Here the ratio of Alfvén to surface speed α = vA/2Ω0R0 equals ϵ − 1/2 as assumed in the derivation of Eq. (27). |
| In the text | |
 |
Fig. 6 Upper panels: numerical solutions of Eq. (11) for two different values of ϵ and corresponding normalized frequency λ = ω/2Ω0. μ = cosθ, where θ is co-latitude, hence μ = 0 corresponds to the equator and μ = 1 corresponds to the northern pole. We take s = 1 and |
| In the text | |
 |
Fig. 7 Schematic picture of connection between Rossby waves and polar spots in rapidly rotating stars. Magnetic Rossby waves are concentrated near the polar regions in tachoclines of rapidly rotating stars. The erupted magnetic flux tubes lead to the appearance of polar spots at the stellar surfaces. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.