EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 532 (August 2011) A&A, 532 (2011) A67 Full HTML
Free Access
Issue
A&A
Volume 532, August 2011
Article Number A67
Number of page(s) 5
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201117025
Published online 22 July 2011

© ESO, 2011

1. Introduction

It is no news that the properties of neutrinos affect the history of the universe. For example, the first limits on the number of neutrino flavours came from big bang nucleosynthesis (BBN) (Steigman et al. 1977). And because measurements of the statistical distribution of matter in the universe and the anisotropies in the cosmic microwave background (CMB) have improved, it has become possible to put increasingly stringent upper bounds on the sum of the neutrino masses (Komatsu et al. 2011; Thomas et al. 2010). The strongest bounds result, of course, when one starts from the simplest cosmological model with a handful of parameters fitted to a selection of the most important data sets and then includes the sum of the neutrino masses as an additional degree of freedom.

However, there are good reasons to take the cosmological mass limits with a grain of salt. For one thing, the cause of the apparent accelerated expansion of the universe is unknown. Although the cosmological constant is consistent with all existing data (Komatsu et al. 2011), we cannot exclude alternative explanations like scalar fields (Mota & Shaw 2007), modified gravity (Tsujikawa 2010) or void models (Mattsson 2010). Furthermore, neutrino experiments suggest that the neutrino sector of the Standard Model of particle physics may be more complicated and interesting than the simplest picture with three massive flavour states consisting of a superposition of three mass eigenstates (Aguilar et al. 2001; Aguilar-Arevalo et al. 2010; Mueller et al. 2011). In this paper our point of departure is that the simplest realizations of massive neutrinos do not seem to explain the results of experiments with neutrinos from nuclear reactors and from the LSND and MiniBooNE experiments. Recently it has been suggested that two sterile neutrinos, which are neutrinos that only interact gravitationally with matter, give a good description of the data if their masses are in the eV-range (Kopp et al. 2011).

The ability of present and future cosmological data sets to constrain light sterile neutrinos was investigated in Gonzalez-Garcia et al. (2010), Calabrese et al. (2011), and Giusarma et al. (2011). We choose to approach the problem from the opposite direction: given the uncertain nature of the dark energy and the somewhat model-dependent interpretation of cosmological data, we would argue, as we have done in the past (Kristiansen & Elgarøy 2008; Kristiansen et al. 2010), that neutrino experiments have greater authority than cosmology. If the latter find that light, sterile neutrinos are required, cosmologists have to find room for them in their models. Knowing full well that the question is far from settled, we nevertheless find it worthwhile to consider what changes in the cosmological concordance model a scenario with three active and two light, sterile neutrinos lead to. We therefore investigate the scenario where the proposal in (Kopp et al. 2011) is assumed to be correct and factor their result into an analysis of current cosmological data.

Our paper is organized as follows. In Sects. 2 and 3 we summarize the theoretical background and describe our method, but only briefly since it follows procedures that are standard in the literature. Section 4 is the most important section where we present our results and the inferences we draw from them. We summarize and conclude in Sect. 5.

2. Sterile neutrinos and cosmology

The number of neutrino species whose masses are below the GeV scale and which couple to the Z0 boson, i.e., interact weakly, was determined to be 2.984 ± 008 from LEP data (Nakamura & Particle Data Group 2010). If there are more neutrino types than the three we already know about, they must be very heavy or only couple to gravity, or both. Neutrinos that do not participate in the weak interaction are known as sterile. They appear in the so-called seesaw mechanism (Zuber 2004) for generating low neutrino masses, and are typically very heavy there, much heavier than the electroweak scale, in order to explain how low the masses of the ordinary, active neutrinos are.

However, as long as it only interacts gravitationally there are no a priori constraints on the mass of a putative sterile neutrino. Sterile neutrinos with keV masses have been of great interest as dark matter candidates in cosmology (Kusenko 2009). And recently it has been suggested that one or two sterilie neutrinos with masses of a few eV lie behind some puzzling features in neutrino oscillation experiments (Kopp et al. 2011). Ever since the LSND experiment found indications of 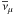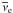νμ\hbox{$\overline{\nu}_{\mu}$}–νe\hbox{$\overline{\nu}_{\rm e}$} transitions (Athanassopoulos et al. 1998), there have been speculations about the existence of a light, sterile neutrino. The MiniBooNE experiment (Aguilar-Arevalo et al. 2010) provided support for the LSND result, but found no evidence of oscillations in the νμ–νe channel. A recent re-evaluation (Mueller et al. 2011) of the expected antineutrino flux from nuclear reactors hint at neutrino oscillations over length scales of tens to hundreds of meters. All of these results have been shown to be accommodated within a model with two eV-mass sterile neutrinos that are quite strongly mixed with electron-type neutrinos. A single sterile species is compatible with all the results except the negative MiniBooNE result for the νμ–νe channel. We take the best-fit models of (Kopp et al. 2011) as our point of departure for investigating both the models with one and two sterile neutrino species.

An important question when we turn to the cosmological implications of these two scenarios is whether these light, sterile neutrinos were thermalized in the early universe. We assume that they were, since several studies (Hamann et al. 2010; Melchiorri et al. 2009; Kainulainen 1990) suggest that this was the case for the masses and mixing parameters we consider. This means that the standard relation between the sum of the neutrino masses and their contribution to the cosmic mass density parameter applies.

Adding two light sterile neutrinos may cause some problems with BBN since the increased relativistic energy density results in a higher neutron-to-proton ratio, and leads to an increased He/H mass fraction. For example, a recent analysis (Mangano & Serpico 2011) found that BBN constrains the number of relativistic degrees of freedom to be Neff < 4.2 at 95% confidence, so the 3 + 1 model is just within the bounds, and the 3 + 2 model is just outside it. If the neutrino oscillation data ends up pointing unequivocally to the existence of two light, sterile neutrinos, this would mean that the standard BBN scenario has to be modified, but this is beyond the scope of this paper.

In contrast to the relatively tight upper bound on Neff from BBN, several recent papers have suggested that additional relativistic species are allowed, and in fact preferred, by a wide range of cosmological data. Specifically, Neff = 5 is within the allowed region (Hamann et al. 2010; Dunkley et al. 2010; Giusarma et al. 2011). The allowed mass range of the sterile neutrinos has also been studied. In Hamann et al. (2010) a scenario with massless flavour neutrinos and two thermalized sterile neutrinos with a common mass is investigated. Using a combination of different cosmological probes, including the CMB and the galaxy power spectrum, they find a 95% upper bound of 0.45 eV for each sterile neutrino. For a single sterile neutrino, the upper bound is 0.48 eV. There is some tension between these limits and the best-fit masses of the sterile neutrinos that we adopt from Kopp et al. (2011). However, we note that the limits in Hamann et al. (2010) are derived assuming a flat universe with a cosmological constant, while we allow for both spatial curvature and a dark energy equation of state, w ≠  − 1 in our analysis.

3. Method

We studied two different cosmological scenarios, the standard flat ΛCDM model and an extended model where we allowed the dark energy equation of state and the spatial curvature of the universe to vary, which we refer to as wCDM+k. For both of these models we estimated the model parameters when including zero, one (1νs), or two (2νs) sterile neutrino species. We assumed the sterile neutrinos to be fully thermalized, and adopted the best-fit masses for the sterile neutrinos from reactor experiments found in Kopp et al. (2011), which is mνs = 1.33 eV in the 1νs scenario and 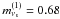mνs(1)=0.68\hbox{$m^{(1)}_{\nu_{\rm s}} = 0.68$} eV and 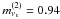mνs(2)=0.94\hbox{$m^{(2)}_{\nu_{\rm s}} = 0.94$} eV in the 2νs scenario. We assumed the three species of flavour neutrinos to be massless, which should be a good approximation when the sterile neutrino masses are at the high end of their cosmologically allowed mass range (see e.g. Giusarma et al. 2011).

We used a modified version of the publicly available cosmological Markov chain Monte Carlo sampler CosmoMC (Lewis & Bridle 2002) to compute the parameter limits. For the ΛCDM model we varied the parameter set {ωb, ωc, θ, τ, ns, ln1010AS}, and for the wCDM+k model we also included w and Ωk as free parameters. The ωb and ωc parameters denote the physical baryon and cold dark matter densities, respectively. The θ parameter is the ratio of the sound horizon to the angular diameter distance, τ is the optical depth, ns and As are the primordial scalar spectral index and amplitude (at k = 0.05   Mpc-1). The dark energy equation of state (assumed to be constant) is denoted by w, and Ωk is the curvature density. For exact parameter definitions we refer to the CosmoMC code. We marginalize over the SZ amplitude. All the listed parameters are given flat priors.

We also used two different combinations of data sets. First, we only used CMB data from the WMAP 7 year data release (Komatsu et al. 2011; Larson et al. 2011), which we refer to as WMAP7. Then we also included data on large scale structures from the Sloan Digital Sky Survey DR7 luminous red galaxy sample (Reid et al. 2010), Supernova 1A data from SDSS-II (Kessler et al. 2009) and a prior on the Hubble parameter of H0 = 73.8 ± 2.4   kms-1   Mpc-1 (Riess et al. 2011). We refer to this combination of data sets as WMAP7++. For the wCDM+k model we only use the WMAP7++ data sets, as WMAP7 data alone have very little constraining power for this extended parameter space.

4. Results

In Fig. 1 we show one-dimensional marginalized probability distributions for a few selected parameters for the ΛCDM, ΛCDM+1νs, and ΛCDM+2νs cases, and the corresponding numerical limits are given in Table 1.

Interestingly, we see that including sterile neutrinos with their masses fitted to reactor experiments will shift the age of the universe significantly. While ΛCDM favours an age of the universe of 13.75 ± 0.13 Gyr with WMAP7, including two sterile neutrinos leads to a preferred age of only 12.77 ± 0.11 Gyr. For the WMAP7++ data, the corresponding age estimates are 13.70 ± 0.10 Gyr and 12.55 ± 0.09 Gyr. The reason for these large shifts can be found in the corresponding shifts in the dark energy density, ΩΛ. The shift in ΩΛ can be understood by considering changes in the time of matter-radiation equality, teq. At the time of equality the sterile neutrinos were still relativistic, thus they contributed to the relativistic (radiation) energy denisity, and keeping all other parameters constant, additional sterile neutrinos will shift teq to later times. The CMB power spectrum is quite sensitive to teq (see e.g. Lesgourgues & Pastor 2006), and to shift teq back, the matter density must be increased. When we require a flat universe, this will lead to a reduction of ΩΛ and thus a younger universe.

thumbnail Fig. 1

Marginalized parameter distributions for ΛCDM with and without additional sterile neutrinos. Solid red lines: no sterile neutrinos. Dashed blue lines: 1 sterile neutrino. Dotted, black lines: 2 sterile neutrinos. Thin lines show results from using WMAP7 data only. Results from WMAP7++ are shown with thick lines.

Table 1

One-dimensional marginalized parameter limits for ΛCDM with and without sterile neutrinos.

In Fig. 2 and Table 2 we show the corresponding results for the wCDM+k model, but only for the WMAP7++ data sets. We basically find the same shifts in ΩDE (corrsponding to ΩΛ) and in the age of the universe, for the same reasons as explained above. When we apply the tight prior on H0 from Riess et al. (2011), WMAP data will constrain the universe to be close to flat for all models, as can be seen in the resulting limits on Ωk.

When including sterile neutrinos, we notice that w is shifted into the w <  −1 phantom regime. For decreasing ΩDE, w is forced to lower, i.e., more negative values to obtain the late time acceleration required by the supernova data.

In Fig. 3 we show two-dimensional 68% and 95% confidence contours for a few strongly correlated parameters. We see from the Ωk–w contours that, for no sterile neutrinos, the ΛCDM model (Ωk = 0 and w =  −1) falls within the 68% contours, while with sterile neutrinos, the ΛCDM  + νs model falls just outside the 95% contours. This indicates that, if further oscillation experiments confirm the existence of sterile neutrinos with properties close to what was found in Kopp et al. (2011), this will imply some tension between the cosmological constant as dark energy and cosmological data. One might argue that models with w <  −1 are unphysical. However several physically more viable dark energy models exist that will give an effective equation of state w <  −1 at late times and thus be able to accommodate the current cosmological data better than the ΛCDM model in a cosmology with more mass in the neutrino sector (see e.g. La Vacca et al. 2009). A discussion of different dynamical dark energy models are outside the scope of this paper, but our results indicate that sterile neutrinos with the properties derived in Kopp et al. (2011) would call the cosmological constant into question as the explanation for dark energy.

thumbnail Fig. 2

Marginalized parameter distributions for wCDM+k with and without additional sterile neutrinos. Labels are the same as in Fig. 1. Since these models are very poorly constrained when using WMAP7 data alone, we only show the results from WMAP7++.

Table 2

One-dimensional marginalized parameter distributions for the wCDM+k model with and without sterile neutrinos.

thumbnail Fig. 3

Marginalized 2D parameter distributions for wCDM+k with and without additional sterile neutrinos. Labels are the same as in Fig. 1. Since these models are very poorly constrained when using WMAP7 data only, we only show the results from WMAP7++.

In Tables 1 and 2 we also show the Δχ2 between the best-fit models in the cases with and without the added massive sterile neutrinos. We see that the addition of sterile neutrinos decreases the fit to the data, especially when using the WMAP7++ data sets and the ΛCDM model, giving Δχ2 =  −22.6 for the 2νs case. When opening for the Ωk and w degrees of freedom, the Δχ2 reduces to –9.3, underlining the need to look beyond a flat ΛCDM model if the existence of the sterile neutrinos in Kopp et al. (2011) is confirmed. It is interesting to notice that the worsening of χ2 from introducing 2νs in our analysis, is of the same order as the improvement of the fit by introducing the same sterile neutrinos in Kopp et al. (2011). As previously stated, our point of departure in this work is that neutrino oscillation experiments are less prone to systematical errors than cosmological observations, justifying the use of the results from Kopp et al. (2011) as input in the cosmological models.

5. Discussion and conclusions

To summarize, we have investigated how the presence of one or two sterile neutrinos with the properties estimated in Kopp et al. (2011) changes the preferred values of cosmological parameters. Rather than deriving constraints on neutrino properties from cosmology, we chose the opposite approach of using neutrino experiments to constrain cosmology. We think our approach can be justified, since the uncertain factors in cosmology, like the nature of the dark energy, are arguably greater than those in neutrino physics.

We analysed the ΛCDM model and the wCDM model with spatial curvature as an added parameter and for two data sets: WMAP7 alone and WMAP7 plus large-scale structure, supernovae type Ia, and the HST result for the Hubble parameter. The most interesting changes from the standard ΛCDM model with no sterile neutrinos were in the equation-of-state parameter w and in the age of the universe.

In the wCDM+k+2νs model we found a preferred age of  ~ 12.5 Gyr. One might question whether such a young universe would be in conflict with other cosmological observations. Regarding observations of high-redshift objects, whose ages are derived from their redshifts, this should not be a problem. As an example, the age of the universe at redshift 12 in the mean parameter value wCDM+k+2νs model from WMAP7++ is only 16% lower than for a standard ΛCDM model.

One may also put lower limits on the age of the universe by measuring the age of the oldest objects independent of the cosmological model. A common way to do this is by main sequence fitting in globular clusters. Gratton et al. (2003) use this technique and estimate the age of the oldest globular cluster in the galaxy to be 13.4 ± 0.8 ± 0.6 Gyr (statistical/systemetic errors), which leaves the 2νs models within the error bars. In Wang et al. (2010) nine clusters with estimated ages of around 14 Gyr were found in M 31. Frebel et al. (2007) use decay rates of radioactive isotopes in nearby stars to estimate a stellar age of 13.4 Gyr. However, the uncertainties in these kinds of measurements are large, and the authors estimate an uncertainty of  ~ 2 Gyr, which also places the model with two massive sterile neutrinos well within the allowed range.

We found that the three active + two sterile neutrinos scenario prefers an equation of state parameter for dark energy w <  − 1, with the cosmological constant being ruled out at 2σ. That w <  − 1 should not be taken as an indication of phantom energy. It more likely means that the correct dark energy model cannot be described by a constant w. If the evidence for sterile neutrinos from oscillation experiments becomes conclusive, the implication could be that the cosmological constant is ruled out as dark energy.

Acknowledgments

We thank Frode K. Hansen for useful discussions. The results described in this paper were produced using the Titan High Performance Computing facilities at the University of Oslo.

References

  1. Aguilar, A., Auerbach, L. B., Burman, R. L., et al. 2001, Phys. Rev. D, 64, 112007 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aguilar-Arevalo, A. A., Anderson, C. E., Brice, S. J., et al. 2010, Phys. Rev. Lett., 105, 181801 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Athanassopoulos, C., Auerbach, L. B., Burman, R. L., et al. 1998, Phys. Rev. Lett., 81, 1774 [Google Scholar]
  4. Calabrese, E., Huterer, D., Linder, E. V., Melchiorri, A., & Pagano, L. 2011, Phys. Rev. D, 83, 123504 [NASA ADS] [CrossRef] [Google Scholar]
  5. Dunkley, J., Hlozek, R., Sievers, J., et al. 2010 [arXiv:1009.0866v1] [Google Scholar]
  6. Frebel, A., Christlieb, N., Norris, J. E., et al. 2007, ApJ, 660, L117 [NASA ADS] [CrossRef] [Google Scholar]
  7. Giusarma, E., Corsi, M., Archidiacono, M., et al. 2011, Phys. Rev. D, 83, 115023 [NASA ADS] [CrossRef] [Google Scholar]
  8. Gonzalez-Garcia, M. C., Maltoni, M., & Salvado, J. 2010, J. High Energy Phys., 8, 117 [NASA ADS] [CrossRef] [Google Scholar]
  9. Gratton, R. G., Bragaglia, A., Carretta, E., et al. 2003, A&A, 408, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Hamann, J., Hannestad, S., Raffelt, G. G., Tamborra, I., & Wong, Y. Y. Y. 2010, Phys. Rev. Lett., 105, 181301 [CrossRef] [Google Scholar]
  11. Kainulainen, K. 1990, Phys. Lett. B, 244, 191 [NASA ADS] [CrossRef] [Google Scholar]
  12. Kessler, R., Becker, A. C., Cinabro, D., et al. 2009, ApJS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
  13. Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
  14. Kopp, J., Maltoni, M., & Schwetz, T. 2011 [arXiv:1103.4570] [Google Scholar]
  15. Kristiansen, J. R., & Elgarøy, Ø. 2008, J. Cosmology Astropart. Phys., 1, 7 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kristiansen, J. R., La Vacca, G., Colombo, L. P. L., Mainini, R., & Bonometto, S. A. 2010, New Astron., 15, 609 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kusenko, A. 2009, Phys. Rep., 481, 1 [NASA ADS] [CrossRef] [Google Scholar]
  18. LaVacca, G., Kristiansen, J. R., Colombo, L. P. L., Mainini, R., & Bonometto, S. A. 2009, J. Cosmology Astropart. Phys., 4, 7 [NASA ADS] [CrossRef] [Google Scholar]
  19. Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
  20. Lesgourgues, J., & Pastor, S. 2006, Phys. Rept., 429, 307 [NASA ADS] [CrossRef] [Google Scholar]
  21. Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
  22. Mangano, G., & Serpico, P. D. 2011, Phys. letters B, 701, 296 [Google Scholar]
  23. Mattsson, T. 2010, Gen. Rel. Grav., 42, 567 [NASA ADS] [CrossRef] [Google Scholar]
  24. Melchiorri, A., Mena, O., Palomares-Ruiz, S., et al. 2009, J. Cosmology Astropart. Phys., 1, 36 [NASA ADS] [CrossRef] [Google Scholar]
  25. Mota, D. F., & Shaw, D. J. 2007, Phys. Rev. D, 75, 063501 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mueller, T. A., Lhuillier, D., Fallot, M., et al. 2011, Phys. Rev. C, 83, 054615 [NASA ADS] [CrossRef] [Google Scholar]
  27. Nakamura, K., & Particle Data Group 2010, J. Phys. G Nucl. Phys., 37, 075021 [NASA ADS] [CrossRef] [Google Scholar]
  28. Reid, B. A., Percival, W. J., Eisenstein, D. J., et al. 2010, MNRAS, 404, 60 [NASA ADS] [CrossRef] [Google Scholar]
  29. Riess, A. G., Macri, L., Casertano, S., et al. 2011, ApJ, 730, 119 [NASA ADS] [CrossRef] [Google Scholar]
  30. Steigman, G., Schramm, D. N., & Gunn, J. E. 1977, Phys. Lett. B, 66, 202 [NASA ADS] [CrossRef] [Google Scholar]
  31. Thomas, S. A., Abdalla, F. B., & Lahav, O. 2010, Phys. Rev. Lett., 105, 031301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Tsujikawa, S. 2010, in Lect. Notes Phys. 800, ed. G. Wolschin (Berlin: Springer Verlag), 99 [Google Scholar]
  33. Wang, S., Fan, Z., Ma, J., de Grijs, R., & Zhou, X. 2010, AJ, 139, 1438 [NASA ADS] [CrossRef] [Google Scholar]
  34. Zuber, K. 2004, Neutrino Phys. (Institute of Physics Publ.) [Google Scholar]

All Tables

Table 1

One-dimensional marginalized parameter limits for ΛCDM with and without sterile neutrinos.

In the text
Table 2

One-dimensional marginalized parameter distributions for the wCDM+k model with and without sterile neutrinos.

In the text

All Figures

thumbnail Fig. 1

Marginalized parameter distributions for ΛCDM with and without additional sterile neutrinos. Solid red lines: no sterile neutrinos. Dashed blue lines: 1 sterile neutrino. Dotted, black lines: 2 sterile neutrinos. Thin lines show results from using WMAP7 data only. Results from WMAP7++ are shown with thick lines.

In the text
thumbnail Fig. 2

Marginalized parameter distributions for wCDM+k with and without additional sterile neutrinos. Labels are the same as in Fig. 1. Since these models are very poorly constrained when using WMAP7 data alone, we only show the results from WMAP7++.
In the text
thumbnail Fig. 3

Marginalized 2D parameter distributions for wCDM+k with and without additional sterile neutrinos. Labels are the same as in Fig. 1. Since these models are very poorly constrained when using WMAP7 data only, we only show the results from WMAP7++.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.