EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 532 (August 2011) A&A, 532 (2011) A40 Full HTML
Free Access
Issue
A&A
Volume 532, August 2011
Article Number A40
Number of page(s) 7
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201116653
Published online 20 July 2011

© ESO, 2011

1. Introduction

The presence of a dark haze situated principally in the stratosphere of the gas giant Jupiter was first established by Voyager photometric observations (Hord et al. 1979). A higher aerosol concentration was derived for the polar regions in which the production is supposedly enhanced by the magnetosphere, which precipitates large amounts of high-energy particles into the polar atmosphere, giving rise to intense auroras. The determination of the optical and physical properties of these aerosols is critical because, for instance, they play a major role in the radiative heat budget. Haze particles may also potentially be used to trace stratospheric circulation (West et al. 2004).

In spite of decades of observations, the origin and the composition of the haze remain elusive. Several possible pathways for aerosol formation have been proposed. The condensation of hydrazine (N2H4) arising from ammonia photolysis in the lower stratosphere was evoked early on (Atreya et al. 1977; Strobel 1983). As on Titan (Wilson & Atreya 2003; Wong et al. 2003), polyyne polymerization (C2n+2H2, n ≥ 1) initiated with the photodissociation of acetylene, creating the ethynyl radical (C2H) through hydrogen abstraction, was also considered, as well as HCN polymerization (Kuhn et al. 1977). The detection by the Voyager Infrared Interferometer Spectrometer (IRIS) of the first ring compound, benzene (C6H6), in the north polar region (Kim et al. 1985) and the recent observation of significant amounts of benzene at mid latitudes in the upper atmosphere by the Infrared Space Observatory (Bézard et al. 2001) promote a scenario in which aromatics play a key role in haze formation.

Aromatic-based chemical schemes developed to investigate aerosol formation in polar regions (Wong et al. 2000; Friedson et al. 2002; Wong et al. 2003) and in the northern equatorial belt (Lebonnois 2005) find their inspiration in combustion studies and models of polycyclic aromatic hydrocarbon (PAH) and soot formation in flames (Wang & Frenklach 1994). Several of the radical-neutral reactions considered have little or no energy entrance barrier and are therefore still relevant at the low temperatures characterizing the atmosphere of Jupiter. The chemical schemes also include, to various extents, ion chemistry, which is generally neglected in combustion flames. The breakdown of methane by charged energetic particle bombardment and by photo-dissociation triggers the whole chain of events. The primary driving force is dissociative recombination of methane ions that are produced from interaction with high energy particles. Small hydrocarbons such as acetylene, C2H2, are considered key products of methane photolysis and ion chemistry.

Photochemical models gradually increased in complexity from just the C and C2 species to include most hydrocarbons up to the C4 level (Gladstone et al. 1996). A new age began with the implementation of successive additive reactions involving acetylene with n − C4H3 or n − C4H5, and the recombination of the propargyl radical C3H3, which were simultaneously included in a photochemical model of Saturn’s atmosphere (Moses et al. 2000), which led then to the formation of the first aromatic compound. On further reaction with C2H2, this aromatic produces higher hydrocarbons including multi-ring species starting from naphthalene to pyrene. Obviously, recombination of aromatic ions with electrons to form neutral species represents another important mechanism near the poles, because it is a very fast process.

When the concentration of heavy polyaromatic molecules becomes high enough, condensation starts, driven by van der Waals forces. Homogeneous nucleation of the least volatile of the saturated species forms critical nuclei, onto which other molecules may heterogeneously condense. Both the pure and mixed particles subsequently grow by condensation of any remaining vapor and by coagulation. As particles grow, they sediment under the effect of gravity until they reach the troposphere (Wong et al. 2003).

Friedson et al. (2002) coupled the neutral chemical kinetics model of Wong et al. (2000) with an aerosol microphysical model to examine the formation of polar haze with the intention of producing quantitative predictions of polar haze properties that can be compared with observations. Later the model was updated to include ion chemistry (Wong et al. 2003). These authors’ findings indicate that at the high altitude of  ~200 km (corresponding to the 0.2 mbar level), pyrene (C16H10), consisting of four fused hexagonal rings, homogeneously nucleates into primary particles. At lower altitudes, the pressure rises, allowing three- and then two-ring species to condense onto the pyrene nuclei. Friedson et al.’s model suggests that particles grow by additional condensation of naphthalene and by coagulation. The prediction for the altitude at which the aerosols are generated is consistent with most observations. However, the model produces significantly less aerosol loading than that derived from earlier models, hinting at alternative pathways.

The model for formation of haze particles rests on the efficient nucleation of three- and four-ring PAHs at the temperatures that characterize the stratosphere of Jupiter. However, as highlighted by Friedson (2002), much of the critical data for calculating homogeneous nucleation rate of three- and four-ring PAHs were unavailable. In this paper we present state-of-the-art laboratory experiments coupled to high-level theoretical calculations related to the thermodynamics and kinetics of the dimerization of anthracene (C14H10). The three-ring PAH considered in the original model is phenanthrene rather than its isomer anthracene, but very little difference is expected in terms of stability. In the light of present and recent challenging results obtained on pyrene dimerization (Sabbah et al. 2010), we re-examine the condensation of small PAHs in the atmosphere of Jupiter.

2. Laboratory experiments

The objective of the laboratory experiments is to identify the temperature range over which PAH molecules, such as anthracene, dimerize and then measure the kinetics of the process. We follow the same approach that was successfully developed for the study of pyrene dimerization, described previously (Sabbah et al. 2010) and therefore only briefly outlined below. The experiments are performed using a continuous flow CRESU apparatus (Rowe et al. 1984), adapted for condensable species such as PAHs (Goulay et al. 2006). This chemical reactor is designed to generate dense uniform flows using a Laval nozzle over a wide range of temperatures (60 − 470 K) and containing high concentrations of PAH vapors. The time evolution of the chemical species present in the reactor is monitored by a time-of-flight mass spectrometer equipped with a vacuum ultraviolet laser for photoionization of the neutral reagents and products. A schematic diagram of the experimental setup is shown in Fig. 1.

thumbnail Fig. 1

CRESU apparatus dedicated to kinetics studies of reactions involving condensable species combined with a time-of-flight mass spectrometer for the detection of the reactants and products.

The rate constant for the dimerization of anthracene is measured over the available temperature range using a set of convergent-divergent Laval nozzles and carrier gases. Table 1 details the experimental conditions. Briefly, the anthracene is evaporated in an oven and flushed into a heated reservoir with a buffer gas. The expansion of this gas mixture through a Laval nozzle generates a supersonic flow in which the temperature and the density of the gas are uniform over several tens of centimeters, which corresponds to several hundred microseconds. The flow consists of an inert buffer gas and a high (supersaturated) concentration of anthracene vapor. The sudden cooling and resulting supersaturation initiates the formation of anthracene dimers via gas-phase collisions in the cold flow, which is sampled downstream at a known and variable distance by a skimmer, generating a molecular beam in a second, differentially pumped chamber. At this stage, collisions virtually disappear and the reaction is frozen. The resultant molecular beam is then irradiated transversally by VUV radiation at a wavelength of 157 nm from a pulsed excimer laser, and the resulting photoions are extracted into another differentially pumped chamber containing a time-of-flight mass spectrometer (TOFMS) to analyze the ions.

Following appropriate mass selection and integration, this yields signals proportional to the concentration of species within the supersonic flow. Anthracene monomer and anthracene cluster signals can be observed with efficiencies depending on the optimization of the different flight times involved. The anthracene monomer signal, σan, obtained by suitable integration, is proportional to the concentration of anthracene monomer present in the gas flow.

The first stage in the experimental procedure is to determine the onset of nucleation. For this purpose, values of σan are plotted as a function of anthracene concentration at each employed flow temperature. Four different temperatures are provided by the available Laval nozzles in the range of 60 to 470 K.

From 470 K down to 120 K, the monomer ion signal, σan, recorded at a distance d from the nozzle exit, varies linearly with the anthracene monomer concentration as calculated from the relative flow rates of anthracene from the oven and buffer gas, and the total gas density in the flow (Fig. 2). Colder flows reveal a very different picture, however. At the temperature of 60 K, the signal increases linearly with the anthracene concentration up to a density of 9 × 1013 molecule cm-3 and strongly collapses thereafter as shown in Fig. 3. The sudden drop of the monomer signal is interpreted as the onset of nucleation. At these high degrees of supersaturation, dimers may be considered as critical nuclei within the framework of classical nucleation theory. Once they are formed, they proceed to react rapidly with more monomer to form trimers and larger clusters. After the identification of the temperature range over which nucleation is occurring, we can proceed to kinetics measurements on anthracene dimerization within this range, but at lower anthracene monomer concentrations, 6.5 × 1013 molecule cm-3 where catastrophic nucleation does not proceed. The gray zone (Fig. 3) identifies the initial density of anthracene at which the kinetics measurements are performed. The anthracene monomer signal is measured at a series of different distances d from the exit of the Laval nozzle, corresponding to a range of reaction times that are calculated from the supersonic flow speed, determined beforehand via impact pressure measurements.

Table 1

Rate constants for the dimerization of anthracene (C14H10). Quoted errors correspond to 95% confidence limits.

To avoid any substantial contribution to the decay from the reaction of the dimer products with further monomers, we ensure that the fraction of monomer consumed remains relatively small (<15%). The ion signal σan is converted to concentration values by multiplying by a proportionality coefficient, calculated from the ratio of σan at d = 0 to the concentration of anthracene injected in the flow. Finally, the reciprocal anthracene monomer concentration is plotted as a function of reaction time (which is related by the flow speed to the distance d). The slope of the plot represented in Fig. 4 gives the apparent second order rate constant (kba) for the removal of anthracene monomer, according to simple second-order kinetics.

thumbnail Fig. 2

Anthracene monomer signal σan as a function of nominal anthracene density (as calculated from anthracene flow rate, mixing ratio, and total flow density) for flows generated at the temperatures of 120, 235, and 470 K and sampled at different reaction times. The surviving anthracene fraction (right axis) is calculated by a simple nucleation kinetics model (red solid line). Nucleation affects at most a few percent of the monomers under our experimental conditions at these temperatures.

thumbnail Fig. 3

Plot of anthracene monomer signal σan as a function of nominal anthracene density (as calculated from the anthracene flow rate, mixing ratio, and total flow density) in a uniform flow at 60 K. The surviving anthracene fraction (right axis) is calculated by a simple nucleation kinetics model for the reaction time of 73 μs (in red). The gray zone identifies the initial density of anthracene at which the kinetics measurements are performed.

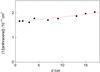thumbnail Fig. 4

1/[anthracene] as a function of distance in a 60 K flow with an initial density of [anthracene]0 = 6.5 × 1013 molecule cm-3 in a buffer of He at a total density of 4.01 × 1016 molecule cm-3. An apparent bimolecular rate constant kba = (2.16 ± 0.8) × 10-11 cm3 molecule-1 s-1 is deduced from the slope of the plot (where the quoted error corresponds to 95% confidence limits).

3. Theoretical calculations

The experimental results are coupled with theoretical calculations that use careful consideration of the intermolecular interaction energies and intermolecular dynamics to estimate the binding energy, equilibrium constant, and rate constant (Sabbah et al. 2010). The theoretical analysis employs a sum of atom-atom potentials to describe the intermolecular interactions. The parameters in this potential are designed to reproduce the equilibrium binding energies from high-level calculations for a range of small PAH dimers, while at the same time accurately modeling the interactions for the large separations that span the transition state region for the association. The analysis focuses on the rigid body dynamics of the two PAH molecules, and employs transition state theory and trajectory simulations to examine the high-pressure addition kinetics. Master equation simulations are performed to obtain pressure- and temperature-dependent rate constants. These simulations assume rapid intramolecular vibrational redistribution among only the transitional modes and the three-lowest frequency conserved modes, where the conserved modes are the internal vibrations of the PAH monomers and the transitional modes are the intermolecular modes describing the rotations and relative translation of the monomers. The results of the master equation simulations are reasonably well reproduced over the 10-3 to 104 mbar pressure range and the 60 to 300 K temperature range by Troe parametrization. In the simple Lindemann-Hinshelwood description of association reactions, the apparent bimolecular rate constant for association, k can be expressed in terms of the limiting low-pressure and high-pressure rate constants k0 and k∞ and the total density  [M]: (1)In practice, the above Lindemann-Hinshelwood fall-off expression has to be modified by a broadening factor F (Atkinson et al. 2008) (2)The broadening factor may be found according to Troe (1979) by (3)with 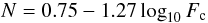(4)where Fc can be calculated from statistical unimolecular rate theory. Thus the three quantities k0, k∞ and Fc characterize the fall-off curve. This yields the following Troe parameterization constants for anthracene: 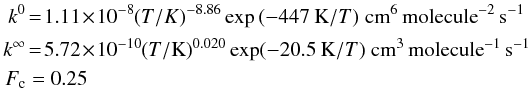(5)and for pyrene: 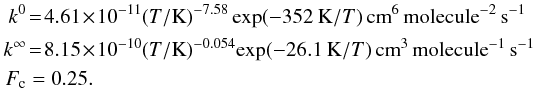(6)Predictions for the equilibrium constant are obtained from a Monte Carlo integration of the classical phase integral representation of the intermolecular partition function. The intramolecular partition functions of the monomer are assumed to be invariant to the dimerization process. The theoretical predictions for the equilibrium constant are determined by the parameters of the model potential and are not adjusted to agree with the present experimental rate measurements. Nevertheless, the accurate reproduction of high-level calculations of the binding energy for a series of related PAHs, coupled with the quantitative determination of the intermolecular partition function (for this model potential) suggests that these equilibrium constants should be quite accurate. The assumed extent of energy transfer is adjusted to reproduce the experimentally measured rate constant. These quantitative coupled anharmonic calculations give an equilibrium constant K (standard state, 1 bar) that can be represented by the expression Kan(T) = 2.04 × 10-16(T/K)3.90exp(4650K/T) for anthracene over the 40 − 500 K temperature range. Similarly, we employ for pyrene the expression of Kpy(T) = 4.58 × 10-12(T/K)2.20exp(5184K/T) calculated by Sabbah et al. (2010) following the same approach.

In an effort to strengthen the connection between our experimental data and calculations even more, we built a simple kinetics model (see, e.g., Hamon et al. 2000) to simulate the onset of nucleation evidenced by the collapse of the monomer ion signal above a certain initial parent concentration (see Fig. 3). Collisions between oligomers of any size are included but dissociation is ignored at temperatures below 470 K because the equilibrium constant for the first step is very large (K = kf/kr ≫ 1). The dimerization rate constants used in the model are given by the temperature – and pressure – dependent theoretical calculations given above.The number of transitional modes in the cluster, and the binding energy increase dramatically with the number of monomers in the cluster. This change strongly impacts on the expected pressure dependence. The production of the trimer and larger clusters is therefore assumed to proceed at a rate close to the capture rate. In our model, we unilaterally adopt the value of 4.2 × 10-10 cm3 molecule-1 s-1 for the formation of larger oligomers. Note that the temperature and size dependence of the capture rate has not been considered in the model, but is expected to be quite weak. We numerically integrate the coupled set of n = 50 rate equations, each expressing the rate of change of concentration of species containing a different number n of anthracene molecules. 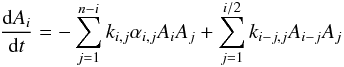(7)with 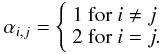(8)The concentration of surviving anthracene monomers is calculated for different reaction times and examined against the initial anthracene concentration. Simulation of a cold 60 K flow after a reaction time of 73 μs predicts significant nucleation above 1014 molecule cm-3 in qualitative agreement with the experimental data (Fig. 3). The calculations do not satisfactorily reproduce the experimental collapse of the anthracene monomer signal, however. This discrepancy could result from a loss mechanism that is as yet unaccounted for. When the formation of clusters is truncated at n = 2, only allowing the formation of dimers, the calculated survival fraction is increased, which indicates the role played by larger oligomers. Simulations of warmer flows (Fig. 2) reveal that nucleation at 120 and 235 K for reaction times of 176 and 144 μs concerns at the most a few percent of the monomers under our experimental conditions. The kinetics model is provided to reinforce the link between theory and experiment and is certainly oversimplified. However, it does show a change in behavior from approximately linear down to 120 K (the 15% deviation for the highest anthracene concentration used is not really significant given a combination of experimental and theoretical uncertainties) to strongly nonlinear at 60 K. The relatively small deviation from linearity in the simulation at 120 K and at the highest concentrations used may arise from an overestimated rate constant for the second condensation step corresponding to the monomer-dimer association. These simulations point to the initial reactions as the nucleation bottleneck. This could explain the influence of the dimer-monomer association on the whole nucleation process.

4. Implications for haze formation in the stratosphere of Jupiter

The combined laboratory/theoretical results are used to investigate the thermodynamics of PAH dimers in the north polar region and in the northern equatorial belt of the atmosphere of Jupiter. We adopt the temperature map retrieved from Cassini Composite InfraRed Spectrometer observations performed during the Jupiter 2000−2001 flyby (Simon-Miller et al. 2006). In order to account for latitudinal variations in aerosol concentration, two distinct regions are examined, 73° North and 10° North. The section of the considered atmosphere starts in the upper troposphere and ends in the upper stratosphere. It extends from the altitude of 20 km (500 mbar) to 220 km (0.5 mbar) with the reference altitude level taken as p = 1 bar. The two temperature profiles, displayed in Fig. 5, follow the same pattern, which reveals three regimes. Going up from 20 km, the temperature first cools from  ~135 K down to 110 − 115 K at 70 km. The temperature then rises back up to reach 165−175 K at the altitude of  ~170 km, where it stabilizes up to 215 km. The north polar region temperature profile exhibits the largest excursions.

thumbnail Fig. 5

10°N and 73°N temperature profiles retrieved from CIRS measurements (Simon-Miller et al. 2006)

The equilibrium constants for pyrene (Sabbah et al. 2010) and anthracene dimerization determined from the combined experimental/theoretical work outlined above, are used to calculate the minimum PAH number density for condensing a fraction, x, of the PAH monomers at a given temperature following the relationship: 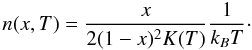(9)The resulting minimum abundances for x = 0.1 are converted into mole fractions and are plotted in Fig. 6. The most striking feature is the steepness of the mole fraction curves, which span 12 orders of magnitude going from 220 km down to 50 km. This behavior is explained by the catastrophic nature of nucleation processes embodied by the relationship between the equilibrium constant K(T) and the change in Gibbs free energy ΔRG°: K(T) = exp( − ΔRG°/RT). At an altitude of 200 km, at which homogeneous nucleation begins according to Friedson et al. (2002), Fig. 6 shows that pyrene mole fractions of 3 × 10-5 and 4 × 10-6 are required to condense 10% of the initial population in the north pole and near the equator, respectively. These values are three to four orders of magnitude higher than the mole fraction of 2 × 10-9 derived, for instance, for the smallest aromatic, benzene, in the north polar region by Voyager (Kim et al. 1985). According to the coupled chemical-microphysical model, the steady state volume mixing ratio of pyrene never goes beyond half this value (Wong et al. 2003). Adopting for the pyrene mixing ratio the value derived for benzene from the observations, we clearly see that pyrene molecules may readily undergo homogeneous nucleation only in the lower stratosphere, below  ~120 km (with a small 3 km difference between the two latitudinal regions considered).

thumbnail Fig. 6

Minimum initial mole fraction of pyrene (blue) and anthracene (red) for homogenous nucleation of 10% of the monomers. The curves with filled symbols correspond to the 73°N temperature profile.

At this altitude, the temperature has cooled down to 140 K and the pressure has risen noticeably higher (>10-2 bar). The altitude at which anthracene can homogenously nucleate, considering the same mixing ratio, is 90 km. This is about 20 km above the tropopause level. Figure 6 also shows that below the altitude of 65 km, the minimum anthracene and pyrene mole fractions for condensing 10% of the monomers differ by a factor of 3 between the northern equatorial belt and the polar region. This conclusion rests on the assumption of homogenous benzene concentration through the stratosphere. Bézard et al. (2001) suggested that the ion-related chemistry proposed by Wong et al. (2000) was probably inadequate to explain the observed C6H6 abundance at midlatitudes. Spatially resolved astronomical observations of benzene, as a tracer of PAH production, could be very helpful in this regard.

The exploration of the kinetics of this association reaction could help us to refine the picture. Collisions between cold PAH molecules lead to the formation of an energized complex, which either relaxes by emission of infrared photons, relaxes by collision with a third body, or breaks apart. The process will then obviously depend on the pressure of the environment.Based on the pressure- and temperature- dependent rate constants given by Eqs. (5) − (6), we can derive a characteristic dimer formation time for anthracene and pyrene assuming initial mole fractions ranging from 2 × 10-11 to 2 × 10-9 corresponding to 1 to 100% of the benzene mole fraction derived from observations. The calculations are performed for altitudes for which the association is faster than the dissociation for a given initial mole fraction, identified on Fig. 6 and illustrated for the northern equatorial belt. Note that the results are very similar for higher latitudes. At the altitude of 118 km and corresponding pressure of 15.8 mbar, these calculations yield an apparent bimolecular rate constant for pyrene association of  ~3.4 × 10-11 cm3 molecule-1 s-1, one order of magnitude below the high pressure limit. This translates into a characteristic time for formation of about 18 s for the maximum initial mole fraction of 2 × 10-9 (see Fig. 7). Similar calculations carried out for anthracene reveal more stringent conditions illustrated by a smaller area. To assess the plausibility of this formation process, we should compare it with dissociation mechanisms, which are dominated by photo-evaporation.

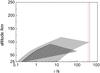thumbnail Fig. 7

Formation times of anthracene (hatched) and pyrene (gray) dimers for the northern equatorial belt considering initial mole fraction in the 2 × 10-11 − 2 × 10-9 interval. The calculations are performed for altitudes for which the association is faster than dissociation for the same range of initial mole fractions. The lines represent the photo-evaporation times for anthracene (solid red line) and pyrene (dotted blue line) dimers.

Laboratory experiments on the photophysics studies of PAH clusters have shown thatmultiphoton excitation of coronene clusters produced in a gas aggregation source leads to the ejection of van der Waals bonded units (Bréchignac et al. 2005; Schmidt et al. 2006). The loss of a monomer in the cluster, characterized by a  ~0.76 eV binding energy (Podeszwa 2010), is much more likely to happen upon absorption of a low-energy photon than the breaking of chemical bonds, which require more than 4.8 eV of energy (Pino et al. 2007). However, some chemical routes cannot be excluded. Schmidt et al. (2006) pointed out that the resonant excitation of the C-H bond by monochromatic light may dehydrogenate the coronene molecules in the cluster and induce coronene-coronene reactions. Quantitative information on dissociation rates remains mostly unavailable from laboratory studies. This can be contrasted with theoretical studies on larger coronene clusters conducted by Rapacioli et al. (2006), who calculated the evaporation rates in the framework of the phase space theory, supplemented with molecular dynamics. For (C24H12)4 they show that below a deposited total energy of 10.5 eV, infrared cooling dominates over the evaporation of a single unit. Effective evaporation requires either multiphoton absorption on a timescale shorter than infrared emission, typically 1 s, or absorption of a VUV photon. An upper limit for the photo-dissociation lifetime can be estimated by making a few assumptions. The first is that the absorption cross section of the dimer σ(λ), equals the absorption cross section of the monomer. Spectroscopy of both PAH molecules reveals intense electronic absorption bands located in the 200−400 nm window that dominate the whole UV-NIR region (Szczepanski et al. 1993; Halasinski et al. 2005) and that are orders of magnitude more intense than mid-infrared vibrational bands (Szczepanski & Vala 1993). Measurements of the gas phase absorption cross section of anthracene and pyrene have been carried out over the 200−400 nm wavelength range and the 423 − 873 K temperature range by Thony et al. (1997). Although the temperatures considered here are much lower, the authors showed that the integrated absorbance does not significantly vary with temperature. The second is that the absorption of a photon with an energy slightly higher than the binding energy of the dimer hν ≥ E + δE with E = 0.39 eV and 0.43 eV for anthracene and pyrene respectively, and δE ~ 50−200 cm-1 depending on the altitude (or the pressure that controls the time between collisions) will lead to dissociation. If the excess energy becomes higher than δE, then the rate of dissociation kdiss of the dimer increases dramatically. The dissociation pathway then dominates over the stabilization by collisions with molecules composing the atmosphere. The quantum yield φ(λ) is therefore taken equal to 1 and all the other possible chemical pathways (such as photo-induced chemistry) ignored. From there, we calculate the mean annual photodissociation rate for equatorial latitude for this channel: 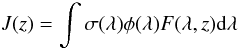(10)over the 0 − 200 km altitude range, with F(λ,z) the solar flux received at the altitude z. Because of the absence of complete quantitative gas-phase mid-infrared absorption spectra, the wavelength integration is performed over the more restricted UV-NIR range. Because VUV photons ( ≤ 180 nm) do not penetrate deep into the atmosphere and because the solar flux peaks in the visible, the lack of experimental quantitative spectra in the VUV and mid-infrared regions should not change dramatically the picture proposed hereafter.The flux is calculated over this window using simple absorption of the incident beam in a plane-parallel atmosphere (Lebonnois 2011, priv. comm.) adopting the vertical profiles of the main constituents derived by Lebonnois in his photochemical model (2005). Rayleigh and aerosol scattering are neglected, which may affect the effective photon flux in the lower layers of the atmosphere and therefore the photodissociation rate. This approximation gives characteristic photo-dissociation times for anthracene and pyrene, which are represented in Fig. 7 along with the formation times. Clearly, in the nucleation zone dimer production dominates over photo-dissociation.

5. Conclusion

The thin atmospheric layer of Jupiter is the only region accessible to direct investigation by remote sensing and in situ sampling. Its exploration may provide insights into the interior structure, bulk composition, and formation history of most of our solar system. It may also serve as the paradigm for extrasolar giant planets. Understanding the origin and composition of the haze contributes to this exploration.

The haze in the atmosphere of Jupiter has been proposed to originate mostly from the physical condensation of low-mass PAH molecules. Friedson et al. built a model in which pyrene dimerization is specifically invoked for generating critical nuclei in the upper stratosphere, which is characterized by temperatures in the 165 − 175 K range. Once these critical pyrene nuclei formed, lower mass PAH molecules can then condense and promote a rapid growth of the aerosol.

We acquired laboratory data supplemented by theoretical calculations on anthracene and pyrene (Sabbah et al. 2010) dimerization that can be used to critically assess this scenario. Thermodynamic considerations based on the determination of the equilibrium constant show that pyrene molecules do not significantly nucleate over the 120 − 220 km altitude window in which condensation has been postulated to start. Polar haze particles occupy the 65 − 175 km region (Pryor & Hord 1991) and concentrate near 100 km (Wong et al. 2000). This means that pyrene dimers are ruled out as aerosol nuclei generated at high altitudes. This automatically moves down the region where heterogeneous condensation of anthracene onto the nuclei may proceed. Through the determination of the pressure- and temperature- dependent rate constant for dimerization, we also show that, assuming an initial mole fraction of 2 × 10-9, the kinetics of anthracene and pyrene dimer formation is not hindered by photo-dissociation at altitudes lower than 90 and 120 km, respectively.

If larger PAH nuclei were to be considered, the outcome would probably differ significantly. One question would then arise, however. How can the PAH monomers be generated in large amount under the physical conditions prevailing in Jupiter’s stratosphere?

Alternatively, ion chemistry may play an even greater role in the north polar region by inducing in the upper stratosphere the formation of chemically bound nuclei – either neutral or ionized. This would not account for the production of haze particles at mid-latitudes, however. Further progress in our understanding of photochemistry at low temperatures and low pressures in hydrogen-dominated atmospheres hinges on the acquisition of high-quality kinetics data (Moses et al. 2005).

Acknowledgments

The authors thank I. W. M. Smith for fruitful discussions and S. Lebonnois for the calculation of the photon flux throughout the atmosphere. L.B. and B.R.R. acknowledge funding from the Indo-French Centre for the Promotion of Advanced Research (Project number 3405-3). This work is also

supported by the French Programmes of Physique Stellaire and of Physique et Chimie du Milieu Interstellaire. The theoretical work (S.J.K.) has been supported by NASA’s Planetary Atmospheres Program through grant NNH09AK24I and by the US Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences under Contract No. DE-AC02-06CH11357. We thank Amy Simon-Miller for providing CIRS temperature maps of Jupiter. We are finally very grateful to B. Bézard who greatly contributed through his remarks to the improvement of the manuscript.

References

  1. Atkinson, R., Baulch, D. L., Cox, R. A., et al. 2008, Atmos. Chem. Phys. 8, 4141 [Google Scholar]
  2. Atreya, S. K., Donahue, T. M., & Kuhn, W. R. 1977, Icarus, 31, 348 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bézard, B., Drossart, P., Encrenaz, T., & Feuchtgruber, H. 2001, Icarus, 154, 492 [Google Scholar]
  4. Bréchignac, Ph., Schmidt, M., Masson, A., et al. 2005, A&A, 442, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Friedson, A. J., Wong, A.-S., & Yung, Y. L. 2002, Icarus, 158, 389 [NASA ADS] [CrossRef] [Google Scholar]
  6. Gladstone, G. R., Allen, M., & Yung, Y. L. 1996, Icarus, 119, 1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Goulay, F., Rebrion-Rowe, C., Biennier, L., et al. 2006, J. Phys. Chem. A, 110, 3132 [CrossRef] [PubMed] [Google Scholar]
  8. Halasinski, T. M., Salama, F., & Allamandola, L. J. 2005, ApJ, 628, 555 [NASA ADS] [CrossRef] [Google Scholar]
  9. Hamon, S., Le Picard, S. D., Canosa, A., Rowe, B. R., & Smith, I. W. M. 2000, J. Chem. Phys., 112, 4506 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hord, C. W., West, R. A., Simmons, K. E., et al. 1979, Science, 206, 956 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Kim, S. J., Caldwell, J., Rivolo, A. R., Wagener, R., & Orton, G. S. 1985, Icarus, 64, 233 [NASA ADS] [CrossRef] [Google Scholar]
  12. Kuhn, W. R., Atreya, S. K., & Chang, S. 1977, Geophys. Res. Lett., 4, 203 [NASA ADS] [CrossRef] [Google Scholar]
  13. Lebonnois, S. 2005, Planet. Space Sci., 53, 486 [NASA ADS] [CrossRef] [Google Scholar]
  14. Moses, J. I., Bézard, B., Lellouch, E., et al. 2000, Icarus, 143, 244 [NASA ADS] [CrossRef] [Google Scholar]
  15. Moses, J. I., Fouchet, T., Bézard, B., et al. 2005, J. Geophys. Res., 110, E08001 [NASA ADS] [CrossRef] [Google Scholar]
  16. Pino, T., Parneix, P., Calvo, F., & Bréchignac, P. 2007, J. Phys. Chem. A, 111, 4456 [CrossRef] [PubMed] [Google Scholar]
  17. Podeszwa, R. 2010, J. Chem. Phys., 132, 044704 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  18. Pryor, W. R., & Hord, C. W. 1991, Icarus, 91, 161 [NASA ADS] [CrossRef] [Google Scholar]
  19. Rapacioli, M., Calvo, F., Joblin, C., et al. 2006, A&A, 460, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Rowe, B. R., Dupeyrat, G., Marquette, J. B., & Gaucherel, P. 1984, J. Chem. Phys., 80, 4915 [NASA ADS] [CrossRef] [Google Scholar]
  21. Sabbah, H., Biennier, L., Klippenstein, S. J., Sims, I. R., & Rowe, B. R. 2010, J. Phys. Chem. Lett., 17, 2962 [CrossRef] [Google Scholar]
  22. Schmidt, M., Masson, A., & Bréchignac, C. 2006, Int. J. Mass Spectrom., 252, 173 [Google Scholar]
  23. Simon-Miller, A. A., Conrath, B. J., Gierasch, P. J., et al. 2006, Icarus, 180, 98 [NASA ADS] [CrossRef] [Google Scholar]
  24. Strobel, D. F. 1983, Int. Rev. Phys. Chem., 3, 145 [Google Scholar]
  25. Szczepanski, J., & Vala, M. 1993, ApJ, 414, 646 [NASA ADS] [CrossRef] [Google Scholar]
  26. Szczepanski, J., Vala, M., Talbi, D., Parisel, O., & Ellinger, Y. 1993, J. Chem. Phys., 98, 4494 [NASA ADS] [CrossRef] [Google Scholar]
  27. Thony, A., & Rossi, M. J. 1997, J. Photochem. Photobiol. A: Chem., 104, 25 [CrossRef] [Google Scholar]
  28. Troe, J. 1979, J. Phys. Chem., 83, 114 [CrossRef] [Google Scholar]
  29. Wang, H., & Frenklach, M. 1994, J. Phys. Chem., 98, 11465 [NASA ADS] [CrossRef] [Google Scholar]
  30. West, R. A., Baines, K. H., Friedson, A. J., et al. 2004, Jovian clouds and haze, ed. F. Bagenal, 79 [Google Scholar]
  31. Wilson, E. H., & Atreya, S. K. 2003, Planet. Space Sci., 51, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  32. Wong, A.-S., Lee, A. Y. T., Yung, Y. L., & Ajello, J. M. 2000, ApJ, 534, L215 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  33. Wong, A.-S., Yung, Y. L., & Friedson, J. A. 2003, Geophys. Res. Lett., 30, 1447 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Rate constants for the dimerization of anthracene (C14H10). Quoted errors correspond to 95% confidence limits.

In the text

All Figures

thumbnail Fig. 1

CRESU apparatus dedicated to kinetics studies of reactions involving condensable species combined with a time-of-flight mass spectrometer for the detection of the reactants and products.
In the text
thumbnail Fig. 2

Anthracene monomer signal σan as a function of nominal anthracene density (as calculated from anthracene flow rate, mixing ratio, and total flow density) for flows generated at the temperatures of 120, 235, and 470 K and sampled at different reaction times. The surviving anthracene fraction (right axis) is calculated by a simple nucleation kinetics model (red solid line). Nucleation affects at most a few percent of the monomers under our experimental conditions at these temperatures.
In the text
thumbnail Fig. 3

Plot of anthracene monomer signal σan as a function of nominal anthracene density (as calculated from the anthracene flow rate, mixing ratio, and total flow density) in a uniform flow at 60 K. The surviving anthracene fraction (right axis) is calculated by a simple nucleation kinetics model for the reaction time of 73 μs (in red). The gray zone identifies the initial density of anthracene at which the kinetics measurements are performed.

In the text
thumbnail Fig. 4

1/[anthracene] as a function of distance in a 60 K flow with an initial density of [anthracene]0 = 6.5 × 1013 molecule cm-3 in a buffer of He at a total density of 4.01 × 1016 molecule cm-3. An apparent bimolecular rate constant kba = (2.16 ± 0.8) × 10-11 cm3 molecule-1 s-1 is deduced from the slope of the plot (where the quoted error corresponds to 95% confidence limits).

In the text
thumbnail Fig. 5

10°N and 73°N temperature profiles retrieved from CIRS measurements (Simon-Miller et al. 2006)

In the text
thumbnail Fig. 6

Minimum initial mole fraction of pyrene (blue) and anthracene (red) for homogenous nucleation of 10% of the monomers. The curves with filled symbols correspond to the 73°N temperature profile.
In the text
thumbnail Fig. 7

Formation times of anthracene (hatched) and pyrene (gray) dimers for the northern equatorial belt considering initial mole fraction in the 2 × 10-11 − 2 × 10-9 interval. The calculations are performed for altitudes for which the association is faster than dissociation for the same range of initial mole fractions. The lines represent the photo-evaporation times for anthracene (solid red line) and pyrene (dotted blue line) dimers.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.