| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201116530 | |
| Published online | 14 July 2011 | |
Magnetic coupling of planets and small bodies with a pulsar wind
1
LUTH, Observatoire de Paris, CNRS, Unviersité Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
e-mail: fabrice.mottez@obspm.fr
2
Observatoire Astronomique, Université de Strasbourg, 11 rue de l’Université, 67000 Strasbourg, France
e-mail: jean.heyvaerts@astro.unistra.fr
Received: 17 January 2011
Accepted: 25 May 2011
Aims. We investigate the electromagnetic interaction of a relativistic stellar wind with a planet or a smaller body in orbit around the star. This may be relevant to objects orbiting a pulsar that are expected to hold a planetary system, such as PSR B1257+12 and PSR B1620-26, or to pulsars with suspected asteroids or comets.
Methods. We extend the theory of Alfvén wings to relativistic winds.
Results. When the wind is relativistic but slower than the total Alfvén speed, a system of electric currents carried by a stationary Alfvénic structure is driven by the planet or by its surroundings.For an Earth-like planet around a “standard” second pulsar, the associated current can reach the same magnitude as the Goldreich-Julian current that powers the pulsar’s magnetosphere.
Key words: plasmas / relativistic processes / methods: analytical / pulsars: general / planets and satellites: dynamical evolution and stability / planet-star interactions
© ESO, 2011
1. Introduction
Precise pulsar timing measurents proved that the pulsars PSR B1257+12 and PSR B1620-26 host planets at distances of the order of an astronomical unit (Wolszczan & Frail 1992; Thorsett et al. 1993). Moreover, accretion discs are expected to form at some phase of the evolution of neutron stars in a binary system, possibly giving birth to second-generation planets. Small bodies such as planetoids, asteroids, or comets may also orbit pulsars and occasionally fall onto them.
Circum-pulsar objects move in the centrifugally driven relativistic pulsar wind. The angular velocity Ω∗ of a rotating neutron star typically is higher than 10 rad s-1. The star behaves like an antenna (Deutsch 1955) emitting a power by magnetic dipole radiation that causes it to lose rotational energy at a rate 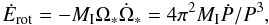 (1)where MI ≈ (2/5)MR2 is the neutron star’s moment of inertia (Lyne & Graham-Smith 1998). This power can be compared to the orbital energy of a pulsar planet. Consider, for example, the case of PSR B1257+12 and its planet “a”. Using the data in Tables 1 and 2, we can estimate the moment of inertia to be MI = 1. × 1038 kg m2, the star’s rotational energy loss to be Ėrot = −2. × 1027 W, and the planet’s orbital energy to be EG = GM∗MP/2a = 4. × 1032 J, where a stands for the planet’s semi-major axis. The planet and its environment intercept a fraction higher than or of the order of
(1)where MI ≈ (2/5)MR2 is the neutron star’s moment of inertia (Lyne & Graham-Smith 1998). This power can be compared to the orbital energy of a pulsar planet. Consider, for example, the case of PSR B1257+12 and its planet “a”. Using the data in Tables 1 and 2, we can estimate the moment of inertia to be MI = 1. × 1038 kg m2, the star’s rotational energy loss to be Ėrot = −2. × 1027 W, and the planet’s orbital energy to be EG = GM∗MP/2a = 4. × 1032 J, where a stands for the planet’s semi-major axis. The planet and its environment intercept a fraction higher than or of the order of 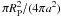 of this power. This captured power is used to heat the planet, to generate the current system described below, and to work on the planet’s motion as described in the accompanying paper (Mottez & Heyvaerts 2011, hereafter MH2). The planet’s radius can be inferred from its mass by assuming a terrestrial density (5000 kg m-3). The intercepted power Ėcapt is
of this power. This captured power is used to heat the planet, to generate the current system described below, and to work on the planet’s motion as described in the accompanying paper (Mottez & Heyvaerts 2011, hereafter MH2). The planet’s radius can be inferred from its mass by assuming a terrestrial density (5000 kg m-3). The intercepted power Ėcapt is 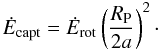 (2)For planet “a” of PSR B1257+12, we find, Ėcapt = 1.74 × 1018 Watt. If a substantial part of this power goes into planet’s motion, an orbital evolution time-scale of about 8 × 106 years may be expected. This is a short time scale by astronomical standards. It scales with the mass MP of the planet as
(2)For planet “a” of PSR B1257+12, we find, Ėcapt = 1.74 × 1018 Watt. If a substantial part of this power goes into planet’s motion, an orbital evolution time-scale of about 8 × 106 years may be expected. This is a short time scale by astronomical standards. It scales with the mass MP of the planet as 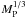 .
.
In this paper, we examine the interaction of these planets with the magnetized wind of their pulsar and discuss in MH2 the effect of this interaction on the long-term evolution of their orbital elements.
The energy flux carried by the wind of an ordinary star, such as the Sun, is low enough to have but negligible effect on the orbits of its planets. Stellar winds usually are asymptotically super-Alfvénic, by which we mean that they eventually become faster than the total Alfvén speed, which is associated with the modulus of the magnetic field. As a result, the planets are protected from a direct contact with the wind by a bow shock.
Pulsar winds are much different. In a first approximation, oblique rotator pulsars may be regarded as magnetic dipoles rotating at high angular velocity in vacuo, which causes a low frequency and large amplitude electromagnetic wave to be emitted, the wave character of which reveals itself in the wave zone, beyond the light cylinder, of radius r = c/Ω∗. In this zone, magnetic field lines become spiral-shaped and the azimuthal component of the magnetic field decreases as Bφ ~ r-1 while its radial component decreases as Br ~ r-2. The magnetic field becomes mostly azimuthal at large distances and at the equatorial latitudes were the planets are expected to be found. Aligned rotators are essentially rotating unipolar inductors that generate a highly relativistic MHD wind beyond the light cylinder in which the magnetic field also becomes predominantly azimuthal at large distances from the rotation axis. The field components Bφ and Br essentially vary with distance as indicated above, at least near the equatorial plane and when the flow is close to being radial. The power emitted by these objects is also of the order of Ėrot, given by Eq. (1) because the Poynting flux emitted through the light cylinder is comparable for wind or wave emission. We only consider aligned rotators in this paper. Their analysis is simplified because the magnetic field of the wind observed in the planet’s frame is close to being time-independent. The origin, acceleration, and structure of pulsar winds are not fully understood. A number of models have been proposed in the literature (Michel 1969; Henriksen & Rayburn 1971; Contopoulos et al. 1999; Michel 2005; Bucciantini et al. 2006). In spite of their diversity, they all conclude that the wind is dominated by the Poynting flux, although observations indicate that they turn into matter-dominated high-energy flows at large distances (Kirk et al. 2009). At distances of the order of an astronomical unit, pulsar winds are expected to still be Poynting-flux-dominated.This means that the electromagnetic energy density ~ 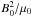 , μ0 being the magnetic permeability of vacuum, is much higher than the plasma energy density γ0ρ0c2, γ0 being its Lorentz factor and ρ0 the rest-mass density of this supposedly cold wind. These quantities refer to the observer’s frame. In these circumstances, Alfvénic perturbations propagate at a phase velocity close to the speed of light (Eq. (3)). Therefore, although it is highly relativistic, the wind flow may nevertheless be sub-Alfvénic, in the sense defined above. A planet in a Poynting-flux-dominated wind may remain unscreened from the wind by a bow shock and thus enter in direct contact with it.
, μ0 being the magnetic permeability of vacuum, is much higher than the plasma energy density γ0ρ0c2, γ0 being its Lorentz factor and ρ0 the rest-mass density of this supposedly cold wind. These quantities refer to the observer’s frame. In these circumstances, Alfvénic perturbations propagate at a phase velocity close to the speed of light (Eq. (3)). Therefore, although it is highly relativistic, the wind flow may nevertheless be sub-Alfvénic, in the sense defined above. A planet in a Poynting-flux-dominated wind may remain unscreened from the wind by a bow shock and thus enter in direct contact with it.
The interaction of a planet with a sub-Alfvénic plasma flow has been considered for moderately magnetized non-relativistic flows in connection with the interaction of the satellite Io with the plasma and magnetic field present in Jupiter’s magnetospheric environment. This interaction is driven by the inductive electromotive field that results from the motion of the satellite across Jupiter’s corotational magnetic field and plasma flow. The satellite acts as a (uniformly moving) unipolar inductor. Neubauer (1980) derived a nonlinear theory of this interaction. The Alfvén wing connecting Io and Jupiter is the only explored case of such a structure in the universe up to now, and it has been the object of recent studies concerning its overall structure (Chust et al. 2005; Hess et al. 2010), the possibility of particle acceleration (Hess et al. 2007b, 2009b), and its consequences on the radio emissions (Queinnec & Zarka 1998; Hess et al. 2007a, 2009a). In the present paper, we develop a theory that generalizes some of Neubauer’s results to highly magnetized (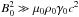 ) and relativistic plasma flows with Lorentz factors γ0 ≫ 1, when a planet immersed in the magnetized pulsar wind acts as a unipolar inductor and generates two stationary Alfvénic structures that emerge from the planet and extend far into the wind.
) and relativistic plasma flows with Lorentz factors γ0 ≫ 1, when a planet immersed in the magnetized pulsar wind acts as a unipolar inductor and generates two stationary Alfvénic structures that emerge from the planet and extend far into the wind.
2. A unipolar inductor in the pulsar wind
Let us consider a planet orbiting a pulsar in the relativistic flow of the emitted wind. Different reference frames can be involved in the description of the fluid motion. The frame where the neutron star is at rest is the observer’s frame. We denote it by RO. Because the planet velocity is low compared to the wind velocity, we may consider the planet to be at rest with respect to the neutron star, except when discussing the planet’s motion. The reference frame RO can then also be regarded as being the planet’s rest frame. Quantities observed in this frame are denoted by letters without any superscript, such as ρ or v. The unperturbed wind’s instantaneous rest frame in the vicinity of the planet is the “wind’s frame” RW. Quantities observed in this frame are denoted by letters with a prime superscript, such as ρ′. An index 0 refers to quantities associated with the unperturbed wind. The unperturbed wind velocity in RO is v0, its associated Lorentz factor is γ0, the unperturbed magnetic field is B0 and the wind’s density is ρ0. Because the wind plasma is supposedly cold, this mass density reduces to the (apparent) rest-mass density of particles. In the wind frame RW, the unperturbed wind density is its proper rest-mass density 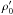 and its magnetic field is
and its magnetic field is 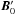 . They both differ from ρ0 and B0. In the presence of a perturbation, the instantaneous rest frame of the fluid is not RW, but another rest frame, RF. Quantities observed in this instantaneous rest frame are indicated by a subscript F.
. They both differ from ρ0 and B0. In the presence of a perturbation, the instantaneous rest frame of the fluid is not RW, but another rest frame, RF. Quantities observed in this instantaneous rest frame are indicated by a subscript F.
The perturbation generated by the planet in this flow is time-dependent in the wind’s frame. Because in the tenuous and highly magnetized pulsar wind the formal Alfvén velocity cA may exceed the speed of light, the derivation of the propagation velocity 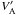 of Alfvénic perturbations must take into account the displacement current. In the wind’s rest frame:
of Alfvénic perturbations must take into account the displacement current. In the wind’s rest frame: 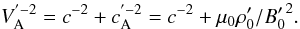 (3)If the flow is faster than the Alfvén velocity VA, the planet is preceded by a shock wave that defines a confined area where the flow is strongly modified. But if the flow is sub-Alfvénic, the planet is directly in contact with the wind. In the instantaneous rest frame of the wind plasma we expect, following the MHD approximation, the electric field to vanish. In the planet’s rest frame an electromotive field E = −v × B is generated, where B and v are the magnetic field and fluid velocity in the planet’s frame.
(3)If the flow is faster than the Alfvén velocity VA, the planet is preceded by a shock wave that defines a confined area where the flow is strongly modified. But if the flow is sub-Alfvénic, the planet is directly in contact with the wind. In the instantaneous rest frame of the wind plasma we expect, following the MHD approximation, the electric field to vanish. In the planet’s rest frame an electromotive field E = −v × B is generated, where B and v are the magnetic field and fluid velocity in the planet’s frame.
Using a model pulsar wind, it is possible to make an estimate of the electric field. One of the simplest such models was developed by Michel (1969). It includes the magnetic field and the star’s rotation as well as wind particles masses, but neglects the dipole inclination and the gravitation and assumes the wind flow to be radial. The unperturbed magnetic field B0 only has a radial poloidal component 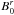 and an azimuthal toroidal component
and an azimuthal toroidal component 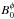 . The neglect of the latitudinal component
. The neglect of the latitudinal component 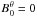 is justified near the equatorial plane and far enough from the inner magnetosphere (Contopoulos et al. 1999). For bodies orbiting near this plane, as circumpulsar planets probably do, this geometrical restriction is unimportant. Other models for steady-state axisymmetric winds have been developed since then (Beskin et al. 1998; Bucciantini et al. 2006). The stationary equations of an axisymmetric perfect MHD flow admit a set of integrals of motion along stream lines, such as the mass flux f and the magnetic flux Ψ, which for cold radial flows and radial poloïdal fields are defined by
is justified near the equatorial plane and far enough from the inner magnetosphere (Contopoulos et al. 1999). For bodies orbiting near this plane, as circumpulsar planets probably do, this geometrical restriction is unimportant. Other models for steady-state axisymmetric winds have been developed since then (Beskin et al. 1998; Bucciantini et al. 2006). The stationary equations of an axisymmetric perfect MHD flow admit a set of integrals of motion along stream lines, such as the mass flux f and the magnetic flux Ψ, which for cold radial flows and radial poloïdal fields are defined by  where all quantities refer to the unperturbed wind as seen in the observer’s frame. The MHD approximation E0 + v0 × B0 = 0 and the Faraday equation imply (Mestel 1961)
where all quantities refer to the unperturbed wind as seen in the observer’s frame. The MHD approximation E0 + v0 × B0 = 0 and the Faraday equation imply (Mestel 1961) 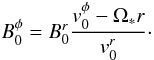 (6)In order to judge whether the planet is in superalfvénic motion with respect to the wind, we should assess whether the modulus of its velocity in the wind’s frame, which equals that of the wind in the observer’s frame, v0, is faster or slower than the propagation speed in the wind’s frame,
(6)In order to judge whether the planet is in superalfvénic motion with respect to the wind, we should assess whether the modulus of its velocity in the wind’s frame, which equals that of the wind in the observer’s frame, v0, is faster or slower than the propagation speed in the wind’s frame, 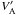 , defined by Eq. (3). The square of the ratio of these two velocities is given for an asymptotically radial wind by
, defined by Eq. (3). The square of the ratio of these two velocities is given for an asymptotically radial wind by 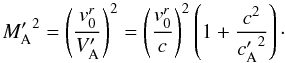 (7)Because the wind is supposedly radial,
(7)Because the wind is supposedly radial, 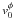 vanishes. This simplifies Eq. (6), which also shows that at distances much larger than the light cylinder radius,
vanishes. This simplifies Eq. (6), which also shows that at distances much larger than the light cylinder radius,
Input data of the pulsars.
the radial component of the magnetic field can be neglected compared to the azimuthal one. The Alfvén speed cA calculated in the observer’s frame is given using Eqs. (4) and (5) to express 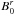 and ρ0 by
and ρ0 by 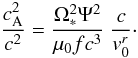 (8)The square of the Alfvén speed
(8)The square of the Alfvén speed 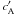 in the wind’s frame is a factor γ0 smaller than the square of the Alfvén speed cA in the observer’s frame because
in the wind’s frame is a factor γ0 smaller than the square of the Alfvén speed cA in the observer’s frame because 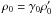 and
and 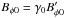 . The latter relation is a result of the vanishing of the electric field in the wind’s frame and of the velocity v0 being perpendicular to the azimuthal field. Then
. The latter relation is a result of the vanishing of the electric field in the wind’s frame and of the velocity v0 being perpendicular to the azimuthal field. Then ![\begin{equation} \label{eq_mach_a} {M'_{\rm A}}^2 = \left(\frac{v_{0}^r}{c}\right)^2 \left[1 + \frac{\gamma_0}{\sigma_0} \left(\frac{v_0^r}{c}\right)\right], \end{equation}](/articles/aa/full_html/2011/08/aa16530-11/aa16530-11-eq80.png) (9)where σ0 is the magnetization parameter:
(9)where σ0 is the magnetization parameter: 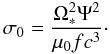 (10)In highly relativistic Poynting-flux-dominated outflows, as is expected for pulsar winds, σ0 ≫ 1. The models show that asymptotically the Lorentz factor γ0 approaches
(10)In highly relativistic Poynting-flux-dominated outflows, as is expected for pulsar winds, σ0 ≫ 1. The models show that asymptotically the Lorentz factor γ0 approaches 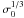 and thus (v0/c)2 approaches
and thus (v0/c)2 approaches 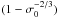 . From Eq. (9) it is found that to lowest order in an expansion in
. From Eq. (9) it is found that to lowest order in an expansion in 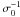 , the asymptotic value of
, the asymptotic value of 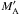 is
is 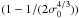 . Therefore the pulsar wind remains slower than the total Alfvén speed (3).
. Therefore the pulsar wind remains slower than the total Alfvén speed (3).
Because this result applies at distances much larger than the light cylinder radius, it is essentially valid wherever orbiting planets may be found. We therefore consider that the planets detected around pulsars orbit in a sub-Alfvénic relativistic pulsar wind.
In the numerical computations, we are less subtle and state that at the planetary distances, v0 ~ c and VA ~ c, every time it makes sense. Then, in first approximation, the unipolar inductor electric potential drop U (along the θ axis, i.e. perpendicular to the orbital plane) is 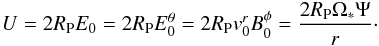 (11)Figure 1 provides a representation of the geometric configuration of the unipolar inductor.
(11)Figure 1 provides a representation of the geometric configuration of the unipolar inductor.
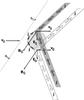 |
Fig. 1 Schematic view of a unipolar inductor. |
The rotation period of the pulsar PSR 1257+12 is P = 0,006s, which corresponds to Ω∗ = 1010 397 rad s-1 and its surface magnetic field is estimated to B∗ ≃ 8.8 × 108 G (Taylor et al. 2000). We assume a star radius R∗ = 10 km and a mass M∗ = 1.4 M⊙ (see Table 1).Data concerning this planet can be read in Table 2. We assumean Earth-like density of 5000 kg m-3. The flux 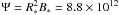 Wb. The semi-major axis, the planetary radius RP = (3MP/4πρP)1/3 and an estimate of U are given for each planet “a”, “b”, “c” orbiting this pulsar in Tables 2 and 3. Evidently, the inductor electric potential drop U (from pole to pole along the planet) is of the order of 1012 V.
Wb. The semi-major axis, the planetary radius RP = (3MP/4πρP)1/3 and an estimate of U are given for each planet “a”, “b”, “c” orbiting this pulsar in Tables 2 and 3. Evidently, the inductor electric potential drop U (from pole to pole along the planet) is of the order of 1012 V.
Input data concerning the planets: mass, radius, orbital period, semi-major axis, excentricity.
Electric potential drop and total electric current associated to the Alfvén wing.
For the pulsar PSR 1620-26, the rotation period is P = 0.011s, Ω∗ = 567 rad s-1, the surface magnetic field is estimated to B∗ = 3. × 109 G (Taylor et al. 2000). Still assuming that R∗ = 10 km, we find that Ψ = 3 × 1013 Wb. This pulsar has a white dwarf companion star. The neutron star mass can be estimated to M∗ = 1.35 M⊙ (Thorsett & Arzoumanian 1999; Sigurdsson et al. 2003). The planet is more distant from its star than in the case of PSR 1257+12 but the planetary radius is larger. The resulting potential drop U is still of the same order of magnitude.
We show in Sects. 3 − 5 that a planet in the wind generates two current systems that propagate far in space, forming a so-called Alfvén wing.
3. Equations of special-relativistic ideal MHD
In this section, the equations up to Eq. (23) are general to special relativity, and valid for quantities defined in any inertial reference frame. We use notations without prime and subscript. After Eq. (23), quantities without prime and subscript refer, as in the previous sections, only to the observer’s frame RO defined at the beginning of Sect. 2.
A condition for MHD to be valid is that the typical length scale L relevant to the flow be much longer than the particles Larmor radii ρL = γv⊥/ωc, where v⊥ is the typical velocity perpendicular to the magnetic field in the fluid’s frame, ωc the gyrofrequency and γ the particle’s Lorentz factor in the same frame. The energy of particles in a pulsar wind is a priori very high because the wind’s bulk Lorentz factor γ0 may be as high as 105 to 107. If, however, in the wind’s frame a significant part of this energy resided in perpendicular motions, particles would very quickly loose it by synchrotron radiation, even in a moderate magnetic field. Therefore, we may consider the pulsar wind particles to have negligible Larmor radii in the rest frame of the wind’s bulk flow, so that MHD is applicable on almost any scale.
The fourth component of position in space time is x4 = ct, t being the time measured in seconds in the given reference frame and c the speed of light. Greek indices label four-dimensional coordinates and components and Latin indices label Euclidean three-dimensional ones. The metric tensor of Minkowskian space is diagonal, with components η44 = + 1 and η11 = η22 = η33 = −1. ∇μ designates the partial derivative with respect to the space-time coordinate xμ. The notation ∇ designates the three-dimensional nabla operator. We use the dummy index rule. Special-relativistic MHD equations associate fluid equations with Maxwell’s equations, in which the displacement current and Poisson’s equation should be retained. The fluid equations consist of a conservation equation for particle number, valid in the absence of reactions among particle species, and of the four components of the energy and momentum conservation equations. The law of conservation of particle number is written as: 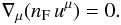 (12)The density nF is the proper spatial number density of particles, that is, their density measured in the instantaneous rest frame of the fluid. The four components uμ are those of the dimensionless four-velocity of the fluid in the considered rest frame:
(12)The density nF is the proper spatial number density of particles, that is, their density measured in the instantaneous rest frame of the fluid. The four components uμ are those of the dimensionless four-velocity of the fluid in the considered rest frame: 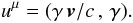 (13)The Lorentz factor γ refers here to the bulk fluid motion. The number density in the observer’s frame is the fourth component of the density-flux four-vector, nFγ. The equations of conservation of energy and momentum of matter are lumped in the four-tensorial equation:
(13)The Lorentz factor γ refers here to the bulk fluid motion. The number density in the observer’s frame is the fourth component of the density-flux four-vector, nFγ. The equations of conservation of energy and momentum of matter are lumped in the four-tensorial equation: 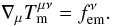 (14)The
(14)The 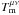 ’s are the components of the energy-momentum tensor of matter and the components
’s are the components of the energy-momentum tensor of matter and the components 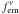 are those of the electromagnetic force density four-vector. By using Maxwell’s equations, this four-vector can be written in conservative form and Eq. (14) can be given the form:
are those of the electromagnetic force density four-vector. By using Maxwell’s equations, this four-vector can be written in conservative form and Eq. (14) can be given the form: 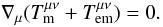 (15)The
(15)The 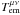 ’s are the components of the electromagnetic energy-momentum tensor. They can be expressed in terms of the electromagnetic field strength tensor F or in terms of the electric and magnetic fields observed in the chosen reference frame. Its time-time component is the electromagnetic energy density, its space-time components are the three components of the Poynting vector divided by c and its space-space components form a second-rank tensor of the three-dimensional Euclidean space, the Maxwell stress tensor:
’s are the components of the electromagnetic energy-momentum tensor. They can be expressed in terms of the electromagnetic field strength tensor F or in terms of the electric and magnetic fields observed in the chosen reference frame. Its time-time component is the electromagnetic energy density, its space-time components are the three components of the Poynting vector divided by c and its space-space components form a second-rank tensor of the three-dimensional Euclidean space, the Maxwell stress tensor: 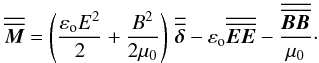 (16)The symbol δ represents the second rank unit tensor. The matter energy-momentum tensor of a cold pressureless fluid can be written in the absence of non-ideal effects such as viscosity as
(16)The symbol δ represents the second rank unit tensor. The matter energy-momentum tensor of a cold pressureless fluid can be written in the absence of non-ideal effects such as viscosity as 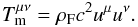 (17)Without internal heat, the number conservation Eq. (12) reduces to a conservation equation for proper mass, because in this case ρF = m nF, m being the rest mass of particles. Equation (12) can then be written in three-dimensional notations as
(17)Without internal heat, the number conservation Eq. (12) reduces to a conservation equation for proper mass, because in this case ρF = m nF, m being the rest mass of particles. Equation (12) can then be written in three-dimensional notations as 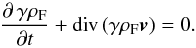 (18)Here, we need not solve the energy conservation equation because the medium is regarded as cold. We only consider the spatial components of the equivalent Eqs. (14) or (15). From Eq. (14) we obtain, denoting the charge and current density by ρe and j respectively:
(18)Here, we need not solve the energy conservation equation because the medium is regarded as cold. We only consider the spatial components of the equivalent Eqs. (14) or (15). From Eq. (14) we obtain, denoting the charge and current density by ρe and j respectively: 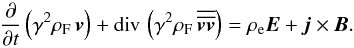 (19)From Eq. (15) we obtain the equivalent equation:
(19)From Eq. (15) we obtain the equivalent equation: 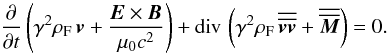 (20)The components of the Maxwell stress tensor
(20)The components of the Maxwell stress tensor 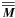 may be transformed to account for the perfect MHD relation
may be transformed to account for the perfect MHD relation  (21)The components of the electric field and those of the Maxwell stress tensor are easily calculated in a frame where the x-axis is taken to be along the direction of the fluid velocity v. Some algebra then yields the following expression, where the indices t (transverse) and l (longitudinal) refer to a component of a vector perpendicular or parallel to the velocity v of the fluid:
(21)The components of the electric field and those of the Maxwell stress tensor are easily calculated in a frame where the x-axis is taken to be along the direction of the fluid velocity v. Some algebra then yields the following expression, where the indices t (transverse) and l (longitudinal) refer to a component of a vector perpendicular or parallel to the velocity v of the fluid: 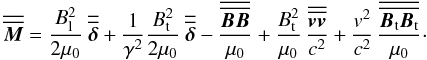 (22)The magnetic field evolution equation, deduced from Faraday’s equation and the perfect MHD relation, writes
(22)The magnetic field evolution equation, deduced from Faraday’s equation and the perfect MHD relation, writes 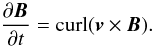 (23)The non-relativistic theory of Neubauer (1980) only considers the Alfvénic wake of the satellite. Indeed, fast MHD disturbances propagate isotropically in the low-βP limit and decrease in amplitude with distance from the source (βP is the ratio of the plasma pressure to the magnetic pressure). These disturbances do not create any concentrated current system. The slow mode propagates in a low-βP plasma much slower than Alfénic perturbations and the associated disturbances, though channelled by the magnetic field, soon become spatially separated from the Alfénic wake. Actually, slow-mode perturbations barely propagate at all in a cold pulsar wind and carry negligible current. The effects of compressive perturbations in the non-relativistic situation have been discussed by Wright & Schwartz (1990), who have shown that compressive plasma wave modes, though necessarily excited, contribute one order of magnitude less to the current flow and to the energy budget than shear Alfvén perturbations do. We therefore follow Neubauer in concentrating on purely Alfvénic motions. We assume that the fluid motions triggered when the planet passes by are sub-relativistic in the rest frame RW of the unperturbed wind and that the changes of the formal Alfvén velocity are similarly sub-relativistic. We do not assume, however, that the formal Alfvén speed calculated from the total field, B′/(μ0ρ′)1/2, is less than the speed of light. Our assumption of non-relativistic Alfvénic motions in RW implies that div v′ = 0. It does not follow, however, that the same relation also holds true in the observer’s frame RO because the wind flow is relativistic in this frame. In RW, the electric terms of the Maxwell stress tensor are of the order of v′2/c2 less than the magnetic terms and can be neglected. Accounting for the relation div v′ = 0, Eq. (23) can be written as
(23)The non-relativistic theory of Neubauer (1980) only considers the Alfvénic wake of the satellite. Indeed, fast MHD disturbances propagate isotropically in the low-βP limit and decrease in amplitude with distance from the source (βP is the ratio of the plasma pressure to the magnetic pressure). These disturbances do not create any concentrated current system. The slow mode propagates in a low-βP plasma much slower than Alfénic perturbations and the associated disturbances, though channelled by the magnetic field, soon become spatially separated from the Alfénic wake. Actually, slow-mode perturbations barely propagate at all in a cold pulsar wind and carry negligible current. The effects of compressive perturbations in the non-relativistic situation have been discussed by Wright & Schwartz (1990), who have shown that compressive plasma wave modes, though necessarily excited, contribute one order of magnitude less to the current flow and to the energy budget than shear Alfvén perturbations do. We therefore follow Neubauer in concentrating on purely Alfvénic motions. We assume that the fluid motions triggered when the planet passes by are sub-relativistic in the rest frame RW of the unperturbed wind and that the changes of the formal Alfvén velocity are similarly sub-relativistic. We do not assume, however, that the formal Alfvén speed calculated from the total field, B′/(μ0ρ′)1/2, is less than the speed of light. Our assumption of non-relativistic Alfvénic motions in RW implies that div v′ = 0. It does not follow, however, that the same relation also holds true in the observer’s frame RO because the wind flow is relativistic in this frame. In RW, the electric terms of the Maxwell stress tensor are of the order of v′2/c2 less than the magnetic terms and can be neglected. Accounting for the relation div v′ = 0, Eq. (23) can be written as 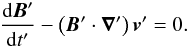 (24)Considering Eqs. (21) and (22), the equation of motion (20) becomes, in RW,
(24)Considering Eqs. (21) and (22), the equation of motion (20) becomes, in RW, 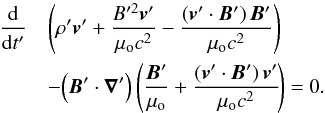 (25)
(25)
4. An Alfvénic first integral
The computation of the non relativistic Alfvén wing given by Neubauer (1980) is based upon the fact that in simple non-linear Alfvénic wave motions, the velocity Vs = v − s cA is a first integral. In this relation, v is the fluid’s velocity, cA the vectorial Alfvén velocity associated with the perturbed field, and the sign s = ± 1 depends on the sense of propagation of the perturbation. This relation can be transposed in a differential form as dB = kdv, where k = (μ0ρ)1/2. Moreover, the modulus of the magnetic field is a time invariant and, because of the uniform boundary conditions B = B0, this modulus is constant over the whole space.
As Neubauer, we look for a solution where dB′ = kdv′ and where B′ is constant. Then, setting b′ = B′/B′ and 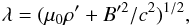 (26)we can write Eqs. (24) and (25) in the form
(26)we can write Eqs. (24) and (25) in the form ![\begin{eqnarray} && \lambda^2 \frac{{\rm d} \vec{v}'}{ {{\rm d}} t'} \!-B'^2 (\vec{b}'\cdot\nabla') \vec{b}' \! -\!\frac{B'^2}{c^2} \left[\frac{{\rm d} v'_\parallel \vec{b}'}{{\rm d} t'} \! + \! (\vec{b}'\cdot\nabla') (v'_\parallel \vec{v}')\right]\!=0 \label{motionAlfrefvent_2} \\ \label{inducdsurdt_2} && \frac{{\rm d} {\vec{b}}' }{{\rm d} t'} - ({\vec{b}}' \cdot {\boldsymbol{\nabla}}') {\vec{v}}' = 0, \end{eqnarray}](/articles/aa/full_html/2011/08/aa16530-11/aa16530-11-eq200.png) where
where 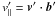 . The two first terms of Eq. (27) are analogous to those of classical MHD, when VA ≪ c. The two others are specific to fast variations of the electric field, when the displacement current is taken into account. We solve this system in the following way: we first ignore the last two terms of Eq. (27) and solve the resulting system (27) − (28), which can then be written as
. The two first terms of Eq. (27) are analogous to those of classical MHD, when VA ≪ c. The two others are specific to fast variations of the electric field, when the displacement current is taken into account. We solve this system in the following way: we first ignore the last two terms of Eq. (27) and solve the resulting system (27) − (28), which can then be written as 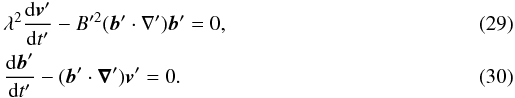 We then check whether the last two terms in Eq. (27) vanish or are negligible. These terms are
We then check whether the last two terms in Eq. (27) vanish or are negligible. These terms are ![\begin{equation} \label{motionAlfrefvent_complement} \frac{B'^2}{c^2} \left[ \frac{{\rm d} v'_\parallel \vec{b}'}{{\rm d} t'} + (\vec{b}'\cdot\nabla') (v'_\parallel \vec{v}')\right] \, . \end{equation}](/articles/aa/full_html/2011/08/aa16530-11/aa16530-11-eq204.png) (31)Considering Eqs. (29) and (30), the proportionality of dB′ and dv′ is obtained for k = sλ, and these two equations become equivalent to
(31)Considering Eqs. (29) and (30), the proportionality of dB′ and dv′ is obtained for k = sλ, and these two equations become equivalent to  Equation (32) has a first integral
Equation (32) has a first integral 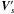 ,
, 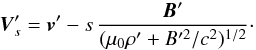 (34)In the region not perturbed by the planet, v′ = 0, and
(34)In the region not perturbed by the planet, v′ = 0, and 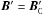 . Therefore,
. Therefore,  In order of magnitude, λ ~ B′/c, and the approximation v′ ≪ c implies that
In order of magnitude, λ ~ B′/c, and the approximation v′ ≪ c implies that 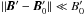 . Therefore, this is equivalent to an hypothesis of linear perturbation. This remark also holds for the computations of Neubauer (1980). At this stage, it is necessary to evaluate the terms in Eq. (31). Using the above relations, these terms are
. Therefore, this is equivalent to an hypothesis of linear perturbation. This remark also holds for the computations of Neubauer (1980). At this stage, it is necessary to evaluate the terms in Eq. (31). Using the above relations, these terms are 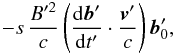 (38)where
(38)where 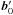 is the direction of the unperturbed magnetic field in the wind’s frame of reference. The quantity in Eq. (38) does not vanish but it is negligible as long as v′ ≪ c in comparison to the terms in Eq. (29), which are of the order of (B′2/c)db′/dt′. Therefore, in the linear approximation, the solution given by Eqs. (32 − 37) is correct.
is the direction of the unperturbed magnetic field in the wind’s frame of reference. The quantity in Eq. (38) does not vanish but it is negligible as long as v′ ≪ c in comparison to the terms in Eq. (29), which are of the order of (B′2/c)db′/dt′. Therefore, in the linear approximation, the solution given by Eqs. (32 − 37) is correct.
The first integral of Eq. (34) must now be computed in the observer’s frame of reference RO. It will be used in the next section to derive the value of the electric current associated to the Alfvén wings.Let us write the velocity and the magnetic field as the sum of a longitudinal component, parallel to v0, and a transverse vector component.  The transforms of the velocity and of the magnetic field are
The transforms of the velocity and of the magnetic field are 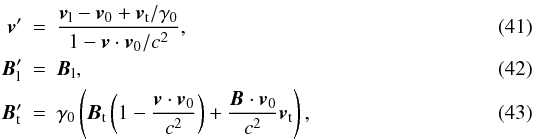 where γ0 is the Lorentz factor of the unperturbed wind. For the transform of the magnetic field, Eq. (21) has been taken into account. Equation (34) becomes
where γ0 is the Lorentz factor of the unperturbed wind. For the transform of the magnetic field, Eq. (21) has been taken into account. Equation (34) becomes 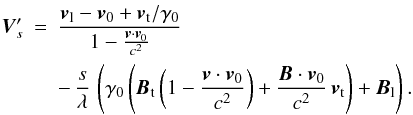 (44)For a first order development, we note
(44)For a first order development, we note 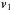 the velocity perturbation and
the velocity perturbation and 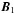 the magnetic perturbation,
the magnetic perturbation,  (45)To the first order, Eq. (44) becomes
(45)To the first order, Eq. (44) becomes 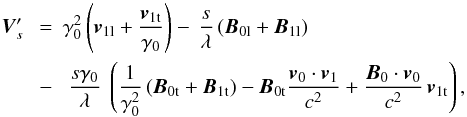 (46)which can be rewritten
(46)which can be rewritten 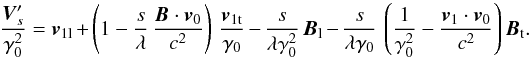 Considering the purely geometric relation
Considering the purely geometric relation 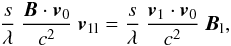 (47)we have
(47)we have 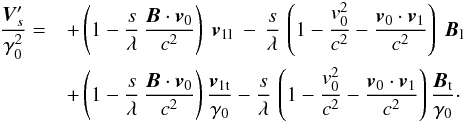 (48)Because this vector is constant, its longitudinal and transverse parts relatively to the constant vector v0 are also two distinct constant entities. We can recombine the longitudinal and transverse components in the following way
(48)Because this vector is constant, its longitudinal and transverse parts relatively to the constant vector v0 are also two distinct constant entities. We can recombine the longitudinal and transverse components in the following way 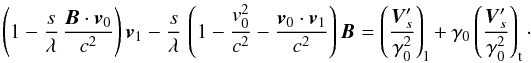 Then we can define a new first integral vector,
Then we can define a new first integral vector, 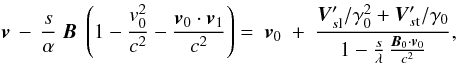 (49)where the constant number α is defined by
(49)where the constant number α is defined by 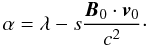 (50)In spite of a greater complexity, this vector presents some analogy with the first integral found in the non-relativistic case by Neubauer (written in the first lines of the present section). This will be used in the next section to derive the current flowing along the Alfvén wing, in a similar way to those developed in Neubauer (1980). The parameter λ, given in Eq. (26), can be expressed as a function of the unperturbed wind parameters,
(50)In spite of a greater complexity, this vector presents some analogy with the first integral found in the non-relativistic case by Neubauer (written in the first lines of the present section). This will be used in the next section to derive the current flowing along the Alfvén wing, in a similar way to those developed in Neubauer (1980). The parameter λ, given in Eq. (26), can be expressed as a function of the unperturbed wind parameters, ![\begin{equation} \lambda = \left[\mu_0 \rho_0'+c^{-2} {B}_{{\rm l} 0}^2+ c^{-2} \gamma_0^{-2} B_{{\rm t} 0}^2 \right] ^{1/2}. \end{equation}](/articles/aa/full_html/2011/08/aa16530-11/aa16530-11-eq236.png) (51)Because ∇·v′ = 0, the density ρ′ is invariant along any line of flow; that is why we noted it
(51)Because ∇·v′ = 0, the density ρ′ is invariant along any line of flow; that is why we noted it 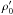 instead. We set
instead. We set  These are mixtures of the magnetic field in the frame RO of the observer and of the density in the proper frame RW of the wind in terms of which the factor λ can be written as
These are mixtures of the magnetic field in the frame RO of the observer and of the density in the proper frame RW of the wind in terms of which the factor λ can be written as 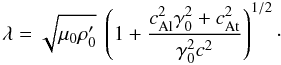 (55)
(55)
5. Current carried by an Alfvén wing
Neubauer (1980) has shown that the electric current density carried by an Alfvén wing is related to the divergence of the electric field through the relation μ0 j·Vs = Σ div E, where the conductance 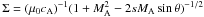 , cA being the classical Alfvén velocity, and MA = v0/cA. In this section, we derive an analogous relation for the relativistic plasma flow, keeping our previous assumptions. From the perfect MHD relation (21) we calculate div E in the observer’s frame RO:
, cA being the classical Alfvén velocity, and MA = v0/cA. In this section, we derive an analogous relation for the relativistic plasma flow, keeping our previous assumptions. From the perfect MHD relation (21) we calculate div E in the observer’s frame RO: 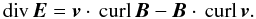 (56)To the first order,
(56)To the first order, 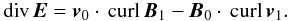 (57)From Eq. (49), the curl of the velocity is
(57)From Eq. (49), the curl of the velocity is ![\begin{eqnarray} \label{curl_v} {\mathrm{curl}} \, {\vec{v}_1} &=& \frac{s}{\gamma_0^2 \alpha} \, {\mathrm{curl}} \, {\vec{B}_1} -\frac{s}{\alpha c^2} {\mathrm{curl}} \, [{\vec{B}_0} ({\vec{v}_0} \cdot {\vec{v}_1})] \\ &=& \frac{s}{\alpha \gamma_0^2} \, {\mathrm{curl}} \, {\vec{B}_1} -\frac{s}{\alpha c^2} {\vec{N}} \times {\vec{B}_0}, \end{eqnarray}](/articles/aa/full_html/2011/08/aa16530-11/aa16530-11-eq247.png) where
where 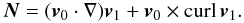 (60)Including Eqs. (58) in (57), we find
(60)Including Eqs. (58) in (57), we find 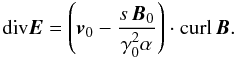 (61)For further convenience, we note
(61)For further convenience, we note 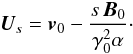 (62)In RO, the Alfvén wave is stationary, therefore the partial time derivatives are null, and Ampère’s equation is simply
(62)In RO, the Alfvén wave is stationary, therefore the partial time derivatives are null, and Ampère’s equation is simply 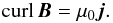 (63)Then, from Eq. (61),
(63)Then, from Eq. (61), 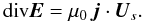 (64)Let Js be the projection of the current density along the direction of the constant vector Us of Eq. (49). Equation (64) can be written as
(64)Let Js be the projection of the current density along the direction of the constant vector Us of Eq. (49). Equation (64) can be written as 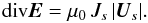 (65)Let θ = π/2 − (B0,v0) be the complement of the angle made in RO by the ambient magnetic field and the flow velocity. The modulus of Us (Eq. (49)) is
(65)Let θ = π/2 − (B0,v0) be the complement of the angle made in RO by the ambient magnetic field and the flow velocity. The modulus of Us (Eq. (49)) is 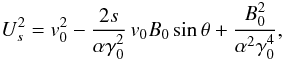 (66)and then
(66)and then ![\begin{eqnarray} J_s &=& \Sigma_{\rm A} \ {\mathrm{div}}\, {\vec{E}} \label{JsSigmaA},\\ \Sigma_{\rm A} &=& \frac{ \gamma_0^2 \left[ \left( 1+\frac{c_{{\rm A l}}^2 \gamma_0^2+c_{{\rm A t}}^2}{ \gamma_0^2 c^2}\right)^{1/2} -s \frac{v_0 c_{\rm A}}{c^2} \sin \theta \right] }{\mu_0 c_{\rm A} \left( 1 + X_{\rm A}^2 -2 s X_{\rm A} \sin \theta \right)^{1/2} }, \label{SigmaA}\\ X_{\rm A} &=& \frac{v_0 \alpha \gamma_0^2}{B_0}= \frac{v_0}{c_{\rm A}} \gamma_0^2 \left( 1+\frac{c_{{\rm A l}}^2 \gamma_0^2+c_{{\rm A t}}^2}{ \gamma_0^2 c^2}\right)^{1/2} -s \frac{v_0^2 \gamma_0^2}{c^2} \sin \theta. \end{eqnarray}](/articles/aa/full_html/2011/08/aa16530-11/aa16530-11-eq258.png) When cA ≪ c, we are in the conditions studied by Neubauer, and we find the same result as in his paper (given in the beginning of this section). If γ0 ≫ 1 and cA ≫ c, that is relevant for a pulsar’s wind, XA ≫ 1 and
When cA ≪ c, we are in the conditions studied by Neubauer, and we find the same result as in his paper (given in the beginning of this section). If γ0 ≫ 1 and cA ≫ c, that is relevant for a pulsar’s wind, XA ≫ 1 and 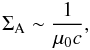 (70)a conductance that is associated with the impedance of vacuum, equal to ℛ∞ ≡ μ0c = 377 Ohm. The two directions of the current flows correspond to the invariant vectors U + and U − . The geometrical configuration of this solution is shown in Fig. 2.
(70)a conductance that is associated with the impedance of vacuum, equal to ℛ∞ ≡ μ0c = 377 Ohm. The two directions of the current flows correspond to the invariant vectors U + and U − . The geometrical configuration of this solution is shown in Fig. 2.
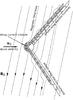 |
Fig. 2 Alfvénic wake of the planet seen from above the equatorial plane. |
Now, we can quite directly adapt the conclusions of Neubauer (1980) to the relativistic inductor. This author considers a specific model of the wake-aligned currents in the Alfvén wing, which he assumes to be flowing on the surface of an infinite cylinder tangent to the planet’s surface, with its axis parallel to Alfvénic characteristics. Equation (67) implies that for these currents the divergence of the electric field vanishes except on the cylinder’s surface. The electric potential can then be found by solving Laplace’s equation, assuming the electric field inside the cylinder to be constant, of intensity Ei. This simple assumption is motivated by the difficulty to solve for the electromagnetic and flow structure in the immediate vicinity of the solid body. The free parameter Ei is the electric field along the planet caused by its ionosphere or surface internal resistance. At large distances from the wake, the electric field converges to the convection field E0 given by the perfect MHD relation (21) in the unperturbed wind. Once the electric potential is found, the magnetic field and current distribution in the wake can be deduced, using in particular Eq. (67).
Neubauer gives useful expressions for the total current I flowing along an Alfvén wing and for the Joule dissipation power in the solid body, ĖJ. Writing RP for the planet’s radius, he obtains 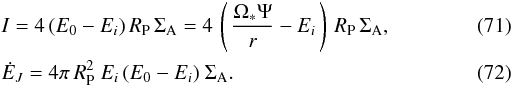 \arraycolsep1.75ptThe Joule dissipation is maximum when Ei = E0/2. In our estimations, we shall use Neubauer’s values for I and ĖJ. Up to unimportant numerical factors, the results (71) − (72) are simply obtained by considering the current I to be driven in a resistive load of resistance
\arraycolsep1.75ptThe Joule dissipation is maximum when Ei = E0/2. In our estimations, we shall use Neubauer’s values for I and ĖJ. Up to unimportant numerical factors, the results (71) − (72) are simply obtained by considering the current I to be driven in a resistive load of resistance 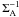 by a generator of electromotive force U0 = 2E0RP applied on two opposite sides of a planet of internal resistance ℛP. Neubauer’s parameter Ei is related to ℛP by
by a generator of electromotive force U0 = 2E0RP applied on two opposite sides of a planet of internal resistance ℛP. Neubauer’s parameter Ei is related to ℛP by 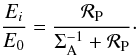 (73)It is very difficult to know precisely the value of ℛP. We therefore regard it, or Ei, as unspecified parameters. The planet’s electrical resistance depends on its constitution, on the path of electric currents in it, and on the existence or absence of some form of ionosphere. The conductivity of terrestrial silicate rock is of the order of σrock = 10-3 Mho m-1 (Cook 1973). Assuming that the wake current closes through a layer of thickness h at the surface of the planet, the electrical resistance ℛP of the latter would be of the order of
(73)It is very difficult to know precisely the value of ℛP. We therefore regard it, or Ei, as unspecified parameters. The planet’s electrical resistance depends on its constitution, on the path of electric currents in it, and on the existence or absence of some form of ionosphere. The conductivity of terrestrial silicate rock is of the order of σrock = 10-3 Mho m-1 (Cook 1973). Assuming that the wake current closes through a layer of thickness h at the surface of the planet, the electrical resistance ℛP of the latter would be of the order of 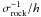 , which numerically amounts to ℛP ~ (hkm)-1. As soon as h exceeded a few meters, which for this low conductivity is reached in a very short time, ℛP would be comparable to or less than ℛ∞, even though the rock intrinsically is a poor conductor. A second-generation planet, which could be partly metallic or a partly molten body, could have lower resistances.
, which numerically amounts to ℛP ~ (hkm)-1. As soon as h exceeded a few meters, which for this low conductivity is reached in a very short time, ℛP would be comparable to or less than ℛ∞, even though the rock intrinsically is a poor conductor. A second-generation planet, which could be partly metallic or a partly molten body, could have lower resistances.
6. Discussion and conclusion
We showed that a planet orbiting a pulsar develops a system of Alfvén wings caused by its interaction with the sub-Alfvénic Poynting-flux-dominated pulsar wind. A system of strong electric currents is set. Although this current cannot reach the inner pulsar’s magnetosphere, it is nevertheless interesting to compare it to the current at the origin of the pulsar’s magnetospheric activity, the Goldreich-Julian current JGJ. This latter current results from the electromotive field generated by the fast rotation of the highly magnetized neutron star and its surrounding magnetosphere. For a dipole magnetic field, the Goldreich-Julian current density is 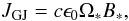 (74)and the total current is of the order of
(74)and the total current is of the order of 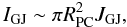 (75)where
(75)where 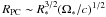 is the polar cap radius (Kirk et al. 2009). Various values of the Goldreich-Julian current IGJ are given in Table 1. A look at Table 3 allows for comparisons between IAW and IGJ. Obviously, for the four known planets the electric current in the Alfvén wings is lower than the Goldreich-Julian current by three orders of magnitude. It is also much lower for small bodies. But a planet orbiting a “standard” pulsar with a typical 1 second period and 1012 G magnetic field would have an Alfvén wing current IAW of similar amplitude as the Goldreich-Julian current IGJ. This is not negligible when we see that IGJ is the basic engine of the pulsar’s electrodynamics.
is the polar cap radius (Kirk et al. 2009). Various values of the Goldreich-Julian current IGJ are given in Table 1. A look at Table 3 allows for comparisons between IAW and IGJ. Obviously, for the four known planets the electric current in the Alfvén wings is lower than the Goldreich-Julian current by three orders of magnitude. It is also much lower for small bodies. But a planet orbiting a “standard” pulsar with a typical 1 second period and 1012 G magnetic field would have an Alfvén wing current IAW of similar amplitude as the Goldreich-Julian current IGJ. This is not negligible when we see that IGJ is the basic engine of the pulsar’s electrodynamics.
The practical consequences of such a current are expected to be of two kinds: we show in a companion paper (Mottez & Heyvaerts 2011) that it can exert an ortho-radial force upon the planet that can, if the magnetic to mechanical energy coupling is efficient enough, have an incidence on the orbit of small circum-pulsar objects such as asteroids or comets. The second incidence, more relevant to massive objects such as planets, is a possibly associated electromagnetic signature, which might be detectable.
Does the Alfvén wing dominate in terms of energy, the direct mechanical action exerted by the wind on the companion? To answer this question, we can compare the flux of magnetic energy, FM with the flux of mechanical energy, FK, received the companion by direct impingement. The ratio of the Poynting flux to the mechanical energy flux is 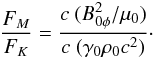 (76)Introducing σ0 and Ψ with the Eqs. ((5), (6), (10)), and v0r ~ c,
(76)Introducing σ0 and Ψ with the Eqs. ((5), (6), (10)), and v0r ~ c, 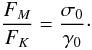 (77)In the case discussed above, where
(77)In the case discussed above, where 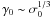 , and σ0 ≫ 1,
, and σ0 ≫ 1, 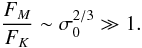 (78)Therefore, we expect that for a Poynting-flux-dominated wind most of the energy exchange with the pulsar’s companion comes from the magnetic field. Equation (72) provides a more precise insight of what is effectively involved in the wind-companion interaction. Considering Ei = E0 and E0 ~ cBφ,
(78)Therefore, we expect that for a Poynting-flux-dominated wind most of the energy exchange with the pulsar’s companion comes from the magnetic field. Equation (72) provides a more precise insight of what is effectively involved in the wind-companion interaction. Considering Ei = E0 and E0 ~ cBφ, 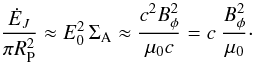 (79)This amounts to the totality of the Poynting flux intercepted by the pulsar’s companion. It is therefore higher (by a factor
(79)This amounts to the totality of the Poynting flux intercepted by the pulsar’s companion. It is therefore higher (by a factor 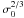 ) than the mechanical energy captured by direct impigement.
) than the mechanical energy captured by direct impigement.
We assume that the wind velocity v0 is slower than the Alfvén wave velocity VA. Otherwise, there would be no Alfvén wing. For an ideal MHD radial wind, the Lorentz factor asymptotically approaches 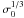 and Eq. (9) shows that the wind remains sub-Alfvénic at any distance. If, however, it is formally considered that the asymptotic Lorentz factor γ0∞ scales as σa instead, with an exponent a ≠ 1/3, then if a > 1/3, MA∞ = 1 + σa − 1 − σ − 2a ~ 1 + σa − 1 > 1. Therefore, in that case, a transition from a sub-Alfvénic to a super-Alfvénic wind occurs at a finite distance. Observations of the equatorial sectors of winds driving pulsar wind nebulae show lower values of the asymptotic magnetization (Kennel & Coroniti 1984a,b; Gaensler et al. 2002), and various authors suggest that the asymptotic value of the Lorentz factor is rather γ∞ ~ σ0. Arons (2004) argues that dissipation must occur in the asymptotic wind zone to understand the observed high Lorentz factors and the low magnetization. Begelman & Li (1994) show that when the flux tubes diverge faster than radially, the fast magnetosonic point can occur closer to the light cylinder, implying an even closer Alfvénic point. Then, the existence of Alfvén wings would depend on the distance from the star to the planet, combined with the effect of a non-radial diverging wind flow, or dissipation.
and Eq. (9) shows that the wind remains sub-Alfvénic at any distance. If, however, it is formally considered that the asymptotic Lorentz factor γ0∞ scales as σa instead, with an exponent a ≠ 1/3, then if a > 1/3, MA∞ = 1 + σa − 1 − σ − 2a ~ 1 + σa − 1 > 1. Therefore, in that case, a transition from a sub-Alfvénic to a super-Alfvénic wind occurs at a finite distance. Observations of the equatorial sectors of winds driving pulsar wind nebulae show lower values of the asymptotic magnetization (Kennel & Coroniti 1984a,b; Gaensler et al. 2002), and various authors suggest that the asymptotic value of the Lorentz factor is rather γ∞ ~ σ0. Arons (2004) argues that dissipation must occur in the asymptotic wind zone to understand the observed high Lorentz factors and the low magnetization. Begelman & Li (1994) show that when the flux tubes diverge faster than radially, the fast magnetosonic point can occur closer to the light cylinder, implying an even closer Alfvénic point. Then, the existence of Alfvén wings would depend on the distance from the star to the planet, combined with the effect of a non-radial diverging wind flow, or dissipation.
Let us return to the hypothesis of a planet in a sub-Alfvénic wind. The present work provides only orders of magnitude estimates for the emitted current. The behaviour of the Alfvén wing at close vicinity of the planet would need a more detailed study. We considered here, as in many other papers concerning pulsars, the case of a neutron star magnetic field that is aligned with the rotation axis. The study of oblique rotators raises more complicated problems. The pulsar wind may have different properties and carry even in the equatorial plane a non-zero Bθ component that oscillates at the pulsar rotation rate Ω∗. An Alfvén wavelength (propagating at ~ c) with P = 6 ms (case of PSR B1257+12) is of the order of 1800 km, which is less than a typical planetary radius. This would question the assumption of stationarity, though less severely for a standard pulsar with P ~ 1s, where the wavelength (about 300 000 km) would be much larger than the planetary radius.
In spite of the preliminary character of our model, our study shows that the consideration of Alfvén wings associated to planets that orbit pulsars deserve some attention.
The question of the radio emissions that are possibly associated to the Alfvén wings will be addressed in a
forthcoming paper. These emissions would provide astronomers with observational data relevant to the wind/planet interaction.
Acknowledgments
This paper was inspired by discussions with Silvano Bonazzola (LUTH, Obs. Paris-Meudon). This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and The Extrasolar Planets Encyclopaedia (http://exoplanet.eu/index.php), maintained by Jean Schneider at the LUTH, and the SIO, at the Observatoire de Paris, France.
References
- Arons, J. 2004, Adv. Space Res., 33, 466 [Google Scholar]
- Begelman, M. C., & Li, Z. 1994, ApJ, 426, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, V. S., Kuznetsova, I. V., & Rafikov, R. R. 1998, MNRAS, 299, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Thompson, T. A., Arons, J., Quataert, E., & Del Zanna, L. 2006, MNRAS, 368, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Chust, T., Roux, A., Kurth, W. S., et al. 2005, Planet. Space Sci., 53, 395 [Google Scholar]
- Contopoulos, I., Kazanas, D., & Fendt, C. 1999, ApJ, 511, 351 [Google Scholar]
- Cook, A. H. 1973, Phys. Earth Planets [Google Scholar]
- Deutsch, A. J. 1955, Ann. Astrophys., 18, 1 [NASA ADS] [Google Scholar]
- Gaensler, B. M., Arons, J., Kaspi, V. M., et al. 2002, ApJ, 569, 878 [CrossRef] [Google Scholar]
- Henriksen, R. N., & Rayburn, D. R. 1971, MNRAS, 152, 323 [NASA ADS] [Google Scholar]
- Hess, S., Mottez, F., & Zarka, P. 2007a, J. Geophys. Res., 112, 11212 [NASA ADS] [CrossRef] [Google Scholar]
- Hess, S., Zarka, P., & Mottez, F. 2007b, Planet. Space Sci., 55, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Hess, S., Mottez, F., & Zarka, P. 2009a, Geophys. Res. Lett., 36, 14101 [NASA ADS] [CrossRef] [Google Scholar]
- Hess, S., Zarka, P., Mottez, F., & Ryabov, V. B. 2009b, Planet. Space Sci., 57, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Hess, S. L. G., Delamere, P., Dols, V., Bonfond, B., & Swift, D. 2010, J. Geophys. Res., 115, 6205 [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984a, ApJ, 283, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984b, ApJ, 283, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Lyubarsky, Y., & Petri, J. 2009, in Astrophys. Space Sci. Lib., ed. W. Becker, 357, 421 [Google Scholar]
- Lyne, A. G., & Graham-Smith, F. 1998, Pulsar astronomy (Cambridge University Press), Cambridge Astrophys. Ser., 31 [Google Scholar]
- Mestel, L. 1961, MNRAS, 122, 473 [NASA ADS] [Google Scholar]
- Michel, F. C. 1969, ApJ, 158, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C. 2005, in Rev. Mex. Astron. Astrofis. Conf. Ser., 23, ed. S. Torres-Peimbert, & G. MacAlpine, 27 [Google Scholar]
- Mottez, F., & Heyvaerts, J. 2011, A&A, 532, A22 [Google Scholar]
- Neubauer, F. M. 1980, J. Geophys. Res., 85, 1171 [Google Scholar]
- Queinnec, J., & Zarka, P. 1998, J. Geophys. Res., 103, 26649 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., Richer, H. B., Hansen, B. M., Stairs, I. H., & Thorsett, S. E. 2003, Science, 301, 193 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Taylor, J. H., Manchester, R. N., & Lyne, A. G. 2000, VizieR Online Data Catalog, 7189, [Google Scholar]
- Thorsett, S. E., & Arzoumanian, Z. 1999, in Pulsar Timing, General Relativity and the Internal Structure of Neutron Stars, ed. Z. Arzoumanian, F. Van der Hooft, & E. P. J. van den Heuvel, 73 [Google Scholar]
- Thorsett, S. E., Arzoumanian, Z., & Taylor, J. H. 1993, ApJ, 412, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, A. N., & Schwartz, S. J. 1990, J. Geophys. Res., 95, 4027 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Input data concerning the planets: mass, radius, orbital period, semi-major axis, excentricity.
Electric potential drop and total electric current associated to the Alfvén wing.
All Figures
 |
Fig. 1 Schematic view of a unipolar inductor. |
| In the text | |
 |
Fig. 2 Alfvénic wake of the planet seen from above the equatorial plane. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


