| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200913788 | |
| Published online | 02 August 2011 | |
Probing dark matter haloes of spiral galaxies at poorly explored distances using satellite kinematics⋆
1
European Southern Observatory, Alonso de Cordova 3107, Santiago, Chile
e-mail: iyegorov@eso.org
2
Dipartimento di Astronomia, Università di Padova, Padova, Italy
e-mail: alessandro.pizzella@unipd.it
3
SISSA International School for Advanced Studies, via Beirut 4, 34013 Trieste, Italy
e-mail: salucci@sissa.it
Received: 2 December 2009
Accepted: 1 June 2011
Aims. We present the results of a pilot project designed to study the distribution of dark matter haloes out to very large radii in spiral galaxies. As dynamical probe, we use their rotation curves and the motions of satellite galaxies. In this pilot stage, we observed seven late-type spiral galaxies of about the same luminosity MR ~ −22 (and approximately the same mass). We investigate the kinematics of these galaxies, and the radial and angular distribution of their satellites.
Methods. Using VIMOS at the VLT, we carried out a spectroscopic survey in seven 14′ × 14′ fields each around a late-type isolated spiral galaxy. We obtained radial velocities and spatial distributions for 77 candidate satellites. After removing the interlopers, we are left with 61 true satellites. In combination with the rotation curves of the primary galaxies, satellites are used to probe the gravitational potential of the primaries and derive the dark matter halo properties by means of standard mass modeling techniques.
Results. We find (a) that the dark matter haloes of luminous spirals (MR ~ −22) have virial radii of ~400 kpc and virial masses of 3.5 × 1012 M⊙; (b) that the radial velocity and angular distributions of the satellites around the primaries are isotropic; and (c) that the resulting mass distribution is in good agreement with that found in the optical regions of spirals and described by the universal rotation curve of spirals once extrapolated to large radii. The results obtained in this pilot phase of the project are already interesting and limited only by small number statistics. The full project involving an order of magnitude more targets, would very likely provide us with a definitive picture of the dark matter distribution around spirals out to their virial radii and beyond.
Key words: galaxies: kinematics and dynamics / galaxies: halos / galaxies: dwarf / galaxies: structure / dark matter
© ESO, 2011
1. Introduction
In the past few decades, it has been revealed that dark matter (DM) haloes extend far beyond the optical boundaries of galaxies. However, their actual “sizes” and, above all, their density distribution outside the luminous regions, are still quite unknown. The inner regions of DM haloes are studied using several methods including the analysis of both rotation curves for spiral galaxies (Rubin et al. 1980; Bosma 1981; Persic et al. 1996), and velocity dispersions for ellipticals (Kronawitter et al. 2000; Cappellari et al. 2006; Thomas et al. 2007). Different tracers of the gravitational field must be used to investigate the external regions, which are relatively void of luminous matter. These include planetary nebulae (Coccato et al. 2009) and globular clusters in ellipticals (Spitler et al. 2009), weakly lensed background galaxies, and the satellites populating the outer parts of the DM haloes. These objects are likely to be the remnants of the halo formation process and provide us with an efficient dynamical probe, out to the “edge” of the halo and beyond, as they are bright, numerous, and radially extended test particles. By measuring the satellite-primary relative velocity for a sufficient number of objects, we can derive the mass distribution of the halo out to very large radii. The results are complementary to those obtained from the analysis of weak lensing data, not only because the measurements involved and their related biases are independent, but because the satellite motions lead to a measure of V(R) = (GMh(R)/R)0.5 i.e. the halo mass inside a given radius, while the observed tangential shear derived from the weak lensing measures a more complex quantity, the (average – local) halo surface density at a given radius 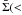 R) − Σ(R). Since (GMh(R)/R)0.5 in the regions under study at most decreases as R-0.25, the sensitivity of the dynamical measurements performed using satellite kinematics does not depend on radius, in contrast to what occurs for the majority of tracers of the gravitational potential including weak lensing. Finally, comparing different mass models derived from various kind of measurements, provides a valuable consistency check.
R) − Σ(R). Since (GMh(R)/R)0.5 in the regions under study at most decreases as R-0.25, the sensitivity of the dynamical measurements performed using satellite kinematics does not depend on radius, in contrast to what occurs for the majority of tracers of the gravitational potential including weak lensing. Finally, comparing different mass models derived from various kind of measurements, provides a valuable consistency check.
The virial radius Rvir is an important characteristic scale-length of dark matter haloes. In the current concordance cosmology (where ΩCDM ~ 0.3, ΩΛ ~ 0.7, and h = 0.72 represent the dark matter, dark energy densities, and Hubble parameter, respectively), this scale-length is defined as the radius that encompasses 330 times the background mass 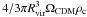 , with ρc ~ 10-29 g/cm3 the critical density of the Universe. For historical reasons R200, i.e. the radius that encompasses a mass
, with ρc ~ 10-29 g/cm3 the critical density of the Universe. For historical reasons R200, i.e. the radius that encompasses a mass 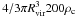 , is also often considered, where Rvir is related to all halo structural properties (concentration and mass) and can be taken as the reference size of a DM halo (e.g. Navarro et al. 2010). Moreover, simulations show that it approximately marks the transition between the virialized matter of a halo and the infalling material. In detail, for a virialized structure of mass Mvir, at redshift zero, Rvir = 260(Mvir/(1012 M⊙))1/3 kpc defines the typical scale-length relevant to this study.
, is also often considered, where Rvir is related to all halo structural properties (concentration and mass) and can be taken as the reference size of a DM halo (e.g. Navarro et al. 2010). Moreover, simulations show that it approximately marks the transition between the virialized matter of a halo and the infalling material. In detail, for a virialized structure of mass Mvir, at redshift zero, Rvir = 260(Mvir/(1012 M⊙))1/3 kpc defines the typical scale-length relevant to this study.
From an observational point of view, the distribution of the DM outside the inner luminous regions out to Rvir is still poorly known, and data suitable for investigating these issues are scarce. Invaluable data is provided by weak lensing measurements (e.g. Mandelbaum et al. 2008), which indicate that Rvir is some hundreds of kpc, although the precise value is uncertain because of the weakness of the signal at these distances coupled with the uncertainties in the DM density profile.
In this pilot study, we show that it is possible to investigate the DM distribution of spiral galaxies out to Rvir by combining the internal kinematics of the spirals and the radial velocities of their satellites.
It is well known that the spatial and kinematical distribution of satellites around their host galaxies provide important information about the DM halo properties. Previous investigations have also noted that further analysis is possible only if the angular distribution of satellites is homogeneous. It is extremely difficult to recover the gravitational potential of the galaxy halo from the kinematics of satellite systems if their distribution is not (roughly) isotropic. Zaritsky et al. (1997) studied a sample of 69 spiral galaxies and their 115 satellites, and found a tendency for the satellites to lie preferentially close to the minor axis of their hosts, a phenomenon called the Holmberg effect (Holmberg 1969). Brainerd (2005, hereafter B05) studied a sample of 2000 primaries and their 3300 satellites selected from the Sloan Digital Sky Survey Data Release 3 (SDSS DR3; York et al. 2000), and found instead a tendency for satellites to lie near the major axis, a result confirmed by Faltenbacher et al. (2007) using SDSS DR4 data. Agustsson & Brainerd (2010) studied a large sample of SDSS DR7 galaxies (4487 hosts and 7399 satellites) and for blue hosts found that at projected radii rp ≲ 150 kpc satellites are distributed close to the major axes, while at rp ≳ 300 kpc satellites are found close to the minor axes. Azzaro et al. (2006) found an isotropic distribution of satellites based on a sample of 193 satellites and 144 isolated spiral galaxies, though they issued a caution about the insufficient quality of their statistics. Using SDSS DR5 data, Bailin et al. (2008) confirmed this result with 273 late-type primaries hosting 321 satellites.
We believe that the contradictory results found so far have the following causes. First, most of these studies rely on data for a very small number of satellites per host. The average primary galaxy often possesses data for only two satellites, which is a very small fraction of the true total number, as we can see just by looking at the Local Group (Hartwick 2000; Kroupa et al. 2005; Willman et al. 2005; Koch et al. 2006). Second, to combine the kinematics of systems composed of primaries of different masses and halo sizes is very complex and the subsequent analysis is far from trivial and can become easily biased.
This uncertain situation has suggested to us a new observational approach to the problem. First, we select a relatively small number of primary galaxies (compared to previous studies), and all in a quite narrow range of luminosity − 21.6 ≤ MR ≤ − 22.7. For each of them, we then detect a larger number of satellites by using powerful instruments (VIMOS at the VLT). The characteristic halo mass will eventually be sampled by 30 primaries in that luminosity range, and their gravitational potential will be reconstructed by means of a) the disk kinematics and b) the kinematics of their about 300 possibly detected satellites.
In this pilot paper, which is also a feasibility study, we carry out about 25% of the project. To complete the project and investigate the mass distribution around spirals of different masses, we plan to replicate the investigation around objects of significantly lower luminosity (e.g. with − 20 ≤ MR ≤ − 20.5).
We measure the rotation curves (RCs) of seven primaries to help us reconstruct the mass distribution in the inner regions of galaxies and eventually ensure that the systems have approximately the same total mass (2 − 5 × 1012 M⊙). We then measure the primary-satellite relative velocities for the candidate satellites and, after removing interlopers, we build for the latter the velocity dispersion profile of the co-added system. The method has a number of advantages: a) since the primaries have almost the same mass, we can co-add the kinematical measurements from different objects as they would belong to a single one. This leads to a very precise measure of the rotation curve in the optical region, a good hint of the satellite number profile, and a fair measure of their velocity dispersions; b) since we detect objects down to a very low (MR = −16) limiting magnitude, our dynamical analysis is not affected by possible luminosity-dependent biases in the positions and in the motions of satellites; c) we can easily reach the virial radius and beyond.
In this paper, we report the first results of the pilot phase of our project, obtained with seven hours of VIMOS at the VLT, followed later by a program totaling 53 h at the VLT (VIMOS) and NTT (EMMI). In this phase, we obtain valuable information about the properties at the outer radii of dark and luminous components around spirals, but we are also particularly interested in demonstrating the feasibility of the project. We anticipate that, once completed, our project will be able to unravel most of the distribution of DM within the haloes surrounding spiral galaxies out to their “edges”.
The layout of the paper is the following. In Sect. 2, we describe observations and data reduction of primary galaxies and their satellite candidates. In Sect. 3, we perform the data analysis: in Sect. 3.1 of the structural properties of the primaries, using their rotation curves; in Sect. 3.2 identifying interlopers in the satellite candidates; in Sect. 3.3 studying the radial distribution of satellites; in Sect. 3.4 studying the angular distribution of the satellites; in Sect. 3.5 estimating the velocity dispersion profile; and in Sect. 3.6 performing mass modeling of the primary galaxies. We discuss the results in Sect. 4.
2. Observations and data reduction
Primary galaxies characteristics and observing blocks.
The selection criteria of the primary galaxies were the following: (1) all galaxies are late-type spirals; (2) they have an inclination between 40° and 70°; (3) they are isolated: all objects within a radius of 700 kpc and 1000 km s-1 in relative radial velocity have a luminosity at least 2.5 mag below that of the primary galaxy; (4) they have a redshift 0.029 < z < 0.085; and (5) they have at least four known satellites (from the SDSS). To select the isolated primaries, we used the catalog of host galaxies and satellites from B05.
The observations were conducted with two instruments: the kinematics of primary galaxies were measured using data acquired with EMMI at the NTT, while the hunt for satellites and the measurement of their radial velocity was done with the VIMOS at the VLT. Redshifts and luminosities of the primary galaxies, and the observing log, are presented in Table 1.
2.1. Kinematics of primary galaxies
The major-axis ionized gas rotation curves of the primary galaxies were obtained by means of long-slit spectroscopy at the ESO-NTT 3.5 m telescope in La Silla (077.B-0767), using the ESO Multi-Mode Instrument (EMMI) in the REd Medium Dispersion (REMD) configuration. Grating No. 6 with 1200 grooves mm-1 blazed at 6890 Å was used in the first order in combination with the two red-arm mosaicked MIT/LL and a 1″ × 330″ slit. Data reduction was done with MIDAS1 and IRAF2 standard routines. Wavelength calibration was performed using observations of a helium-argon calibration lamp. All frames were bias subtracted, flat-field corrected, cosmic-ray cleaned, and wavelength calibrated. Quartz lamp and twilight sky flat-fields were used to remove pixel-to-pixel variations and large-scale illumination patterns. After wavelength calibration, repeated exposures of the same target were aligned and summed. We used the night-sky emission lines to assess the quality of the wavelength calibration and spectral resolution. We use these data not only to derive the rotation curve of the galaxies but also to define their recession velocity. This velocity is later compared with the one measured for the satellites using VIMOS. The instrumental resolution is 1.3 Å (FWHM), corresponding to a resolution of σ = 27 km s-1 at Hα. The ionized gas kinematics was measured by simultaneous Gaussian fits to Hα, [N ii], and [S ii] lines by means of a self-written IDL routine and then folded around their centers and deprojected for the disk inclination as done by Pizzella et al. (2004). The derived velocity curves are plotted in Fig. 1.
 |
Fig. 1 Rotation curves of the seven primary galaxies deprojected for the disk inclination and folded around their centers. |
2.2. Satellites radial velocity
Observations were carried out in service mode with the VIsual MultiObject Spectrograph (VIMOS) operated at Cerro Paranal (075.B-0794; 077.B-0767). To identify satellites orbiting selected primary galaxies and measure their radial velocity, the instrument was used in MOS configuration. After pre-imaging, we constructed the masks for the MOS observations selecting the brightest non-stellar objects in the field.
We adopted grism “HR orange” on the four arms of the instrument. The grism is used in combination with the order sorting filter GG435. The grism is characterized by a dispersion of 0.6 Å px-1, which corresponds to a spectral resolution of 2150 for a 1′′ slit. We could accommodate, on average, about 50 slits in each quadrant for a total of about 200 slits for each primary galaxy. We organized the observations by repeating the same pointing with the same mask several times. Each exposure is 2180 s long. Some exposures that did not fulfill our observational requirements were repeated. For this reason, we obtained more exposures than requested. Extra exposures, executed under weather conditions not complying with our constraints, were only used if the data quality was good. The exposures reported in Table 1 are the ones used in our final data reduction.
We started our data reduction from frames that were bias subtracted, flat-field corrected, and wavelength calibrated by the ESO data reduction pipeline. Further data reduction was done with MIDAS. The first step was to assess the quality of each integration. Once the selection was done and the low quality spectra discarded, we computed the average spectrum for all frames. The second step was to approximately derive, in the sky-subtracted spectra, the redshift of all targets. To this aim, we used emission and absorption lines listed in Table 2.
Emission and absorption lines used in the preliminary redshift determination.
This second step allowed us to select possible satellites and reject all other background or foreground objects characterized by a radial velocity difference (with respect to the primary galaxy) more than Vout = 1000 km s-1 (McKay et al. 2002; B05). We refer to these galaxies as candidate satellites throughout the paper.
In designing the masks containing the slits, we did not constrain the wavelength range. Slit positioned on the north side of each quadrant produced spectra in the red range, with wavelengths longer than 5500 Å. Slit positioned on the south side of each quadrant produced spectra in the blue range, with wavelengths shorter than 6500 Å. Our strategy is to derive the redshift of satellites either from the Hα, [N ii] emission lines or from the Hβ, [O iii] emission lines that always fall in the observed spectral range. We were typically able to identify about 150 redshifts for each primary galaxy.
After the satellite candidates of a primary galaxy were identified, we proceeded with the accurate measurement of their radial velocity. We again, used all available emission lines (typically Hα, [N ii] or Hβ, [O ii]) and used the sky emission lines to refine the wavelength calibration. We first spatially averaged the spectrum of each satellite and derived its one-dimensional spectrum. We then measured the wavelengths of a number of night-sky and target emission lines. We later, computed the difference between the expected night-sky wavelength values and the measured ones, which were fit with a one-degree polynomial. This was used to correct the wavelength of the satellite emission lines. To have independent measurements, when possible we measured the radial velocity separately for each exposure and for each emission line and then averaged the measurements. The radial velocities were measured with a typical uncertainty of 10 km s-1. All radial velocities were reported with respect to the heliocentric rest-frame.
The last step consisted of identifying the positions of all the 200 slits on both the pre-imaging frame and the SDSS images and, in particular, the positions of the satellites.
In view of future observations with the same instrument, we note, that we can easily increase the fraction of observed extragalactic sources, and therefore satellites, by using different MOS masks for the same primary instead of repeating the same mask several times as we did in this pilot project. In very few cases, we added the spectra before measuring the redshift and we found that two independent 45 min spectra per target would have provided a velocity measurements with uncertainties not significatively larger than what we obtained with several exposures.
3. Distribution of satellites
At the end of the data reduction phase, we found a total of 77 objects (considering both VIMOS and B05 data) that fall in a projected circle in the sky of about 1000 kpc of radius and have a velocity that is at most 1000 km s-1 smaller or larger than that of the primary galaxy. In Table 3, we indicate the number of satellite candidates found for each primary galaxy (for J003828+000720 the quality of the data was insufficient for the analysis). Not all objects are physical satellites since outliers may be present (see Sect. 3.2). To assess the completeness of our sample, we estimate the fraction of objects that we observed over the total number of objects present in the field. For each VIMOS field, we derived the r-band magnitude distribution of all extended sources, regardless of their redshift, from the SDSS DR7 photometric catalog. We then identified in the latter the objects that we had observed and found that, in the magnitude range between 18 and 21 r-band, they are about half of those present in the SDSS photometric catalog (see Fig. 2) and this ratio is roughly constant with the apparent magnitude. Only for objects fainter than 21 the ratio start to increase. The discontinuity visible at magnitude ~16−17 is caused by our having for these objects an SDSS redshift and we selected only the few galaxies with a recession velocity similar to the one of the primary galaxy. We can assume that, by adopting different masks in our observations, we could spectroscopically observe twice the number of objects we actually observed. Since we placed the slits on targets with no particular criteria other than that they are extended sources, the real number of candidate satellites (galaxies with a radial velocity Vr in the interval Vprimary − 1000 km s-1 < Vr < Vprimary + 1000 km s-1) present in the field is about twice the number we counted. We have to take into account this factor of about two when estimating the number density of objects.
Number of candidate and confirmed satellites found for each galaxy.
 |
Fig. 2 Lower panel: SDSS DR7 number counts of galaxies averaged in a 14′ × 14′ field around each primary galaxy (blue dotted line), number counts of the galaxies that have been observed with VIMOS (black line, magnitudes from SDSS), and number counts of the physical satellites (shaded region). Upper panel: ratio of the number of galaxies present in the field to the one observed with VIMOS. |
3.1. Structural properties of the primaries from their rotation curves
A crucial advantage of this study is that by measuring the RCs of the primaries, we can estimate their inner gravitational field. As a first step, from their velocity-position diagrams and inclinations i, we derive their corrected rotation curves. Secondly, we compute the average velocity of all curves at radius Ropt = 3.2 RD (where RD is the exponential disk scale-length). We define this velocity ⟨ V(Ropt) ⟩ , and we use it to normalize every RC to a same representative amplitude and radius. We found ⟨ V(Ropt) ⟩ = (255 ± 16) km s-1 and ⟨ Ropt ⟩ = (19.8 ± 2.0) kpc. Because of the small luminosity range of the primaries, both quantities lie in a relatively small range of values, in agreement with the Tully-Fisher relation. Following Persic, Salucci & Stel (1996, hereafter PSS), for each primary we plot V(R ⟨ Ropt ⟩ /Ropt) ⟨ V(Ropt) ⟩ /V(Ropt) (see Figs. 11 and 12), a quantity which is proper when comparing rotation curves of objects of (slightly) different luminosity. We find, in agreement with PSS and Salucci et al. (2007, hereafter S07), that the optical RCs of the primaries have similar shapes and define universal curve VURC(R/Ropt,L) that accurately represents each of them. This implies that these galaxies have similar disks embedded in similar dark matter haloes. Therefore their RCs and the recessional velocities of their satellites probe the dark matter halo around a spiral of luminosity ⟨ MR ⟩ with characteristic radius ⟨ Ropt ⟩ . The virial mass, virial radius, and halo escape velocity can roughly be estimated by extrapolating its representative RC out to large radii according to V(R) = V(Ropt)(R/Ropt)-0.2, i.e. by adopting the velocity profile suggested by observations in S07 and found in ΛCDM simulated haloes.
We find Mvir ~ 3.5 × 1012 M⊙ and Rvir ~ 400 kpc, which we consider as indicative values of the virial masses and radii of the primaries. Furthermore, we can estimate the escape velocity as 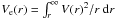 , because it mainly depends on the gravitational potential at small radii, which can be accurately mapped by the (co-added) RC. This estimate is robust in spite of the uncertainty in the RC extrapolation: even if we truncated the halo at 1/2 Rvir, Ve(r) would be smaller by only 20%. We also note that the value of Ve(r) varies with halo mass only as
, because it mainly depends on the gravitational potential at small radii, which can be accurately mapped by the (co-added) RC. This estimate is robust in spite of the uncertainty in the RC extrapolation: even if we truncated the halo at 1/2 Rvir, Ve(r) would be smaller by only 20%. We also note that the value of Ve(r) varies with halo mass only as 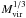 .
.
We use these estimates just as templates of these quantities and Ve(r) helps us to distinguish interlopers from true satellites. We note that the actual circular velocity curve leading to the gravitational potential for our galaxies will be derived from the velocity dispersion of the satellite population. No result of this paper depends on the details of the above RC extrapolation.
 |
Fig. 3 Satellites velocities with respect to the primary (open circles) versus radius. Black points are outliers. The red curves are the caustics identifying satellites and outliers. Vertical red lines indicate the bin locations and sizes. |
3.2. Interlopers
Not all the galaxies detected around the seven primaries are their satellites: the distribution of objects around a target galaxy is contaminated by the presence of a background population of interlopers/outliers, i.e. of objects physically unrelated to the galaxy targets but at a small projected distance from them. That we investigate haloes of approximately the same mass and virial radius, and that these quantities are roughly known, allows us to infer the membership status of nearby objects according to their location and relative velocity with respect to the primary. Moreover, we can also distinguish the background of “false satellites” in outliers, galaxies around the primaries whose large value of relative velocity Vrel show that they are systems unbound to the primaries, and true velocity interlopers, i.e. objects with Vrel and projected locations similar to those of true satellites.
In general, the removal of interlopers is quite complicated and uncertain. However, according to Chen et al. (2006) and Azzaro et al. (2006) for haloes of 1012 − 1013 M⊙, the removal of outliers can be routinely done and the contamination of velocity interlopers becomes important only at projected radius of R > 400 kpc ~ Rvir.
A modern and efficient way of identifying member satellites is the caustic method introduced by Diaferio (1999) (later improved in Serra et al. 2010, 2011). The method uses relative velocities Vrel and projected radii to delineate the caustic curves that represent the escape velocity of the system (for details, see Serra et al. 2010, 2011). We applied it to our data identifying the interloper galaxies and removed them from our sample. In Fig. 3, we present the Vrel versus R for all objects, along with the caustic defined by Diaferio (1999). We also show the locations of the bins adopted (ten objects per bin) in computing the satellites mean velocity and velocity dispersion.
Since the present work is limited by the relatively small number of satellites, we investigate this issue by means of a further method to identify objects gravitationally unbound to our primaries. We also used the negative binding energy criterium: we resorted to the negative binding energy criterium that uses the Ve(r) profiles by obtaining a very similar result in the selection.
With the above considerations, we removed from our sample, at any projected radius R, the unbound/unrelated objects to the primaries whose inclusion strongly affects the estimate of the velocity dispersion. These outliers are galaxies more distant than 5 Mpc from the primaries, which happen to lie on a line of sight passing close to their centers (i.e. < 1000 kpc). In Fig. 4, we give the histogram of our objects after we performed the velocity clipping described above, i.e. we show the number of candidate satellites for each radial bin and the number of outliers. Because of small numbers, the cosmic variance of outliers cannot be estimated in this study.
The clipping does not remove objects that are physically unrelated to the primaries, but reside at a smaller distance (1 Mpc < D < 5 Mpc). In this case, Vrel, which is the resultant of redshift and peculiar velocity, can take similar values in a true satellite or in a physically unrelated object. This population of velocity interlopers affects in particular the satellite’s surface density (at outer radii); we investigate its bias of our measured projected satellite surface density by following Azzaro et al. (2006) and assuming that it provides a constant background (Chen et al. 2006; Azzaro et al. 2006; Mamon et al. 2010). We estimate the latter with the SDSS r-band luminosity function (Blanton et al. 2003), i.e. a Schechter function Φ(M) = 0.4Φ∗log (10) 100.4(M∗ − M)(α + 1)exp(−100.4(M∗ − M)), with the parameters Φ∗ = 0.0074 Mpc-3, M∗ = −21.31, and α = −0.89.
In detail, we estimate the number of velocity interlopers Nvi(R), i.e. of the objects that lie within a projected distance R from the center of a primary galaxy but at a redshift distance De ≤ Ve/72 Mpc. Assuming that Ve is constant with radius, we get 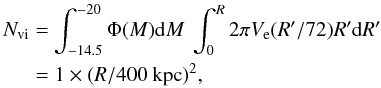 (1)where MR = −14.5 is the limiting magnitude in our observations, and 72 km s-1 Mpc-1 is the Hubble constant. In agreement with Azzaro et al. (2006), we consider the radial dependence of Ve (see Sect. 3.1) and find that Nvi ~ 1 × (R/1 Mpc)1.75 i.e. in our case the number of interlopers inside Rvir ≃ 400 kpc is at most one, while in the region between Rvir and 2Rvir (that corresponds to the three outermost radial bins) the expected number of interlopers is a few. In terms of number surface density, we find that μvi ~ 5 × 10-7 kpc-2, with an uncertainty of a factor of two. Thus, the number of objects with MR > −14.5 after a Ve clipping represents a fair estimate of the number of satellites around spirals of MR ~ −22.
(1)where MR = −14.5 is the limiting magnitude in our observations, and 72 km s-1 Mpc-1 is the Hubble constant. In agreement with Azzaro et al. (2006), we consider the radial dependence of Ve (see Sect. 3.1) and find that Nvi ~ 1 × (R/1 Mpc)1.75 i.e. in our case the number of interlopers inside Rvir ≃ 400 kpc is at most one, while in the region between Rvir and 2Rvir (that corresponds to the three outermost radial bins) the expected number of interlopers is a few. In terms of number surface density, we find that μvi ~ 5 × 10-7 kpc-2, with an uncertainty of a factor of two. Thus, the number of objects with MR > −14.5 after a Ve clipping represents a fair estimate of the number of satellites around spirals of MR ~ −22.
 |
Fig. 4 Number of candidate satellites (top panel) and outliers (bottom panel) as a function of radius. |
 |
Fig. 5 Surface density of candidate satellites (filled circles) as a function of radius. The full line is the surface density of satellites after accounting for position interlopers. The dotted line indicates the surface density radial slope of a NFW halo. The full and open triangles represent the surface density of satellites found by Sales et al. (2005) and Chen et al. (2006), respectively. The dashed lines show the estimate of the interlopers velocity for μ = 3 × 10-7 kpc-2 and μ = 10-6 kpc-2. |
3.3. The radial distribution of satellites
The radial distribution of satellites was analyzed with bin sizes of ~100−200 kpc (ten satellites per bin), starting with the total number of satellites detected around all primaries. To get a representative number for an individual galaxy, the frequencies were later multiplied by the factor of 2/7, where 7 is the number of primaries in the present work and 2 is the completeness factor discussed above. In the full project, we aim to reduce the latter factor down to ≃1. In Fig. 5, we plot the number surface density μ(R) before (filled circles) and after (full line) the removal of interlopers.
The first can be written as 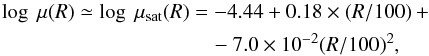 (2)where R is in kpc and μ in kpc-2, the above holding inside ~500 kpc. We can remove the velocity interlopers, although they contribute in a negligible way for R < 700 kpc thus, to a first approximation, we take Eq. (2) as the estimate of the surface density of satellites.
(2)where R is in kpc and μ in kpc-2, the above holding inside ~500 kpc. We can remove the velocity interlopers, although they contribute in a negligible way for R < 700 kpc thus, to a first approximation, we take Eq. (2) as the estimate of the surface density of satellites.
The projected radial distribution of galactic satellites around high luminosity primaries has been measured with the SDSS (Chen et al. 2006) and the 2dFGRS (Sales et al. 2005). Sales et al. (2005) also distinguished the case of blue (spiral) and red (elliptical) primaries. In both surveys, the limiting flux of the satellites is 2−3 mag brighter than that of our study and halo masses around primaries are a factor 2 − 5 smaller than the mass of the halo around our primaries. In view of this, the smaller amplitude of the satellite surface density found in the quoted surveys is unsurprising. It may indicate a bias in the radial distribution of satellites that depends on their luminosity. We see that μ(R) is not a power law: there is a central region of constant value, extending for ~100 kpc. A similar trend can be seen in the quoted surveys, especially for the subsamples of red primaries in 2dFGRS, and high luminosity primaries in SDSS.
Outside 500 kpc, μ(R) is subject to the increasingly limited quality of the statistics. However, the primary inner kinematics guarantees that the density profile represents objects related to the primary but not virialized. The distribution of satellites associated with an 3 × 1012 M⊙ halo seems to be cut off at about 700 kpc. The observed fall-off in number density (see Fig. 5) is real: we could have detected objects at R > 2Rvir, if they existed.
The satellite surface density distribution cannot be reproduced by a projected Navarro-Frenk-White (NFW) profile (μ ∝ R-1.5) for 0.1 < R/Rvir < 1 (see Fig. 5). In other words, it is not compatible with the predicted density distribution of dark matter haloes in a ΛCDM scenario. In particular, the predicted ~200 subhaloes around a 3 × 1012 M⊙ halo exceeds the number of observed satellites by one order of magnitude, a situation we also find for Local Group galaxies. However, astrophysical processes in the late stages of galaxy assembly might depopulate most subhaloes (e.g., Macciò et al. 2010) and the distribution of visible satellites might have no resemblance with that of existing DM sub-unities.
We might try and compare our radial distribution with those predicted by state-of-the-art simulations of galaxy formation with models based on cold dark matter (CDM). The results of simulations using N-body techniques as well as different semi-analytic models of galaxy formation can be found in the literature (e.g., Moore 1999; Baugh 2006). However, these codes do not produce unique results. We can add as a general comment, that these models may have difficulties in explaining the rapid increase in the cumulative number of satellites inside 100 kpc (Macciò et al. 2010).
3.4. Angular distribution of the satellites
From the R-band photometry, we measured the position angle (PA) of the primaries and derived ΔPA = PAsatellite − PAgalaxy for each satellite. In Fig. 6, we plot the number of satellites as a function of ΔPA and in Fig. 7 ΔPA as a function of the distance to the primaries. We compared the PA distribution to a uniform distribution by means of a Kolmogorov-Smirnov test. The probability that the PA distribution and the uniform distribution have a common origin is ~ 98% (see Fig. 8). Hence, the observed distribution is consistent with being isotropic at current levels of uncertainty. In any case, it is clear that the distribution of satellites around primary galaxy in Figs. 6 and 7 do not show any preferential alignment, i.e. they are distributed isotropically.
 |
Fig. 6 Number of satellites against position angle differences. The total distribution is given by the upper histogram, while that of approaching satellites is represented by the unshaded area. In each bin, the rest of the contribution is due to receding satellites (shaded area). |
 |
Fig. 7 Distribution of satellites around primary galaxies. Radius and position angle with respect to the major axis are shown for approaching (open circles) and receding (crosses) satellites. |
 |
Fig. 8 The cumulate vector of ΔPA (broken curve) is compared to that of a uniform distribution (straight line). A Kolmogorov-Smirnov test shows that the probability that the two distributions are coming from and identical underlying one is ≃ 98%. |
3.5. Velocity dispersion profile and rotation velocity at large radii
Velocities and dispersion versus radius.
 |
Fig. 9 Mean velocity of satellites as a function of radius. |
 |
Fig. 10 Velocity dispersion as a function of radius. |
We estimate the velocity dispersion σ(R) of the seven co-added systems by binning the satellites into groups of ten objects. For each bin, we compute the average velocity ⟨ Vrel ⟩ and the velocity dispersion σ. We report them in Table 4 and plot them in Figs. 9 and 10. The average difference ⟨ Vrel ⟩ is compatible with zero at any radius (see Fig. 9). In addition, along the line-of-sight the velocities are isotropic. This is confirmed by the finding that ⟨ Vrel ⟩ ~ 0.2σ at any radius (see Table 4). The flat radial trend also implies that the satellite system has a negligible rotation.
In view of the considerably large rms of σ(R), we chose the simplest linear function to fit data from 100 kpc to 500 kpc ![\begin{equation} \sigma(R)= [265 - 0.35 (R - 100)] ~{\rm km~s^{-1}}, \end{equation}](/articles/aa/full_html/2011/08/aa13788-09/aa13788-09-eq144.png) (3)where R is in kpc.
(3)where R is in kpc.
The inner RCs of the primaries indicate, following Salucci et al. (2007), for our co-added system a virial mass of ~ 3.5 × 1012 M⊙ and a virial radius of 400 kpc. Inside this radius, σ measures the kinetic energy of a unit mass test particle in gravitational equilibrium inside the galaxy potential. At larger radii in the range 400 < R < 800 kpc, we have two cases: 1) σ still measures the kinetic energy, but of objects out of equilibrium or 2) σ is totally contaminated by velocity interlopers.
The velocity dispersion measures the circular velocities well beyond the extent of the rotation curves. We assume that the satellites have isotropic motions. This assumption is supported (albeit not proven) by the isotropic angular distribution and velocity dispersion along the line of sight. The co-addition procedure would of course also smear out any velocity anisotropies if they had different structure galaxy by galaxy. In this framework, we derive the circular velocity V2(R) = RdΦ/dR where Φ is the gravitational potential, from the velocity dispersion in two different ways.
First, we apply the usual argument that velocity dispersion has three degrees of freedom while rotation has just two, and we set V(R) = (3/2)1/2σ(R). Rotation velocities computed this way are plotted in Fig. 11 together with the inner RCs.
Second, we adopt the fully correct procedure: we solve the Jeans equation for the 3D distribution of satellite ns(R) that we get from an Abel-integral deconvolution of μ(R). We note that in this pilot study the quality of the statistics is still low and this is done just to illustrate the feasibility of the full project (which involves several times more data). The deconvolution yields 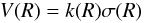 (4)with k = ( − dlog ns(R)/dlog R − 2 dlog σ/dlog R)0.5. For r < 400 kpc, i.e. for velocity dispersions of the three innermost bins we find k = 1.0,1.4,1.8. For the outer three bins in which very likely the Jeans equation cannot be applied, we allow V to range between (3/2)1/2σ and σ (an object radially infalling) and we do not estimate a value. Figure 12 shows the inner RCs together with velocities computed with this second procedure.
(4)with k = ( − dlog ns(R)/dlog R − 2 dlog σ/dlog R)0.5. For r < 400 kpc, i.e. for velocity dispersions of the three innermost bins we find k = 1.0,1.4,1.8. For the outer three bins in which very likely the Jeans equation cannot be applied, we allow V to range between (3/2)1/2σ and σ (an object radially infalling) and we do not estimate a value. Figure 12 shows the inner RCs together with velocities computed with this second procedure.
The last two bins illustrate a steep, large increase in the velocity dispersion. This is likely to indicate that most, perhaps all objects, are not physically bound to the primary galaxy. The detected sharp decrease in the number of true satellites might indicate at ~ 600 kpc the edge of the dark matter halo. With the full sample that is four times larger, we hope of course to have consequently a more accurate determination of the mass distribution.
3.6. Mass modeling
The radial profiles of circular velocities shown in Figs. 11 and 12 were fit with the universal rotation curve (URC) with ⟨ RD ⟩ = 6.2 kpc and halo mass Mvir = 3.5 × 1012 M⊙ that closely fits the inner RCs. The URC has no free parameters to fit the present outer data, therefore its success is remarkable. The URC depends only on the disk scale-length RD and the halo mass Mvir, which also controls the disk mass (Shankar et al. 2006). The URC mass model fits well the data points in both cases for Mvir = 3.5 × 1012 M⊙.
 |
Fig. 11 RCs of primaries and circular velocities obtained from the velocity dispersions of the satellites (black squares) (V(R) = (3/2)1/2σ(R), see text for details). The URC is shown (as a black line) out to the virial radius. |
 |
Fig. 12 RCs of primaries and circular velocities obtained from velocity dispersions and Jeans equation (black squares, see text for details). The URC is shown (as a black line) out to the virial radius. |
4. Discussion and conclusions
In this pilot project, we have searched for satellites around seven spiral galaxies of comparable luminosity (MR ~ −22). We have found 61 objects that, based on their velocity relative to the primary galaxies, are their satellites. By combining results, we have investigated several properties of these satellites, which allow us to draw a number of conclusions.
We find that our target dark matter haloes have about 15 satellites (down to MR = −16) inside their virial radius. Their measured inner kinematics show that, as intended, they have similar halo masses, of about 3.5 × 1012 M⊙ and the embedded luminous spirals have luminosities MR ≃ −22. Therefore this result is comparable to what we observe for M31 and the Milky Way (MW) in the Local Group. As in those cases, this small number of satellites represents a problem for “naive” ΛCDM theories, which predict an order of magnitude larger number of objects orbiting around dark haloes of this size. To reconcile observations and theory, one has to assume that most of the galaxy subhaloes have become unobservable. This possibility, related also to the apparent lack of subhaloes around the Milky Way, is being investigated (e.g. Kravtsov et al. 2004; Libeskind et al. 2009). Could a long list of physical processes occurring in subhaloes during their history jeopardize (while perhaps also introducing a radial bias) their ability to host luminous objects? In this respect, we note that our primaries have a mass 3 − 4 times higher that of the MW and the combined sample has already 102 objects and in the future will have ten times more. We will be able to investigate the “missing subhaloes problem” also in subhaloes with a mass 1 order of magnitude larger than that of the Large Magellanic Cloud (LMC), and therefore in subhaloes that should host normal and not dwarf galaxies. It will be interesting to see whether, at these high masses, the problem remains, and can be tackled by the explanations put forward in the case of MW.
By considering a composite system including all detected satellites, we are able to study their radial distribution with respect to the central galaxy. The surface density has a shallower profile than found in previous surveys, based on fewer satellites per primary. We propose that this is due to a bias in the radial distribution of satellites that depends on their luminosity.
We also find that the angular distribution of satellites around primary spirals is isotropic. Furthermore, the relative velocity along the line of sight is isotropically distributed around zero. Based on this observation, we can use the velocity dispersion profile to estimate rotation velocities far beyond the extent of the inner rotation curves.
An additional result of this study is that the RCs of the primaries appear very similar. Because we targeted objects with the same absolute luminosity, our finding confirms that RCs mainly depend on an object’s mass. It follows that the mass distribution inside the optical region is the same for all our objects. It also justifies combining the satellite relative motions to derive the velocity dispersion and probe the mass distribution of a “stacked” halo. The outer RC obtained from the velocity dispersion results is smooth and continuous with respect to the inner measured RCs and, over two orders of magnitude in distance, is very well reproduced by the S07 universal mass model that holds for spirals. In this paper, the model is tested for the first time with kinematical measurements out to the virial radius of the galaxy. The technique we have applied is therefore very promising.
In the future, we plan to test our findings by enlarging our sample of primary galaxies. We estimate that by co-adding the satellite distribution and kinematics of ~20 systems of a same high mass we can infer the mass distribution of the underlying
DM halo. The full project aims to replicate this procedure for haloes of intermediate and low mass (8 × 1011 M⊙ and 2 × 1011 M⊙ respectively), to derive the mass dependence of the DM distribution.
Acknowledgments
We thank Teresa Brainerd for kindly providing the catalog of the primaries with satellites obtained from the SDSS survey. We thank Antonaldo Diaferio for kindly computing the caustics curves to identify satellites and outliers. We are grateful to the anonymous referee for valuable comments that truly improved the paper. A.P. acknowledge findings through grant CPDA089220/08 by Padua University. We are pleased to thank Michael West for improving the style of the manuscript and for the helpful comments. We thank Ivo Saviane for his reading of the manuscript that considerably improved the presentation of this work. The Sloan Digital Sky Survey (SDSS) is a joint project of The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, Los Alamos National Laboratory, the Max-Planck Institute for Astronomy (MPIA), the Max-Planck Institute for Astrophysics (MPA), New Mexico State University, Princeton University, the United States Naval Observatory, and the University of Washington. Apache Point Observatory, site of the SDSS telescopes, is operated by the Astrophysical Research Consortium (ARC). Funding for the project has been provided by the Alfred P. Sloan Foundation, the SDSS member institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/
References
- Agustsson, I., & Brainerd, T. 2010, ApJ, 709, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Azzaro, M., Zentner, A. R., Prada, F., & Klypin, A. A. 2006, ApJ, 645, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Bailin, J., Power, Ch., Norberg, P., Zaritsky, D., & Gibson, B. K. 2008, MNRAS, 390, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Baugh, C. M. 2006, Rep. Progress Phys., 69, 3101 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Hogg, D. W., Bahcall, N. A., et al. 2003, ApJ, 592, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Bosma, A. 1981, AJ, 86, 1791 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, T. 2005, ApJ, 628, 101 (B05) [Google Scholar]
- Cappellari, M., Bacon, R., Bureau, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J., Kravtsov, A. V., Prada, F., et al. 2006, ApJ, 647, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A. 1999, MNRAS, 309, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Faltenbacher, A., Li, Ch., Mao, S., et al. 2007, ApJ, 662, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Hartwick, F. D. A. 2000, AJ, 119, 2248 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, E. 1969, Ark. Astron., 5, 305 [Google Scholar]
- Koch, A., & Grebel, E. 2006, AJ, 131, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Gnedin, O. Y., & Klypin, A. A. 2004, ApJ, 609, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Kronawitter, A., Saglia, R. P., Gerhard, O., & Bender, R. 2000, A&A, 144, 53 [Google Scholar]
- Kroupa, P., Theis, C., & Boily, C. M. 2005, A&A, 431, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libeskind, N. I., Frenk, C. S., Cole, S., Jenkins, A., & Helly, J. C. 2009, MNRAS, 399, 550L [NASA ADS] [CrossRef] [Google Scholar]
- Macciò, A. V., Kang, X., Fontanot, F., et al. 2010, MNRAS, 402, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G., Biviano, A., & Murant, G. 2010, A&A, 520, 30 [Google Scholar]
- Mandelbaum, R., Seljak, U., & Hirata, Ch. M. 2008, JCAP, 08, 006 [CrossRef] [Google Scholar]
- McKay, T. A., Sheldon, E. S., Johnston, D., et al. 2002, ApJ, 571, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Navarro J. F., Ludlow, A., Springel, V., et al. 2010, MNRAS, 402, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., Salucci, P., & Stel, F. 1996, MNRAS, 281, 27 (PSS) [NASA ADS] [CrossRef] [Google Scholar]
- Pizzella, A., Corsini, E. M., Vega Beltrán, J. C., & Bertola, F. 2004, A&A, 424, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubin, V. C., Ford, W. K., Jr., & Thonnard, N. 1980, ApJ, 238, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L., & Lambas, D. G. 2005, MNRAS, 356, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Salucci, P., Lapi, A., Tonini, C., et al. 2007, MNRAS, 378, 41 (S07) [NASA ADS] [CrossRef] [Google Scholar]
- Serra, A. L., Angus, G. W., & Diaferio, A. 2010, A&A, 524, 16S [Google Scholar]
- Serra, A., Diaferio, A., Murante, G., & Borgani, S. 2011, MNRAS, 412, 800 [NASA ADS] [Google Scholar]
- Shankar, F., Lapi, A., Salucci, P., De Zotti, G., & Danese, L. 2006, ApJ, 643, 14 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Spitler, L. R., & Forbes, D. A. 2009, MNRAS, 392L, 1 [Google Scholar]
- Thomas, J., Saglia, R. P., Bender, R., et al. 2007, MNRAS, 382, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Willman, B., Dalcanton, J. J., Martinez-Delgado, D., et al. 2005, ApJ, 626, L85 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zaritsky, D., Smith, R., Frenk, C. S., & White, S. D. M. 1997, ApJ, 478, L53 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Rotation curves of the seven primary galaxies deprojected for the disk inclination and folded around their centers. |
| In the text | |
 |
Fig. 2 Lower panel: SDSS DR7 number counts of galaxies averaged in a 14′ × 14′ field around each primary galaxy (blue dotted line), number counts of the galaxies that have been observed with VIMOS (black line, magnitudes from SDSS), and number counts of the physical satellites (shaded region). Upper panel: ratio of the number of galaxies present in the field to the one observed with VIMOS. |
| In the text | |
 |
Fig. 3 Satellites velocities with respect to the primary (open circles) versus radius. Black points are outliers. The red curves are the caustics identifying satellites and outliers. Vertical red lines indicate the bin locations and sizes. |
| In the text | |
 |
Fig. 4 Number of candidate satellites (top panel) and outliers (bottom panel) as a function of radius. |
| In the text | |
 |
Fig. 5 Surface density of candidate satellites (filled circles) as a function of radius. The full line is the surface density of satellites after accounting for position interlopers. The dotted line indicates the surface density radial slope of a NFW halo. The full and open triangles represent the surface density of satellites found by Sales et al. (2005) and Chen et al. (2006), respectively. The dashed lines show the estimate of the interlopers velocity for μ = 3 × 10-7 kpc-2 and μ = 10-6 kpc-2. |
| In the text | |
 |
Fig. 6 Number of satellites against position angle differences. The total distribution is given by the upper histogram, while that of approaching satellites is represented by the unshaded area. In each bin, the rest of the contribution is due to receding satellites (shaded area). |
| In the text | |
 |
Fig. 7 Distribution of satellites around primary galaxies. Radius and position angle with respect to the major axis are shown for approaching (open circles) and receding (crosses) satellites. |
| In the text | |
 |
Fig. 8 The cumulate vector of ΔPA (broken curve) is compared to that of a uniform distribution (straight line). A Kolmogorov-Smirnov test shows that the probability that the two distributions are coming from and identical underlying one is ≃ 98%. |
| In the text | |
 |
Fig. 9 Mean velocity of satellites as a function of radius. |
| In the text | |
 |
Fig. 10 Velocity dispersion as a function of radius. |
| In the text | |
 |
Fig. 11 RCs of primaries and circular velocities obtained from the velocity dispersions of the satellites (black squares) (V(R) = (3/2)1/2σ(R), see text for details). The URC is shown (as a black line) out to the virial radius. |
| In the text | |
 |
Fig. 12 RCs of primaries and circular velocities obtained from velocity dispersions and Jeans equation (black squares, see text for details). The URC is shown (as a black line) out to the virial radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


