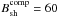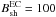EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 530 (June 2011) A&A, 530 (2011) A49 Full HTML
Free Access
Issue
A&A
Volume 530, June 2011
Article Number A49
Number of page(s) 10
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201116549
Published online 05 May 2011

© ESO, 2011

1. Introduction

Eta Carinae is the highest mass binary system detected up to now. It contains a star with a mass estimated in the range 80−120 M⊙ (Davidson & Humphreys 1997; Hillier et al. 2001) up to 200 M⊙ (Kashi & Soker 2010). The basic parameters of this star remain uncertain. Its luminosity is equal to 4.5 × 106 L⊙, and the surface temperature to 2 × 104 K. The radius estimates of Eta Carinae can differ by a factor of a few, between 40−180 R⊙ (Hillier et al. 2001). The star creates a very strong wind with a terminal velocity of  ~500−700 km s-1. The mass loss rate is estimated to be in the range from 2.5 × 10-4 M⊙ yr-1 (Pittard & Corcoran 2002) up to 10-3 M⊙ yr-1 (Hillier et al. 2001). Moreover, this mass loss rate seems to change rapidly (Martin et al. 2010; Corcoran et al.  2010). Eta Carinae is suspected to be a binary system with a period of  ~2022.7    ±    1.3 days (Daminelli et al. 2008), characterised by high eccentricity e ~ 0.9 (Nielsen et al. 2007) and the semi-major axis of a = 16.64 AU (Hillier et al. 2001). The parameters of the companion star are even more uncertain. It is a WR type or an O type supergiant with a luminosity 9 × 105 L⊙, and a surface temperature  ~4 × 104 K (Verner et al. 2005; Mehner et al. 2010). The radius of the companion star estimated for the above parameters is  ~1.4 × 1012 cm. The mass loss rate of the companion star is estimated to be Ṁcomp ~ 10-5 M⊙/yr and the wind velocity to be  ~3000 km s-1 (Pittard & Corcoran 2002). The timing of the periastron passage is defined as T0 = JD   24   528   19.8 (Damineli et al. 2008). The binary system is immersed in the massive nebula (Mneb ~ 12 M⊙, Smith et al. 2003), which likely originated in the huge outburst observed in this system in the year 1843. The radius of the nebula is estimated to be 3.4 × 1017 cm (Smith et al. 1998).

The GeV γ-ray emission has been recently reported from the direction of Eta Carinae by the AGILE telescope (Tavani et al. 2009). The γ-ray flux was steady during the period of over one year corresponding to the pre-periastron passage except for a single flare lasting for about two days. The analysis of the whole Fermi-LAT data shows the γ-ray source to be consistent with the AGILE discovery (Abdo et al. 2010; Farnier et al. 2010). These observations, covering also the period of the periastron passage, suggest a steady nature of the source. The γ-ray spectrum extends up to  ~ 100 GeV, showing two distinct components. The first one is consistent with a power law spectrum (spectral index 1.6 ± 0.2) and a cut-off at 1.6 GeV. The second one is described by a power law with spectral index  ~1.9 without evidence of a cut-off. The non-thermal nature of the source is also confirmed by the hard X-ray observations with the Beppo-Sax (Viotti et al. 2004), the INTEGRAL (Leyder et al. 2008) and the SUZAKU (Sekiguchi et al. 2009) satellites. This hard X-ray emission creates an additional flat component above the extended soft thermal X-rays which dominate below 1.5 keV. The X-ray emission from Eta Carinae in the 22 − 100 keV energy range is very hard (differential spectral index equal to  ≅ 1 ± 0.4, Leyder et al. 2008). More recent observations with INTEGRAL show that the hard X-ray component is well described by a power law spectrum (with photon index 1.8) without any strong variability at the periastron passage (Leyder et al. 2010).

In general, non-thermal high-energy radiation from massive binary systems is interpreted as radiation from particles accelerated at the stellar wind shock (e.g. Eichler & Usov 1993; Benaglia & Romero 2003; Bednarek 2005; Reimer et al. 2006; Pittard & Dougherty 2006; or Farnier et al. 2010). Both, leptons and hadrons can contribute to the γ-ray emission from the binary systems in the considered scenarios. Particles might also be accelerated in the large-scale blast wave produced during the Eta Carinae explosion in the year 1843 (e.g. Ohm et al. 2010). It is argued that accelerated hadrons cannot find enough targets for efficient γ-ray production. However, accelerated electrons are able to produce GeV γ-rays in the inverse-Compton process by scattering infrared radiation from the nebula.

In this paper we analyse different scenarios for the high-energy production in the general wind shock model with an application to the most massive compact binary system Eta Carinae. In contrast to previous works, we consider the acceleration of particles in two shocks with different properties appearing from the side of the Eta Carinae star and the companion star.

2. General scenario

We consider a simple scenario for the high-energy production within the binary system of two massive stars similar to what was already discussed in the papers mentioned above. The massive stars produce very strong winds, which collide within the binary system and create a double shock structure (see Fig. 1). The location of the shock within the binary system, Rsh, can be estimated for the known value of the coefficient η = Ṁcompvcomp/(ṀECvEC), which describes the pressure ratio of the winds from both stars. For the Eta Carinae binary system the wind pressure from the side of the Eta Carinae dominates. The value of η is estimated to be  ~0.2 by Pittard & Corcoran (2002) for the following parameters of Eta Carinae, vEC ~ 500 − 700 km s-1 and ṀEC ~ 2.5 × 10-4 M⊙ yr-1, and the companion star, Ṁcomp ~ 10-5 M⊙/yr and the wind velocity on vcomp ~ 3000 km s-1. This means that the shock is bound around the companion star but it is closer to the surface of the Eta Carinae star than to the surface of the companion star considering their stellar radii. In the example modelling we present, we apply the above parameters for the stars and their stellar radii equal to REC = 1.2    ×    1013 cm and Rcomp = 1.4    ×    1012 cm. The distance of the shock from the companion star can be obtained from 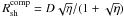Rshcomp=Dη/(1+η)\hbox{$R_{\rm sh}^{\rm comp} = D\sqrt{\eta}/(1 + \sqrt{\eta})$} and from Eta Carinae 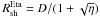RshEta=D/(1+η)\hbox{$R_{\rm sh}^{\rm Eta} = D/(1 + \sqrt{\eta})$}, where D is the separation of the stars. For the periastron passage, D = (1 − e)a ≈ 1.7 AU. Then, 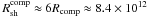Rshcomp≈6Rcomp≈8.4×1012\hbox{$R_{\rm sh}^{\rm comp}\approx 6R_{\rm comp}\approx 8.4\times 10^{12}$} cm and 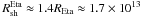RshEta≈1.4REta≈1.7×1013\hbox{$R_{\rm sh}^{\rm Eta}\approx 1.4R_{\rm Eta}\approx 1.7\times 10^{13}$} cm. For the apastron passage, the shock is located about an order of magnitude farther from both stars owing to the highly eccentric orbit. However, the fractions of their wind powers, which are intercepted by the shock structure, are comparable. The above mentioned estimates are obtained on the base of a simplified scenario. They may not correspond to the real situation as it occurrs in very close binary systems. At first, the stellar winds accelerate from the stellar surface. They are slower close to the stellar surfaces and reach the terminal speeds only at some distance from the stars. This may influence the localization of the shock within the binary system. Secondly, the radii of the companion stars are not preciously known. This means that in reality the distances of the acceleration region from the stellar surfaces may differ from the values estimated above. Thirdly, at the periastron passage the winds may not even balance. Owing to the instabilities in the wind, the shock surface can obtain a very complicated structure or it may even collapse onto one of the stars (e.g. Parkin et al. 2011). Therefore, the above estimated values should be taken with caution. They are applied as example values, but whether they correspond to the real situation in the Eta Carinae binary system is uncertain.

It is believed that shocks produced in collisions of stellar winds are able to accelerate particles to relativistic energies. Note, however, that the conditions at the shocks from the sides of both stars can be quite different. The mechanical pressure of the winds has to balance at the shock, i.e., parts of the power provided to the shock region from the sides of both stars are comparable. However, other physical parameters such as the magnetic field strength, the density of the wind or the wind velocity, can differ significantly. Therefore, it is expected that spectra of leptons and hadrons accelerated at the shocks from the sides of both stars can have different properties because of the differences in the efficiency of the acceleration process, magnetic field strengths and energy losses of particles that can determine their maximum energies. The density of stellar photons in both shocks is expected to be similar owing to relatively small thickness of the double shock structure.

In principle both shocks can accelerate leptons and hadrons to different maximum energies. Particles accelerated in different shocks can produce radiation at different energy ranges and at different dominant radiation processes. We also expect that depending on the shock (from the Eta Carinae or the companion star), particles can already lose energy close to the shock (i.e. within the binary system) or escape to the surrounding large-scale nebula. Therefore, high-energy radiation with very different properties can be expected in this relatively simple scenario of the two stellar wind interactions.

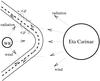thumbnail Fig. 1

Schematic representation of the supermassive binary system Eta Carinae. Electrons (e) and hadrons (p) can be accelerated on both shocks to different maximum energies due to different conditions at the shocks from the sides of the Eta Carinae star and the companion star. The details of the considered scenario are given in the main text of the paper.

3. Acceleration of particles

In general, the acceleration rate of particles at the shock can be parametrised by 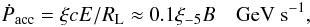Ṗacc=ξcE/RL≈0.1ξ-5B    GeV s-1,\begin{eqnarray} {\dot P}_{\rm acc} = \xi cE/R_{\rm L}\approx 0.1\xi_{-5} B~~~{\rm~GeV~s^{-1}}, \label{eq1} \end{eqnarray}(1)where ξ = 10-5ξ-5 is the acceleration parameter, E is the energy of particle (in GeV), RL is the Larmor radius of particles in the magnetic field B (in Gauss), and c is the velocity of light. We can estimate the characteristic acceleration time scale of particles from 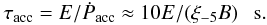τacc=E/Ṗacc≈10E/(ξ-5B)   s.\begin{eqnarray} \tau_{\rm acc} = E/{\dot P}_{\rm acc}\approx 10E/(\xi_{-5}B)~~~{\rm s}. \label{eq2} \end{eqnarray}(2)This acceleration process can be limited either by the advection of particles along the shock surfaces with the stellar winds or by their energy losses through different radiation processes. The characteristic time scale for the advection process along the shock is, 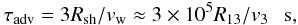τadv=3Rsh/vw≈3×105R13/v3   s,\begin{eqnarray} \tau_{\rm adv} = 3R_{\rm sh}/v_{\rm w}\approx 3\times 10^5R_{13}/v_3~~~{\rm s}, \label{eq3} \end{eqnarray}(3)where Rsh = 1013R13 cm is the distance of the shock from the centre of the star and vw = 108v3 cm s-1 is the stellar wind velocity. The radiation energy losses of particles can determine their maximum energies. Below we estimate the energy loss time scales for electrons and hadrons and their maximum allowed energies at the shocks from the sides of the Eta Carinae and the companion star.

3.1. Electrons

The synchrotron and ICS processes for the electrons are important. The cooling time scale of electrons on the synchrotron and IC (in the Thomson regime) processes can be estimated from, τsyn/IC = Ee/Ṗsyn/IC, where Ee is the electron energy and Ṗsyn/IC are the energy loss rates of electrons on both processes. These time scales are estimated as, 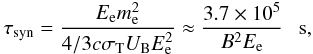τsyn=Eeme24/3cσTUBEe2≈3.7×105B2Ee   s,\begin{eqnarray} \tau_{\rm syn} = {{E_{\rm e}m_{\rm e}^2}\over{4/3c\sigma_{\rm T}U_{\rm B}E_{\rm e}^2}}\approx {{3.7\times 10^5}\over{B^2E_{\rm e}}}~~~{\rm s}, \label{eq4} \end{eqnarray}(4)and τIC/T=Eeme24/3cσTUradEe2≈170Ee[(T44Rsh2)comp+(T44Rsh2)EC]-1   s,\begin{eqnarray} \tau_{\rm IC/T} = {{E_{\rm e}m_{\rm e}^2}\over{4/3c\sigma_{\rm T}U_{\rm rad}E_{\rm e}^2}}\approx {{170}\over{E_{\rm e}}}\left[\left({{T_4^4}\over{R_{\rm sh}^2}}\right)_{\rm comp} + \left({{T_4^4}\over{R_{\rm sh}^2}}\right)_{\rm EC}\right]^{-1}~~~{\rm s}, \label{eq5} \end{eqnarray}(5)where σT is the Thomson (T) cross section, UB and Urad is the energy density of the magnetic and radiation fields, me is the electron mass, Rsh is the distance of the shock from a specific star expressed in units of the stellar radius of the specific star, and T = 104T4 K is the surface temperature of the specific star. 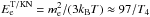The cooling time scale in the Klein-Nishina (KN) regime can be roughly estimated by introducing the energy of electrons into the above formula for the IC losses, corresponding to the transition between the Thomson and the Klein-Nishina regimes, EeT/KN=me2/(3kBT)≈97/T4\hbox{$E_{\rm e}^{\rm T/KN} = m_{\rm e}^2/(3k_{\rm B}T)\approx 97/T_4$} GeV. Then, the cooling time scale of electrons in the KN regime in the radiation field of both stars is approximately given by τICKN=3Eeme24cσTUrad(EeT/KN)2≈0.27Ee[(T44Rsh2)comp+(T44Rsh2)EC]-1 s.\begin{equation} \tau_{\rm IC}^{\rm KN} = {{3E_{\rm e}m_{\rm e}^2}\over{4c\sigma_{\rm T}U_{\rm rad}(E_{\rm e}^{\rm T/KN})^2}}\approx 0.27E_{\rm e}\left[\left({{T_4^4}\over{R_{\rm sh}^2}}\right)_{\rm comp} + \left({{T_4^4}\over{R_{\rm sh}^2}}\right)_{\rm EC}\right]^{-1}~{\rm s}. \label{eq6} \end{equation}(6)The cooling time scale of electrons on the bremsstrahlung process is almost independent of the electron energy. 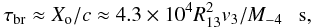It can be estimated from τbr≈Xo/c≈4.3×104R132v3/M-4   s,\begin{eqnarray} \tau_{\rm br}\approx X_{\rm o}/c\approx 4.3\times 10^4R_{13}^2v_3/M_{-4}~~~{\rm s}, \label{eq7} \end{eqnarray}(7)where Xo = 3.9 × 1025/ρw cm is the electron radiation length in hydrogen, 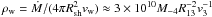ρw=Ṁ/(4πRsh2vw)≈3×1010M-4R13-2v3-1\hbox{$\rho_{\rm w} = {\dot M}/(4\pi R_{\rm sh}^2v_{\rm w})\approx 3\times 10^{10}M_{-4}R_{13}^{-2}v_3^{-1}$} cm-3 is the concentration of matter in the stellar wind, and the mass loss rate of the star is Ṁ = 10-4M-4 M⊙ yr-1.

The synchrotron and IC cooling time scales are clearly shorter than the advection time scale of electrons along the shock and their bremsstrahlung energy loss time scale for the applied parameters of the stars in the binary system. Therefore, the maximum energies of accelerated electrons should be determined by balancing the energy gains from the acceleration process with the energy losses on the synchrotron and IC processes. The efficiency of these two processes depends on the energy density of the magnetic and radiation fields in the acceleration region. The synchrotron losses dominate over the IC losses in the T regime for the magnetic field Bsh>40[(T44/Rsh2)comp+(T44/Rsh2)EC]1/2\hbox{$B_{\rm sh} > 40[(T_4^4/R_{\rm sh}^2)_{\rm comp} + (T_4^4/R_{\rm sh}^2)_{\rm EC}]^{1/2}$} G. For the part of the shock that is the closest to the stars at the periastron passage, this limiting value is Bsh > 160 G. Depending on the specific parameters of the companion stars, we expect a variety of radiation scenarios from the binary systems:

  • 1.

    the synchrotron energy losses always dominate over the IC process;

  • 2.

    the synchrotron energy losses dominate only at the highest energies (whereas the IC scattering occurs in the Klein-Nishina regime);

  • 3.

    the IC energy losses dominate for the whole energy range of accelerated electrons.

These radiation processes can occur in a different way on both sides of the double shock structure.

By balancing the synchrotron energy losses with the acceleration energy gains, we obtain the limit of the maximum energies of accelerated electrons at the shock, 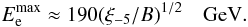Eemax≈190(ξ-5/B)1/2    GeV.\begin{eqnarray} E_{\rm e}^{\rm max}\approx 190(\xi_{-5}/B)^{1/2}~~~{\rm~GeV}. \label{eq8} \end{eqnarray}(8)On the other hand, by balancing the acceleration time scale with the IC energy loss time scale (in the T regime), we estimate the maximum energies of electrons as Eemax≈4(ξ-5Bsh)1/2[(T44/Rsh2)comp+(T44/Rsh2)EC]−1/2    GeV.\begin{eqnarray} E_{\rm e}^{\rm max}\approx 4(\xi_{-5}B_{\rm sh})^{1/2}\left[\left(T_4^4/R_{\rm sh}^2\right)_{\rm comp} + \left(T_4^4/R_{\rm sh}^2\right)_{\rm EC}\right]^{-1/2}~~~{\rm~GeV}. \label{eq9} \end{eqnarray}(9)To consider the high-energy processes in the Eta Carinae binary system, we have to fix the basic parameter that describes the considered scenario, which is the strength of the surface magnetic field of both stars. As an example, we use the value of 2 × 103 G for the surface magnetic field of the companion star and 200 G for the Eta Carinae star. 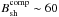Then, the magnetic field at the shock from the companion star is estimated to be Bshcomp~60\hbox{$B_{\rm sh}^{\rm comp}\sim 60$} G and at the shock from the Eta Carinae star as 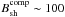Bshcomp~100\hbox{$B_{\rm sh}^{\rm comp}\sim 100$} G. We also fixed the values of the acceleration parameter ξ for both shocks by estimating them from ξ ~ (vw/c)2. Because the velocity of the winds from both stars differs significantly, we obtain, ξEC ~ 5 × 10-6 and ξcomp ~ 10-4. Because of large differences between these acceleration coefficients and magnetic field strengths at the shocks, the maximum energies of the electrons accelerated on both shocks (from the sides of Eta Carinae and the companion star) differ significantly.

The magnetic field strength in the winds of stars has a complicated dependence on the distance from the star. In a small region close to the stellar surface the magnetic field has a dipole structure, i.e., B(R) ∝ R-3 (Usov & Melrose 1992). However, in most cases this region is very small and it can be neglected. At larger distances the magnetic field has a radial structure. Then, its strength drops as B(R) ∝ R-2. This dependence dominates for distances characteristic for the periastron and apastron passages of the stars in the Eta Carinae binary system. The above dependence of the magnetic field strength on the distance from the star has interesting consequences. The maximum energies of electrons, determined by the balance between their acceleration efficiency and the synchrotron energy losses, should increase proportionally with the distance of the shock from the stellar surface provided that the acceleration efficiency is independent of the magnetic field strength (see Eq. (8)). Note however that at uncertain distance from the stars the adiabatic losses can dominate over the hadron energy losses. On the other hand, the maximum energies of electrons, determined by the IC energy losses in the T regime, should stay independent ofthe distance from the star (see Eq. (9)). We conclude that if the acceleration process is saturated by the synchrotron energy losses, the spectra of electrons should extend to higher energies for the parts of the shock farther from the star or for the apastron passage of stars when the whole shock structure is at a larger distance from the stars. However, the maximum energies should be independent of the shock location if the electron acceleration is saturated by the IC energy losses in the T regime. This conclusion is valid provided that the acceleration efficiency of electrons does not depend on the distance from the stars and the advection time scale of electrons is always longer than the energy loss time scales.

3.2. Hadrons

On the other hand, hadrons lose energy mainly on collisions with the matter of the stellar winds. The time scale for the energy losses on pion production in proton-proton collisions can be estimated from 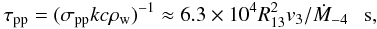τpp=(σppkcρw)-1≈6.3×104R132v3/Ṁ-4   s,\begin{eqnarray} \tau_{\rm pp} = (\sigma_{\rm pp} k c \rho_{\rm w})^{-1}\approx 6.3\times 10^4R_{13}^2v_3/{\dot M}_{-4}~~~{\rm s}, \label{eq10} \end{eqnarray}(10)where σpp ≈ 3 × 10-26 cm2 is the cross section for p − p → π production, k = 0.5 is the in-elasticity coefficient in this collision, and ρw is the density of the stellar wind at the shock region defined above. This energy loss time scale for the shock from the side of the Eta Carinae star is estimated to be  ~4 × 104 s and from the side of the companion star as  ~3.4 × 105 s at the closest region of the shock to the stars and at their periastron passage. The time scales for energy losses by hadrons and their escape (advection) from the acceleration site do not depend on their energy. By comparing these time scales (τpp = τadv), we determine the condition under which hadrons can interact close to the shock within the binary system. The following condition has to be fulfilled 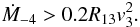Ṁ-4>0.2R13v32.\begin{eqnarray} {\dot M}_{-4} > 0.2R_{13}v_3^2. \label{eq11} \end{eqnarray}(11)This condition is clearly fulfilled at the periastron passage of the binary stars in the region of the shock from the side of the Eta Carinae star but is not fulfilled at the shock from the side of the companion star. Therefore, we expect that hadrons accelerated at the shock from the side of the Eta Carinae star interact efficiently within the binary system but those accelerated from the side of the companion star escape from the binary system to the surrounding nebula and interact there with the matter of expanding winds and the matter expelled during the past outbursts in the binary system (i.e., in the years 1843 and 1890).

The maximum energies of accelerated hadrons can be estimated by comparing the energy gains from the shock with energy losses on hadronic interactions or the advection from the acceleration site. The comparison of τacc with τpp allows us to estimate the maximum energies of hadrons 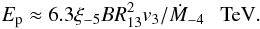Ep≈6.3ξ-5BR132v3/Ṁ-4   TeV.\begin{eqnarray} E_{\rm p}\approx 6.3\xi_{-5}BR_{13}^2v_3/{\dot M}_{-4}~~~{\rm TeV}. \label{eq12} \end{eqnarray}(12)If the condition given by Eq. (11) is not fulfilled, then the maximum energies of hadrons are determined by the escape along the shock. Then, the maximum energies are estimated as 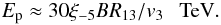Ep≈30ξ-5BR13/v3   TeV.\begin{eqnarray} E_{\rm p}\approx 30\xi_{-5}BR_{13}/v_3~~~{\rm TeV}. \label{eq13} \end{eqnarray}(13)Hadrons are expected to be accelerated at the shock not only at the periastron passage but also at other phases of the binary system. The advection time of hadrons scales proportionally to the distance between the companion stars but the collision time of hadrons is only proportional to the square of the distance (owing to the dependence of density of the wind with the distance from the star). We expect that hadrons are accelerated at the shock from the side of the Eta Carinae star to the maximum energies, which are independent on the phase of the binary system. However, their collision rate with the matter of the wind decreases at larger separation of the stars within the binary system. On the other hand, hadrons, accelerated at the shock from the side the the companion star and farther from the periastron passage (or at the parts of the shock laying father from the star), should be accelerated to lower maximum energies. This is a consequence of the mainly radial structure of the magnetic field around the stars within the binary system (B(r) ∝ R-2). As a result, hadrons injected into the Eta Carinae nebula will have a complicated spectrum, which can only be limited by the extreme values. The more precise determination of this spectrum is difficult due to the unknown dependence of the efficiency of hadron acceleration in different parts of the shock and at different phases of the binary system. Therefore, we calculate the expected radiation output below only from the hadrons at limiting distances from the star.

4. Scenarios for gamma-ray production

The complicated double shock structure of the collision region of the stellar winds, the possibile acceleration of electrons and hadrons, and the possible domination of different types of radiation mechanisms, that are responsible for the saturation of the acceleration process of particles provide the reach range of scenarios in which particles can produce high-energy radiation in the context of the massive binary systems. Here we consider the production of high-energy radiation in some possible scenarios in the context of massive binary system with an elongated orbit. They will be tested by the available high-energy observations of Eta Carinae. They also predict some specific features, which will allow us to distinguish between them with the future more systematic X-ray and GeV-TeV γ-ray and neutrino observations.

At first, we conclude that the hard X-ray emission detected by Beppo-SAX, INTEGRAL, and SUZAKU cannot be produced by electrons in the synchrotron process. The maximum energies of synchrotron photons produced by electrons whose acceleration is saturated by the synchrotron energy losses can be estimated from 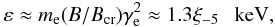ε≈me(B/Bcr)γe2≈1.3ξ-5   keV,\begin{eqnarray} \varepsilon \approx m_{\rm e}(B/B_{\rm cr})\gamma_{\rm e}^2\approx 1.3\xi_{-5} ~~~{\rm keV}, \label{eq14} \end{eqnarray}(14)where γe is the Lorentz factor of electrons estimated from Eq. (8), and Bcr = 4.4 × 1013 G is the critical magnetic field. Because the maximum energies of observed hard X-ray emission is at least ε ~ 0.1 MeV, the acceleration efficiency has to fulfil the condition ξ-5 > 76 (see Eq. (14)). This condition cannot be fulfilled in the shocks either from the side from the companion star or from the side of the Eta Carinae star. If the acceleration of primary electrons is saturated by the synchrotron energy losses, we should observe a strong synchrotron component in the Eta Carinae spectrum from the central source peaking at  ~1 keV. This is in-consistent with the observations of Eta Carinae because the detected soft X-ray emission has a thermal nature and is clearly extended. Therefore, we conclude that the hard X-ray emission cannot be produced by electrons in the synchrotron process, which are directly accelerated at the shocks.

Below we consider the two most likely scenarios for the high-energy emission from the Eta Carinae binary system, i.e., the production of the whole γ-ray spectrum only by electrons (our model A) and the production of the γ-ray spectrum in a composite model, part of the spectrum by electrons and part by hadrons (model B).

4.1. Model A: electrons

The non-thermal multiwavelength spectrum measured from the Eta Carinae binary system has its maximum in the γ-ray energy range. We expect that the energy losses of accelerated electrons in the synchrotron process are less than their energy losses in the IC process. As we noted above, both shocks present within the binary system are characterised by different values of the acceleration efficiency (ξcomp ~ 10-4 and ξEC ~ 5 × 10-6) and different values of the magnetic field strength at the shock. We fixed the values for the surface magnetic field of the companion star as Bcomp = 2 × 103 G and of the Eta Carinae star as BEC = 200 G, and assumed a mainly radial structure of the magnetic field in the stellar winds within the binary system (i.e. B(r) ∝ r-2). With these assumptions, we estimated the magnetic field strength at the shock from the companion star to be B ≈ 60 G, and from the Eta Carinae star as B ≈ 100 G at the periastron passage. We compare the characteristic time scales important for acceleration of electrons and their energy losses for the parameters mentioned above (see Fig. 2). The acceleration of those electrons at the parts of the shock that are the closest to the companion stars at their periastron passage is considered. We find that electrons can be accelerated at the shock from the side of the companion star to the maximum energies 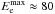Eemax≈80\hbox{$E_{\rm e}^{\rm max}\approx 80$} GeV. These energies are owing to the saturation by the synchrotron energy losses (Fig. 2). The saturation of electron acceleration by the synchrotron energy losses happens for energies close to the transition between the dominance of the synchrotron and the IC energy losses in the KN regime. Therefore, in spite of the saturation of electron acceleration by synchrotron process, these electrons lose energy mainly on the IC scattering in the KN regime (see Fig. 2). The acceleration process of electrons at the parts of the shock at larger distances from the stars should also be saturated by the synchrotron energy losses because their acceleration time scale depends on the distance from the stars in a similar way as their energy loss time in the KN regime (i.e. τacc ∝ τIC/KN ∝ R2, see Eqs. (2) and (6)). However, the maximum energies of electrons accelerated at the parts of the shock at larger distances from the stars should increase proportionally to R (see Eq. (8)).

The maximum energies of electrons at the shock from the side of the Eta Carinae star are determined by the balance between the acceleration process and the IC energy loss process in the T regime. For the parameters mentioned above, they are estimated to be 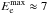Eemax≈7\hbox{$E_{\rm e}^{\rm max}\approx 7$} GeV (see Eq. (9)). These maximum energies should not change in the parts of the shock farther from the stars or at other phases because they are independent of the distance from the stars (see Eq. (9)). Electrons accelerated at the shock from the side of the Eta Carinae star lose energy mainly on the IC scattering of stellar radiation in the Thomson regime. The energy density of the radiation at the shock region from the Eta Carinae star and the companion star are comparable. Therefore, γ-rays produced in the IC process should have a quite isotropic distribution.

In conclusion, we expect the presence of two components in the electron spectrum, which are accelerated by different shocks created in the collision of the winds from the sides of both stars. These electrons can cool efficiently in the radiation field of the companion stars. These two components in the electron spectrum are responsible in our Model A for the two-component γ-ray spectra observed from the Eta Carinae binary system.

thumbnail Fig. 2

Characteristic time scales for electrons in the acceleration process in the shock from the side of the companion star (dot-dashed line) and the side of the Eta Carinae star (solid), the synchrotron cooling time of electrons at the shock from the side of the companion star (dotted), the IC cooling time scale in the Thomson regime (dot-dot-dashed) and in the Klein-Nishina regime (dashed). The intersection of the acceleration time scale with the IC cooling time scale in the Thomson regime gives the maximum energies of electrons accelerated at the shock from the side of the Eta Carinae star. The intersection of the acceleration time scale with the synchrotron cooling time scale gives the maximum energies of electrons accelerated at the shock from the side of the companion star. The parameters defining the acceleration scenario are Bshcomp=60\hbox{$B_{\rm sh}^{\rm comp} = 60$} G, BshEC=100\hbox{$B_{\rm sh}^{\rm EC} = 100$} G, ξcomp = 10-4, and ξEC = 5 × 10-6.

thumbnail Fig. 3

Optical depths for γ-rays in the radiation field of the Eta Carinae star (left panel) and its companion star (middle panel) as a function of energy of injected γ-ray photons. Specific curves show the results for the propagation angle of the γ-ray photon (measured from the direction defined by the injection place and the center of specific star) equal to: α = 0o (dot-dot-dashed curve, direction outwards of the specific star), 30o (dot-dashed), 60o (dotted), 90o (dashed), 120o (solid). γ-rays are injected at the distance of 1.4REC from the surface of Eta Carinae and at the distance of 6Rcomp from the surface of the companion star. The dependence of the optical depths on the distance from the Eta Carinae star is shown in the right panel for the injection angle of α = 60o and the distances 1.4REC (dotted), 2REC (solid), 3REC (dashed), 5REC (dot-dashed), and 10REC (dot-dot-dashed), respectively.

4.2. Model B: electrons and hadrons

In the second model we assume that the sub-GeV γ-rays are produced by electrons as in the case of model A. However, the second higher energy component in the γ-ray spectrum is expected to be produced by hadrons (see also Leyder et al. 2010). Acceleration of hadrons at the shock from the side of the Eta Carinae star is saturated by their energy losses on pion production. Their maximum energies are estimated from Eq. (12) on 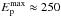Epmax≈250\hbox{$E_{\rm p}^{\rm max}\approx 250$} TeV. These hadrons cool close to the acceleration site within the binary system, producing high-energy γ-rays and neutrinos. On the other hand, acceleration of hadrons at the shock from the side of the companion star is limited by their convection along the shock. Then, the maximum energies of hadrons in the part of the shock that is the closest to the stars at the periastron passage, are estimated to be 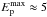Epmax≈5\hbox{$E_{\rm p}^{\rm max}\approx 5$} PeV (see Eq. (13)). These hadrons escape to the nebula surrounding the Eta Carinae binary system and eventually interact with the matter within the nebula, producing high-energy gamma-rays and neutrinos. In principle, hadrons accelerated in both shocks can contribute to the observed hard γ-ray emission. However, their relative contribution is difficult to estimate because of it depends on the details of the acceleration process, which are mainly unknown. On the other hand, hadrons accelerated at the shock from the side of the companion star accumulate within the nebula. They interact with the matter of expending winds of the stars and the matter entrained within the nebula during the past outbursts.

Note that in principle the efficiencies of the particle acceleration in both shocks can differ as can the efficiencies of the acceleration of electrons and hadrons. Therefore, a different combination of processes can produce a variety of radiation outputs from these binary systems.

5. Absorption of gamma-rays

The TeV γ-rays produced within the compact binary systems should be absorbed in a complicated way in the soft radiation of luminous stars (e.g. Bednarek 1997). These absorption effects should be taken into account for the case of the γ-ray production within  ~10 stellar radii from both stars. Therefore, we calculated the optical depths for γ-rays injected close to the shock region in the radiation field of both stars as a function of their propagation angle and for their different injection distances from the stars. We applied the parameters of both stars as mentioned in the introduction. The optical depths are shown in Fig. 3. The angles for the Eta Carinae star and the companion star are counted outwards from the specific star. Clearly even in the most favourable case defined by the angle α = 90°, the γ-rays with energies above a few tens of GeV should be efficiently absorbed (the optical depth above unity). These absorption effects should be taken into account when comparing the γ-ray spectra produced close to the periastron passage of the stars with the observations of the Eta Carinae binary system. However, closer to the apastron passage, most of the shock structure lies at distances larger than  ~10 stellar radii. At these distances the optical depths drop below unity (see Fig. 3 for the dependence of the optical depth on the distance). Therefore, it is expected that absorption of γ-rays produced close to the shock region will result in a clear modulation of the γ-ray signal from the Eta Carinae binary system already at sub-TeV energies.

6. Comparison with observations of Eta Carinae

We discuss the radiation output expected in terms of the model A and B (defined above) for different locations of the acceleration site from the companion stars, i.e. for different parts of the shock and different phases of the binary system. The calculated hard X-ray to γ-ray spectra are compared with the recent observations of the Eta Carinae binary system (described in the introduction).

thumbnail Fig. 4

X-ray and γ-ray spectra expected for the model A (left) and model B (right) at the periastron passage of the stars in the binary system Eta Carinae compared with the high-energy observations of this system. The measurements in the hard X-rays by the INTEGRAL satellite (Leyder et al. 2010) are marked by squares and those in the γ-ray energy range by the Fermi-LAT detector (Farnier et al. 2010; Abdo et al. 2010) are marked by triangles. The results of the calculations are shown for the model A (left panel): γ-rays from electrons accelerated at the shock from the side of the Eta Carinae star (solid) and from electrons accelerated at the shock from the side of the companion star: without any absorption (thin dashed), with absorption for the γ-ray propagating at the angle equal to 50o (towards the star) at distance from the star D = 1.4REC (dashed), and at the same angle but for the parts of the shock at the distance from the star D = 10REC (dot-dashed). For Model B (right panel): γ-rays from electrons, accelerated at the shock from the side of the Eta Carinae star, scattering stellar radiation in the T regime (solid), γ-rays from decay of neutral pions produced by hadrons accelerated at the shock from the side of the Eta Carinae star: unabsorbed spectrum (thin dashed curve extending to lower energies), spectra absorbed in the stellar radiation for distances from the star: D = 1.4REC (thick dashed) and D = 10REC (dot-dashed). Secondary leptons from decay of charged pions (produced in hadronic collisions) lose energy on the synchrotron radiation (dot-dot-dashed curve). The γ-ray spectrum produced by hadrons, which are accelerated at the shock from the side of the companion star and produce pions in the interactions within the Eta Carinae nebula, are shown by the thin dashed curve extending to higher energies.

6.1. Model A

In this model we assumed that the GeV γ-ray emission is produced by electrons accelerated at the shock from the side of the Eta Carinae star and the multi-GeV hard γ-ray emission is produced by electrons accelerated at the shock from the side of the companion star. As an example, we assume that electrons are accelerated with the power law spectrum defined by the spectral index αinj = 2 up to the maximum energies as estimated in Sect. 3.1.

For electrons accelerated at the shock from the side of the Eta Carinae star, the main energy loss mechanism is the IC scattering in the T regime. This process is efficient enough already close to the acceleration site because the cooling time scale of electrons on the IC process is clearly shorter than their advection time scale (see Eqs. (3) and (5)). As a result, the equilibrium spectrum of electrons reaches the spectral index αeq = 3 and the γ-ray spectra from these electrons should have a spectral index close to 2. However, at low electron energies, the cooling time scale of the IC process starts to become comparable to the cooling time scale of the bremsstrahlung process (see Eqs. (5) and (7)). The transition between which of these two radiation processes dominates occurs for electrons with energies of a few tens of MeV. Therefore, the photon spectrum from the IC process should steepen at energies somewhere in the soft γ-ray to hard X-ray energy range. The precise break energy in the IC spectrum is difficult to estimate because of the uncertain density of the matter in the shock region (it varies by a factor of  ~100, see Pittard 2009). For low-energy electrons, for which the bremsstrahlung energy losses dominate, the equilibrium spectrum should be close to the injection spectrum 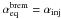αeqbrem=αinj\hbox{$\alpha_{\rm eq}^{\rm brem} = \alpha_{\rm inj}$}. Therefore, the IC spectrum produced by these electrons should steepen to the spectral index  ~ 1.5. We compare the hard X-ray to γ-ray IC spectrum expected from the electrons accelerated at the shock from the side of the Eta Carinae star with the observations of this binary system in Fig. 4 (see solid curve in the left panel). γ-rays from the bremsstrahlung process are produced with energies comparable to energies of their parent electrons. The power in this emission only contains a small part of the whole power of accelerated electrons. Therefore, its contribution to the spectrum observed from Eta Carinae is on a much lower level.

On the other hand, electrons accelerated at the shock from the side of the companion star can reach energies of the order of  ~100 GeV. The electron energies can be even higher, provided that their acceleration occurs in the part of the shock at larger distances from the stars (Sect. 3.1). Electrons also lose energy in the IC scattering process, which in this case occurs in the T and in the KN regimes (the synchrotron energy losses are neglected, see Fig. 2 for details of the derivation of maximum energies of accelerated electrons). We show that this IC emission can be responsible for the the hard multi-GeV γ-ray spectrum observed from the direction of the Eta Carinae binary system. For the injection spectrum of electrons with the spectral index αinj = 2, the IC γ-ray spectrum is also produced with the spectral index αγ = 2, both in the T and KN regimes (see e.g. Blumenthal & Gould 1970). However, as we showed above, γ-rays produced at the part of the shock relatively close to the companion stars are efficiently absorbed in the stellar radiation field. We take these absorption effects into account by applying the optical depths for the γ-rays in the radiation fields of the Eta Carinae and companion stars and using simple absorption law,  ∝ exp [−τ(Eγ) ] . Because the inclination angle of the Eta Carinae binary system is estimated to be  ~40o, we show as an example the γ-ray spectra with the absorption effects in the radiation of the Eta Carinae star for the angle α = 50o (see dashed and dot-dashed curves in left Fig. 4). The unabsorbed γ-ray spectrum (produced at distances  > 10REC from the Eta Carinae star) are shown by the dotted curves. We conclude that the considered model predicts a clear modulation of the γ-ray signal at energies above  ~100 GeV with the period of the binary system. The γ-ray spectrum produced at the periastron passage by electrons accelerated at the part of the shock that are the closest to the Eta Carinae star should cutoff just below  ~100 GeV.

6.2. Model B

In this model the GeV γ-ray peak is also produced by electrons accelerated at the shock from the side of the Eta Carinae star (as in model A). But the multi-GeV hard γ-ray emission is proposed to be produced by hadrons that are also accelerated at the shock from the side of the Eta Carinae star (see also Farnier et al. 2010). At the periastron passage the hadrons accelerated at this shock can reach energies  ~250 TeV for the magnetic field strength at the shock from the side of the Eta Carinae star (see Eq. (12)). These maximum energies are independent of the distance from the stars in the case of the radial structure of the magnetic field. The number of collisions of relativistic hadrons with the matter of the Eta Carinae wind, already close to the acceleration site within the binary system, can be estimated as, 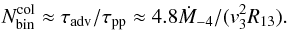Nbincol≈τadv/τpp≈4.8Ṁ-4/(v32R13).\begin{eqnarray} N_{\rm bin}^{\rm col}\approx \tau_{\rm adv}/\tau_{\rm pp}\approx 4.8{\dot M}_{-4}/(v_3^2R_{13}). \label{eq15} \end{eqnarray}(15)For the parts of the shock close to the Eta Carinae star at the periastron passage, the collision rate is estimated to be  ~15, and at the distance of 10REC it is still  ~1.5. Therefore, we conclude that these hadrons are efficiently cooled already close to the shock within the binary system through the large range of the binary phases. As a consequence, γ-ray spectra from the decay of the neutral pions produced by hadrons accelerated at the Eta Carinae shock should not depend strongly on the phase of the binary system. We calculate the spectra of γ-rays and secondary leptons from the decay of the pions produced in hadronic collisions assuming the power law spectrum of hadrons with the spectral index αp = 2. In Fig. 4, γ-ray spectra from decay of πo are compared with the γ-ray observations of the Eta Carinae binary system.

The γ-ray spectrum from decay of pions clearly extends through the TeV energy range. However, as in the previous model, the TeV γ-rays produced within  ~10 stellar radii should be efficiently absorbed in the thermal radiation of the Eta Carinae star (Sect. 5). We take this absorption effect into account by showing in Fig. 4 the unabsorbed γ-ray spectra (thin dashed curves) and absorbed spectra for the parameters of the binary system as for model A. The maximum energies of the accelerated hadrons should not depend on the distance from the stars for the radial structure of the magnetic field, provided that the acceleration coefficient does not depend on the distance (see Eq. (12)). Therefore, at locations close to apastron, the γ-ray emission extending up to a few TeV is in principle possible. We conclude that the Cherenkov telescopes should detect a clear modulation of the γ-ray signal at energies above  ~100 GeV with the orbital period of the binary system because of the different absorption conditions within the binary system.

The secondary leptons, from decay of charged pions produced in hadronic collisions, efficiently lose energy in the synchrotron process, reaching the equilibrium spectrum with the spectral index 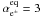αe±eq=3\hbox{$\alpha_{\rm e^\pm}^{\rm eq} = 3$}. They produce synchrotron radiation with the spectral index 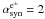αsyne±=2\hbox{$\alpha_{\rm syn}^{\rm e^\pm} = 2$}. The spectral index of the hard X-ray emission from the Eta Carinae binary system is not precisely known (Viotti et al. 2004; Leyder et al. 2008, 2010; Sekiguchi et al. 2009). However, it is reported to be not far from the above value. The synchrotron emission from secondary leptons should extend through the hard X-ray energy range. The spectrum of secondary leptons, from decay of charged pions produced in hadronic collisions, extends up to 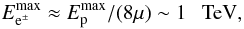Ee±max≈Epmax/(8μ)~1   TeV,\begin{eqnarray} E_{{\rm e}^\pm}^{\rm max}\approx E_{\rm p}^{\rm max}/(8\mu)\sim 1~~~{\rm TeV}, \label{eq16} \end{eqnarray}(16)where μ is the multiplicity of pion production by protons given in Orth & Buffington (1976). Electrons with these energies (Ee = meγe) are able to produce synchrotron radiation at the shock from the side of the Eta Carinae star with energies up to 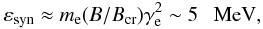εsyn≈me(B/Bcr)γe2~5   MeV,\begin{eqnarray} \varepsilon_{\rm syn} \approx m_{\rm e}(B/B_{\rm cr})\gamma_{\rm e}^2\sim 5 ~~~{\rm MeV}, \label{eq17} \end{eqnarray}(17)i.e., consistent with the observations of the hard X-ray emission from the Eta Carinae binary system (see Fig. 4). The level of this emission should also be comparable to the level of the hard γ-ray component from Eta Carinae, which is indeed the case (see Abdo et al. 2010; and Farnier et al. 2010). Therefore, secondary leptons can contribute to (or even be responsible for) the hard X-ray emission from the Eta Carinae binary system. The spectral index of the IC component in the hard X-ray energy range produced by primary electrons accelerated at the shock from the side of the Eta Carinae star is predicted to be clearly flatter than 2 (see Model A). Therefore, precise measurements in this energy range should indicate the origin of this lower energy emission, i.e., either it is produced by primary electrons in the IC process or by secondary leptons in the synchrotron process.

In principle, the hard γ-ray component could be also produced by hadrons accelerated at the shock from the side of the companion star. However, these hadrons escape to the Eta Carinae nebula from the binary system without significant energy losses close to the acceleration site. The Larmor radii of hadrons escaping to the nebula are always much smaller than the characteristic distance scale of the system (which is of the order of the distance from the binary system) for the magnetic field around the massive stars with the toroidal structure at a distance above  ~ 10REC (Usov & Melrose 1992). Hadrons are frozen in the stellar winds moving outwards from the binary system. We can distinguish two regions within the nebula in which hadrons interact with the matter, i.e., the inner region where the density of matter is dominated by the direct stellar winds and the outer region where the density of the wind drops below the average density of the Eta Carinae nebula created during the outburst about 170 years ago. We assume that at larger distances from the binary system the winds from the Eta Carinae star and the companion star can mix through the rotation of the binary system. The characteristic collision rate of hadrons can be estimated from 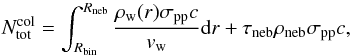Ntotcol=∫RbinRnebρw(r)σppcvwdr+τnebρnebσppc,\begin{eqnarray} N_{\rm tot}^{\rm col} = \int_{R_{\rm bin}}^{R_{\rm neb}}{{\rho_{\rm w}(r)\sigma_{\rm pp}c}\over{v_{\rm w}}}{\rm d}r + \tau_{\rm neb}\rho_{\rm neb}\sigma_{\rm pp}c, \label{eq18} \end{eqnarray}(18)where Rbin is the radius of the binary system assumed to be equal to  ~1014 cm, Rneb = 3 × 1017 cm, ρw(r) is the density of the wind from the binary system (see above), vw is the velocity of the stellar wind, ρneb is the average density of the nebula  ~104 cm-3, and τneb ≈ 5 × 109 s is the age of the Eta Carinae nebula. For the applied parameters, 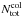Ntotcol\hbox{$N_{\rm tot}^{\rm col}$} can reach the values of a few, i.e., hadrons can completely cool within the nebula. In principle, hadrons injected into the expanding wind from the star could suffer from adiabatic energy losses. To check whether this process can significantly change the energies of the injected hadrons we estimate the distance, Rout, from the binary system up to which hadrons interact at least once with the matter of the wind. The following equation has to be checked: 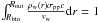Rbin∫Routρw(r)σppcvwdr=1\hbox{$\int_{R_{\rm bin}}^{R_{\rm out}}{{\rho_{\rm w}(r)\sigma_{\rm pp}c}\over{v_{\rm w}}}{\rm d}r = 1$}. For the example parameters applied in our calculations we estimate that hadrons should mainly interact relatively close to the binary system, where the density of the wind is still high. Therefore, adiabatic energy losses of hadrons through the expansion of the wind can be safely neglected. We conclude that hadrons injected into the nebula surrounding the Eta Carinae binary system should interact efficiently, producing γ-rays and neutrinos. This conclusion is in contrast to the expectations of Ohm et al. (2010), who predicted inefficient interaction of hadrons in the large-scale nebula with relatively low average density. However, we consider the inner, denser nebula with the radius of a few times smaller than applied in their case. This inner nebula is dominated by the matter from the dense wind of the Eta Carinae star produced at the present time.

The maximum energies of hadrons escaping from the binary system can be as high as  ~ 5 PeV (see Eq. (13)) for the part of the shock that is closest to the companion star at the periastron passage. These maximum energies drop with the distance of the shock from the companion star if the radial dependence of its magnetic field reaches values of  ~250 TeV for the distance of 20REC. As an example, we calculate the γ-ray spectrum expected from hadrons within the nebula with the power law spectrum, applying the spectral index equal to 2 and the maximum energies of hadrons equal to 5 PeV (Fig. 4). If hadrons are accelerated efficiently at the shock from the side of the companion star, a γ-ray emission extending up to multi-TeV energies is expected. This emission component should be steady, i.e., independent of the phase of the binary system because the absorption effects in the stellar radiation fields within the Eta Carinae nebula are not important.

The total energy content in relativistic hadrons, which are responsible for the observed γ-ray luminosity, can be estimated from, 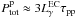Ptotp≈3LγECτpp\hbox{$P_{\rm tot}^{\rm p}\approx 3L_\gamma^{\rm EC} \tau_{\rm pp}$}, where 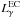LγEC\hbox{$L_\gamma^{\rm EC}$} is the γ-ray luminosity observed from the Eta Carinae binary system above  ~ 10 GeV, τpp is the cooling time scale for hadronic collisions given by Eq. (10), and the factor of 3 is there because only about one third of the produced pion energy goes to γ-rays. For 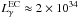LγEC≈2×1034\hbox{$L_\gamma^{\rm EC}\approx 2\times 10^{34}$} erg s-1 derived for the distance to Eta Carinae equal to 2 kpc (Abdo et al. 2010) and the density of matter characteristic at the border of the binary system, ρw(Rbin = 1014   cm) ~ 109 cm-3, we estimate the total energy content in relativistic hadrons within the inner nebula to be 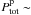Ptotp~\hbox{$P_{\rm tot}^{\rm p}\sim$}1041 erg. Because the energy losses of hadrons are very efficient in this model, hadrons reach a steady-state distribution in the inner nebula. Then, the power radiated in γ-rays is comparable to the power converted from the acceleration mechanism to relativistic hadrons, 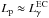Lp≈LγEC\hbox{$L_{\rm p}\approx L_\gamma^{\rm EC}$}. We conclude that to provide the hard γ-ray luminosity observed from the Eta Carinae binary system, hadrons have to take only  ~10-3 of the power of the wind from the Eta Carinae star, which is estimated to be 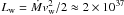Lw=Ṁvw2/2≈2×1037\hbox{$L_{\rm w} = {\dot M}v_{\rm w}^2/2\approx 2\times 10^{37}$} erg s-1.

Hadrons might also be accelerated at the large-scale blast wave produced during the past explosion of the Eta Carinae star (e.g. Ohm et al. 2010). This injection process can provide an additional source of high-energy hadrons within the nebula which was not considered in the present paper.

7. Neutrinos from Eta Carinae

Hadrons accelerated at both shocks should also produce neutrinos in collisions with dense matter of the Eta Carinae wind and the matter entrained within the Eta Carinae nebula during past outbursts. In model B, we propose that hadrons accelerated at the shock from the side of the Eta Carinae star can interact efficiently with the matter of the stellar wind, producing γ-rays via decay of pions from hadronic interactions through the large range of the binary phases. The maximum energies of accelerated hadrons are estimated to be  ~250 TeV. They should not depend strongly on the distance of the shock from the Eta Carinae star. We calculate the muon neutrino spectra produced by these hadrons by applying the scaling break model, which is suitable for hadrons with the above estimated energies (Wdowczyk & Wolfendale 1987). It is assumed that hadrons have a power law spectrum with the spectral index equal to 2. Such a flat spectrum is motivated by the very flat hard GeV γ-ray emission observed from the Eta Carinae. We compare the neutrino spectra with the atmospheric neutrino background and the sensitivity of 1 km2 neutrino detector of the IceCube type (see Fig. 5). Unfortunately, the level of this neutrino emission is comparable to the level of the atmospheric neutrino background. Therefore, these neutrinos will be difficult to detect even with a 1 km2 neutrino detector.

thumbnail Fig. 5

Muon neutrino spectra produced by hadrons which are accelerated at the shocks from the side of the companion star up to energies of 5 PeV (solid curve) and the side of the Eta Carinae star up to energies of 250 TeV (dashed). Hadrons from the side of the Eta Carinae star interact with the matter of dense wind close to the shock region within the binary system. Hadrons from the side of the companion star escape from the shock region into the nebula and interact with the matter of expanding stellar wind and the matter within the nebula expelled in the past. The power law spectrum of hadrons is applied with the spectral index equal to 2. The neutrino spectra are normalized to the hard γ-ray spectrum observed from the Eta Carinae binary system assuming its hadronic origin via pion production. The range of the atmospheric neutrino background (vertical and horizontal) within 1o degree of the source is marked by dot-dashed curves (Lipari 1993). The 1 yr sensitivity of the km2 neutrino detector (expected for the IceCube detector) is marked by the thin dotted line.

Hadrons accelerated at the shock from the side of the companion star can also produce neutrinos in collisions with the matter of the Eta Carinae nebula. We show that this scenario can be tested by the future neutrino observations of the Eta Carinae binary system. By assuming that γ-rays, also produced by these hadrons, are responsible for the observed hard GeV γ-ray emission from the Eta Carinae binary system, we estimate the expected muon neutrino spectrum from hadrons accelerated at the shock from the side of the companion star. The neutrino signal should result as a contribution from hadrons accelerated at the shock during the whole range of phases of the binary system. Their maximum energies at these different locations vary between 5 PeV (periastron) to 250 TeV (at distance of the shock equal to D = 20REC). Therefore, the total neutrino flux from hadrons, accelerated at the shock from the side of the companion star and interacting with the matter of the Eta Carinae nebula, should be contained within the range defined by the dashed and solid curves in Fig. 5. There is a chance that these neutrinos would be detected by the 1 km2 detector because the predicted spectrum is above the atmospheric neutrino background and above the sensitivity of the 1 km2 neutrino detector at energies between a few TeV and a few tens of TeV. Non-detection of the muon neutrino signal in this energy range (or detection on lower level) will give us important information on the acceleration efficiency of hadrons at the shock from the companion star.

8. Discussion and conclusion

We investigated the consequences of the acceleration of particles (electrons, hadrons) at the shocks appearing within the binary system of two massive stars as a result of stellar wind collisions. In contrast to previous studies, we considered the acceleration of particles in two shock structures which appear on both sides of the contact discontinuity from the sides of the Eta Carinae star and the companion star. These two shocks have different properties owing to differences in the surface magnetic field strengths (BEC = 200 G and Bcomp = 2 × 103 G) and acceleration efficiencies depending on the stellar wind velocities (ξEC = 5 × 10-6 and ξcomp = 10-4). The possibility of acceleration of particles in both shocks, either electrons or hadrons or both, can turn into a variety of radiation scenarios in which the high-energy γ-rays can be produced. As an example, we considered in a more detail two general scenarios for some specific values of the surface magnetic fields of the stars and acceleration efficiencies at the shocks created from the sides of the Eta Carinae star and the companion star. In the first one (model A), all high-energy emission comes from electrons accelerated in these two shocks. In the second model (model B), soft γ-ray emission comes from electrons and the higher energy γ-ray component is produced by hadrons. Both models can successfully describe the γ-ray spectral features of the Eta Carinae (e.g., two-component spectrum, lack of strong variability at the multi-GeV energies). However, the leptonic model predicts a clear variability of the γ-ray emission above  ~ 100 GeV with the period of the binary system. This variability is caused by the strong absorption of the produced γ-rays in the stellar radiation fields of both stars. On the other hand, TeV γ-ray emission produced by hadrons in terms of the model B can either show variability in the case of their acceleration at the shock from the side of the Eta Carinae star (γ-rays from within the binary system) or not show variability if they are accelerated at the shock from the side of the companion star (γ-rays produced within the larger scale nebula surrounding the binary system).

We have considered only a part of possible radiation scenarios that could be expected in this type of a wind collision model. For other values of the surface magnetic field of the companion stars, locations of the shocks, or acceleration efficiencies, the acceleration of electrons and hadrons can be saturated at other energies. Therefore, a variety of spectral behaviours might be expected from other massive binaries. The general spectral features of the Eta Carinae could also be investigated with other parameters of the stars. Therefore, the set of parameters applied in our example modelling may not be unique.

It is fairly difficult to conclude on the type of accelerated and radiating particles in the Eta Carinae binary system. In general, the leptonic model (model A) does not predict significant γ-ray emission above a few TeV at any phase of the binary system. But the hadronic model (model B) predicts γ-ray emission at energies up to  ~10−100 TeV. Moreover, γ-ray spectra produced by hadrons injected into the Eta Carinae nebula should be independent of the phase of the binary system. The most evident confirmation of the hadronic origin of γ-ray emission could come from the detection of a neutrino signal from this source. Therefore, we calculated the neutrino spectra expected for the model B and compared them with the sensitivity of the 1 km2 telescope. We showed that the neutrino spectra produced by hadrons within the nebula

can be above the atmospheric neutrino background and within the sensitivity of the 1 km2 telescope. However, the exact neutrino event rate in these telescopes is difficult to predict because the energies of the injected hadrons depend on the phase of the binary system. The dependence of the injection rate of particles on the phase of the binary system cannot be reliably predicted at present. Only future precise measurements of the γ-ray flux from the Eta Carinae as a function of the phase of this binary system may allow us to put limits on the injection rate of hadrons at different phases and thus allow us to estimate the expected neutrino event rates in large-scale neutrino telescopes more precisely.

Acknowledgments

We would like to thank the anonymous referee for valuable comments. This work is supported by the Polish MNiSzW grant N N203 390834 and NCBiR grant ERA-NET-ASPERA/01/10. Project co-funded by the European Union under the European Social Fund, POKL “Człowiek najlepsza inwestycja”.

References

  1. Abdo, A. A., Ackermann, M., Ajerb, M., et al. 2010, ApJ, 723, 649 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bednarek, W. 1997, A&A, 322, 523 [NASA ADS] [Google Scholar]
  3. Bednarek, W. 2005, MNRAS, 363, 46 [Google Scholar]
  4. Benaglia, P., & Romero, G. E. 2003, A&A, 399, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
  6. Damineli, A., Hillier, D. J., Corcoran, M. F., et al. 2008, MNRAS, 384, 1649 [NASA ADS] [CrossRef] [Google Scholar]
  7. Davidson, K., & Humphreys, R. M. 1997, ARA&A, 35, 1 [NASA ADS] [CrossRef] [Google Scholar]
  8. Eichler, D., & Usov, V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef] [Google Scholar]
  9. Farnier, C., Walter, R., & Leyder, J.-C. 2010, A&A, 526, A57 [Google Scholar]
  10. Hillier, D. J., Davidson, K., Ishibashi, K., & Gull, T. 2001, ApJ, 553, 837 [NASA ADS] [CrossRef] [Google Scholar]
  11. Kashi, A., & Soker, N. 2010, ApJ, 723, 602 [NASA ADS] [CrossRef] [Google Scholar]
  12. Leyder, J.-C., Walter, R., & Rauw, G. 2008, A&A, 477, L29 [Google Scholar]
  13. Leyder, J.-C., Walter, R., & Rauw, G. 2010, A&A, 524, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Lipari, P. 1993, APh, 1, 195 [Google Scholar]
  15. Martin, J. C., Davidson, K., Humphreys, R. M., & Mehner, A. 2010, AJ, 139, 2056 [NASA ADS] [CrossRef] [Google Scholar]
  16. Mehner, A., Davidson, K., Ferland, G. J., & Humphreys, R. M. 2010, ApJ, 710, 729 [NASA ADS] [CrossRef] [Google Scholar]
  17. Nielsen, K. E., Corcoran, M. F., Gull, T. R., et al. 2007, ApJ, 660, 669 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ohm, S., Hinton, J. A., & Domainko, W. 2010, ApJ, 718, 1610 [Google Scholar]
  19. Orth, C. D., & Buffington, A. 1976, ApJ, 206, 312 [NASA ADS] [CrossRef] [Google Scholar]
  20. Parkin, E. R., Pittard, J. M., Corcoran, M. F., & Hamaguchi, K. 2011, ApJ, 726, 105 [NASA ADS] [CrossRef] [Google Scholar]
  21. Pittard, J. M. 2009, MNRAS, 396, 1743 [NASA ADS] [CrossRef] [Google Scholar]
  22. Pittard, J. M., & Corcoran, M. F. 2002, A&A, 383, 636 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Pittard, J. M., & Dougherty, S. M. 2006, MNRAS, 372, 801 [NASA ADS] [CrossRef] [Google Scholar]
  24. Reimer, A., Pohl, M., & Reimer, O. 2006, ApJ, 644, 1118 [NASA ADS] [CrossRef] [Google Scholar]
  25. Sekiguchi, A., Tsujimoto, M., Kitamoto, S., et al. 2009, PASJ, 61, 629 [NASA ADS] [Google Scholar]
  26. Smith, N., Gehrz, R. D., & Krautter, J. 1998, AJ, 116, 1332 [NASA ADS] [CrossRef] [Google Scholar]
  27. Smith, N., Gehrz, R. D., Hinz, P. M., et al. 2003, AJ, 125, 1458 [NASA ADS] [CrossRef] [Google Scholar]
  28. Tavani, M., Sabatini, S., Pian, E., et al. 2009, ApJ, 698, L142 [Google Scholar]
  29. Usov, V. V., & Melrose, D. B. 1992, ApJ, 395, 575 [NASA ADS] [CrossRef] [Google Scholar]
  30. Verner, E., Bruhweiler, F., & Gull, T. 2005, ApJ, 624, 973 [NASA ADS] [CrossRef] [Google Scholar]
  31. Viotti, R. F., Antonelli, L. A., Rossi, C., & Rebecchi, S. 2004, A&A, 420, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Wdowczyk, J., & Wolfendale, A. W. 1987, J. Phys. G, 13, 411 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Schematic representation of the supermassive binary system Eta Carinae. Electrons (e) and hadrons (p) can be accelerated on both shocks to different maximum energies due to different conditions at the shocks from the sides of the Eta Carinae star and the companion star. The details of the considered scenario are given in the main text of the paper.
In the text
thumbnail Fig. 2

Characteristic time scales for electrons in the acceleration process in the shock from the side of the companion star (dot-dashed line) and the side of the Eta Carinae star (solid), the synchrotron cooling time of electrons at the shock from the side of the companion star (dotted), the IC cooling time scale in the Thomson regime (dot-dot-dashed) and in the Klein-Nishina regime (dashed). The intersection of the acceleration time scale with the IC cooling time scale in the Thomson regime gives the maximum energies of electrons accelerated at the shock from the side of the Eta Carinae star. The intersection of the acceleration time scale with the synchrotron cooling time scale gives the maximum energies of electrons accelerated at the shock from the side of the companion star. The parameters defining the acceleration scenario are Bshcomp=60\hbox{$B_{\rm sh}^{\rm comp} = 60$} G, BshEC=100\hbox{$B_{\rm sh}^{\rm EC} = 100$} G, ξcomp = 10-4, and ξEC = 5 × 10-6.
In the text
thumbnail Fig. 3

Optical depths for γ-rays in the radiation field of the Eta Carinae star (left panel) and its companion star (middle panel) as a function of energy of injected γ-ray photons. Specific curves show the results for the propagation angle of the γ-ray photon (measured from the direction defined by the injection place and the center of specific star) equal to: α = 0o (dot-dot-dashed curve, direction outwards of the specific star), 30o (dot-dashed), 60o (dotted), 90o (dashed), 120o (solid). γ-rays are injected at the distance of 1.4REC from the surface of Eta Carinae and at the distance of 6Rcomp from the surface of the companion star. The dependence of the optical depths on the distance from the Eta Carinae star is shown in the right panel for the injection angle of α = 60o and the distances 1.4REC (dotted), 2REC (solid), 3REC (dashed), 5REC (dot-dashed), and 10REC (dot-dot-dashed), respectively.
In the text
thumbnail Fig. 4

X-ray and γ-ray spectra expected for the model A (left) and model B (right) at the periastron passage of the stars in the binary system Eta Carinae compared with the high-energy observations of this system. The measurements in the hard X-rays by the INTEGRAL satellite (Leyder et al. 2010) are marked by squares and those in the γ-ray energy range by the Fermi-LAT detector (Farnier et al. 2010; Abdo et al. 2010) are marked by triangles. The results of the calculations are shown for the model A (left panel): γ-rays from electrons accelerated at the shock from the side of the Eta Carinae star (solid) and from electrons accelerated at the shock from the side of the companion star: without any absorption (thin dashed), with absorption for the γ-ray propagating at the angle equal to 50o (towards the star) at distance from the star D = 1.4REC (dashed), and at the same angle but for the parts of the shock at the distance from the star D = 10REC (dot-dashed). For Model B (right panel): γ-rays from electrons, accelerated at the shock from the side of the Eta Carinae star, scattering stellar radiation in the T regime (solid), γ-rays from decay of neutral pions produced by hadrons accelerated at the shock from the side of the Eta Carinae star: unabsorbed spectrum (thin dashed curve extending to lower energies), spectra absorbed in the stellar radiation for distances from the star: D = 1.4REC (thick dashed) and D = 10REC (dot-dashed). Secondary leptons from decay of charged pions (produced in hadronic collisions) lose energy on the synchrotron radiation (dot-dot-dashed curve). The γ-ray spectrum produced by hadrons, which are accelerated at the shock from the side of the companion star and produce pions in the interactions within the Eta Carinae nebula, are shown by the thin dashed curve extending to higher energies.
In the text
thumbnail Fig. 5

Muon neutrino spectra produced by hadrons which are accelerated at the shocks from the side of the companion star up to energies of 5 PeV (solid curve) and the side of the Eta Carinae star up to energies of 250 TeV (dashed). Hadrons from the side of the Eta Carinae star interact with the matter of dense wind close to the shock region within the binary system. Hadrons from the side of the companion star escape from the shock region into the nebula and interact with the matter of expanding stellar wind and the matter within the nebula expelled in the past. The power law spectrum of hadrons is applied with the spectral index equal to 2. The neutrino spectra are normalized to the hard γ-ray spectrum observed from the Eta Carinae binary system assuming its hadronic origin via pion production. The range of the atmospheric neutrino background (vertical and horizontal) within 1o degree of the source is marked by dot-dashed curves (Lipari 1993). The 1 yr sensitivity of the km2 neutrino detector (expected for the IceCube detector) is marked by the thin dotted line.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.