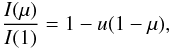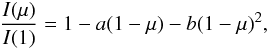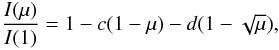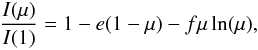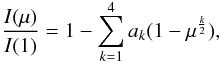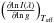EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 529 (May 2011) A&A, 529 (2011) A75 Full HTML
Free Access
Issue
A&A
Volume 529, May 2011
Article Number A75
Number of page(s) 5
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201116451
Published online 05 April 2011

© ESO, 2011

1. Introduction

Accurate modelling of the light curves of eclipsing binaries and planetary transits requires a good knowledge about the intensity distribution of the stellar disc. The complexity of the proximity effects in binary stars is, however, one of the most important challenges in theoretical stellar physics. Usually, the intensity distribution is approximated by limb-darkening laws that are calibrated using modern stellar atmosphere models. At present, there is still some controversy concerning the best numerical method to compute theoretical limb-darkening coefficients (LDCs) using these model atmospheres. A review of the main problems can be found in Díaz-Cordovés et al. (1995) and Claret (2000b); see also Howarth (2010). On the other hand, the scarcity of empirical information about limb-darkening does not give us a robust tool to try to elucidate some points of the mentioned controversy or obtain a reliable inter-comparison between empirical and theoretical LDCs. The situation is getting better with the advent of high-quality light curves of eclipsing binaries and transiting planets obtained with automatic telescopes and space missions such as Kepler and CoRoT, as well as studies of microlensing events (Zub 2011). This input is, however, still insufficient to allow for a reliable comparison between theoretical and empirical LDCs.

In addition to limb-darkening, there are other proximity effects that often have to be taken into account, including distortions by rotation and tides, and mutual irradiation in binary systems. Some efforts were made, for example, to account for the effects of irradiation on the specific intensity distribution (Claret 2007). Concerning stellar distortions, we know that rotation and/or tides change the shapes of stars. Tides elongate stars, while rotation flattens them at the poles. The distortions can be described through spherical harmonics, but not only the changes in the shapes of the stars are important: in 1924 von Zeipel showed that, for configurations in radiative equilibrium, the emerging flux is not constant on the surface of a distorted star and depends on the value of the local gravity. The general equation is 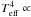Teff4∝\hbox{$T_{\rm eff}^4 \propto$}gβ1 where g is the local gravity, Teff is the effective temperature and β1 is the gravity-darkening exponent GDE (not to be confused with the gravity-darkening coefficient GDC, which is a monochromatic quantity). The value of β1 is 1.0 for envelopes in radiative equilibrium. Lucy (1967) computed GDEs for models with deep convective envelopes and found an average value of β = 0.32. The situation did not change until Claret (1998) introduced a new method to compute β1 that embraces both radiative and convective energy transport. The GDEs were presented, for the first time, as continuous functions of the stellar masses, age, chemical composition, and mixing-length parameter. These theoretical values of β1 are supported by recent observations of double-lined eclipsing binaries and rapidly rotating stars (Pantazis & Niarchos 1998; Niarchos 2000; Djurasevic et al. 2003; Che et al., priv. commun.). However, photometric observations are usually performed in certain wavelength bands instead of bolometrically, and therefore monochromatic (or band) GDCs are to be used in modelling efforts. These bandpass-dependent coefficients were computed by Claret 2003 from realistic atmosphere models instead of black body spectra. It is important to point out that all these comments can also be applied to planetary transits, because they can be considered as a special case of eclipsing binaries.

In this paper we present new calculations of limb-darkening coefficients for five laws by adopting 100 μ points instead of the usually adopted 17 or 15 points. The specific intensities of the ATLAS (Kurucz, priv. commun.) and PHOENIX (Hauschildt, priv. commun.) models were used to compute the limb-darkening coefficients. The calculations cover the passbands of the Kepler, CoRoT and Spitzer space missions as well as the commonly used uvby (Strömgren), UBVRIJHK (Johnson-Cousins) and Sloan filter systems. We also perform the calculations for the bi-parametric approximations by adopting by adopting the flux conservation method (FCM) to provide users with an additional tool to estimate the theoretical error bars.

New values of the gravity-darkening coefficients y(λ) are also computed using the same grids of stellar atmosphere models. The calculations were carried out by adopting a more general differential equation, which now also takes into account the contributions of the dependence of the intensities on the local gravity and, more importantly, the effect of convection. The new tables presented in this paper supersede our old values of y(λ), which were computed with a simpler equation.

2. The limb-darkening coefficients for ATLAS and PHOENIX models

We have computed limb-darkening coefficients for several models that mainly cover the transmission curves of the Kepler, CoRoT, and Spitzer space missions although we also provide LDCs for the traditional passbands. The calculations for the Spitzer space mission were carried out considering the full array average spectral responses for four bands. As usual, we have used the least-square method (LSM) to fit the following five limb-darkening laws to the specific intensities of the models:

the linear law I(μ)I(1)=1−u(1−μ),\begin{equation} {I(\mu)\over{ I(1)}} = 1 - u(1 - \mu), \end{equation}(1)

the quadratic law

I ( μ ) I ( 1 ) = 1 − a ( 1 − μ ) − b ( 1 − μ ) 2 , \begin{equation} {I(\mu)\over{I(1)}} = 1 - a(1 - \mu) - b(1 - \mu)^2, \end{equation}(2)

the square root law

I ( μ ) I ( 1 ) = 1 − c ( 1 − μ ) − d ( 1 − μ ) , \begin{equation} {I(\mu)\over{I(1)}} = 1 - c(1 - \mu) - d(1 - \sqrt{\mu}), \end{equation}(3)

the logarithmic law

I ( μ ) I ( 1 ) = 1 − e ( 1 − μ ) − fμ ln ( μ ) , \begin{equation} {I(\mu)\over{I(1)}} = 1 - e(1 - \mu) - f\mu\ln(\mu), \end{equation}(4)

and a more general law with four terms

I ( μ ) I ( 1 ) = 1 − ∑ k = 1 4 a k ( 1 − μ k 2 ) , \begin{equation} {I(\mu)\over{I(1)}} = 1 - \sum_{k=1}^{4} {a_k} (1 - \mu^{k\over{2}}), \end{equation}(5)

where I(1) is the specific intensity at the centre of the disc, and u,a,b,c,d,e,f, and ak are the corresponding LDCs. The quantity μ is defined by μ = cos(γ), where γ is the angle between the line of sight and the emergent intensity. The model atmosphere intensities were convolved with a response function that takes into account the filter transmission curves for Kepler, CoRoT, and Spitzer and the reflection from an aluminium-coated mirror, as explained in our previous papers on the subject. The LDC calculations were performed for 19 metallicities ranging from 10-5 up to 10+1 times the solar abundance, for gravities 0.0 ≤ log    g ≤ 5.0, and for effective temperatures 2000   K ≤ Teff ≤ 50   000 K. Five microturbulent velocities (Vξ = 0,1,2,4,8 km s-1) were used.

The limb-darkening law described in Eq. (5) has important advantages compared to the linear or bi-parametric approximations: the other laws are useful only for limited effective temperature ranges, while the law in Eq. (5) fits well to the modelled specific intensities for the whole ranges of log g and Teff for which ATLAS and PHOENIX models are available. As this 4-parameter law reproduces the intensity distributions very well and conserves flux within very small tolerances, we recommend the users to adopt it whenever the quality of the light curves does not allow one to derive empirical values.

As explained in the introduction, the adopted numerical method to derive the LDCs is still a matter of discussion. To provide a more extensive set of tools to the observers, we have also computed LDCs by adopting the FCM that conserves, by definition, the flux, but the corresponding intensity distributions are not well described. It would be interesting if observers could test both possibilities (as well as comparing the LDCs derived from ATLAS and PHOENIX models). Although the LDCs computed by adopting the ATLAS and PHOENIX models are similar, at least for the linear fitting (Claret 1998) such a variety of numerical methods and atmosphere models may provide a good tool to evaluate the theoretical errors in the LDC more realistically.

thumbnail Fig. 1

Linear LDC for Kepler. The continuous line represents the present calculations by adopting LSM, the dashed line denotes calculations using FCM, and the dashed-dotted line those by Sing (2010). All calculations are based on the Kurucz atmosphere models, with log g = 4.5, log [A/H] = 0.0 and Vξ = 2 km s-1. Right upper corner: observations of I(0) for six extra-solar planetary systems from CoRoT (error bars) and the linear theoretical LDC for CoRoT (same symbols as for the main figure). The full line shows the theoretical LDC computed following Eq. (5). Numbers indicate the CoRoT target star (CoRoT-n).

As commented in the introduction, observational data of limb-darkening that can be compared with theoretical predictions is scarce. An example of these data is presented in Claret (2008), in which a systematic disagreement between theoretical predictions and semi-empirical linear LDCs was shown based on observations of nine double-lined eclipsing binaries. However, the linear limb-darkening law does not describe the specific intensities well and as such the paper’s conclusions cannot be considered to be robust. Also for the transits of the planetary system HD 209458, systematic disagreements between the theoretical and empirical LDCs for the linear and quadratic cases were found (Claret 2009). Even taking into account uncertainties in the metallicity, microturbulent velocity, and effective temperature in the calculation of the theoretical LDCs, the corresponding theoretical predictions cannot match the empirical data.

Specifically for transits obtained with the CoRoT space mission, Sing (2010) used his method – which combines LSM and exclusion of limb intensities – to compare his theoretical predictions with semi-empirical LDCs. To compare the present calculations with those performed by Sing, we show Sing’s results in Fig. 1 together with our theoretical results obtained using both LSM and FCM. For the sake of clarity, we only analyse the linear case, although we recall that this approach is not the most adequate, because limb-darkening is clearly a non-linear phenomenon. Our calculations coincide with those by Sing only in a small range of effective temperatures. Our linear LDCs are systematically smaller for log Teff > 3.8. We can also note from that figure (right upper corner) that excluding the limb intensities does not really generally improve the comparison with observations: the calculations by Sing “fit the observations better” for only two systems and in this range of effective temperatures the differences with our calculations are not significant. The LDC computed by adopting the FCM present the “most acceptable fit”. This was also noticed by Claret (2009) for the HD 209458 planetary system. However, when a bi-parametric law was investigated, the FCM disagreed with observations.

The full line in the right upper corner of Fig. 1 denotes the theoretical predictions adopting Eq. (5). As we have seen before, this equation provides the best fit for all atmosphere models investigated here, but it disagrees with the empirical data. It is true that it is not directly comparable with these data, but this may indicate a problem with the atmosphere models and/or with the empirical data themselves. Taking into account the above comments, we do not consider the comparison with observations shown in Fig. 1 as a definitive one. In any case, we think that the differences shown in the main frame of Fig. 1 may be a good tool to investigate and delineate more realistic theoretical error bars in LDC studies. It would be very interesting to have semi-empirical LDC determinations for systems with effective temperatures larger than 8000 K, for which the differences between our calculations and those by Sing are higher.

3. The passband gravity-darkening coefficients y(λ)

The values of β1 that appear in the von Zeipel equation refer to bolometric quantities. However, photometric observations are performed in bands. Kopal (1959) introduced the gravity-darkening coefficients, y(λ), which were derived assuming that the distorted configurations radiate like a black body and by expanding the ratio between the monochromatic and total radiation in a Taylor series. However, the black body radiation is a poor approximation and more elaborate stellar atmosphere models have to be used, as was discussed in Claret (2003). The equation for y(λ) used in Claret (2003), taken from Martynov (1973), is

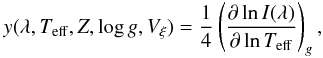y(λ,Teff,Z,logg,Vξ)=14(∂lnI(λ)∂lnTeff)g,\begin{equation} y(\lambda, T_{\rm eff}, Z, \log g, V_{\xi}) = {1\over 4} \left(\partial\ln I(\lambda)\over \partial\ln T_{\rm eff}\right)_{g}, \end{equation}(6)where λ denotes the wavelength, Z the metal content, Vξ the microturbulent velocity and I the intensity at a given wavelength (or passband) at the centre of the stellar disc. The subscript g indicates that the derivatives are calculated at a constant surface gravity.

However, this expression is only valid for some special situations, because it implicitely assumes that β1 = 1.0 and that the specific intensities do not depend on the local gravity. Previous investigations indicated that the value of the bolometric β1 strongly depends on the effective temperature, and an inspection of the stellar atmosphere models also shows that the specific intensities do depend on the local surface gravity. As presented by Bloemen et al. (2011), a more general expression for y(λ) can be written as 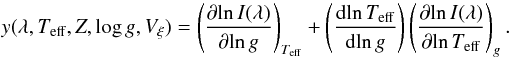y(λ,Teff,Z,logg,Vξ)=(∂lnI(λ)∂lng)Teff+(dlnTeffdlng)(∂lnI(λ)∂lnTeff)g.\begin{equation} y(\lambda, T_{\rm eff }, Z, \log g, V_{\xi}) = \left(\partial{\ln I(\lambda)} \over{\partial{\ln g}}\right)_{T_{\rm eff}} + \left({\rm d}\!\ln T_{\rm eff }\over{{\rm d}\!\ln g}\right) \left(\partial{\ln I(\lambda)}\over{\partial{\ln T_{\rm eff }}}\right)_{g}. \end{equation}(7)

thumbnail Fig. 2

Bolometric β1 (continuous line) and the quantity (∂lnI(λ)∂lng)Teff\hbox{$\left(\partial{\ln I(\lambda)} \over{\partial{\ln g}}\right)_{T_{\rm eff}}$} (dashed-asterisks) as a function of the effective temperature for the Kurucz atmosphere models with log g = 4.0, log [A/H] = 0.0 and Vξ = 2 km s-1.

This equation reduces to Eq. (6) if one assumes that β1 = 1.0 for any effective temperature and that 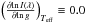(∂lnI(λ)∂lng)Teff≡0.0\hbox{$\left(\partial{\ln I(\lambda)}\over{\partial{\ln g}}\right)_{T_{\rm eff}} \equiv 0.0$}. As illustrated in Fig. 2, the contribution of the partial derivative to the local gravity is not large for main-sequence stars, but it is not negligible (this was first noted in Claret 2003). Indeed, for cool PHOENIX models with log g = 3.5, this contribution can be significant. For ATLAS models with the same log g, Teff, metallicity and microturbulent velocity, however, the contribution is smaller. On the other hand, the correction introduced by the effects of the convection is very important for cooler models. The derivative 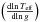(dlnTeffdlng)\hbox{$\left({\rm d}\! \ln T_{\rm eff }\over{{\rm d}\! \ln g}\right)$} of the right side of Eq. (7) can be easily computed by using the general von Zeipel law and it is equal to β1/4. To take into account the effects of the convection on β1 (and consequently on y(λ)), we considered the bolometric GDE previously calculated in some of our earlier papers (Claret 2000a, 2004). We have revised our old computations of y(λ) by recomputing the values of the GDC using Eq. (7). The same atmosphere models as used to generate the limb-darkening coefficients are adopted. As for the LDCs, the GDCs are available for the Kepler, CoRoT, and Spitzer photometric systems, and for the most widely used photometric systems.

Table 1

Limb-darkening coefficients for the Kepler, CoRoT, Spitzer, U   B   V   R   I   J   H   K, u   v   b   y, and Sloan photometric systems.

Table 2

Gravity-darkening coefficients y(λ) for the Kepler, CoRoT, Spitzer, U   B   V   R   I   J   H   K, u   v   b   y, and Sloan photometric systems.

As shown in Claret (2003), using black body spectra is not a good approach, except in some small intervals of effective temperatures. For a given filter, the differences may be large, especially for passbands with short effective wavelengths. The differences between the y(λ)s computed by adopting the ATLAS (continuous lines) and PHOENIX models (dashed lines) are not large for the same input parameters (Fig. 3). The effect of the convection on y(λ) (primarily on β1) is very important, as can be seen in Fig. 3. Note the differences between the y(λ)s computed adopting the Kurucz models and Eq. (7) (continuous line) and those computed using the same models, but using Eq. (6) (asterisks). Taking into account the effects of convection reduces the values of y(λ) most drastically for log Teff ≈  3.89 (see also Fig. 2). One natural question is whether the values of the bolometric β1 used to correct for the influence of convection in Eq. (7) are reliable. Fortunately, in the last years, several investigations were carried out concerning the semi-empirical determination of the GDE. For example, Fig. 3 in Claret (2003) shows an exhaustive comparison between the theoretical and observed β1 for W Uma-type binaries carried out by Pantazis & Niarchos (1998), Niarchos (2000) and Djurasevic et al. (2003) and the agreement can be considered as good, mainly concerning the detection of the transition zone. Previously, the semi-empirical values of β1 obtained by Rafert & Twigg (1980) also showed a similar consistency (Claret 1998). More recently, the investigations of interferometric imaging of rapid rotators (for example, Che et al., priv. comm.) also confirmed the main characteristics of β1, including the transition zone. Finally, one should note that Eq. (7) indicates that y(λ) also depends on other input parameters of the atmosphere models: metallicity and microturbulent velocity. Generally speaking, these effects are detected at shorter wavelengths and for low effective temperatures, as explained in Claret (2003).

thumbnail Fig. 3

Gravity-darkening coefficient y (Kepler) versus effective temperature. The continuous line represents the Kurucz models (Eq. (7)), the dashed one denotes the PHOENIX plan-parallel models (Eq. (7)), and asterisks represent the results from Kurucz models by adopting Eq. (6). We used models with log g = 4.5, log [A/H] = 0.0, Vξ = 2 km s-1.

4. Summary and final comments

We have computed limb-darkening and gravity-darkening coefficients for the ATLAS and PHOENIX ( plane-parallel) atmosphere models spanning a log g range between 0.0 and 5.0, a metallicity range of –5.0  ≤  log [M/H]  ≤  +1, effective temperatures 2000 K  ≤ Teff ≤ 50   000 K and five values for the microturbulent velocity. Our new tables of coefficients now cover the transmission curves of the Kepler, CoRoT, and Spitzer space missions as well as the traditional Johnson-Cousins, Strömgren, and Sloan passbands.

The LDC were computed with a higher numerical resolution (100 μ points instead of 15/17 often used in the ATLAS models). Five equations were used to describe the specific intensities (linear, quadratic, root-square, logarithmic, and that containing four terms introduced by Claret 2000b). In addition to these computations we performed the calculations for the bi-parametric approximations by adopting the FCM to provide users with an additional tool to estimate the theoretical error bars. Considering the discussion in Sect. 2 on the best numerical approach to LDC, we strongly recommend the use of Eq. (5) when the quality of the light curves does not allow one to derive empirical values.

The new values of the gravity-darkening coefficients y(λ) are computed with a more general differential equation, which now also takes into account the contribution of the variation of the local gravity and the effects of convection. The GDC tables presented in this paper supersede our old values of y(λ), which were computed with a simpler equation.

Table 1 summarises the results for limb-darkening coefficients calculations (Tables 3–32), and Table 2 for the gravity-darkening coefficients. All these tables are available electronically at CDS. The implementation of the tables of LDCs and y(λ)s in codes to model light curves of eclipsing binaries and transiting extrasolar planets is straightforward and we are able to provide calculations for additional photometric systems on request.

Acknowledgments

The authors would like to thank V. Costa, T. Marsh, C. Lazaro, G. Torres and an anonymous referee for useful suggestions. The Spanish MEC (AYA2006-06375, AYA2009-14000-C03-01) is gratefully acknowledged for its support during the development of this work. The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement n°227224 (PROSPERITY), as well as from the Research Council of K.U.Leuven grant agreement GOA/2008/04. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Abstract Service.

References

  1. Bloemen, S., Marsh, T. R., Østensen, R. H., et al. 2011, MNRAS, 410, 1787 [NASA ADS] [Google Scholar]
  2. Claret, A. 1998, A&AS, 131, 395 [Google Scholar]
  3. Claret, A. 2000a, A&A, 359, 289 [NASA ADS] [Google Scholar]
  4. Claret, A. 2000b, A&A, 363, 1081 [NASA ADS] [Google Scholar]
  5. Claret, A. 2003, A&A, 406, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Claret, A. 2007, A&A, 470, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Claret, A. 2008, A&A, 482, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Claret, A. 2009, A&A, 506, 1335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Díaz-Cordovés, J., Claret, A., & Giménez, A. 1995, A&AS, 110, 329 [NASA ADS] [Google Scholar]
  10. Djurasevic, G., Rovithis-Livaniou, H., Rovithis, P., Georgiades, N., & Erkapic, S. 2003, A&A, 402, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Howarth, I. D. 2010 [arXiv:1011.2631] [Google Scholar]
  12. Lucy, L. B. 1967, Zeitschritft für Astrophysik, 65, 89 [Google Scholar]
  13. Kopal, Z. 1959, Close Binary Systems, Chapman & Hall [Google Scholar]
  14. Niarchos, P. G. 2000, in Variable Stars as Essential Astrophysical Tools, ed. C. Ibanoglu, 631 [Google Scholar]
  15. Martynov, D. Ya. 1973, in Eclipsing Variable Stars, 128, IPST Astrophysics Library, ed. V. P. Tsesevich [Google Scholar]
  16. Pantazis, G., & Niarchos, P. G. 1998, A&A, 335, 199 [NASA ADS] [Google Scholar]
  17. Rafert, J. B., & Twigg, L. W. 1980, MNRAS, 193, 79 [NASA ADS] [CrossRef] [Google Scholar]
  18. Sing, D. K. 2010, A&A, 510, A21 [Google Scholar]
  19. von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
  20. Zub, M., Cassan, A., Heyrovsky, D., et al. 2011, A&A, 525, L5 [Google Scholar]

All Tables

Table 1

Limb-darkening coefficients for the Kepler, CoRoT, Spitzer, U   B   V   R   I   J   H   K, u   v   b   y, and Sloan photometric systems.

In the text
Table 2

Gravity-darkening coefficients y(λ) for the Kepler, CoRoT, Spitzer, U   B   V   R   I   J   H   K, u   v   b   y, and Sloan photometric systems.

In the text

All Figures

thumbnail Fig. 1

Linear LDC for Kepler. The continuous line represents the present calculations by adopting LSM, the dashed line denotes calculations using FCM, and the dashed-dotted line those by Sing (2010). All calculations are based on the Kurucz atmosphere models, with log g = 4.5, log [A/H] = 0.0 and Vξ = 2 km s-1. Right upper corner: observations of I(0) for six extra-solar planetary systems from CoRoT (error bars) and the linear theoretical LDC for CoRoT (same symbols as for the main figure). The full line shows the theoretical LDC computed following Eq. (5). Numbers indicate the CoRoT target star (CoRoT-n).
In the text
thumbnail Fig. 2

Bolometric β1 (continuous line) and the quantity (∂lnI(λ)∂lng)Teff\hbox{$\left(\partial{\ln I(\lambda)} \over{\partial{\ln g}}\right)_{T_{\rm eff}}$} (dashed-asterisks) as a function of the effective temperature for the Kurucz atmosphere models with log g = 4.0, log [A/H] = 0.0 and Vξ = 2 km s-1.
In the text
thumbnail Fig. 3

Gravity-darkening coefficient y (Kepler) versus effective temperature. The continuous line represents the Kurucz models (Eq. (7)), the dashed one denotes the PHOENIX plan-parallel models (Eq. (7)), and asterisks represent the results from Kurucz models by adopting Eq. (6). We used models with log g = 4.5, log [A/H] = 0.0, Vξ = 2 km s-1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.