EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 529 (May 2011) A&A, 529 (2011) A14 Full HTML
Free Access
Issue
A&A
Volume 529, May 2011
Article Number A14
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201016256
Published online 21 March 2011

© ESO, 2011

1. Introduction

4U 1907+09 is a high-mass X-ray binary (HMXB), consisting of an X-ray pulsar (neutron star) accreting from a late O-type supergiant companion star (Giacconi et al. 1971; Schwartz et al. 1980; Marshall & Ricketts 1980; Makishima et al. 1984; van Kerkwijk et al. 1989; Cox et al. 2005; Nespoli et al. 2008). Like other HMXBs, 4U 1907+09 is the descendant of a massive binary, whose primary (initially more massive) star experienced a supernova explosion (van den Heuvel & Heise 1972; Tutukov & Yungelson 1973). That the binary has remained bound after the supernova explosion implies either that the system lost less than half of its initial (pre-supernova) mass (in the case of a symmetric supernova explosion, Boersma 1961) or that the kick attained by the neutron star at birth had a favourable orientation and magnitude (if the explosion was asymmetric, Hills 1983; Tauris & Takens 1998). In both cases, the HMXB attains a recoil velocity, which could be high enough (i.e.  ≥ 30   km   s-1) to classify the system as a runaway (Blaauw 1961). The distribution of HMXBs in the Galaxy and their kinematic properties are consistent with the possibility that most of them are runaways (van Oijen 1989; Chevalier & Ilovaisky 1998). A similar conclusion was derived by Coe (2005) for HMXBs in the Small Magellanic Cloud.

The high peculiar velocities of HMXBs could be revealed directly, via measurement of their radial velocities (van Oijen 1989) and/or proper motions (Chevalier & Ilovaisky 1998), or indirectly, through the detection of the secondary attributes of runaway stars – the bow shocks (e.g. van Buren & McCray 1988; van Buren et al. 1995; Gvaramadze & Bomans 2008; Gvaramadze et al. 2010a; Gvaramadze et al. 2011). The first-ever detection of a bow shock associated with a HMXB was reported by Kaper et al. (1997), who discovered a very symmetric Hα arc around the HMXB Vela X-1 (a system similar to 4U 1907+09). This discovery unambiguously showed that at least for Vela X-1 the system got its high space velocity owing to the binary-supernova explosion (an alternative mechanism for the origin of runaway stars (including binaries) is based on dynamical three- and four-body encounters in dense star clusters, Poveda et al. 1967; Gies & Bolton 1986).

Huthoff & Kaper (2002) used the high-resolution IRAS maps to search for bow shocks around 11 high-velocity HMXBs and detected only an infrared counterpart to the already known bow shock generated by Vela X-1. The paucity of bow shock-producing HMXBs is consistent with the observational fact that only a minority of runaway OB stars are associated with (detectable) bow shocks (van Buren et al. 1995). The most reliable explanation of this is that the majority of runaway stars are moving through a low density, hot medium, so that the emission measure of their bow shocks is below the detection limit or the bow shocks cannot be formed at all because the sound speed in the local interstellar medium (e.g. the hot gas within large-scale bubbles around OB associations) is higher than the stellar space velocity (Kaper et al. 1999; Huthoff & Kaper 2002). For bow shocks with small emission measure, one might expect to detect them with modern infrared telescopes.

Motivated by the above arguments, we have undertaken a search for bow shocks around the HMXBs from the sample of Huthoff & Kaper (2002, see their Table 1) using the archival Spitzer Space Telescope data. We have discovered a bow shock around the HMXB 4U 1907+09 and detected the already known bow shock associated with Vela X-1 (Sect. 3). The orientation of the bow shock generated by 4U 1907+09 is consistent with ejection of this HMXB from the Galactic plane. To confirm the runaway nature of the system, we have measured its proper motion using archival data over a total time baseline of 50 yr (Sect. 4). Section 5 discusses the results obtained in the previous sections. We summarize and conclude in Sect. 6.

2. 4U 1907+09: general data

The HMXB 4U 1907+09 was discovered with Uhuru as a discrete X-ray source (Giacconi et al. 1971). The X-ray source was subsequently identified with a highly reddened early-type star with broad, strong Hα emission (Schwartz et al. 1980). Schwartz et al. (1980) hypothesized that 4U 1907+09 is a binary system composed of an OB supergiant star and a compact object, and that accretion of the stellar wind onto the compact object is responsible for the X-ray emission. This hypothesis was proved by Marshall & Ricketts (1980), who revealed a binary period of  ≃ 8.38 day in the X-ray light curve of 4U 1907+09, confirming that the system is a new member of a class of HMXBs (see, e.g., Kaper & van der Meer 2007, for a review on these objects). Makishima et al. (1984) discovered a 437.5 s X-ray pulsations from 4U 1907+09, establishing this system as a binary X-ray pulsar.

Follow-up optical spectroscopy of 4U 1907+09 by Cox et al. (2005) showed that the companion of the X-ray pulsar is a late O-type supergiant star (O8 Ia-O9 Ia, cf. van Kerkwijk et al. 1989; Iye 1986). This classification was refined by Nespoli et al. (2008), who got the infrared spectrum of 4U 1907+09 and derived the spectral type of O9.5 Iab.

The distance to 4U 1907+09 still remains uncertain (cf. van Kerkwijk et al. 1989; Cox et al. 2005; Nespoli et al. 2008).

Using the optical photometry from Schwartz et al. (1980), V = 16.37 ± 0.02 mag, B − V = 3.17 ± 0.06 mag, and adopting the intrinsic (B − V)0 colour of an O9.5 I star of  − 0.26 mag (Martins & Plez 2006), one finds the interstellar reddening towards 4U 1907+09 E(B − V) = 3.43 ± 0.06 mag. Then taking AV = 3.1E(B − V), one obtains AV ≃ 10.6 ± 0.2 mag, which for MV =  −6.34 ± 0.45 mag (Martins & Plez 2006) leads to a distance 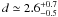d≃2.6-0.5+0.7\hbox{$d\simeq 2.6^{+0.7}_{-0.5}$} kpc.

Similarly, using J and Ks magnitudes of 4U 1907+09 (10.00 ± 0.02 and 8.77 ± 0.02, respectively) from 2MASS (Skrutskie et al. 2006), (J − Ks)0 =  −0.21 mag and MKs =  −5.52 ± 0.20 mag from Martins & Plez (2006), and adopting the extinction law from Rieke & Rebofsky (1985), one finds AKs = 0.66 [(J − Ks) − (J − Ks)0]  = 0.95 ± 0.02 mag1, suggesting a distance of 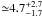≃4.7-1.7+2.7\hbox{${\simeq} 4.7^{+2.7}_{-1.7}$} kpc. The large discrepancy between the distance estimates based on the visual and near infrared photometry could be understood if the reddening towards 4U 1907+09 is anomalous, i.e. the total-to-selective absorption ratio RV < 3.1 (cf. Cox et al. 2005).

Using a similar procedure and adopting the intrinsic colours and absolute magnitudes from Wegner (1994, 2006), Nespoli et al. (2008) derived a distance to 4U 1907+09 of 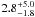2.8-1.8+5.0\hbox{$2.8^{+5.0} _{-1.8}$} kpc, where the quoted errors stem mainly from the uncertainty in the absolute magnitudes.

A distance d = 2.1 − 2.6 kpc was derived by van Kerkwijk et al. (1989) and Cox et al. (2005) from interstellar absorption of sodium in the spectrum of 4U 1907+09, while the detection of a high-velocity (~60   km   s-1) component in the K i absorption line in the line-of-sight towards 4U 1907+09 suggests a distance of  ≥ 4 kpc (Cox et al. 2005). The latter estimate is based on the model of Galactic rotation by Brand & Blitz (1993), which assumes that, to first order, the Galactic velocity field is axisymmetric. Note, however, that 4U 1907+09 is located in the direction of the Sagittarius arm tangent region and that our line-of-sight towards this HMXB passes through the spiral arm over a distance of several kpc. One cannot, therefore, exclude that random (non-circular) motions (up to several tens of    km   s-1) caused by outflows from star-forming regions could contribute to the origin of the high-velocity components in the K i absorption line, thereby affecting the kinematic distance estimate.

Finally, we note that the interstellar extinction cannot be constrained by using the empirical relationships between AV and the interstellar column density NH (derived from modelling the X-ray spectrum of the neutron star), because the total column density towards 4U 1907+09 contains a variable contribution from the circumstellar material of a magnitude comparable to that of the interstellar one (Cook & Page 1987; in ’t Zand et al. 1997; Rivers et al. 2010).

As a compromise between the different distance estimates, we adopt a distance to 4U 1907+09 of 4 kpc in the following.

3. 4U 1907+09: bow shock

To search for bow shocks around HMXBs from the sample of Huthoff & Kaper (2002), we utilized the imaging data from the Spitzer Space Telescope archive, obtained with the Multiband Imaging Photometer for Spitzer (MIPS, Rieke et al. 2004) and the Infrared Array Camera (IRAC, Fazio et al. 2004). The publicly available data cover the fields containing 5 of the 11 HMXSs (namely, GX 301-2, 4U 1907+09, Cyg X-1, Vela X-1 and V615 Cas). Visual inspection of the MIPS and IRAC images results in a discovery of a bow shock generated by 4U 1907+09.

Figure 1 shows the MIPS 24   μm, IRAC 8, 5.8, 4.5 and 3.6 μm, and DSS-II (red band) images2 of the field around the HMXB 4U 1907+09. Like many other bow shocks discovered with Spitzer (e.g. Gvaramadze et al. 2010a,b, 2011; Gvaramadze & Gualandris 2011), the bow shock associated with 4U 1907+09 is only visible at 24   μm (although the IRAC 5.8 and 8 μm images show the gleam of emission possibly associated with the bow shock). The bow shock has a clear arcuate shape with the apex at 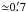\hbox{${\simeq} 0\farcm7$} from 4U 1907+09, which at the distance to the system of 4 kpc corresponds to the linear separation Robs ≃ 0.8 pc (see Sect. 5.3).

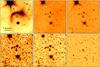thumbnail Fig. 1

From left to right, and from top to bottom: Spitzer MIPS 24   μm, IRAC 8, 5.8, 4.5 and 3.6 μm, and DSS-II (red band) images of the field around the HMXB 4U 1907+09. The arrow shows the direction of peculiar velocity of 4U 1907+09, as suggested by the proper motion measurement (see text for details). A bright infrared source to the north is the maser source IRAC 19071+0946. In all panels the position of 4U 1907+09 is indicated by a circle.

thumbnail Fig. 2

Spitzer MIPS 24   μm (left) and IRAC 8   μm images of the bow shock around the HMXB Vela X-1. The arrow shows the direction of peculiar velocity of Vela X-1 (see Sect. 5.3 for details).

We also detected the already known bow shock associated with Vela X-1 (see Kaper et al. 1997; and Huthoff & Kaper 2002, for the Hα and IRAS 60 μm images of the bow shock, respectively). Unlike 4U 1907+09, the bow shock produced by Vela X-1 is visible not only at 24 μm, but also at all four IRAC bands, i.e. at 3.6, 4.5, 5.8 and 8   μm. In Fig. 2 we present for the first time the MIPS 24 μm and IRAC 8 μm images of the bow shock (Program Id.: 30088, PI: A.Noriega-Crespo)3 showing its fine structure (most prominent at 8 μm) similar to that detected in Hα by Kaper et al. (1997). Using the IRAC 8   μm image of the bow shock, we estimated Robs ≃ 0.5   d1.9 pc, where d1.9 is the distance to Vela X-1 in units of 1.9 kpc (Sadakane et al. 1985).

The symmetry axis of a bow shock generated by a supersonically moving star reflects the direction of motion of the star with respect to the ambient medium, which also could be in motion relative to the local standard of rest at the location of the star. For example, high-velocity outflows driven from young star clusters by the collective effect of stellar winds can create bow shocks around (low-velocity) stars in the cluster’s halo (e.g., bow shocks around LL Ori and several other stars in the Orion Nebula, all of which are faced towards the central Trapezium cluster, Bally et al. 2000). For runaway stars located far from star-forming regions and their associated gas outflows (caused by stellar winds and supernovae), one can assume that the peculiar velocity of the ambient medium is negligible compared with the space velocity of the star, meaning that the symmetry axis of the bow shock coincides well with the direction of stellar motion. In this case, the orientation of the bow shock can be used to back-trace the trajectory of the star to the parent cluster even for those stars whose proper motions cannot be measured with a high confidence (Gvaramadze & Bomans 2008; Gvaramadze et al. 2010a,b, 2011).

Figure 3 shows the Midcourse Space Experiment (MSX) satellite (Price et al. 2001) image of a 3° × 2° region of the Galactic plane (centred at 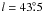\hbox{$l=43\fdg5$}, b = 0°), with the position of 4U 1907+09 indicated by a circle (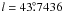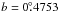\hbox{$l=43\fdg7436$}, \hbox{$b=0\fdg4753$}). The symmetry axis of the bow shock around 4U 1907+09 (see Fig. 1, whose orientation is the same as for Fig. 3) suggests that this HMXB is moving away from the Galactic plane. To prove unambiguously that the origin of the bow shock is caused by the high space velocity of 4U 1907+09, we searched for existing proper motion measurements for this system using the Vizier catalogue access tool4. We found three catalogues that provided proper motions for 4U 1907+09, USNO-B1 (Monet et al. 2003), UCAC3 (Zacharias et al. 2010) and PPMXL (Röser et al. 2010). All three give huge proper motions, which, if real, would correspond to the peculiar velocity of several thousands of    km   s-1. We discovered, however, that USNO-B1 has two entries separated by less than 2″ at the position of 4U 1907+09, which (possibly) originate from mismatching of plates from different epochs and cause the huge proper motion. PPMXL followed the cross-matching of USNO-B1, hence the star is one of the 10% (Röser et al. 2010) of double entries in PPMXL. Also, it turns out that the UCAC3 proper motion is marked “with doubts” because it relies on “less than two good matches”. Thus, an individual determination of the proper motion of 4U 1907+09 became necessary.

thumbnail Fig. 3

3° × 2° MSX 8.3   μm image of the Galactic plane (shown by a dashed line) centred at \hbox{$l=43\fdg5$}, b = 0°, with the position of the HMXB 4U 1907+09 indicated by a circle. The arrow shows the direction of motion of 4U 1907+09. The orientation of this figure is the same as for Fig. 1. The brightest nebula on the image is the background star-forming region W 49A.

4. 4U 1907+09: proper motion measurement

With its intermediate optical magnitudes, 4U 1907 + 09 is not saturated on photographic Schmidt plates (see Fig. 1), which provide different epoch observations over five decades, and it is well measured in the CCD-based Carlsberg Meridian Catalog 14 (CMC14)5. However, there are several difficulties in the field around the target: 1) overlap of star images, which already change with the different optical passbands and lead to a completely different appearance of the field in the near infrared owing to strong reddening; 2) absence of reference galaxies for direct absolute proper motion measurement; 3) different location of the target on the Schmidt plates, which results in different residual geometric distortions after any full Schmidt plate calibration.

We collected all available Schmidt plate data, POSS-1 blue (O) and red (E), POSS Quick V, and POSS-2 B,R, and I, nine plates altogether, and extracted small 15 × 15 arcmin2 FITS images from the DSS6. For the POSS-1 red (E) plate we also extracted the FITS file from the SuperCOSMOS Sky Survey7 (Hambly et al. 2001), which we preferred because of its higher resolution. To overcome the above mentioned difficulties, we used 14 reference stars (of magnitudes similar to those of 4U 1907+09) that are distributed closely around the target within about 3 arcmin for a new local astrometric calibration of the Schmidt plates with respect to the CMC14 positions of the reference stars. The astrometric measurements and transformations from the Schmidt plates to the CMC14 system were carried out using the ESO SkyCat Tool8. To avoid colour-dependent effects, we finally preferred to combine only the E,R and V plates with the CMC14 (r′)-band data.

The resulting proper motion from simple linear fitting of the target positions at five epochs (1952.395, 1983.611, 1987.411, 1992.586, 2001.956) is μαcosδ =  −4.1 ± 5.5   mas   yr-1, μδ = 4.9 ± 4.4   mas   yr-1. For the absolutisation of this relative proper motion we investigated the proper motions of the reference stars as given in the PPMXL catalogue (Röser et al. 2010), which is on the International Celestial Reference System. The individual PPMXL proper motions of the 14 stars are all smaller than 10   mas   yr-1, and their mean PPMXL proper motion is μαcosδ =  −3.6 ± 3.0   mas   yr-1, μδ =  −3.4 ± 3.0   mas   yr-1. The quoted errors are conservative estimates including the systematic PPMXL uncertainty of 1 to 2   mas   yr-1 in any small field (~1 square degree) of the sky due to the small number density of Hipparcos stars (Röser et al. 2010). Taking into account the mean proper motion of the 14 reference stars, we then computed an absolute proper motion of 4U 1907+09: μαcosδ =  −7.7 ± 6.3   mas   yr-1, μδ = 1.5 ± 5.3   mas   yr-1, or in Galactic coordinates: 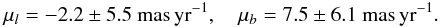μl=−2.2±5.5 mas yr-1, μb=7.5±6.1 mas yr-1.\begin{eqnarray} \mu_l = -2.2 \pm 5.5\masyr, \quad \mu_b = 7.5 \pm 6.1\masyr. \nonumber \end{eqnarray}

5. Discussion

5.1. 4U 1907+09 as a runaway HMXB

To convert the observed proper motion of 4U 1907+09 into the transverse peculiar velocity, we used the Galactic constants R0 = 8.0 kpc and Θ0 = 240   km   s-1 (Reid et al. 2009) and the solar peculiar motion (U⊙,V⊙,W⊙) = (10.0,11.0,7.2)   km   s-1 (McMillan & Binney 2010). We found the components of the peculiar velocity: 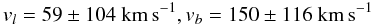vl=59±104 km s-1,vb=150±116 km s-1\begin{equation} v_l = 59\pm 104\kms, v_b =150\pm 116\kms \label{eqn:vel} \end{equation}(1)(here we assumed that the errors are due to errors in the proper motion measurement). Taken at face value, these velocity components suggest that 4U 1907+09 is running away from the Galactic plane in the direction consistent with the orientation of the symmetry axis of the bow shock (see Figs. 3 and 1; recall that the orientation of both figures is the same).

By tracing back the trajectory of 4U 1907+09 and assuming that this HMXB originated in the Galactic plane, we inferred that the system was ejected from the region around 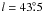\hbox{$l=43\fdg5$}, b = 0°. We did not, however, find any known young (≲ 10 Myr) star cluster or association (located at a distance comparable to that of 4U 1907+09) in this region (of radius of 1°). (The only young star-forming region in this area is the background one W 49A.) This could simply be owing to the huge interstellar extinction in the Galactic plane. Another possibility is that the progenitor massive binary was dynamically expelled from the parent cluster well before the primary exploded as a supernova and that the system changed the direction of its motion because of a kick caused by the supernova explosion (cf. Pflamm-Altenburg & Kroupa 2010). In this case, the parent cluster could be located at several degrees from the region inferred from the proper motion measurement and orientation of the bow shock.

We also searched for the parent diffuse supernova remnant in the same area of the Galactic plane using the catalogue of Galactic supernova remnants by Green (2009)9. The only supernova remnant listed in the catalogue in this area is the background one W 49B. The non-detection is not surprising, however, because the kinematic age of 4U 1907+09 (i.e. the time elapsed since the supernova explosion), tkin = dsinb/vb ~ 105 yr, is comparable to the typical lifetime of diffuse supernova remnants (e.g. Shull et al. 1989).

5.2. Origin of a high peculiar velocity of 4U 1907+09

5.2.1. Symmetric supernova explosion

Boersma (1961) showed that a post-supernova binary remains bound if the mass of the supernova ejecta, Mej, comprises less than a half of the system’s initial mass, i.e. Mej < (1/2)(M1 + M2), where M1 and M2 are the pre-supernova masses of the primary and secondary stars, respectively. In response to the instant mass loss caused by the supernova explosion, the binary system recoils with a velocity, given by (Gott et al. 1970; Iben & Tutukov 1997) 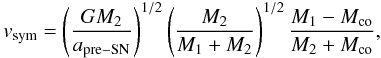vsym=(GM2apre−SN)1/2(M2M1+M2)1/2M1−McoM2+Mco,\begin{equation} v_{\rm sym} =\left({GM_2 \over a_{\rm pre-SN}}\right)^{1/2} \left({M_2 \over M_1 +M_2}\right)^{1/2} {M_1 -M_{\rm co} \over M_2 +M_{\rm co}}, \label{eqn:velsym} \end{equation}(2)where G is the gravitational constant, apre − SN is the pre-supernova semimajor axis of the binary, and Mco = M1 − Mej is the mass of the compact object (a neutron star or black hole). For 4U 1907+09, the stellar supernova remnant is a neutron star and we assume that it has a canonical mass Mco = 1.4   M⊙.

It follows from Eq. (2) that the HMXB achieves the highest peculiar velocity if the pre-supernova binary was as tight as possible, i.e. if the secondary star of radius R2 was close to filling its Roche lobe, R2 ~ RL, where RL is the radius of the Roche lobe, given by (Eggleton 1983) 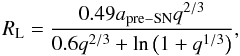RL=0.49apre−SNq2/30.6q2/3+ln(1+q1/3),\begin{equation} R_{\rm L} = {0.49a_{\rm pre-SN}q^{2/3} \over 0.6q^{2/3} +\ln \left(1+q^{1/3}\right)}, \end{equation}(3)and q = M2/M1. Equation (2) also shows that the larger Mej = M1 − Mco the higher vsym. Assuming that at the moment of supernova explosion the secondary was a 26   M⊙ main-sequence star (cf. Cox et al. 2005) of radius 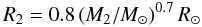R2=0.8(M2/M⊙)0.7R⊙\begin{equation} R_2 = 0.8\left(M_2 /M_\odot\right)^{0.7}R_\odot \label{eqn:rad} \end{equation}(4)(Habets & Heintze 1981) and adopting the maximum pre-supernova mass of the exploding star of 17   M⊙ (see Fig. 6 of Meynet & Maeder 2003), one finds from Eqs. (2) − (4) that apre − SN ≃ 2.4RL ≃ 20   R⊙ and the maximum possible systemic velocity 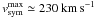vsymmax≃230 km s-1\hbox{$v_{\rm sym} ^{\rm max} \simeq 230\kms$}. The latter figure, when compared with the total peculiar (transverse) velocity of 4U 1907+09, 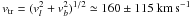vtr=(vl2+vb2)1/2≃160±115 km s-1\hbox{$v_{\rm tr} =(v_l ^2 +v_b ^2)^{1/2} \simeq 160\pm 115\kms$} (see Eq. (1)), means that the symmetric supernova explosion could be responsible for the origin of the high space velocity of 4U 1907+09.

The maximum recoil velocity would be lower if at the moment of the supernova explosion the secondary star already entered the supergiant stage of evolution. Adopting RL ~ R2 = 26   R⊙ (Cox et al. 2005), one finds 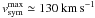vsymmax≃130 km s-1\hbox{$v_{\rm sym}^{\rm max} \simeq 130\kms$}. Still, the “measured” peculiar velocity of 4U 1907+09 within the 1σ error bar is consistent with the maximum possible recoil velocity. Note, however, that apre − SN is related to the post-supernova semimajor axis, apost − SN, through the relationship 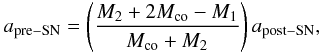apre−SN=(M2+2Mco−M1Mco+M2)apost−SN,\begin{eqnarray} a_{\rm pre-SN} = \left({M_2 +2M_{\rm co} -M_1 \over M_{\rm co} +M_2}\right) a_{\rm post-SN}, \nonumber \label{eqn:semi} \end{eqnarray}from which it follows that apre − SN ≃ 24   R⊙ if one uses the stellar masses adopted above and the present semimajor axis of 4U 1907+09 of  ≃ 50   R⊙. This estimate suggests that at the moment of the supernova explosion the secondary star was still on the main-sequence and left it later on.

5.2.2. Asymmetric supernova explosion

The recoil velocity could be higher if the supernova explosion was asymmetric and the stellar remnant received a kick at birth. In this case, the systemic velocity of the post-supernova binary also depends on the magnitude and orientation of the kick, and is given by (Stone 1982): 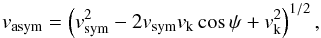vasym=(vsym2−2vsymvkcosψ+vk2)1/2,\begin{equation} v_{\rm asym} = \left(v_{\rm sym} ^2 -2v_{\rm sym} v_{\rm k} \cos \psi + v_{\rm k} ^2 \right)^{1/2}, \label{eqn:velasym} \end{equation}(5)where vsym is given by Eq. (2), vk = Mcow/(Mco + M2), w is the kick velocity, and ψ is the angle between the kick velocity and the pre-explosion relative orbital velocity (note that Eq. (5) neglects the mass loss from the secondary star owing to stripping and ablation of the stellar material caused by the passing supernova shock wave; see Tauris et al. 1999, for details).

Table 1

Summary of parameters related to 4U 1907+09 and Vela X-1.

It follows from Eq. (5) that vasym is maximum if the kick velocity attained by the stellar supernova remnant was oriented in the opposite direction to the relative orbital velocity, i.e. cosψ =  −1. In this case 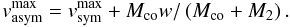vasymmax=vsymmax+Mcow/(Mco+M2).\begin{equation} v_{\rm asym}^{\rm max} = v_{\rm sym} ^{\rm max} + M_{\rm co} w/\left(M_{\rm co} +M_2\right). \label{eqn:full} \end{equation}(6)Equation (6) shows that for HMXBs comprising a neutron star, i.e. for systems with Mco/(Mco + M2) ≪ 1, the effect of asymmetry of supernova explosion on the systemic velocity is modest and could be substantial (larger than several tens of    km   s-1) only for extremely high kick velocities, w ≥ 1000   km   s-1. It is generally believed that neutron stars can obtain kick velocities of this magnitude. This belief was boosted after Chatterjee et al. (2005) derived a space velocity of  ~1000   km   s-1 for the pulsar PSR B1508+55 by measuring its proper motion and parallax. Still, the existence of a population of extremely high-velocity neutron stars can be explained without exploiting the idea of asymmetric supernova explosion – they simply could be the remnants of massive hypervelocity runaway stars (Gvaramadze 2007, 2009; Gvaramadze et al. 2008, 2009).

Assuming that the neutron star in 4U 1907+09 attained a kick velocity of 200−400   km   s-1 at birth (typical of radio pulsars; e.g. Hobbs et al. 2005) and adopting Mco = 1.4   M⊙ and M2 = 26   M⊙ (Cox et al. 2005), one finds from Eq. (6) that the asymmetry of the supernova explosion can increase the systemic velocity only by  ≃ 10−20   km   s-1 (provided that the kick velocity was of favourable orientation; see above). We therefore conclude that the asymmetric supernova explosion did not contribute significantly to the space velocity of 4U 1907+09, unless the kick velocity was higher than 1000   km   s-1.

5.3. 4U 1907+09 and Vela X-1

In many aspects, 4U 1907+09 is similar to Vela X-1: both systems host OB supergiants of almost equal mass and radius, the orbital periods of both systems are almost equal to each other as well, and both systems are bow shock-producing runaways. Below we compare the bow shocks associated with these HMXBs.

The geometry of a bow shock generated by a supersonically moving star is characterized by two main parameters, the Mach number M = v∗/cs (where v∗ is the velocity of the star relative to the ambient medium and cs is the sound speed of the ambient medium) and the stand-off distance Rs. The higher M (or the higher v∗) the smaller the opening angle, α, of the bow shock, which is related to the Mach number through the relationship: α = 2arcsin(1/M). In practice, however, this angle is difficult to determine owing to the low-emission measure of the flanks of bow shocks. Still, a comparison of Figs. 1 and 2 suggests that the opening angle of the bow shock generated by 4U 1907+09 is much smaller than that of the bow shock associated with Vela X-1, meaning that the peculiar velocity of the former system is much higher than that of the latter one (see also below).

Let us estimate the space velocity of Vela X-1 using the proper motion of this HMXB from the new reduction of the Hipparcos data by van Leeuwen (2007), μαcosδ =  −5.48 ± 0.35   mas   yr-1, μδ = 8.79 ± 0.40   mas   yr-1, and the generally accepted distance to Vela X-1 of 1.9 kpc (Sadakane et al. 1985). Using the Galactic constants and the solar peculiar motion adopted in Sect. 5.1, we found the transverse peculiar velocity of Vela X-1: 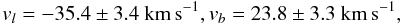vl=−35.4±3.4 km s-1,vb=23.8±3.3 km s-1,\begin{equation} v_l = -35.4\pm 3.4\kms, v_b =23.8\pm 3.3\kms, \label{eqn:velo} \end{equation}(7)or vtr = 42.7 ± 3.4   km   s-1 (cf. Moffat et al. 1998; Huthoff & Kaper 2002). To this velocity one should add the peculiar radial velocity vrad =  −27   km   s-1, inferred from the heliocentric one of  −4   km   s-1 (Gies & Bolton 1986), so that the total (three-dimensional) velocity of Vela X-1 v∗ ≃ 50   km   s-1, and its vector is inclined to the plane of the sky by an angle of  ≃ 32°.

The second parameter characterizing a bow shock is the stand-off distance, i.e. the minimum distance from the star at which the ram pressure of the stellar wind is balanced by the ram pressure of the ambient interstellar medium (e.g., Baranov et al. 1971): 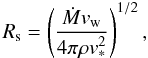Rs=(Ṁvw4πρv∗2)1/2,\begin{equation} R_{\rm s} = \left({\dot{M} v_{\rm w} \over 4\pi \rho v_\ast^2}\right)^{1/2}, \label{eqn:stand} \end{equation}(8)where Ṁ and vw are the stellar mass-loss rate and the wind velocity, ρ = 1.4mHn, mH is the mass of a hydrogen atom, and n is the number density of the ambient medium. Rs is related to the observed angular separation between the apex of the bow shock and the star, θ, through the relationship 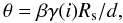θ=βγ(i)Rs/d,\begin{equation} \theta = \beta \gamma (i) R_{\rm s} /d, \end{equation}(9)where β > 1 is a factor of order unity taking into account the finite thickness of the layers occupied by the shocked gas coming from the ambient medium and the stellar wind (see, e.g., Fig. 1 in Comerón & Kaper 1998, for a schematic view of the multi-layer structure of a wind bow shock), 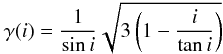γ(i)=1sini3(1−itani)\begin{equation} \gamma (i) = {1 \over \sin i} \sqrt{3\left(1-{i \over \tan i}\right)} \label{eqn:gamma} \end{equation}(10)is a geometric factor taking into account the inclination of the bow shock to the plane of the sky (see Wilkin 1996), where i = arctan(vrad/vtr) is the angle between the vector of the space velocity of the star and the plane of the sky. Note that for small inclination angles (i < 45°) the factor γ is  ≃ 1.

Using Eqs. (8) − (10), one can estimate the number density of the ambient medium: 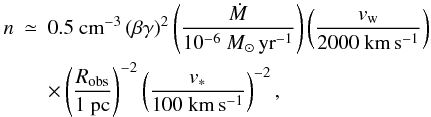n≃0.5 cm-3 (βγ)2(Ṁ10-6 M⊙ yr-1)(vw2000 km s-1)\begin{eqnarray} n &\simeq& 0.5~{\rm cm}^{-3} \, (\beta \gamma)^2 \left({\dot{M} \over 10^{-6}~M_{\odot}\,{\rm yr}^{-1}}\right) \left({v_{\rm w} \over 2000~{\rm km }\,{\rm s}^{-1}}\right) \nonumber \\ && \times \left({R_{\rm obs} \over 1~{\rm pc}}\right)^{-2} \left({v_{\ast} \over 100\kms}\right)^{-2}, \label{eqn:den} \end{eqnarray}(11)where Robs = θd. Inserting parameters of 4U 1907+09 and Vela X-1 (given in Table 1) in Eq. (11), one finds the number density of the interstellar medium surrounding these HMXBs,  ≃ 2 and 10   cm-3, respectively (we assumed here that βγ ~ 1). Note that despite the much larger separation of Vela X-1 from the Galactic plane (≃ 130 pc versus  ≃ 30 pc for 4U 1907+09) it is located in a denser medium than 4U 1907+09, implying that Vela X-1 met a density enhancement (a cloudlet) on its way (cf. Gvaramadze & Bomans 2008; Gvaramadze et al. 2009). This implication is supported by the presence of an extended (of angular radius of 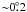\hbox{${\sim}0\fdg2$}) IRAS source at the position of Vela X-1, suggesting that this source might be a Strömgren zone created by the ultraviolet emission of Vela X-1 (Kaper et al. 1997). Assuming that the gas in the H ii region is fully ionized and its temperature is 104 K, one can obtain an estimate of the gas number density (e.g. Lequeux 2005) 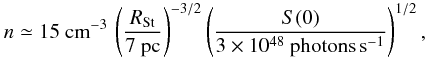n≃15 cm-3 (RSt7 pc)−3/2(S(0)3×1048 photons s-1)1/2,\begin{equation} n \simeq 15~{\rm cm}^{-3} \, \left({R_{\rm St} \over 7~{\rm pc}}\right)^{-3/2} \left({S(0) \over 3\times 10^{48}~{\rm photons} \, {\rm s}^{-1}}\right)^{1/2}, \label{eqn:str} \end{equation}(12)where RSt is the Strömgren radius (derived from the angular radius of the H ii region and the distance to Vela X-1 of 1.9 kpc) and S(0) is the total ionizing-photon luminosity of an B0.5 Iab star (cf. Martins et al. 2005). The good agreement between the two independent estimates derived from Eqs. (11) and (12) supports the interpretation of the extended infrared emission around Vela X-1 and its bow shock as the H ii region (Kaper et al. 1997; see also Fig. 5 in Gvaramadze & Bomans 2008, for another example of a bow shock within an H ii region).

It should be noted that the geometric factor γ(i) (given by Eq. (10)) was derived in the thin-shell approximation, i.e. under the assumption that the thickness of the region occupied by the shocked gas is  ≪ Rs (Wilkin 1996). This approximation, however, could be valid only for bow-shocks generated in the very dense medium (e.g. cometary ultra-compact H ii regions, Mac Low et al. 1991) or for bow shocks produced by stars with dense, slow winds (e.g. red supergiants). In both cases, the shocked gas could be dense enough to rapidly cool and collapse into a thin shell. The thin-shell approximation can hardly be used to describe the shape of adiabatic bow shocks, i.e. the bow shocks generated by massive stars possessing fast, hot winds and/or moving through the space with high peculiar velocities. For these bow shocks, the thickness of the layers occupied by the shocked stellar wind (the inner layer) and the shocked ambient medium (the outer layer) constitutes a significant fraction of Rs (Raga et al. 1997; Comerón & Kaper 1998).

Because 4U 1907+09 and Vela X-1 both contain supergiant stars with strong winds (see Table 1), one can expect that at least the inner layer of the bow shocks generated by these HMXBs is adiabatic. To check this, we use the following back-of-the-envelope estimates. The shocked gas in a bow shock will collapse into a thin shell if the characteristic time-scale for radiative cooling of the gas, 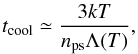tcool≃3kTnpsΛ(T),\begin{equation} t_{\rm cool} \simeq {3kT \over n_{\rm ps} \Lambda (T)}, \label{eqn:cool} \end{equation}(13)is much shorter than the characteristic dynamical time-scale of the bow shock, 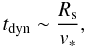tdyn~Rsv∗,\begin{equation} t_{\rm dyn} \sim {R_{\rm s} \over v_{\ast}}, \label{eqn:dyn} \end{equation}(14)where k is the Boltzmann constant, Tps and nps are the initial post-shock temperature and number density, and Λ(T)={0,T<104 K1.0×10-24T0.55,104 K<T<105 K6.2×10-19T-0.6,105 K<T<4×107 K2.5×10-27T0.5,T>4×107 K\begin{equation} \label{eqn:lam} \Lambda (T)=\left\{ \begin{array}{l} 0, T<10^4~{\rm K} \\[0.5mm] 1.0\times 10^{-24} T^{0.55}, 10^4~{\rm K} <T<10^5~{\rm K} \\[0.5mm] 6.2\times 10^{-19} T^{-0.6}, 10^5~{\rm K} <T<4\times 10^7~{\rm K} \\[0.5mm] 2.5\times 10^{-27} T^{0.5}, T>4\times 10^7~{\rm K} \end{array} \right. \end{equation}(15)is the cooling function (Raymond et al. 1976; Cowie et al. 1981). 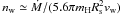For the (inner) layer of the bow shock occupied by the shocked stellar wind, Tps ≃ 1.4 × 107(vw/1000   km   s-1)2 and nps = 4nw, where nw≃Ṁ/(5.6πmHRs2vw)\hbox{$n_{\rm w} \simeq \dot{M}/(5.6\pi m_{\rm H} R_{\rm s}^2 v_{\rm w})$}. Using Eqs. (13) − (15) and parameters of the stellar winds from Table 1, one finds that tcool ≫ tdyn for both bow shocks, i.e. the inner layer of the bow shocks is adiabatic. Similarly, adopting for the shocked ambient gas Tps ≃ 1.4 × 105(v∗/100   km   s-1)2 and nps = 4n, one finds that tcool ~ tdyn for 4U 1907+09 and tcool ≪ tdyn for Vela X-1, so that the outer layer of the bow shock produced by 4U 1907+09 is adiabatic, while that of the bow shock around Vela X-1 is radiative. From this it follows that the shape of both bow shocks cannot be described by the thin-shell solution of Wilkin (1996). Indeed, the Wilkin’s solution predicts that the radial extent of a bow shock in the direction perpendicular to the direction of motion R(π/2) = γ(π/2)Rs ≃ 1.7Rs, while from Figs. 1 and 2 we found R(π/2) ≃ 1.5Rs for 4U 1907+09 and R(π/2) ≃ 2.4Rs for Vela X-1.

It is also instructive to compare the geometry of the bow shocks produced by 4U 1907+09 and Vela X-1 with that of model bow shocks from Comerón & Kaper (1998), namely with their case D and case E bow shocks (generated by stars with space velocities of 50 and 150   km   s-1, respectively, which are almost identical to those of Vela X-1 and 4U 1907+09). One can show that like in the case of 4U 1907+09 and Vela X-1, the inner layer of both model bow shocks is adiabatic (cf. Comerón & Kaper 1998), while the outer one is radiative in the case D bow shock and adiabatic in the case E bow shock. It is not surprising, therefore, that the bow shock around Vela X-1 shows a close similarity to the case D bow shock, while the shape of the bow shock associated with 4U 1907+09 recalls that of the case E bow shock (cf. Figs. 2 and 1 with the upper and the lower panels of Fig. 13 in Comerón & Kaper 1998, respectively). The more thorough study of the bow shocks associated with 4U 1907+09 and Vela X-1 requires numerical simulations (similar to those carried out by Comerón & Kaper 1998), which is beyond the scope of the present paper.

The inference that the outer layer of the bow shock around Vela X-1 is radiative is consistent with the observational fact that just this of the two bow shocks manifests itself in Hα. On the other hand, the non-detection of the Hα emission from the bow shock associated with 4U 1907+09 could be used to somewhat constrain the distance to this HMXB. The space velocity of 4U 1907+09 approximately scales with the distance as  ~d, so that n ~ d-4, and correspondingly, tcool ∝ d7.2 (for 105   K < T < 4 × 107   K) and tdyn ∝ d0. The strong dependence of tcool on d implies that the outer layer of the bow shock would be radiative, while the bow shock itself would be visible in Hα if the distance to 4U 1907+09 is shorter than 4 kpc, say comparable to that of Vela X-1 (≃ 2 kpc). This implication, however, suffers from the large error bar in the proper motion measurements, which causes the correspondingly large uncertainties in estimates of the space velocity of the HMXB and the cooling time-scale of the bow shock. And on the related note, for distances much larger than 4 kpc, the outer layer of the bow shock would remain adiabatic, while the space velocity of the system would become too high to be explained within the binary-supernova scenario (see Sect. 5.2).

Finally, we note that the IRAC 8 μm image of the bow shock produced by Vela X-1 (right panel of Fig. 2) shows filamentary (cirrus-like) structures beyond the main body of the bow shock. We speculate that these filaments are due to interstellar dust grains aligned with the local interstellar magnetic field and heated by the radiation of Vela X-1.

6. Summary and conclusion

We have searched for bow shocks around 5 HMXBs (GX 301-2, 4U 1907+09, Cyg X-1, Vela X-1 and V615 Cas) using the Spitzer Space Telescope archival data. We found two bow shocks, one of which (produced by Vela X-1) was already known, while the second one (generated by 4U 1907+09) was detected for the first time. The detection of the bow shock around 4U 1907+09 provides strong evidence that this HMXB is a runaway system, which supports the general belief that most of HMXBs possess high space velocities caused by supernova explosion of one of the components of the progenitor massive binary. To prove the runaway nature of 4U 1907+09, we have measured its proper motion using archival data over a total time baseline of 50 yr. Although suffering from large error bars, our measurements support the runaway interpretation of 4U 1907+09, and suggest that this system was expelled from the Galactic plane about 105 yr ago. Using the observed parameters of 4U 1907+09, we found that the high space velocity of this HMXB could be well explained within the framework of the symmetric binary-supernova explosion. We found also that the possible asymmetry in the supernova explosion does not contribute significantly to the space velocity of 4U 1907+09. We have compared the bow shocks produced by 4U 1907+09 and Vela X-1 and showed that the cooling of the shocked stellar wind is inefficient in both shocks. We showed also that the layer of the shocked ambient gas is adiabatic in the former bow shock and is radiative in the latter one. This allowed us to explain qualitatively why the shapes of both bow shocks do not follow the thin-shell solution by Wilkin (1996).

To conclude, we expect that the future proper motion and parallax measurements for 4U 1907+09 with the space astrometry mission Gaia will considerably improve the estimate of its space velocity, and thereby will allow us to better understand the evolution and pre-supernova configuration of its progenitor binary system. With the new proper motion and distance measurements in hands we will also be able to refine the parameters of the bow shock around 4U 1907+09 and to confront them with numerical simulations.

1

We also tried to estimate AKs using the Spitzer photometry of 4U 1907+09 and the Stellar Performance Estimation Tool (http://ssc.spitzer.caltech.edu/warmmission/propkit/pet/starpet/ index.html), but found that the fluxes predicted by this tool (based on Kurucz-Lejeune atmospheric models) cannot be reconciled with the observed ones.

2

The MIPS and IRAC images were obtained within the framework of the 24 and 70 Micron Survey of the Inner Galactic Disk with MIPS (MIPSGAL, Carey et al. 2009) and the Galactic Legacy Infrared Mid-Plane Survey Extraordinaire (GLIMPSE, Benjamin et al. 2003), respectively.

3

Note that the bow shock produced by Vela X-1 was independently observed with Spitzer by R.Iping (Program Id.: 30174).

Acknowledgments

We are grateful to the referee for comments allowing us to improve the presentation and the content of the paper. V.V.G. acknowledges financial support from the Deutscher Akademischer Austausch Dienst. This research has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, the SIMBAD database, and the VizieR catalogue access tool, both operated at CDS, Strasbourg, France.

References

  1. Bally, J., O’Dell, C. R., & McCaughrean, M. J. 2000, AJ, 119, 2919 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baranov, V. B., Krasnobaev, K. V., & Kulikovskii, A. G. 1971, Sov. Phys. Dokl., 15, 791 [NASA ADS] [Google Scholar]
  3. Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] [Google Scholar]
  4. Blaauw, A. 1961, Bull. Astron. Inst. Netherlands, 15, 265 [NASA ADS] [Google Scholar]
  5. Boersma, J. 1961, Bull. Astron. Inst. Netherlands, 15, 291 [Google Scholar]
  6. Brand, J., & Blitz, L. 1993, A&A, 275, 67 [NASA ADS] [Google Scholar]
  7. Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chatterjee, S., Vlemmings, W. H. T., Brisken, W. F., et al. 2005, ApJ, 630, L61 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chevalier, C., & Ilovaisky, S. A. 1998, A&A, 330, 201 [NASA ADS] [Google Scholar]
  10. Coe, M. J. 2005, MNRAS, 358, 1379 [NASA ADS] [CrossRef] [Google Scholar]
  11. Comerón, F., & Kaper, L. 1998, A&A, 338, 273 [NASA ADS] [Google Scholar]
  12. Conti, P. S. 1978, A&A, 63, 225 [NASA ADS] [Google Scholar]
  13. Cook, M. C., & Page, C. G. 1987, MNRAS, 225, 381 [NASA ADS] [Google Scholar]
  14. Cowie, L. L., McKee, C. F., & Ostriker, J. P. 1981, ApJ, 247, 908 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cox, N. L. J., Kaper, L., & Mokiem, M. R. 2005, A&A, 436, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
  18. Giacconi, R., Kellogg, E., Gorenstein, P., Gursky, H., & Tananbaum, H. 1971, ApJ, 165, L27 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gies, D. R., & Bolton, C. T. 1986, ApJS, 61, 419 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gott, J. R., Gunn, J. E., & Ostriker, J. P. 1970, ApJ, 160, L91 [NASA ADS] [CrossRef] [Google Scholar]
  21. Green, D. A. 2009, Bull. Astron. Soc. India, 37, 45 [Google Scholar]
  22. Gvaramadze, V. V. 2007, A&A, 470, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gvaramadze, V. V. 2009, MNRAS, 395, L85 [NASA ADS] [Google Scholar]
  24. Gvaramadze, V. V., & Bomans, D. J. 2008, A&A, 490, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gvaramadze, V. V., & Gualandris, A. 2011, MNRAS, 410, 304 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gvaramadze, V. V., Gualandris, A., & Portegies Zwart, S. 2008, MNRAS, 385, 929 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gvaramadze, V. V., Gualandris, A., & Portegies Zwart, S. 2009, MNRAS, 396, 570 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gvaramadze, V. V., Kroupa, P., & Pflamm-Altenburg, J. 2010a, A&A, 519, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Gvaramadze, V. V., Kniazev, A. Y., Hamann, W.-R., et al. 2010b, MNRAS, 403, 760 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gvaramadze, V. V., Pflamm-Altenburg, J., & Kroupa, P. 2011, A&A, 525, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Habets, G. M. H. J., & Heintze, J. R. W. 1981, A&AS, 46, 193 [NASA ADS] [Google Scholar]
  32. Hambly, N. C., MacGillivray, H. T., Read, M. A., et al. 2001, MNRAS, 326, 1279 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hills, J. G. 1983, ApJ, 267, 322 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
  35. Huthoff, F., & Kaper, L. 2002, A&A, 383, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Iben, I., & Tutukov, A. V. 1997, ApJ, 491, 303 [NASA ADS] [CrossRef] [Google Scholar]
  37. in ’t Zand, J. J. M., Strohmayer, T. E., & Baykal, A. 1997, ApJ, 479, L47 [NASA ADS] [CrossRef] [Google Scholar]
  38. Iye, M. 1986, PASJ, 38,463 [NASA ADS] [Google Scholar]
  39. Kaper, L., & van der Meer, A. 2007, in Massive Stars in Interactive Binaries, ed. N. St.-Louis, & A. F. J. Moffat, ASP Conf. Ser., 367 (San Francisco: ASP), 447 [Google Scholar]
  40. Kaper, L., van Loon, J. Th., Augusteijn, T., et al. 1997, ApJ, 475, L37 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kaper, L., Comerón, F., & Barziv, O. 1999, in Wolf-Rayet Phenomena in Massive Stars and Starburst Galaxies, ed. K. A. van der Hucht, G. Koenigsberger, & P. R. J. Eenens, IAU Symp., 193 (San Francisco: ASP), 316 [Google Scholar]
  42. Lequeux, J. 2005, The Interstellar Medium (Berlin: Springer) [Google Scholar]
  43. Mac Low, M.-M., van Buren, D., Wood, D. O. S., & Churchwell, E. 1991, ApJ, 369, 395 [NASA ADS] [CrossRef] [Google Scholar]
  44. Makishima, K., Kawai, N., Koyama, K., et al. 1984, PASJ, 36, 679 [NASA ADS] [Google Scholar]
  45. Marshall, N., & Ricketts, M. J. 1980, MNRAS, 193, 7P [NASA ADS] [CrossRef] [Google Scholar]
  46. Martins, F., & Plez, B. 2006, A&A, 457, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. McMillan, P. J., & Binney, J. J. 2010, MNRAS, 402, 934 [NASA ADS] [CrossRef] [Google Scholar]
  49. Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Moffat, A. F. J., Marchenko, S. V., Seggewiss, W., et al. 1998, A&A, 331, 949 [NASA ADS] [Google Scholar]
  51. Monet, D. G., Levine, S. E., Casian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
  52. Nespoli, E., Fabregat, J., & Mennickent, R. E. 2008, A&A, 486, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Pflamm-Altenburg, J., & Kroupa, P. 2010, MNRAS, 404, 1564 [NASA ADS] [Google Scholar]
  54. Poveda, A., Ruiz, J., & Allen, C. 1967, Bol. Obs. Tonantzintla Tacubaya, 4, 86 [NASA ADS] [Google Scholar]
  55. Price, S. D., Egan, M. P., Carey, S. J., Mizuno, D. R., & Kuchar, T. A. 2001, AJ, 121, 2819 [NASA ADS] [CrossRef] [Google Scholar]
  56. Prinja, R. K., Barlow, M. J., & Howarth, I. D. 1990, ApJ, 361, 607 [NASA ADS] [CrossRef] [Google Scholar]
  57. Raga, A. C., Noriega-Crespo, A., Cantó, J., et al. 1997, Rev. Mex. Astron. Astrofis., 33, 73 [NASA ADS] [Google Scholar]
  58. Raymond, J. C., Cox, D. P., & Smith, B. W. 1976, ApJ, 204, 290 [NASA ADS] [CrossRef] [Google Scholar]
  59. Reid, M. J., Menten, K. M., Zheng, X. W., Brunthaler, A., & Xu, Y. 2009, ApJ, 705, 1548 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
  61. Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
  62. Rivers, E., Markowitz, A., Pottschmidt, K., et al. 2010, ApJ, 709, 179 [NASA ADS] [CrossRef] [Google Scholar]
  63. Röser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
  64. Sadakane, K., Hirata, R., Jugaku, J., et al. 1985, ApJ, 288, 284 [NASA ADS] [CrossRef] [Google Scholar]
  65. Schwartz, D. A., Griffiths, R. E., Bowyer, S., Thorstensen, J. R., & Charles, P. A. 1980, AJ, 85, 549 [NASA ADS] [CrossRef] [Google Scholar]
  66. Shull, J. M., Fesen, R. A., & Saken, J. M. 1989, ApJ, 346, 860 [NASA ADS] [CrossRef] [Google Scholar]
  67. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  68. Stone, R. C. 1982, AJ, 87, 90 [NASA ADS] [CrossRef] [Google Scholar]
  69. Tauris, T. M., & Takens, R. J. 1998, A&A, 330, 1047 [NASA ADS] [Google Scholar]
  70. Tauris, T. M., Fender, R. P., van den Heuvel, E. P. J., Johnston, H. M., & Wu, K. 1999, MNRAS, 310, 1165 [NASA ADS] [CrossRef] [Google Scholar]
  71. Tutukov, A., & Yungelson, L. R. 1973, Nauchn. Inform., 27, 86 [NASA ADS] [Google Scholar]
  72. van Buren, D., & McCray, R. 1988, ApJ, 329, L93 [NASA ADS] [CrossRef] [Google Scholar]
  73. van Buren, D., Noriega-Crespo, A., & Dgani, R. 1995, AJ, 110, 2914 [NASA ADS] [CrossRef] [Google Scholar]
  74. van den Heuvel, E. P. J., & Heise, J. 1972, Nat. Phys. Sci., 239, 67 [Google Scholar]
  75. van Kerkwijk, M. H., van Oijen, J. G. J., & van den Heuvel, E. P. J. 1989, A&A, 209, 173 [NASA ADS] [Google Scholar]
  76. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. van Oijen, J. G. J. 1989, A&A, 217, 115 [NASA ADS] [Google Scholar]
  78. Watanabe, S., Sako, M., Ishida, M., et al. 2006, ApJ, 651, 421 [NASA ADS] [CrossRef] [Google Scholar]
  79. Wegner, W. 1994, MNRAS, 270, 229 [NASA ADS] [CrossRef] [Google Scholar]
  80. Wegner, W. 2006, MNRAS, 371, 185 [NASA ADS] [CrossRef] [Google Scholar]
  81. Wilkin, F. 1996, ApJ, 459, L31 [NASA ADS] [CrossRef] [Google Scholar]
  82. Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Summary of parameters related to 4U 1907+09 and Vela X-1.

In the text

All Figures

thumbnail Fig. 1

From left to right, and from top to bottom: Spitzer MIPS 24   μm, IRAC 8, 5.8, 4.5 and 3.6 μm, and DSS-II (red band) images of the field around the HMXB 4U 1907+09. The arrow shows the direction of peculiar velocity of 4U 1907+09, as suggested by the proper motion measurement (see text for details). A bright infrared source to the north is the maser source IRAC 19071+0946. In all panels the position of 4U 1907+09 is indicated by a circle.
In the text
thumbnail Fig. 2

Spitzer MIPS 24   μm (left) and IRAC 8   μm images of the bow shock around the HMXB Vela X-1. The arrow shows the direction of peculiar velocity of Vela X-1 (see Sect. 5.3 for details).
In the text
thumbnail Fig. 3

3° × 2° MSX 8.3   μm image of the Galactic plane (shown by a dashed line) centred at \hbox{$l=43\fdg5$}, b = 0°, with the position of the HMXB 4U 1907+09 indicated by a circle. The arrow shows the direction of motion of 4U 1907+09. The orientation of this figure is the same as for Fig. 1. The brightest nebula on the image is the background star-forming region W 49A.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.