| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201015551 | |
| Published online | 21 March 2011 | |
Spectropolarimetric forward modelling of the lines of the Lyman-series using a self-consistent, global, solar coronal model
1
Dipartimento di Fisica e Astronomia, SASSUniversità degli Studi di Firenze, Largo E. Fermi 2, 50125 Firenze, Italy
e-mail: khan@arcetri.astro.it
2
Instituto de Astrofísica de Canarias, C/ via Láctea s/n, 38205 La Laguna, Tenerife, Spain
3 INAF - Osservatorio Astronomico di Torino, Strada Osservatorio 20, Pino Torinese (TO), Italy
Received: 9 August 2010
Accepted: 17 November 2010
Context. The presence and importance of the coronal magnetic field is illustrated by a wide range of phenomena, such as the abnormally high temperatures of the coronal plasma, the existence of a slow and fast solar wind, the triggering of explosive events such as flares and CMEs.
Aims. We investigate the possibility of using the Hanle effect to diagnose the coronal magnetic field by analysing its influence on the linear polarisation, i.e. the rotation of the plane of polarisation and depolarisation.
Methods. We analyse the polarisation characteristics of the first three lines of the hydrogen Lyman-series using an axisymmetric, self-consistent, minimum-corona MHD model with relatively low values of the magnetic field (a few Gauss).
Results. We find that the Hanle effect in the above-mentioned lines indeed seems to be a valuable tool for analysing the coronal magnetic field. However, great care must be taken when analysing the spectropolarimetry of the Lα line, given that a non-radial solar wind and active regions on the solar disk can mimic the effects of the magnetic field, and, in some cases, even mask them. Similar drawbacks are not found for the Lβ and Lγ lines because they are more sensitive to the magnetic field. We also briefly consider the instrumental requirements needed to perform polarimetric observations for diagnosing the coronal magnetic fields.
Conclusions. The combined analysis of the three aforementioned lines could provide an important step towards better constrainting the value of solar coronal magnetic fields.
Key words: polarisation / scattering / Sun: corona / magnetic fields
© ESO, 2011
1. Introduction
In 1908, Hale succeeded in measuring the magnetic field of a sunspot for the first time by taking two separate spectra in right and left circular polarisation, and interpreted his observations in terms of the Zeeman effect, then recently discovered by Zeeman where a magnetic field splits a spectral line into several differently polarised components. As a result he pioneered the field of magnetometry, i.e., the art of measuring the magnetic fields of the solar atmosphere.
Despite its usefulness for photospheric field measurements, the method developed by Hale cannot be readily applied to magnetic field determinations in the higher layers of the solar atmosphere (upper chromosphere, transition region, and corona). The reason for this is that the splitting effect of the magnetic field, which is proportional to λ2B where λ is the wavelength and B the field intensity, has to be compared to the Doppler width of the line, which, because of the temperature increase beginning in the chromosphere, dominates, thus rendering the Zeeman effect unobtrusive.
In 1924 however, Hanle discovered that the laws of resonance scattering of polarised radiation are modified in the presence of a magnetic field. This modification consists mostly of a depolarisation, but can, for certain geometries, even become a hyperpolarisation of the scattered radiation accompanied by a rotation of the plane of polarisation.
The first proposal to use the Hanle effect for astrophysical purposes, e.g. magnetic field diagnostics of solar prominences, was made by Öhman (1929). The same proposal was later placed on more solid grounds by Hyder (1965) and House (1971), but it was not until the late seventies that detailed observations were reported (Leroy et al. 1977; House & Smartt 1979), and progress made in the theoretical interpretation of the observations of the helium D3 emission line (Bommier 1977; Sahal-Bréchot et al. 1977; Bommier & Sahal-Bréchot 1978; Bommier 1980; Landi Degl’Innocenti 1982). Bommier & Sahal-Bréchot (1982) worked out the full quantum mechanical theory of resonance scattering in the presence of a magnetic field for the specific case of one of the strongest lines of the solar spectrum, namely the 1215.16 Å Lα line, making the bold suggestion of using their results to enter previously uncharted territory: the diagnostics of the ever-elusive magnetic field of the solar corona. In their seminal paper, the authors show that a linear polarisation degree of up to about 20% can be expected in the solar corona at heights of about one solar radius above the solar surface, and calculate the depolarisation and rotation of the plane of polarisation with respect to the solar limb for various directions and intensities of the magnetic field vector. The final line of their abstract reads: “After integrating along the line of sight, these formulae could be used for magnetic field determination in the solar corona from measurements of the linear polarisation of the Lα line”.
The recipe is apparently very simple, i.e. in the absence of a magnetic field, the plane of linear polarisation is parallel to the solar limb, and if it were possible to measure the rotation of the plane of polarisation, then, through the algorithms developed, one could deduce the magnetic field vector. The authors do however point out that this type of analysis cannot provide a complete description of the three components of the magnetic field vector because only two linear polarisation parameters can be measured. We note that this subtlety was already tackled in a previous paper (Bommier et al. 1981), in which the authors investigate various methods of adding supplementary information to those resulting from the Hanle effect analysis of linear polarisation measurements of an emission line to provide the three components of the magnetic field.
A first implementation of a line-of-sight (LOS) integration of the hydrogen Lα line was undertaken by Fineschi and coworkers. In a series of papers (Fineschi et al. 1991, 1992, 1993, 1999), these authors thoroughly examine the feasibility of diagnosing the coronal magnetic field after a LOS integration, and simultaneously address the problem from an experimental point of view, defining and investigating the relevant parameters and even suggesting instruments capable of achieving the necessary measurement sensitivity. They recommend that polarimetric measurements be undertaken at relatively low altitudes (~1.1 solar radii), and show that the bulk of the emission comes predominantly from the high-density scattering points along the LOS that are close to the plane of the sky, i.e. the plane perpendicular to the LOS passing through the Sun’s centre. In their 1993 paper, they model a typical coronal large-scale structure, i.e., a loop connecting two large sunspots of opposite polarity, and simulate the magnetic field placing a magnetic dipole below the solar surface, demonstrating that the averaging effects of the LOS integration do not cancel out the Hanle effect. They also argue that the solar wind at these distances (~1.1 solar radii) is rather slow thus eliminating the need to take into account the effects of Doppler-dimming when comparing with the Hanle effect caused by the relatively strong magnetic field of the active region. To assess the disturbing effects of magnetic fields in the coronal fore-and background with respect to the plane of the sky, they model an array of loops along the LOS simulating a “random” field configuration. Despite this morphological complexity, and taking into account measuring uncertainties, they show that the difference between the LOS integrated signal and that produced by only one loop is negligible, suggesting that “to first order” one can interpret the LOS integration as stemming only from the plane of the sky, thus facilitating the identification of two of the three components of the magnetic field1. To overcome the dimensional problem of having a magnetic field with three components, they suggest applying a cluster of far ultraviolet (FUV) coronagraphs/polarimeters operating at different wavelengths and making simultaneous observations of the Hanle effect in various lines. In their 1999 paper, the authors analyse the Hanle effect for two additional lines of the Lyman-series, the 1025 Å Lβ and the 972 Å Lγ lines, which are more sensitive to the Hanle effect, and show how the Lγ seems to be a particularly promising line, given that the rotation angle of the linear polarisation at a heliocentric distance of 1.1 solar radii is close to 13 degrees for a magnetic field of 4 G, which, as will be shown later, is quite a substantial rotation. The value of the magnetic field just quoted was validated by Lin et al. (2004), using Zeeman-splitting observations of infrared coronal emission lines for the above-mentioned height.
Various groups have modelled the corona assuming simple magnetic field configurations, i.e. dipoles in the Sun’s interior and current sheets in the Sun’s equatorial plane, or photospheric field extrapolations. With these simplified models, they preformed LOS integrations of the transfer equation of polarised radiation finding the rotation of the plane of polarisation and depolarisation for the Lα line (Derouich et al. 2010), and both Lα and Lβ (Raouafi et al. 2009).
To date, however, the polarimetric properties of the radiation expected from self-consistent, magneto-hydrodynamical coronal models and the detailed influence of a non-radial solar wind on the same properties have not yet been fully investigated. It is to fill this gap in our understanding of the complete spectrum of forward modelling results of more realistic, self-consistent coronal models, accounting for the presence of magnetic fields, of non-radial outflow velocities (solar wind), and of active regions, that we revisit the Hanle effect in the first three spectral lines of the Lyman-series. In this paper, we report on the results obtained using a self-consistent 2.5-D, MHD global coronal model with a solar minimum-like magnetic field topology, i.e. a global dipole field directed along the Sun’s polar regions with a current-sheet-like structure in the equatorial plane, and strengths that lie in the realistic range of a few Gauss, thus taking forward modelling of the Hanle effect in the Lyman-series one step further in predicting the outcome of real solar coronal observations.
In Sect. 2, we review the theory of resonance polarisation and the Hanle effect, and in Sect. 3 we present and discuss our simulation results. In Sect. 4, we analyse aspects of the instrumental requirements for doing spectropolarimetric observations in the solar minimum corona, and finally present our conclusions in Sect. 5.
2. Theory
The physical problem we wish to address is the following: what are the scattering polarisation properties of neutral hydrogen atoms situated in the solar corona in the presence of the pumping, anisotropic radiation field coming from the solar chromosphere, magnetic fields, collisions, (non-radial) outflow velocities, and active regions?
After the intervention of some simplifying assumptions, the algorithm for solving the problem is quite straightforward. Once the physical boundary conditions are specified, the excitation state of the atom is found by solving the statistical equilibrium equations, thus enabling the determination of its emissivity, which is then integrated along the LOS, given that the corona is optically thin for FUV lines.
The phenomenon of polarisation in resonance scattering is the emission of linearly polarised radiation by atoms that are illuminated anisotropically. In a cylindrically symmetric solar corona, the degree of linear polarisation is an increasing function of the height above the solar surface and its direction is parallel to the closest solar limb. In the following, we describe how it is possible to incorporate into our modelling three different mechanisms capable of modifying the degree of linear polarisation and rotating the plane of polarisation. These mechanisms stem from the presence of magnetic fields, non-radial outflow velocities, and active regions on the solar surface. For each case, we briefly present the initial assumptions and show the equations used to calculate the polarisation signatures these mechanisms produce in the radiation emitted by the hydrogen atoms in the first three spectral lines of the Lyman-series.
For additional details about the theory of resonance scattering of polarised radiation, we recommend that the interested reader consult the monograph “Polarisation in Spectral Lines” by Landi Degl’Innocenti & Landolfi (2004), hereafter LL04.
2.1. Resonance polarisation
We now present the most important equations describing the phenomenon of resonance polarisation. We state the approximations used and end up finding the Stokes parameters I, Q, and U of the radiation emitted in the scattering processes as a function of the incident radiation field2.
The hydrogen atoms are described in terms of the multipole moments of the density matrix in the spherical statistical tensor representation, and are modelled as having only three levels, two upper levels with Ju = 3/2 and Ju = 1/2, respectively, and a lower one with Jℓ = 1/2, where J is the total angular momentum. This model is well suited to describing Lα, whereas for Lβ and Lγ it represents a first-order approximation that could be improved by considering more sophisticated models involving further atomic levels and the effect of the pumping photospheric radiation in H-α (for the Lβ case) and in H-α, H-β, and Paschen-α (for the Lγ case). Given the exploratory nature of our investigation, we have, at this stage, chosen not to consider these sophistications in our model calculations. Owing to the large difference in energy between the two upper levels relative to their natural width, we neglect quantum interferences between them and assume that they are independent. One is left with a couple of equivalent two-level atoms whose upper level has either Ju = 3/2 or Ju = 1/2. According to Bommier & Sahal-Bréchot (1982), the hyperfine structure can also be safely neglected, and, with this approximation, only the upper level for which Ju = 3/2 can harbour atomic polarisation. We assuming the lower level to be unpolarised, ignore for the moment the effects of collisions (elastic, inelastic, and super-elastic) on the upper levels, and neglect stimulation effects due to the dilution of the solar radiation in the FUV. After solving the statistical equilibrium equations, the multipole moments of the upper level are given by3![\begin{eqnarray} \rho^K_{Q}\left(\alpha_{\rm u} J_{\rm u}\right) &=& \sqrt{\frac{2J_{\ell}+1}{2J_{\rm u}+1}}\, \frac{B\left(\alpha_{\ell} J_{\ell} \rightarrow \alpha_{\rm u} J_{\rm u}\right)} {A\left(\alpha_{\rm u} J_{\rm u} \rightarrow \alpha_{\ell} J_{\ell}\right)} \, w^{(K)}_{J_{\rm u} J_{\ell}}\nonumber \\[2.5mm] \label{eq1} &&\times (-1)^Q \, J^K_{-Q}\left(\nu_0\right) \, \rho^0_{0}\left(\alpha_{\ell} J_{\ell}\right), \end{eqnarray}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq16.png) (1)where A(αℓJℓ → αuJu) and B(αuJu → αℓJℓ) are the Einstein coefficients for spontaneous emission and absorption, respectively. The symbols
(1)where A(αℓJℓ → αuJu) and B(αuJu → αℓJℓ) are the Einstein coefficients for spontaneous emission and absorption, respectively. The symbols 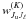 , introduced by Landi Degl’Innocenti (1984), are a sort of “efficiency factor” characterising the transfer of the K-th order multipole moment from the radiation field to the atomic density matrix in the absorption process from the lower to the upper level, while
, introduced by Landi Degl’Innocenti (1984), are a sort of “efficiency factor” characterising the transfer of the K-th order multipole moment from the radiation field to the atomic density matrix in the absorption process from the lower to the upper level, while 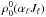 is the multipole moment of the unpolarised lower level proportional to the number density of hydrogen atoms, and α is a set of quantum numbers related to the spectroscopic properties of the energy level. The frequency ν0 corresponds to the transition between the upper and lower level.
is the multipole moment of the unpolarised lower level proportional to the number density of hydrogen atoms, and α is a set of quantum numbers related to the spectroscopic properties of the energy level. The frequency ν0 corresponds to the transition between the upper and lower level.
The tensor 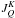 that appears in Eq. (1) describes the incoming radiation field. It is usually called the radiation field tensor and is given by
that appears in Eq. (1) describes the incoming radiation field. It is usually called the radiation field tensor and is given by ![\begin{eqnarray} J^K_{Q}\left(\nu_0\right) &=& \int^{\infty}_{-\infty} f(\vec{v}-\vec{w}) \, {\rm d}^3 \vec{v}\nonumber \\[1.5mm] \label{jkq} &&\times \oint\frac{{\rm d} \Omega^\prime}{4\pi}\, \mathcal{T}^K_{Q}\left(0,\vec{\Omega^\prime}\right) \, I \left( \nu_0 \left( 1+\frac{\vec{v} \cdot \vec{\Omega^\prime}}{c} \right), \vec{\Omega^\prime} \right) . \end{eqnarray}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq24.png) (2)We assume the radiation field to be unpolarised and independent of the heliocentric angle. The absence of limb-darkening or limb-brightening in the pumping chromospheric radiation is indeed consistent with observations to a good degree of approximation. Furthermore, in Eq. (2), we have to perform an integration over the velocity distribution function of the hydrogen atoms, f(v − w), which we assume to be Maxwellian. The velocity, v, is the vector sum of the thermal velocity, and of the solar wind velocity, w, and in the expression for the intensity we have taken into account the Doppler effect to first order in v/c.
(2)We assume the radiation field to be unpolarised and independent of the heliocentric angle. The absence of limb-darkening or limb-brightening in the pumping chromospheric radiation is indeed consistent with observations to a good degree of approximation. Furthermore, in Eq. (2), we have to perform an integration over the velocity distribution function of the hydrogen atoms, f(v − w), which we assume to be Maxwellian. The velocity, v, is the vector sum of the thermal velocity, and of the solar wind velocity, w, and in the expression for the intensity we have taken into account the Doppler effect to first order in v/c.
Finally, the quantities 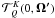 are spherical tensors pertaining to the geometry of the scattering event.
are spherical tensors pertaining to the geometry of the scattering event.
These two expressions, Eqs. (1) and (2) for the upper-level statistical tensors and the radiation field tensor, can now be used to find the frequency-integrated emission coefficients (Stokes parameters) given by (cf. Eq. (10.15) of LL04) 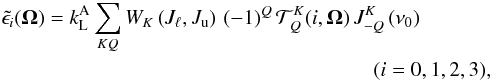 where
where 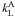 is the frequency-integrated absorption coefficient of the line, given by
is the frequency-integrated absorption coefficient of the line, given by 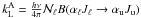 , hν is the energy of the scattered photons, and
, hν is the energy of the scattered photons, and 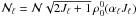 is the number of hydrogen atoms per unit volume in the lower level,
is the number of hydrogen atoms per unit volume in the lower level, 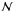 being the overall number density of atoms. Finally,
being the overall number density of atoms. Finally, 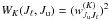 .
.
Given that the corona is an optically thin plasma in the FUV, to obtain the emergent signals, we simply have to perform an integration along the LOS of the emission coefficient, and get for any one of the Stokes parameters 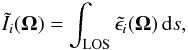 (5)where s is the coordinate along the LOS.
(5)where s is the coordinate along the LOS.
2.2. The Hanle effect in resonance polarisation
The Hanle effect is the modification of the polarisation parameters of a spectral line in the presence of a magnetic field. Its consequences, relative to the non-magnetic case, are a modification (usually a decrease) of the linear polarisation degree and a simultaneous rotation of the plane of polarisation that depends on both the strength and direction of the field in a non-linear manner. The usual way to depict the Hanle effect is in a so-called Hanle diagram, which for various values of the field strength and orientation (horizontal field) shows the depolarisation along the y-axis and the rotation of the plane of polarisation along the x-axis, as shown, for instance, in Fig. 5 of Bommier & Sahal-Bréchot (1982).
If one relaxes the condition of considering only horizontal fields, and allows the polar angle to vary, one can also achieve a hyper polarisation as shown in Figs. 6b − d of Fineschi et al. (1993).
With the same assumptions as in the previous section, the solution of the statistical equilibrium equations in the presence of a magnetic field is ![\begin{eqnarray} \rho^K_{Q}\left(\alpha_{\rm u} J_{\rm u}\right) &=& \sqrt{\frac{2J_{\ell}+1}{2J_{\rm u}+1}} \frac{B\left(\alpha_{\ell} J_{\ell} \rightarrow \alpha_{\rm u} J_{\rm u}\right)} {A\left(\alpha_{\rm u} J_{\rm u} \rightarrow \alpha_{\ell} J_{\ell}\right)+ 2\pi {\rm i} \nu_{\rm L} g_{\alpha_{\rm u} J_{\rm u}} Q}\nonumber \\[2.5mm] \label{rb} &&\times w^{(K)}_{J_{\rm u} J_{\ell}} \, (-1)^Q \, J^K_{-Q}\left(\nu_0\right) \, \rho^0_{0}\left(\alpha_{\ell} J_{\ell}\right), \end{eqnarray}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq42.png) (6)where all the tensors are now defined in the reference system in which the z-axis is directed along the magnetic field, gαuJu is the Landé factor of the upper level, and νL is its Larmor frequency, which is proportional to the magnetic field intensity.
(6)where all the tensors are now defined in the reference system in which the z-axis is directed along the magnetic field, gαuJu is the Landé factor of the upper level, and νL is its Larmor frequency, which is proportional to the magnetic field intensity.
Defining the dimensionless parameter Hu as 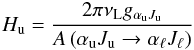 (7)allows us to recast Eq. (6) as
(7)allows us to recast Eq. (6) as ![\begin{equation} \rho^K_{Q}\left(\alpha_{\rm u} J_{\rm u}\right) = \frac{1}{1+{\rm i}Q H_{\rm u}} \left[ \rho^K_{Q} \right]_{B=0}, \end{equation}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq48.png) (8)where
(8)where ![\hbox{$[\rho^K_{Q}]_{B=0}$}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq49.png) are the multipole moments in the non-magnetic case. This expression embodies the Hanle effect both qualitatively and quantitatively, i.e. coherences with Q = 0 (populations of the Zeeman sub-levels) are unaffected by the magnetic field, while the absolute values of these with Q ≠ 0 are reduced by a factor
are the multipole moments in the non-magnetic case. This expression embodies the Hanle effect both qualitatively and quantitatively, i.e. coherences with Q = 0 (populations of the Zeeman sub-levels) are unaffected by the magnetic field, while the absolute values of these with Q ≠ 0 are reduced by a factor 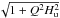 , with respect to the non-magnetic case.
, with respect to the non-magnetic case.
The frequency-integrated emission coefficients are easily found to be 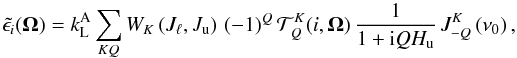 (9)and, as in the previous case, we obtain the emergent Stokes parameters by integrating the emissivity along the LOS.
(9)and, as in the previous case, we obtain the emergent Stokes parameters by integrating the emissivity along the LOS.
2.3. Resonance polarisation in the presence of non-radial outflow velocities
We now turn our attention to the second of the three phenomena capable of modifying the polarisation parameters of a spectral line, i.e. a non-radial solar wind.
This problem was tackled for the first time by Sahal-Bréchot et al. (1998) for the 1032 Å O VI line. In their paper, as in ours, the thermal velocity distribution was assumed to be isotropic. The SUMER (Solar UV Measurement of Emitted Radiation) instrument on SOHO (Solar and Heliospheric Observatory), which provided the first, and to date only, detection of UV resonance-line polarisation in the solar corona, found that H0 and O5 + ions have anisotropic distributions of their unresolved velocities (see Kohl et al. 1998). This prompted Fineschi (2001) to study resonance polarisation in the presence of “anisotropic Doppler-width dimming” and demonstrate that this effect amplifies considerably the variation in the polarimetric outcome (see also Raouafi & Solanki 2003 for a discussion of the same effect). In the present paper, however, we do not take into account the effects of anisotropic Doppler velocities.
To understand the effects of a non-radial solar velocity on the polarisation characteristics of the emitted light in a scattering process, we must examine in detail the expression for the radiation field tensor, Eq. (2). The first argument of the unpolarised intensity contains the Doppler-effect, v·Ω′, where v is the atom velocity and Ω′ is the propagation direction of the chromospheric radiation. Because of the nature of the profile, for non-radial velocities of the solar wind, the atoms will experience different intensities coming from different directions, a phenomenon known as Doppler-dimming or Doppler-brightening. For a purely radial velocity, because of the cylindrical symmetry of the radiation field, the only non-zero components of the radiation field tensor in a reference system in which the z-axis is directed along the vertical are 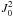 and
and 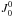 , thus causing the linear polarisation to be parallel to the solar limb. This property obviously holds in the absence of magnetic fields and/or active regions, whose polarisation signatures will be discussed in the following section. The scalar product v·Ω′ can in general be written as
, thus causing the linear polarisation to be parallel to the solar limb. This property obviously holds in the absence of magnetic fields and/or active regions, whose polarisation signatures will be discussed in the following section. The scalar product v·Ω′ can in general be written as 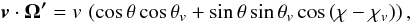 (10)where θ and χ are the angles of the propagation direction Ω′ of the radiation impinging on the atom of velocity v with direction θv and χv (see Fig. 12.10 in LL04).
(10)where θ and χ are the angles of the propagation direction Ω′ of the radiation impinging on the atom of velocity v with direction θv and χv (see Fig. 12.10 in LL04).
When this expression is inserted into Eq. (2), one sees that additional components of the radiation field tensor, besides 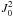 and
and 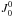 , differ from zero. These components can now be inserted into Eqs. (1) and (4) in order to find the frequency-integrated Stokes parameters in the non-magnetic case, or into Eqs. (6) and (9) in the presence of a magnetic field. The effect is very similar to that of a magnetic field, i.e. non-radial outflows can depolarise or hyperpolarise and rotate the plane of polarisation and one must be very careful when interpreting observations in order to differentiate the effects of velocities from those of the Hanle effect.
, differ from zero. These components can now be inserted into Eqs. (1) and (4) in order to find the frequency-integrated Stokes parameters in the non-magnetic case, or into Eqs. (6) and (9) in the presence of a magnetic field. The effect is very similar to that of a magnetic field, i.e. non-radial outflows can depolarise or hyperpolarise and rotate the plane of polarisation and one must be very careful when interpreting observations in order to differentiate the effects of velocities from those of the Hanle effect.
2.4. The polarimetric signature of active regions
The third possible way in which the polarisation parameters of a spectral line can be modified, is by the presence of active regions on the solar surface. As mentioned in the previous section, at a given point P of the solar corona, owing to the cylindrical symmetry of the chromospheric radiation, the only non-zero components of the radiation field tensor, defined in a reference system whose z-axis is directed along the vertical, are 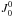 and
and 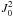 .
.
In addition to a non-radial solar wind, a number of phenomena can, however, break this symmetry, an example of which is the presence of active regions characterised by an intensity contrast with respect to the quiet chromosphere. Other examples are granulation, faculae, or, in general, any of the typical structures of solar activity capable of rendering the radiation field tensor less homogeneous, but since their typical dimensions and lifetimes are small compared to active regions they are neglected in the following.
An active region whose “centre” has coordinates δ and φ in the above-mentioned coordinate system (see Fig. 12.8 in LL04) is seen under the small solid angle ΔΩ from a point P of the corona. If we denote by ΔIν the intensity variation in the active region with respect to its surroundings, then the radiation field tensor components at P are, to a first order approximation, given by ![\begin{eqnarray} J^0_{0}(\nu) & = & \left[ J^0_{0}(\nu) \right]_{\rm cyl.s} + \frac{\Delta \Omega}{4 \pi} \, \Delta I_\nu, \\[1.5mm] J^2_{0}(\nu) & = & \left[ J^2_{0}(\nu) \right]_{\rm cyl.s} + \frac{1}{2 \sqrt{2}} \, \left(3\cos^2 \theta_0 -1\right) \, \frac{\Delta \Omega}{4 \pi} \, \Delta I_\nu, \\[1.5mm] J^2_{\pm1}(\nu) & = & \mp \frac{\sqrt{3}}{2} \sin \theta_0 \cos\theta_0\, {\rm e}^{\pm {\rm i} \chi_0} \, \frac{\Delta \Omega}{4 \pi} \, \Delta I_\nu, \\[1.5mm] J^2_{\pm2}(\nu) & = & \frac{\sqrt{3}}{4} \sin^2 \theta_0 \, {\rm e}^{\pm 2 {\rm i} \chi_0} \, \frac{\Delta \Omega}{4 \pi} \, \Delta I_\nu, \end{eqnarray}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq69.png) where the quantities
where the quantities ![\hbox{$[J^K_{Q}(\nu)]_{\rm cyl.s}$}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq70.png) are the components of the radiation field tensor in the cylindrically symmetric case, and the angles θ0 and χ0 are related to the sunspot coordinates by χ0 = φ − π, and
are the components of the radiation field tensor in the cylindrically symmetric case, and the angles θ0 and χ0 are related to the sunspot coordinates by χ0 = φ − π, and ![\hbox{$\theta_0 = {\rm arctan} \big[ \frac{\sin \delta}{1-\cos \delta +h/R_*} \big]$}](/articles/aa/full_html/2011/05/aa15551-10/aa15551-10-eq74.png) , h being the height of P above the solar surface and R∗ the solar radius.
, h being the height of P above the solar surface and R∗ the solar radius.
These are the expressions for the radiation field tensor that can now be inserted into either Eqs. (1) and (4) in order to find the frequency-integrated Stokes parameters in the non-magnetic case, or, into Eqs. (6) and (9) in the presence of a magnetic field.
As for non-radial outflow velocities, but in this case owing to a difference in intensity caused by active regions, the consequences are a modification of the Stokes parameters leading to either a depolarisation or hyperpolarisation and a simultaneous rotation of the plane of polarisation.
3. Results
We chose to visualise our simulation results using three different kinds of graphs. The blue graphs represent the logarithm of the number of photons per unit area, per unit time, and per steradians. The inclination and length of the little black segments on top represent the angle and degree of the fractional linear polarisation. The number of photons is obviously given by the intensity of the scattered radiation divided by the energy per photon. The fractional linear polarisation is obtained via 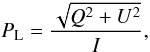 (15)and the polarisation angle, α, is obtained from
(15)and the polarisation angle, α, is obtained from 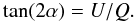 (16)The red graphs represent the difference in angle of the linear polarisation direction with respect to the solar limb, caused by magnetic fields, active regions, solar wind, or any combination of them. The angle is expressed in degrees and measured counterclockwise. Finally, the green graphs represent the fractional change in percent of the linear polarisation, defined by (P0 − PL)/P0, where P0 is the degree of linear polarisation in the absence of symmetry-breaking effects.
(16)The red graphs represent the difference in angle of the linear polarisation direction with respect to the solar limb, caused by magnetic fields, active regions, solar wind, or any combination of them. The angle is expressed in degrees and measured counterclockwise. Finally, the green graphs represent the fractional change in percent of the linear polarisation, defined by (P0 − PL)/P0, where P0 is the degree of linear polarisation in the absence of symmetry-breaking effects.
The substrate for our polarimetric forward modelling is a series of 2.5-D MHD self-consistent coronal models by Wang et al. (1993), in particular their steady-state solutions that evolve from an initial dipole magnetic field configuration. The magnetic and velocity field configurations are shown in Figs. 2a and 6a of their paper. The profiles and intensities of the chromospheric Lα and Lβ lines are taken from Lemaire et al. (2005), while the Lγ line profile is assumed to be equal to that of the Lβ line with the difference in peak intensity taken from Raymond et al. (1997). These lines are all formed by doublets at almost the same wavelength, and each doublet has the same lifetime, but, as already mentioned, only the Ju = 3/2 → Jℓ = 1/2 transition can be linearly polarised in resonance scattering.
The hydrogen Lα is one of the brightest lines of the solar corona. According to Gabriel et al. (1971), the dominant excitation mechanism is almost exclusively caused by the resonant photo-excitation of coronal neutral hydrogen by the chromospherically produced Lα photons. For the Lβ line, there is a slightly dominant contribution from collisional excitations relative to photo-excitations, which in contrast for the Lγ line by far dominates (see Table 4 of Raymond et al. 1997). Only in the case of photo-excitation can the scattered radiation become linearly polarised. Atoms that are collisionally excited (mostly by electrons) are not able to emit polarised light since the collisions are believed to be isotropic. This results in a decrease in the degree of linear polarisation, leaving, however, the direction of the plane of polarisation and the relative depolarisation unaffected. The advantage of the Lα line is on the one hand its brightness, and on the other hand its ratio of photo-excitation to collisional excitation. The Lβ and Lγ lines are much fainter and the contribution coming from the collisional excitation is unfortunately not negligible thus producing much less linearly polarised light than the Lα line. To account for the effect of collisions, we added an extra contribution of unpolarised radiation equal to x times the scattered radiation itself, with x being equal to two for Lβ and ten for Lγ.
We start by looking at the simulation results for the Lα line. Figure 1 is just a simple “warm-up” graph depicting the static solar corona (no solar wind) in the absence of active regions and a magnetic field4. We note how the degree of polarisation is an increasing function of the height above the solar surface, reaching a maximum value of 21.3% for the distances considered in the plot, and how the linear polarisation is parallel everywhere to the solar limb.
 |
Fig. 1 Resonance polarisation of the Lα line in the static, non-magnetic solar corona. |
In Fig. 2, we display the red graph obtained from a simulation relative to a model evolved from an initial magnetic dipole-field, with a maximum value of roughly 4 G just above the solar poles (for the exact values see Fig. 7a of Wang et al. 1993), but no active regions or solar wind. The combination of this rather weak value of the magnetic field with the sensitivity of the Lα line to the Hanle effect results in very small changes in angle, i.e. ± 0.11 degrees. The relative depolarisation ranges from zero to 2.23%. We note how the effect is predominant at both the Sun’s poles and relatively low altitudes, right from the surface up to roughly 0.2 solar radii.
 |
Fig. 2 The Hanle effect in the Lα line. |
In Fig. 3, we “turned off” the magnetic field and show the simulation results of the effect of the non-radial solar wind. We find a rotation of the plane of polarisation that is quantitatively almost identical to that of the magnetic field. The rotation is already present at very low heights above the solar surface and lasts all the way out to distances of about one solar radius. The relative depolarisation ranges from − 3.48 to 0.25% and shows that the effect of a non-radial solar wind is mostly a polarising one, i.e. it creates polarisation.
 |
Fig. 3 Resonance polarisation in the presence of a non-radial solar wind in the Lα line. |
In Fig. 4, we “turned off” both the magnetic field and solar wind and show the effect of active regions on the solar surface by placing eight active regions symmetrically on both hemispheres at latitudes of ± π/4 and longitudes (measured from the plane of the sky) of 0, π/2, π, and 3π/2, respectively, reflecting more or less the starting configuration of activity at the beginning of the solar cycle.
 |
Fig. 4 Resonance polarisation in the presence of active regions in the Lα line. |
The values for the intensity contrast were taken from Raymond et al. (1997), and the active regions are all assumed to have the same diameter of 30 000 km. We find rotations that locally attain values of the same order of magnitude as those found for magnetic fields and the solar wind, i.e. ± 0.44 degrees. As in the case of the solar wind, the effect of the active regions is to polarise, rather than depolarise, with values of the depolarisation parameter that range from −7.8 to 0.7%. As expected, only the effect of the regions of longitude 0 and π are seen in the graph.
As can be seen from the previous four graphs, and also expected theoretically, not only do magnetic fields, active regions, and non-radial outflow velocities have almost the same polarisation signature, but, for the values used in our simulations, the quantitative outcome is painstakingly similar, alerting us to be very cautious when attributing a polarisation signal to any of the aforementioned “polarimetrically active” agents, whose combined effect is shown in Fig. 5.
 |
Fig. 5 The Hanle effect combined with a non-radial solar wind and active regions in the Lα line. |
This panorama completely changes when one looks at the same simulation results (including magnetic field, non-radial outflow velocities, and active regions) using the Lβ and Lγ lines, which are shown in Figs. 6 and 7, respectively.
 |
Fig. 6 The Hanle effect combined with a non-radial solar wind and active regions in the Lβ line. |
 |
Fig. 7 The Hanle effect combined with a non-radial solar wind and active regions in the Lγ line. |
 |
Fig. 8 Relative depolarisation of the Hanle effect combined with a non-radial solar wind and active regions in the Lγ line. |
For Lβ, we get a rotation of ± 1.32 and a relative depolarisation ranging from −3.7 to 22.3%, and for Lγ the same values are ± 4.58 and from −3.6 to 57.6%. As an example of a green graph, we show the relative depolarisation of the Lγ line in Fig. 8.
This abrupt change in the polarimetric parameters for these lines is due to their differential sensitivity to the magnetic field. The critical value of the magnetic field at which the Hanle effect appears is found by setting the previously defined parameter Hu ~ 1. This leads to a sensitivity of the Lα line to the magnetic field for values that range from roughly 10 G to 70 G, for Lβ to values that range from 2 G to 15 G, and finally for Lγ to values from 1 G to 7 G, leading us to conclude that these last two lines are the most suitable for magnetic field diagnostics in the solar corona, at least for observations around the solar minimum.
As previously mentioned, the drawbacks of the Lβ and Lγ lines are their faintness and that they have a smaller amount of linear polarisation caused by the predominant collisional excitation mechanism, and it remains to be seen whether these lines can be set to work for magnetic field diagnostics in the solar corona. If, for technical reasons, it were not possible to use the Lβ and Lγ lines, and one only had information from the Lα line, everything would however not be lost. The problem of the contribution from the active regions could be solved by simultaneously tracking their presence and position, and, armed with the knowledge of their effect on the polarisation signals, one could subtract their contribution from the observations. Given that only the largest active regions have a detectable influence and that their longevity outlasts the solar rotation, even those present on the Sun’s backside should not cause major problems.
As to the solar wind, one could use different methods to assess its value (see e.g. Cranmer et al. 1999) and thereby likewise subtract its contribution.
The philosophy of forward modelling is to use an analytical description of all the complex physics involved in the scattering process in the presence of magnetic fields, and by making fine tunings in parameter space, find the simulation results that most closely reproduce the observations. It is clear that one could in principle encounter many situations in which the magnetic field vectors might vary along the LOS, cancelling the Hanle effect locally, and thus rendering the interpretation of the polarisation signal in terms of the magnetic field extremely ambiguous, if not outright spurious. The same obviously holds true for non-radial outflow velocities and active regions. The interpretation of LOS integrated data is inherently a risky business and extreme care is warranted when one attempts to use it for deducing physical observables.
For now, we limit ourselves here to presenting the expected spectropolarimetric outcome based on our models, but in a follow-up paper we plan to use a multi-line approach in a different sense from what we have done here, i.e. separating the effects of the magnetic field from those caused by non-radial outflow velocities and active regions by shifting from the Lα line to the Lβ and, preferably, Lγ lines, to address the problem of what kind of information on the topology and intensity of the magnetic field can actually be extracted from LOS integrations in forward modelling.
We close this section by briefly commenting on the results obtained from the simulation with the solar wind shown in Fig. 3, and those pertaining to the effects of active regions shown in Fig. 4. Until now, the effects of the solar wind have been considered negligible compared to the Hanle effect due to the magnetic field of an active region, both from a theoretical (e.g. Beckers & Chipman 1974; Fineschi et al. 1993), and an observational point of view (e.g. Withbroe et al. 1982). Our simulations, which have much lower values of the magnetic field corresponding to solar minimum conditions, demonstrate that one cannot neglect the effects of the solar wind when considering the Lα line, but that they are negligible when one considers the Lβ and Lγ lines, again due to their augmented sensitivity to the magnetic field. Another interesting thing to note in Fig. 3 is how the polarisation signal can be used as a diagnostic tool for elucidating the direction of the magnetic field in the interface region between the open field lines of the coronal holes and the closed ones of the streamers.
Our results for active regions on the solar surface are in line with those of Sahal-Bréchot et al. (1986) where the authors investigate the effects of active regions on magnetic field diagnostics in the solar corona using the 1032 Å O VI line and show that for the most realistic values of the involved parameters one would overestimate or underestimate the actual field value by 30 − 40% if one did not take into account the presence of active regions. They, as we, conclude that the polarisation parameters measured by an UV-corona graph/polarimeter should be associated with spectroheliograms to elucidate the true values of the radiation field tensor and thereby render the magnetic field diagnostics more realistic.
4. Instrumental requirements
We briefly digress and address the issue of instrumental requirements in terms of a hypothetical instrument’s parameters to be able to detect the differences in the Stokes parameters that our simulation results suggest.
We note that an instrument capable of performing polarimetry in the FUV, thus making the observations needed to confirm our results has never previously existed. After performing the simulations and arriving at certain values of the Stokes parameters I, Q and U, we ask ourselves how many photons a measuring device would have to pick up for the data analysts to have an unequivocal confirmation of a magnetic field, or more generally, active regions on the solar surface and/or non-radial outflow velocities. The number of counts, Ni, that a given measuring device detects in any one of the components of the Stokes vector is a function of the five parameters given by 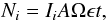 (17)where Ii is any Stokes vector component, in units of photons per unit area per unit time and per steradians, A is the instrument’s collection area, Ω is the spatial sampling in steradians, ϵ is the instrument’s efficiency, and t is the exposure time. We assume Ii, A, Ω, and ϵ to be fixed, leaving t as the only leftover parameter controlling the value of Ni.
(17)where Ii is any Stokes vector component, in units of photons per unit area per unit time and per steradians, A is the instrument’s collection area, Ω is the spatial sampling in steradians, ϵ is the instrument’s efficiency, and t is the exposure time. We assume Ii, A, Ω, and ϵ to be fixed, leaving t as the only leftover parameter controlling the value of Ni.
To assess how many counts one should have to be sure that the signal in the presence of “rotation-active” agents differs from the “uncontaminated” quiet Sun signal we demand that the distance between two points in the (Q,U)-plane (one being the result of a simulation with a magnetic field and the other without a magnetic field) be greater than 3σ, where 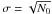 is the standard deviation of the polarimetric error assuming that this is due only to Poisson statistics in the number of counts.
is the standard deviation of the polarimetric error assuming that this is due only to Poisson statistics in the number of counts.
As an example, we consider the specific case of a model evolved from an initial dipole configuration and analyse it for the first three resonance lines of the Lyman-series. The results are shown in Fig. 9, where we plot the logarithm of the observation time as a function of the radial distance for A = 500 cm2, with an angle of 20 arc sec subtended by the resolution element, and an instrument efficiency, ϵ, of 0.01.
 |
Fig. 9 Observation time as a function of radial distance for the Lα (lowest curve), Lβ (centre curve) and Lγ (top curve) lines. |
For the radial direction, we chose the symmetry line that bisects the first quadrant in the plane of the sky, i.e. with polar angle equal to π/4. From Fig. 9, we see that for this set of parameters, at ~1.1 solar radii one would need an exposure time of about ~17 min for the Lα line, ~1.4 h for the Lβ line, and roughly 4.7 h for the Lγ line, which is quite acceptable (i.e. we do not expect the phenomena that we wish to study to have timescales shorter than this). The trend shown in Fig. 9 is quite clear, that is, the further out one goes, the more the observation time increases. This is obviously due to the exponential decline in the density of emitting atoms, thus restricting our possibilities of doing measurements at heights definitively no more than 1.5 solar radii. If it were possible to increase the instrumental efficiency, aperture, and pixel size, maybe one could realistically push the limit all the way out to two solar radii.
Needless to say, the above outlined procedure can easily be generalised to any other of the remaining parameters while fixing the observation time beforehand. In the preceding section, we showed that the expected rotation angle, α, for the Lα case amounts to some tenths of a degree, thus setting a very stringent limit on the necessary sensitivity of the instrument. We also showed that the Lβ and Lγ lines are more sensitive to the magnetic field, causing more substantial rotations of the plane of polarisation, and we advocate the use of these lines if the rotation angles for the Lα line turn out to be unmeasurable. The following analysis shows, however, that the Lα could be the most suitable line.
The instrumental polarimetric sensitivity, ΔP, needed to measure the rotation of the plane of polarisation, P, with an error, Δδ, is given by5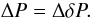 (18)In the Lα case, the line is bright (P ∝ brightness of the line), but the rotation is small (Δδ ∝ the rotation angle, α), whereas in the Lβ and Lγ cases the lines are faint and the rotation is bigger. This means that our previous comment about the Lα line placing heavy demands on the instruments sensitivity is also valid for the Lβ and Lγ lines.
(18)In the Lα case, the line is bright (P ∝ brightness of the line), but the rotation is small (Δδ ∝ the rotation angle, α), whereas in the Lβ and Lγ cases the lines are faint and the rotation is bigger. This means that our previous comment about the Lα line placing heavy demands on the instruments sensitivity is also valid for the Lβ and Lγ lines.
We now attempt to estimate the value of ΔδLα. It can be shown that the accuracy of the measurement of the rotation angle for a given line intensity is inversely proportional to the number of counts that the measuring device detects 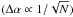 . This means that
. This means that 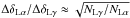 , which gives
, which gives 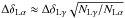 . In the solar corona, the typical value of
. In the solar corona, the typical value of 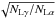 is roughly 0.01. If we set ΔδLγ to be equal to one third of its maximum rotation found in our simulations, then ΔδLα ≈ 0.02 degrees, which is about five times smaller than the actual value for the maximum rotation. An instrument with this accuracy might actually measure rotation angles as small as one tenth of a degree, the typical values we found in our simulations.
is roughly 0.01. If we set ΔδLγ to be equal to one third of its maximum rotation found in our simulations, then ΔδLα ≈ 0.02 degrees, which is about five times smaller than the actual value for the maximum rotation. An instrument with this accuracy might actually measure rotation angles as small as one tenth of a degree, the typical values we found in our simulations.
This is quite a remarkable result for this rather simple analysis based purely on Poisson statistics. The overpowering brightness of the Lα line compensates for the small rotation angle and makes a more suitable diagnostic of the physical parameters of the solar corona6.
These are very interesting findings for future solar FUV polarimetry space missions, because it means that instruments with the parameters used in this section would have the necessary sensitivity for at least the first three lines of the Lyman-series. A coronagraph with the same parameters as the ones we have used here was suggested in 2007 as part of a mission (Compass) proposed to the ESA cosmic vision program. An improved version of a similar coronagraph has recently been suggested as part of a future ESA mission (SolmeX).
5. Conclusions
We have presented our forward modelling results of the effects of magnetic fields (Hanle effect), non-radial outflow velocities (solar wind), and the presence of active regions on the first three Stokes parameters of the radiation scattered by the solar corona in the first three lines of the Lyman-series using a self-consistent 2.5-D global MHD model of the corona with realistic low field values of a few Gauss. We have shown that all three of these “polarimetrically active” agents have the same effect, i.e. they rotate the plane of linear polarisation and cause a depolarisation (in a few cases hyperpolarisation) of the scattered light, and that their effects, even after a line-of-sight integration, are still detectable. The use of a global MHD model has for the first time (previously these effects had only been studied separately, or pairwise) enabled us to compare the relative contributions of the three effects that in the Lα case indicate that besides being qualitatively are also quantitatively almost identical, producing rotations of a few tenths of a degree.
We have also discussed how to circumvent the possible confusion caused by the simultaneous presence of all three agents and show how, because of the augmented sensitivity to the magnetic field, the Lβ and especially the Lγ lines produce rotation angles that in principle should be measurable.
Finally, we have briefly turned our focus to the instrumental side of the problem by showing how the observation time of a hypothetical instrument varies as a function of height above the solar surface. At the most suitable distances for observations, ~1.1 solar radii, and a realistic set of instrument parameters, we have presented substantial arguments in favour of being able to measure rotation angles with an error of 0.02 degrees, making the tiny rotations in the Lα case possibly measurable.
In conclusion, forward modelling can be a very valuable tool for elucidating the physics of the solar corona as demonstrated convincingly by Cranmer et al. (1999), who succeeded in deriving outflow velocities in polar coronal holes by combining forward modelling with UVCS/SOHO data. In this paper, we
have shown how a similar derivation can be accomplished for the magnetic field vector.
In spite of all the proposals that have been advanced by various groups to the different space agencies to make coronal polarimetric observations in the FUV possible, (see, e.g., the response by Trujillo Bueno et al. 2005, to ESA’s call for ideas in the framework of the “Cosmic Vision 2020” program; Fineschi 2001), the only mission has been the SUMER instrument on SOHO.
We hope that the results presented in this paper and the references cited herein will stimulate the space agencies to commission the building of instruments capable of doing the necessary measurements, in order to be able to assess the full potential of this promising approach that has been the main subject of the present paper.
See Sect. 3.2 in Fineschi et al. (1993) for a discussion of the formulae used in the following.
Acknowledgments
The authors wish to thank G. Poletto, G. Noci, K. Biazzo and T. S. Wu for helpful discussions.
References
- Beckers, J. M., & Chipman, E. 1974, Sol. Phys., 34, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Bommier, V. 1977, Thèse de 3ème cycle, Paris VI University [Google Scholar]
- Bommier, V. 1980, A&A, 87, 109 [NASA ADS] [Google Scholar]
- Bommier, V., & Sahal-Bréchot, S. 1978, A&A, 69, 57 [NASA ADS] [Google Scholar]
- Bommier, V., Leroy, J. L., & Sahal-Bréchot, S. 1981, A&A, 100, 231 [NASA ADS] [Google Scholar]
- Bommier, V., & Sahal-Bréchot, S. 1982, Sol. Phys., 78, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., Kohl, J. L., Noci, G., et al. 1999, ApJ, 511, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Derouich, M., Auchère, F., Vial, J. C., & Zhang, M. 2010, A&A, 511, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fineschi, S. 2001, ASP Conf. Ser., 248, 597 [NASA ADS] [Google Scholar]
- Fineschi, S., et al. 2007, COMPASS, submitted to the ESA Cosmic Vision, call for Proposals [Google Scholar]
- Fineschi, S., Hoover, R. B., Fontenla, J. M., & Walker, A. B. C. 1991, Opt. Eng. 30, 1161 [Google Scholar]
- Fineschi, S., Hoover, R. B., & Walker, A. B. C. 1992, SPIE, 1546, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Fineschi, S., Hoover, R. B., Zukic, M., et al. 1993, SPIE, 1742, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Fineschi, S., van Ballegoijen, A., & Kohl, J. L. 1999, ESASP, 446, 317 [Google Scholar]
- Gabriel, A. H., Garton, W. R. S., Goldberg, L., et al. 1971, ApJ, 169, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Hanle, W. 1924, Z. Phys., 30, 93 [Google Scholar]
- House, L. L. 1971, in Solar Magnetic Fields, ed. R. Howard, IAU Symp., 43, 130 [Google Scholar]
- House, L. L., & Smartt, R. N. 1979, in Physics of Solar Prominences, ed. E. Jensen, P. Maltby, & F. Q. Orrall, IAU Colloq., 44, 81 [Google Scholar]
- Hyder, C. L. 1965, ApJ, 141, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., Noci, G., Antonucci, E., et al. 1998, ApJ, 501, 127 [Google Scholar]
- Landi Degl’Innocenti, E. 1982, Sol. Phys., 79, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E. 1984, Sol. Phys., 91, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) (LL04) [Google Scholar]
- Lemaire, P., Emerich, C., Vial, J. C., et al. 2005, Adv. Space Res., 35, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, J. L., Ratier, G., & Bommier, V. 1977, A&A, 54, 811 [NASA ADS] [Google Scholar]
- Lin, H., Kuhn, J. R., & Coulter, R. 2004, ApJ, 613, L177 [NASA ADS] [CrossRef] [Google Scholar]
- Öhman, Y. 1929, Mon. Not. Roy. Astron. Soc., 89, 479 [Google Scholar]
- Raouafi, N. E. & Solanki, S. K. 2003, A&A, 412, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raouafi, N. E., Solanki, S. K., & Wiegelmann, T. 2009, in Solar Polarization 5, ed. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli, ASP Conf. Ser., 405, 429 [Google Scholar]
- Raymond, J. C., Kohl, J. L., Noci, G., et al. 1997, Sol. Phys., 175, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Sahal-Bréchot, S., Bommier, V., & Leroy, J. L. 1977, A&A, 59, 223 [NASA ADS] [Google Scholar]
- Sahal-Bréchot, S., Malinovski, M., & Bommier, V. 1986, A&A, 168, 284 [NASA ADS] [Google Scholar]
- Sahal-Bréchot, S., Bommier, V., & Feautrier, N. 1998, A&A, 340, 579 [NASA ADS] [Google Scholar]
- Trujillo Bueno, J., Landi Degl’Innocenti, E., Casini, R., & Martinez Pillet, V. 2005, in 39th Eslab Symposium on Trends in Space Science and Cosmic Vision 2020, ed. F. Favata, J. Sanz-Forcada, A. Giménez, & B. Battrick, ESA SP, 588, 203 [Google Scholar]
- Wang, A. H., Wu, T. S., Suess, S. T., & Poletto, G. 1993, Sol. Phys., 147, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Withbroe, G. L., Kohl, J. L., Weiser, H., Noci, G., & Munro, R. H. 1982, ApJ, 254, 361 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Resonance polarisation of the Lα line in the static, non-magnetic solar corona. |
| In the text | |
 |
Fig. 2 The Hanle effect in the Lα line. |
| In the text | |
 |
Fig. 3 Resonance polarisation in the presence of a non-radial solar wind in the Lα line. |
| In the text | |
 |
Fig. 4 Resonance polarisation in the presence of active regions in the Lα line. |
| In the text | |
 |
Fig. 5 The Hanle effect combined with a non-radial solar wind and active regions in the Lα line. |
| In the text | |
 |
Fig. 6 The Hanle effect combined with a non-radial solar wind and active regions in the Lβ line. |
| In the text | |
 |
Fig. 7 The Hanle effect combined with a non-radial solar wind and active regions in the Lγ line. |
| In the text | |
 |
Fig. 8 Relative depolarisation of the Hanle effect combined with a non-radial solar wind and active regions in the Lγ line. |
| In the text | |
 |
Fig. 9 Observation time as a function of radial distance for the Lα (lowest curve), Lβ (centre curve) and Lγ (top curve) lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


