| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201116534 | |
| Published online | 15 March 2011 | |
Research Note
Habitability of the Goldilocks planet Gliese 581g: results from geodynamic models
1
Potsdam Institute for Climate Impact Research,
PO Box 60 12 03,
14412
Potsdam,
Germany
e-mail: bloh@pik-potsdam.de
2
Department of Physics, University of Texas at
Arlington, Box
19059, Arlington,
TX
76019,
USA
Received:
18
January
2011
Accepted:
14
February
2011
Aims. In 2010, detailed observations have been published that seem to indicate another super-Earth planet in the system of Gliese 581, which is located in the midst of the stellar climatological habitable zone. The mass of the planet, known as Gl 581g, has been estimated to be between 3.1 and 4.3 M⊕. In this study, we investigate the habitability of Gl 581g based on a previously used concept that explores its long-term possibility of photosynthetic biomass production, which has already been used to gauge the principal possibility of life regarding the super-Earths Gl 581c and Gl 581d.
Methods. A thermal evolution model for super-Earths is used to calculate the sources and sinks of atmospheric carbon dioxide. The habitable zone is determined by the limits of photosynthetic biological productivity on the planetary surface. Models with different ratios of land/ocean coverage are pursued.
Results. The maximum time span for habitable conditions is attained for water worlds at a position of about 0.14 ± 0.015 AU, which deviates by just a few percent (depending on the adopted stellar luminosity) from the actual position of Gl 581g, an estimate that does however not reflect systematic uncertainties inherent in our model. Therefore, in the framework of our model an almost perfect Goldilock position is realized. The existence of habitability is found to critically depend on the relative planetary continental area, lending a considerable advantage to the possibility of life if Gl 581g’s ocean coverage is relatively high.
Conclusions. Our results are another step toward identifying the possibility of life beyond the Solar System, especially concerning super-Earth planets, which appear to be more abundant than previously surmised.
Key words: stars: individual: Gliese 581 / astrobiology
© ESO, 2011
1. Introduction
The nearby M-type dwarf Gliese 581 is an important target of previous and ongoing planetary search efforts, and so far four, but possibly up to six planets around this star have been discovered. It is noteworthy that until recently the possible existence of Earth-type and super-Earth planets in extrasolar systems has been highly speculative (e.g., Butler et al. 2006). Bonfils et al. (2005) reported the detection of a Neptune-size planet around Gl 581 (M3 V). Gl 581 is at a distance of 6.26 pc; it has a mass of about 0.31 M⊙ and a luminosity of 0.013 ± 0.002 L⊙ (see below).
Later on, Udry et al. (2007) announced the detection of two so-called “super-Earth” planets in this system, Gl 581c and Gl 581d, with minimum masses of 5.06 and 8.3 M⊕ and with semi-major axes of 0.073 and 0.25 AU, respectively. In 2009, Gl 581e was discovered, another super-Earth planet (Mayor et al. 2009). Meanwhile the position of Gl 581d has been re-identified as 0.22 AU. Finally, in 2010, Vogt et al. (2010) reported a still controversial discovery. The authors argue in favor of the existence of two additional super-Earth planets, namely Gl 581f and Gl 581g. Note that Gl 581g is of particular interest for the study of planetary science and astrobiology because it is positioned in the midst of the stellar climatological habitable zone. Its mass is estimated to be between 3.1 and 4.3 M⊕, noting that the putative upper mass limit is partially constrained by the assumption that none of the planetary orbital eccentricities exceeds 0.2. The distance of Gl 581g is estimated to be 0.14601 ± 0.00014 AU, and its eccentricity is almost identical to zero.
According to Valencia et al. (2006), super-Earths are rocky planets from one to about ten Earth masses with a chemical and mineral composition akin to that of Earth. In the following, we adopt the hypothesis that this is indeed the case, and consider for Gl 581g our model previously developed for the Earth, using scaling laws if appropriate. This approach has already been applied to Gl 581c and Gl 581d (von Bloh et al. 2007), as well as to simulations of hypothetical super-Earth planets in systems undergoing red giant branch evolution (von Bloh et al. 2009).
The main question is whether Gl 581g, if existing, offers the principal possibility of life, i.e., whether it lies within the stellar habitable zone (HZ), as already argued by Vogt et al. (2010). Typically, stellar HZs are defined as regions around the central star where the physical conditions are favourable for liquid water to exist at the planet’s surface for a period of time sufficient for biological evolution to occur. Kasting et al. (1993) calculated the HZ boundaries for the luminosity and effective temperature of the present Sun as Rin = 0.82 AU and Rout = 1.62 AU. They defined the HZ of an Earth-like planet as the region where liquid water is present at the surface.
According to this definition, the inner boundary of the HZ is determined by the loss of water via photolysis and hydrogen escape. The outer boundary of the HZ is determined by the condensation of CO2 crystals out of the atmosphere that attenuate the incident sunlight by Mie scattering. The critical CO2 partial pressure for the onset of this effect is about 5 to 6 bar. However, the cooling effect of CO2 clouds has been challenged by Forget & Pierrehumbert (1997). CO2 clouds have the additional effect of reflecting the outgoing thermal radiation back to the surface. The precise inner and outer limits of the climatic habitable zone are still unknown owing to the limitations of the existing climate models. Recently, Heller et al. (2011) extended the concept of the HZ by including constraints arising from tidal processes due to the planet’s spin orientation and rate. Effects caused by tilt erosion, tidal heating, and tidal equilibrium rotation seem to be especially important for potentially habitable planets (as Gl 581d and Gl 581g) around low-mass stars. For limitations of the planetary habitability of M-type stars see, e.g., Tarter et al. (2007), Guinan & Engle (2009), and Segura et al. (2011).
The luminosity and age of the central star play important roles in the manifestation of habitability. The luminosity of Gl 581 can be obtained by (1) photometry (Bonfils et al. 2005; Udry et al. 2007), and (2) the application of the mass-radius relationship (Ribas 2006) together with the spectroscopically determined stellar effective temperature of Te = 3480 K (Bean et al. 2006). Both methods yield L = 0.013 ± 0.002 L⊙. Selsis et al. (2007) estimated the stellar age as at least 7 Gyr based on the non-detection of Gl 581’s X-ray flux considering the sensitivity limit of ROSAT (Schmitt et al. 1995; Voges et al. 2000).
In the following, we adopt a definition of the HZ previously used by Franck et al. (2000a,b). Here habitability at all times does not just depend on the parameters of the central star, but also on the properties of the planet. In particular, habitability is linked to the photosynthetic activity of the planet, which in turn depends on the planetary atmospheric CO2 concentration together with the presence of liquid water, and is thus strongly influenced by the planetary dynamics. We call this definition the photosynthesis-sustaining habitable zone, pHZ. In principle, this leads to additional spatial and temporal limitations of habitability because the pHZ (defined for a specific type of planet) becomes narrower with time owing to the persistent decrease of the planetary atmospheric CO2 concentration.
2. Habitability of super-Earth planets
2.1. Photosynthesis-sustaining habitable zone (pHZ)
The climatic habitable zone at a given time for a star with luminosity L and effective temperature Te different from the Sun can be calculated following Underwood et al. (2003) based on previous work by Kasting et al. (1993) as 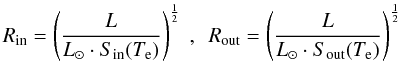 (1)with Sin(Te) and Sout(Te) described as second-order polynomials.
(1)with Sin(Te) and Sout(Te) described as second-order polynomials.
To assess the habitability of a terrestrial planet, an Earth-system model is applied to calculate the evolution of the temperature and atmospheric CO2 concentration. On Earth, the carbonate-silicate cycle is the crucial element for a long-term homeostasis under increasing solar luminosity. On geological time-scales, the deeper parts of the Earth are considerable sinks and sources of carbon.
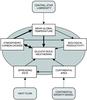 |
Fig. 1 Earth system box model. The arrows indicate the different forcing and feedback mechanisms. The bold arrows indicate negative feedback that operates toward climate stabilization. |
Our numerical model previously applied to Gl 581c and Gl 581d (von Bloh et al. 2007) couples the stellar luminosity L, the silicate-rock weathering rate Fwr and the global energy balance to obtain estimates of the partial pressure of atmospheric carbon dioxide PCO2, the mean global surface temperature Tsurf, and the biological productivity Π as a function of time t (Fig. 1). The main point is the persistent balance between the CO2 sink in the atmosphere-ocean system and the metamorphic (plate tectonic) sources. This is expressed through the dimensionless quantities 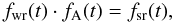 (2)where fwr(t) ≡ Fwr(t)/Fwr,0 is the weathering rate, fA(t) ≡ Ac(t)/Ac,0 is the continental area, and fsr(t) ≡ S(t)/S0 is the areal spreading rate, which are all normalized by their present values of Earth. Equation (2) can be rearranged by introducing the geophysical forcing ratio GFR (Volk 1987) as
(2)where fwr(t) ≡ Fwr(t)/Fwr,0 is the weathering rate, fA(t) ≡ Ac(t)/Ac,0 is the continental area, and fsr(t) ≡ S(t)/S0 is the areal spreading rate, which are all normalized by their present values of Earth. Equation (2) can be rearranged by introducing the geophysical forcing ratio GFR (Volk 1987) as 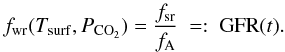 (3)Here we assume that the weathering rate only depends on the global surface temperature and the atmospheric CO2 concentration. For the investigation of a super-Earth under external forcing, we adopt a model planet with a prescribed continental area. The fraction of continental area with respect to the total planetary surface fA is varied between 0.1 and 0.9.
(3)Here we assume that the weathering rate only depends on the global surface temperature and the atmospheric CO2 concentration. For the investigation of a super-Earth under external forcing, we adopt a model planet with a prescribed continental area. The fraction of continental area with respect to the total planetary surface fA is varied between 0.1 and 0.9.
Size and gravity parameters of the Gl 581g models.
The connection between the stellar parameters and the planetary climate can be obtained by using a radiation balance equation (Williams 1998) ![\begin{equation} \frac{L}{4\pi R^2} [1- a (T_{\mathrm{surf}}, P_{\mathrm{CO}_2})] = 4I_R (T_{\mathrm{surf}}, P_{\mathrm{CO}_2}), \label{L} \end{equation}](/articles/aa/full_html/2011/04/aa16534-11/aa16534-11-eq37.png) (4)where a denotes the planetary albedo, IR the outgoing infrared flux, and R the distance from the central star. The climate model does not include clouds, which are particularly important for determining the inner boundary of the HZ (Selsis et al. 2007). Equations (3) and (4) constitute a set of two coupled equations with two unknowns, Tsurf and PCO2, if the parameterization of the weathering rate, the luminosity, the distance to the central star and the geophysical forcing ratio are specified. Therefore, a numerical solution can be attained in a straightforward manner.
(4)where a denotes the planetary albedo, IR the outgoing infrared flux, and R the distance from the central star. The climate model does not include clouds, which are particularly important for determining the inner boundary of the HZ (Selsis et al. 2007). Equations (3) and (4) constitute a set of two coupled equations with two unknowns, Tsurf and PCO2, if the parameterization of the weathering rate, the luminosity, the distance to the central star and the geophysical forcing ratio are specified. Therefore, a numerical solution can be attained in a straightforward manner.
The photosynthesis-sustaining HZ around Gl 581 is defined as the spatial domain of all distances R from the central star where the biological productivity is greater than zero, i.e., 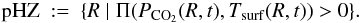 (5)In our model, biological productivity is considered to be solely a function of the surface temperature and the CO2 partial pressure in the atmosphere. Our parameterization yields zero productivity for Tsurf ≤ 0 °C or Tsurf ≥ 100 °C or PCO2 ≤ 10-5 bar (Franck et al. 2000a). The inner and outer boundaries of the pHZ do not depend on the detailed parameterization of the biological productivity within the temperature and pressure tolerance window.
(5)In our model, biological productivity is considered to be solely a function of the surface temperature and the CO2 partial pressure in the atmosphere. Our parameterization yields zero productivity for Tsurf ≤ 0 °C or Tsurf ≥ 100 °C or PCO2 ≤ 10-5 bar (Franck et al. 2000a). The inner and outer boundaries of the pHZ do not depend on the detailed parameterization of the biological productivity within the temperature and pressure tolerance window.
2.2. Comments on the thermal evolution model
Parameterized convection models are the simplest models for investigating the thermal evolution of terrestrial planets and satellites. They have been successfully applied to the evolution of Mercury, Venus, Earth, Mars, and the Moon (Stevenson et al. 1983; Sleep 2000). Franck & Bounama (1995) studied the thermal and volatile history of Earth and Venus in the framework of comparative planetology. The internal structure of massive terrestrial planets with one to ten Earth masses has been investigated by Valencia et al. (2006) to obtain scaling laws for the total radius, mantle thickness, core size, and average density as a function of mass. Similar scaling laws were found for different compositions. We will use these scaling laws for the mass-dependent properties of super-Earths and also the mass-independent material properties given by Franck & Bounama (1995).
The thermal history and future of a super-Earth has to be determined to calculate the spreading rate for solving key Eq. (2). A parameterized model of whole mantle convection including the volatile exchange between the mantle and surface reservoirs (Franck & Bounama 1995; Franck 1998) is applied. The key equations used in our present study are in accord with our previous work focused on Gl 581c and Gl 581d; see von Bloh et al. (2007), for details. A key element is the computation of the areal spreading rate S; note that S is a function of the average mantle temperature Tm, the surface temperature Tsurf, the heat flow from the mantle qm, and the area of ocean basins A0 (Turcotte & Schubert 2002). It is given as 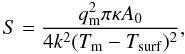 (6)where κ is the thermal diffusivity and k the thermal conductivity. To calculate the spreading rate, the thermal evolution of the mantle has be to computed:
(6)where κ is the thermal diffusivity and k the thermal conductivity. To calculate the spreading rate, the thermal evolution of the mantle has be to computed: 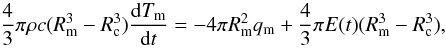 (7)where ρ is the density, c is the specific heat at constant pressure, E is the energy production rate by decay of radiogenic heat sources in the mantle per unit volume, and Rm and Rc are the outer and inner radii of the mantle, respectively. To calculate the thermal evolution for a planet with several Earth masses, i.e., 3.1 and 4.3 M⊕ as pursued for Gl 581g in our present study, the planetary parameters have to be adjusted. Thus we assume
(7)where ρ is the density, c is the specific heat at constant pressure, E is the energy production rate by decay of radiogenic heat sources in the mantle per unit volume, and Rm and Rc are the outer and inner radii of the mantle, respectively. To calculate the thermal evolution for a planet with several Earth masses, i.e., 3.1 and 4.3 M⊕ as pursued for Gl 581g in our present study, the planetary parameters have to be adjusted. Thus we assume 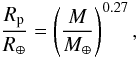 (8)where Rp is the planetary radius, see Valencia et al. (2006). The total radius, mantle thickness, core size, and average density are all functions of mass, with the subscript ⊕ denoting Earth values. The exponent of 0.27 has been obtained for super-Earths. The values of Rp, Rm, Rc, as well as the other planetary properties are scaled accordingly. It means that Rp, Rm and Rc increase by a factor of 1.36 for M = 3.1 M⊕ and 1.48 for M = 4.3 M⊕.
(8)where Rp is the planetary radius, see Valencia et al. (2006). The total radius, mantle thickness, core size, and average density are all functions of mass, with the subscript ⊕ denoting Earth values. The exponent of 0.27 has been obtained for super-Earths. The values of Rp, Rm, Rc, as well as the other planetary properties are scaled accordingly. It means that Rp, Rm and Rc increase by a factor of 1.36 for M = 3.1 M⊕ and 1.48 for M = 4.3 M⊕.
Table 1 gives a summary of the size parameters for the models of the planets with 3.1 and 4.3 M⊕; see the study by von Bloh et al. (2007) for additional information. The values for an Earth-size planet are included for comparison. The onset of plate tectonics on massive terrestrial planets is a topic of controversy. While O’Neill & Lenardic (2007) stated that they might be in an episodic or stagnant lid regime, Valencia & O’Connell (2009) proposed that a more massive planet is likely to convect in a plate tectonic regime similar to Earth. Thus, the more massive the planet is, the higher the Rayleigh number that controls convection, the thinner the top boundary layer (lithosphere), and the higher the convective velocities. In the framework of our model, a plate-tectonic-driven carbon cycle is considered necessary for carbon-based life. This approach follows the previous work by von Bloh et al. (2007), who gave a detailed discussion of the equations and parameters used in their study for the super-Earths with 5 and 8 M⊕, identified as Gl 581c and Gl 581d, respectively.
 |
Fig. 2 The pHZ of Gl 581 for a super-Earth of a) M = 3.1 M⊕ and b) M = 4.3 M⊕ as a function of planetary age. The relative continental area is varied from 0.1 to 0.9. The stellar luminosity is assumed to be 0.013 L⊙. Following Selsis et al. (2007) and references therein, the stellar age is at least 7 Gyr, indicated by a dashed line. For comparison, we show the positions of Venus, Earth, and Mars scaled to the luminosity of Gl 581. Note that the position of Gl 581g almost exactly coincides with the luminosity-scaled position of Earth. |
 |
Fig. 3 Life span for Gl 581g with M = 3.1 M⊕ ( + ) and M = 4.3 M⊕ ( × ) as a function of the relative continental area. For comparison the dashed curve denotes the life span of an Earth-mass planet. The horizontal line indicates the lower limit for the age estimate of 7 Gyr. |
3. Results and discussion
The photosynthesis-sustaining habitable zone is calculated for super-Earth planets with 3.1 and 4.3 M⊙ and the results are depicted in Fig. 2. The maximum life span of a biosphere is given at the point in time when the pHZ vanishes. This maximum life span strongly depends on the relative continental area r and increases with decreasing r. Therefore, “water worlds” are favored in the facilitation of habitability as previously obtained in models of fictitious Earth-mass planets for 47 UMa and 55 Cnc (Cuntz et al. 2003; Franck et al. 2003; von Bloh et al. 2003). In this context, water worlds are planets of non-vanishing continental area mostly covered by oceans. The climate of a planet fully covered by oceans is not stabilized by the carbonate-silicate cycle. The maximum life span for a water world with r = 0.1 and a planetary mass of M = 3.1 M⊕ is 15.4 Gyr, whereas it is 16.3 Gyr for M = 4.3 M⊕. Both times are considerably longer than the estimated age limit of Gl 581, which is 7 Gyr (Selsis et al. 2007).
This maximum life span can be realized for a super-Earth at a distance from the central star of about 0.14 ± 0.015 AU. This uncertainty reflects the uncertainty in the luminosity estimate of Gl 581, noting however that our models are also subject to various systematic uncertainties (see Sect. 2). A full assessment of those uncertainties, which are expected to be larger than the impact of the uncertainty in the stellar luminosity, can best be obtained by a comparison with future alternative models. It is noteworthy that the orbital position of Gl 581g at 0.146 AU, if existing, is largely consistent with this ideal position. Thus, we can conclude that Gl 581g has an almost perfect Goldilock position in the star-planet system of Gl 581, and it is the best candidate for extra-terrestrial habitability so far. Because of the Goldilock position, located well within the HZ, clouds play no major role for our results. Any shift (within limits) of the inner or outer boundary of the HZ will not affect the maximum life span obtained by our model. The optimum position is not only the geometric mean of the pHZ, but it is also the position where the maximum life span of the biosphere is realized.
But the pHZ also strongly depends on the planetary age. Figure 3 depicts the life span for a super-Earth with 3.1 and 4.3 M⊕ at 0.146 AU as a function of the relative continental area r. For a relative continental area larger than 0.6, the realized life span is shorter than 7 Gyr, which is the estimated lower limit for the stellar age of the Gl 581 star-planet system. In this case, no habitable conditions on Gl 581g would exist in the framework of the adopted geodynamic model. If we place an Earth twin (r ≃ 0.29) at the orbital position of Gl 581g, habitable conditions would cease just at an age of 7 Gyr. In conclusion, we have to await future missions to identify the pertinent geodynamical features of Gl 581g (in case it does exist) and to search for biosignatures in its atmosphere to gain insight into whether or not Gl 581g harbors life.
References
- Bean, J. L., Benedict, G. F., & Endl, M. 2006, ApJ, 653, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Forveille, T., Delfosse, X., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Cuntz, M., von Bloh, W., Bounama, C., & Franck, S. 2003, Icarus, 162, 215 [Google Scholar]
- Forget, F., & Pierrehumbert, R. T. 1997, Science, 278, 1273 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Franck, S. 1998, Tectonophysics, 291, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Franck, S., & Bounama, C. 1995, Phys. Earth Planet. Inter., 92, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Franck, S., Block, A., von Bloh, W., et al. 2000a, Tellus, 52B, 94 [NASA ADS] [Google Scholar]
- Franck, S., von Bloh, W., Bounama, C., et al. 2000b, J. Geophys. Res., 105 (E1), 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Franck, S., Cuntz, M., von Bloh, W., & Bounama, C. 2003, Int. J. Astrobiol., 2, 35 [Google Scholar]
- Guinan, E. F., & Engle, S. G. 2009, in Proc. 8th Pacific Rim Conference on Stellar Astrophysics, in press [arXiv:0901.1860] [Google Scholar]
- Heller, R., Leconte, J., & Barnes, R. 2011, A&A, 528, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Neill, C., & Lenardic, A. 2007, Geophys. Res. Lett., 34, L19204 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I. 2006, Ap&SS, 304, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., Fleming, T. A., & Giampapa, M. S. 1995, ApJ, 450, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Segura, A., Kasting, J. F., Meadows, V., et al. 2011, Astrobiology, in press [Google Scholar]
- Selsis, F., Kasting, J. F., Levrard, B., et al. 2007, A&A, 476, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sleep, N. H. 2000, J. Geophys. Res., 105, 17563 [Google Scholar]
- Stevenson, D. J., Spohn, T., & Schubert, G. 1983, Icarus, 54, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Tarter, J. C., Backus, P. R., Mancinelli, R. L., et al. 2007, Astrobiology, 7, 30 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Turcotte, D. L., & Schubert, G. 2002, Geodynamics (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Underwood, D. R., Jones, B. W., & Sleep, P. N. 2003, Int. J. Astrobiol., 2, 289 [Google Scholar]
- Valencia, D., & O’Connell, R. J. 2009, EPSL, 286, 492 [Google Scholar]
- Valencia, D., O’Connell, R. J., & Sasselov, D. 2006, Icarus, 181, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 2000, IAU Circ., 7432, 1 [NASA ADS] [Google Scholar]
- Vogt, S. S., Butler, R. P., Rivera, E. J., et al. 2010, ApJ, 723, 954 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volk, T. 1987, Am. J. Sci., 287, 763 [CrossRef] [Google Scholar]
- von Bloh, W., Cuntz, M., Franck, S., & Bounama, C. 2003, Astrobiology, 3, 681 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- von Bloh, W., Bounama, C., Cuntz, M., & Franck, S. 2007, A&A, 476, 1365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Bloh, W., Cuntz, M., Schröder, K.-P., Bounama, C., & Franck, S. 2009, Astrobiology, 9, 593 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Williams, D. M. 1998, Ph.D. Thesis, Pennsylvania St. Univ. [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Earth system box model. The arrows indicate the different forcing and feedback mechanisms. The bold arrows indicate negative feedback that operates toward climate stabilization. |
| In the text | |
 |
Fig. 2 The pHZ of Gl 581 for a super-Earth of a) M = 3.1 M⊕ and b) M = 4.3 M⊕ as a function of planetary age. The relative continental area is varied from 0.1 to 0.9. The stellar luminosity is assumed to be 0.013 L⊙. Following Selsis et al. (2007) and references therein, the stellar age is at least 7 Gyr, indicated by a dashed line. For comparison, we show the positions of Venus, Earth, and Mars scaled to the luminosity of Gl 581. Note that the position of Gl 581g almost exactly coincides with the luminosity-scaled position of Earth. |
| In the text | |
 |
Fig. 3 Life span for Gl 581g with M = 3.1 M⊕ ( + ) and M = 4.3 M⊕ ( × ) as a function of the relative continental area. For comparison the dashed curve denotes the life span of an Earth-mass planet. The horizontal line indicates the lower limit for the age estimate of 7 Gyr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


