| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201116533 | |
| Published online | 25 February 2011 | |
Letters to the Editor
HD 5388 b is a 69 MJup companion instead of a planet
Observatoire de Genève, Université de Genève,
51 chemin des Maillettes,
1290
Sauverny,
Switzerland
e-mail: johannes.sahlmann@unige.ch
Received:
18
January
2011
Accepted:
8
February
2011
We examined six exoplanet host stars with non-standard Hipparcos astrometric solution,
which may be indicative of unrecognised orbital motion. Using Hipparcos intermediate
astrometric data, we detected the astrometric orbit of HD 5388 at a significance level of
99.4% (2.7 σ). HD 5388 is a metal-deficient star and hosts a planet
candidate with a minimum mass of 1.96 MJ discovered in 2010.
We determined its orbit inclination to be 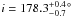 and
the corresponding mass of its companion HD 5388 b
to be M2 = 69 ± 20 MJ. The orbit
is seen almost face-on and the companion mass lies at the upper end of the brown-dwarf
mass range. A mass lower than 13 MJ was excluded at the
3 σ-level. The astrometric motions of the five other stars had been
investigated by other authors revealing two planetary companions, one stellar companion,
and two statistically insignificant orbits. We conclude that HD 5388 b is not a planet but
most likely a brown-dwarf companion. In addition, we find that the inclinations of the
stellar rotation axis and the companion’s orbital axis differ significantly.
and
the corresponding mass of its companion HD 5388 b
to be M2 = 69 ± 20 MJ. The orbit
is seen almost face-on and the companion mass lies at the upper end of the brown-dwarf
mass range. A mass lower than 13 MJ was excluded at the
3 σ-level. The astrometric motions of the five other stars had been
investigated by other authors revealing two planetary companions, one stellar companion,
and two statistically insignificant orbits. We conclude that HD 5388 b is not a planet but
most likely a brown-dwarf companion. In addition, we find that the inclinations of the
stellar rotation axis and the companion’s orbital axis differ significantly.
Key words: stars: individual: HD 5388 / planetary systems / brown dwarfs / astrometry
© ESO, 2011
1. Introduction
For most extrasolar planets detected with the radial-velocity (RV) method, only their minimum masses are known because of their unknown orbit inclinations. Although the large number of planets allows us to draw statistically sound conclusions about their mass distribution (Udry & Santos 2007; Howard et al. 2010), it is highly desirable to derive this distribution without the inclination incertitude. Astrometric measurements can resolve this ambiguity. For instance, Sahlmann et al. (2011) used Hipparcos data to analyse the astrometric motion of stars with potential brown-dwarf companions and found that about half of the candidates are low-mass stars. Here, we extend this work to stars with planet candidates and non-standard Hipparcos solution, and discover the astrometric orbit of HD 5388, which hosts a recently announced planet candidate.
2. Target selection and astrometric analysis
In September 2010, the list of RV-planets at exoplanet.eu contained 461 entries around 389 stars. Only 286 host stars are included in the new Hipparcos reduction (van Leeuwen 2007). Many host stars of transiting exoplanets discovered in transit surveys (e.g., Kepler, CoRoT, HAT, WASP) and confirmed by RV are fainter than the completeness limit of Hipparcos. We selected the stars for which the new Hipparcos reduction found a non-standard solution and that were not flagged as member of a multiple system, thus having solution types “1”, “7”, or “9”. Type “1” solutions are termed stochastic and adopted when the standard five-parameter solution (type “5”) is not satisfactory and neither orbital nor acceleration models improve the solution in terms of χ2. The types “7” and “9” are given, when the model has to include proper-motion derivatives of first and second order to obtain a reasonable fit. Six stars satisfied these criteria and are listed in Table 4.
The astrometric analysis was performed as described in Sahlmann et al. (2011), where a detailed description of the method can be found. We briefly recall the main elements of the analysis. Using the orbital parameters known from RV measurements, the intermediate astrometric data of the new Hipparcos reduction was fitted with a seven-parameter model depending on the inclination i, the longitude of the ascending node Ω, the parallax ϖ, and offsets to the coordinates (Δα ⋆ , Δδ) and proper motions (Δμα ⋆ , Δμδ) given in the published catalogue of van Leeuwen (2007). A two-dimensional search grid in i and Ω defined starting values for a standard nonlinear χ2-minimisation procedure identifying the global minimum. The uncertainties in the RV parameters are propagated to the astrometric solution by means of Monte Carlo simulations. The statistical significance of each astrometric orbit was determined by the distribution-free permutation test employing 1000 pseudo orbits. Uncertainties in the solution parameters were derived by Monte Carlo simulations. This approach has proven to be reliable in detecting orbital signatures in the Hipparcos astrometric data and efficiently distinguishing a significant orbit in the present low signal-to-noise ratio regime (Sahlmann et al. 2011).
3. The orbit of HD 5388
HD 5388 (HIP 4311) is listed with a stochastic solution in the catalogue of the new Hipparcos reduction. Santos et al. (2010) used the HARPS spectrograph to discover a massive planet candidate around this F6V-star. Figure 1 shows the radial velocities from the discovery paper. The companion has a minimum mass of M2sini = 1.96 MJ and orbits its host in an eccentric orbit (e = 0.4) with an orbital period of P = 777 days. The time of periastron passage T0, the longitude of periastron ω, the radial-velocity semi-amplitude K1, and the minimum semimajor axis of the star’s astrometric motion asini are given in Table 1. The residuals of the RV solution (3.3 ms-1) are larger than the average measurement error (2.8 ms-1). By considering the star’s spectral type and projected rotational velocity and analysing the bisector inverse slope, Santos et al. (2010) conclude that the excess RV noise is insignificant.
We detected the astrometric orbit with a significance of 99.4% (2.7σ),
which means that Hipparcos measured the stellar orbit induced by a companion with the
orbital characteristics given in Table 1. The derived
astrometric orbit with a = 1.7 ± 0.5 milli-arcsec (mas) is small compared
to the median single-measurement precision σΛ = 3.8 mas given by
the new Hipparcos reduction. However, the large number of measurements
Nmes = 191 covering more than one orbital revolution
(Norb = 1.5) resulted in an effective signal-to-noise ratio of
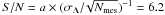 allowing the detection to be
possible. With a reduced chi-square value of
allowing the detection to be
possible. With a reduced chi-square value of 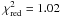 the
final seven-parameter fit is good and the derived offsets to positions, parallax, and proper
motions are small. The values of Ω and the inclination iorbit
are well constrained at
the
final seven-parameter fit is good and the derived offsets to positions, parallax, and proper
motions are small. The values of Ω and the inclination iorbit
are well constrained at 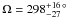 and
and
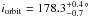 .
Using a stellar mass of 1.2 M⊙ (Santos et al. 2010), we derived the companion mass to be
M2 = 69.2 ± 19.9 MJ. The
astrometric orbit of HD 5388 is shown in Fig. 2 and its
characteristics are summarised in Table 2. Reffert & Quirrenbach (2011) found an upper mass
limit of 124 MJ for the companion of HD 5388, which is
compatible with our result.
.
Using a stellar mass of 1.2 M⊙ (Santos et al. 2010), we derived the companion mass to be
M2 = 69.2 ± 19.9 MJ. The
astrometric orbit of HD 5388 is shown in Fig. 2 and its
characteristics are summarised in Table 2. Reffert & Quirrenbach (2011) found an upper mass
limit of 124 MJ for the companion of HD 5388, which is
compatible with our result.
 |
Fig. 1 Phase-folded radial velocities of HD 5388 as published by Santos et al. (2010). Red circles indicate the HARPS measurements and the solid line corresponds to the best-fit solution. |
Orbital parameters of HD 5388 (Santos et al. 2010).
Assuming that the orbit orientations are randomly oriented in space, the probability of measuring an inclination smaller than 2° is only 0.06%. However, the number of planets detected in RV-surveys reached several hundreds making our detection reasonably probable. HD 5388 is a metal-deficient star with [ Fe/H ] = −0.27 ± 0.02. The hydrogen-burning mass limit, commonly used to distinguish between stars and brown dwarfs, increases with decreasing metallicity and reaches 87 MJ (0.083 M⊙) for [Fe/H] < −1 (Chabrier & Baraffe 1997). Because of the moderate metal-deficiency of HD 5388, we used a limit of 80 MJ and found that the probability that the companion of HD 5388 has a mass below this limit is 71%. The companion of HD 5388 is thus most likely a brown dwarf. This adds HD 5388 to the very few known Sun-like stars that have a brown-dwarf companion and a well-determined astrometric orbit.
 |
Fig. 2 Top: astrometric orbit of HD 5388 projected on the sky. North is up and east is left. The solid red line shows the model orbit, which is orientated clockwise, and open circles mark the individual Hipparcos measurements. Bottom: O–C residuals for the normal points of the orbital solution (filled blue circles) and the standard five-parameter model without companion (crosses). |
 |
Fig. 3 Probability density functions of orbit inclination (iorbit, dark-grey histogram) and stellar spin axis inclination (irot, light-grey histogram). The orbit inclination PDF is very sharply peaked with its maximum at 0.18 and is truncated for display clarity. The PDF of ψ = iorbit − irot is shown as dashed line. The bin size is 0.2°. |
Parameters of the astrometric solution for HD 5388.
3.1. Spin-orbit alignment
After determining the orbital inclination from astrometry, we compared it to the
orientation of the stellar spin axis. The inclination irot of
the stellar spin axis is defined with respect to the line of sight
(irot = 0° or 180° for a pole-on view) and can be derived
from the spectroscopic estimate of
υsinirot = 4.2 km s-1 (Santos et al. 2010). The authors did not give an error
bar for this measurement and we assumed a conservative uncertainty of 1 km s-1.
On the basis of the activity indicator 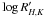 determined from the
HARPS spectra, we used the calibration of Mamajek &
Hillenbrand (2008) to derive the stellar rotation period
Prot. Assuming an effective temperature of
Teff = 6297 ± 32 (Santos
et al. 2010), the apparent visual magnitude
mV = 6.839 ± 0.001 (van Leeuwen 2007), and the parallax ϖ given in
Table 2, we derived the star’s absolute
magnitude, luminosity (L = 4.5 ± 0.3 L⊙),
and radius (R = 1.8 ± 0.1 R⊙), using
standard formulae and Monte Carlo resampling. Bolometric corrections were computed using
the Flower (1996) parameters given by Torres (2010). Using the stellar radius and rotation
period, we derived the equatorial rotation velocity to be
υ = 10 ± 3 km s-1, and then the inclination of the spin axis
by calculating
irot = arcsin(υsinirot/υ).
determined from the
HARPS spectra, we used the calibration of Mamajek &
Hillenbrand (2008) to derive the stellar rotation period
Prot. Assuming an effective temperature of
Teff = 6297 ± 32 (Santos
et al. 2010), the apparent visual magnitude
mV = 6.839 ± 0.001 (van Leeuwen 2007), and the parallax ϖ given in
Table 2, we derived the star’s absolute
magnitude, luminosity (L = 4.5 ± 0.3 L⊙),
and radius (R = 1.8 ± 0.1 R⊙), using
standard formulae and Monte Carlo resampling. Bolometric corrections were computed using
the Flower (1996) parameters given by Torres (2010). Using the stellar radius and rotation
period, we derived the equatorial rotation velocity to be
υ = 10 ± 3 km s-1, and then the inclination of the spin axis
by calculating
irot = arcsin(υsinirot/υ).
Because we cannot determine the star’s sense of rotation, the angle
irot has a 180° ambiguity and we first considered the value
that falls into the same quadrant as iorbit, i.e. a prograde
configuration. The astrometric analysis yielded the distribution of
iorbit, obtained from 100 000 Monte Carlo simulations. To
obtain the irot-distribution, we performed 106
Monte Carlo simulations. We finally compared these two distributions by drawing
2 × 107 pairs of values [ iorbit,
irot ] and obtained the distribution of the orbit obliquity
or spin-orbit angle ψ by computing
ψ = iorbit − irot.
Figure 3 shows the probability density functions
(PDF) of iorbit, irot, and
ψ. The iorbit-distribution is very narrow
and peaks around 178.3°, whereas the irot-distribution is
broad with its maximum at ~155° and the two distributions show a very small
overlap. The median values and confidence intervals of irot,
iorbit, and the obliquity ψ are given in
Table 3. We found that ψ is
larger than 4.4° and 19.3° with a probability of 99.7% and 68.3%, respectively, and its
nominal value with 1 σ confidence intervals is
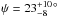 in prograde configuration, which indicates that the orientations of stellar spin and
orbital axis differ substantially. In retrograde configuration, the obliquity would be
in prograde configuration, which indicates that the orientations of stellar spin and
orbital axis differ substantially. In retrograde configuration, the obliquity would be
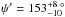 .
We note that these values of ψ and ψ′ are lower limits,
because the ascending node Ωrot of the spin axis is not constrained and we
assumed that Ω = Ωrot in their derivation. As illustrated in Fig. 4, ψ increases if the two ascending
nodes Ωrot and Ω do not coincide, creating an additional uncertainty in
ψ of 2 × (180° − iorbit) = 3.4° in the
prograde configuration. For a retrograde orbit, this uncertainty is larger at 51°. In
summary, the obliquity is
.
We note that these values of ψ and ψ′ are lower limits,
because the ascending node Ωrot of the spin axis is not constrained and we
assumed that Ω = Ωrot in their derivation. As illustrated in Fig. 4, ψ increases if the two ascending
nodes Ωrot and Ω do not coincide, creating an additional uncertainty in
ψ of 2 × (180° − iorbit) = 3.4° in the
prograde configuration. For a retrograde orbit, this uncertainty is larger at 51°. In
summary, the obliquity is ![\hbox{$\psi= 23_{- 8}^{+10\,[+3.4]\,\circ}$}](/articles/aa/full_html/2011/04/aa16533-11/aa16533-11-eq106.png) and
and ![\hbox{$\psi'=153_{-10}^{+ 8\, [+51]\,\circ}$}](/articles/aa/full_html/2011/04/aa16533-11/aa16533-11-eq107.png) for prograde and retrograde orbits, respectively, where the additional uncertainties are
denoted in square brackets.
for prograde and retrograde orbits, respectively, where the additional uncertainties are
denoted in square brackets.
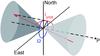 |
Fig. 4 Possible spin-orbit configurations. The astrometric motion in the sky plane defined by the north and east axes is observed from location P. The orbit orientation vector (red arrow) is defined by the angles iorbit and Ω. The stellar spin orientation vector can lie on either the dark-grey cone (prograde configurations) or the light-grey cone (retrograde configurations) with identical opening angles 2 × (180° − irot) = 51°. |
Spin inclination, orbital inclination, and obliquity.
We performed these calculations using the Prot-calibration by
Noyes et al. (1984), which yielded a value of
8.8 ± 1.6 days and an obliquity of 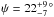 ,
in agreement with the result obtained with the calibration of Mamajek & Hillenbrand (2008). The isochrones of Marigo et al. (2008)1 indicated that HD 5388 is at the end of the core-H burning phase just past the
turn-off point. Therefore, HD 5388 may be about to leave the main sequence or even be
slightly evolved. This would introduce additional uncertainties and possibly biases into
our estimates of
,
in agreement with the result obtained with the calibration of Mamajek & Hillenbrand (2008). The isochrones of Marigo et al. (2008)1 indicated that HD 5388 is at the end of the core-H burning phase just past the
turn-off point. Therefore, HD 5388 may be about to leave the main sequence or even be
slightly evolved. This would introduce additional uncertainties and possibly biases into
our estimates of 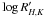 ,
Prot, the stellar radius, and eventually
irot, and may therefore alter the above findings.
,
Prot, the stellar radius, and eventually
irot, and may therefore alter the above findings.
4. The orbits of five additional selected stars
In addition to HD 5388, we examined five other stars that satisfied our selection criteria in Sect. 2. They are listed in Table 4 and although their astrometric motions were previously studied in the literature, we describe our findings below:
-
55 Cnc has five planetary companions an-nounced by Fischer et al. (2008).The planet 55 Cnc d has aminimum mass of M2sini = 3.84 MJ. Using HST astrometry, McArthuret al. (2004) derived an orbit in-clination of 53 ± 7° for the d-planet, an astrometric perturbation size ofa = 1.9 ± 0.4 mas, and a mass of M2 = 4.9 ± 1.1 MJ. Compared to the measurementprecision of σΛ = 1.4 mas, the stellar orbit is large enoughto have been measured by Hipparcos, which explains the non-standard solution type. Because the Hipparcos data only covers20% of the 5200 day orbital period, we did not attemptto fit an astrometric orbit.
-
HD 81040 hosts a massive planet with M2sini = 6.86 MJ (Sozzetti et al. 2006). We did not detect orbital signature because the obtained orbit has a very low significance of 68%, in agreement with the result of Sozzetti et al. (2006). As in that work, we used the Hipparcos astrometric data to set an upper limit to the companion mass of 47.5 MJ, thus excluding that the companion has a stellar nature.
-
HD 179949 hosts a planet candidate with M2sini = 0.84 MJ (Tinney et al. 2001). We did not detect an orbital signature because the obtained orbit has a very low significance of 71%, which confirms the result of Zucker & Mazeh (2001).
-
HD 195019 hosts a planet candidate with M2sini = 3.70 MJ (Wright et al. 2007). We detected the astrometric orbit with a high significance of 98% and a very low inclination of 0.3 ± 0.1°, which renders a stellar companion and confirms the result of Zucker & Mazeh (2001).
-
γ Cep (HD 222404) hosts a planet candidate with M2sini = 1.7 MJ (Hatzes et al. 2003). We did not treat this system because an exhaustive analysis, including the use of Hipparcos astrometry, was performed by Torres (2007), who set an upper mass limit of 16.9 MJ to the planetary companion.
Stars with candidate RV-planets and non-standard Hipparcos astrometric solutions.
5. Discussion
Among the potential planets around the six stars selected in Sect. 2, one turned out to be a star (HD 195019 b), two are likely planets (55 Cnc d and γ Cep b), and one is a brown-dwarf companion (HD 5388). The astrometric orbits of two stars were not detected with Hipparcos and the companions remain planetary candidates. The significant fraction of one third of non-planetary companions found in this small sample is a selection effect and does not reflect the properties of the planetary population. That a large population of non-planetary companions is observed with low orbital inclinations, hence mistaken for planets, is statistically unlikely and would have been detected with Hipparcos (Zucker & Mazeh 2001). At the individual level, however, a planet detected by RV remains a planet candidate until its mass range is confined by complementary constraints derived for instance from a transit lightcurve, dynamical interactions, by direct imaging, or from astrometric data, as in the case of HD 5388. In the future, as the data of the GAIA astrometry satellite becomes available, we will be able to measure the astrometric orbits of many planetary systems, thus obtaining an accurate census of the planetary mass distribution. A few more planet candidates may then turn out to be brown-dwarf companions.
We have detected the astrometric orbit of HD 5388, which harboured a planet candidate of
minimum mass
M2sini = 1.96 MJ.
We found an almost face-on orbit with an inclination of
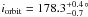 .
Consequently, we determined the mass of the companion HD 5388 b to be
M2 = 69 ± 20 MJ. A mass
lower than 13 MJ was excluded at the 3σ
confidence level. Thus, HD 5388 b can no longer be considered a planet. It is instead a
close brown-dwarf companion, which is remarkable because at most 0.6% of Sun-like stars have
close brown-dwarf companions (Sahlmann et al. 2011).
In particular, it is one of the very few brown-dwarf companions for which the astrometric
orbit could be measured and whose orbital motion is therefore fully characterised, such as
HD 38529 (Benedict
et al. 2010).
.
Consequently, we determined the mass of the companion HD 5388 b to be
M2 = 69 ± 20 MJ. A mass
lower than 13 MJ was excluded at the 3σ
confidence level. Thus, HD 5388 b can no longer be considered a planet. It is instead a
close brown-dwarf companion, which is remarkable because at most 0.6% of Sun-like stars have
close brown-dwarf companions (Sahlmann et al. 2011).
In particular, it is one of the very few brown-dwarf companions for which the astrometric
orbit could be measured and whose orbital motion is therefore fully characterised, such as
HD 38529 (Benedict
et al. 2010).
The measurement of the spin-orbit alignment in planetary and binary systems, e.g., Triaud et al. (2010) and Albrecht et al. (2011), gives insight into the formation of these systems. The
most frequently applied technique uses spectroscopic measurements during the transit of
eclipsing systems and only determines the projected spin-orbit angle. Because it is
restricted to eclipsing systems, it favours small-separation, short-period systems (another
method relies on interferometric imaging of the stellar surface, see Hinkley et al. 2011). We determined the stellar spin axis inclination on
the basis of the spectroscopic estimate of
υsinirot and the rotation period calibration
using 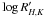 . We found
evidence of non-zero spin-orbit angles with numerical values of
. We found
evidence of non-zero spin-orbit angles with numerical values of
![\hbox{$\psi= 23_{- 8}^{+10\,[+3.4]\,\circ}$}](/articles/aa/full_html/2011/04/aa16533-11/aa16533-11-eq106.png) and
and ![\hbox{$\psi'=153_{-10}^{+ 8\, [+51]\,\circ}$}](/articles/aa/full_html/2011/04/aa16533-11/aa16533-11-eq107.png) for prograde and retrograde orbits, respectively. Thus, for both orientations of the unknown
stellar spin, we found substantial non-coplanarity between the stellar and orbital axes.
Spin-orbit angle measurements obtained from the determination of the astrometric orbit and
the spectroscopic υsini offer the opportunity to access
this information for non-eclipsing systems.
for prograde and retrograde orbits, respectively. Thus, for both orientations of the unknown
stellar spin, we found substantial non-coplanarity between the stellar and orbital axes.
Spin-orbit angle measurements obtained from the determination of the astrometric orbit and
the spectroscopic υsini offer the opportunity to access
this information for non-eclipsing systems.
The interface is http://stev.oapd.inaf.it/cgi-bin/cmd.
Acknowledgments
J.S. thanks A. Triaud for his contributions to the discussion on spin-orbit angles.
References
- Albrecht, S., Winn, J. N., Carter, J. A., et al. 2011, ApJ, 726, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Bean, J. L., et al. 2010, AJ, 139, 1844 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
- Fischer, D. A., Marcy, G. W., Butler, R. P., et al. 2008, ApJ, 675, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2003, ApJ, 599, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkley, S., Monnier, J. D., Oppenheimer, B. R., et al. 2011, ApJ, 726, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McArthur, B. E., Endl, M., Cochran, W. D., et al. 2004, ApJ, 614, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., et al. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Reffert, S., & Quirrenbach, A. 2011, A&A, 527, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Benz, W., et al. 2010, A&A, 512, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Udry, S., Zucker, S., et al. 2006, A&A, 449, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2001, ApJ, 551, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G. 2007, ApJ, 654, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., & Santos, N. C. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Van Leeuwen, F. 2007, Astrophysics and Space Science Library, Hipparcos, the New Reduction of the Raw Data, 350 [Google Scholar]
- Wright, J. T., Marcy, G. W., Fischer, D. A., et al. 2007, ApJ, 657, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S., & Mazeh, T. 2001, ApJ, 562, 549 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Stars with candidate RV-planets and non-standard Hipparcos astrometric solutions.
All Figures
 |
Fig. 1 Phase-folded radial velocities of HD 5388 as published by Santos et al. (2010). Red circles indicate the HARPS measurements and the solid line corresponds to the best-fit solution. |
| In the text | |
 |
Fig. 2 Top: astrometric orbit of HD 5388 projected on the sky. North is up and east is left. The solid red line shows the model orbit, which is orientated clockwise, and open circles mark the individual Hipparcos measurements. Bottom: O–C residuals for the normal points of the orbital solution (filled blue circles) and the standard five-parameter model without companion (crosses). |
| In the text | |
 |
Fig. 3 Probability density functions of orbit inclination (iorbit, dark-grey histogram) and stellar spin axis inclination (irot, light-grey histogram). The orbit inclination PDF is very sharply peaked with its maximum at 0.18 and is truncated for display clarity. The PDF of ψ = iorbit − irot is shown as dashed line. The bin size is 0.2°. |
| In the text | |
 |
Fig. 4 Possible spin-orbit configurations. The astrometric motion in the sky plane defined by the north and east axes is observed from location P. The orbit orientation vector (red arrow) is defined by the angles iorbit and Ω. The stellar spin orientation vector can lie on either the dark-grey cone (prograde configurations) or the light-grey cone (retrograde configurations) with identical opening angles 2 × (180° − irot) = 51°. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


