| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 6 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201116507 | |
| Published online | 17 March 2011 | |
uvbyβ photometry of early type open cluster and field stars⋆,⋆⋆
Institut für Astronomie, Universität Wien,
Türkenschanzstraße 17,
1180
Wien,
Austria
e-mail: gerald.handler@univie.ac.at
Received:
13
January
2011
Accepted:
27
January
2011
Context. The β Cephei stars and slowly pulsating B (SPB) stars are massive main sequence variables. The strength of their pulsational driving strongly depends on the opacity of iron-group elements. As many of those stars naturally occur in young open clusters, whose metallicities can be determined in several fundamental ways, it is logical to study the incidence of pulsation in several young open clusters.
Aims. To provide the foundation for such an investigation, Strömgren-Crawford uvbyβ photometry of open cluster target stars was carried out to determine effective temperatures, luminosities, and therefore cluster memberships.
Methods. In the course of three observing runs, uvbyβ photometry for 168 target stars was acquired and transformed into the standard system by measurements of 117 standard stars. The list of target stars also included some known cluster and field β Cephei stars, as well as β Cephei and SPB candidates that are targets of the asteroseismic part of the Kepler satellite mission.
Results. The uvbyβ photometric results are presented. The data are shown to be on the standard system, and the properties of the target stars are discussed: 140 of these are indeed OB stars, a total of 101 targets lie within the β Cephei and/or SPB star instability strips, and each investigated cluster contains such potential pulsators.
Conclusions. These measurements will be taken advantage of in a number of subsequent publications.
Key words: stars: early-type / stars: fundamental parameters / open clusters and associations: general / techniques: photometric / stars: oscillations / asteroseismology
Tables 3–6 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/528/A148
© ESO, 2011
1. Introduction
The β Cephei stars are a group of pulsating main sequence variables with early B spectral types. They oscillate in radial and nonradial pressure modes with typical periods of several hours. Stankov & Handler (2005) provide an overview of those stars. Pigulski & Pojmański (2008) doubled the number of class members to about 200. As these are young massive stars (and are thus progenitors of type II supernovae), they naturally occur in the galactic plane, in open clusters, and stellar associations. In general, this statement also holds for the less massive slowly pulsating B (SPB) stars. They neighbour the β Cephei stars in the HR diagram, but they are cooler and less luminous, and they pulsate in gravity modes with periods of a few days (see, e.g., De Cat 2007).
The physical origin of pulsation driving of the β Cephei and SPB stars is well established (Moskalik & Dziembowski 1992), and is caused by the huge number of transitions inside the thin structure of the electron shells in excited ions of the iron-group elements (Rogers & Iglesias 1994): the κ mechanism. Obviously, the power of pulsational driving will strongly depend on the abundance of iron-group elements and on their opacities in the driving zone. Credible pulsational models must reflect the conditions inside the real stars, reproducing all observables such as the extents of the β Cephei and SPB instability strips and their metallicity dependence. These depend on the input data used in the models, which can therefore be tested.
The metallicities of stellar aggregates can be determined in several fundamental ways. The incidence of core hydrogen-burning B-type pulsators among open cluster stars can then yield important constraints on what abundance of metals (and, by extrapolation, amount of iron group elements) is required to drive their oscillations. The aim of the present and subsequent works is to determine observationally the incidence of β Cephei and SPB stars in a number of open clusters exactly for this purpose.
Ground-based measurements of stellar variability are hampered by the presence of the Earth’s contaminated atmosphere. Scintillation and variable transparency of the night sky limit the precision of stellar brightness measurements. Therefore, the level at which the presence of oscillations in a given star can be detected is finite. Although there are techniques that optimize the precision of ground-based photometric measurements (again, often taking advantage of stellar clusters), observations from space are superior given a large enough telescope.
The Kepler mission, the most powerful instrument for measuring stellar brightness variations to date (Koch et al. 2010), aims at detecting transits of extrasolar planets in the habitable zone around their host stars. As the only inhabited planet known so far revolves around a middle-aged main sequence G star, the sample of target stars of the Kepler mission was chosen to observe as many similar stars as possible to the highest precision. Stars at such an age do not dominate the population at low galactic latitudes, so the Kepler field was chosen to be some 10° off the galactic plane (Batalha et al. 2010, and references therein). β Cephei and SPB stars with magnitudes of V > 7.5 formed in the galactic plane would hardly reach these galactic latitudes within their main sequence life times and are thus expected to be unusual. Therefore, characterizing Kepler β Cephei and SPB star candidates is important.
The present paper reports the results of a study of bona fide and candidate field and open cluster β Cephei stars in the Strömgren photometric system: 168 target stars were measured, 107 of them being open cluster stars, 17 known cluster and field β Cephei stars, and 42 Kepler targets. To transform the data into the standard system, 117 Strömgren photometric standards were measured as well. The outcome of this study will be used in subsequent papers.
2. Observations
2.1. Measurements and reductions
The measurements were obtained with the 2.1-m telescope at McDonald Observatory in Texas. Three observing runs were carried out in October 2008, March 2009, and August/September 2010. The first two observing runs were dedicated to stars in open clusters and known field β Cephei stars, whereas the third run focused on Kepler targets and on supplementary Hβ measurements of previous targets missing this information.
In all runs, a two-channel photoelectric photometer was used, but only channel 1 was employed. The same filter set, the same photomultiplier tube, and the same operating voltage were used during all observations. The only variables in the observational setup were the reflectivities of the telescope’s mirrors: the primary mirror was not cleaned or aluminized within the time span of the observing runs, but dust on the secondary mirror is blown off on a monthly basis.
Photometric apertures of 14.5 and 29′′ were used in most cases, depending on the brightness of the target and sky background as well as on crowding of the field. In a few cases of extreme crowding or of a close companion, a 11′′ aperture and extremely careful (offset) guiding had to be used. As the photometer’s filter wheel can only carry four filters at once, the uvby measurements had to be taken separately from the Hβ data. No Hβ measurements were taken for open cluster targets that were immediately identified as non-OB stars from their Strömgren “bracket quantities” (see Sect. 4 for details).
As the measurements aimed at obtaining estimates of the effective temperatures and luminosities of most targets possible rather than establishing new standard stars, most stars were observed only once. A few exceptions were made for standard and target stars that were used for purposes of determining extinction coefficients, for target stars that were deemed the most interesting astrophysically, or where a previous measurement appeared suspicious.
2.2. Selection of standard stars
A set of standard stars was selected to span the whole parameter range of the targets in terms of (b − y), m1, c1, β, and E(b − y). It was observed for transforming the measurements into the standard system. For reasons of homogeneity in the colour transformations, the majority of the adopted standard Strömgren indices were taken from the work of a single group of researchers. The standard stars were chosen from the papers on NGC 1502 (Crawford 1994), IC 4665 (Crawford & Barnes 1972), NGC 2169 (Perry et al. 1972), NGC 6910 and NGC 6913 (Crawford et al. 1977), O-type stars (Crawford 1975), h and χ Per (Crawford et al. 1970), Cep OB3 (Crawford & Barnes 1970), Lac OB1 (Crawford & Warren 1976), and on three field stars (Crawford et al. 1972; Knude 1977).
2.3. Data reduction
The data were reduced in a standard way. The instrumental system’s deadtime of 33 ns was determined by measuring the twilight sky, and then was used to correct for coincidence losses. Sky background subtraction was done next, followed by nightly extinction corrections determined from measurements of extinction stars that also served as standards. The applied extinction coefficients varied between 0.14−0.18 in y, 0.054−0.069 in (b − y), 0.050−0.064 in m1, and 0.126−0.157 in c1.
3. Transformation equations
The equation for (b − y) only has two parameters, so we only needed to calculate a linear fit to the data. However, as it turned out, the photometric zeropoints of the three individual observing runs and seasons were different (most likely as a consequence of the large temporal gaps between the observing runs) and had to be determined separately. After adjustment of the zeropoints, the slope of the transformation was re-determined, and the procedure repeated until convergence. The final transformation equation was 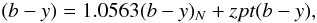 (1)where the subscript N denotes the colour in the natural system, and zpt(b − y) is the zeropoint of the transformation equation, listed in Table 1. The rms residual scatter of a single standard star measurement in (b − y) is an unsatisfactory 13.4 mmag.
(1)where the subscript N denotes the colour in the natural system, and zpt(b − y) is the zeropoint of the transformation equation, listed in Table 1. The rms residual scatter of a single standard star measurement in (b − y) is an unsatisfactory 13.4 mmag.
(b − y) colour transformation zeropoints.
However, this high residual scatter does not mean that the present measurements are imprecise. Some standard stars were measured more than once, which indicates the precision of the data. The average rms scatter of the (b − y) values of standard stars that were measured three times is only 2.0 mmag.
It is worth noting that the (b − y) transformation zeropoints are different by up to 6σ when standard stars from different publications are considered (upper part of Table 1). This comparison only uses data from the most fruitful observing run in Autumn 2008, where several of the different groups of standard stars were measured in the same nights. The total 13.4 mmag residual scatter in (b − y) may therefore be due to a combination of underestimation of the precision of the data and of imperfections in the standard values adopted.
Because accuracy is more important than precision (see, e.g., Bevington 1969, for the distinction between these two terms) in the present case, the same transformation slope was used for all (b − y) measurements, but seasonal (lower part of Table 1) zeropoints were applied. In other words, it is assumed that the changes in the seasonal zeropoints of the colour equations are dominated by variations in the instrumental system.
The remaining transformation equations are to be determined by a (simultaneous) three-parameter fit to the measurements of the standard stars as a colour correction by means of the (b − y) data is necessary. The equation for m1 derived by simultaneously fitting three parameters appears biased from correlations in the m1 and b − y indices due to reddening: E(m1) = −0.32E(b − y). The range spanned by the m1 values of the standard stars is 0.37 mag, the range in (b − y) is 0.89 mag, 2.4 times larger.
Therefore, the measured and standard m1 values were linearly fitted first, and only then were the (b − y) correction term and the zeropoint fixed. This resulted in the following transformation equation 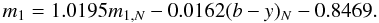 (2)Statistically insignificant variations occurred in the zeropoint when different ensembles of comparison stars were considered. The rms residual of a single standard m1 measurement is 12.1 mmag.
(2)Statistically insignificant variations occurred in the zeropoint when different ensembles of comparison stars were considered. The rms residual of a single standard m1 measurement is 12.1 mmag.
Concerning c1, correlations between the coefficients in the transformation equation due to reddening are also to be expected, but are less severe than in m1 because the c1 values have a much wider spread than m1 and because c1 is less affected by reddening than m1. A simultaneous three-parameter linear fit yielded 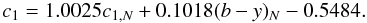 (3)The seasonal zeropoints were roughly, but not fully satisfactorily, consistent. Again, as accuracy is more important than precision, a single zeropoint was adopted for all data sets. The residual scatter of the standard star measurements transformed in this way is 15.6 mmag per single point.
(3)The seasonal zeropoints were roughly, but not fully satisfactorily, consistent. Again, as accuracy is more important than precision, a single zeropoint was adopted for all data sets. The residual scatter of the standard star measurements transformed in this way is 15.6 mmag per single point.
No difficulties with varying zeropoints were encountered when determining the transformation equation for the β value. This is no surprise as it is a differential measurement at the same effective wavelength. The transformation equation for β is 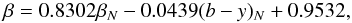 (4)leaving a residual scatter of 11.4 mmag per single measurement. Finally, the transformation equations for the V magnitude require nightly zeropoints (Table 2) to take variable sky transparency into account. As some papers reporting standard Strömgren colour indices do not quote V magnitudes, these values were supplemented by literature data as supplied by the SIMBAD data base and cross-checked with the original references. The final transformation was
(4)leaving a residual scatter of 11.4 mmag per single measurement. Finally, the transformation equations for the V magnitude require nightly zeropoints (Table 2) to take variable sky transparency into account. As some papers reporting standard Strömgren colour indices do not quote V magnitudes, these values were supplemented by literature data as supplied by the SIMBAD data base and cross-checked with the original references. The final transformation was 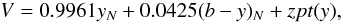 (5)resulting in a residual scatter of 22.2 mmag per single measurement. Observations yielding statistically significant outliers in each of the transformation equations were excluded from the determination of its parameters and are marked as such in the data tables that follow. It cannot be judged whether this indicates a problem with the present measurements or with the standard values used.
(5)resulting in a residual scatter of 22.2 mmag per single measurement. Observations yielding statistically significant outliers in each of the transformation equations were excluded from the determination of its parameters and are marked as such in the data tables that follow. It cannot be judged whether this indicates a problem with the present measurements or with the standard values used.
Nightly V magnitude transformation zeropoints.
4. Results
With the transformation equations in place, the colour indices in the standard system can be determined for all standard and target stars. The results are listed in Tables 3–6. Table 3 contains the present measurements of the standard stars themselves, transformed into the standard system. Table 4 reports the uvbyβ photometry for open cluster target stars not previously known to pulsate. Table 5 lists the Strömgren-Crawford photometry for known β Cephei stars plus a few other targets. Finally, Table 6 contains the results for stars in the Kepler field.
Stars in open clusters are always designated with the cluster name followed by their identification in the WEBDA1 data base. Measurements of standard stars that were rejected for computing the transformation equations (or where no V magnitudes or Hβ values were available in the literature) were treated in the same way as target star observations and are marked with asterisks in Table 3.
 |
Fig. 1 Distributions of the different Strömgren-Crawford colour indices amongst standard (thick histogram bars) and target (thin histogram bars) stars. |
 |
Fig. 2 Comparison of the present measurements and published Johnson photometry. Circles are open cluster targets not yet known to pulsate, diamonds are known β Cephei stars with new Strömgren colour indices, and star symbols are early-type targets in the Kepler field. The dotted line is the relation defined by unreddened B stars, whereas the full line is the relation inferred for reddened OB stars. See text for more information. |
Some of the stars used as standards have been shown to be intrinsically variable in the literature. However, standard stars must have temperatures and luminosities similar to the targets that would ideally be pulsating variables. Therefore the use of variable standard stars of low amplitude cannot be avoided. Intrinsic variability of standard stars not exceeding the accuracy of the present data is therefore tolerable and measurements that are significantly off the limits would be rejected anyway.
4.1. Comments on individual stars
BD+36 4867 was mistakenly observed when intending to measure the uvbyβ standard star BD+36 4868. This error came from confusion of the coordinates of the two stars in the SIMBAD data base at the time of the measurements. The Strömgren indices of BD+36 4867 are listed for completeness in Table 6, indicating a mid G-type star.
The published V magnitudes of NGC 1893 196 vary between 12.30 and 12.79. This unusually wide range raises the suspicion of stellar variability. Table 4 lists V = 12.637 and β = 2.441. The latter value indicates strong hydrogen-line emission, as demonstrated spectroscopically (Marco et al. 2001).
5. Analysis and discussion
5.1. Validity of the transformation equations
The ranges in which the transformation equations are valid are examined in Fig. 1. It shows the distributions of the standard and target star measurements with respect to the different uvbyβ colour indices and reddening. The routines by Napiwotzki et al. (1993) were used to derive the latter.
The (b − y) values of all but one target star (Roslund 2 13, a very red object) are contained within the range spanned by the standard stars. The same comment is true for the c1 parameter and reddening E(b − y). Sixteen (i.e. 10%) of the targets have more positive m1 values than any standard star. These are stars of later spectral types than A0 which are not the prime interest of this work.
As far as Hβ is concerned, five stars with values below 2.55 were observed, including two (supposed) standard and three target stars. Both standard stars were rejected after determining the transformation equations due to high residual deviations. It is suspected that all five of these stars are Be stars. The hydrogen line emission of such stars is often variable (e.g., McSwain et al. 2009) which explains the high residuals and makes the tabulated values unreliable. They are listed for completeness only.
Considering the distribution in E(b − y), about two thirds of the stars with the smallest reddening are among the Kepler targets: the satellite’s field of view deliberately excludes the central galactic plane. Two of the remaining targets are β Cephei stars of rather high galactic latitude, and the remainder are cool main sequence stars in the foreground of some of the target open clusters. In Tables 4–6 the colour indices that are outside the range of those spanned by the standard stars are marked with colons and should be used with caution.
5.2. Are the present data on the standard system?
Before inferring physical parameters of the targets, it must be made sure that the data are commensurate with the standard system. It is a subtle process to obtain accurate standard photometry of reddened early-type stars, see, e.g., Crawford (1994) for a discussion.
One test is to compare published (U − B) colours with (u − b) values from Strömgren indices (see Crawford 1994) and to compare the resulting relation with the one defined by standard stars. This is done in Fig. 2, using the results for target stars with existing UBV photometry. The (U − B) values for the target stars were taken from the General Catalogue of Photometric Data (Mermilliod et al. 1997).
For easier visual inspection, the slope of the (U − B) vs. (u − b) relation was removed by a linear fit. The residuals are compared with those of the standard values for reddened O-type stars (Crawford 1975) and for bright stars earlier than B5 (Crawford et al. 1971), which are on the average considerably less reddened than the O stars. For better illustration, we only show a fit to the relations defined by the standard stars for comparison with the data of the target stars.
The fits for the O and B-type stars in Fig. 2 are somewhat different. However, the relation for the more strongly reddened target stars are not systematically different from the one defined by the reddened O-type standards, and the relation for the less reddened targets shows no systematic offset from the one defined by the mildly reddened B-type standards. The present uvbyβ photometry is therefore on the standard system.
5.3. Distinguishing OB stars from cooler ones
OB stars can be separated from objects of later spectral type by using the reddening independent Strömgren “bracket quantities” [m1] = m1 + 0.32(b − y) and [c1] = c1 − 0.2(b − y). As a rule of thumb, stars with [m1] < 0.14 are B type stars and stars with [m1] > 0.22 are of spectral type A3 and later. Astrophysically, this separation is caused by the changing curvature of the stellar energy distribution depending on temperature. Figure 3 shows the distribution of the target and standard stars in an [m1], [c1] diagram.
 |
Fig. 3 Plot of the Strömgren “bracket quantities”. These reddening-free indices allow an easy separation between OB and cooler stars; all objects with [m1] ≳ 0.14 are non-OB stars. One very cool star lies outside the borders of this diagram. Filled circles are for standard stars, open circles for the target stars. |
All but one standard star were chosen to be of no later type than early A: 83% of the targets are in the same domain. Of the 30 target stars that cannot be OB stars, twelve have been associated with the open cluster Berkeley 4, and should therefore be foreground stars. Seven non-OB stars are Kepler targets, and six were mentioned in connection with NGC 7380, therefore also not being cluster members.
5.4. Effective temperatures and luminosities of the target stars
The effective temperatures and absolute magnitudes of the target stars can be determined with the routines by Napiwotzki et al. (1993, see their paper for accurate descriptions of the calibrations employed). Bolometric corrections by Flower (1996) and a bolometric magnitude of Mbol = 4.74 for the Sun (Livingston 2000) were used to derive stellar luminosities. Figure 4 shows the targets’ locations in a log Teff − log L diagram, in comparison with theoretical pulsational instability strips (Zdravkov & Pamyatnykh 2008).
 |
Fig. 4 log Teff − log L diagram with the positions of the target stars, derived as explained in the text, indicated. Circles are open cluster targets not yet known to pulsate, diamonds are known β Cephei stars with new Strömgren colour indices, and star symbols are early-type targets in the Kepler field. Some model evolutionary tracks are shown for comparison and are marked with the corresponding masses. The slanted full line is the zero age main sequence, the dotted line defines the theoretical SPB star instability strip, and the dashed-dotted line is the theoretical β Cephei star instability strip. |
All targets previously known as β Cephei stars are located within the corresponding instability strip. The catalogue of Galactic β Cephei stars (Stankov & Handler 2005) only contains one object with a mass above 17 M⊙, which could be a Be star, hence have overestimated luminosity from Hβ photometry. In contrast, the present, considerably smaller, sample contains three stars with 17.5 < M/M⊙ < 21. There is one Kepler target in the high mass domain, which, however, appears to be a close binary with no pulsational light variation (Balona et al. 2011).
Table 7 summarizes how many of our target stars lie within the β Cephei and SPB star instability strips, respectively, and how many are located in either and may therefore show both types of oscillations. Each of the open clusters observed contains potential pulsators and is therefore worthy of a variability search. As expected, the Kepler field contains only a few high-mass stars.
Numbers of target stars within the β Cephei or SPB star instability strip, or both.
Two stars in Fig. 4 appear to be post main sequence objects. Berkeley 4 513 is also known as LS I +63 98 and has been classified as an OBe star (Hardorp et al. 1959). The low Hβ value for the star supports this interpretation. A similar comment applies to NGC 7380 4 that has been spectrally classified as B6Vne (Hoag & Applequist 1965). The post main sequence evolutionary status of these two stars may therefore just be apparent: the calibrations of uvbyβ photometry are not applicable to emission line stars.
6. Summary
New uvbyβ photometry was acquired for 168 open cluster and field stars, and was transformed into the standard system by means of measurements of 117 standard stars. The data were demonstrated to be on the standard system, and the limits in which these photometric results are valid were determined. Most target stars are indeed OB stars, and each cluster contains several stars that are located in the pulsational instability strips of main sequence B stars.
These measurements are required to determine the effective temperatures and luminosities of the targets. Published uvbyβ photometry of the target clusters may now be tied into the standard system, allowing investigations of the clusters themselves, in terms of (differential) reddening, distance, etc. This is the foundation for several forthcoming papers devoted to individual clusters, including searches for stellar variability. Balona et al. (2011) discuss the variability of the Kepler targets in detail.
Acknowledgments
This research is supported by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung under grant P20526-N16. This research has made use of the WEBDA database, operated at the Institute for Astronomy of the University of Vienna.
References
- Balona, L. A., Pigulski, A., De Cat, P., et al. 2011, MNRAS, in press [Google Scholar]
- Batalha, N. M., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 713, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. R. 1969, Data reduction and error analysis for the physical sciences (New York: McGraw-Hill), 3 [Google Scholar]
- Crawford, D. L. 1975, PASP, 87, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L. 1994, PASP, 106, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L. 1999, in CCD Precision Photometry Workshop, ed. R. Craine et al., ASP Conf. Ser., 189, 6 [Google Scholar]
- Crawford, D. L., & Barnes, J. V. 1970, AJ, 75, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Barnes, J. V. 1972, AJ, 77, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Warren, W. H. 1976, PASP, 88, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., Glaspey, J. W., & Perry, C. L. 1970, AJ, 75, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., Barnes, J. V., & Golson, J. C. 1971, AJ, 76, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., Barnes, J. V., Gibson, J., et al. 1972, A&AS, 5, 109 [Google Scholar]
- Crawford, D. L., Barnes, J. V., & Hill, G. 1977, AJ, 82, 606 [NASA ADS] [CrossRef] [Google Scholar]
- De Cat, P. 2007, CoAst, 150, 167 [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Hardorp, J., Rohlfs, K., Slettebak, A., & Stock, J. 1959, Publ. Hamburger Sternw., Warner & Swasey Obs., 1 [Google Scholar]
- Hoag, A. A., & Applequist, N. L. 1965, ApJS, 12, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Knude, J. K. 1977, A&AS, 30, 297 [NASA ADS] [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W. C. 2000, in Allen’s Astrophysical Quantities, 4th edition, ed. A. N. Cox (Springer Verlag), 341 [Google Scholar]
- Marco, A., Bernabeu, G., & Negueruela, I. 2001, AJ, 121, 2075 [NASA ADS] [CrossRef] [Google Scholar]
- McSwain, M. V., Huang, W., & Gies, D. R. 2009, ApJ, 700, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moskalik, P., & Dziembowski, W. A. 1992, A&A, 256, L5 [NASA ADS] [Google Scholar]
- Napiwotzki, R., Schönberner, D., & Wenske, V. 1993, A&A, 268, 653 [NASA ADS] [Google Scholar]
- Perry, C. L., Lee, P. D., & Barnes, J. V. 1978, PASP, 90, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Pigulski, A., & Pojmański, G. 2008, A&A, 477, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1994, Science, 263, 50 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stankov, A., & Handler, G. 2005, ApJS, 158, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zdravkov, T., & Pamyatnykh, A. A. 2008, JPhCS, 118, 012079 [Google Scholar]
All Tables
Numbers of target stars within the β Cephei or SPB star instability strip, or both.
All Figures
 |
Fig. 1 Distributions of the different Strömgren-Crawford colour indices amongst standard (thick histogram bars) and target (thin histogram bars) stars. |
| In the text | |
 |
Fig. 2 Comparison of the present measurements and published Johnson photometry. Circles are open cluster targets not yet known to pulsate, diamonds are known β Cephei stars with new Strömgren colour indices, and star symbols are early-type targets in the Kepler field. The dotted line is the relation defined by unreddened B stars, whereas the full line is the relation inferred for reddened OB stars. See text for more information. |
| In the text | |
 |
Fig. 3 Plot of the Strömgren “bracket quantities”. These reddening-free indices allow an easy separation between OB and cooler stars; all objects with [m1] ≳ 0.14 are non-OB stars. One very cool star lies outside the borders of this diagram. Filled circles are for standard stars, open circles for the target stars. |
| In the text | |
 |
Fig. 4 log Teff − log L diagram with the positions of the target stars, derived as explained in the text, indicated. Circles are open cluster targets not yet known to pulsate, diamonds are known β Cephei stars with new Strömgren colour indices, and star symbols are early-type targets in the Kepler field. Some model evolutionary tracks are shown for comparison and are marked with the corresponding masses. The slanted full line is the zero age main sequence, the dotted line defines the theoretical SPB star instability strip, and the dashed-dotted line is the theoretical β Cephei star instability strip. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


