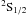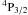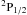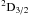| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 15 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201016417 | |
| Published online | 03 March 2011 | |
R-matrix electron-impact excitation data for the Li-like iso-electronic sequence including Auger and radiation damping⋆
Department of PhysicsUniversity of Strathclyde, Glasgow, G4 0NG, UK
e-mail: guiyun.liang@strath.ac.uk
Received: 28 December 2010
Accepted: 27 January 2011
We present results for the electron-impact excitation of all Li-like ions from Be+ to Kr33+ which we obtained using the radiation- and Auger-damped intermediate-coupling frame transformation R-matrix approach. We have included both valence- and core-electron excitations up to the 1s25l and 1s2l4l′ levels, respectively. A detailed comparison of the target structure and collision data has been made for four specific ions (O5+, Ar15+, Fe23+ and Kr33+) spanning the sequence so as to assess the accuracy for the entire sequence. Effective collision strengths (Υs) are presented at temperatures ranging from 2 × 102(z + 1)2 K to 2 × 106(z + 1)2 K (where z is the residual charge of the ions, i.e. Z − 3). Detailed comparisons for the Υs are made with the results of previous calculations for several ions which span the sequence. The radiation and Auger damping effects were explored for core-excitations along the iso-electronic sequence. Furthermore, we examined the iso-electronic trends of effective collision strengths as a function of temperature.
Key words: atomic data / atomic processes / plasmas
These data are made available in the archives of APAP via http://www.apap-network.org, OPEN-ADAS via http://open.adas.ac.uk, as well as anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/528/A69
© ESO, 2011
1. Introduction
Li-like ions are of importance both in astrophysics and in theoretical and experimental atomic physics. Satellite lines arising from transitions of the type 1s2lnl′ → 1s22l (where the generation of 1s2lnl′ states could be from dielectronic recombination of He-like ions or inner-shell excitation of Li-like ions), were observed in solar flare spectra by the Rentgenowsky Spektrometr s Izognutymi Kristalami (RESIK) instrument on the Russian CORONAS-F mission, launched on 2001 July 31 (Phillips et al. 2006). These satellite lines complicate the analysis of the spectrum around the He-like transition lines but they are important diagnostics of the electron density and temperature of a plasma (Phillips et al. 2006; Nahar et al. 2009; Oelgoetz et al. 2009, and references therein). Atomic data for the dielectronic recombination process populating the 1s2lnl′ levels has been reported by Bautista & Badnell (2007).
For the case of outer-shell transitions, some n = 2 → 2 transition lines in Mg9+–Ni25+ were recorded in the early solar flare observation by Widing & Purcell (1976). These have been extensively used in a variety of diagnostic applications, for which accurate atomic data are needed.
The group of Sampson carried-out early work to provide comprehensive atomic data for Li-like ions using the non-resonant relativistic distorted-wave (DW) method. Zhang et al. (1990) calculated collision strengths (Ω) for n = 2 → n = 3,4,5 excitations for the 85 ions with nuclear charge number Z: 8 ≤ Z ≤ 92. These data are still extensively used by current astrophysical modelling codes, e.g. CHIANTI v6 (Dere et al. 2009). Sampson and co-authors (1985a,b; Zhang et al. 1986; Goett & Sampson 1983) reported the collision strengths of inner-shell (n ≤ 3) excitations in the Li-like ions with Z: 6 ≤ Z ≤ 74. These were obtained using a Coulomb-Born-Exchange (CBE) method. Their data is the main source used by CHIANTI v6 to model the satellite lines of He-like ions.
We turn next to R-matrix calculations, which take account of resonances normally omitted by the DW and CBE methods. Berrington & Tully (1997) calculated the valence-electron impact excitation of Fe23+ (up to n = 5) using the Breit-Pauli R-matrix method. Gorczyca & Badnell (1996) demonstrated significant reduction of the resonance contribution due to radiation damping in the K-shell excitation of Fe25+ and Mo41+. Subsequently, Ballance et al. (2001) performed a Breit-Pauli R-matrix calculation including radiation damping for the inner-shell excitations (1s2nl → 1s2ln′l′, where n,n′ ≤ 3) in Fe22+ and Fe23+. Furthermore, taking Auger damping into account, Whiteford et al. (2002) performed new calculations for these (to n = 3) inner-shell excitations in Ar15+ and Fe23+, using an intermediate-coupling frame transformation (ICFT) R-matrix method. A complete excitation dataset for the Ar15+ and Fe23+ ions was presented in their work by incorporating data from a separate calculation for outer-shell excitations up to levels of the n = 5 complex. There appears to be no previous inner-shell electron-impact excitation work using the close-coupling method for all other ions in this iso-electronic sequence.
For valence-electron excitations, Griffin et al. (2000) carried-out LS-coupling R-matrix with pseudo-states (RMPS) calculations for C3+ and O5+. Similar calculations for Be+ (n ≤ 5) were performed by Ballance et al. (2003). Aggarwal and co-authors (2004a,b, 2010) reported results for n ≤ 5 for N4+, O5+, F6+, Ne7+, Na8+, Ar15+ and Fe23+ which were obtained by using the Dirac R-matrix method as implemented in darc.
Here, we report-on calculations for the electron-impact excitation of the Li-like iso-electronic sequence ions from Be+ to Kr33+ which were made using the ICFT R-matrix method. The main focus of the present work is on the inner-shell transitions to n = 4 which contribute to the population of the upper levels (1s2lnl′) of the He-like satellite lines. Separate outer-shell calculations were made which went up to n = 5.
This paper is one of our series of works on iso-electronic sequences: F-like, Witthoeft et al. (2007), Ne-like, Liang & Badnell (2010), Na-like, Liang et al. (2009a,b). This work is part of the UK Atomic Processes for Astrophysical Plasmas (APAP) network1.
The remainder of this paper is organized as follows. In Sect. 2, we discuss details of the calculational method and pay particular attention to comparing our underlying atomic structure results with those of previous workers. The model for scattering calculation is outlined in Sect. 3. The excitation results themselves are discussed in Sect. 4.
2. Sequence calculation
The aim of this work is to perform R-matrix calculations employing the ICFT method (see Griffin et al. 1998) for all Li-like ions from Be+ to Kr33+. Our approach to the valence- and core-excitation data is to perform the two calculations independently and later merge the effective collision strengths (Υ) back together into a single dataset for each ion.
The reason for this approach is that the number of R-matrix continuum basis orbitals required increases with box size (which scales as n2) and also with scattering energy. Inner-shell excitations require a large scattering energy and n = 5 gives rise to a large box size. The two together result-in too large an (N + 1)-electron Hamiltonian for Auger plus radiation damped R-matrix calculations along an entire sequence. There are also numerical stability issues when the number of continuum basis orbitals exceeds 100 per orbital l.
The close-coupling (CC) and configuration interaction (CI) expansions used consist of the 1s2 { 2,3,4,5 } l (14 LS terms, 24 fine-structure levels) and 1s2 { 2,3,4 } l, 1s2l { 2,3,4 } l′ (89 LS terms, 195 fine-structure levels) configurations for the valence- and core-excitation calculations, respectively.
2.1. Structure: level energies
The target wavefunctions (1s − 5g) were obtained from autostructure (AS, Badnell 1986) using the Thomas-Femi-Dirac-Amaldi model potential. Relativistic effects were included perturbatively from the one-body Breit-Pauli operator (viz. mass-velocity, spin-orbit and Darwin) without valence-electron two-body fine-structure operators. This is consistent with the operators included in the standard Breit-Pauli R-matrix suite of codes. The radial scaling parameters, λnl (n = 1 − 5; l ∈ s,p,d, and f, were obtained separately for each ion by a two-step optimization procedure. In the first step, the energy of the 1s22l was minimized by varying the λ1s, λ2s and λ2p scaling parameters. Then, the energy of the 1s2 { 3,4,5 } l configurations was minimized by varying the λ { 3,4,5 } l scaling parameters. In the calculation including doubly-excited configurations, the energy of the 1s2 { 3,4 } l configurations was minimized by varying the λ { 3,4 } l scaling parameters. In order to maintain consistency and so as not to introduce arbitrary changes along the sequence, the optimization procedure is done automatically in autostructure without any manual re-adjustment. The resultant scaling parameters are listed in Table 1. We took λ5g to be unity since it is insensitive to optimization and the atomic structure itself is insensitive to it.
Thomas-Fermi potential scaling factors used by autostructure for the outer-shell calculations (see text for details).
Comparisons of the level energies (Ryd) of 1s2 {2,3,4,5} l (l ∈ s,p,d,f and g), 1s2l2 and 1s2s2p configurations in O5+, Ar15+, Fe23+, and Kr33+ ions.
A comparison of level energies is made with the experimentally derived data available from the compilation of NIST v32 and with other theoretical results for several specific ions (O5+, Ar15+, Fe23+, and Kr33+) spanning the sequence so as to assess the accuracy of our present structure over the entire iso-electronic sequence – see (the composite) Table 2. The low-lying level energies of all ions agree to within about 1%. The present calculations also show a good agreement (1%) with previous results obtained by using grasp (Aggarwal et al. 2004a,b, 2010) and the Dirac-Fock-Slater method (Zhang et al. 1990) for O5+, Ar15+ and Fe23+ 3. It should be noted that there can be large factor differences in energy separations between closely-spaced levels arising from different configurations, e.g. 5fj − 5gj′ etc. For higher-lying levels, our energies differ from NIST’s by at most 0.5% (see Table 2). Checks with AS calculations including both the two-body fine-structure and quantum-electrodynamic (QED) effects revealed the two-body fine-structure contribution to be negligible when compared with those of QED for these Li-like ions. (Two-body fine-structure and QED operators have not yet been incorporated into the present R-matrix codes, but such work is in progress – Eissner, private communication.)
2.2. Structure: line strength S
A further test of our structure calculation is to compare line strengths (Sij for a given i ← j transition). In terms of the transition energy Eji (Ryd) for the j → i transition, the absorption oscillator strength, fij, can be written as 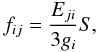 (1)and the transition probability or Einstein’s A-coefficient, Aji, as
(1)and the transition probability or Einstein’s A-coefficient, Aji, as 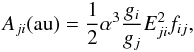 (2)where α is the fine structure constant, and gi, gj are the statistical weight factors of the initial and final states, respectively. Table 3 shows a comparison of line strengths for the most prominent satellite lines (Gabriel 1972) for several ions (O5+, Ar15+, Fe23+ and Kr33+) spanning the sequence.
(2)where α is the fine structure constant, and gi, gj are the statistical weight factors of the initial and final states, respectively. Table 3 shows a comparison of line strengths for the most prominent satellite lines (Gabriel 1972) for several ions (O5+, Ar15+, Fe23+ and Kr33+) spanning the sequence.
Comparisons of line strengths S for K-shell transitions in ions (O5+, Ar15+, Fe23+ and Kr33+) spanning sequence.
To-date, the Li-like inner-shell line-strength data (n = 2p → 1s) calculated by Goett & Sampson (1983) is the main source of data used in astrophysical modelling. So, a comparison with their results, and others, has been made to assess the present structure results for S over the iso-electronic sequence – see Table 3. For O5+, results for most (76%) of the listed transitions agree to within 15% . For Ar15+, there is good agreement with Goett & Sampson (1983) – about 86% of transitions are within 15%. The present results also show excellent agreement with the data of Whiteford et al. (2002) also obtained using autostructure. For Fe23+, almost all transition lines show excellent agreement (to within 5%) with the results of Whiteford et al. (2002) except for the s-line – there is somewhat of a spread of results for this line. Most of transitions (64%) show agreement to within 15% between the present AS and the multiconfiguration Dirac-Fock (MCDF) calculation of Chen (1972), in which the Breit and QED contributions have been included in the transition energy. Bautista et al. (2003) took the relativistic two-body operator and term-energy corrections (TECs) into account in their autostructure calculation, resulting-in their line strengths being slightly larger than the present AS ones. Yet, they are still within 15% for most transitions (63%). For the highly-charged ion, Kr33+, 73% of transitions agree to within 15% with the results of Goett & Sampson (1983).
Furthermore, a comparison of the line strength has been done here for outer-shell (dipole) transitions of ions spanning the sequence, see Fig. 1. For O5+, the data of Zhang et al. (1990) is still the main source for astrophysical modelling and 66% of available transitions agree to within 5% of the present results. An excellent agreement is obtained between the present results and those of the grasp calculation by Aggarwal & Keenan (2004a): 97% of available dipole transitions agree to within 5%. For Ar15+, a comparison with the previous AS (Whiteford et al. 2002) and grasp calculations (McKeown et al. 2004b) has been made: around 93% and 81%, respectively, of available transitions agree to within 5%. For Fe23+, 98% of available outer-shell transitions from the ADAS database4 (Whiteford et al. 2002) show agreement to within 5%. The present AS calculation also shows good agreement with the grasp calculation performed by McKeown et al. (2004b) – 75% of available transitions show agreement to within 5%. For Kr33+, somewhat worse agreement appears with the results of Zhang et al. (1990) which were obtained using Dirac-Slater atomic-structure approach. However, there are still about 57% of available transition showing agreement to within 10%.
 |
Fig. 1 Comparison of the line strength (S) of outer-shell dipole transitions for ions spanning the sequence. MAK04 corresponds to the grasp calculation done by McKeown et al. (2004b). The horizontal dashed lines correspond to agreement within 5%. [Colour online] |
Thus, we believe that the atomic structure of the ions spanning the sequence is reliable, and expect the uncertainty in collision strengths (Ωs) due to inaccuracies in the target structure to be correspondingly small.
3. Scattering
As demonstrated for inner-shell excitations of the Na-like iso-electronic sequence, including the astrophysically abundant Fe15+, (Liang et al. 2008; 2009b) and the Li-like ions Ar15+ and Fe23+ (Ballance et al. 2001; Whiteford et al. 2002), the radiation- and Auger-damping effects significantly reduce the resonant enhancement of the collision strengths. In the Na-like iso-electronic sequence, the Auger damping effect was found to be the dominant damping mechanism over the entire sequence although the radiation damping increased quickly with increasing nuclear charge. The radiation- and Auger-damping effects have been incorporated into the present ICFT and Breit-Pauli R-matrix suite code via a complex optical potential as detailed by Gorczyca & Robicheaux (1999) and Robicheaux et al. (1995). For clarity, we give a brief description of the two damping effects for the specific case of Li-like ions. Over the sequence Be+–Kr33+, the four-electron resonance configurations are of the form 1s [ 2s,2p ] [ 2s − 4f ] nl, and they can decay via the following channels: ![\begin{eqnarray} {\rm 1s[2s,2p][2s-4f]}nl & \to & {\rm 1s^2[2s-4f] + e}^- \label{eqn_path_ap}\\ & \to & {\rm 1s^2}nl + {\rm e}^- \label{eqn_path_as}\\ & \to & {\rm 1s^2[2s,2p][2s-4f]}+h\nu \label{eqn_path_rp}\\ & \to & {\rm 1s^2[2s-4f]}nl+h\nu. \label{eqn_path_rs} \end{eqnarray}](/articles/aa/full_html/2011/04/aa16417-10/aa16417-10-eq123.png) The participator KLn/KMn/KNn Auger channel (Eq. (3)) scales as n-3 and is automatically described in the R-matrix method by the contribution to the close-coupling expansion from the right-hand side of Eq. (3). However, the spectator KLL/KLM/KLN Auger pathway (Eq. (4)) is independent of n and only low-n resonances (n ≤ 4 here) are included explicitly in the close-coupling expansion. The higher-n are accounted-for by the complex optical potential which acts as a loss mechanism. The last two channels, Eqs. (5) and (6), represent radiation damping.
The participator KLn/KMn/KNn Auger channel (Eq. (3)) scales as n-3 and is automatically described in the R-matrix method by the contribution to the close-coupling expansion from the right-hand side of Eq. (3). However, the spectator KLL/KLM/KLN Auger pathway (Eq. (4)) is independent of n and only low-n resonances (n ≤ 4 here) are included explicitly in the close-coupling expansion. The higher-n are accounted-for by the complex optical potential which acts as a loss mechanism. The last two channels, Eqs. (5) and (6), represent radiation damping.
Our ICFT R-matrix calculations employed 40 (core-electron excitation) or 60 (valence-electron excitation) continuum basis orbitals per angular momentum to represent the (N + 1)th-electron, over most of the sequence. For lower-charged ions, the number of continuum basis orbitals was increased. For example, the values were 46 and 65 in B2+ for the valence- and core-electron excitations, respectively. All partial waves from J = 0 to 41 were included explicitly and contributions from higher J-values were included using a “top-up” procedure (Burgess 1974; Badnell & Griffin 2001). The contributions from partial waves up to J = 10 were included in the exchange R-matrix, while those from J = 11 to 41 where included via a non-exchange R-matrix calculation. For the exchange calculation, a fine energy mesh (less than 0.005 Ryd, and even finer to 0.0002 Ryd for lower-charged ions) was used to resolve the majority of narrow resonances below the highest excitation threshold, which has been tested to be sufficient for the convergence of the effective collision strength. From just above the highest threshold excitation to a maximum energy of ten times the ionization potential for each ion, a coarse energy mesh (1.0 × 10-2z2 Ryd, where z = Z − 3 is the residual charge of ion) was employed. For the non-exchange calculation, a step of 1.0 × 10-2z2 Ryd was used over the entire energy range.
We then used the infinite energy Born limits (non-dipole allowed) and line strengths (dipole allowed) from autostructure so that higher energy reduced collision strengths (Ω), as defined by Burgess & Tully (1992), can be found from interpolation in Burgess-Tully space for all additional higher energies. The effective collision strengths at 13 electron temperatures ranging from 2 × 102(z + 1)2 K to 2 × 106(z + 1)2 K are produced as the end product. The data were stored in the ADAS adf04 format (Summers 2004).
 |
Fig. 2 Comparison of collision strengths Ω from the present ICFT R-matrix calculation in with those of Goett & Sampson (1983). a) O5+: 1s22s 2S1/2 → 1s2s2p 4P3/2 excitation (u line in Table 3); b) Ar15+: 1s22s 2S1/2 → 1s2p2 2P1/2 excitation (1-37, ID is as list in Table 2); c) Fe23+: 1s22s 2S1/2 → 1s2s2p 2P1/2 excitation (r line in Table 3). AS-DW corresponds to the present Breit-Pauli distorted-wave calculation using autostructure; d) Kr33+: 1s22p 2P1/2 → 1s2p2 2D3/2 excitation (k line in Table 3). [Colour online] |
 |
Fig. 3 Comparison of the effective collision strength Υ between the present ICFT R-matrix calculation and previous results of Goett & Sampson (1983) and Whiteford et al. (2002). a) O5+: 1s22s |
A separate Breit-Pauli DW calculation has been done for Fe23+ to study the importance of the effect of resonance enhancement. We find that it is still significant and widespread after Auger-plus-radiation damping has been taken into account. The DW approach has recently been incorporated into the autostructure code by Badnell (2011, see also autostructure code-log in APAP website1). It is self-consistent with the present R-matrix ICFT method in its calculation of the target structure.
4. Results and discussions
4.1. Comparisons with previous calculations for core-excitations
The present ICFT R-matrix results are compared with those of previous works for four ions (O5+, Ar15+, Fe23+ and Kr33+) which span the range of calculated data for this iso-electronic sequence. Here we select a few inner-shell transition lines to test the accuracy of the present ICFT R-matrix calculations. An extensive comparison (all available excitation data from the ground level 1s22s 2S1/2) between the present ICFT R-matrix and previous calculations has been made for the four ions to check the broad accuracy and the resonant enhancement (when compared with distorted-wave data) of the present ICFT R-matrix data. Earlier sequence calculations of core-electron impact excitation from the 1s2 {2,3} l states were by Goett & Sampson (1983, hereafter GS83) and Sampson et al. (1985b) using the Coulomb-Born exchange method.
-
O5+ To-date, there is no R-matrix calculation available for this ion. The background of the ordinary collision strength Ω of the present ICFT R-matrix calculation agrees well with that from the Coulomb-Born exchange method by Goett & Sampson (1983), as shown in Fig. 2 for the 1s2s2p 4P3/2 → 1s22s 2S1/2 transition line (the u line in Table 3). The resultant effective collision strengths (Υ) are in agreement to within 10% over the entire temperature range, which is due to the scarce and weak resonances left after the Auger-plus-radiation damping has been taken into account. The undamped Υ is higher than the results of Goett & Sampson (1983) by ~20–35% for the temperature range 4 × 102(z + 1)2–4 × 103(z + 1)2 K.
-
Ar15+ A weak non-dipole transition line, due to 1s2p2 2P1/2 → 1s22s 2S1/2, was selected for this ion. Figure 2b demonstrates that the background of the present calculation agrees well with the results of Goett & Sampson (1983). Strong resonances appear as expected for forbidden transitions, which significantly enhances the effective collision strengths over the temperature range 103(z + 1)2–105(z + 1)2 K. We also find strong Auger and radiation damping effects on the Ω/Υ for this transition, that will be discussed in detail later. At higher temperatures, the resonance contribution to the present R-matrix results becomes negligible, which leads-to good agreement with those of Goett & Sampson (1983). In a comparison with previous R-matrix data (Whiteford et al. 2002), our results with Auger-plus-radiation damping also show a good agreement over the entire temperature range, see Fig. 3b. A complete dataset from Whiteford et al. (2002) is available from the OPEN-ADAS database5. Thus we have made an extensive comparison (all core-excitation data from the 1s22l states) with them at the temperature (5.0 × 106 K) of peak Ar15+ fractional abundance in equilibrium (Bryans et al. 2009), as well as at a lower (5.0 × 105 K) and a higher (2.0 × 107 K) temperature. In this comparison, we adopt the configuration, total angular momentum, and energy ordering as the “good” quantum numbers to match the transitions from the two different calculations. Recall, Whiteford et al. (2002) did not include any n = 4 states. We find that the Υ results for 73% of core-excitations agree to within 20% at Te = 5.0 × 106 K. This slightly large difference between the two calculations with same method, is attributed to the different atomic models (n = 3 vs. n = 4). There are 88% of core-excitations to n = 2 levels showing agreement to within 20%, whereas the percentage is about 70% for core-excitations to n = 3 levels. This is consistent with the expectation that the influence of n = 4 states is stronger for the core-excitations to n = 3 than to n = 2. At the low and high temperatures, the percentage is 59% and 78%, respectively.
-
Fe23+ A strong transition (the r line), due to 1s2s2p 2P1/2 → 1s22s 2S1/2, was selected for this ion. The ordinary collision strength Ω of Goett & Sampson (1983) shows a good agreement with the background of the present ICFT R-matrix calculation, as well as the present Breit-Pauli DW calculation using autostructure (AS-DW), see Fig. 2. For this ion, earlier R-matrix excitation data is available (Ballance et al. 2001; Whiteford et al. 2002). The present radiation damped calculation agrees well with the smaller-scale calculation by Ballance et al. (2001, see Fig. 7a in their work). Their corresponding Maxwellian-averaged Υ is also in agreement with the present Auger-plus-radiation damping results and with those likewise of Whiteford et al. (2002). Due to the weak resonance contribution for this excitation, the calculation from the Coulomb-Born exchange method (GS83) also agrees well with the result of R-matrix calculation, see Fig. 3. A complete dataset of Whiteford et al. (2002) is available from the OPEN-ADAS database5. Thus we make an extensive comparison as just done for Ar15+ at three temperatures (2.0 × 106 K, 2.0 × 107 K and 1.0 × 108 K). The percentage agreements are 68%, 78% and 81% at the low, middle (corresponding to peak abundance) and high temperatures, respectively.
-
Kr33+ Another satellite line (the k line in Table 3) is selected to test the accuracy of the present calculation. Figure 2 displays that the background of the present ICFT R-matrix results is slightly lower than the Coulomb-Born exchange results of Goett & Sampson (1983) by ~10%. This mirrors the reduction of the line strength demonstrated in Table 3. The resulting effective collision strengths agree with those from the Coulomb-Born exchange approach to within ~10% over the entire temperature range, which is due to the scarcity of resonances for this satellite (k) line following damping. Auger-plus-radiation damping is significant for this line (see Fig. 2) and so the final damped resonance contribution is not significant for the effective collision strength at any temperature.
From the above comparison for the four specified ions (O5+, Ar15+, Fe23+ and Kr33+) spanning the sequence, we believe that the present ICFT R-matrix results (Ω and Υ) are reliable. For ions near neutral (below O5+), R-matrix with pseudostates calculations are needed to consider ionization loss in the excitation, but the present are the best data to be made available to-date for these inner-shell transitions.
 |
Fig. 4 Collision strengths Ω from the present ICFT R-matrix calculation and DW data (Zhang et al. 1990) for the dipole 1s24p 2P1/2 → 1s22s 2S1/2 transition (left) and non-dipole 1s24d 2D3/2 → 1s22s 2S1/2 transition (right) of ions (O5+, Ar15+, Fe23+ and Kr33+) spanning the sequence. Note: The scattered electron energy is in unit of z2 Ryd (z is the residual charge). [Colour online] |
4.2. Comparisons with previous calculations for valence-excitations
As mentioned in the introduction, most available valence-excitation data is from the (relativistic) distorted-wave method (Zhang et al. 1990). We select one dipole transition line (1s24p 2P1/2 → 1s22s 2S1/2) and one non-dipole transition line (1s24d 2D3/2 → 1s22s 2S1/2) to test the accuracy of the present ICFT R-matrix calculations, see Fig. 4. The background of the collision strength Ω agrees well with the distorted-wave calculation for ions (O5+, Ar15+, Fe23+ and Kr33+) spanning the sequence.
For the cosmic abundant ion Fe23+, various R-matrix calculations including Breit-Pauli (Berrington & Tully 1997), ICFT (Whiteford et al. 2002) and darc (McKeown 2005) are available. In the results of Whiteford et al. (2002), McKeown (2005, see Figs. 7.13–7.16) noticed that there are strong resonances, resonance shifts and background enhancement around thresholds for some outer-shell transitions when compared with her darc calculation. The ordinary and effective collision strengths for 1s24d 2D3/2 → 1s24d 2D5/2 are shown in Fig. 5 to illustrate this problem. A hard-copy comparison of Ω indicates that the present ICFT R-matrix calculation agrees well with the darc calculation by McKeown (2005) – electronic results for McKeown (2005) are not available – which is confirmed by the effective collision strength Υ, see the inset panel. The numerical problem in the work of Whiteford et al. (2002) has been traced to the treatment of the inner-region exchange integrals for high-L partial waves. The problem and solution is discussed in detail by Berrington (2006) and was incorporated into the Breit-Pauli R-matrix codes at the time (2006) – the ICFT method uses the standard inner-region Breit-Pauli codes. Moreover, an extensive comparison (see Table 46) has been made for transitions with a large disagreement as reported by McKeown (2005) and they show good agreement between the present ICFT and darc calculations. This demonstrates that the present results for outer-shell excitations are reliable for diagnostic modelling application.
 |
Fig. 5 Collision strength Ω for the 1s24d 2D3/2 → 1s24d 2D5/2 excitation, as well as the comparison of resultant effective collision strength Υ with previous works of McKeown (2005) using darc R-matrix suite code and Whiteford et al. (2002). [Colour online] |
A complete set of effective collision strengths for O5+ obtained using darc (Aggarwal & Keenan 2004a) is available electronically. Comparison with the present results shows agreement to within 20% for 97% of all excitations at the temperature (Te = 3.2 × 105 K) of peak fractional abundance in equilibrium (Bryans et al. 2009). This provides further support that the present results are reliable over the sequence. For ions near neutral, viz. C3+, Griffin et al. (2000) performed an LS-coupling R-matrix with 32 pseudostates (5s, 5p, 5d, 5f ··· 12s, 12p, 12d and 12f) calculation to determine ionization loss in the valence-excitations, and found the reduction of the effective collision strengths to be less than 10% for excitations up to n = 3. For excitations to the n = 4 shell, the pseudostate results are typically 20% smaller, with one transition (2s−4d) being 30%. However, the present are the best J-resolved data to be made available to-date.
Finally, we note that dipole transitions between closely-spaced levels, e.g. 5fj − 5gj′, are dominated by contributions from high angular momentum and these come mainly from the Coulomb-Bethe “top-up”. The top-up is inversely proportional to the energy separation. Our sequence work makes use of calculated energies. This can give rise to large errors in the top-up. This has no practical consequences. The excitation rates are very large and so, along with proton collisions, establish statistical values for these level populations independently of the precise value of the excitation rate.
4.3. Damping effects along the sequence
As shown in Fig. 2, radiation damping significantly reduces the resonance strength of inner-shell transitions. The inclusion of Auger damping further reduces the resonance strength. Correspondingly, the resonance enhancement of the effective collision strengths is reduced, see Fig. 3. For some strong excitations, the resonance contribution to the Υ decreases to the level of 10%, e.g. the 1s22s 2S1/2 → 1s2s2p 2P1/2 excitation line of Fe23+ shown in Fig. 3. However, for some weak transition lines, the damped resonance contribution to the effective collision strength is still non-negligible and leads to significantly higher results than those without resonances (see Fig. 3 for Ar15+), e.g. the work of Goett & Sampson (1983) using the Coulomb-Born exchange method.
In the inner-shell excitations for the Na-like iso-electronic sequence, Liang et al. (2009b) clearly demonstrated that radiation damping increases steadily with increasing of nuclear charge Z, but the Auger damping effect still plays an important role on the reduction of the resonance enhancement of Υ over the iso-electronic sequence.
Here we illustrate the radiation and Auger-plus-radiation damping effects along the sequence by a scatter plot of the ratios of damped to undamped (or only radiation damped) Υ at Te = 104(z + 1)2 K for dipole transitions of O5+ (Fig. 6a), Ar15+ (Fig. 6c), Fe23+ (Fig. 6e) and Kr33+ (Fig. 6g). The widespread effect of the radiation and Auger-plus-radiation damping effects is illustrated. For the low-charge ion (O5+) the radiation damping is small, being less than 10% for 99% of all dipole core-excitations at the temperature of 104(z + 1)2 K. The Auger damping is the prominent factor for the reduction of resonance enhancement of Υ. It can up to a factor of 5 for a few dipole transitions. For Ar15+, the radiation damping is less than 10% for most (94%) of the dipole transitions. The Auger damping is stronger and larger than a factor of 2 for 30% of the illustrated dipole transitions. For Fe23+, the radiation damping increases, but the Auger damping is still the dominant and stronger damping effect in the reduction of resonance enhancement of Υ. About 30% of dipole transitions show an Auger damping reduction of over a factor of 2 when compared with the radiation damped Υ. For higher-charge ions, e.g. Kr33+, the radiation damping is greater than 30% for 10% of the dipole transitions. But, Fig. 6g demonstrates that Auger damping is still the dominant resonance damping reduction of Υs at Te = 104(z + 1)2 K. Additionally, we notice that there are a few weak transitions with the ΥR/ΥU ratio being slightly larger than unity. This was found to be due to the low resolution of the undamped resonances. Recall, damping both broadens and reduces the height of resonance profiles.
 |
Fig. 6 Left-hand panels: scatter plots showing the ratio of the effective collision strength Υ with Auger-plus-radiation damping (ΥA + R) or radiation damping (ΥR) to without damping (ΥU) or with radiation damping alone, as a function of line strength for dipole core-excitation of O5+a), Ar15+c), Fe23+e) and Kr33+g) at temperature of 104(z + 1)2 K, where z is the ionic charge. Right-hand panels: percentage of the corresponding transitions where the effect of damping exceeds 10%, 20% and 30%. [ Colour online] |
An illustrative way to quantify the information in the scatter plot is to count how many transitions differ by more than a given value. In Figs. 6b, d, f and h, we show the percentage of the dipole transitions where the Auger-plus-radiation damping effect, or radiation or Auger damping effects alone, are at least 10%, 20% and 30% for the four ions. Here, 0%, < 1%, 3% and 10% of dipole transitions show a radiation damping effect of more than 30% at Te = 104(z + 1)2 K for O5+, Ar15+, Fe23+ and Kr33+, respectively. The percentage for higher-charge ions, e.g. Fe23+ and Kr33+, is higher than that of lower-charge ions. This illustrates that the radiation damping is more widespread for higher-charge ions, as one would expect. There are about 36%, 43%, 41% and 37% of dipole transitions showing a further Auger damping of more than 30% at the temperature of 104(z + 1)2 for O5+, Ar15+, Fe23+ and Kr33+, respectively. This means that the Auger damping is still the dominant damping effect over the entire sequence.
4.4. Resonant enhancement for core-excitations
The Auger-plus-radiation damping effect significantly reduces the resonance enhancement of the effective collision strength for core-excitations. Does this mean that one can use non-resonant excitation data such as DW? Here we investigate it statistically by comparing distorted-wave (AS-DW) and R-matrix (ICFT) calculations for Fe23+. The exact same atomic structure was used for the AS-DW calculation as has been described and used in the R-matrix calculation. This eliminates differences in the collision data due to the use of different atomic structures. The scatter plot in Fig. 7 demonstrates that the resonant enhancement can be larger than a factor of 2 for some core-excitations. The percentage is about 66% and 59% of all core-excitations at Te = 2.0 × 105 and 2.0 × 107 K, respectively. So a complete sequence calculation with resonances is still necessary. The non-resonant DW results could be supplemented by resonances calculated perturbatively. This is just the complement of dielectronic recombination. It is beyond the scope of the present work.
 |
Fig. 7 The ratio of the effective collision strengths Υ for all core-excitations in Fe23+ between the present ICFT R-matrix and Breit-Pauli DW (autostructure) calculations at the temperature of 2.0 × 105 and 2.0 × 107 K. The filled and dashed regions correspond to a agreement of 20% and a factor 2, respectively. [Colour online] |
4.5. Iso-electronic trends
As noted in the previous sequence works (Witthoeft et al. 2007; Liang et al. 2009b; 2010), the level mixing effect for higher excited levels strongly affects the behaviour of the Υ along the sequence. Here, we also take configuration, total angular momentum J and energy ordering for level matching in the comparison between different calculations and the investigation of Υ along the iso-electronic sequence. This satisfactorily eliminates uncertainty originating from the non-continuity of level-ordering along the sequence. The choice of reference ion, Fe here, is irrelevant of course.
 |
Fig. 8 Effective collision strengths Υ at temperatures of Te = 5 × 102(z + 1)2, 103, 104 K (here, z = Z − 3) along the iso-electronic sequence. Left-hand panels: 1s2s2p 4P3/2 → 1s22s 2S1/2 (u line), 1s2s2p 2P1/2 → 1s22s 2S1/2 (r line) and 1s2s2p 4P1/2 → 1s22p 2P3/2 (3-26) transitions. Right-hand panels: 1s2p2 4P1/2 → 1s22p 2P3/2 (h line), 1s2p2 2D3/2 → 1s22p 2P1/2 (k line) and 1s2s2 2S1/2 → 1s22p 2P3/2 (3-25) transitions. [Colour online] |
In Fig. 8, we show the effective collision strength Υ at Te/(z + 1)2 = 5 × 102, 103 and 104 K along the sequence for a few satellite lines in Li-like ions: at the low temperature of 5 × 102(z + 1)2 K, spikes and/or dips are observed at low charges for some transitions, e.g. 1s22p 2P3/2 → 1s2s2p 4P1/2 (3 − 26). With increasing temperature, the spikes and/or dips disappear, as expected, because the resonance contribution becomes weaker and eventually negligible. For K-shell excitations, the behaviour of Υ along the sequence differs from the L-shell, for example F-like (Witthoeft et al. 2007) and Ne-like sequences (Liang & Badnell 2010). The irregularity appears only for the low-charged ions. Above Z ~ 14, the effective collision strengths show a smooth behaviour. This is due to the high core-excitation energy. KMn resonances are all positioned well above threshold while KLn can only Auger to the final-state for high-n at high-charge and so there is little variation. Only at low-charge do low-n KLn resonances come into play. The “precise” n-value can be estimated from the Rydberg formula: 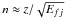 , where f is the final state and j is an intermediate parent resonant state to which the Rydberg series of resonances converges. For example, for O5+ (z = 5) from Table 2 we have Efj = 2.36 Ryd for the 40 → 25 (j → f) core-Auger, giving n = 4 as the lowest KLn resonance for any excitation transition i − 25. The variation in n and energy spacing is relatively largest for the smallest n-values. This variation can then be seen in the Maxwell-averaged results.
, where f is the final state and j is an intermediate parent resonant state to which the Rydberg series of resonances converges. For example, for O5+ (z = 5) from Table 2 we have Efj = 2.36 Ryd for the 40 → 25 (j → f) core-Auger, giving n = 4 as the lowest KLn resonance for any excitation transition i − 25. The variation in n and energy spacing is relatively largest for the smallest n-values. This variation can then be seen in the Maxwell-averaged results.
5. Summary
We have performed 195-level (24-level) ICFT R-matrix calculations the of core- (valence-) electron-impact excitation of all ions of the Li-like iso-electronic sequence from Be+ to Kr33+.
Good agreement with the available experimentally derived data and the results of others for level energies and line strengths S for several specific ions (O5+, Ar15+, Fe23+, and Kr33+) spanning the iso-electronic sequence supports the reliability of the present R-matrix excitation data. This was confirmed specifically by detailed comparisons (including previously available R-matrix calculations) of Ω and Υ for O5+, Ar15+, Fe23+ and Kr33+.
A problem for some Fe23+ outer-shell excitation transitions in the earlier ICFT calculation by Whiteford et al. (2002) was checked-for in the present calculations by comparison with the fully relativistic darc calculation by McKeown (2005) and not found. It had been solved by a previous correction (Berrington 2006) to the inner-region Breit-Pauli codes which the ICFT method makes use of.
The present R-matrix excitation data is expected to be an important improvement on the current data (from Coulomb-Born exchange approximation) extensively used by the spectroscopic diagnostic modelling communities in astrophysics and magnetic fusion.
The Auger-plus-radiation damping effect along the sequence was examined, it is significant and widespread over the entire sequence and more-so for the higher-charge ions. For some inner-shell transitions (39% of available DW data to 1s22l levels in Ar15+), the damped effective collision strengths are still larger than those without the inclusion of resonances (by 20%). The Auger damping effect was found to be dominant in the reduction of resonance enhancement on the electron-impact excitation over the entire sequence, whereas the radiation damping is small for lower-charge ions but increases with increasing nuclear charge.
By excluding the level crossing effects on the Υ, we examined the iso-electronic trends of the effective collision strengths. A complicated pattern of spikes and dips of Υ at low temperatures was noted again along the sequence for some transitions with strong resonances, which precludes the generality of interpolation in Z. With increasing temperature, the resonance effects decrease as expected. Such irregular effects are only seen at low-charges for inner-shell transitions since low-n resonances cannot straddle thresholds in high-charge ions.
The data are made available in the ADAS adf04 format (Summers 2004) at the archives of the APAP1, OPEN-ADAS5 and and will be included in CHIANTI7 database.
In conclusion, we have generated an extensive set of reliable excitation data, utilizing the ICFT R-matrix method, for spectroscopy/diagnostic research within the astrophysical and fusion communities. This will replace data from DW and Coulomb-Born exchange approaches presently used by these communities and its use can be expected to identify new lines and may overcome some shortcomings in present astrophysical modelling, as we have seen for Mg8+ (Del Zanna et al. 2008), Fe6+, Fe7+ and Fe10+ (Del Zanna 2009a,b, 2010), Si9+ (Liang et al. 2009c) and Fe7+–Fe15+ (Liang & Zhao 2010).
Acknowledgments
The work of the UK APAP Network is funded by the UK STFC under grant no. PP/E001254/1 with the University of Strathclyde.
References
- Aggarwal, K. M., & Keenan, F. P. 2004a, Phys. Scr., 70, 222 [Google Scholar]
- Aggarwal, K. M., Keenan, F. P., & Heeter, R. F. 2010, Phys. Scr., 81, 015303 [Google Scholar]
- Badnell, N. R. 1986, J. Phys. B At. Mol. Opt. Phys., 19, 3827 [Google Scholar]
- Badnell, N. R. 2011, Comp. Phys. Comm., accepted [Google Scholar]
- Badnell, N. R., & Griffin, D. C. 2001, J. Phys. B At. Mol. Opt. Phys., 34, 681 [Google Scholar]
- Ballance, C. P., Badnell, N. R., & Berrington, K. A. 2001, J. Phys. B At. Mol. Opt. Phys., 34, 3287 [NASA ADS] [CrossRef] [Google Scholar]
- Ballance, C. P., Griffin, D. C., Colgan, J., Loch, S. D., & Pindzola, M. S. 2003, Phys. Rev. A, 68, 062705 [CrossRef] [Google Scholar]
- Bautista, M. A., & Badnell, N. R. 2007, A&A, 466, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bautista, M. A., Mendoza, C., Kallman, T. R., & Palmeri, P. 2003, A&A, 403, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berrington, K. A. 2006, J. Phys. B At. Mol. Opt. Phys., 39, 3837 [Google Scholar]
- Berrington, K. A., & Tully, J. A. 1997, A&AS, 126, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryans, P., Landi, E., & Savin, D. W. 2009, ApJS, 167, 343 [Google Scholar]
- Burgess, A. 1974, J. Phys. B At. Mol. Opt. Phys., 7, L364 [Google Scholar]
- Burgess, A., & Tully, J. A. 1991, A&A, 254, 436 [Google Scholar]
- Chen, M. H. 1986, Atom. Data Nucl. Data Tables, 34, 301 [Google Scholar]
- Del Zanna, G. 2009a, A&A, 508, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G. 2009b, A&A, 508, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G. 2010, A&A, 514, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Rozum, I., & Badnell, N. R. 2008, A&A, 487, 1203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabriel, A. H. 1972, MNRAS, 160, 99 [NASA ADS] [Google Scholar]
- Goett, S. J., & Sampson, D. H. 1983, Atom. Data Nucl. Data Tables, 29, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Gorczyca, T. W., & Badnell, N. R. 1996, J. Phys. B At. Mol. Opt. Phys., 29, L283 [NASA ADS] [CrossRef] [Google Scholar]
- Gorczyca, T. W., & Robicheaux, F. 1999, Phys. Rev. A, 60, 1216 [CrossRef] [Google Scholar]
- Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B At. Mol. Opt. Phys., 31, 3713 [Google Scholar]
- Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 2000, J. Phys. B At. Mol. Opt. Phys., 33, 1013 [CrossRef] [Google Scholar]
- Liang, G. Y., & Badnell, N. R. 2010, A&A, 518, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, G. Y., & Zhao, G. 2010, MNRAS, 405, 1987 [Google Scholar]
- Liang, G. Y., Whiteford, A. D., & Badnell, N. R. 2008, J. Phys. B At. Mol. Opt. Phys., 41, 235203 [Google Scholar]
- Liang, G. Y., Whiteford, A. D., & Badnell, N. R. 2009a, A&A, 500, 1263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, G. Y., Whiteford, A. D., & Badnell, N. R. 2009b, J. Phys. B At. Mol. Opt. Phys., 42, 225002 [Google Scholar]
- Liang, G. Y., Whiteford, A. D., & Badnell, N. R. 2009c, A&A, 499, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKeown, K. 2005, Ph.D. Thesis, Queen’s University, Belfast [Google Scholar]
- McKeown, K., Aggarwal, K. M., Keenan, F. P., & Rose, S. J. 2004b, Phys. Scr., 70, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N., Oelgoetz, J., & Pradhan, A. K. 2009, Phys. Scr., 79, 055301 [NASA ADS] [CrossRef] [Google Scholar]
- Oelgoetz, J., Fontes, C. J., Zhang, H. L., Nahar, S. N., & Pradhan, A. K. 2009, MNRAS, 394, 742 [CrossRef] [Google Scholar]
- Phillips, K. J. H., Dubau, J., Sylwester, J., & Sylwester, B. 2006, ApJ, 638, 1154 [NASA ADS] [CrossRef] [Google Scholar]
- Robicheaux, F., Gorczyca, T. W., Pindzola, M. S., & Badnell, N. R. 1995, Phys. Rev. A, 51, 1319 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sampson, D. H., Goett, S. J., Petrou, G. V., Zhang, H. L., & Clark, R. E. H. 1985a, Atom. Data Nucl. Data Tables, 32, 343 [Google Scholar]
- Sampson, D. H., Petrou, G. V., Goett, S. J., & Clark, R. E. H. 1985b, Atom. Data Nucl. Data Tables, 32, 403 [CrossRef] [Google Scholar]
- Summers, H. P. 2004, The ADAS User manual version 2.6, http://www.adas.ac.uk/ [Google Scholar]
- Zhang, H. L., Sampson, D. H., & Clark, R. E. H. 1986, Atom. Data Nucl. Data Tables, 35, 267 [CrossRef] [Google Scholar]
- Zhang, H. L., Sampson, D. H., & Fontes, C. J. 1990, Atom. Data Nucl. Data Tables, 44, 31 [Google Scholar]
- Whiteford, A. D., Badnell, N. R., Ballance, C. P., et al. 2002, J. Phys. B At. Mol. Opt. Phys., 3, 3729 [Google Scholar]
- Widing, K. G., & Purcell, J. D. 1976, ApJ, 204, L151 [CrossRef] [Google Scholar]
- Witthoeft, M. C., Whiteford, A. D., & Badnell, N. R. 2007, J. Phys. B At. Mol. Opt. Phys., 40, 2969 [Google Scholar]
All Tables
Thomas-Fermi potential scaling factors used by autostructure for the outer-shell calculations (see text for details).
Comparisons of the level energies (Ryd) of 1s2 {2,3,4,5} l (l ∈ s,p,d,f and g), 1s2l2 and 1s2s2p configurations in O5+, Ar15+, Fe23+, and Kr33+ ions.
Comparisons of line strengths S for K-shell transitions in ions (O5+, Ar15+, Fe23+ and Kr33+) spanning sequence.
All Figures
 |
Fig. 1 Comparison of the line strength (S) of outer-shell dipole transitions for ions spanning the sequence. MAK04 corresponds to the grasp calculation done by McKeown et al. (2004b). The horizontal dashed lines correspond to agreement within 5%. [Colour online] |
| In the text | |
 |
Fig. 2 Comparison of collision strengths Ω from the present ICFT R-matrix calculation in with those of Goett & Sampson (1983). a) O5+: 1s22s 2S1/2 → 1s2s2p 4P3/2 excitation (u line in Table 3); b) Ar15+: 1s22s 2S1/2 → 1s2p2 2P1/2 excitation (1-37, ID is as list in Table 2); c) Fe23+: 1s22s 2S1/2 → 1s2s2p 2P1/2 excitation (r line in Table 3). AS-DW corresponds to the present Breit-Pauli distorted-wave calculation using autostructure; d) Kr33+: 1s22p 2P1/2 → 1s2p2 2D3/2 excitation (k line in Table 3). [Colour online] |
| In the text | |
 |
Fig. 3 Comparison of the effective collision strength Υ between the present ICFT R-matrix calculation and previous results of Goett & Sampson (1983) and Whiteford et al. (2002). a) O5+: 1s22s |
| In the text | |
 |
Fig. 4 Collision strengths Ω from the present ICFT R-matrix calculation and DW data (Zhang et al. 1990) for the dipole 1s24p 2P1/2 → 1s22s 2S1/2 transition (left) and non-dipole 1s24d 2D3/2 → 1s22s 2S1/2 transition (right) of ions (O5+, Ar15+, Fe23+ and Kr33+) spanning the sequence. Note: The scattered electron energy is in unit of z2 Ryd (z is the residual charge). [Colour online] |
| In the text | |
 |
Fig. 5 Collision strength Ω for the 1s24d 2D3/2 → 1s24d 2D5/2 excitation, as well as the comparison of resultant effective collision strength Υ with previous works of McKeown (2005) using darc R-matrix suite code and Whiteford et al. (2002). [Colour online] |
| In the text | |
 |
Fig. 6 Left-hand panels: scatter plots showing the ratio of the effective collision strength Υ with Auger-plus-radiation damping (ΥA + R) or radiation damping (ΥR) to without damping (ΥU) or with radiation damping alone, as a function of line strength for dipole core-excitation of O5+a), Ar15+c), Fe23+e) and Kr33+g) at temperature of 104(z + 1)2 K, where z is the ionic charge. Right-hand panels: percentage of the corresponding transitions where the effect of damping exceeds 10%, 20% and 30%. [ Colour online] |
| In the text | |
 |
Fig. 7 The ratio of the effective collision strengths Υ for all core-excitations in Fe23+ between the present ICFT R-matrix and Breit-Pauli DW (autostructure) calculations at the temperature of 2.0 × 105 and 2.0 × 107 K. The filled and dashed regions correspond to a agreement of 20% and a factor 2, respectively. [Colour online] |
| In the text | |
 |
Fig. 8 Effective collision strengths Υ at temperatures of Te = 5 × 102(z + 1)2, 103, 104 K (here, z = Z − 3) along the iso-electronic sequence. Left-hand panels: 1s2s2p 4P3/2 → 1s22s 2S1/2 (u line), 1s2s2p 2P1/2 → 1s22s 2S1/2 (r line) and 1s2s2p 4P1/2 → 1s22p 2P3/2 (3-26) transitions. Right-hand panels: 1s2p2 4P1/2 → 1s22p 2P3/2 (h line), 1s2p2 2D3/2 → 1s22p 2P1/2 (k line) and 1s2s2 2S1/2 → 1s22p 2P3/2 (3-25) transitions. [Colour online] |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.