| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015783 | |
| Published online | 03 March 2011 | |
Effects of quark matter nucleation on the evolution of proto-neutron stars
1 Dipartimento di Fisica “E.
Fermi”Università di Pisa, Largo B.
Pontecorvo 3, 56127 Pisa, Italy
e-mail: bombaci@df.unipi.it
2 INFN, Sezione di Pisa, Largo B.
Pontecorvo 3, 56127
Pisa,
Italy
3 Centro de Física Computacional,
Department of Physics, University of Coimbra, 3004-516
Coimbra,
Portugal
Received: 18 September 2010
Accepted: 3 December 2010
Context. A phase of strong interacting matter with deconfined quarks is expected in the core of a massive neutron star. If this deconfinement phase transition is of the first order, as suggested by many models inspired by quantum chromodynamics, then it will be triggered by the nucleation of a critical size drop of the (stable) quark phase in the metastable hadronic phase. Within these circumstances it has been shown that cold (T = 0) pure hadronic compact stars above a threshold value of their gravitational mass (central pressure) are metastable with respect to the “decay” (conversion) to quark stars (i.e., compact stars made at least in part of quark matter). This stellar conversion process liberates a huge amount of energy (a few 1053 erg), and it could be the energy source of some of the long gamma ray bursts.
Aims. The main goal of the present work is to establish whether a newborn hadronic star (proto-hadronic star) could survive the early stages of its evolution without “decaying” to a quark star. To this aim, we study the nucleation process of quark matter in hot (T ≠ 0) β-stable hadronic matter, with and without trapped neutrinos, using a finite temperature equation of state (EOS) for hadronic and quark matter.
Methods. The finite-temperature EOS for the hadronic and for the quark phases were calculated using the nonlinear Walecka model and the MIT bag model, respectively. The quantum nucleation rate was calculated making use of the Lifshitz & Kagan nucleation theory. The thermal nucleation rate was calculated using the Langer nucleation theory.
Results. We calculate and compare the nucleation rate and the nucleation time due to thermal and quantum nucleation mechanisms. We compute the crossover temperature above which thermal nucleation dominates the finite temperature quantum nucleation mechanism. We next discuss the consequences of quark matter nucleation for the physics and the evolution of proto-neutron stars. We introduce the new concept of limiting conversion temperature and critical mass Mcr for proto-hadronic stars, and we show that proto-hadronic stars with a mass M < Mcr could survive the early stages of their evolution without decaying to a quark star. We extend the concept of maximum mass of a “neutron star” with respect to the classical one introduced by Oppenheimer & Volkoff to account for the existence of two distinct families of compact stars (hadronic stars and quark stars) as predicted by the present scenario.
Key words: dense matter / equation of state / stars: neutron
© ESO, 2011
1. Introduction
According to quantum chromodynamics (QCD) a phase transition from hadronic matter to a deconfined quark phase should occur at a density of a few times nuclear matter saturation density ρ0 ~ 2.8 × 1014 g/cm3. Neutron star structure calculations, based on a wide variety of modern equations of state (EOS) of hadronic matter (Lattimer & Prakash 2001; Bombaci 2007), predict a maximum stellar central density (the one for the maximum mass star configuration) in the range of 4–8 times ρ0. Consequently, the core of neutron stars is one of the best candidates in the universe where a phase of strong interacting matter with deconfined up, downand strange quarks could be found.
In the region of high density (high baryon chemical potential) and low temperature (which is the one relevant for neutron star physics) many QCD-inspired models suggest the deconfinement transition to be a first-order phase transition (Hsu & Schwetz 1998; Fodor & Katz 2004). As is well known, first-order phase transitions are triggered by the nucleation of a critical size drop of the new (stable) phase in a metastable mother phase.
In recent years there has been a growing interest in studying the nucleation process of quark matter in the core of massive neutron stars. The nucleation rate of quark matter in cold (T = 0) β-stable nuclear matter has been calculated by Iida & Sato (1997) wthin the Lifshitz-Kagan quantum nucleation theory (Lifshitz & Kagan 1972). The same authors (Iida & Sato 1998) have later on studied quark matter nucleation in β-stable hyperonic matter within a relativistic extension of the Lifshitz-Kagan theory. Various significant astrophysical implications of quark matter nucleation in neutron stars have been explored in a series of subsequent papers (Berezhiani et al. 2002, 2003; Bombaci et al. 2004; Drago et al. 2004; Lugones & Bombaci 2005; Bombaci et al. 2007, 2008; Drago et al. 2008; Bambi & Drago 2008). In particular, in these studies it has been shown that, above a threshold value of the central pressure, a pure hadronic compact star (HS) is metastable to the decay (conversion) to a quark star (QS), i.e. to a hybrid neutron star or to a strange star (Bodmer 1971; Witten 1984), depending on the details of the EOS for quark matter used to model the phase transition. This stellar conversion process releases (Bombaci & Datta 2000) an extraordinarily large amount of energy (a few 1053 erg) and it could be the energy source of some of the long gamma ray bursts (GRBs).
The research reported in these papers has focused on the quark deconfinement phase transition in cold and neutrino-free neutron stars. In this case the formation of the first drop of QM could take place solely via a quantum nucleation process.
A neutron star at birth (proto-neutron star) is very hot (T = 10–30 MeV) with neutrinos being still trapped in the stellar interior (Burrow & Lattimer 1986; Prakash et al. 1997; Pons et al. 1999). Subsequent neutrino diffusion causes deleptonization and heats the stellar matter to an approximately uniform entropy per baryon 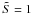 –2 (in units of the Boltzmann’s constant kB). Depending on the stellar composition, during this stage neutrino escape can lead the more “massive” stellar configurations to the formation of a black hole (Bombaci 1996; Prakash et al. 1997). However, if the mass of the star is sufficiently low, the star will remain stable and will cool to temperatures well below 1 MeV within a cooling time tcool ~ a few 102 s, as the neutrinos continue to carry energy away from the stellar material (Burrow & Lattimer 1986; Prakash et al. 1997; Pons et al. 1999). Thus in a proto-neutron star, the quark deconfinement phase transition will likely be triggered by a thermal nucleation process. In fact, for sufficiently high temperatures, thermal nucleation is a much more efficient process than the quantum nucleation mechanism.
–2 (in units of the Boltzmann’s constant kB). Depending on the stellar composition, during this stage neutrino escape can lead the more “massive” stellar configurations to the formation of a black hole (Bombaci 1996; Prakash et al. 1997). However, if the mass of the star is sufficiently low, the star will remain stable and will cool to temperatures well below 1 MeV within a cooling time tcool ~ a few 102 s, as the neutrinos continue to carry energy away from the stellar material (Burrow & Lattimer 1986; Prakash et al. 1997; Pons et al. 1999). Thus in a proto-neutron star, the quark deconfinement phase transition will likely be triggered by a thermal nucleation process. In fact, for sufficiently high temperatures, thermal nucleation is a much more efficient process than the quantum nucleation mechanism.
Some of the earlier studies of quark matter nucleation (see e.g., Horvath et al. 1992; Horvath 1994; Olesen & Madsen 1994; Heiselberg 1995; Harko et al. 2004) have already dealt with thermal nucleation in hot and dense hadronic matter. In these studies, it has been found that the prompt formation of a critical size drop of quark matter via thermal activation is possible above a temperature of about 2–3 MeV. As a consequence, it was inferred that pure hadronic stars are converted to quark stars within the first seconds after their birth. However, these works (Horvath et al. 1992; Horvath 1994; Olesen & Madsen 1994; Heiselberg 1995) reported an estimate of the thermal nucleation based on “typical” values for the thermodynamic properties characterizing the central part of neutron stars. Quark matter nucleation during the early post-bounce stage of core collapse supernova has been lately examined by Sagert et al. (2009) and Mintz et al. (2010).
The main goal of the present paper is to establish whether a newborn hadronic star (proto-hadronic star) could survive the early stages of its evolution without “decaying” to a quark star. To this aim, we calculated the thermal nucleation rate of quark matter in hot (T ≠ 0) β-stable hadronic matter using a finite temperature EOS for hadronic and quark matter. In addition, we calculated the quantum nucleation rate at finite temperature, and compared the thermal and quantum nucleation time at different temperatures and pressures characterizing the central conditions of metastable proto-hadronic compact stars. We computed the crossover temperature above which thermal nucleation dominates the finite temperature quantum nucleation mechanism. An exploratory study of this issue has been recently reported (Bombaci et al. 2009) for the case of neutrino-free hadronic matter. Here, we extend our analysis and our numerical investigation to the case of hadronic matter with trapped neutrinos, and we make a systematic study of the finite temperature nucleation process on the value of the Bag constant in the EOS for the quark phase. Finally, we discuss the relevant consequences of quark matter nucleation for the evolution of proto-neutron stars.
2. Equation of state
Within a fundamental approach, the EOS for neutron star matter should be derived by solving numerically the equations of QCD on a space-time lattice. Lattice calculations at zero baryon chemical potential (zero baryon density) suggest that at high temperature and for physical values of the quark masses, the transition to quark gluon plasma is a “crossover” (Fodor & Katz 2004; Karsch 2005) rather than a phase transition, which would be signaled by singularities in the thermodynamic observables. Unfortunately, present lattice QCD calculations at finite density (baryon chemical potential) are plagued with the notorius “sign problem”, which makes them unrealizable by all presently known lattice methods (see e.g. Lombardo 2007, and references therein). Thus, to explore the QCD phase diagram at low temperature T and high baryon chemical potential μ, it is necessary to invoke some approximations in QCD or to apply some QCD effective model. In this region of the T-μ plane, many QCD inspired models suggest the deconfinement transition to be a first-order phase transition (Hsu & Schwetz 1998; Fodor & Katz 2004). In this domain of the QCD phase diagram, many possible color superconducting phases of quark matter are expected (see e.g. Casalbuoni & Nardulli 2004; Alford et al. 2008, and references therein). The effects of these color superconducting phases on the properties of proto-neutron stars have been investigated in (Aguilera et al. 2004; Sandin & Blaschke 2007; Gu et al. 2008; Lugones et al. 2009).
Very recently, a new phase of QCD, named quarkyonic phase, has been predicted (McLerran & Pisarski 2007; Hidaka et al. 2008). This matter phase is characterized by chiral symmetry and confinement.
Here, we have adopted a more traditional view, assuming a single first-order phase transition between the confined (hadronic) and deconfined phase of dense matter, and we used rather common models for describing them.
For the hadronic phase we used the nonlinear Walecka model (NLWM) (Walecka 1974; Serot & Walecka 1986). This model is based on a relativistic Lagrangian of baryons interacting via the exchange of various mesons. We considered a version of the NLWM in which the baryon octet particles (n, p, Λ, Σ − , Σ0, Σ + , Ξ − , Ξ0) interact via the exchange of the scalar σ, the vector-isoscalar ωμ and the vector-isovector ρμ meson fields (see e.g. Prakash et al. 1997; Glendenning 2000; Menezes & Providência 2003).
The Lagrangian density of the model reads as 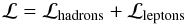 (1)where the hadronic contribution is
(1)where the hadronic contribution is 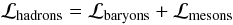 (2)with
(2)with ![\begin{equation} {\cal L}_{\rm baryons}=\sum_{\rm baryons} \bar \psi\left[\gamma^\mu D_\mu -M^*_B\right]\psi, \end{equation}](/articles/aa/full_html/2011/04/aa15783-10/aa15783-10-eq31.png) (3)where
(3)where 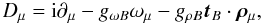 (4)and
(4)and 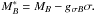 The quantity tB designates the isospin of baryon B. The mesonic contribution reads as
The quantity tB designates the isospin of baryon B. The mesonic contribution reads as 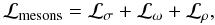 (5)with
(5)with 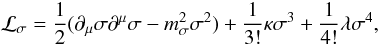 (6)
(6)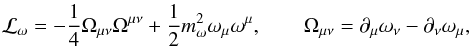 (7)
(7)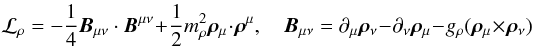 (8)for the lepton contribution we take
(8)for the lepton contribution we take 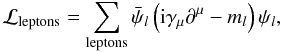 (9)where the sum is over electrons, muons and neutrinos for matter with trapped neutrinos. In uniform matter, we get for the baryon Fermi energy
(9)where the sum is over electrons, muons and neutrinos for matter with trapped neutrinos. In uniform matter, we get for the baryon Fermi energy 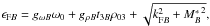 with the baryon effective mass
with the baryon effective mass 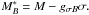
In the present work we used one of the parametrizations of the NLWM given by Glendenning & Moszkowski (2001) (hereafter the GM1 equation of state). The parameters of the GM1 EOS are fitted to the saturation properties of symmetric nuclear matter: binding energy per nucleon B/A = −16.3 MeV, saturation density ρ0 = 0.153 fm-3, incompressibility K = 300 MeV, nucleon effective mass M∗ = 0.7, and to the nuclear symmetry energy at saturation density asym = 32.5 MeV.
Including hyperons involves new couplings, i.e., the hyperon-nucleon couplings: gσB = xσB gσ, gωB = xωB gω, gρB = xρB gρ. For nucleons we take xσB, xωB, xρB = 1 and for hyperons we will consider the couplings proposed by Glendenning & Moszkowski (2001). They consider the binding energy of the Λ in nuclear matter, BΛ, 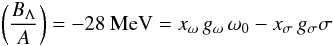 (10)to establish a relation between xσ and xω. Moreover, known neutron star masses restrict xσ to the range 0.6–0.8. We take xρ = xσ and consider xσ = 0.6.
(10)to establish a relation between xσ and xω. Moreover, known neutron star masses restrict xσ to the range 0.6–0.8. We take xρ = xσ and consider xσ = 0.6.
For the quark phase, we adopted a phenomenological EOS (Farhi & Jaffe 1984) that is based on the MIT bag model for hadrons and considered different possible values for the bag constant B. The remaining model parameters have been fixed to: mu = md = 0, ms = 150 MeV for the masses of the up, down, and strange quark, respectively, and αs = 0 for the QCD structure constant.
The two models for the EOS have been generalized to the case of finite temperature (see e.g. Menezes & Providência 2003).
3. Phase equilibrium
For a first-order phase transition, the conditions for phase equilibrium are given by the Gibbs’ phase rule  (11)
(11)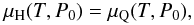 (12)where
(12)where 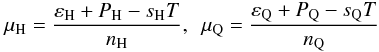 (13)are the Gibbs’ energies per baryon (average chemical potentials) for the hadron and quark phase respectively, and εH (εQ), PH (PQ), sH (sQ) and nH (nQ) respectively denote the total (i.e., including leptonic contributions) energy density, total pressure, total entropy density, and baryon number density for the hadron (quark) phase. Above the “transition point” (P0), the hadronic phase is metastable, and the stable quark phase will appear as a result of a nucleation process.
(13)are the Gibbs’ energies per baryon (average chemical potentials) for the hadron and quark phase respectively, and εH (εQ), PH (PQ), sH (sQ) and nH (nQ) respectively denote the total (i.e., including leptonic contributions) energy density, total pressure, total entropy density, and baryon number density for the hadron (quark) phase. Above the “transition point” (P0), the hadronic phase is metastable, and the stable quark phase will appear as a result of a nucleation process.
Small localized fluctuations in the state variables of the metastable hadronic phase will give rise to virtual drops of the stable quark phase. These fluctuations are characterized by a time scale 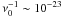 s. It is set by the strong interactions (responsible for the deconfinement phase transition), and it is many orders of magnitude shorter than the typical time scale for the weak interactions. Quark flavor must therefore be conserved during the deconfinement transition. We refer to this form of deconfined matter, in which the flavor content is equal to that of the β-stable hadronic system at the same pressure and temperature, as the Q*-phase. Soon after a critical size drop of quark matter is formed, the weak interactions will have enough time to act, changing the quark flavor fraction of the deconfined droplet to lower its energy, and a droplet of β-stable quark matter is formed (hereafter the Q-phase).
s. It is set by the strong interactions (responsible for the deconfinement phase transition), and it is many orders of magnitude shorter than the typical time scale for the weak interactions. Quark flavor must therefore be conserved during the deconfinement transition. We refer to this form of deconfined matter, in which the flavor content is equal to that of the β-stable hadronic system at the same pressure and temperature, as the Q*-phase. Soon after a critical size drop of quark matter is formed, the weak interactions will have enough time to act, changing the quark flavor fraction of the deconfined droplet to lower its energy, and a droplet of β-stable quark matter is formed (hereafter the Q-phase).
This first seed of quark matter will trigger the conversion (Olinto 1987; Heiselberg et al. 1991; Bombaci & Datta 2000; Drago et al. 2010) of the pure hadronic star to a hybrid star or to a strange star. Thus, pure hadronic stars with values of the central pressure higher than P0 are metastable to the decay (conversion) to hybrid stars or to strange stars (Berezhiani et al. 2002, 2003; Bombaci et al. 2004; Drago et al. 2004; Lugones & Bombaci 2005; Bombaci et al. 2007). The mean lifetime of the metastable stellar configuration is related to the time needed to nucleate the first drop of quark matter in the stellar center, and it depends dramatically on the value of the stellar central pressure.
 |
Fig. 1 (Color online) Gibbs energy per baryon, in neutrino-free matter, as a function of pressure for the hadronic and quark phases at different temperatures. Lines with the steeper slope refer to the hadronic phase. Full dots indicate the transition pressure P0 for each temperature. GM1 EOS for the hadronic phase and MIT bag model EOS with B = 85 MeV/fm3 for the quark phase. |
In Figs. 1 and 2, we plot the Gibbs’ energies per baryon for the hadron-phase and the Q*-phase in neutrino-free matter, at different temperatures (T = 0, 10, 20, 30 MeV) and for two different values of the bag constant B = 85 MeV/fm3 (Fig. 1) and B = 100 MeV/fm3 (Fig. 2). Lines with the steeper slope refer to the hadron phase. As we see, the transition pressure P0 (indicated by a full dot) decreases when the hadronic matter temperature is increased.
 |
Fig. 3 Phase equilibrium curve for the hadron to Q*-matter phase transition. The continuous curve is relative to neutrino-free matter, the dashed curve to matter with trapped neutrinos. EOS: GM1 plus MIT Bag model with B = 85 MeV/fm3. |
The phase equilibrium curve P0(T) for the hadron-quark phase transition (in the case B = 85 MeV/fm3) is shown in Fig. 3 for neutrino-free matter and matter with trapped neutrinos. The region of the P0–T plane above each curve represents the deconfined Q*-phase. As expected (Prakash et al. 1997; Lugones & Benvenuto 1998; Vidaña et al. 2005; Lugones et al. 2009) neutrino trapping in β-stable hadronic matter inhibits the quark deconfinement phase transition, thus the global effect of neutrino-trapping is to produce a shift of the phase equilibrium curve toward higher values of the pressure in the P0–T plane.
As is well known, for a first-order phase transition the derivative dP0/dT is related to the specific (i.e. per baryon) latent heat 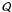 of the phase transition by the Clapeyron-Clausius equation
of the phase transition by the Clapeyron-Clausius equation 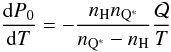 (14)
(14)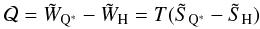 (15)where
(15)where 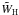 (
(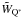 ) and
) and 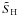 (
(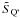 ) denote the enthalpy per baryon and entropy per baryon for the hadron (quark) phase, respectively. The specific latent heat
) denote the enthalpy per baryon and entropy per baryon for the hadron (quark) phase, respectively. The specific latent heat 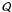 and the phase numbers densities nH and nQ∗ at phase equilibrium are reported in Tables 1 and 2 for the case of neutrino-free matter and for two different values of the bag constant B = 85 MeV/fm3 (Table 1) and B = 100 MeV/fm3 (Table 2). As expected for a first-order phase transition, one has a discontinuity jump in the phase number densities: in our particular case nQ∗(T,P0) > nH(T,P0). This result, together with the positive value of
and the phase numbers densities nH and nQ∗ at phase equilibrium are reported in Tables 1 and 2 for the case of neutrino-free matter and for two different values of the bag constant B = 85 MeV/fm3 (Table 1) and B = 100 MeV/fm3 (Table 2). As expected for a first-order phase transition, one has a discontinuity jump in the phase number densities: in our particular case nQ∗(T,P0) > nH(T,P0). This result, together with the positive value of 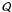 (i.e. the deconfinement phase transition absorbs heat), tells us (see Eq. (14)) that the phase transition temperature (11) decreases with pressure (as in the melting of ice).
(i.e. the deconfinement phase transition absorbs heat), tells us (see Eq. (14)) that the phase transition temperature (11) decreases with pressure (as in the melting of ice).
The specific latent heat 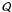 and the phase number densities nH and nQ∗ at phase equilibrium.
and the phase number densities nH and nQ∗ at phase equilibrium.
To explore the effect of neutrino trapping on the phase equilibrium properties of the system, in Table 3 we report the quantities 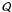 , nH, nQ∗ and P0 at different temperatures, for a bag constant B = 85 MeV/fm3 (compare with the results in Table 1). As we see, the phase number densities nH and nQ∗ at phase equilibrium are shifted to higher values, and the specific latent heat
, nH, nQ∗ and P0 at different temperatures, for a bag constant B = 85 MeV/fm3 (compare with the results in Table 1). As we see, the phase number densities nH and nQ∗ at phase equilibrium are shifted to higher values, and the specific latent heat 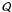 is increased with respect to the neutrino-free matter case.
is increased with respect to the neutrino-free matter case.
We also made systematic calculations of the phase equilibrium properties varying the value of the bag constant in the EOS of the Q*-phase. These results are summarized in Fig. 4 where we plot the phase equilibrium pressure P0 between the hadron phase and the Q* phase at zero temperature as a function of B for neutrino-free matter and neutrino-trapped matter. As expected, a higher value of B makes the deconfinemnt transition more difficult, increasing the value of the transition pressure.
 |
Fig. 4 Phase equilibrium pressure P0 between the hadron phase and the Q* phase at T = 0, as a function of the bag constant B. The continuous curve refers to neutrino-free matter, and the dashed curve refers to neutrino-trapped matter. |
4. Quantum and thermal nucleation rates
Above the phase equilibrium pressure P0 the β-stable hadron phase is metastable, and the formation of the stable (with respect to the strong interactions) Q*-phase will occur via a nucleation process. The main effect of finite temperature on the quantum nucleation mechanism of quark matter is to modify the energy barrier separating the quark phase from the metastable hadronic phase. This energy barrier, which represents the difference in the free energy of the system with and without a Q*-matter droplet, can be written as 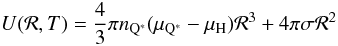 (16)where ℛ is the radius of the droplet (supposed to be spherical), and σ is the surface tension for the surface separating the hadron from the Q*-phase. The energy barrier has a maximum at the critical radius ℛc = 2σ/ [nQ∗(μH − μQ∗) ] . We neglected the term associated with the curvature energy, and also the terms connected with the electrostatic energy, since they are known to only introduce small corrections (Iida & Sato 1998; Bombaci et al. 2004). The value of the surface tension σ for the interface separating the quark and hadron phase is poorly known, and typically values used in the literature range within 10–50 MeV fm-2 (Heiselberg et al. 1993; Iida & Sato 1998). We assume σ to be temperature independent and we take σ = 30 MeV fm-2.
(16)where ℛ is the radius of the droplet (supposed to be spherical), and σ is the surface tension for the surface separating the hadron from the Q*-phase. The energy barrier has a maximum at the critical radius ℛc = 2σ/ [nQ∗(μH − μQ∗) ] . We neglected the term associated with the curvature energy, and also the terms connected with the electrostatic energy, since they are known to only introduce small corrections (Iida & Sato 1998; Bombaci et al. 2004). The value of the surface tension σ for the interface separating the quark and hadron phase is poorly known, and typically values used in the literature range within 10–50 MeV fm-2 (Heiselberg et al. 1993; Iida & Sato 1998). We assume σ to be temperature independent and we take σ = 30 MeV fm-2.
The quantum nucleation time τq can be straightforwardly evaluated within a semi-classical approach (Lifshitz & Kagan 1972; Iida & Sato 1997, 1998). First one computes the ground state energy E0 in the WKB approximation and the oscillation frequency ν0 of the drop in the potential well U(ℛ,T). Then, the probability of tunneling is given by ![\begin{equation} p_0=\exp\left[-\frac{A(E_0)}{\hbar}\right] \label{eq:prob} \end{equation}](/articles/aa/full_html/2011/04/aa15783-10/aa15783-10-eq98.png) (17)where A(E) is the action under the potential barrier, which in a relativistic framework reads as (Iida & Sato 1998)
(17)where A(E) is the action under the potential barrier, which in a relativistic framework reads as (Iida & Sato 1998) ![\begin{equation} A(E)=\frac{2}{c}\int_{{\cal R}_-}^{{\cal R}_+}\sqrt{[2m({\cal R})c^2 +E-U({\cal R})][U({\cal R})-E]} \label{eq:action} \end{equation}](/articles/aa/full_html/2011/04/aa15783-10/aa15783-10-eq100.png) (18)with ℛ ± the classical turning points and m(ℛ) the droplet effective mass. The quantum nucleation time is then equal to
(18)with ℛ ± the classical turning points and m(ℛ) the droplet effective mass. The quantum nucleation time is then equal to 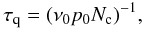 (19)with Nc ~ 1048 the number of nucleation centers expected in the innermost part (r ≤ Rnuc ~ 100 m) of the hadronic star, where the pressure and temperature can be considered constant and equal to their central values.
(19)with Nc ~ 1048 the number of nucleation centers expected in the innermost part (r ≤ Rnuc ~ 100 m) of the hadronic star, where the pressure and temperature can be considered constant and equal to their central values.
The thermal nucleation rate can be written (Langer & Turski 1973) as 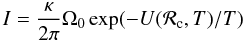 (20)where κ is the so-called dynamical prefactor, which is related to the growth rate of the drop radius ℛ near the critical radius (ℛc); Ω0 is the so-called statistical prefactor, which measures the phase-space volume of the saddle-point region around ℛc; and U(ℛc,T) is the activation energy, i.e. the change in the free energy of the system required to activate the formation of a critical size droplet. The Langer theory (Langer 1968, 1969; Langer & Turski 1973; Turski & Langer 1980) of homogeneous nucleation has been extended in Csernai & Kapusta (1992) and Venugopalan & Vischer (1994) to the case of first-order phase transitions occurring in relativistic systems, as in the case of the quark deconfinement transition. The statistical prefactor can be written (Csernai & Kapusta 1992) as
(20)where κ is the so-called dynamical prefactor, which is related to the growth rate of the drop radius ℛ near the critical radius (ℛc); Ω0 is the so-called statistical prefactor, which measures the phase-space volume of the saddle-point region around ℛc; and U(ℛc,T) is the activation energy, i.e. the change in the free energy of the system required to activate the formation of a critical size droplet. The Langer theory (Langer 1968, 1969; Langer & Turski 1973; Turski & Langer 1980) of homogeneous nucleation has been extended in Csernai & Kapusta (1992) and Venugopalan & Vischer (1994) to the case of first-order phase transitions occurring in relativistic systems, as in the case of the quark deconfinement transition. The statistical prefactor can be written (Csernai & Kapusta 1992) as 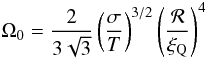 (21)where ξQ is the quark correlation length, which gives a measure of the thickness of the interface layer between the two phases (the droplet “surface thickness”). In the present calculation, we take ξQ = 0.7 fm according to the estimate given in Csernai & Kapusta (1992) and Heiselberg (1995). For the dynamical prefactor, we have used a general expression, which has been derived by Venugopalan & Vischer (1994)
(21)where ξQ is the quark correlation length, which gives a measure of the thickness of the interface layer between the two phases (the droplet “surface thickness”). In the present calculation, we take ξQ = 0.7 fm according to the estimate given in Csernai & Kapusta (1992) and Heiselberg (1995). For the dynamical prefactor, we have used a general expression, which has been derived by Venugopalan & Vischer (1994) ![\begin{equation} \kappa = \frac{2 \sigma} {{\cal R}_{\rm c}^3 (\Delta w)^2} \left [ \lambda T + 2 \left(\frac{4}{3} \eta + \zeta \right)\right] , \label{eq:kappa} \end{equation}](/articles/aa/full_html/2011/04/aa15783-10/aa15783-10-eq115.png) (22)where Δw = wQ ∗ − wH is the difference between the enthalpy density of the two phases, λ the thermal conductivity, and η and ζ are the shear and bulk viscosities respectively of hadronic matter. The nucleation prefactor used in the present work differs significantly from the one used in previous works (Horvath et al. 1992; Horvath 1994; Olesen & Madsen 1994), where based on dimensional grounds, the prefactor was taken to be equal to T4.
(22)where Δw = wQ ∗ − wH is the difference between the enthalpy density of the two phases, λ the thermal conductivity, and η and ζ are the shear and bulk viscosities respectively of hadronic matter. The nucleation prefactor used in the present work differs significantly from the one used in previous works (Horvath et al. 1992; Horvath 1994; Olesen & Madsen 1994), where based on dimensional grounds, the prefactor was taken to be equal to T4.
There are not many calculations of the transport properties of dense hadronic matter. With a few exceptions (see e.g. van Dalen & Dieperink 2004; Chattaerjee & Bandyopadhyay 2006) most of them are relative to nuclear or pure neutron matter (Flowers & Itho 1979; Danielewicz 1984; Sedrakian et al. 1994; Benhar & Valli 2007; Shternin & Yakovlev 2008; Benhar et al. 2010; Zhang et al. 2010). These quantities have been calculated by Danielewicz (1984) in the case of nuclear matter. According to the results of Danielewicz (1984), the dominant contribution to the prefactor κ comes from the shear viscosity η. Therefore, we take λ and ζ equal to zero, and we use the following relation for the shear viscosity (Danielewicz 1984): 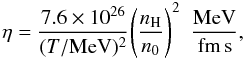 (23)with n0 = 0.16 fm-3 the saturation density of normal nuclear matter.
(23)with n0 = 0.16 fm-3 the saturation density of normal nuclear matter.
The thermal nucleation time τth, relative to the innermost stellar region (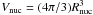 ) where almost constant pressure and temperature occur, can thus be written as
) where almost constant pressure and temperature occur, can thus be written as 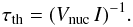 (24)In Fig. 5, we represent the energy barrier for a virtual drop of the Q*-phase (with B = 85 MeV/fm3) in the neutrino-free hadronic phase as a function of the droplet radius and for different temperatures at a fixed pressure P = 57 MeV/fm3. As expected, from the results plotted in Fig. 1, the energy barrier U(ℛ,T) and the droplet critical radius ℛc decrease as the matter temperature is increased. This effect favors the Q*-phase formation and, in particular, increases (decreases) the quantum nucleation rate (nucleation time τq) with respect to the corresponding quantities calculated at T = 0.
(24)In Fig. 5, we represent the energy barrier for a virtual drop of the Q*-phase (with B = 85 MeV/fm3) in the neutrino-free hadronic phase as a function of the droplet radius and for different temperatures at a fixed pressure P = 57 MeV/fm3. As expected, from the results plotted in Fig. 1, the energy barrier U(ℛ,T) and the droplet critical radius ℛc decrease as the matter temperature is increased. This effect favors the Q*-phase formation and, in particular, increases (decreases) the quantum nucleation rate (nucleation time τq) with respect to the corresponding quantities calculated at T = 0.
 |
Fig. 5 Energy barrier for a virtual drop of the Q*-phase in β-stable neutrino-free hadronic matter as a function of the droplet radius and for different temperatures for a fixed pressure P = 57 MeV/fm3. The bag constant takes the value B = 85 MeV/fm3. |
In Fig. 6 we plot the quantum and thermal nucleation times of the Q*-phase (with B = 85 MeV/fm3) in β-stable neutrino-free hadronic matter as a function of temperature and at a fixed pressure P = 57 MeV/fm3. As expected, we find a crossover temperature Tco above which thermal nucleation is dominant with respect to the quantum nucleation mechanism. For the case reported in Fig. 6, we have Tco = 7.05 MeV and the corresponding nucleation time is log 10(τ/s) = 54.4. The crossover temperature for different values of the pressure of β-stable hadronic matter is reported in Table 4 (second column), together with the nucleation time calculated at T = Tco (third column).
 |
Fig. 6 (Color online) Thermal (τth) and quantum (τq) nucleation time of the Q*-phase (with B = 85 MeV/fm3) in β-stable neutrino-free hadronic matter as a function of temperature at fixed pressure P = 57 MeV/fm3. The crossover temperature is Tco = 7.05 MeV. The limiting conversion temperature for the proto-hadronic star is, in this case, Θ = 10.3 MeV, obtained from the intersection of the thermal nucleation time curve (continuous line) and the dot-dashed line representing log 10(τ/s) = 3. |
Crossover temperature Tco (in MeV), for different fixed values of the pressure P (in MeV/fm3) of neutrino-free hadronic matter.
5. Evolution of proto-hadronic stars
Keeping in mind the physical conditions in the interior of a proto-hadronic star (Burrow & Lattimer 1986; Prakash et al. 1997) (see Sect. 1 of the present paper) to establish whether this star will survive the early stages of its evolution without “decaying” to a quark star, one has to compare the quark matter nucleation time τ = min(τq,τth) with the cooling time tcool ~ a few 102 s. If τ ≫ tcool then quark matter nucleation is not likely to occur in the newly formed star, and this star will evolve into a cold deleptonized configuration. We thus introduce the concept of limiting conversion temperature Θ for the proto-hadronic star and define it as the value of the stellar central temperature Tc for which the Q*-matter nucleation time is equal to 103 s. The limiting conversion temperature Θ will clearly depend on the value of the stellar central pressure (and thus on the value of the stellar mass).
 |
Fig. 7 (Color online) The limiting conversion temperature Θ for a newborn hadronic star as a function of the central stellar pressure. The lines labeled TS represent the stellar matter temperature as a function of pressure at fixed entropies per baryon |
Gravitational (Mcr) and baryonic (MB,cr) critical mass (see text for more details) for proto-hadronic stars at different entropy per baryon 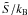 .
.
The limiting conversion temperature Θ is plotted in Fig. 7 as a function of the stellar central pressure P. A proto-hadronic star with a central temperature Tc > Θ(P) will likely nucleate a Q*-matter drop during the early stages of its evolution, will finally evolve to a cold and deleptonized quark star, or will collapse to a black hole (depending on the particular model adopted for the matter EOS).
For an isoentropic stellar core (Burrow & Lattimer 1986; Prakash et al. 1997), the central temperature of the proto-hadronic star is given for the present EOS model by the lines labeled by TS in Fig. 7, relative to the case 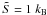 and
and 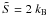 . The intersection point (PS,ΘS) between the two curves Θ(P) and TS(P) thus gives the central pressure and temperature of the configuration that we denote as the critical mass configuration of the proto-hadronic stellar sequence. The value of the gravitational critical mass Mcr = M(PS,ΘS) and baryonic critical mass MB,cr are reported in Table 5 for three different choices of the entropy per baryon,
. The intersection point (PS,ΘS) between the two curves Θ(P) and TS(P) thus gives the central pressure and temperature of the configuration that we denote as the critical mass configuration of the proto-hadronic stellar sequence. The value of the gravitational critical mass Mcr = M(PS,ΘS) and baryonic critical mass MB,cr are reported in Table 5 for three different choices of the entropy per baryon, 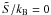 (corresponding to a cold hadronic star)1, 1 and 2 in the case of a bag constant B = 85 MeV/fm3 and for σ = 30 MeV/fm2. In the same table, we also report the value of the gravitational mass ℳ of the cold hadronic star with baryonic mass equal to MB,cr. This configuration is stable (τ = ∞) with respect to Q*-matter nucleation in the case
(corresponding to a cold hadronic star)1, 1 and 2 in the case of a bag constant B = 85 MeV/fm3 and for σ = 30 MeV/fm2. In the same table, we also report the value of the gravitational mass ℳ of the cold hadronic star with baryonic mass equal to MB,cr. This configuration is stable (τ = ∞) with respect to Q*-matter nucleation in the case 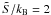 , and it is essentially stable (having a nucleation time enormously longer than the age of the universe) in the case
, and it is essentially stable (having a nucleation time enormously longer than the age of the universe) in the case 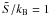 .
.
 |
Fig. 8 (Color online) The limiting conversion temperature Θ for a newborn hadronic star as a function of the central stellar pressure for different values of the bag constant B. The lines labeled TS represent the stellar matter temperature as a function of pressure at fixed entropies per baryon |
The limiting conversion temperature Θ for a newborn hadronic star is plotted in Fig. 8 for different values of the bag constant. The increase in B produces a growth of the region of the P-T plane where the proto-hadronic star could survive Q* nucleation and thus evolve to a cold hadronic star.
To explore the role of neutrino trapping on the limiting conversion temperature Θ and on the critical mass of the proto-hadronic star, we plot in Fig. 9 the results of our calculations for Θ and for the stellar matter temperature TS at fixed entropies per baryon (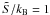 , and 2) in the case of neutrino-free matter and neutrino-trapped matter. Results in Fig. 9 are relative to the GM1 EOS for the hadronic phase and the bag model EOS with B = 85 Mev/fm3 for the quark phase. As we see, neutrino trapping has a conspicuous effect on Θ, and ultimately strongly suppresses the nucleation of Q*-matter in the proto-hadronic star. There is also a relatively small effect of neutrino trapping on TS.
, and 2) in the case of neutrino-free matter and neutrino-trapped matter. Results in Fig. 9 are relative to the GM1 EOS for the hadronic phase and the bag model EOS with B = 85 Mev/fm3 for the quark phase. As we see, neutrino trapping has a conspicuous effect on Θ, and ultimately strongly suppresses the nucleation of Q*-matter in the proto-hadronic star. There is also a relatively small effect of neutrino trapping on TS.
 |
Fig. 9 (Color online) Effects of neutrino trapping on the limiting conversion temperature Θ for a newborn hadronic star as a function of the central stellar pressure. |
 |
Fig. 10 (Color online) Evolution of a proto-hadronic star in the gravitational-baryonic mass plane for B = 85 MeV/fm3 and σ = 30 MeV/fm2. The upper (red) line represents the stellar equilibrium sequence for neutrino-free proto-hadronic stars (PHS) with |
 |
Fig. 11 (Color online) Same as Fig. 10, but with the additional stellar sequence (upper (black) line) for proto-hadronic stars with trapped neutrinos (νPHSs) with a lepton fraction YL = 0.4 and |
The evolution of a proto-hadronic star (PHS) within our scenario is delineated in Fig. 10, where we plot the appropriate stellar equilibrium sequences in the gravitational-baryonic mass plane obained from the GM1 EOS for the hadronic phase and the bag model EOS with B = 85 MeV/fm3 for the quark phase. In particular, we plot the PHS sequence, i.e. isoentropic HSs (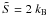 ) and neutrino-free matter (upper line), and the cold HS sequence (middle line). The asterisk and the full circle on these lines identify respectively the stellar configuration with τ = ∞ and the critical mass configuration. We denote as
) and neutrino-free matter (upper line), and the cold HS sequence (middle line). The asterisk and the full circle on these lines identify respectively the stellar configuration with τ = ∞ and the critical mass configuration. We denote as 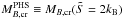 the baryonic critical mass for the PHS sequence and as
the baryonic critical mass for the PHS sequence and as 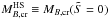 the baryonic critical mass for the cold hadronic star sequence. Finally, the lower line represents the cold QS sequence. We assume (Bombaci & Datta 2000) MB = const. during these stages of the stellar evolution)2. Thus according to the results in Fig. 10, proto-hadronic stars with a baryonic mass
the baryonic critical mass for the cold hadronic star sequence. Finally, the lower line represents the cold QS sequence. We assume (Bombaci & Datta 2000) MB = const. during these stages of the stellar evolution)2. Thus according to the results in Fig. 10, proto-hadronic stars with a baryonic mass 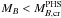 ( = 1.492 Msun within the present EOS parametrzation) will survive Q*-matter early nucleation (i.e. nucleation within the cooling time tcool ~ a few 102 s) and in the end will form stable (τ = ∞) cold hadronic stars. Proto-hadronic stars with
( = 1.492 Msun within the present EOS parametrzation) will survive Q*-matter early nucleation (i.e. nucleation within the cooling time tcool ~ a few 102 s) and in the end will form stable (τ = ∞) cold hadronic stars. Proto-hadronic stars with 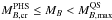 (the maximum baryonic mass of the cold QS sequence, 1.813 Msun for the present EOS) will experience early nucleation of a Q*-matter drop and will ultimately form a cold deleptonized quark star. The last possibility is for PHSs having
(the maximum baryonic mass of the cold QS sequence, 1.813 Msun for the present EOS) will experience early nucleation of a Q*-matter drop and will ultimately form a cold deleptonized quark star. The last possibility is for PHSs having 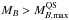 . In this case the early nucleation of a Q*-matter drop will trigger a stellar conversion process to a cold QS configuation with
. In this case the early nucleation of a Q*-matter drop will trigger a stellar conversion process to a cold QS configuation with 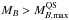 , thus these PHSs will finally form black holes.
, thus these PHSs will finally form black holes.
The outcomes of this scenario are not altered by neutrino trapping effects in hot β-stable hadronic matter as illustrated in Fig. 11 where (in addition to the stellar sequence curves of Fig. 10) we plot the stellar sequence for proto-hadronic stars with trapped neutrinos (νPHSs) with a lepton fraction YL = 0.4 and 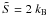 . For the νPHS stellar sequence in Fig. 11 we find a critical baryonic mass
. For the νPHS stellar sequence in Fig. 11 we find a critical baryonic mass 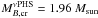 . Thus νPHSs with
. Thus νPHSs with 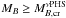 after neutrino escape and cooling will finally evolve to black holes. The fate of a νPHS with
after neutrino escape and cooling will finally evolve to black holes. The fate of a νPHS with 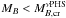 is the same as the corresponding neutrino-free PHS with equal baryonic mass.
is the same as the corresponding neutrino-free PHS with equal baryonic mass.
Finally, in Fig. 12 we plot the PHS, cold HS, and cold QS sequences in the gravitational-baryonic mass plane for the case of a bag constant B = 70.9 MeV/fm3. (All the other EOS parameters are the same as for the results in Fig. 10) Apart from changes in the numerical values of the maximum masses of the various stellar sequences and of the values of the stellar critical masses, the evolutionary scenario of a proto-hadronic star is qualitatively similar to the one previously discussed for the results in Fig. 10.
An interesting situation comes up when a PHS with 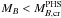 is formed in a binary stellar system. In this case, as we have just seen, a stable (case of Fig. 10) or a metastable (case of Fig. 12) cold HS is formed. Long-term accretion from the companion star will start to populate the portion of the cold HS sequence with
is formed in a binary stellar system. In this case, as we have just seen, a stable (case of Fig. 10) or a metastable (case of Fig. 12) cold HS is formed. Long-term accretion from the companion star will start to populate the portion of the cold HS sequence with 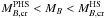 . If the star accretes enough matter (~0.1–0.3 M⊙, see Figs. 10 and 12), it could possibly reach the critical mass
. If the star accretes enough matter (~0.1–0.3 M⊙, see Figs. 10 and 12), it could possibly reach the critical mass 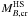 . At this point a quantum nucleation process will trigger the conversion of this critical mass cold HS to a QS (Berezhiani et al. 2002, 2003; Bombaci et al. 2004). The time delay between the supernova explosion forming the PHS, and the second “explosion” (neutrino burst or/and GRB) forming the QS will actually depend on the mass accretion rate, which modifies the quark matter nucleation time via an explicit time dependence of the stellar central pressure.
. At this point a quantum nucleation process will trigger the conversion of this critical mass cold HS to a QS (Berezhiani et al. 2002, 2003; Bombaci et al. 2004). The time delay between the supernova explosion forming the PHS, and the second “explosion” (neutrino burst or/and GRB) forming the QS will actually depend on the mass accretion rate, which modifies the quark matter nucleation time via an explicit time dependence of the stellar central pressure.
Within the present scenario, there is thus a stellar mass range 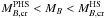 where it is possible to find two different types of “neutron stars” in the Universe: pure hadronic compact stars with large radii in the range 12–20 km, and quark stars with small radii in the range of 6–9 km (Bombaci et al. 2004; Drago & Lavagno 2010). Accurate measurements of both the mass and radius of a few individual “neutron stars” (Bhattacharyya 2010; Steiner et al. 2010) could shed light on the validity of this presumptive scenario.
where it is possible to find two different types of “neutron stars” in the Universe: pure hadronic compact stars with large radii in the range 12–20 km, and quark stars with small radii in the range of 6–9 km (Bombaci et al. 2004; Drago & Lavagno 2010). Accurate measurements of both the mass and radius of a few individual “neutron stars” (Bhattacharyya 2010; Steiner et al. 2010) could shed light on the validity of this presumptive scenario.
6. Limiting mass of compact stars
The possibility of having metastable hadronic stars, together with the feasible existence of two distinct families of compact stars (pure hadronic stars and quark stars), demands an extension of the concept of maximum mass of a “neutron star” with respect to the classical one introduced by Oppenheimer & Volkoff (1939). Since metastable HS with a “short” mean-life time are very unlikely to be observed, an extended concept of maximum mass has to be introduced in view of the comparison with the values of the mass of compact stars deduced from direct astrophysical observation. With this operational definition in mind, Bombaci et al. (2004) define the limiting mass (Mlim) of a compact star in the case of cold stellar configurations. This concept of limiting mass can be straightforwardly extended to the present case, i.e. taking the effects of proto-neutron stars evolution into account. For the two cases reported in Figs. 10 and 12, the limiting mass is the highest between the gravitational critical mass 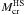 of the cold HS sequence and the gravitational maximum mass
of the cold HS sequence and the gravitational maximum mass 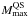 of the cold QS sequence. Thus
of the cold QS sequence. Thus 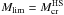 (case in Fig. 10) and
(case in Fig. 10) and 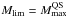 (case in Fig. 12).
(case in Fig. 12).
The very recent measurement (Demorest et al. 2010) of the Shapiro delay in the binary millisecond pulsar J1614-2230 has helped to obtain the mass of the associated neutron star. The calculated mass is M = (1.97 ± 0.04) M⊙ (Demorest et al. 2010), making PSR J1614-2230 the most massive neutron star known to date.
As is well known (see e.g. Lattimer & Prakash 2001; Bombaci 2007), neutron star mass measurements give one of the most stringent tests of the composition and EOS of strong interacting matter at very high densities. Here, we very briefly address some possible implications of the high mass of PSR J1614-2230 in connection with the feasibility of the scenario discussed in present work. To this aim we consider two almost diametrical situations for the stiffness of the EOS.
The first possibility is for the case of a stiff hadronic EOS and a soft quark matter EOS. This is the case, for example, for the GM1 model with xσ = xρ = 0.8, xω = 0.913 for hyperonic matter, and the MIT bag model EOS (Farhi & Jaffe 1984) with B = 100–150 MeV/fm3 for quark matter. For these EOS models, the limiting mass is given by the gravitational critical mass of the HS sequence, and it is in the range Mlim = 1.9 − 2.1 M⊙ (Bombaci et al. 2008). Thus, in this case, PSR J1614-2230 can be interpreted as a pure hadronic star (hyperon star), and quark matter nucleation, in HS with 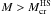 , will produce stellar configurations which will form black holes.
, will produce stellar configurations which will form black holes.
The second possibility is for a soft hadronic EOS and a stiff quark matter EOS. This is the case, for example, of the microscopic Brueckner-Hartree-Fock EOS for hyperonic matter (Baldo et al. 2000; Vidaña et al. 2000; Schulze et al. 2006) and the recent perturbative calculations of the quark matter EOS by (Kurkela et al. 2010) which include quark interaction effects up to the second order in the QCD coupling αs (see also Fraga et al. 2001; Alford et al. 2005). For these EOS models, the limiting mass is likely given by the gravitational maximum mass of the cold QS sequence, which according to the results of (Kurkela et al. 2010) is 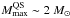 (hybrid stars),
(hybrid stars), 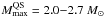 (strange stars). Thus, for this second case, PSR J1614-2230 could be interpreted as a quark star (Özel et al. 2010).
(strange stars). Thus, for this second case, PSR J1614-2230 could be interpreted as a quark star (Özel et al. 2010).
7. Conclusions
In summary, in this work we have studied the quark deconfinement phase transition in hot β-stable hadronic matter and explored some of its consequences for the physics of neutron stars at birth. We calculated and compared the nucleation time due to thermal and quantum nucleation mechanisms, and computed the crossover temperature above which thermal nucleation dominates the finite temperature quantum nucleation mechanism. In addition, we introduced the new concept of limiting conversion temperature Θ for proto-hadronic stars and extended the concept of critical mass (Berezhiani et al. 2002, 2003; Bombaci et al. 2004) to the case of finite temperature hadronic stars.
Our main finding is that proto-hadronic stars with a gravitational mass lower than the critical mass Mcr could survive the early stages of their evolution without decaying to a quark star. This outcome contrasts with the predictions of the earlier studies (Horvath et al. 1992; Horvath 1994; Olesen & Madsen 1994; Heiselberg 1995; Harko et al. 2004) where it was inferred that all the pure hadronic compact stars, with a central temperature above 2–3 MeV, are converted to quark stars within the first seconds after their birth.
However, the prompt formation of a critical size drop of quark matter could take place when M > Mcr. These proto-hadronic stars evolve to cold and deleptonized quark stars or collapse to a black holes.
Finally, if quark matter nucleation occurs during the post-bounce stage of core-collapse supernova, then the quark deconfinement phase transition could trigger a delayed supernova explosion characterized by a peculiar neutrino signal (Sagert et al. 2009; Mintz et al. 2010; Nakazato et al. 2008; Dasgupta et al. 2010).
In reference (Berezhiani et al. 2002, 2003; Bombaci et al. 2004; Drago et al. 2004; Lugones & Bombaci 2005; Bombaci et al. 2007, 2008), the critical mass for cold (T = 0) metastable hadronic stars has been defined as the value of the gravitational mass for which the quantum nucleation time is equal to one year: Mcr(T = 0) = M(τq = 1 yr). It is worth recalling that the nucleation time τq is an extremely steep function of the hadronic star mass (Berezhiani et al. 2002, 2003; Bombaci et al. 2004), therefore the exact value of τq chosen in the definition of Mcr(T = 0) is not crucial (one must take a “reasonable low” value of τq, much shorter than the age of young pulsars as the Crab pulsar). We have verified that changing τq from 1 yr to 103 s modifies Mcr(T = 0) by ~ 0.02%. On the other hand, the nucleation time τ = min(τq,τth) entering in the definition of the critical mass of proto-hadronic stars 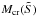 must be comparable to the proto-hadronic star cooling time tcool.
must be comparable to the proto-hadronic star cooling time tcool.
Acknowledgments
This work has been partially supported by FCT (Portugal) under grants SFRH/BD/62353/2009, PTDC/FIS/64707/2006 and FCOMP-01-0124-FEDER-008393 with FCT reference CERN/FP/109316/2009, and by COMPSTAR, an ESF Research Networking Programme.
References
- Aguilera, D. N., Blaschke, D., & Grigorian, H. 2004, A&A, 416, 991 [Google Scholar]
- Alford, M. G., Braby, M., Paris, M., & Reddy, S. 2005, ApJ, 629, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., Schmitt, A., Rajagopal, K., & Schafer, T. 2008, Rev. Mod. Phys., 80, 455 [Google Scholar]
- Baldo, M., Burgio, G. F., & Schulze, H.-J. 2000, Phys. Rev. C, 61, 055801 [NASA ADS] [CrossRef] [Google Scholar]
- Bambi, C., & Drago, A. 2008, Astropart. Phys., 29, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Benhar, O., & Valli, M. 2007, Phys. Rev. Lett., 99, 232501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Benhar, O., Polls, A., Valli, M., & Vidaña, I. 2010, Phys. Rev. C, 81, 024305 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhiani, Z., Bombaci, I., Drago, A., Frontera, F., & Lavagno, A. 2002, Nuclear Physics B – Proceedings Supplements, 113, 268 [Google Scholar]
- Berezhiani, Z., Bombaci, I., Drago, A., Frontera, F., & Lavagno, A. 2003, ApJ, 586, 1250 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya, S. 2010, Adv. Space Res., 45, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Bodmer, A. R. 1971, Phys. Rev. D, 4, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I. 1996, A&A, 305, 871 [Google Scholar]
- Bombaci, I. 2007, Eur. Phys. J. A, 31, 810 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bombaci, I., & Datta, B. 2000, ApJ, 530, L69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bombaci, I., Parenti, I., & Vidaña, I. 2004, ApJ, 614, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., Lugones, G., & Vidaña, I. 2007, A&A, 462, 1017 [Google Scholar]
- Bombaci, I., Panda, P. K., Providência, C., & Vidaña, I. 2008, Phys. Rev. D, 77, 083002 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., Logoteta, D., Panda, P. K., Providência, C., & Vidaña, I. 2009, Phys. Lett. B, 680, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., & Lattimer, J. M. 1986, ApJ, 307, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Casalbuoni, R., & Nardulli, G. 2004, Rev. Mod. Phys., 76, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Chattaerjee, D., & Bandyopadhyay, D. 2006, Phys. Rev. D, 74, 023003 [NASA ADS] [CrossRef] [Google Scholar]
- Csernai, L., & Kapusta, J. I. 1992, Phys. Rev. D, 46, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Danielewicz, P. 1984, Phys. Lett. B, 146, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Dasgupta, B., Fischer, T., Horiuchi, S., Liebendörfer, M., & Mirizzi, A. 2010, Phys. Rev. D, 81, 103005 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessel, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Drago, A., & Lavagno, A. 2010, [arXiv:1004.0325] [Google Scholar]
- Drago, A., Lavagno, A., & Pagliara, G. 2004, Phys. Rev. D, 69, 057505 [NASA ADS] [CrossRef] [Google Scholar]
- Drago, A., Lavagno, A., & Parenti, I. 2007, ApJ, 659, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Drago, A., Pagliara, G., & Schaffner-Bielich, J. 2008, J. Phys. G, 35, 014052 [NASA ADS] [CrossRef] [Google Scholar]
- Farhi, E., & Jaffe, R. L. 1984, Phys. Rev. D, 30, 2379 [NASA ADS] [CrossRef] [Google Scholar]
- Fodor, Z., & Katz, S. D. 2004, Prog. Theor. Suppl., 153, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Flowers, E., & Itho, N. 1979, ApJ, 230, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Fraga, E. S., Pisarski, R. D., & Schaffner-Bielich, J. 2001, Phys. Rev. D, 63, 121702(R) [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 2000, Compact Stars: Nuclear Physics, Particle Physics, and General Relativity (New York: Springer) [Google Scholar]
- Glendenning, N. K., & Moszkowski, S. 1991, Phys. Rev. Lett., 67, 2414 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gu, J.-F., Guo, H., Lee, X.-G, Liu Y.-X., & Xu, F.-R. 2008, Commun. Theor. Phys., Beijing, China, 49, 461 [Google Scholar]
- Harko, T., Cheng, K. S., & Tang, P. S. 2004, ApJ, 608, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Heiselberg, H., Baym, G., & Pethick, C. J. 1991, Nucl. Phys. B, Proc. Suppl., 24, 144 [Google Scholar]
- Heiselberg, H., Pethick, C. J., & Staubo, E. F. 1993, Phys. Rev. Lett., 70, 1355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Heiselberg, H. 1995, in Strangeness and Quark Matter, ed. G. Vassiliadis (World Scientific), 338, [arXiv:hep-ph/9501374] [Google Scholar]
- Hidaka, Y., McLerran, L., & Pisarski, R. D. 2008, Nucl. Phys. A, 808, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Horvath, J. E., Benvenuto, O. G., & Vucetich, H. 1992, Phys. Rev. D, 45, 3865 [NASA ADS] [CrossRef] [Google Scholar]
- Horvath, J. E. 1994, Phys. Rev. D, 49, 5590 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, S. D. H., & Schwetz, M. 1998, Phys. Lett. B, 432, 2003 [Google Scholar]
- Iida, K., & Sato, K. 1997, Prog. Theor. Phys., 98, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Iida, K., & Sato, K. 1998, Phys. Rev. C, 58, 2538 [Google Scholar]
- Karsch, F. 2005, J. Phys. G, 31, S633 [NASA ADS] [CrossRef] [Google Scholar]
- Kurkela, A., Romatschke, P., & Vuorinen, A. 2010, Phys. Rev. D, 81, 105021 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, J. S. 1968, Phys. Rev. Lett., 21, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, J. S. 1969, Ann. Phys. (N.Y.), 54, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, J. S., & Turski, L. A. 1973, Phys. Rev. A, 8, 3230 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426 [Google Scholar]
- Lifshitz, I. M., & Kagan, Y. 1972, Sov. Phys. JETP, 35, 206 [NASA ADS] [Google Scholar]
- Lombardo, M. P. 2007, Mod. Phys. Lett., A, 22, 457 [Google Scholar]
- Lugones, G., & Benvenuto, O. G. 1998, Phys. Rev. D, 58, 083001 [NASA ADS] [CrossRef] [Google Scholar]
- Lugones, G., & Bombaci, I. 2005, Phys. Rev. D, 72, 065021 [NASA ADS] [CrossRef] [Google Scholar]
- Lugones, G., Grunferld, A. G., Scoccola N. N., & Villavicencio, C. 2009, Phys. Rev. D, 80, 045017 [NASA ADS] [CrossRef] [Google Scholar]
- Lugones, G., do Carmo, T. A. S., Grunferld, A. G., & Scoccola, N. N. 2010, Phys. Rev. D, 81, 085012 [NASA ADS] [CrossRef] [Google Scholar]
- McLerran, L., & Pisarski, R. D. 2007, Nucl. Phys. A, 796, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Menezes, D. P., & Providência, C. 2003, Phys. Rev. C, 68, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Mintz, B. W., Fraga, E. S. Pagliara, G., & Schaffner-Bielich, J. 2010, Phys. Rev. D, 81, 123012 [NASA ADS] [CrossRef] [Google Scholar]
- Nakazato, K., Sumiyoshi, K., & Yamada, S. 2008, Phys. Rev. D, 77, 103006 [NASA ADS] [CrossRef] [Google Scholar]
- Olesen, M. L., & Madsen, J. 1994, Phys. Rev. D, 49, 2698 [NASA ADS] [CrossRef] [Google Scholar]
- Olinto, A. V. 1987, Phys. Lett. B, 192, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, J. R., & Volkoff, G. M. 1939, Phys. Rev., 55, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., Psaltis, D., Ransom, S., Demorest, P., & Alford, M. 2010, ApJ, 724, L199 [Google Scholar]
- Prakash, M., Bombaci, I., Prakash, M., et al. 1997, Phys. Rep., 280, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Pons, J. A., Reddy, S., Prakash, M., Lattimer, J. M., & Miralles, J. A. 1999, ApJ, 513, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Sagert, I., Fischer, T., Hempel, M., et al. 2009, Phys. Rev. Lett., 102, 081101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sandin, F., & Blaschke, D. 2007, Phys. Rev. D, 75, 125013 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, H.-J., Polls, A., Ramos, A., & Vidaña, I. 2006, Phys. Rev. C, 73, 058801 [NASA ADS] [CrossRef] [Google Scholar]
- Sedrakian, A. D., Blaschke, D., Röpke, G., & Schultz, H. 1994, Phys. Lett. B, 338, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Serot, B. D., & Walecka, J. D. 1986, Adv. Nucl. Phys., 16, 1 [Google Scholar]
- Turski, L. A., & Langer, J. S. 1980, Phys. Rev. A, 22, 2189 [NASA ADS] [CrossRef] [Google Scholar]
- van Dalen, E. N. E., & Dieperink, A. E. L. 2004, Phys. Rev. C, 69, 025802 [NASA ADS] [CrossRef] [Google Scholar]
- Venugopalan, R., & Vischer, A. P. 1994, Phys. Rev. E, 49, 5849 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Polls, A., Ramos, A., Engvik, L., & Hjorth-Jensen, M. 2000, Phys. Rev. C, 62, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Bombaci, I., & Parenti, I. 2005, J. Phys. G, 31, S1165 [NASA ADS] [CrossRef] [Google Scholar]
- Walecka, J. D. 1974, Ann. Phys. (N.Y.), 83, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Witten, E. 1984, Phys. Rev. D, 30, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Shternin, P. S., & Yakovlev, D. G. 2008, Phys. Rev. D, 78, 063006 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H. F., Lombardo, U., & Zuo, W. 2010, Phys. Rev. C, 82, 015805 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
The specific latent heat 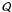 and the phase number densities nH and nQ∗ at phase equilibrium.
and the phase number densities nH and nQ∗ at phase equilibrium.
Crossover temperature Tco (in MeV), for different fixed values of the pressure P (in MeV/fm3) of neutrino-free hadronic matter.
Gravitational (Mcr) and baryonic (MB,cr) critical mass (see text for more details) for proto-hadronic stars at different entropy per baryon 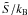 .
.
All Figures
 |
Fig. 1 (Color online) Gibbs energy per baryon, in neutrino-free matter, as a function of pressure for the hadronic and quark phases at different temperatures. Lines with the steeper slope refer to the hadronic phase. Full dots indicate the transition pressure P0 for each temperature. GM1 EOS for the hadronic phase and MIT bag model EOS with B = 85 MeV/fm3 for the quark phase. |
| In the text | |
 |
Fig. 2 Same as Fig. 1, but with a bag constant B = 100 MeV/fm3. (Color online) |
| In the text | |
 |
Fig. 3 Phase equilibrium curve for the hadron to Q*-matter phase transition. The continuous curve is relative to neutrino-free matter, the dashed curve to matter with trapped neutrinos. EOS: GM1 plus MIT Bag model with B = 85 MeV/fm3. |
| In the text | |
 |
Fig. 4 Phase equilibrium pressure P0 between the hadron phase and the Q* phase at T = 0, as a function of the bag constant B. The continuous curve refers to neutrino-free matter, and the dashed curve refers to neutrino-trapped matter. |
| In the text | |
 |
Fig. 5 Energy barrier for a virtual drop of the Q*-phase in β-stable neutrino-free hadronic matter as a function of the droplet radius and for different temperatures for a fixed pressure P = 57 MeV/fm3. The bag constant takes the value B = 85 MeV/fm3. |
| In the text | |
 |
Fig. 6 (Color online) Thermal (τth) and quantum (τq) nucleation time of the Q*-phase (with B = 85 MeV/fm3) in β-stable neutrino-free hadronic matter as a function of temperature at fixed pressure P = 57 MeV/fm3. The crossover temperature is Tco = 7.05 MeV. The limiting conversion temperature for the proto-hadronic star is, in this case, Θ = 10.3 MeV, obtained from the intersection of the thermal nucleation time curve (continuous line) and the dot-dashed line representing log 10(τ/s) = 3. |
| In the text | |
 |
Fig. 7 (Color online) The limiting conversion temperature Θ for a newborn hadronic star as a function of the central stellar pressure. The lines labeled TS represent the stellar matter temperature as a function of pressure at fixed entropies per baryon |
| In the text | |
 |
Fig. 8 (Color online) The limiting conversion temperature Θ for a newborn hadronic star as a function of the central stellar pressure for different values of the bag constant B. The lines labeled TS represent the stellar matter temperature as a function of pressure at fixed entropies per baryon |
| In the text | |
 |
Fig. 9 (Color online) Effects of neutrino trapping on the limiting conversion temperature Θ for a newborn hadronic star as a function of the central stellar pressure. |
| In the text | |
 |
Fig. 10 (Color online) Evolution of a proto-hadronic star in the gravitational-baryonic mass plane for B = 85 MeV/fm3 and σ = 30 MeV/fm2. The upper (red) line represents the stellar equilibrium sequence for neutrino-free proto-hadronic stars (PHS) with |
| In the text | |
 |
Fig. 11 (Color online) Same as Fig. 10, but with the additional stellar sequence (upper (black) line) for proto-hadronic stars with trapped neutrinos (νPHSs) with a lepton fraction YL = 0.4 and |
| In the text | |
 |
Fig. 12 (Color online) Same as Fig. 10, but with a bag constant B = 70.9 MeV/fm3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


