| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 6 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201015375 | |
| Published online | 21 February 2011 | |
Relativistic satellite astrometry: the stellar radial velocity
1
Dipartimento di Fisica “Galileo Galilei”Università degli Studi di
Padova,
via Marzolo 8,
35131
Padova,
Italy
e-mail: defelice@pd.infn.it; preti@pd.infn.it; crosta@to.astro.it; vecchiato@to.astro.it
2
INFN, Sezione di Padova, via Marzolo 8,
35131
Padova,
Italy
3 Osservatorio Astronomico di Torino, strada Osservatorio 20,
10125 Pino Torinese (TO), Italy
Received:
12
July
2010
Accepted:
6
January
2011
We present a general-relativistic analysis that allows the stellar radial velocities to be determined from a suitable implementation of the spectroscopic data with the astrometric ones shortly to be provided by new generations of astrometric satellites at μarcsec levels of accuracy at least. This analysis leads to an enhancement of the c-1 Doppler-shift formula presently planned for the Gaia mission to an all-inclusive, general-relativistic formula at the c-3 level, consistently with the expected accuracy. From this formula, which is shown to provide relevant corrections already at the c-2 level to a previously proposed one, we are then able to derive the explicit expression for the stellar radial velocity in terms of the spectroscopic and astrometric data, thereby accounting for all the necessary relativistic corrections up to and including the c-3 level.
Key words: gravitation / methods: analytical / techniques: high angular resolution / techniques: spectroscopic / astrometry / stars: kinematics and dynamic
© ESO, 2011
1. Introduction
The new generation of astrometric satellites – like Gaia, which is going to be launched by ESA within the next few years – will be able to provide astronomers with a wealth of information about the structure of the Galaxy, thanks to the impressive accuracy in the measurement capabilities (Turon et al. 2005). For instance, Gaia is expected to reach μarcsec precision in measuring the angular distances, thus outperforming the presently employed Hipparcos data by a factor of 103 and thereby providing us with an accurate description of the star positions up to the boundary of the Galaxy, some 10 kpc away.
Such a high accuracy in the expected astrometric performance implies that the general-relativistic effects must be taken into account in analysing the experimental data provided by these satellites, since the c-3 level of precision is mandatory for this analysis to be consistent with the μarcsec accuracy of their astronomical observations. To this end, a “Relativistic Astrometric MODel” (RAMOD) has been conceived and developed – see de Felice et al. (1998), de Felice et al. (2001), Bini & de Felice (2003), Bini et al. (2003), de Felice et al. (2004), de Felice et al. (2006), de Felice & Preti (2006), de Felice & Preti (2008), Crosta & Vecchiato (2010), and Preti & de Felice (2010) – providing a fully general-relativistic analysis of the inverse ray-tracing problem at the required c-3 level from the observational data (the direction cosines of the detector’s line-of-sight) back to the position of the light-emitting star. Resting on this theoretical framework, we derive here an explicit formula for determining the stellar radial velocity, taking advantage of both the spectroscopic and the astrometric data supplied by the observations.
As a matter of fact, this new generation of astrometric satellites will not only allow us to greatly enhance our knowledge of the Galactic structure as far as the stellar positions are concerned, but also provide precise information allowing astronomers to frame a much more detailed kinematical picture of our Galaxy than the presently available one. To this end, these satellites will also be equipped with high-precision spectrometers, allowing determination of the stellar radial velocities on the basis of the Doppler shift of the stellar spectral lines. The interpretation of these observational data in terms of radial velocities is by no means a trivial task yet (Gullberg & Lindegren 2002; Lindegren & Dravins 2003). Moreover, as we note in Sect. 2, the Doppler-shift formula that is planned for the spectroscopic data analysis (de Bruijne et al. 2005) in the case of the first of these new-generation satellites, Gaia, does not take advantage of the high accuracy of its expected astrometric performance at all. After recalling in Sect. 3 the general-relativistic astrometric framework in which we operate, we thus introduce in Sect. 4 an entirely new method that allows implementing the spectroscopic data with the astrometric ones, thus leading to determining the exact general-relativistic Doppler-shift formula at the required c-3 level. In Sect. 5, this formula will be compared to a previously proposed one (Lindegren & Dravins 2003), and this comparison will reveal how our consistently general-relativistic analysis will correct the latter. The issue of separating the radial velocity contribution from that of the proper motion is discussed in Sect. 6. In Sect. 7 an explicit solution of the c-3 equation for the radial velocity is obtained, and in Sect. 8 we finally draw the conclusions of our paper.
As notation and conventions, the metric signature + 2 is employed. Greek (spacetime)
indices run from 0 to 3, while Latin (space) indices run from 1 to 3. From now on, the
expression 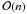 is used to indicate terms of the order of
c − n; moreover, in all the formulae the
G and c factors will be set equal to 1.
is used to indicate terms of the order of
c − n; moreover, in all the formulae the
G and c factors will be set equal to 1.
2. The Doppler-shift formula
Comparison of the observed spectrum of a star with a reference one allows the stellar radial velocity to be determined via the cross-correlation method, based on measurement of the frequency shift between the pairs (ω∗,ωobs) of corresponding frequencies, where ω∗ is the frequency of a photon as emitted by the star, and ωobs the corresponding (“cross-correlated”) frequency measured by the satellite rest observer.
In the case of Gaia and according to the official specifications for its
spectroscopic performance (de Bruijne et al. 2005),
the stellar radial velocity v∗rad will be
determined as 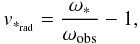 (1)hence employing a
Doppler-shift formula that does not take any relativistic corrections at all into account,
even if they are primary for the expected astrometric observations. These corrections,
however, cannot be provided simply by the well-known special-relativistic formula
(1)hence employing a
Doppler-shift formula that does not take any relativistic corrections at all into account,
even if they are primary for the expected astrometric observations. These corrections,
however, cannot be provided simply by the well-known special-relativistic formula
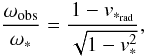 (2)because the genuinely
general-relativistic regime in which the future astrometric missions will operate naturally
calls for a fully general-relativistic Doppler-shift formula, including all the corrections
due to the gravitoelectric and gravitomagnetic effects that a dynamical curved spacetime
background has on the motion of the photon from the star to the satellite. The simple
local comparison of ω∗ with the
corresponding ωobs, as implied by Eq. (2), does not consider the whole story of the
light ray from its origin to its observation, which causes relevant terms to be neglected in
the determination of the stellar velocities. As we see, implementing the Doppler-shift data
with the information coming from the astrometric observations allows all the necessary
relativistic corrections to be naturally included in a general-relativistic Doppler-shift
formula that is fully consistent with the
(2)because the genuinely
general-relativistic regime in which the future astrometric missions will operate naturally
calls for a fully general-relativistic Doppler-shift formula, including all the corrections
due to the gravitoelectric and gravitomagnetic effects that a dynamical curved spacetime
background has on the motion of the photon from the star to the satellite. The simple
local comparison of ω∗ with the
corresponding ωobs, as implied by Eq. (2), does not consider the whole story of the
light ray from its origin to its observation, which causes relevant terms to be neglected in
the determination of the stellar velocities. As we see, implementing the Doppler-shift data
with the information coming from the astrometric observations allows all the necessary
relativistic corrections to be naturally included in a general-relativistic Doppler-shift
formula that is fully consistent with the  accuracy, at least, of the new generation of astrometric satellites.
accuracy, at least, of the new generation of astrometric satellites.
3. The relativistic astrometric framework
We have already recalled that the use of a general-relativistic environment is mandatory
for consistent dealing with μarcsec-precision data; accordingly, the
behaviour of the light ray stemming from a distant star and reaching the satellite detector
must be analysed in terms of geodesic propagation in a curved spacetime. The expression for
the background metric in which the light ray propagates is written in the form 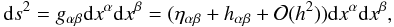 (3)corresponding to
the weak-field, slow-motion approximation; the sources of gravity are assumed to be the
bodies of the solar system alone. In Eq. (3),
the hαβ terms represent perturbations to the
Minkowski metric ηαβ, and the expression
(3)corresponding to
the weak-field, slow-motion approximation; the sources of gravity are assumed to be the
bodies of the solar system alone. In Eq. (3),
the hαβ terms represent perturbations to the
Minkowski metric ηαβ, and the expression
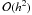 denotes nonlinear terms in these perturbations. The
hαβ terms encapsulate the gravitoelectric
and gravitomagnetic potentials of the gravitational sources, whose contributions we need to
retain up to and including the
denotes nonlinear terms in these perturbations. The
hαβ terms encapsulate the gravitoelectric
and gravitomagnetic potentials of the gravitational sources, whose contributions we need to
retain up to and including the 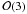 level, in order to comply with the accuracy of the astrometric measurements, as in the case
of Gaia. To the required order of precision, we have
level, in order to comply with the accuracy of the astrometric measurements, as in the case
of Gaia. To the required order of precision, we have 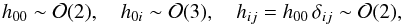 (4)and the metric components
of Eq. (3) are given by
(4)and the metric components
of Eq. (3) are given by  Following
the IAU resolution B1.3 (2000), we introduce a family of locally baricentric observers
u who fill the spacetime (cf. de Felice et al. 2006), each of them at rest with respect to the
Barycentric Celestial Reference System (BCRS). Explicitly, we have
Following
the IAU resolution B1.3 (2000), we introduce a family of locally baricentric observers
u who fill the spacetime (cf. de Felice et al. 2006), each of them at rest with respect to the
Barycentric Celestial Reference System (BCRS). Explicitly, we have 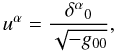 (8)where
g00 is evaluated at the specific spacetime point where the
particular observer u belonging to this family is located.
With respect to u, we can define a spacelike vector
(8)where
g00 is evaluated at the specific spacetime point where the
particular observer u belonging to this family is located.
With respect to u, we can define a spacelike vector
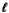 which represents u’s local line of sight. The explicit
expression for
which represents u’s local line of sight. The explicit
expression for 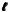 reads as
reads as 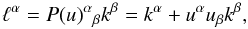 (9)where
k is the tangent vector to the null geodesic followed by
the light ray,
(9)where
k is the tangent vector to the null geodesic followed by
the light ray, 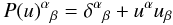 (10)is the spatial
projector on the local rest space of u, and relation
(10)is the spatial
projector on the local rest space of u, and relation
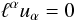 (11)obviously holds.
(11)obviously holds.
Using Eqs. (3)–(7) for the metric, and introducing the convenient
rescaled quantity 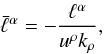 (12)which satisfies
(12)which satisfies
 (13)we are able to
obtain (see de Felice et al. 2006) the equations of
motion describing, at the required
(13)we are able to
obtain (see de Felice et al. 2006) the equations of
motion describing, at the required 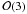 ,
the behaviour of the local line of sight along the light-ray path connecting the star with
the observer. These “RAMOD master equations” explicitly read as
,
the behaviour of the local line of sight along the light-ray path connecting the star with
the observer. These “RAMOD master equations” explicitly read as 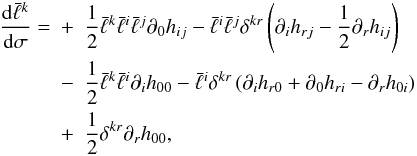 (14)where
σ is a parameter suitably chosen along the null geodesic. The inverse
ray-tracing algorithm based on Eq. (14)
allows us to determine the stellar positions, the stellar motions, and the comprehensive
error budget due to the uncertainties in the boundary conditions (de Felice & Preti
20062008).
(14)where
σ is a parameter suitably chosen along the null geodesic. The inverse
ray-tracing algorithm based on Eq. (14)
allows us to determine the stellar positions, the stellar motions, and the comprehensive
error budget due to the uncertainties in the boundary conditions (de Felice & Preti
20062008).
4. The stellar velocity
As shown in de Felice & Preti (2006), all the
components of the stellar velocities with respect to the BCRS can be determined directly
from astrometric observations alone. However, when the astrometric satellites are also
equipped with a high-precision spectrometer, as in the case of Gaia, a
primary source of information will obviously come from the Doppler-shift data as well. We
have seen above that the Doppler formula (1)
that is actually going to be employed for Gaia’s data analysis (de Bruijne
et al. 2005) contains the Newtonian contribution
alone; on the other hand, we have also seen that a μarcsec astrometric
performance implies that one has to consider the relativistic corrections up to and
including the 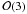 level. As we now show, the relativistic astrometric model outlined in Sect. 3 is able to
provide a Doppler-shift formula that naturally includes all these corrections and allows
determining the stellar radial velocity at this same
level. As we now show, the relativistic astrometric model outlined in Sect. 3 is able to
provide a Doppler-shift formula that naturally includes all these corrections and allows
determining the stellar radial velocity at this same  .
.
The spatial three-velocity of a star relative to the local baricentric observer
u located at the emission event is obtained from
projecting the stellar four-velocity u∗ on the
rest space of this observer: 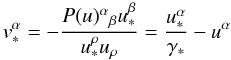 (15)(cf. de Felice
et al. 1990), where
(15)(cf. de Felice
et al. 1990), where
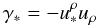 (16)is
the Lorentz factor of the star in the rest frame of u.
Recalling that the tangent four-vector to the light trajectory is
k, the emission frequency ω∗
of a light signal is defined (cf. de Felice et al. 1990) as the frequency measured by the observer
u∗ comoving with the star, namely
(16)is
the Lorentz factor of the star in the rest frame of u.
Recalling that the tangent four-vector to the light trajectory is
k, the emission frequency ω∗
of a light signal is defined (cf. de Felice et al. 1990) as the frequency measured by the observer
u∗ comoving with the star, namely 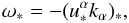 (17)a quantity that is
obviously evaluated at the star position in the asymptotic region of metric (3). The effect of the gravitational field of the
emitting star can easily be taken into account via corrections to the background metric
(3) at the star position as
(17)a quantity that is
obviously evaluated at the star position in the asymptotic region of metric (3). The effect of the gravitational field of the
emitting star can easily be taken into account via corrections to the background metric
(3) at the star position as 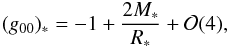 (18)which can be evaluated
using estimates for the mass M∗ and radius
R∗ of the star on the basis of the photometric data.
(18)which can be evaluated
using estimates for the mass M∗ and radius
R∗ of the star on the basis of the photometric data.
The scalar quantity ω∗ defined in Eq. (17) represents the emission frequency to be
cross-correlated with the observational value ωobs measured by
the Gaia satellite. (The considerations made here about the single
frequencies obviously apply to the whole spectrum, which is per se the observed object.)
From Eqs. (15) and (17) it follows that, in terms of quantities
defined in the rest frame of the local baricentric observer u
at the event of emission, the reference data reads as 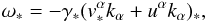 (19)which, recalling
Eqs. (8) and (18), gives
(19)which, recalling
Eqs. (8) and (18), gives ![\begin{equation} \label{1.4} {\omega}_*=-\gamma_*\left[v_*^\alpha k_\alpha+(1+M_*/R_*)k_0\right]_*. \end{equation}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq51.png) (20)At the event of
observation, the emitted spectrum with the single frequencies (20) will be compared with the observed spectrum whose single frequencies
are obtained in a frame comoving with the satellite by the observer
uobs according to the formula
(20)At the event of
observation, the emitted spectrum with the single frequencies (20) will be compared with the observed spectrum whose single frequencies
are obtained in a frame comoving with the satellite by the observer
uobs according to the formula 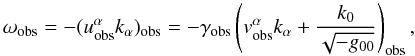 (21)where
(21)where
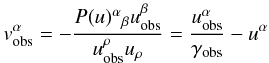 (22)and
(22)and
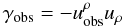 (23)are
the spatial three-velocity of the satellite and the corresponding Lorentz factor,
respectively, relative to the local baricentric observer u
located at the observation event.
(23)are
the spatial three-velocity of the satellite and the corresponding Lorentz factor,
respectively, relative to the local baricentric observer u
located at the observation event.
Equations (20) and (21) are both expressed in terms of the spatial
three-dimensional velocities of the star and of the satellite, relative to the respective
local baricentric observers. While the components 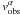 refer to the
motion of the satellite, which is expected to be known, the
refer to the
motion of the satellite, which is expected to be known, the
 represent the
unknowns of our problem. Recalling Eq. (9),
from Eq. (21) it follows that
represent the
unknowns of our problem. Recalling Eq. (9),
from Eq. (21) it follows that 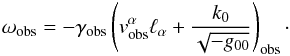 (24)Since the
frequencies ω∗ and ωobs represent
two observables, their ratio
(24)Since the
frequencies ω∗ and ωobs represent
two observables, their ratio ![\begin{equation} \label{1.7} \frac{{\omega}_*}{\omega_{\rm obs}}=\frac{\gamma_*\left[v_*^\alpha\ell_{\alpha}+(1+M_*/R_* )k_0\right]_*} {\gamma_{\rm obs}\left(v_{\rm obs}^\alpha\ell_{\alpha}+{k_0}/{\sqrt{-g_{00}}}\,\right)_{\rm obs}} \end{equation}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq59.png) (25)is
an experimentally measurable quantity. Using Eqs. (8)–(12) we obtain
(25)is
an experimentally measurable quantity. Using Eqs. (8)–(12) we obtain }{\gamma_{\rm obs}(1-v_{\rm obs}^\alpha\bar\ell_{(0)\alpha})/\sqrt{(-g_{00})_{\rm obs}}}, \end{equation}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq60.png) (26)where
(26)where
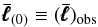 (27)is
directly deducible from the observational data (de Felice & Preti 2006).
(27)is
directly deducible from the observational data (de Felice & Preti 2006).
The components  of the spatial
three-velocity of the star with respect to the local baricentric observer can be decomposed
in a radial plus a trasversal component relative to
of the spatial
three-velocity of the star with respect to the local baricentric observer can be decomposed
in a radial plus a trasversal component relative to 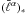 , as follows:
, as follows:
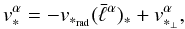 (28)where
(28)where 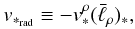 (29)provides the
stellar radial velocity. The minus sign in definition (29) – which causes the minus sign in decomposition (28) – has been introduced for consistency with
the usual conventions, according to which the radial velocity is positive when the star is
moving away from the observer. (Recall that the direction of
(29)provides the
stellar radial velocity. The minus sign in definition (29) – which causes the minus sign in decomposition (28) – has been introduced for consistency with
the usual conventions, according to which the radial velocity is positive when the star is
moving away from the observer. (Recall that the direction of
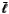 is the incoming one, cf. Fig. 1 of de Felice et al. 2006.)
is the incoming one, cf. Fig. 1 of de Felice et al. 2006.)
Indicating with v∗ the modulus of Eq. (28), and recalling that
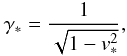 (30)we see that Eq. (26) can be rewritten as
(30)we see that Eq. (26) can be rewritten as 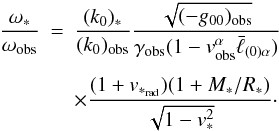 (31)We
now need to evaluate the ratio
(k0)∗ / (k0)obs.
The coordinate time direction is defined by the vector field
(31)We
now need to evaluate the ratio
(k0)∗ / (k0)obs.
The coordinate time direction is defined by the vector field
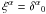 , which is
not a Killing field of spacetime (3). This implies that the scalar
kαξα = k0
is not a constant of motion along the null geodesic with tangent field
k; in fact, we have
, which is
not a Killing field of spacetime (3). This implies that the scalar
kαξα = k0
is not a constant of motion along the null geodesic with tangent field
k; in fact, we have 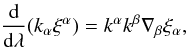 (32)where
∇β is the covariant derivative with respect to
xβ in the given metric, and
λ is a generic parameter along the null ray path. From the definition of
covariant derivative, and recalling relations (4)–(7), we have
(32)where
∇β is the covariant derivative with respect to
xβ in the given metric, and
λ is a generic parameter along the null ray path. From the definition of
covariant derivative, and recalling relations (4)–(7), we have 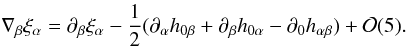 (33)Noting that, according to
Eq. (9), the vector field
k admits the decomposition
(33)Noting that, according to
Eq. (9), the vector field
k admits the decomposition
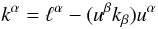 (34)and that
(34)and that
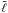 ,
defined in Eqs. (12) and (13), is a unit vector, we can write Eq. (33) as
,
defined in Eqs. (12) and (13), is a unit vector, we can write Eq. (33) as 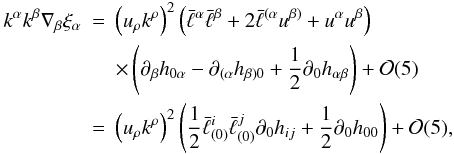 (35)where
the last equivalence also follows from recalling that
(35)where
the last equivalence also follows from recalling that 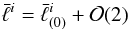 (36)(cf. de Felice
& Clarke 1990). With a little algebra and
observing that
(36)(cf. de Felice
& Clarke 1990). With a little algebra and
observing that 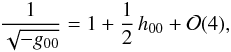 (37)we see that, at the
relevant
(37)we see that, at the
relevant 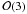 ,
Eq. (32) becomes
,
Eq. (32) becomes 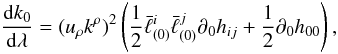 (38)which since
(38)which since
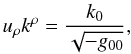 (39)and setting
(39)and setting
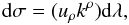 (40)can also be written as
(40)can also be written as
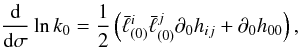 (41)thus leading to
(41)thus leading to
![\begin{equation} \label{1.17} \frac{(k_0)_{\rm obs}}{(k_0)_*}=\exp\left[\frac12 \int_{\sigma_*}^{\sigma_0}\left(\bar\ell^i_{(0)}\bar\ell^j_{(0)}\partial_0 h_{ij}+\partial_0h_{00}\right){\rm d}\sigma\right] \end{equation}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq86.png) (42)where
σ0 ≡ σobs.
(42)where
σ0 ≡ σobs.
Now, using Eq. (42) and recalling
Eq. (18), we see that Eq. (31) can be rewritten as ![\begin{eqnarray} \label{dervel} \frac{{\omega}_*}{\omega_{\rm obs}}&=& \frac{\sqrt{(-g_{00})_{\rm obs}}}{\gamma_{\rm obs}(1-v_{\rm obs}^\alpha\bar\ell_{(0)\alpha})}\cdot \frac{(1+v_{*_{\rm rad}})(1+M_*/R_*)}{\sqrt{1-v_*^2}}\nonumber\\ &&\times\exp\left[-\frac12\int_{\sigma_*}^{\sigma_0}\left(\bar\ell^i_{(0)}\bar\ell^j_{(0)}\partial_0 h_{ij}+\partial_0h_{00}\right){\rm d}\sigma\right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq88.png) (43)which
includes all the relevant contributions that must be taken into account for
consistently dealing with the observational data from the new generation of astrometric
satellites.
(43)which
includes all the relevant contributions that must be taken into account for
consistently dealing with the observational data from the new generation of astrometric
satellites.
Equation (43) can actually be simplified
further, since only the terms up to and including the
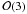 level have to be retained. Recalling Eqs. (18) and (37), and defining
level have to be retained. Recalling Eqs. (18) and (37), and defining
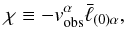 (44)using
(44)using ![\begin{eqnarray} \label{expgs} &&\gamma_{\rm obs}^{-1}=1-\frac{1}{2}v_{\rm obs}^2+{\cal O}(4),\\\nonumber\\ \label{expchi} &&(1+\chi)^{-1}=1-\chi+\chi^2-\chi^3+{\cal O}(4),\\\nonumber\\ \label{expexp} &&\exp\left[-\frac12\int_{\sigma_*}^{\sigma_0}\left(\bar\ell^i_{(0)}\bar\ell^j_{(0)}\partial_0 h_{ij}+\partial_0h_{00}\right){\rm d}\sigma\right]= \nonumber\\ &&\quad1-\frac12\int_{\sigma_*}^{\sigma_0}\left(\bar\ell^i_{(0)}\bar\ell^j_{(0)}\partial_0 h_{ij}+\partial_0h_{00}\right){\rm d}\sigma+{\cal O}(4), \arraycolsep1.75pt \end{eqnarray}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq90.png) and
introducing the shorthand
and
introducing the shorthand ![\begin{eqnarray} \label{defz} \zeta&\equiv&\frac12\bigg[v_{\rm obs}^2+(h_{00})_{\rm obs}\nonumber\\ &&\quad+\int_{\sigma_*}^{\sigma_0}\left(\bar\ell^i_{(0)}\bar\ell^j_{(0)}\partial_0 h_{ij}+\partial_0h_{00}\right){\rm d}\sigma -\frac{2M_*}{R_*}\bigg], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq91.png) (48)we
finally obtain
(48)we
finally obtain 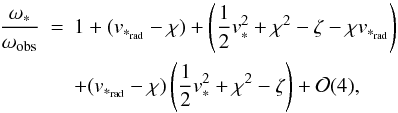 (49)where
the terms in the righthand side have been explicitly grouped according to their progressive
order of magnitude.
(49)where
the terms in the righthand side have been explicitly grouped according to their progressive
order of magnitude.
5. Comparison with a previous formula
In Lindegren & Dravins (2003), a detailed
review of the definition of “radial velocity” in astronomy is presented, with a critical
revision of the equations usually employed to determine this velocity from the spectroscopic
and astrometric measurements. In that paper, a formula for the Doppler shift is also given,
with the aim of including all the corrections caused by the local kinematical and
gravitational effects. This formula reads 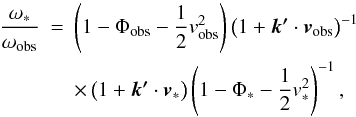 (50)where
use of the BCRS is implied. The Newtonian gravitational potentials are defined as
Φ(r) = G ∑ iMi | r − ri | -1,
Φobs is the Newtonian gravitational potential at the observer location,
Φ∗ is the Newtonian gravitational potential of the star,
vobs and
v∗ are the three-dimensional Euclidean
coordinate velocities of the observer and of the star, respectively,
k′ is the
three-dimensional Euclidean coordinate direction from the observer to the star, and the
scalar products refer to three-dimensional Euclidean space.
(50)where
use of the BCRS is implied. The Newtonian gravitational potentials are defined as
Φ(r) = G ∑ iMi | r − ri | -1,
Φobs is the Newtonian gravitational potential at the observer location,
Φ∗ is the Newtonian gravitational potential of the star,
vobs and
v∗ are the three-dimensional Euclidean
coordinate velocities of the observer and of the star, respectively,
k′ is the
three-dimensional Euclidean coordinate direction from the observer to the star, and the
scalar products refer to three-dimensional Euclidean space.
Given the previous existence of Eq. (50),
it is interesting and instructive to compare its  expansion with our Eq. (49). This comparison
will reveal the importance of a consistently general-relativistic analysis for determining a
Doppler-shift formula adequate for the capabilities of the new generation of astrometric
satellites and for the need of interpreting their spectroscopic observables in terms of the
stellar radial velocities.
expansion with our Eq. (49). This comparison
will reveal the importance of a consistently general-relativistic analysis for determining a
Doppler-shift formula adequate for the capabilities of the new generation of astrometric
satellites and for the need of interpreting their spectroscopic observables in terms of the
stellar radial velocities.
If we define 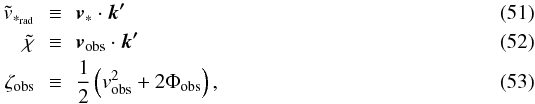 hence
rewrite Eq. (50) as
hence
rewrite Eq. (50) as 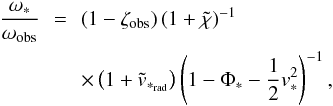 (54)recall
expansion (46), and, finally, define
(54)recall
expansion (46), and, finally, define
![\begin{equation} \label{zetat} \tilde{\zeta}\equiv\zeta_{\mathrm{obs}}-\Phi_*=\frac{1}{2}\left[v_{\mathrm{obs}}^{2}+2(\Phi_{\mathrm{obs}}-\Phi_*)\right], \end{equation}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq102.png) (55)we see that
Eq. (50) power expands into
(55)we see that
Eq. (50) power expands into 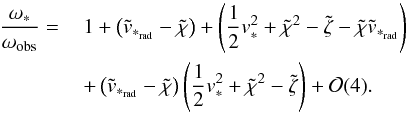 (56)Although
formally analogous to Eq. (49), the above
equation contains some substantial differences from it, and they mirror the differences
existing between the “tilded” quantities (51) and (55), and the corresponding
“untilded” ones (29) and (48). Noting that
(56)Although
formally analogous to Eq. (49), the above
equation contains some substantial differences from it, and they mirror the differences
existing between the “tilded” quantities (51) and (55), and the corresponding
“untilded” ones (29) and (48). Noting that 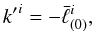 (57)we see that definitions
(44) and (52) agree, namely
(57)we see that definitions
(44) and (52) agree, namely
 (58)but
(58)but 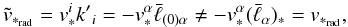 (59)because of Eq. (36); however, because of this same equation we
have
(59)because of Eq. (36); however, because of this same equation we
have 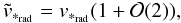 (60)so we recognize that at
first order Eqs. (56) and (43) coincide. Nevertheless, this coincidence is
soon lost, already at second order: if we compare relation (55) with (48), we clearly see that the former completely misses the “history” of
the photon (namely, the integral term appearing in the latter), which only results from a
consistently general-relativistic analysis. Thus, although the velocity and potential terms
in Eqs. (55) and (48) do correspond (note that
(h00)obs = 2Φobs), the absence of the
“photon history” contribution in the former does represent a critical issue. This term does
provide a
(60)so we recognize that at
first order Eqs. (56) and (43) coincide. Nevertheless, this coincidence is
soon lost, already at second order: if we compare relation (55) with (48), we clearly see that the former completely misses the “history” of
the photon (namely, the integral term appearing in the latter), which only results from a
consistently general-relativistic analysis. Thus, although the velocity and potential terms
in Eqs. (55) and (48) do correspond (note that
(h00)obs = 2Φobs), the absence of the
“photon history” contribution in the former does represent a critical issue. This term does
provide a 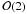 correction, so it is clear that its inclusion is mandatory for a consistent analysis of the
satellite data, which are actually expected to reach the notably higher
correction, so it is clear that its inclusion is mandatory for a consistent analysis of the
satellite data, which are actually expected to reach the notably higher
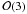 precision. Moreover, we see that at
precision. Moreover, we see that at 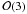 too Eq. (56) misses relevant corrections,
which are provided by Eq. (49): not only the
“photon history” integral, once again, but also the contribution arising from relations
(59)–(60).
too Eq. (56) misses relevant corrections,
which are provided by Eq. (49): not only the
“photon history” integral, once again, but also the contribution arising from relations
(59)–(60).
In conclusion, Eq. (50) is only correct to
 .
It therefore cannot be consistently employed for any higher order analysis. For a consistent
dealing with data from future astrometric satellites, recourse should be made to Eq. (49) instead.
.
It therefore cannot be consistently employed for any higher order analysis. For a consistent
dealing with data from future astrometric satellites, recourse should be made to Eq. (49) instead.
6. Separation of the radial velocity from the proper motion
Wishing to determine the stellar velocity, we see that Eq. (49) alone does not allow this problem to be solved, because it contains two unknowns, namely the radial velocity v∗rad and the total velocity v∗ of the star, or equivalently, the radial velocity v∗rad and the proper motion v∗⊥, according to Eq. (28).
An experimental method for separating the two velocity components, hence obtaining two independent equations for the two unknowns, is provided by the simultaneous observation of the incoming photons along two opposite directions, with the aid of a mirror to be included in the spectroscopic device, following a suggestion originally given by Ives & Stilwell (1938) and also employed in Hasselkamp et al. (1979) for determining the special-relativistic transverse Doppler shift.
However, should such a direct spectroscopic measurement of the proper motion not be allowed by the satellite equipment, we could rely on the astrometric determination of the same, reducing Eq. (43) to an equation where the only unknown is the radial velocity v∗rad, which can thus be determined in terms of both the astrometric and the spectroscopic data. In fact, it can be noted that the total velocity v∗ introduced so far – which is the instantaneous spatial three-velocity of the star with respect to the locally baricentric observer u at the emission event – actually coincides with the one determined in de Felice & Preti (2006) via astrometric methods alone. This is because the local baricentric observer has no spatial velocity with respect to the BCRS, and the background metric for the stellar motion is the asymptotic form of Eq. (3); by the very definition of the instantaneous relative spatial velocity, these two total velocities do coincide, and the expression found for the latter can be correctly employed for the former as well.
7. Explicit solution of the general-relativistic Doppler-shift formula
The general-relativistic Doppler-shift formula (49) obtained above contains all the relativistic corrections up to
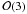 included, in agreement with the expected satellite astrometric capabilities. If we now write
included, in agreement with the expected satellite astrometric capabilities. If we now write
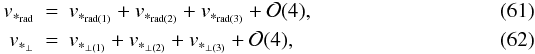 and
solve Eq. (49) in successive approximations,
we find an explicit expression for the radial velocity in terms of the astrometric and
spectroscopic data, namely
and
solve Eq. (49) in successive approximations,
we find an explicit expression for the radial velocity in terms of the astrometric and
spectroscopic data, namely ![\begin{eqnarray} \label{evalvrad} v_{*_{\rm rad}}= &&\left(\frac{{\omega}_*}{\omega_{\rm obs}}-1\right)+\chi\nonumber\\ &-&\frac12\left[\left(\frac{{\omega}_*}{\omega_{\rm obs}}-1\right)^2+\chi^2-2\zeta+v_{*_{\perp(1)}}^2\right]\nonumber\\ &-&\left\{\left[\left(\frac{{\omega}_*}{\omega_{\rm obs}}-1\right)+\chi\,\right] \left(\frac{{\omega}_*}{\omega_{\rm obs}}-1\right)\chi+v_{*_{\perp(1)}}v_{*_{\perp(2)}}\right\}\nonumber\\ &+&{\cal O}(4), \end{eqnarray}](/articles/aa/full_html/2011/04/aa15375-10/aa15375-10-eq113.png) (63)which
accounts for all the necessary first-, second-, and third-order corrections to Eq. (1) caused by the motion of the satellite, its
position in spacetime, the photon history from the star to the satellite, and the surface
gravity and the proper motion of the star itself.
(63)which
accounts for all the necessary first-, second-, and third-order corrections to Eq. (1) caused by the motion of the satellite, its
position in spacetime, the photon history from the star to the satellite, and the surface
gravity and the proper motion of the star itself.
8. Conclusions
Using the Newtonian formula (1) to interpret
the spectroscopic data is clearly unable to account for any relativistic effects. Working in
the RAMOD framework, we have shown how the spectroscopic and astrometric data that will be
provided by the new generation of satellites can be implemented with one another, thus
leading to a general-relativistic Doppler formula – Eq. (49) – which is exact up to and including the
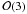 terms, namely the order of magnitude consistent with the expected μarcsec
performance of the future astrometric satellite measurements. We also showed that a
previously proposed Doppler-shift formula, Eq. (50), is definitely not adequate to this task, since it misses relevant
relativistic corrections already at
terms, namely the order of magnitude consistent with the expected μarcsec
performance of the future astrometric satellite measurements. We also showed that a
previously proposed Doppler-shift formula, Eq. (50), is definitely not adequate to this task, since it misses relevant
relativistic corrections already at 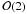 and is therefore correct only at
and is therefore correct only at  .
Finally, by solving Eq. (49) we have been
able to provide an explicit
.
Finally, by solving Eq. (49) we have been
able to provide an explicit 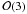 expression – Eq. (63) – for the stellar
radial velocity, in terms of the astrometric and spectroscopic data, where all the relevant
relativistic contributions are now considered.
expression – Eq. (63) – for the stellar
radial velocity, in terms of the astrometric and spectroscopic data, where all the relevant
relativistic contributions are now considered.
References
- Bini, D., Crosta, M. T., & de Felice, F. 2003, Class. Quantum Grav., 20, 4695 [Google Scholar]
- Crosta, M. T., & Vecchiato, A. 2010, A&A, 509, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Bruijne, J., Perryman, M., Lindegren, L., et al. 2005, Gaia astrometric, photometric, and radial-velocity performance assessment methodologies to be used by the industrial system-teams, Technical Note Gaia-JdB-022, June 9 [Google Scholar]
- de Felice, F., & Clarke, C. J. S. 1990, Relativity on Curved Manifolds (New York: Cambridge University Press) [Google Scholar]
- de Felice, F., & Preti, G. 2006, Class. Quantum Grav., 23, 5467 [Google Scholar]
- de Felice, F., & Preti, G. 2008, Class. Quantum Grav., 25, 165015 [Google Scholar]
- de Felice, F., Lattanzi, M. G., Vecchiato, A., & Bernacca, P. L. 1998, A&A, 332, 1133 [NASA ADS] [Google Scholar]
- de Felice, F., Lattanzi, M. G., & Vecchiato, A. 2001, A&A, 373, 336 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Felice, F., Crosta, M. T., Vecchiato, A., Bucciarelli, B., & Lattanzi, M. G. 2004, ApJ, 607, 580 [NASA ADS] [CrossRef] [Google Scholar]
- de Felice, F., Vecchiato, A., Crosta, M. T., Bucciarelli, B., & Lattanzi, M. G. 2006, ApJ, 653, 1552 [NASA ADS] [CrossRef] [Google Scholar]
- Gullberg, D., & Lindegren, L. 2002, A&A, 390, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasselkamp, D., Mondry, E., & Scharmann, A. 1979, Z. Phys. A, 289, 151 [Google Scholar]
- IAU 2000, Definition of Barycentric Celestial Reference System and Geocentric Celestial Reference System, IAU Resolution B1.3 adopted at the 24th General Assembly, Manchester, August [Google Scholar]
- Ives, H. E., & Stilwell, G. R. 1938, J. Opt. Soc. Am., 28, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., & Dravins, D. 2003, A&A, 401, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preti, G., & de Felice, F. 2010, A&A, 513, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turon, C., O’Flaherty, K. S., & Perryman, M. A. C. 2005, The Three-dimensional Universe with Gaia (The Netherlands: ESA Publication Division), SP-576 [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


