| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201015011 | |
| Published online | 09 March 2011 | |
High-contrast observations of (136108) Haumea
A crystalline water-ice multiple system⋆
1
European Southern Observatory. Alonso de Córdova 3107,
Vitacura, Casilla 19001,
Santiago de Chile,
Chile
e-mail: cdumas@eso.org
2
LESIA, Observatoire de Paris, CNRS, 5 place Jules Janssen, 92195
Meudon Cedex,
France
e-mail: benoit.carry@sciops.esa.int
3
European Space Astronomy Centre, ESA, PO Box 78, 28691 Villanueva
de la Cañada, Madrid,
Spain
4
IMCCE, Observatoire de Paris, CNRS. 77,
Av.
Denfert-Rochereau, 75014
Paris,
France
e-mail: hestro@imcce.fr
5
Universit Paris 7 Denis Diderot, 4 rue Elsa Morante, 75013
Paris,
France
e-mail: frederic.merlin@obspm.fr
Received:
18
May
2010
Accepted:
6
January
2011
Context. The trans-Neptunian region of the Solar System is populated by a wide variety of icy bodies showing great diversity in orbital behavior, size, surface color, and composition. One can also see there are dynamical families and binary systems. One surprising feature detected in the spectra of some of the largest trans-Neptunians is the presence of crystalline water-ice. This is the case for the large TNO (136 108) Haumea (2003 EL61).
Aims. We seek to constrain the state of the water ice of Haumea and its satellites and to investigate possible energy sources that maintain the water ice in its crystalline form.
Methods. Spectro-imaging observations in the near infrared were performed with the integral field spectrograph SINFONI mounted on UT4 at the ESO Very Large Telescope. The spectra of both Haumea and its larger satellite Hi’iaka were analyzed. Relative astrometry of the components was also measured, providing a check of the orbital solutions and equinox seasons.
Results. We describe the physical characteristics of the crystalline water-ice present on the surface of Haumea and its largest satellite Hi’iaka and analyze possible sources of heating to maintain water in a crystalline state: tidal dissipation in the system components vs. radiogenic source. The surface of Hi’iaka appears to be covered by large grains of water ice, almost entirely in its crystalline form. Under some restricted conditions, both radiogenic heating and tidal forces between Haumea and Hi’iaka could provide the energy needed to maintain the ice in its crystalline state.
Key words: Kuiper belt objects: individual: (136108) Haumea / techniques: high angular resolution / techniques: imaging spectroscopy / methods: observational / infrared: planetary systems
Based on observations collected at the European Southern Observatory, Paranal, Chile - 60.A-9235.
© ESO, 2011
1. Introduction
The planetesimals orbiting beyond Neptune, the trans-Neptunian objects (TNOs), are remnants of the Solar System’s formation in its outer part. They are thought to be among the most pristine objects in our solar system, although their outer surface layers have been altered by irradiation and collisions over the age of the solar system. Currently, the TNOs population accounts for ~1300 known objects, which are difficult to observe owing to their extreme heliocentric distances and relatively small size. Our knowledge of their physical characteristics is limited for now to studying the few largest and brightest objects, which still reveal that this population displays a large number of binary and multiple systems when compared to other small solar system bodies such as main belt asteroids (e.g., Noll et al. 2008). Transneptunian binaries can be found as gravitationally bound systems with similar mass components, but systems harboring smaller moons, which are by definition harder to detect, have also been discovered around (134 340) Pluto, (136 108) Haumea (2003 EL61), (50 000) Quaoar, (90 482) Orcus, etc. (Noll et al. 2008). Thanks to their binary nature, the total mass of these systems can be inferred, which provides a valuable tool for characterizing their surface and internal physical properties when combined with spectroscopy and radiometric sizes.
Haumea is the largest member of a TNO family, which is likely the outcome of a collision (Brown et al. 2007; Ragozzine & Brown 2007; Schaller & Brown 2008; Rabinowitz et al. 2008; Snodgrass et al. 2010). Here we report spectro-imaging observations of all three components of the Haumea system performed in 2007 at the ESO Very Large Telescope. Our data and related compositional modeling show that the surface of the outer satellite Hi’iaka is mostly coated with crystalline water ice, as in the case of the central body Haumea (Trujillo et al. 2007; Merlin et al. 2007; Pinilla-Alonso et al. 2009). We also discuss the effects of tidal torques as a possible source of energy that is responsible for the crystalline state of the water-ice of Hi’iaka.
2. Observations and data reduction
Haumea was observed in H and K bands on 2007 March 15 UT, using the laser guide-star facility (LGSF) and the SINFONI instrument (Spectrograph for INtegral Field Observations in the Near Infrared), both installed at the 8 m “Yepun” unit of the ESO Very Large Telescope. The use of SINFONI for the observations of the large TNOs Haumea and Eris has been described in earlier papers (Merlin et al. 2007; Dumas et al. 2007), and more information about this instrument can be found in Eisenhauer et al. (2003) and Bonnet et al. (2004). In a nutshell, SINFONI is an integral field spectrometer working in the [1.0−2.5] μm range, which is also equipped with an adaptive optics (AO) system with Natural Guide Star (NGS) and Laser Guide Star (LGS) channels. While our previous published observations were obtained in non-AO mode (seeing-limited), the results presented in this paper made use of the AO system and the LGS facility. The laser produces an artificial visible-light star of Rmag ~ 13.4 in the line of sight of Haumea (Vmag ~ 17.4), thus returning a gain of four magnitudes for characterizing the higher orders of the wavefront in comparison to non-laser observations. Haumea itself was used as a reference source for the tip-tilt, delivering optimal correction by the AO-LGS system. The atmospheric conditions were extremely good during the observations, with an uncorrected seeing varying between 0.5 and 0.6″. On 2007 March 15, between 6h34 UT and 7h24 UT, six exposures of 300 s each were obtained on Haumea (total integration time of 0.5 h), interspaced by 3 exposures of 300 s to record the sky background. We used the H+K spectral grating (spectral resolution of ~1500) covering both H and K bands simultaneously, and a plate scale of 100 mas/spaxel (3″ × 3″ total field). Calibrations to correct our spectra from the solar response and telluric absorption features were obtained immediately after Haumea by observing the local telluric standard HD 142093 (Vmag ~ 7.3, G2V) in NGS mode at similar airmass and with the same instrumental setting.
The data (science target and telluric standard) were mainly reduced using the ESO pipeline 1.9.3 (Modigliani et al. 2006). We first corrected all raw frames from the noise pattern of dark and bright horizontal lines introduced when reading the detector. We then used the ESO pipeline to produce all master files needed by the data reduction, such as the badpixel masks, master darks and flats, and the wavelength and distortion calibration files, which respectively associate a wavelength value to each pixel and reconstruct the final image cubes. Each object frame was subtracted from the sky frame recorded closest in time and the quality of the sky subtraction was improved by enabling the correction of sky residuals in the pipeline, i.e. by subtracting the median value of each image slice in the reconstructed, sky-corrected, spectro-image cube.
 |
Fig. 1 Comparison of H+K band SINFONI images of Haumea obtained under similar conditions but in seeing-limited observations (A, left) and LGS-AO corrected mode (B, right). The spatial and intensity scales are similar and the intensity is given in ADU. The improved contrast and spatial resolution of the AO image (B) is apparent in comparison to the non-AO image (A), making possible the detection of the two faint satellites: Namaka (faintest, just below Haumea) and Hi’iaka (brightest, bottom of image). The images were obtained by summing all the slices of our data-cube to produce the equivalent of a broad H+K band image. |
 |
Fig. 2 Spectrum of Haumea (thin dashed line) obtained with the SINFONI instrument using LGS-AO assisted observations, and our spectral model (solid line, see text). |
Figure 1 shows two H+K-band images of Haumea obtained in seeing-limited and LGS modes. The improvement in contrast returned by the LGS is immediately apparent, as the two satellites of Haumea are visible in the LGS image, allowing us to carry out a detailed spectroscopic and astrometric study of the components of this system.
We thus were able to extract the spectra of Haumea and its brighter satellite Hi’iaka separately. The faintest satellite Namaka could not be spectrophotometrically isolated from Haumea owing to its too close proximity at the time of these observations. Nevertheless, we could neglect the contribution of the satellite to the overall spectrum as its H magnitude is ~24.9 (Fraser & Brown 2009), i.e., within the noise level for a given wavelength bin of our data cube. The individual spectra were then corrected from the remaining bad pixels, combined, and finally divided by the spectrum of the local telluric standard HD 142093. A detailed analysis of the cube and subsequent modeling of the spectra revealed that division of our spectra by the solar analog had the effect of introducing a small artifact in the spectrum of Haumea in the [1.65−1.8] μm range. This particular feature came from the contamination of our spectra by a faint background object within the close vicinity of the standard star. We characterized the impact of the contaminant by dividing our spectrum of HD 142093 by the spectrum of a good solar analog, HD 11532 (Vmag ~ 9.7, G5) used by our ESO Large Program (Prog. ID 179.C-0171, PI: Barucci) and obtained with a similar setup and airmass (Δairmass ~ 0.03). We then applied correction to our final spectra of Haumea and Hi’iaka by dividing both of them by the relative response of the two telluric standard stars over the [1.65−1.8] μm range.
3. Structure of the water ice
3.1. Spectral behavior
Our spectra of Haumea (Fig. 2) and of its brightest satellite (Fig. 3) reveal clear absorption bands of water ice as reported by Barkume et al. (2006) around 1.5 and 2.0 μm. Previous reports (e.g. Trujillo et al. 2007; Merlin et al. 2007) had also shown that the spectrum of Haumea displays the clear signature of crystalline water ice at 1.65 μm. Here, these LGS-assisted VLT observations clearly show that water ice in its crystalline state is similarly present on the brightest of the satellites. The crystalline ice on Hi’iaka was also reported previously by Takato et al. (unpublished) from seeing-limited observations carried out at Subaru under very good atmospheric conditions, while this paper reports LGS-assisted observations of Haumea’s satellite and Hapke modeling of its reflectance spectrum. The primary object spectrum does not display other major absorption bands in the 1.45−2.35 μm range. We can suspect a couple of absorption bands around 2.21 μm and 2.25 μm in the spectrum of Haumea, which, if real, might be explained by the presence of NH3·H2O and, tentatively, NH4+, on the surface, with the latter the likely product of irradiation of ammonia hydrate (Cook et al. 2009). Better data are needed to confirm these bands. The spectrum of Hi’iaka is still too noisy to search for the signature of any additional compounds.
 |
Fig. 3 Spectra of Haumea (top, offsetted by +1 unit for clarity) and of Hi’iaka (bottom), the largest of Haumea’s satellites. The spectrum of the satellite (thin dashed line) was extracted from the same data set as in Fig. 2. Our spectral model (solid line) is described in the text. |
Depth of the water ice absorption bands in the spectra of Haumea and its outermost satellite Hi’iaka.
The crystalline water ice band (at 1.65 μm) is very deep in the spectrum of both objects. This behavior is similar to those of pure crystalline water ice at low temperatures (see Grundy & Schmitt 1998). Considering the high albedo of the primary object (Stansberry et al. 2008), we can assume that crystalline water ice is the major compound on the surface of Haumea and Hi’iaka (and likely Namaka as well). For both spectra, we analyzed the relative depth of the water ice absorption bands at 1.5 μm, 1.65 μm, and 2.0 μm in comparison to the continuum flux estimated at each band center. This continuum was first removed from our measured spectrum before estimating the depth of each band. The results are given in Table 1.
The absorption bands of the spectrum of the satellite are deeper than those of the spectrum of Haumea by a factor ~1.5 for the wide absorption bands (1.5 and 2 μm) and more than 2.5 for the finer 1.65 μm band. This implies a larger grain size for the water ice on the surface of the satellite. Concerning the depth of the absorption band at 1.65 μm, we can suggest that the surface of the satellite has suffered less from the irradiation processes than the surface of Haumea (see Merlin et al. 2007, for a discussion about the shape and location of the 1.65 μm band).
3.2. Spectral modeling
To investigate the surface properties of Haumea and Hi’iaka, we ran a radiative transfer model, based on Hapke theory (Hapke 1981). We computed the geometric albedo at a zero phase angle from Eq. (44) of Hapke (1981). The phase function, which describes the angular distribution of light scattered from a body, is represented by a single Henyey-Greenstein function (Henyey & Greenstein 1941) with an asymmetry parameter of v = −0.4. The backscattering parameter is B = 0.7. These values are close to those used by Verbiscer & Helfenstein (1998) for the icy satellites of the giant planets, which exhibit similar strong water ice features. We follow the formalism of Emery & Brown (2004) to compute the geometric albedo from different compounds, assuming a salt and pepper or an intimate mixture. The free parameters of our models are the grain size and the relative amount of each chemical compound. The lowest reduced χ2 values between the observed spectra and our synthetic spectra were reached using the Marqvardt-Levenberg algorithm, although it is important to note that our model results are not unique and only show the most probable surface composition from our initial set of probable chemical analogs (see Barucci et al. 2008a, on a discussion of the limits of this model).
To perform our spectral modeling, we used optical constants for the several ices at low temperature (close to 40 K) that are suspected to be present on the surface of these icy bodies, including pure and amorphous water ice (Grundy & Schmitt 1998), as well as pure methane ice (Quirico & Schmitt 1997). We also used optical constants of dark compounds, such as amorphous black carbon (Zubko et al. 1996) and Titan Tholin (Khare et al. 1986), which reproduce the low albedo of a large portion of these objects (Stansberry et al. 2008).
Our best result, obtained by assuming an albedo of 0.6 (normalized over the 1.6−1.7 μm region of the spectrum), includes 73% (particle size of 9 μm) of crystalline water ice, 25% (particle size of 10 μm) of amorphous water ice, and 2% (particle size of 10 μm) of Titan Tholin. No other major compound seem to be present on the surface of Haumea. The albedo value in the near infrared was determined from its V albedo (Stansberry et al. 2008), its V − J color and the reflectance ratio reported between the CH4 band at 1.6 μm (CH4s) and J band (Lacerda et al. 2008). We normalized our spectra by convolving them with the response curve of the CH4s filter used by Lacerda et al. (2008) in the H-band region. For the satellite, we treated its albedo as a free parameter in our model, and the best fit was obtained for an albedo of 0.4 in CH4s band and a composition made of 100% of crystalline water ice (particle size of 20 μm). The results of our spectral modeling are given in Figs. 2 and 3.
3.3. Discussion
Our observations and modeling results clearly show that crystalline water ice is present on the surface of the largest satellite, and probably more abundantly than on the surface of the central body (larger particle size and greater amount). Even though our results would require an independent determination of Hi’iaka’s albedo, it is highly probable that the surface of the satellite is completely covered by crystalline water ice, especially if the exact albedo in the CH4s band is close to, or even larger than, the value of 40%. The presence of crystalline water ice on the surface of Hi’iaka demonstrates that crystalline ice can be present on the surface of very small bodies. Indeed, if we adopt a 1600 km diameter for the primary (Rabinowitz et al. 2006), a similar visible albedo between the two bodies, and a magnitude difference of 3.3 (Brown et al. 2005), we derive a diameter of 170 km for the largest satellite.
Mastrapa & Brown (2006) and Zheng et al. (2008) show that the crystalline water ice feature almost disappears after irradiation over a time span of only several Myr to several hundred Myr, so the life time of the crystalline state of water ice is expected to be small on outer solar system objects, especially for low-temperature surfaces. Also, crystalline water ice can only be formed from amorphous water ice after episodes of sufficient heating, since this mechanism is very efficient above 100 K (Jewitt & Luu 2004), but still possible at lower temperatures. Based on this, some competitive mechanisms must be involved to explain that water ice is found mostly in its crystalline state over planet satellites and TNOs, including those of small size. As shown here, our spectral modeling results show that crystalline water ice is dominant and “fresh” (less than several Myr) on the surface of Haumea and its largest satellite. Zheng et al. (2008) shows that the amorphization of crystalline ice by irradiation becomes less efficient with increasing temperature, with the effect of “thermal recrystallization” even becoming dominant at higher temperatures than 40 K. This could partly explain why crystalline ice is still found on small outer solar system bodies. Several authors have also proposed cryovolcanic processes to explain the observation of crystalline water ice (e.g. Jewitt & Luu 2004; Cook et al. 2007). From observations, this assumption could be possible for a few objects where ammonia ice has been detected; for instance: Charon (Brown & Calvin 2000; Buie & Grundy 2000; Dumas et al. 2001; Cook et al. 2007), Quaoar (Jewitt & Luu 2004), or Orcus (Barucci et al. 2008b). Ammonia depresses the melting point and could cause liquid to be compressed and pressurized enough at high depths to reach the surface (Cook et al. 2007). However, the presence of absorption bands due to ammonia is not definitive in our spectra.
Brown et al. (2007) reports the probable discovery of a family of Kuiper belt objects with surface properties and orbits that are nearly identical to those of Haumea, most likely ejected fragments of the parent body’s ice mantle. Recent simulations performed by Ragozzine & Brown (2007) seem to confirm this hypothesis even if the epoch found for the collision seems too ancient (1 Gyr) to conserve the fresh mantle of these bright objects. From photometry, Rabinowitz et al. (2008) show that the members of this family have a common phase curve and have the bluest color among all the TNOs. These observations suggest a high albedo for all of the objects and assume very fresh surfaces. Barkume et al. (2008) show that all observed members of this family show clear absorption features of crystalline water ice, which are not observed in other small TNOs (diameter smaller than ~1000 km), although the number of putative family members has recently been lowered by Snodgrass et al. (2010). Still, the hypothesis of an energetic collisional event could provide a scenario that explains the presence of nearly pure crystalline water ice on the surface of Hi’iaka, especially if we consider that the largest Haumea satellite is still too small to reach the melting point of H2O at any depth. The next section below investigates the possibility of maintaining interior temperatures high enough by involving other scenarios: radiogenic heating and tidal effects between Haumea and Hi’iaka.
 |
Fig. 4 Prediction of the Earth’s elevation (sub-Earth point’s latitude: SEPβ) above the orbital plane for each of the two satellites. Open triangles (blue) indicate the outer satellite S1 Hi’iaka discovered in 2005, filled circles (black) the recently discovered inner satellite S2 Namaka. |
Orbital and physical parameters of the Haumea system.
4. Orbits of Haumea’s satellites
Taking advantage of the imaging capabilities of SINFONI, we extracted the relative astrometric positions of (136 108) Haumea and its two satellites by fitting Gaussian profiles on each of the components. We found the brighter satellite (S1: Hi’iaka) at (−0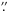 277±.01 E, −1
277±.01 E, −1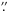 318±.01 N) from (136 108) Haumea, and the faintest satellite (S2: Namaka) at (+ 0
318±.01 N) from (136 108) Haumea, and the faintest satellite (S2: Namaka) at (+ 0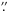 026±.02 E, −0
026±.02 E, −0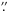 528±.03 N). The large error bars along the SN direction are due to the non-squared shape of SINFONI spaxels, which is twice as large in the SN direction than along the EW direction.
528±.03 N). The large error bars along the SN direction are due to the non-squared shape of SINFONI spaxels, which is twice as large in the SN direction than along the EW direction.
These positions agree with orbits recently determined by Ragozzine & Brown (2009), emphasizing the astrometric quality of the data obtained with SINFONI at the VLT. These orbits lead to mutual events (eclipses) between Haumea and its satellite Namaka within the period ≈2008−2011 (see Fig. 4). There are two equinox seasons during one orbital period of the system around the Sun, hence approximately one each 130 years. Such events are of prime importance because their photometric follow-up can lead directly to a direct determination of the real size of the components, and hence their bulk density, with high accuracy. These events have been indeed predicted by Fabrycky et al. (2008) based on HST and Keck observations. The characteristic modulation of the curves (which depend only on the inclination of the orbit) in Fig. 4 is the effect of the parallax, leading to several favorable opportunities to observe transits and occultation phenomena. It is worth noting that some symmetric solutions for the orbit orientation, although less likely, cannot strictly be ruled out, which would have strong consequences on the prediction of the equinox seasons. Because of scarcity of such occultation events within the transneptunian region, it is important to gather additional astrometric data on the position of the inner satellite for better constraining its orbit orientation, and consequently the prediction of the mutual events.
5. Discussion
This paper shows that crystalline ice is not only present on the largest body of the Haumea multiple system, which could be explained by the long-lived effect of radiogenic heating, but also on the external satellite Hi’iaka (and hence likely on the inner satellite Namaka). Several mechanisms to explain the widespread presence of crystalline ice among primitive small solar system objects have already been proposed (Jewitt & Luu 2004; Grundy et al. 2006; Cook et al. 2007), and all require that some earlier heating events above 80−90 K (Schmitt et al. 1988) might have occurred at large heliocentric distances. In the following, we explore the efficiency of radiogenic heating and tidal dynamical effects as possible heat sources for maintaining water ice in its crystalline state over Hi’iaka.
The radiogenic heating still present in such bodies comes from long-period unstable elements such as 40K, 232Th, and 238U. The heating depends on the volume/surface ratio of the body and mostly the total mass of silicates (for rocks it is 4.5 × 10-12 W kg-1 overall). Assuming a two-layer model for the internal structure of Haumea with a silicate core (density of 3500 kg m-3) and a water ice surface (density of 900 kg m-3), we find that the rock fraction should represent between 88% and 97% of the mass of Haumea (4.00 ± 0.04 × 1021 kg) (Ragozzine & Brown 2009) to comply with the possible density range (2600 to 3300 kg m-3) reported by Rabinowitz et al. (2006). The radiogenic energy presently available is thus on the order of 1010 W, about 10 times what is expected for the asteroid (1) Ceres. In the perspective of a high-impact scenario, the fraction of rock in the satellites should be lower. Still, a 10% rock fraction for the satellites would provide radiogenic energy on the order of 106 W for Namaka, and 107 W for Hi’iaka, which is comparable to the icy satellite of Saturn Tethys (although it is understood that for Tethys, resurfacing processes to maintain water ice in its crystalline state differ and invoke the action of particle bombardment from both the nearby E-ring and Saturn’s magnetosphere).
Assuming now that all the energy involved from the tidal flexure is dissipated, an upper-bound to the crystalline-ice production can be obtained. The amount of thermal energy dissipated in the body is the residual of the transfer of orbital and rotational energy of the deformed body Ėth = |Ẇtide + Ẇrot| . Here we have to consider the more general case of inclined and eccentric orbits, elongated primary (the large lightcurve amplitude observed in Rabinowitz et al. (2006) and Lellouch et al. (2010) is clearly associated to the shape effect, although the object displays albedo markings, see Lacerda et al. (2008)), and non synchronous rotation. However, for the upper-bound computation derived here, we neglect the effect of eccentricity, obliquity, and shape, according to the considerations proposed by Ferraz-Mello et al. (2008) for fast rotators1. As a result, the energy released by the effect of tides can be expressed as 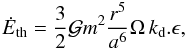 (1)where a is the semi-major axis of the orbit; Ω, m, and r Haumea’s spin rate, mass, and equivalent radius; kd the Love dynamical number, ϵ the phase lag of the tide and
(1)where a is the semi-major axis of the orbit; Ω, m, and r Haumea’s spin rate, mass, and equivalent radius; kd the Love dynamical number, ϵ the phase lag of the tide and 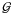 the constant of gravitation.
the constant of gravitation.
Considering the rheology of the material (viscosity, elasticity, and rigidity) and response to forced periodic oscillations through kd·ϵ, only a fraction of this energy will be dissipated. For a typical icy body, one can assume Q ≈ 30−100, which also depends on the temperature of the ice. The Love number scales linearly with the body’s size, and one can assume kd·ϵ ∝ 10-2 for Haumea and ∝ 10-3 for its satellites. Thus, the total energy dissipated inside the outer satellite Hi’iaka (from the tides raised by the central body) can approach 107 W. Conversely, taking the mass, sizes, and different Love numbers into account, the energy dissipated from tides raised by the satellites on Haumea is about 5 × 109 W (somewhat lower than the expected radiogenic energy available).
In comparison, the energy needed to crystallize 95% of amorphous ice (starting from an equilibrium temperature of ≈50 K) corresponds to an increase in temperature of about 40−50 K (with corresponding characteristic times of about 108 and 105 years, respectively) (Schmitt et al. 1988). Taking the water-ice heat capacity (C = 2 × 103 J K-1 kg-1) and the energy found previously, one finds a temperature increase rate δT = 3 × 10-16 K s-1 for a 1019 kg satellite and δT = 6 × 10-16 K s-1 for the ~1020 kg of water ice composing Haumea’s crust. These values lead to an increase of 50 K in two and five Gyrs for Haumea and Hi’iaka respectively.
This scenario is valid for an energy equally distributed inside the whole volume. If, for some reason, the energy is mostly dissipated in some fraction of the mass or conducted to the surface, then the increase in temperature can be even greater. This could be the case if the surface displays cracks in the ice, where the heating could be more concentrated from the friction occurring during the tides. Possible cryovolcanism with a liquid subsurface (Desch et al. 2009) can also be favored by such tidal flexions.
Compared to other systems like Io or Enceladus, the amount of energy involved is very low. However, given the uncertainty of our order of magnitude calculations, it would still be possible, but only under particular conditions, that tides contribute to the generation of crystalline ice on the satellites surface. Knowledge of the spin vector coordinates of Haumea is required to proceed with more specific computations for modeling the tidal effect, the dissipation, heat transfer, and ice crystallization. Besides, if the tides are efficient at producing crystallisation on the outer satellite, one also expects to have crystalline ice on the inner satellite Namaka.
6. Conclusion
We presented spectro-imaging observations of (136 108) Haumea obtained in the near infrared [1.6–2.4 μm] with the integral-field spectrograph SINFONI at the ESO VLT. The presence of crystalline water ice is confirmed on the surfaces of Haumea and Hi’iaka, the largest of the two satellites. Analysis of the spectral bands of water ice and Hapke modeling of our data show that the surface of Hi’iaka is mainly coated with “fresh” ice with larger particles (20 μm), supporting a less altered surface than on Haumea.
Energy sources responsible for the crystallization of the water ice were discussed, and we conclude that radiogenic heating, as well as – under very specific conditions – tidal heating, could explain this observational result.
Improved spectrophotometry of the individual components of the system, and better constraints on Haumea size, shape, and spin state, as well as more detailed modeling of the tidal heating, are now required to proceed in this investigation.
This simplification is based on the following consideration: if the very elongated primary is a fast rotator, the tides it will generate will have high frequencies (see Ferraz-Mello et al. 2008, for more detailed information).
Acknowledgments
The authors wish to thank the referee Josh Emery, for the pertinent comments that improved the manuscript. We thank H. Hussman (DLR, Berlin), N. Rambaux, and V. Lainey (IMCCE) for fruitful discussions about the general treatment of the tides, as well as the whole ESO-Garching commissioning team for the SINFONI LGS system, in particular Stefan Stroebele, Ronald Donaldson, Sylvain Oberti, and Enrico Fedrigo.
References
- Barkume, K. M., Brown, M. E., & Schaller, E. L. 2006, ApJ, 640, 87 [Google Scholar]
- Barkume, K. M., Brown, M. E., & Schaller, E. L. 2008, AJ, 135, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Barucci, M. A., Merlin, F., Guilbert, A., et al. 2008a, A&A, 479, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barucci, M. A., Brown, M. E., Emery, J. P., & Merlin, F. 2008b, in The Solar System Beyond Neptune (Tucson: University of Arizona Press), 143 [Google Scholar]
- Bonnet, H., Abuter, R., Baker, A., et al. 2004, The ESO Messenger, 117, 17 [Google Scholar]
- Brown, M. E., & Calvin, W. M. 2000, Science, 287, 107 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brown, M. E., Bouchez, A. H., Rabinowitz, D., et al. 2005, ApJ, 632, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., Barkume, K. M., Ragozzine, D., & Schaller, E. L. 2007, Nature 446, 294 [Google Scholar]
- Buie, M. W., & Grundy, W. M. 2000, Icarus, 148, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, J. C., Desch, S. J., Roush, T. L., Trujillo, C. A., & Geballe, T. R. 2007, ApJ, 663, 1406 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, J. C., Olkin, C. B., Desch, S. J., et al. 2009, LPSC, 2222 [Google Scholar]
- Desch, S., Cook, J., Doggett, T., & Porter, S. B. 2009, Icarus, 202, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Dumas, C., Smith, B. A., & Terrile, R. J. 2001, AJ, 126, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Dumas, C., Merlin, F., Barucci, M. A., et al. 2007, A&A, 471, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, SPIE, 4841, 1548 [NASA ADS] [Google Scholar]
- Emery, J. P., & Brown, R. H. 2004, Icarus, 170, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., Ragozzine, D., Brown, M. E., & Holman, M. J. 2008, IAU Circ., 8949, 1 [NASA ADS] [Google Scholar]
- Ferraz-Mello, S., Rodríguez, A., & Hussmann, H. 2008, Celest. Mech. Dyn. Astron., 101, 171 [Google Scholar]
- Fraser, W. C., & Brown, M. E. 2009, ApJ, 695, 1 [Google Scholar]
- Grundy, W. M., & Schmitt, B. 1998, JGR, 103, 25809 [Google Scholar]
- Grundy, W. M., Young, L. A., Spencer, J. R., et al. 2006, Icarus, 184, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1981, JGR, 86, 3039 [Google Scholar]
- Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., & Luu, J. 2004, Nature, 432, 731 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Khare, B. N., Sagan, C., Ogino, H., et al. 1986, Icarus, 67, 176 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lacerda, P., Jewitt, D., & Peixinho, N. 2008, AJ, 135, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., Kiss, C., Santos-Sanz, P., et al. 2010, A&A, 518, A147 [Google Scholar]
- Mastrapa, R. M. E., & Brown, R. H. 2006, Icarus, 183, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Merlin, F., Guilbert, A., Dumas, C., et al. 2007, A&A, 466, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Modigliani, A., Hummel, W., Abuter, R., et al. 2006, Proceedings of ADA-4 Conference: Astronomical Data Analysis 4, Marseilles, France, 18−20 Sep. [Google Scholar]
- Noll, K. S., Grundy, W. M., Chiang, E. I., Margot, J. L., & Kern, S. D. 2008, in The Solar System Beyond Neptune, 345 [Google Scholar]
- Pinilla-Alonso, N., Brunetto, R., Licandro, J., et al. 2009, A&A, 496, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirico, E., & Schmitt, B. 1997, Icarus, 127, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Rabinowitz, D. L., Barkume, K., Brown, M. E., et al. 2006, ApJ, 639, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Rabinowitz, D. L., Schaefer, B. E., Schaefer, M., & Tourtellotte, S. W. 2008, AJ, 136, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Ragozzine, D., & Brown, M. E. 2007, AJ, 134, 2160 [NASA ADS] [CrossRef] [Google Scholar]
- Ragozzine, D., & Brown, M. E. 2009, AJ, 137, 4766 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, E. L., & Brown, M. E. 2008, ApJ, 68, 107 [Google Scholar]
- Schmitt, B., Grim, R., & Greenberg, R. 1988, Eslab Symposium on Infrared Spectroscopy in Astronomy [Google Scholar]
- Snodgrass, C., Carry, B., Dumas, C., & Hainaut, O. 2010, A&A, 511, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stansberry, J., Grundy, W., Brown, M., et al. 2008, in The Solar System Beyond Neptune, ed. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, & A. Morbidelli (Tucson: University of Arizona Press), 161 [Google Scholar]
- Trujillo, C. A., Brown, M. E., Barkume, K. M., Schaller, E. L., & Rabinowitz, D. L. 2007, ApJ, 655, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Verbiscer, A., & Helfenstein, P. 1998, in Solar System Ices (Dordrecht: Kluwer Academic Publishers), ASSL, 227, 157 [NASA ADS] [Google Scholar]
- Zheng, W., Jewitt, D., & Kaiser, R. I. 2009, ApJS, 181, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Depth of the water ice absorption bands in the spectra of Haumea and its outermost satellite Hi’iaka.
All Figures
 |
Fig. 1 Comparison of H+K band SINFONI images of Haumea obtained under similar conditions but in seeing-limited observations (A, left) and LGS-AO corrected mode (B, right). The spatial and intensity scales are similar and the intensity is given in ADU. The improved contrast and spatial resolution of the AO image (B) is apparent in comparison to the non-AO image (A), making possible the detection of the two faint satellites: Namaka (faintest, just below Haumea) and Hi’iaka (brightest, bottom of image). The images were obtained by summing all the slices of our data-cube to produce the equivalent of a broad H+K band image. |
| In the text | |
 |
Fig. 2 Spectrum of Haumea (thin dashed line) obtained with the SINFONI instrument using LGS-AO assisted observations, and our spectral model (solid line, see text). |
| In the text | |
 |
Fig. 3 Spectra of Haumea (top, offsetted by +1 unit for clarity) and of Hi’iaka (bottom), the largest of Haumea’s satellites. The spectrum of the satellite (thin dashed line) was extracted from the same data set as in Fig. 2. Our spectral model (solid line) is described in the text. |
| In the text | |
 |
Fig. 4 Prediction of the Earth’s elevation (sub-Earth point’s latitude: SEPβ) above the orbital plane for each of the two satellites. Open triangles (blue) indicate the outer satellite S1 Hi’iaka discovered in 2005, filled circles (black) the recently discovered inner satellite S2 Namaka. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


