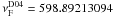© ESO, 2011

1. Introduction

The discovery of the first accreting millisecond pulsar (AMSP) in 1998, SAX J1808.4–3658 (Wijnands & van der Klis 1998), confirmed the predictions of the recycling scenario, according to which millisecond radio pulsars are the end product of a long phase of accretion of matter and angular momentum onto a neutron star (NS) hosted in a low mass X-ray binary (see, e.g., Bhattacharya & van den Heuvel 1991). In the twelve years since the first discovery, the class of AMSPs has grown to thirteen members, all X-ray transients. To perform a timing analysis of different outbursts of the same source allows the estimate of its evolution over a time range of a few years. In the case of SAX J1808.4–3658, the observations of five outbursts over 10 yr have allowed a firm estimate of its spin and orbital evolution. The orbital period has been observed to increase at a rate of nearly two orders of magnitude larger than what is predicted by conservative mass transfer (Di Salvo et al. 2008; Burderi et al. 2009; see also Hartman et al. 2008, H08 hereafter). This has led the authors to argue that a large fraction of the mass transferred by the companion star is ejected by the system taking away the angular momentum needed to match the observed value. A regular NS spin down has also been measured by H08 (see also Hartman et al. 2009) leading to stringent upper limits on the various mechanisms that can brake down a pulsar during quiescence such as magneto-dipole emission, emission of gravitational waves and a propeller effect. These effects, and in particular the spin down torque associated with the emission of gravitational waves, N_GW, crucially depend on the spin frequency of the NS (N_GW ∝ ν⁵). It is therefore very appealing to shed light on the long-term behaviour of the fastest AMSP discovered so far, the 598.89 Hz pulsar IGR J00291+5934 (J00291 in the following). In this paper, we present a timing analysis based on the two outbursts shown by the source in 2008, and observed by the Rossi X-ray Timing Explorer (RXTE). The results thus obtained are compared with the rotational state of J00291 at the end of the outburst exhibited on 2004 December, that is the only other outburst of this source for which high temporal resolution data are available.

2. Observations

The X-ray transient, J00291, was discovered by INTEGRAL on 2004 December 2 (Shaw et al. 2005). The 598.89 Hz pulsations found in its light curve make it the fastest AMSP discovered so far (Galloway et al. 2005, G05 hereinafter).

Renewed activity was detected by RXTE on 2008 August 13 (Chakrabarty et al. 2008). The 2.5–25 keV X-ray flux¹ reaches a peak level of (6.3    ±    0.2)    ×    10^-10 erg cm^-2 s^-1, which is  ≈ 0.5 times the peak flux observed during the 2004 outburst (G05). The flux decreases on a timescale τ ≈ 3 d and the source returns to quiescence  ~5 d after the first detection. The light curve recorded by the PCU2 of the Proportional Counter Array (PCA) aboard RXTE is plotted in Fig. 1. As the nearby source V709 Cas (17 arcmin away) contributes to the X-ray flux detected by RXTE in the direction of J00291 (Markwardt & Swank 2008), the observed count-rate stays at a level of  ~6 c s^-1 PCU^-1 (corresponding to (7 ± 2) × 10^-11 erg cm^-2 s^-1; 2.5–25 keV) even when the J00291 outburst is presumably over. J00291 is again detected in outburst on 2008 September, 21 and the fluence of this second episode is similar to that of the first one.

Fig. 1 Lightcurve of the two outbursts exhibited by J00291 during 2008, as observed by the PCU2 of the PCA aboard RXTE.

To perform a timing analysis on the 598.89 Hz pulsar signal, we consider events recorded by the PCA (Obsid P93013) both in good xenon (1 μs temporal resolution), and event mode (125 μs temporal resolution) configurations. All the arrival times were first corrected with respect to the Solar System barycentre, considering the position of the optical counterpart determined by Torres et al. (2008, T08 hereinafter), RA = 00^h29^m0305  ±  001, Dec = 59°34′1893  ±  005. A re-analysis of the data taken by RXTE during the 2004 outburst (ObsId P90052 and P90425), is also reported. Despite a temporal analysis of the 2004 outburst of J00291 having already been performed by G05, Falanga et al. (2005, F05 in the following) and Burderi et al. (2007, B07), such a re-analysis is aimed at deriving the most accurate estimate of the spin frequency at the end of the outburst that can then be compared to the spin frequency of the source measured in 2008, after  ≈ 3.7 yr of quiescence.

3. Temporal analysis

3.1. The 2008 outbursts

To check the presence of pulsations during the 2008 outbursts of J00291, we first correct the photon-arrival times for the source orbital motion. As no eccentricity was detected as a result of the timing analysis performed on the data of the 2004 outburst (G05, see also Sect. 3.2), we consider a circular orbit to correct photon-arrival times, t_em − t_arr = xsin [l(t_em)] . Here t_arr and t_em are the photon arrival and emission times, respectively, x = asini/c the projected semi-major axis of the NS orbit, l(t_em) = 2π(t_em − T^∗)/P_orb is the mean orbital longitude, P_orb the orbital period, and T^∗ the epoch at which the mean orbital longitude is equal to zero (see Deeter et al. 1981, for a discussion of this choice of orbital epoch²). After a set of values for the orbital parameters is considered, the corrected emission times are obtained by iterating the above relation until the difference between successive steps is of the order of the RXTE absolute timing accuracy (3.4 μs, Jahoda et al. 2006). We first consider the values of x and P_orb given by G05 as orbital evolution is not expected to change them significantly during the time elapsed between the 2004 and 2008 outbursts (≈3.7 yr). The propagation of the error in the value of T^∗ quoted by G05 yields instead an uncertainty of  ~ 80 s. We then use the technique described by Papitto et al. (2005) to improve the estimate of T^∗. The difference of  ≃  − 200 s between the improved estimate we find and the value predicted according to the G05 solution indicates how a correction of  ≃  − 0.015 s (2.5σ from the G05 estimate) to the value of the orbital period has to be applied. Using this improved orbital solution and folding 500 s-long data segments in 12 phase bins around the frequency ${\mathit{\nu }}_{\mathrm{F}}^{\mathrm{A}\mathrm{08}}\mathrm{=}\mathrm{598.89213046}$ Hz, we detect pulsations at the 99% confidence level in the interval MJD 54 691.9−54 696.8, which we refer to as the 2008 August outburst. Pulses are again detected in the interval MJD 54 730.5−54 740.1 (2008 September outburst), after observations have been folded around the frequency ${\mathit{\nu }}_{\mathrm{F}}^{\mathrm{S}\mathrm{08}}\mathrm{=}\mathrm{598.89213060}$ Hz. A detection is assessed according to the criterion stated by Leahy et al. (1983), rejecting the profiles that have a probability larger than 1% of being due to chance.

The pulse profiles have an rms amplitude of  ≃ 8% and are successfully modelled by a sinusoid. We fit the phases thus evaluated with the relation $\mathit{\phi }\mathrm{\left(}\mathit{t}\mathrm{\right)}\mathrm{=}\mathit{\phi }\mathrm{\left(}\mathrm{0}\mathrm{\right)}\mathrm{+}\mathrm{(}{\mathit{\nu }}_{\mathrm{0}}\mathrm{-}{\mathit{\nu }}_{\mathrm{f}}\mathrm{)}\mathrm{(}\mathit{t}\mathrm{-}{\mathit{T}}_{\mathrm{ref}}\mathrm{)}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}\mathit{\nu ̇}{\mathrm{(}\mathit{t}\mathrm{-}{\mathit{T}}_{\mathrm{ref}}\mathrm{)}}^{\mathrm{2}}\mathrm{+}{\mathit{R}}_{\mathrm{orb}}\mathrm{\left(}\mathit{t}\mathrm{\right)}\mathit{,}$(1)where T_ref is the reference epoch for the timing solution, ν₀ and  are the pulsar frequency at the reference epoch and its mean derivative across the outburst, respectively, and R_orb(t) describes the phase residuals due to a difference between the parameters used to correct photon arrival times and the actual orbital parameters of the system. Neglecting second-order terms in the eccentricity, these residuals behave as$\begin{array}{ccc}{\mathit{R}}_{\mathrm{orb}}\mathrm{\left(}\mathit{t}\mathrm{\right)}& \mathrm{=}& \mathit{x}{\mathit{\nu }}_{\mathit{f}}\{\sin \mathrm{\left[}\mathit{l}\mathrm{\right(}\mathit{t}\mathrm{\left)}\mathrm{\right]}\frac{\mathit{\delta x}}{\mathit{x}}\mathrm{-}\frac{\mathrm{1}}{{\mathit{P}}_{\mathrm{orb}}}\left[\mathit{l}\mathrm{\left(}\mathit{t}\mathrm{\right)}\mathit{\delta }{\mathit{P}}_{\mathrm{orb}}\mathrm{+}\mathrm{2}\mathit{\pi \delta }{\mathit{T}}^{\mathrm{\ast }}\right]\cos \mathrm{\left[}\mathit{l}\mathrm{\right(}\mathit{t}\mathrm{\left)}\mathrm{\right]}\\ & & \mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}\sin \mathrm{\left[}\mathrm{2}\mathit{l}\mathrm{\right(}\mathit{t}\mathrm{\left)}\mathrm{\right]}\mathit{h}\mathrm{-}\frac{\mathrm{1}}{\mathrm{2}}\cos \mathrm{\left[}\mathrm{2}\mathit{l}\mathrm{\right(}\mathit{t}\mathrm{\left)}\mathrm{\right]}\mathit{g}\}\mathit{,}\end{array}$(2)where h = ecosω and g = esinω, e is the eccentricity of the orbit, ω the longitude of the periastron measured from the ascending node, and the terms δx, δP_orb, and δT^∗ are the differential corrections to the respective orbital parameter with respect to those used to correct the time series. If significant corrections to the orbital parameters are found, photon arrival times are corrected with the new set of orbital parameters and the phases thus obtained are again fitted using Eq. (1). This procedure is iterated until no orbital residuals are significantly detected.

The results we obtain by fitting the phases of the two outbursts separately are given in the leftmost and central column of Table 1. We consider either a constant frequency model (i.e., ) and also allow for the possibility of a constant spin frequency derivative during each of the outbursts ( model). The addition of a quadratic component to the fit of 2008 August and 2008 September data does not significantly improve the model, and only an upper limit could be set on the spin up term during both outbursts. However, the results obtained with this model are considered as more reliable than those obtained putting , as a non-zero spin frequency derivative is expected on physical grounds and also already observed during the outburst shown by the source during 2004 (F05 and B07; see also Sect. 3.2). We note however that the spin frequency determined in the case is compatible within a 3σ confidence level with that obtained allowing , thus representing a particular case of this more general solution. The evolution of the phases determined for the 2008 August and September outbursts are plotted in Figs. 2 and 3, respectively, together with the residuals with respect to the best-fit models.

Fig. 2 Evolution of the pulse phase delays (in μs) during the August 2008 outburst obtained by folding around the best estimate of the spin frequency at the beginning of that outburst, ${\mathit{\nu }}_{\mathit{F}}^{\mathrm{A}\mathrm{08}}\mathrm{=}\mathrm{598.89213046}$ Hz, the time series preliminarily corrected with the orbital solution listed in the left column of Table 1. The solid line is the best-fit quadratic model, while dashed lines mark the 1σ confidence-level intervals. The bottom panel shows residuals with respect to a model that also includes the spin up term.

Fig. 3 Same as Fig. 2 concerning the phases of the 2008 September outburst. Observations were folded around the best estimate of the spin frequency at the beginning of that outburst, ${\mathit{\nu }}_{\mathrm{F}}^{\mathrm{S}\mathrm{08}}\mathrm{=}\mathrm{598.89213060}$ Hz.

3.2. The 2004 outburst

This work is mainly focused on the study of the spin down experienced by J00291 during the quiescent phase that lasted since the end of the 2004 outburst to the onset of the 2008 August outburst. To this aim, the most accurate estimate of the spin frequency at the end of the 2004 outburst is needed. Previous works relied only on a fraction of the available data: G05 considered only the first three days of data, ObsId P90052, while the solutions of F05 and B07 are valid for the subsequent seven days, ObsId P90425, the only set of which data were publicly available at that time. We re-analysed the 2004 outburst including all the available RXTE data (ObsId P90052 and P90425). Time series were corrected using the position of the optical counterpart (T08), while the position of the proposed radio counterpart (Rupen et al. 2004) was considered in previous works. The results we obtained, applying the same procedure outlined in Sect. 3.1, are listed in the rightmost column of Table 1. Only the parabolic model is presented because the quadratic term is highly significant (Δχ² = 303 over 429 degrees of freedom with respect to a constant frequency model, which has one degree of freedom more). The timing solution is referred to an epoch at the end of the outburst to estimate the spin frequency after the accretion-induced spin-up is over, which can therefore be compared to the frequency at the beginning of the 2008 August outburst. The orbital parameters we obtain are compatible with those previously published by G05, F05, and B07, and are somewhat more precise as they rely on a longer baseline. The addition of three days of data to the data set considered by F05 and B07 indicates an average spin-up term , which is lower with respect to those there evaluated  [(8.5    ±    1.1) × 10^-15   Hz   s^-1] . The phase evolution and residuals with respect to the best-fit model are plotted in Fig. 4.

Fig. 4 Same as Figs. 2 and 3 concerning the phases of the 2004 outburst. The timing solution has been refereed to the epoch at the end of the outburst, MJD 53 352.0, to get the most precise estimate of the spin frequency at that epoch, ${\mathit{\nu }}_{\mathrm{F}}^{\mathrm{D}\mathrm{04}}\mathrm{=}\mathrm{598.89213094}$ Hz, around which the observations are folded.

3.3. The positional uncertainty

The uncertainties quoted in Table 1 are 1σ error based on the modelling of the phase evolution. However, the error in the source position introduces an uncertainty in the determination of the pulse phases $\mathrm{\Delta }{\mathit{\phi }}_{\mathrm{pos}}\mathrm{=}\mathit{\nu y}\left[\sin \mathrm{(}{\mathit{M}}_{\mathrm{0}}\mathrm{+}{\mathit{ϵ}}^{\mathrm{)}}\cos \mathit{\beta \delta \lambda }\mathrm{-}\cos \mathrm{(}{\mathit{M}}_{\mathrm{0}}\mathrm{+}{\mathit{ϵ}}^{\mathrm{)}}\sin \mathit{\beta \delta \beta }\right]\mathit{,}$(3)where y is the Earth distance from the Solar System barycentre in lt-s, λ and β are the ecliptic longitude and latitude, respectively, δλ and δβ the respective uncertainties, M₀ =  [2π(T₀ − T_γ)/P _⊕ ]  − λ, T₀ is the start time of observations considered, T_γ is the nearest epoch of passage at the vernal point, P _⊕  is the Earth orbital period, and ϵ = 2π(t − T₀)/P _⊕  (see, e.g., Lyne & Graham-Smith 1990). For time intervals that are small with respect to the Earth orbital period (i.e. ϵ ≪ 1) such as the ones considered in this work, this expression can be expanded as a polynomial and only the lowest order terms retained. As the value of the spin frequency at the reference epoch of the timing solution depends on the linear term of the temporal evolution of the phases [see Eq. (1)], the systematic uncertainty introduced by the position error in this measure, δν_pos, is $\mathit{\delta }{\mathit{\nu }}_{\mathrm{pos}}\mathrm{\simeq }\mathit{\nu y}\left(\frac{\mathrm{2}\mathit{\pi }}{{\mathit{P}}_{\mathrm{\oplus }}}\right)\left[\cos {\mathit{M}}_{\mathrm{0}}\cos \mathit{\beta \delta \lambda }\mathrm{+}\sin {\mathit{M}}_{\mathrm{0}}\sin \mathit{\beta \delta \beta }\right]\mathit{.}$(4)Considering the uncertainties in the position quoted by T08 [σ_λ ≤ (3.9 × 10^-5)°, σ_β ≤ (2.4 × 10^-5)°], and evaluating this relation for the 2008 and the 2004 outbursts translates into ${\mathit{\sigma }}_{\mathit{\nu }}^{\mathrm{08}}\mathrm{\simeq }\mathrm{1}\mathrm{\times }{\mathrm{10}}^{-8}$ Hz and ${\mathit{\sigma }}_{\mathit{\nu }}^{\mathrm{04}}\mathrm{\simeq }\mathrm{3}\mathrm{\times }{\mathrm{10}}^{-8}$ 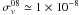Hz, respectively. To get reliable estimates of the uncertainties affecting each measured spin frequency, these systematic errors have to be summed in quadrature with the statistical errors quoted in Table 1. The systematic error in the frequency variation between the two outbursts can instead be estimated as σ_Δνpos ≃ 4 × 10^-8 Hz.

3.4. The spin evolution of J00291 during quiescence

The estimate of the spin frequency of J00291 at the beginning of the 2008 August can be compared with the spin measured at the end of the 2004 outburst to measure the frequency variation experienced by the source during quiescence. Considering the value measured using the model at the onset of the 2008 August outburst (ν^A08 = 598.89213046(13) Hz), we thus obtain Δν = ν^A08 − ν⁰⁴ =  −(0.48    ±    0.13    ±    0.04)   μHz, where the first error quoted is the statistical error given by the difference of the values quoted in Table 1 and the latter reflects the uncertainty on the source position. The average spin-down rate during quiescence is therefore estimated as  Hz s^-1. The large uncertainty affecting this estimate is due to the limited statistics available for the 2008 August outburst which imply loose estimates of the spin frequency at the beginning of that outburst and of the spin frequency derivative during that outburst (see also the discussion).

4. Discussion and conclusions

We have presented a detailed timing analysis concerning the two outbursts shown by J00291 in 2008 August and September as observed by RXTE, as well as a re-analysis of the 2004 outburst using the whole RXTE dataset available.

Our analysis of the 2004 data confirms the significant spin up the source has underwent while accreting as already reported by F05 and B07. The estimate of the spin up rate we have presented here is evaluated on a longer temporal baseline with respect to that considered by those authors and is accordingly more accurate. The magnitude of the spin up is lower by a factor  ~ 0.4 with respect to that quoted by those works, making its interpretation easier in terms of the NS accretion of the supposedly Keplerian disc angular momentum at the flux emitted by the source (see discussion in B07).

In contrast, no derivative is detected significantly during the 2008, August and September, outbursts, with 3σ upper limits on the spin up component of and  Hz s^-1, respectively. These estimates reflect the limited statistics available. An accretion-induced spin-up is expected to depend almost linearly on the mass accretion rate (, where α is the index of the dependence of the inner disk radius on the mass accretion rate, R_in ∝ Ṁ ^− α, α = 2/7 if the inner disc radius is approximated by the Alfven radius). As the peak X-ray flux shown by the source during both 2008 outbursts is roughly half that of the 2004 outburst, the spin up rate is expected to scale accordingly, provided that the flux is a good tracer of the mass accretion rate. We thus expect  Hz s^-1 during each of the outbursts shown by the source in 2008. While the upper limit to the September 2008 outburst spin up is of the same order as this value, the upper limit to the August 2008 data is one order of magnitude larger and can therefore not be considered as a tight constraint. This can also be viewed by considering the 3σ upper limit to the difference between the spin frequencies at the beginning of the 2008 September and August outbursts, ν_S08 − ν_A08 < 0.45   μHz. Neglecting any spin down in-between the two outbursts, the spin up during the 2008 August episode cannot be larger than  Hz s^-1 to account for this difference. This reasonable upper limit is already smaller by a factor of two than the upper limit found from timing analysis of that outburst alone.

The comparison of the spin frequency measured at the beginning of the 2008 August outburst with that of the end of the 2004 episode indicates that the spin frequency has decreased during quiescence. Summing in quadrature the statistical error to the systematics induced by the uncertainty in the source position (see Sect. 3.4), we quote an average spin-down rate during quiescence of  Hz s^-1.

A spin down at a rate of (−5.5 ± 1.2) × 10^-16 Hz s^-1 extending over  ~ 10 yr, has already been measured by Hartman et al. (2009; see also H08), from the 401 Hz AMSP, SAX J1808.4–3658. Riggio et al. (in prep.) found an average spin down rate of (−5.5    ±    1.2)    ×    10^-15 Hz s^-1 for the case of XTE J1751–305, while only an upper limit ( Hz s^-1, 95% confidence level) could be set instead by Patruno et al. (2010), for SWIFT J1756.9–2508. Similarly to H08, we discuss the spin down measured from J00291 in terms of: (i) magneto-dipole radiation, (ii) emission of gravitational waves, and (iii) the propeller effect.

The spin down luminosity of a rotating magnetosphere, , has been evaluated by Spitkovsky (2006) in the limit of force-free magneto-hydrodynamics as, L_sd = (1 + sin²α)μ²(2πν)⁴/c³, where α is the latitude of the magnetic poles, I is the NS moment of inertia and μ is the magnetic dipole. This translates into a spin down rate, , where N_vac =  −(2/3)μ²(2πν/c)³sin²α is the usual expression for the torque acting on a magnetised rotator in vacuum. The estimate of  we have given translates into a value of the magnetic dipole of $\mathit{\mu }\mathrm{\simeq }\mathrm{1.1}\mathrm{\left(}\mathrm{2}\mathrm{\right)}\mathrm{\times }{\mathrm{10}}^{\mathrm{26}}{\mathit{I}}_{\mathrm{45}}^{\mathrm{1}\mathit{/}\mathrm{2}}\mathrm{(}\mathrm{1}\mathrm{+}{\sin }^{\mathrm{2}}\mathit{\alpha }{\mathrm{)}}^{\mathrm{-}\mathrm{1}\mathit{/}\mathrm{2}}$ G cm³, where I₄₅ is the moment of inertia in units of 10⁴⁵ g cm². This estimates translates into a magnetic field, $\mathit{B}\lesssim \mathrm{2.2}\mathrm{\left(}\mathrm{4}\mathrm{\right)}\mathrm{\times }{\mathrm{10}}^{\mathrm{8}}{\mathit{I}}_{\mathrm{45}}^{\mathrm{1}\mathit{/}\mathrm{2}}\mathrm{(}\mathrm{1}\mathrm{+}{\sin }^{\mathrm{2}}\mathit{\alpha }{\mathrm{)}}^{\mathrm{-}\mathrm{1}\mathit{/}\mathrm{2}}$ G at the magnetic poles of a 10 km NS. Considering α = 0, an upper limit of  ≃ 3 × 10⁸ G (3σ confidence level) on the magnetic field is obtained. This estimate fits well into the expected range of magnetic field strengths for the AMSPs to be the progenitors of recycled radio millisecond pulsars ( ≃ 10⁸ − 10⁹ G). It is also compatible with the requirements set on the dipole strength by the maximum and minimum accretion rate experienced by the source while showing pulsations. For pulsations to be observed, the magnetospheric radius has to lie between the NS radius, R_NS, and the corotation radius, R_C = (GM/4π²ν²)^1/3 ($\mathrm{23.6} {\mathit{m}}_{\mathrm{1.4}}^{\mathrm{1}\mathit{/}\mathrm{3}}$ km for J00291, where m_1.4 is the NS mass in units of 1.4 M_⊙). The minimum flux at which we observe pulsations during the 2008 outbursts is F_2.5−25 = (1.8    ±    0.4)    ×    10^-10 erg cm² s^-1 (MJD 54 696.751). Assuming as the bolometric correction factor that derived by G05 (2.54) and that the observed X-ray flux reflects the mass accretion rate, this translates into $\mathit{Ṁ}{}_{\min }\mathrm{\simeq }\mathrm{0.9}\mathrm{\times }{\mathrm{10}}^{-10} {\mathit{m}}_{\mathrm{1.4}}^{-1} {\mathit{R}}_{\mathrm{10}} {\mathit{d}}_{\mathrm{4}}^{\mathrm{2}} {\mathit{M}}_{\mathrm{\odot }} {\mathrm{yr}}^{-1}$, where R₁₀ is the radius of the NS in units of 10 km, and d₄ is the distance to the source in units of 4 kpc. Considering the value quoted by G05 for the peak flux during the 2004 outburst, the maximum accretion rate at which pulsations were observed can be estimated as $\mathit{Ṁ}{}_{\max }\mathrm{\simeq }\mathrm{4.7}\mathrm{\times }{\mathrm{10}}^{-10} {\mathit{m}}_{\mathrm{1.4}}^{-1} {\mathit{R}}_{\mathrm{10}} {\mathit{d}}_{\mathrm{4}}^{\mathrm{2}} {\mathit{M}}_{\mathrm{\odot }} {\mathrm{yr}}^{-1}$. Using the expressions derived by Psaltis & Chakrabarty (1999), the presence of pulsations at these two limiting accretion rates indicates that the magnetic dipole has to lie in the range, (0.2 − 21) × 10²⁶   d₄   G   cm³, fully compatible with our estimate. As the minimum flux at which pulsations are observed is likely overestimated by a factor of  ~2 because of the contribution of V709 Cas, the upper limit to the magnetic dipole is likely to be a factor $\sqrt{\mathrm{2}}$ smaller. Considering also the dynamical estimate of the maximum mass-accretion rate derived by B07 from the spin up rate observed during the 2004 outburst, the lower limit to the dipole strength increases to 0.6 × 10²⁶ G cm^-3, still compatible with the estimate derived here. Our estimate of the magnetic field strength is also compatible with the upper limit estimated by T08 from the X-ray quiescent luminosity,  < 3 × 10⁸ G, using the criteria stated by Burderi et al. (2002) and Di Salvo & Burderi (2003).

The spin down torque associated with the emission of gravitational radiation has been proposed to explain the non-detection of accreting pulsars with frequencies higher than  ≈ 730 Hz (Chakrabarty et al. 2003; see Wagoner 1984; Bildsten 1998; Melatos & Payne 2005, for models describing mechanism that can lead to a non-zero mass quadrupole for an accreting pulsar). In this case, the spin-down torque is, N_GW =  −(32/5) GQ²(2πν/c)⁵ (see, e.g., Thorne 1980). Under the hypotheses that the spin down of J00291 is due only to this mechanism and that the torque due to the GW emission is constant, our measure of the average spin down translates into an estimate of the average mass quadrupole moment, $\mathit{Q}\mathrm{\simeq }\mathrm{1.2}\mathrm{\left(}\mathrm{2}\mathrm{\right)}\mathrm{\times }{\mathrm{10}}^{\mathrm{36}}{\mathit{I}}_{\mathrm{45}}^{\mathrm{1}\mathit{/}\mathrm{2}}$ g cm². Considering the upper limit at the 3σ confidence level, Q ≲ 2 × 10³⁶ g cm², the maximum amplitude at the Earth of the emitted GW is therefore, ${\mathit{h}}_{\mathrm{C}}\lesssim \mathrm{4.6}\mathit{G}\mathrm{(}\mathrm{2}\mathit{\pi \nu }{\mathrm{)}}^{\mathrm{2}}\mathit{Q}\mathit{/}\mathit{d}{\mathit{c}}^{\mathrm{4}}\lesssim \mathrm{3}\mathrm{\times }{\mathrm{10}}^{-28} {\mathit{d}}_{\mathrm{4}}^{-1} {\mathit{I}}_{\mathrm{45}}^{\mathrm{1}\mathit{/}\mathrm{2}}$ (Brady et al. 1998). Assuming that the spin down during quiescence of J00291 and SAX J1808.4–3658 is driven by the emission of GW and that the NS in these systems have a similar mass quadrupole, the spin down driven by the emission of GW should be  ≈ (598.9/401.0)⁵ ≃ 7.6 times larger in J00291 than in SAX J1808.4–3658. The large uncertainties affecting the spin down estimates in both sources do not allow us to check whether this prediction is compatible with observations. However, that the spin down of both sources can be easily explained by magneto-dipole emission of a NS with a magnetic field of the order of that expected for an AMSP makes it unlikely that the spin down during quiescence of AMSPs is dictated by the emission of GW.

The spin down of an accreting NS during quiescence can be also explained by the propeller effect (Illarionov & Sunyaev 1975), that is the centrifugal inhibition of accretion by a magnetosphere that extends beyond the corotation radius. Considering the upper limit at 3σ on the average spin frequency derivative during quiescence that we have measured , the system should eject matter at an average rate Ṁ_ej ≳ 2 × 10^-12   n^-1$\mathrm{(}{\mathit{r}}_{\mathrm{in}}\mathit{/}{\mathit{R}}_{\mathrm{C}}{\mathrm{)}}^{\mathrm{-}\mathrm{1}\mathit{/}\mathrm{2}} {\mathit{I}}_{\mathrm{45}} {\mathit{m}}_{\mathrm{1.4}}^{\mathrm{-}\mathrm{2}\mathit{/}\mathrm{3}} {\mathit{M}}_{\mathrm{\odot }}\hspace{0.17em}{\mathrm{yr}}^{-1}$, if the spin down is explained in terms of the propeller effect alone. Here, R_in is the inner disc radius, and n is the dimensionless torque (Ghosh & Lamb 1979), which takes values n ≈ 1, as soon as r_in ≳ R_C (Ekşi et al. 2005). Assuming that mass is propelled away from the NS at a roughly constant rate, the source quiescent luminosity would then be L_p ≥ GMṀ_ej/2R_C ≃ 6 × 10³³ erg s^-1. As the quiescent flux received from the source is F_q ≲ 1.2 × 10^-13 erg cm^-2 s^-1 (0.5–10 keV, Campana et al. 2008; Jonker et al. 2008), the source should be farther than  ≃ 20 kpc to match this value, and a distance greatly in excess of 10 kpc is obviously to be excluded (see also G05). We thus conclude that it is highly unlikely that the propeller effect alone explains the spin down of J00291.

Observations of future outbursts from this source will be used to monitor the constancy of the long-term spin down, and to derive tighter constraints on the parameters of the NS in J00291.

Acknowledgments

This work is supported by the Italian Space Agency, ASI-INAF I/088/06/0 contract for High Energy Astrophysics, as well as by the operating program of Regione Sardegna (European Social Fund 2007-2013), L.R.7/2007, “Promotion of scientific research and technological innovation in Sardinia”. Soon after this paper was first submitted, other two papers discussing the rotational evolution of this source during quiescence appeared on arXiv.org (Patruno 2010; Hartman et al. 2011). Even if the analysis presented by these authors slightly differs with respect to that presented here (in particular Patruno 2010, derived a timing solution under the preliminary assumption that pulse phases linearly correlate with the X-ray flux), the values they obtain for the spin-down rate of the source during quiescence are entirely compatible with that presented here. We thank Jacob M. Hartman for useful discussions and comments on this paper.

References

All Tables

All Figures

	Fig. 1 Lightcurve of the two outbursts exhibited by J00291 during 2008, as observed by the PCU2 of the PCA aboard RXTE.
In the text

Fig. 2 Evolution of the pulse phase delays (in μs) during the August 2008 outburst obtained by folding around the best estimate of the spin frequency at the beginning of that outburst, ${\mathit{\nu }}_{\mathit{F}}^{\mathrm{A}\mathrm{08}}\mathrm{=}\mathrm{598.89213046}$ Hz, the time series preliminarily corrected with the orbital solution listed in the left column of Table 1. The solid line is the best-fit quadratic model, while dashed lines mark the 1σ confidence-level intervals. The bottom panel shows residuals with respect to a model that also includes the spin up term.

In the text

	Fig. 3 Same as Fig. 2 concerning the phases of the 2008 September outburst. Observations were folded around the best estimate of the spin frequency at the beginning of that outburst, ${\mathit{\nu }}_{\mathrm{F}}^{\mathrm{S}\mathrm{08}}\mathrm{=}\mathrm{598.89213060}$ Hz.
In the text

	Fig. 4 Same as Figs. 2 and 3 concerning the phases of the 2004 outburst. The timing solution has been refereed to the epoch at the end of the outburst, MJD 53 352.0, to get the most precise estimate of the spin frequency at that epoch, ${\mathit{\nu }}_{\mathrm{F}}^{\mathrm{D}\mathrm{04}}\mathrm{=}\mathrm{598.89213094}$ Hz, around which the observations are folded.
In the text