EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 527 (March 2011) A&A, 527 (2011) A59 Full HTML
Free Access
Issue
A&A
Volume 527, March 2011
Article Number A59
Number of page(s) 6
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201016066
Published online 25 January 2011

© ESO, 2011

1. Introduction

Several features of colour-magnitude diagrams (CMDs) and luminosity functions (LFs) of Galactic globular clusters (GCs) can be employed to test the accuracy of low-mass, metal-poor stellar models (see, e.g. Renzini & Fusi Pecci 1988). The bump appearing in the GC red giant branch (RGB) LF is one of these important benchmarks. It is produced by the encounter of the H-burning shell with the H-abundance discontinuity left over by the outer convection at its maximum depth (Thomas 1967; Iben 1968) reached during the first dredge-up. The sharp increase in the H-abundance causes a sudden decrease in the mean molecular weight (μ), which affects the efficiency of the H-burning shell, proportional to a high power of μ (see Kippenhahn & Weigert 1994; Salaris & Cassisi 2005). This occurrence causes a temporary drop in the surface luminosity, before it starts to increase again. As a consequence, a low-mass RGB star crosses the same luminosity interval three times, and a bump (over-density) appears in the RGB differential LF (star counts per magnitude bin) of GCs (for a detailed discussion we refer to Salaris et al. 2002). Given that the RGB-bump brightness depends on the maximum depth attained by the convective envelope and on the chemical profile above the advancing H-burning shell, the comparison between predicted and observed luminosity of the RGB-bump, provides valuable information about the internal structure of low-mass stars at the beginning of their RGB evolution.

Since its first detection in the LF of NGC 104 (47 Tuc – King et al. 1985), the RGB bump has been the subject of several theoretical and observational investigations (Fusi Pecci et al. 1990; Cassisi & Salaris 1997; Alves & Sarajedini 1999; Zoccali et al. 1999; Bono et al. 2001; Riello et al. 2003; Bjork & Chaboyer 2006; Di Cecco et al. 2010). Thanks to these works, we now have accurate measurements of its brightness in many GCs, as well as in Local Group dwarf galaxies (see Monelli et al. 2010, and references therein).

Table 1

The metal content, TO, RGB bump brightness, and age estimates from both TO and ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} for the selected sample of GCs.

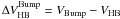The parameter routinely adopted to compare observations with theory is the quantity ΔVHBBump=VBump−VHB\hbox{$\Delta V_{\rm HB}^{\rm Bump} = V_{\rm Bump}-V_{\rm HB}$}, that is, the V-magnitude (or bandpasses similar to Johnson V) difference between the RGB-bump and the horizontal branch (HB) at the RR Lyrae instability strip level (Fusi Pecci et al. 1990; Cassisi & Salaris 1997). This has the advantage of being formally independent of distance and reddening and not affected by any uncertainty in the zero point of the photometry. The most recent comparisons between ΔVHBBump\hbox{$\Delta V_{\rm HB}^{\rm Bump}$} models and observations (see, e.g., Fig. 10 in Di Cecco et al. 2010) seem to confirm a discrepancy (at the level of  ~0.20 mag or possibly more) for GCs with total metallicity [M/H] below  ~ −.5, in the sense that the predicted RGB-bump luminosity is too high. The quantitative estimate of the discrepancy depends on the adopted metallicity scale. At the upper end of the GC metallicity range, the existence of a discrepancy depends on the adopted metallicity scale.

One drawback of using ΔVHBBump\hbox{$\Delta V_{\rm HB}^{\rm Bump}$} as a diagnostic of the RGB-bump luminosity is that uncertainties in the placement of the observed HB level for GCs with blue HB morphologies and in theoretical predictions of the HB luminosity (i.e., due to uncertainties in the calculations of the He-core mass at the He-flash, see e.g. Cassisi 2010) hamper any interpretation of discrepancies between theory and observations.

An alternative avenue explored in this paper is offered by measuring the magnitude difference between the main sequence (MS) turn-off (TO) and the RGB-bump brightness ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} = VTO − Vbump, which bypasses the HB. Observationally, an accurate estimate of the TO brightness requires both very high-quality photometric datasets and a detailed analysis of the uncertainty associated with the presence of binary stars. To the best of our knowledge, only Caputo & Cassisi (2002) and Meissner & Weiss (2006) have so far studied the ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} parameter. 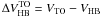Caputo & Cassisi (2002) used ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} in combination with ΔVHBTO=VTO−VHB\hbox{$\Delta V_{\rm HB}^{\rm TO}= V_{\rm TO}-V_{\rm HB}$} to investigate the metallicity scale of a large sample of galactic GCs, but did not attempt to assess the level of agreement between predicted and observed ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} values. More recently, Meissner & Weiss (2006) have used the ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$}, together with other CMD age indicators, to check their mutual self-consistency. As a result, they found that the GC ages estimated from ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} were younger by about 2 Gyr, in comparison with estimates based on the ΔVHBTO\hbox{$\Delta V_{\rm HB}^{\rm TO}$} parameter. This occurrence was interpreted as evidence that stellar models predict too bright an RGB-bump, by  ~0.2–0.3 mag.

We wish to reanalyse this question by employing new, accurate photometry of a large sample of GCs, which enabled us to determine both TO and RGB-bump magnitudes for 12 GCs, covering a wide metallicity range. Our methodological approach is the following. We first determined the apparent magnitudes of both TO and RGB-bump in each GC in our sample and employed the clusters’s relative distances from a theoretical MS-fitting technique. As a second step, we estimated individual cluster ages from the TO absolute magnitudes, obtained by assuming the empirical MS-fitting distance to NGC 6752 by Gratton et al. (2003) as zero point of our relative distance scale. Another set of ages for each cluster is then determined from their observed ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} and compared with the TO ages. The outcome of this comparison constrains the level of agreement between predicted and observed RGB-bump luminosity, without the need of taking into account the HB.

The plan of this paper is as follows. Section 2 briefly presents the observational dataset and the theoretical models adopted in our analysis, and estimates and comparisons of TO and ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} ages are described in Sect. 3, followed by a final discussion.

2. Observational and theoretical framework

We have employed a subsample of F606W and F814W photometries from the ACS GC Survey Treasury Project (Sarajedini et al. 2007), and made use of the ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} parameter, that is the counterpart of ΔVTOBump\hbox{$\Delta V_{\rm TO}^{\rm Bump}$} in the F606W filter. Details of the observations and data reduction have been already discussed in Sarajedini et al. (2007) and Anderson et al. (2008).

This database was collected mainly with the aim of investigating relative and absolute GCs ages and the initial mass function of GC stars. The observational strategy was optimized to obtain accurate photometry of the faint portion of the CMD, and the bright RGB photometry is saturated for many clusters. In other clusters – belonging mainly to the metal poor tail of the GC metallicity distribution – there are so few RGB stars that the RGB-bump detection is impossible. As a consequence, the number of GCs with measurements of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} is reduced compared to the total number of objects in the original database (64 clusters). In addition, we chose to restrict our analysis to those globulars with recent (re)determinations of both [Fe/H] (Carretta et al. 2009) and  [ α / Fe ]  (Carretta et al. 2010a). More in detail, the values of [Fe/H] are obtained from Table A.1 in Carretta et al. (2009), which displays [Fe/H] estimates for 95 GCs, obtained by transforming (and averaging) previous determinations onto the homogeneous scale set by high-resolution spectroscopic measurements on 19 clusters, reported in Table 1 of the same paper. This metallicity scale turns out to be very close to the Zinn & West (1984) estimates. The errors displayed in the same table (which represent the 1σ rms with respect to the metallicity scale set by the high-resolution spectroscopy) are added in quadrature to the average systematic errors in the high-resolution estimates of the 19 reference clusters (reported also in Table 1 of the same paper). As for  [ α / Fe ] , we assign a typical 0.10 dex uncertainty.

These additional constraints on the metallicity estimates reduces our sample to 11 objects, to which we added the NGC 6341 (M92), using HST archive data (program n. 9453, PI T. Brown). For this cluster, three images in each band were used, with exposure times of 0.5, 5, and 90 s in the F606W band and 0.5, 6, and 100 s in F814W. The photometry was reduced with the DAOPHOT/ALLFRAME package (Stetson 1994) and calibrated to the VEGAMAG system following Sirianni et al. (2005). With the inclusion of M 92 we are able to approximately cover the whole metallicity range of Galactic GCs.

Measurements of the apparent TO magnitude and associated uncertainties are from Marín-Franch et al. (2009). In brief, these authors employed a MS-fitting technique to determine the relative distance moduli between the reference cluster NGC 6752 and all other clusters in our sample. We adopt here a zero point for these relative distances set by the empirical MS-fitting distance to NGC 6752 determined by Gratton et al. (2003)1. 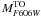The final errors on the absolute magnitudes MF606WTO\hbox{$M^{\rm TO}_{F606W}$} reported in Table 1 have been obtained by adding in quadrature the errors on the determination of the apparent magnitudes, errors on the relative cluster distances (Marín-Franch et al. 2009), and the error on NGC 6752 distance (Gratton et al. 2003). As for determining the RGB-bump level, we employed the following method, illustrated in Fig. 1 for the case of NGC 104. For each cluster, the LF around the bump region is determined using a bin size equal to 0.1 mag. A linear fit (see right panel of Fig. 1) is then performed around the bump – excluding the bump feature – to obtain what we denote as the LF “continuum” (black line in the right panel of Fig. 1). 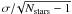Finally, the apparent magnitude of the bump is determined at the maximum of the continuum-subtracted LF, and its uncertainty is computed as σ/Nstars−1\hbox{$\sigma/\!\sqrt{N_{\rm stars}-1}$}, with Nstars and σ denoting the number of bump stars and their standard deviation around the bump luminosity, respectively. Results of these measurements, as well as [Fe/H] spectroscopic estimates and the global metallicity [M/H] obtained from the measurements of [Fe/H] and [α/Fe], are reported in Table 1.

thumbnail Fig. 1

Left panel: CMD of NGC 104. Right panel: the LF around the bump region. The solid line shows the continuum used for the bump determination (see text for more details), while the dotted line marks the bump location.

Our theoretical analysis makes use of the α-enhanced BaSTI2 stellar model library (Pietrinferni et al. 2006) that employs transformations to the ACS/HST photometric system by Bedin et al. (2005). From this extended set of isochrones, we have obtained the theoretical estimates of the TO, RGB-bump brightness, and ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} as a function of age and [M/H], which are displayed in Fig. 23.

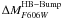It is interesting to investigate the sensitivity of the ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} parameter to the cluster age t, in comparison with ΔMF606WHB−Bump\hbox{$\Delta M_{F606W}^{\rm HB-Bump}$}, i.e. the equivalent of the traditional ΔVHBBump\hbox{$\Delta V_{\rm HB}^{\rm Bump}$}. In the age range typical of GCs, the HB is practically unaffected by the exact value of t, while the RGB-bump becomes fainter with increasing t. 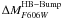As a result ΔMF606WHB−Bump\hbox{$\Delta M_{F606W}^{\rm HB-Bump}$} increases with age by  ~0.03 mag/Gyr. In case of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}, both TO and RGB-bump become fainter with increasing age, but the effect of changing t is greater on the TO luminosity. Overall ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} increases with age by  ~0.08 mag/Gyr at [M/H] =  −2.0, and by  ~0.04 mag/Gyr at [M/H] =  − 0.5.

3. Comparison between theory and observations

The values of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} measured in our sample of 12 clusters are displayed in the lower panel of Fig. 2, over-imposed on the theoretical calibration as a function of [M/H] and age. The cluster ages needed to match the observed ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} generally appear younger than standard GC ages (~12–14 Gyr). The ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} ages and associated errors are reported in Table 1, as obtained by interpolation amongst the theoretical values. A conservative estimate of the associated error has been obtained by considering the rectangle defined in the ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} − [M/H] plane by the uncertainties in both ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} and [M/H]. The error in the age estimate was then determined from the ages of the “youngest” and “oldest” corners of the rectangle. The same approach was followed also to estimate the uncertainties in the ages from the absolute TO magnitude.

thumbnail Fig. 2

Upper panel: absolute MF606W magnitude of the TO as a function of [M/H] for our GC sample (filled circles). Solid and dashed lines display the theoretical calibration from BaSTI α − enhanced isochrones for ages between 6 and 15 Gyr, in steps of 0.5 Gyr. Bottom panel: as the upper panel but for ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}.

The upper panel of Fig. 2 displays a comparison between the theoretical calibration of the TO absolute magnitude (as a function of age and [M/H]) and the cluster TO absolute magnitudes 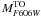MF606WTO\hbox{$M^{\rm TO}_{F606W}$} (also reported in Table 1). A visual comparison of the upper and lower panels of Fig. 2 confirms that ages from ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} tend to be systematically lower than TO ages.

thumbnail Fig. 3

Difference between the cluster ages inferred from the TO absolute magnitude and from ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}.

Figure 3 displays the difference between TO and ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} ages as a function of [M/H]. All points are systematically shifted to positive values of the age difference, and for about half of the clusters in the sample, the difference is significant at the 2σ level or more. Another way to look at this discrepancy is to display the difference between the values of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} expected from the cluster TO ages and the measured values, as shown in Fig. 4. Conservative error bars on these Δ(ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}) values were obtained applying a procedure analogous to the one followed to determine the errors on ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} ages. Figure 4 shows very clearly that the expected ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} values are systematically higher (as can also be inferred from Fig. 2) than observed. The mean value of Δ(ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}) is equal to 0.20 mag, with a 1σ dispersion of  ± 0.1 mag. A linear fit that takes the errors on both Δ(ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}) and [M/H] into account (using the routine fitexy in Press et al. 1992) provides a slope dΔ(ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$})/d[M/H] =  − 0.16 ± 0.12, which is not significantly different from zero. Neglecting the more discrepant cluster with [M/H]  ~  −2.0 (NGC 6341) leaves the mean value of Δ(ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}) almost unchanged (0.19 mag, with a 1σ dispersion of  ± 0.08 mag), whilst the slope of the linear fit is again not statistically significant (dΔ(ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$})/d[M/H]= − 0.14 ± 0.14).

thumbnail Fig. 4

Difference between the values of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} expected from the cluster TO ages, and the measured values, as a function of [M/H].

4. Discussion

The main result of our analysis is summarized by Fig. 4, discussed in the previous section. The values of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} predicted by theoretical models for cluster ages estimated from the TO absolute magnitudes, are larger than observed. Given that the observed TO magnitude is by definition matched by the theoretical isochrones to determine the TO age, this discrepancy implies that the absolute magnitude of the RGB-bump in the models is too bright.

An extension of this type of analysis to a larger, homogeneous sample of GC photometries is obviously desirable; hovewer, our results based on a limited sample of clusters already provide clear evidence of a real “over-luminosity” of the predicted absolute magnitude of the RGB-bump, irrespective of problems with HB modeling and placement of the reference HB level in clusters with only blue HB stars.

The simplest explanation for this discrepancy envisages a systematic underestimate of the cluster metallicities by  ~0.2 dex. A higher [M/H] would eliminate the discrepancy, because it causes a lower TO age and a lower theoretical RGB-bump brightness for each cluster. There is of course no indication that the metallicity scale we adopted is affected by this type of systematics, but this is a point to be considered.

In the following we expand our discussion to see how improvements in the micro- (e.g. opacities, nuclear reaction rates) and macro-physics (e.g., element transport meachanisms) employed in stellar evolution calculations, along with the recently established presence of multiple stellar populations with varying chemical patterns in individual GCs, can account for this discrepancy.

4.1. Improved micro- and macro-physics

A straightforward explanation for the discrepancy highlighted in Fig. 4 could be an underestimate of the radiative opacity at temperatures around a few 106 K – typical temperatures at the lower boundary of the convective envelope. Higher opacities would shift the convection boundary – hence the H-abundance discontinuity – to deeper layers, causing a fainter RGB-bump. However, this solution does not seem plausible for the following reasons: i) radiative opacities in this temperature range should not be affected by an uncertainty larger than  ~5% (see, e.g. Guzik 2008) and this small change is not able to reconcile theory with observations; ii) the discrepancy theory-observations increases with decreasing [M/H], and it does not seem very likely that radiative opacities become less accurate when the metal content decreases.

The isochrones employed to determine both the cluster ages from the TO brightness and the theoretical values of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} do not account for the effect of atomic diffusion (including radiative levitation). Although current spectroscopic observations of globular cluster stars show that atomic diffusion is at least partially inhibited by additional turbulence/mixing (see, i.e. Korn et al. 2007) – induced for example by rotation (see, i.e., Eggenberger et al. 2010) – we summarize here the effect on TO ages and ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} values in case of full efficiency. According to the results by Vandenberg et al. (2002) and Michaud et al. (2010) – expanding upon previous studies by Cassisi et al. (1997, 1998) where the effect of radiative levitation was not considered – atomic diffusion makes the RGB-bump magnitude brighter by 0.03–0.06 mag at fixed age, and also decreases the cluster TO ages by at most  ~1.5 Gyr for the lowest metallicity clusters. The combined effect on ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} would decrease the discrepancy for the most metal-poor cluster in our sample by  ~0.05 mag at most. The effect becomes less significant with increasing metallicity.

On the other hand, the recent redetermination of the 14N(p,γ)15O reaction rate, not included in our adopted models, would increase the cluster ages by  ~1 Gyr, and at the same time make the RGB-bump brighter by  ~0.06 mag at fixed age (Weiss et al. 2005; Pietrinferni et al. 2010). The net result would be an increase in the discrepancy by  ~0.10 mag or more, which would move the mean value of Δ(ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}) up to  ~0.30 mag. Overall, the combined effect of the new 14N(p,γ)15O reaction rate and inclusion of atomic diffusion (plus radiative levitation) would exacerbate the discrepancy between theory and observations, which would become on average of the order of 0.25 mag.

Another possibility for mitigating the discrepancy is to include overshooting beyond the formal boundary of the convective envelope (see, e.g., Alongi et al. 1991). Calculations by Cassisi et al. (2002) show that including convective overshooting decreases the RGB-bump brightness by  ~0.8 mag/HP (where HP denotes the local pressure scale height). The discrepancy between theory and observations would disappear with the inclusion of convective overshooting of the order of  ~0.25 below the Schwarzschild boundary of the convective envelope.

Besides overshooting from the convective boundary, Cassisi et al. (2002) have also investigated the effect on the RGB-bump shape and brightness, of a smoother chemical discontinuity left over by the first dredge-up. A smoother chemical discontinuity could be produced, for example, by turbulent mixing counteracting the efficiency of atomic diffusion. The Cassisi et al.’s results show that the bump luminosity decreases by  ~0.25 mag/Hp, where the smoothing length is expressed in units of the local pressure scale height. Given that smoothing the discontinuity also alters the shape of the RGB luminosity function in the bump region, this hypothesis is potentially testable. As estimated by Cassisi et al. (2002), a sample of more than 120 RGB stars within  ± 0.2 mag of the peak of the RGB-bump, and random photometric errors smaller than 0.03 mag can potentially reveal this effect in the RGB luminosity function.

4.2. The role of GC multipopulations

A very important issue to be considered is the effect on the cluster RGB-bump luminosity and TO ages of subpopulations with varying degrees of the CNONa anticorrelation and the – likely – associated, increased He abundance, as observed in individual GCs (see, e.g., Gratton et al. 2004, for a review). If the sum of the CNO abundance stays constant among all stars in a given cluster – as observed within the measurement errors – the RGB-bump magnitude is only affected by the possible increase in helium. As shown by, e.g., Cassisi & Salaris (1997) and Salaris et al. (2006), increasing the initial He abundance increases the bump brightness at fixed age and [Fe/H]. In a “real” cluster the size of this effect depends on the exact amount of He-enhancement and the fraction of stars involved, but the main point is that this can only exacerbate the discrepancy displayed in Fig. 4. As for the ages from the TO luminosity, one has to notice that within the individual clusters analysed in this paper, there are no clear signs of wide spreads of the initial He abundance, in terms of a split of the MS in the CMD. A reasonable upper limit to the He spread of 0.05 in mass fraction would decrease the TO age by no more than  ~0.5 Gyr (see, i.e., Salaris et al. 2006). As a conclusion, the effect of subpopulations with enhanced He within individual clusters in our sample would not solve the discrepancy highlighted by Fig. 4.

Only NGC 1851 shows a clear split of the subgiant branch in our adopted CMD, whose origin is still debated (see, e.g., Cassisi et al. 2008; Carretta et al. 2010b). The TO measurement has been obtained by considering only the most populated SGB, which should harbour stars with a “standard” He and metal distribution (Cassisi et al. 2008), so that our TO age estimates should be reliable also in the case of this GC.

1

The empirical MS-fitting distance to NGC 6752 derived in Gratton et al. (2003) was obtained by fitting the observed globular cluster mean locus to the colour-magnitude diagram location of local subdwarfs with the same [M/H] of the cluster. Although both [Fe/H] and [α/Fe] values employed by Gratton et al. (2003) are different from the values reported in Table 1 for this cluster, the total metallicity [M/H] turns out to be same within 0.01 dex.

2

The BaSTI stellar evolution library is available at the following URL: http://www.oa-teramo.inaf.it/BASTI.

3

Our analysis relies entirely on the theoretical predictions from the BaSTI models. Although a good agreement does exist among several different stellar model libraries concerning the trend with age of the evolutionary features discussed in this paper, some small, marginal differences can still be present.

Acknowledgments

We warmly thank our referee, Dr. A. Weiss, for his prompt report. S.C. and A.P. acknowledge the partial financial support of INAF through the PRIN INAF 2009 (P.I.: R. Gratton) . This work was supported by the Science and Technology Ministry of the Kingdom of Spain (Consolider-Ingenio 2010 Program CSD 2006-00070, grants AYA2004-06343 and AYA2007-3E3507) and by the IAC (grant 310394).

References

  1. Alongi, M., Bertelli, G., Bressan, A., & Chiosi, C. 1991, A&A, 244, 95 [NASA ADS] [Google Scholar]
  2. Alves, D. R., & Sarajedini, A. 1999, ApJ, 511, 225 [NASA ADS] [CrossRef] [Google Scholar]
  3. Anderson, J., Sarajedini, A., Bedin, L. R., et al. 2008, AJ, 135, 2055 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bedin, L. R., Cassisi, S., Castelli, F., et al. 2005, MNRAS, 357, 1038 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bjork, S. R., & Chaboyer, B. 2006, ApJ, 641, 1102 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bono, G., Cassisi, S., Zoccali, M., & Piotto, G. 2001, ApJ, 546, L109 [NASA ADS] [CrossRef] [Google Scholar]
  7. Carretta, E., Bragaglia, A., Gratton, R., et al. 2009, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Carretta, E., Gratton, R. G., Lucatello, S., et al. 2010, ApJ, 772, L1 [NASA ADS] [CrossRef] [Google Scholar]
  10. Caputo, F., & Cassisi, S. 2002, MNRAS, 333, 825 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cassisi, S. 2010, in Proc. IAU Symp. 262, ed. G. Bruzual, & S. Charlot, 13 [Google Scholar]
  12. Cassisi, S., & Salaris, M. 1997, MNRAS, 285, 593 [NASA ADS] [Google Scholar]
  13. Cassisi, S., Degl’Innocenti, S., & Salaris, M. 1997, MNRAS, 290, 515 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cassisi, S., Castellani, V., Degl’Innocenti, S., & Weiss, A. 1998, A&AS, 129, 267 [Google Scholar]
  15. Cassisi, S., Castellani, V., Degl’Innocenti, S., Salaris, M., & Weiss, A. 1999, A&AS, 134, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Cassisi, S., Salaris, M., & Bono, G. 2002, ApJ, 565, 1231 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] [Google Scholar]
  18. Di Cecco, A., Bono, G., Stetson, P. B., et al. 2010, ApJ, 712, 527 [NASA ADS] [CrossRef] [Google Scholar]
  19. Eggenberger, P., Meynet, G., Maeder, A., et al. 2010, A&A, 519, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Fusi Pecci, F., Ferraro, F. R., Crocker, D. A., Rood, R. T., & Buonanno, R. 1990, A&A, 238, 95 [NASA ADS] [Google Scholar]
  21. Gratton, R. G., Bragaglia, A., Carretta, E., et al. 2003, A&A, 408, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
  23. Guzik, J. A. 2008, Mem. Soc. Astron. It., 79, 481 [NASA ADS] [Google Scholar]
  24. Iben, I., Jr. 1968, ApJ, 154, 581 [NASA ADS] [CrossRef] [Google Scholar]
  25. King, C. R., Da Costa, G. S., & Demarque, P. 1985, ApJ, 299, 674 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kippenhahn, R., & Weigert, A. 1994, Stellar Structure and Evolution, (Germany: Springer-Verlag) [Google Scholar]
  27. Korn, A. J., Grundahl, F., Richard, O., et al. 2007, ApJ, 671, 402 [NASA ADS] [CrossRef] [Google Scholar]
  28. Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
  29. Meissner, F., & Weiss, A. 2006, A&A, 456, 1085 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Michaud, G., Richer, J., & Richard, O. 2010, A&A, 510, 104 [Google Scholar]
  31. Monelli, M., Cassisi, S., Bernard, E. J., et al. 2010, ApJ, 718, 707 [NASA ADS] [CrossRef] [Google Scholar]
  32. Pietrinferni, A., Cassisi, S., Salaris, M., et al. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
  33. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
  34. Pietrinferni, A., Cassisi, S., & Salaris, M. 2010, A&A, 522, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Piotto, G. 2008, Mem. Soc. Astron. It., 79, 334 [NASA ADS] [Google Scholar]
  36. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical recipes in FORTRAN. The art of scientific computing, (Cambridge: University Press), 2nd edn. [Google Scholar]
  37. Renzini, A., & Fusi Pecci, F. 1988, ARA&A, 26, 199 [NASA ADS] [CrossRef] [Google Scholar]
  38. Riello, M., Cassisi, S., Piotto, G., et al. 2003, A&A, 410, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar Populations, (London, Wiley and sons eds.) [Google Scholar]
  40. Salaris, M., Chieffi, A., & Straniero, O. 1993, ApJ, 414, 580 [NASA ADS] [CrossRef] [Google Scholar]
  41. Salaris, M., Cassisi, S., & Weiss, A. 2002, PASP, 114, 375 [NASA ADS] [CrossRef] [Google Scholar]
  42. Salaris, M., Weiss, A., Ferguson, J. W., & Fusilier, D. J. 2006, ApJ, 645, 1131 [NASA ADS] [CrossRef] [Google Scholar]
  43. Sirianni, M., Jee, M. J., Benítez, N., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef] [Google Scholar]
  44. Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
  45. Stetson, P. B. 1994, PASP, 106, 250 [NASA ADS] [CrossRef] [Google Scholar]
  46. Thomas, H. C. 1967, Ph.D. Thesis, L. M. Univ., München [Google Scholar]
  47. VandenBerg, D. A., Richard, O., Michaud, G., & Richer, J. 2002, ApJ, 571, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Weiss, A., Serenelli, A., Kitsikis, A., Schlattl, H., & Christensen-Dalsgaard, J. 2005, A&A, 441, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Zinn, R., & West, M. J. 1984, ApJS, 55 45 [NASA ADS] [CrossRef] [Google Scholar]
  50. Zoccali, M., Cassisi, S., Piotto, G., Bono, G., & Salaris, M. 1999, ApJ, 518, L49 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

The metal content, TO, RGB bump brightness, and age estimates from both TO and ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} for the selected sample of GCs.

In the text

All Figures

thumbnail Fig. 1

Left panel: CMD of NGC 104. Right panel: the LF around the bump region. The solid line shows the continuum used for the bump determination (see text for more details), while the dotted line marks the bump location.
In the text
thumbnail Fig. 2

Upper panel: absolute MF606W magnitude of the TO as a function of [M/H] for our GC sample (filled circles). Solid and dashed lines display the theoretical calibration from BaSTI α − enhanced isochrones for ages between 6 and 15 Gyr, in steps of 0.5 Gyr. Bottom panel: as the upper panel but for ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}.
In the text
thumbnail Fig. 3

Difference between the cluster ages inferred from the TO absolute magnitude and from ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$}.
In the text
thumbnail Fig. 4

Difference between the values of ΔMF606WTO−Bump\hbox{$\Delta M_{F606W}^{\rm TO-Bump}$} expected from the cluster TO ages, and the measured values, as a function of [M/H].
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.