| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 4 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201016028 | |
| Published online | 24 January 2011 | |
Kink and fluting modes of stratified coronal magnetic loops with elliptical cross-sections
Solar Physics and Space Plasma Research Centre
(SP 2RC), University of Sheffield,
Hicks Building, Hounsfield Road,
Sheffield
S3 7RH,
UK
e-mail: r.j.morton@sheffield.ac.uk; m.s.ruderman@sheffield.ac.uk
Received:
29
October
2010
Accepted:
20
December
2010
Aims. We study kink and fluting oscillations of a straight magnetic tube with an elliptic cross-section and density varying along the tube.
Methods. The governing equations for kink and fluting modes in the thin tube approximation are derived. We found that there are two kink modes, polarised along the semimajor and semiminor axes of the elliptic cross-section. We have shown that the ratio of frequencies of the first overtone and fundamental mode is the same for both kink modes and independent of the ratio of the ellipse axes.
Results. On the basis of this result we concluded that the estimates of the atmospheric scale height obtained using simultaneous observations of the fundamental mode and first overtone of the coronal loop kink oscillations are independent of the ellipticity of the loop cross-section.
Key words: magnetohydrodynamics (MHD) / plasmas / Sun: corona / Sun: oscillations / waves
© ESO, 2011
1. Introduction
The solar atmosphere is a highly dynamic and structured plasma that is able to support a wide variety of magneto-acoustic waves and oscillations. Each layer of the solar atmosphere, from the photosphere to the corona, is magnetically connected to the others via the all pervading magnetic field. The omnipresence of the waves throughout the atmosphere is becoming well documented as new and exciting techniques are being developed to help observe and study the waves (see, e.g. Banerjee et al. 2007; Tomczyk et al. 2007).
After transverse coronal loop oscillations were first observed by TRACE in 1998 (Aschwanden et al. 1999; Nakariakov et al. 1999), the phenomenon became one of the hot topics within solar physics. In the first theoretical interpretation of these oscillations, a coronal loop was modelled as a straight magnetic cylinder with the density constant inside and outside. Since then, a number of more complicated and realistic models have been considered. For a recent review on the theory of transverse oscillations of a coronal loop see, e.g., Ruderman & Erdélyi (2009).
Although the transverse coronal loop oscillations are interesting on their own, their main importance is related to the fact that they are a powerful tool of coronal seismology. Nakariakov & Ofman (2001) demonstrated this by using the observations of transverse coronal loop oscillations to estimate the magnitude of the magnetic field in the corona, while Andries et al. (2005) suggested to use these observations to estimate the atmospheric scale height in the corona.
In this paper we continue to study the transverse oscillations of coronal loops. Coronal loops with elliptical cross-sections and a constant density profile have been studied previously in both cold (Ruderman 2003) andfinite-β (Erdélyi & Morton 2009) plasmas. Now, we consider oscillations of loops with the density varying along the loop and a constant elliptic cross-section. The paper is organized as follows. In the next section we formulate the problem. In Sect. 3 we derive the governing equations for kink and fluting oscillations of a coronal loop with an elliptic cross-section in the thin tube approximation. In Sect. 4 we study the implication of our analysis on coronal seismology. Section 5 contains the summary of the obtained results and our conclusions.
2. Problem formulation
We model a coronal loop as a straight magnetic tube with an elliptical cross-section. The cold plasma approximation is used. The density varies along the tube, while the cross-section remains constant. In Cartesian coordinates x,y,z the loop axis coincides with the z-axis. The equilibrium magnetic field is given by 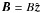 , where B is constant and
, where B is constant and 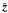 is the unit vector in the z-direction. The plasma motion is governed by the linearised ideal MHD equations,
is the unit vector in the z-direction. The plasma motion is governed by the linearised ideal MHD equations, \arraycolsep1.75ptHere ξ is the plasma displacement, b the magnetic field perturbation, ρ(z) the equilibrium density, and μ0 the magnetic permeability of free space; ρ(z) = ρi(z) inside the tube and ρ(z) = ρe(z) outside the tube.
\arraycolsep1.75ptHere ξ is the plasma displacement, b the magnetic field perturbation, ρ(z) the equilibrium density, and μ0 the magnetic permeability of free space; ρ(z) = ρi(z) inside the tube and ρ(z) = ρe(z) outside the tube.
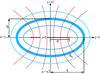 |
Fig. 1 Sketch showing the elliptical coordinate system used to describe the loop cross-section.The open and closed curves show the s and ϕ coordinate lines respectively. The thick closed curve shows the tube boundary. |
Let us introduce the elliptic coordinates s and ϕ in the xy-plane (see Fig. 1). The Cartesian coordinates are expressed in terms of elliptic coordinates as  (3)where σ is a quantity with the dimension of length, s varies from 0 to ∞, and ϕ from −π to π. In the elliptic coordinates the equation of the tube boundary is s = s0. Then the semimajor and semiminor half-axes of the tube elliptic cross-section are in the x and y-direction, and they are given by
(3)where σ is a quantity with the dimension of length, s varies from 0 to ∞, and ϕ from −π to π. In the elliptic coordinates the equation of the tube boundary is s = s0. Then the semimajor and semiminor half-axes of the tube elliptic cross-section are in the x and y-direction, and they are given by  (4)At the tube boundary the normal component of the displacement, ξs, and the magnetic pressure perturbation, P = b·B/μ0, has to be continuous,
(4)At the tube boundary the normal component of the displacement, ξs, and the magnetic pressure perturbation, P = b·B/μ0, has to be continuous, ![\begin{equation} \label{eq:jumps} [[\xi_s]] = 0, \quad [[P]] = 0 \quad \mbox{at} \quad s = s_0, \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq31.png) (5)where [ [ f ] ] indicates the jumps of function f across the boundary defined as
(5)where [ [ f ] ] indicates the jumps of function f across the boundary defined as ![\begin{equation} [[f]] = \lim_{\varepsilon\to 0} [f(s + \varepsilon) - f(s - \varepsilon)]. \label{eq:jump-def} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq34.png) (6)The magnetic field lines at the loop foot points are frozen in the dense photospheric plasma, so that
(6)The magnetic field lines at the loop foot points are frozen in the dense photospheric plasma, so that 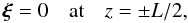 (7)where L is the loop length.
(7)where L is the loop length.
It follows from Eq. (3) that the points with the elliptical coordinates s = 0, ϕ = ϕ0, and s = 0, ϕ = −ϕ0 are the same point in the xy-plane. This implies that P and ξs have to satisfy the boundary conditions  (8)Equations (1) and (2) together with the boundary conditions (5), (7) and (8) will be used in the next section to derive the governing equations for kink and fluting oscillations in the thin tube approximation.
(8)Equations (1) and (2) together with the boundary conditions (5), (7) and (8) will be used in the next section to derive the governing equations for kink and fluting oscillations in the thin tube approximation.
3. Derivation of governing equations
The analysis in this section is similar to one used by Dymova & Ruderman (2005) to derive the governing equation for a thin tube with a circular tube cross-section. We begin by noting that, in accordance with Eq. (1), ξz = 0. The system of Eqs. (1) and (2) can then be transformed to 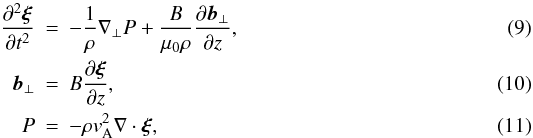 where vA is the Alfvén speed defined by
where vA is the Alfvén speed defined by 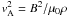 , and the operator ∇⊥ and component of the magnetic field perturbation perpendicular to the z-axis are given by
, and the operator ∇⊥ and component of the magnetic field perturbation perpendicular to the z-axis are given by 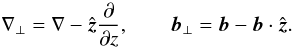 (12)Eliminating b⊥ from Eqs. (9) and (10) yields
(12)Eliminating b⊥ from Eqs. (9) and (10) yields 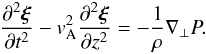 (13)Taking the divergence of this equation and using Eq. (11) we arrive at the equation for P,
(13)Taking the divergence of this equation and using Eq. (11) we arrive at the equation for P, 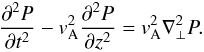 (14)Now we use the thin tube approximation. To do this we note that the characteristic spatial scale in the z-direction is L, and the characteristic time of the problem is
(14)Now we use the thin tube approximation. To do this we note that the characteristic spatial scale in the z-direction is L, and the characteristic time of the problem is 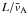 , where
, where 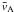 is a typical value of Alfvén speed. In what follows we only consider the perturbations that decay at the distance of a few a from the tube. Then the characteristic spatial scale in the x and y-direction is a. It follows from this analysis that the ratio of the left-hand side of Eq. (14) to its right-hand side is of the order of (a/L)2 ≪ 1, so that we can neglect the left-hand side. Then, using the expression for
is a typical value of Alfvén speed. In what follows we only consider the perturbations that decay at the distance of a few a from the tube. Then the characteristic spatial scale in the x and y-direction is a. It follows from this analysis that the ratio of the left-hand side of Eq. (14) to its right-hand side is of the order of (a/L)2 ≪ 1, so that we can neglect the left-hand side. Then, using the expression for 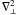 in the elliptical coordinates (e.g. Korn & Korn 1961), we obtain the equation for P in the thin tube approximation,
in the elliptical coordinates (e.g. Korn & Korn 1961), we obtain the equation for P in the thin tube approximation, 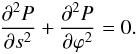 (15)The solution to this equation has to satisfy the first regularity condition in Eq. (8), and the second boundary condition in Eq. (5). Using Eq. (13) we rewrite the second regularity condition in terms of P,
(15)The solution to this equation has to satisfy the first regularity condition in Eq. (8), and the second boundary condition in Eq. (5). Using Eq. (13) we rewrite the second regularity condition in terms of P, 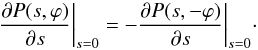 (16)To derive the governing equations for non-axisymmetric tube oscillations we solve Eqs. (13) and (15) inside and outside the tube, and then match the two solutions at the tube boundary. It is straightforward to obtain the general solution to Eq. (15) inside the tube satisfying the regularity conditions Eqs. (8) and (16),
(16)To derive the governing equations for non-axisymmetric tube oscillations we solve Eqs. (13) and (15) inside and outside the tube, and then match the two solutions at the tube boundary. It is straightforward to obtain the general solution to Eq. (15) inside the tube satisfying the regularity conditions Eqs. (8) and (16), ![\begin{equation} P^{\rm i} = \sum_{n=1}^\infty\left[C_n^{\rm i}\cosh(ns)\cos(n\varphi) + D_n^{\rm i}\sinh(ns)\sin(n\varphi)\right], \label{eq:p_int} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq59.png) (17)where
(17)where 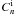 and
and 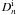 are arbitrary functions of t and z. The solution outside the tube has to decay as s → ∞. Hence, its general form is
are arbitrary functions of t and z. The solution outside the tube has to decay as s → ∞. Hence, its general form is ![\begin{equation} P^{\rm e} = \sum_{n=1}^\infty {\rm e}^{-ns}\left[C_n^{\rm e}\cos(n\varphi) + D_n^{\rm e}\sin(n\varphi)\right], \label{eq:p_ext} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq64.png) (18)where once again
(18)where once again 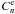 and
and 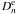 are arbitrary functions of t and z. Substituting Eqs. (17) and (18) in Eq. (13) and using the expression for ∇⊥ in the elliptical coordinates (e.g. Korn & Korn 1961),
are arbitrary functions of t and z. Substituting Eqs. (17) and (18) in Eq. (13) and using the expression for ∇⊥ in the elliptical coordinates (e.g. Korn & Korn 1961), 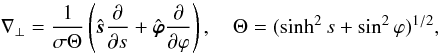 (19)where
(19)where 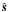 and
and 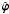 are the unit vectors in the s and ϕ-direction, we obtain the expressions for ξs inside and outside the tube,
are the unit vectors in the s and ϕ-direction, we obtain the expressions for ξs inside and outside the tube, ![\begin{equation} \xi_s^{\rm i} = \frac1{\sigma\Theta}\sum_{n=1}^\infty \left[F_n^{\rm i}\sinh(ns)\cos(n\varphi) + G_n^{\rm i}\cosh(ns)\sin(n\varphi)\right], \label{eq:xi_int} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq70.png) (20)
(20)![\begin{equation} \xi_s^{\rm e} = \frac1{\sigma\Theta}\sum_{n=1}^\infty {\rm e}^{-ns} \left[F_n^{\rm e}\cos(n\varphi) + G_n^{\rm e}\sin(n\varphi)\right]. \label{eq:xi_ext} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq71.png) (21)In these equations
(21)In these equations 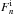 ,
, 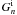 ,
, 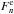 and
and 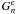 are functions of t and z. They are related to the functions
are functions of t and z. They are related to the functions 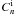
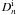 ,
, 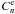 and
and 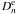 by
by 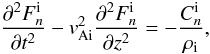 (22)
(22)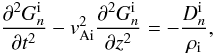 (23)
(23)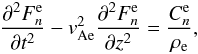 (24)
(24)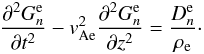 (25)Substituting Eqs. (17) and (18) in the second boundary condition in Eq. (5) we obtain
(25)Substituting Eqs. (17) and (18) in the second boundary condition in Eq. (5) we obtain 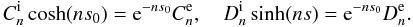 (26)Substituting Eqs. (20) and (21) in the first boundary condition in Eq. (5) yields
(26)Substituting Eqs. (20) and (21) in the first boundary condition in Eq. (5) yields 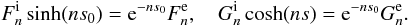 (27)Eliminating
(27)Eliminating 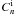 ,
, 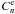 and
and 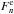 from Eqs. (22), (24), (26) and (27) we obtain the equation for
from Eqs. (22), (24), (26) and (27) we obtain the equation for 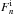 ,
, ![\begin{equation} \frac{\partial^2 F_n}{\partial t^2} - c_{n\rm c}^2\frac{\partial^2 F_n}{\partial z^2} = 0, \quad c_{n\rm c}^2 = \frac{B^2[1+\tanh(ns_0)]} {\mu_0[\rho_{\rm i}+\rho_{\rm e}\tanh(ns_0)]}, \label{eq:govF} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq82.png) (28)where we have dropped the superscript “i”. Eliminating
(28)where we have dropped the superscript “i”. Eliminating 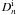 ,
, 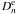 and
and 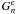 from Eqs. (23), (25), (26) and (27) we obtain the equation for
from Eqs. (23), (25), (26) and (27) we obtain the equation for 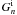 ,
, ![\begin{equation} \frac{\partial^2 G_n}{\partial t^2} - c_{n\rm s}^2\frac{\partial^2 G_n}{\partial z^2} = 0, \quad c_{n\rm s}^2 = \frac{B^2[1+\tanh(ns_0)]} {\mu_0[\rho_{\rm i}\tanh(ns_0)+\rho_{\rm e}]}, \label{eq:govG} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq83.png) (29)where we have once again dropped the superscript “i”. It follows from Eqs. (7) and (20) that Fn and Gn have to satisfy the boundary conditions
(29)where we have once again dropped the superscript “i”. It follows from Eqs. (7) and (20) that Fn and Gn have to satisfy the boundary conditions 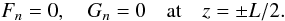 (30)In Eqs. (28) and (29) n = 1 corresponds to kink modes, and n > 1 to fluting modes.
(30)In Eqs. (28) and (29) n = 1 corresponds to kink modes, and n > 1 to fluting modes.
In the elliptical coordinates the loop axis (x = y = 0) is defined by s = 0 and ϕ = π/2. It follows from Eq. (20) that the kink mode described by Eq. (28) does not displace the loop axis in the s-direction which, at the loop axis, coincides with the y-direction. Hence, the loop axis displacement is in the x-direction, i.e. this mode is polarised in the direction of the semimajor axis of the tube cross-section. The kink mode described by Eq. (29) displaces the loop axis in the s-direction. It is straightforward to show that it does not displace it in the ϕ-direction which, at the loop axis, coincides with the x-direction. Hence, the loop axis displacement is in the y-direction, i.e. this mode is polarised in the direction of the semiminor axis of the tube cross-section.
When the density is constant, we can use Eqs. (28) and (29) with the boundary conditions Eq. (30) to recover the results obtained by Ruderman (2003). Let us look for the eigenmodes and restrict the analysis to the fundamental modes in the z-direction. This implies that we take Fn and Gn proportional to e−iωtcos(πz/L). Then we immediately obtain that the eigenfrequencies of the boundary value problem defined by Eq. (28) and the boundary conditions (30) are given by ![\begin{equation} \omega_{n\rm c}^2 = \frac{\pi^2 c_{n\rm c}^2}{L^2} = \frac{\pi^2 B^2[1+\tanh(ns_0)]} {\mu_0 L^2[\rho_{\rm i}+\rho_{\rm e}\tanh(ns_0)]}, \quad n = 1,2,\dots, \label{eq:Feigen} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq92.png) (31)and the eigenfrequencies of the boundary value problem defined by Eq. (29) and the boundary conditions (30) are given by
(31)and the eigenfrequencies of the boundary value problem defined by Eq. (29) and the boundary conditions (30) are given by ![\begin{equation} \omega_{n\rm s}^2 = \frac{\pi^2 c_{n\rm s}^2}{L^2} = \frac{\pi^2 B^2[1+\tanh(ns_0)]} {\mu_0 L^2[\rho_{\rm i}\tanh(ns_0)+\rho_{\rm e}]}. \quad n = 1,2,\dots \label{eq:Geigen} \end{equation}](/articles/aa/full_html/2011/03/aa16028-10/aa16028-10-eq93.png) (32)In particular, the squares of eigenfrequencies of the kink modes are given by
(32)In particular, the squares of eigenfrequencies of the kink modes are given by 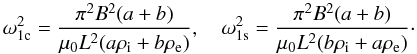 (33)It is straightforward to see that the eigenfrequencies satisfy
(33)It is straightforward to see that the eigenfrequencies satisfy  (34)
(34)
4. Implication on coronal seismology
After Verwichte et al. (2004) reported two cases of observations of the transverse coronal loop oscillations where, in addition to the fundamental mode, the first overtone was also observed, Andries et al. (2005) suggested observations of this nature could be used to estimate the scale height in the solar corona. Andries et al. (2005) assumed that an oscillating loop has a half-circle shape and a circular cross-section, and it is in the vertical plane. They also assumed that the atmosphere is isothermal. In that case, the dependence of the plasma density on z is given by 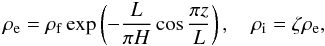 (35)where H is the atmospheric scale height, ρf the plasma density at the loop foot points outside the loop, and ζ > 1 a constant. Andries et al. (2005) calculated the ratio of frequencies of the first overtone and fundamental mode and found that this ratio is a monotonically decreasing function of the parameter L/H. Hence, if we know the ratio of frequencies and L, we can determine H. For a recent review of coronal seismology using kink oscillation overtones see Andries et al. (2009).
(35)where H is the atmospheric scale height, ρf the plasma density at the loop foot points outside the loop, and ζ > 1 a constant. Andries et al. (2005) calculated the ratio of frequencies of the first overtone and fundamental mode and found that this ratio is a monotonically decreasing function of the parameter L/H. Hence, if we know the ratio of frequencies and L, we can determine H. For a recent review of coronal seismology using kink oscillation overtones see Andries et al. (2009).
A very important question is how robust is this method. Dymova & Ruderman (2006) and Morton & Erdélyi (2009a) have found that the account of the loop shape can moderately affect the estimates of the atmospheric scale height. Ruderman (2007) has shown that the twist of magnetic field lines in the loop can be safely neglected when estimating the atmospheric scale height in the corona. Robertson et al. (2010) found that the estimates of the atmospheric scale height obtained using the two-thread model are exactly the same as those obtained using the model of a monolithic coronal loop with a circular cross-section of constant radius when the two threads have the same scale height. Recently Ruderman (2010) showed that the account of stationary time independent siphon flows in coronal loops have little influence on the estimates of the coronal scale height found using the frequency ratio. On the other hand, Ruderman et al. (2008) and Verth et al. (2008) found that the account of the loop expansion can strongly affect these estimates.
In this section we study what the effect the elliptic cross-section has on the estimates of the coronal scale height. As we have already seen, when a loop has an elliptic cross-section, its kink oscillations are polarised along the axes of the cross-section. The kink mode polarised in the direction of the semimajor axis is described by Eq. (28) with n = 1, while the kink mode polarised in the direction of the semiminor axis is described by Eq. (29) with n = 1. Let us consider the solutions to these equations in the form of eigenmodes and take F1 and G1 proportional to exp(−iωt). Using Eq. (35) we obtain 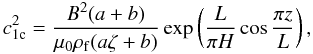 (36)
(36)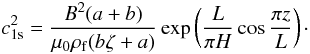 (37)Then, introducing
(37)Then, introducing 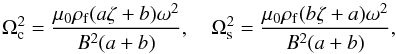 (38)we reduce Eqs. (28) and (29) with n = 1 to
(38)we reduce Eqs. (28) and (29) with n = 1 to 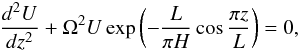 (39)where either U = F1 and Ω = Ωc, or U = G1 and Ω = Ωs, and U satisfies the boundary conditions U = 0 at z = ± L/2. If a = b then we have a circular cross-section and it can be seen from Eqs. (38) that
(39)where either U = F1 and Ω = Ωc, or U = G1 and Ω = Ωs, and U satisfies the boundary conditions U = 0 at z = ± L/2. If a = b then we have a circular cross-section and it can be seen from Eqs. (38) that 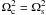 . Since Eq. (39) does not contain a and b, the equation remains the same for the elliptical cross-section. Hence, the eigenvalues of the boundary value problem for U are independent of a and b and independent of whether the loop has a circular or elliptical cross-section. With respect to observations, the eigenvalue Ω is related to the observable quantity ω by a constant scaling factor, where the scaling factor depends upon a and b for the elliptical cross-section. Hence, ω2/ω1 = Ω2/Ω1 due to the cancelation of the constant scaling factor. Since
. Since Eq. (39) does not contain a and b, the equation remains the same for the elliptical cross-section. Hence, the eigenvalues of the boundary value problem for U are independent of a and b and independent of whether the loop has a circular or elliptical cross-section. With respect to observations, the eigenvalue Ω is related to the observable quantity ω by a constant scaling factor, where the scaling factor depends upon a and b for the elliptical cross-section. Hence, ω2/ω1 = Ω2/Ω1 due to the cancelation of the constant scaling factor. Since
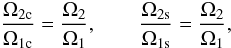 it follows that we obtain the same estimates of the atmospheric scale height no matter if we use the observation of the kink oscillations polarised in the direction of the semimajor or semiminor axis. Further, due to the estimates also being independent of a and b, they are the same as those obtained for a loop with the circular cross-section.
it follows that we obtain the same estimates of the atmospheric scale height no matter if we use the observation of the kink oscillations polarised in the direction of the semimajor or semiminor axis. Further, due to the estimates also being independent of a and b, they are the same as those obtained for a loop with the circular cross-section.
5. Summary and conclusions
In this paper we have studied kink and fluting oscillations of straight magnetic loops with a constant elliptic cross-section and density varying along the loop. We derived the governing equations for kink and fluting modes in the thin tube approximation. All these equations are similar to the equation describing kink oscillations of a straight tube with the circular cross-section. We found that there are two sets of kink and fluting modes, one set polarised in the direction of semimajor axis of the elliptic cross-section, and the other set polarised in the direction of the semiminor axis. The frequencies of fundamental mode and overtones of these two kinds of kink oscillation are different. However, the ratio of frequencies of the first overtone and the fundamental mode is the same for both kink oscillations, and it is independent of the ratio of the ellipse half-axes a/b. This result implies that we obtain the same estimates of the atmospheric scale height no matter if we use the observation of the kink oscillations polarised in the direction of semimajor or semiminor axis. The estimates are also the same as those obtained for a loop with the circular cross-section. This demonstrates that the model shows a very robust nature when considering a static plasma. However, if the plasma in the loops is dynamic (i.e. time dependent) then the ability of the static model to provide accurate estimates may become questionable (see e.g. Morton & Erdélyi 2009b).
It should be noted that the model for coronal loops used here is simplified, with the observed structure of loops appearing to be more complicated. López Fuentes et al. (2006) modelled coronal loops using magnetic extrapolation and observational data. They found that cross-sectional area and shape changed along the axis of the modelled loop. Analytical work by Ruderman (2009), who modelled a curved coronal loop with a potential magnetic field, found that the introduction of curvature caused the cross-section of a coronal loop to change shape, from a circular cross-section at the footpoints to an elliptical cross-section at the apex. Such a model influenced the transverse oscillations of the loop. It was shown by Andries et al. (2005) that the frequency ratio is dependent upon quantities that influence the degree of stratification. In the present discussion, the variable a and b are independent of z so do not influence the frequency ratio. It is possible that the introduction of a variable cross-section and area along a coronal loop could influence the ratio ω2/ω1.
Acknowledgments
The authors thank the Science and Technology Facilities Council (STFC), UK for the financial support they received. We also thank the referee for a number of useful suggestions.
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Andries, J., van Doorsselaere, T., Roberts, B., et al. 2009, Space Sci. Rev., 149, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, D., Erdélyi, R., Oliver, R., & O’Shea, E. 2007, Sol. Phys., 246, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2005, Sol. Phys., 229, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2006, A&A, 459, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erdélyi, R., & Morton, R. J. 2009, A&A, 494, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korn, G., & Korn, T. 1961, Mathematical Handbook for Scientists and Engineers (New York: McGraw-Hill) [Google Scholar]
- López Fuentes, M. C., Klimchuk, J. A., & Démoulin, P. 2006, ApJ, 639, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, R., & Erdélyi, R. 2009a, A&A, 605, 493 [Google Scholar]
- Morton, R. J., & Erdélyi, R. 2009b, ApJ, 707, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Robertson, D., Ruderman, M. S., & Taroyan, Y. 2010, A&A, 515 [Google Scholar]
- Ruderman, M. S. 2003, A&A, 409, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S. 2007, Sol. Phys., 246, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2009, A&A, 506, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S. 2010, Sol. Phys., 267, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Erdélyi, R. 2009, Space Sci. Rev., 149, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., Verth, G., & Erdélyi, R. 2008, ApJ, 686, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verth, G., Erdélyi, R., & Jess, D. B. 2008, ApJ, 687, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Sketch showing the elliptical coordinate system used to describe the loop cross-section.The open and closed curves show the s and ϕ coordinate lines respectively. The thick closed curve shows the tube boundary. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


