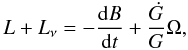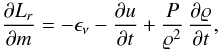| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015849 | |
| Published online | 27 January 2011 | |
Research Note
The evolution of white dwarfs with a varying gravitational constant
1
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La
Plata,
Paseo del Bosque s/n, (1900)
La Plata,
Argentina
2
Instituto de Astrofísica La Plata, IALP, CONICET-UNLP, Argentina
e-mail: althaus@fcaglp.unlp.edu.ar; acorsico@fcaglp.unlp.edu.ar
3
Member of the Carrera del Investigador Científico y Tecnológico,
CONICET,
Argentina
4
Departament de Física Aplicada, Universitat Politècnica de
Catalunya, c/Esteve Terrades,
5, 08860
Castelldefels,
Spain
e-mail: santi@fa.upc.edu; loren@fa.upc.edu; garcia@fa.upc.edu
5
Institute for Space Studies of Catalonia,
c/Gran Capità 2–4, Edif. Nexus
104, 08034
Barcelona,
Spain
6
Institut de Ciències de l’Espai (CSIC),
Campus UAB,
08193
Bellaterra,
Spain
e-mail: isern@ieec.cat
Received: 30 September 2010
Accepted: 26 December 2010
Context. Within the theoretical framework of some modern unification theories the constants of nature are functions of cosmological time. White dwarfs offer the possibility of testing a possible variation of G and, thus, to place constraints on these theories.
Aims. We present full white dwarf evolutionary calculations for a scenario where G decreases with time.
Methods. White dwarf evolution is computed in a self-consistent way, including the most up-to-date physical inputs, non-gray model atmospheres and a detailed core chemical composition that results from the calculation of the full evolution of progenitor stars.
Results. We find that the mechanical structure and the energy balance of white dwarfs are strongly modified by a varying G. In particular, for a rate of change of G higher than Ġ/G = −1 × 10-12 yr-1, the evolution of cool white dwarfs is markedly affected. The impact of a varying G is more pronounced for more massive white dwarfs.
Conclusions. In view of the recent results reporting that a very accurate white dwarf cooling age can be derived for the old and metal-rich open cluster NGC 6791, our study suggests that this cluster could be a potential target to constrain or detect a hypothetical secular variation of G.
Key words: stars: interiors / stars: evolution / white dwarfs
© ESO, 2011
1. Introduction
One of the principles of General Relativity – the equivalence principle – requires that the fundamental constants should be independent of location. However, in several modern grand-unification theories, the constants of nature are supposed to be functions of low-mass dynamical scalar fields – see, for instance, Lorén-Aguilar et al. (2003) and references therein. If these theories are correct, we expect them to experience slow changes over cosmological timescales, and thus to also depend on location. In recent years, several constraints have been placed on the variation of the fine structure constant – see the review papers of Uzan (2003) and García-Berro et al. (2007) for recent revisions of the most stringent upper limits to their rate of change. In sharp contrast with the vivid debate about whether (or not) there is evidence for a varying fine structure constant, relatively few works have been devoted to study a hypothetical variation of G. The reason probably lies on the intrinsic difficulty of measuring the value of this constant (Mohr et al. 2008). Actually, G is the fundamental constant for which we have the less accurate determination, and the several measures of G differ considerably. The tightest constraints on the rate of variation of G come from lunar laser ranging, Ġ/G ≲ (2 ± 7) × 10-13 yr-1 (Müller & Biskupek 2007), but these are purely local. At intermediate cosmological ages the Hubble diagram of Type Ia supernovae can also be used to constrain the rate of variation of the gravitational constant, Ġ/G ≲ 10-11 yr-1 at z ~ 0.5 (Gaztañaga et al. 2002). Finally, Big Bang nucleosynthesis also provides limits on possible variations in Newton’s constant, −3 × 10-13 yr-1 ≲ (Ġ/G) ≲ 4 × 10-13 yr-1 (Copi et al. 2004).
White dwarfs provide an independent way of constraining any hypothetical variation of G. There are several reasons for this. First, white dwarfs are extremely long-lived stars. Thus, the effects of a varying G can become prominent, even for very low rates of change. Second, white dwarfs are the end-point of stellar evolution for the vast majority of stars. Hence, they are numerous. Third, white dwarfs are compact objects, and their structure is very sensitive to the precise value of G. Finally, the evolution of white dwarfs is relatively well understood, and can be well described as a simple gravothermal process. Hence, for sufficiently low temperatures, their luminosity is derived entirely from a close balance between the thermal and the gravitational energies. Consequently, a secularly varying G largely affects the gravothermal balance of white dwarfs and, thus, their luminosities.
One of the ways in which white dwarfs can be used to constrain a variation of G considers the dependence of the secular rate of change of the period of pulsation of variable white dwarfs on its cooling rate (Benvenuto et al. 2004; Biesiada & Malec 2004). It has been shown that their secular rate of change of the period not only depends on the cooling rate, but also on the rate of change of G. Benvenuto et al. (2004) applied this method to the well studied variable white dwarf G117-B15A and obtained a rather loose bound, − 2.5 × 10-10 yr-1 ≤ Ġ/G ≤ 0. Another method to constrain a possible variation of G is to use the white dwarf luminosity function. The number counts of white dwarfs depend sensitively on the characteristic cooling time of white dwarfs in the corresponding luminosity interval, as does the position of the cut-off of the white dwarf luminosity function at low luminosities. García-Berro et al. (1995) used a simplified treatment to check what the effects of a slowly varying G in the white dwarf luminosity function could be. They assumed that Ġ/G was low enough to ensure that white dwarfs have time to adjust their mechanical structure to the present value of G on a timescale much shorter than that of the cooling timescale. Under this assumption, energy conservation leads to (García-Berro et al. 1995)
where B is the binding energy of the white dwarf, B = U + Ω, U is the total internal energy, Ω is the total gravitational energy and Lν is the neutrino luminosity. The evolution of the luminosity was then obtained from a series of static models, not from fully evolutionary calculations, assuming a relationship between the luminosity and the core temperature obtained from fits to evolutionary calculations with constant G. Despite this simplified treatment they were able to obtain an upper limit Ġ/G ≤ −(1.0 ± 1.0) × 10-11 yr-1. Later, Biesiada & Malec (2004) cast doubts on this treatment. In particular, they claimed that the last term in Eq. (1), involving Ġ/G, cancels out when the expression for the expansion work is further expanded. However, their criticism was incorrect because all relevant terms in the energy conservation equation were carefully taken into account in García-Berro et al. (1995).
What neither García-Berro et al. (1995) nor Biesiada & Malec (2002) took into account is that the relationship between the core temperature and the luminosity of white dwarfs also depends on G. For instance, adopting the simplified Mestel cooling law (Mestel 1952), it turns out that L ∝ G. This means that a full stellar evolutionary code is needed if an accurate treatement of white dwarf cooling for G changing with time is to be done. To our knowledge, the only calculations of cooling white dwarfs with a time-varying G employing an up-to-date stellar evolutionary code are those of Benvenuto et al. (1999), but their analysis turned out to be flawed. Specifically, in this work the energy conservation equation for a running G included the differential version of the last term of Eq. (1), which is incorrect. In summary, although the evolutionary properties of white dwarfs can be potentially used to set upper bounds to the rate of variation of G, very few studies have been done up to now, and they are incomplete or flawed. Moreover, none of these works took into account that if G varies, its value in the past differs from its present value, and all calculations were made with the present value of G, thus neglecting a potentially important effect. This paper aims at filling this gap.
2. Input physics
We follow in a self-consistent way the evolution of white dwarfs for a varying G. In the interest of simplicity we have assumed that Ġ/G remains constant with time. All the calculations were made with the LPCODE stellar evolutionary code – see Althaus et al. (2010) and Renedo et al. (2010) for recent applications of this code. The main physical inputs considered in LPCODE comprise the following. We included 22Ne diffusion and its associated energy release – see García-Berro et al. (2008, 2010) and Althaus et al. (2010) for details. The energy sources arising from crystallization of the white dwarf core – namely, the release of latent heat and of gravitational energy associated with carbon-oxygen phase separation (García-Berro et al. 1988; Isern et al. 1997, 2000) – are fully taken into account following the treatment of Althaus et al. (2010). We used the carbon-oxygen phase diagram of Segretain & Chabrier (1993). Other phase diagrams for the carbon-oxygen mixture have been recently computed (Horowitz et al. 2010), but as long as we are concerned with relative differences in the white dwarf cooling times when a running G is adopted, the impact of a different choice of the phase diagram on the bounds on Ġ/G should be minor. For the 12C(α,γ)16O reaction rate we adopt the prescription of Angulo et al. (1999). Again, we stress that although the precise value of this poorly known reaction rate – see, for instance Assunção et al. (2006) – is important to obtain the chemical stratification of white dwarf progenitors and thus to compute absolute white dwarf cooling ages, the relative effect of a varying G in the models does not appreciably depend on it. We use non-gray model atmospheres to provide accurate outer boundary conditions for our models. Our atmospheres include non-ideal effects in the gas equation of state and chemical equilibrium based on the occupation probability formalism. They also consider collision-induced absorption caused by H2-H2, H2-He, and H-He pairs, and the Lyα quasi-molecular opacity that results from perturbations of hydrogen atoms by interactions with other particles, mainly H and H2 (Rohrmann et al. 2010). Our sequences also incorporate element diffusion in the outer layers (Althaus et al. 2003).
The radiative opacities used are those of the OPAL project (Iglesias & Rogers 1996), and include carbon- and oxygen-rich compositions. These opacities are supplemented at low temperatures with the molecular opacities for pure hydrogen composition of Marigo & Aringer (2009). The conductive opacities of Cassisi et al. (2007) were used as well. Neutrino emission rates for pair, photo, and bremsstrahlung processes are those of Itoh et al. (1996), while for plasma processes we include the treatment of Haft et al. (1994). We use the equation of state of Segretain et al. (1994) for the high-density regime. For the low-density regime, we used an updated version of the equation of state of Magni & Mazzitelli (1979).
Given that our aim is to self-consistently compute the cooling of white dwarfs in the presence of a varying G, we write the local luminosity equation as
and we allow G to vary. This is a fair approach and has been adopted in previous studies of this kind (degl’Innocenti et al. 1996). Consequently, the density profile of the white dwarf now varies not only because the white dwarf cools, but also because G varies. Naturally, this influences the white dwarf cooling ages.
White dwarf evolutionary sequences computed in this work.
3. Evolutionary results
We computed the evolution of white dwarf sequences of masses 0.525, 0.609 and 1.0 M⊙ considering three values for the rate of change of G, namely Ġ/G = −5 × 10-11 yr-1, Ġ/G = −1 × 10-11 yr-1, and Ġ/G = −1 × 10-12 yr-1. As will become clear later, the evolution with a varying G is strongly dependent on the initial value of G at the beginning of the cooling phase. Accordingly, for each value of Ġ/G we computed several sequences with different values of Gi/G0, where Gi stands for the value of G at the beginning of the cooling track at high effective temperature, and G0 corresponds to the present value of G. To obtain starting white dwarf configurations with the appropriate value of G, we simply changed G0 by Gi at the beginning of the cooling phase and calculated the resulting structure. After a brief transitory stage, we obtain the initial configurations for our sequences. This artificial procedure to obtain the initial white dwarf configurations is justified since the subsequent evolution does not depend on the way the initial white dwarf structures are obtained. All in all, we computed 30 white dwarf evolutionary sequences, which are listed in Table 1. In addition, we also list in this table the surface luminosity (in solar units) for which G = G0. Note that the election of the values of Gi was made in a way that the present value of G occurs at advanced stages of white dwarf evolution, when the surface luminosity ranges from log (L/L⊙) = −3 to −5, the typical luminosities of field white dwarfs. All sequences were computed down to log (L/L⊙) = −5, a luminosity lower than that of the dimmest field white dwarfs.
 |
Fig. 1 Surface luminosity versus age for a 0.609 M⊙ white dwarf assuming Ġ/G = −5 × 10-11 yr-1 and different initial values of G at the start of the cooling track. We also show with square symbols the luminosity and age at which the present value of G is reached in the cooling track. |
 |
Fig. 2 Surface luminosity versus age for a 1.0 M⊙ white dwarf assuming Ġ/G = −5 × 10-11 yr-1 and different initial values of G at the start of the cooling track. We also show with square symbols the luminosity and age at which the present value of G is reached in the cooling track. |
Despite the low rates of change of G adopted here, the evolution of our white dwarf sequences is strongly modified. Because we adopted Ġ/G < 0, the central density of the cooling sequences decreases with time. This is at odds with the evolution of standard models, in which white dwarfs cool at approximately constant density. Because the energy of cool white dwarfs is essentially of gravothermal origin, this has important implications for the evolution of old white dwarfs, and even a small change in G alters the energy balance of the star and thus its luminosity. In addition, because of the higher value of G at the beginning of the cooling track, 22Ne sedimentation in the liquid phase and crystallization of the white dwarf core occur at higher luminosities. Hence, the gravitational energy released by these processes takes place much earlier, and therefore strongly modifies the cooling rate when compared with that obtained for a constant G.
The white dwarf cooling times are sensitive to the value of G at the beginning of the cooling track. This can be better understood by examining Figs. 1 and 2, which show the relation between the surface luminosity and the age for the 0.609 M⊙ and 1.0 M⊙ white dwarf sequences assuming Ġ/G = −5 × 10-11 yr-1 and different values of Gi/G0. In these figures we also show with square symbols the luminosity and age at which the present value of G is reached in the cooling track. Note that the higher the value of Gi/G0, the lower the luminosity at which Gi = G0 occurs. Obviously, this means that if the correct value of G is to be obtained at present time, an initially more compact white dwarf is needed. Also, it is worth noting that the cooling ages for a varying G are much smaller at low luminosities than the cooling ages obtained when G is constant. Finally, because of the stronger gravity of massive white dwarfs, the impact of a decreasing G on the cooling time increases markedly with the stellar mass.
 |
Fig. 3 Surface luminosity versus age for several 0.609 M⊙ white dwarf sequences, adopting different values of Ġ/G. See text for details. |
To illustrate the dependence of cooling on the rate of change of G, we show in Figs. 3 and 4 the temporal evolution of the luminosity for the 0.609 M⊙ and 1.0 M⊙ white dwarf sequences assuming Ġ/G = −1 × 10-12 yr-1, −1 × 10-11 yr-1, and −5 × 10-11 yr-1. The initial values of G were selected in a way that for each sequence the present value of G occurs at log (L/L⊙) ≈ −4.0. To further quantify the effects of a varying G we also show in Table 2 the white dwarf cooling ages at log (L/L⊙) = −4.0 of these evolutionary sequences and the corresponding ages for the models in which Ġ/G = 0. As can be seen in these figures, and in Table 2, there is a marked dependence of the white dwarf ages on the assumed rate of change of G. This dependence is more pronounced for massive white dwarfs. However, for Ġ/G = −1 × 10-12 yr-1 the evolution is almost indistinguishable from that of the standard case of constant G, particularly for the low-mass white dwarf. This value of Ġ/G constitutes a lower limit for the rate of change of G above which we can expect that the evolution of white dwarfs will be influenced by a varying G.
4. Discussion and conclusions
Recently, García-Berro et al. (2010) have demonstrated that the slow-down of the white dwarf cooling rate owing to the release of gravitational energy from 22Ne sedimentation and carbon-oxygen phase separation upon crystallization is of fundamental importance to reconcile the age discrepancy in the very old, metal-rich open cluster NGC 6791. This raises the possibility of using this cluster to constrain a hypothetical variation of G with time. In a step forward to do this, we computed a new set of white dwarf evolutionary sequences in which we allow G to vary. We assumed that Ġ/G remains constant with time and followed the evolution of white dwarf model sequences of masses 0.525, 0.609 and 1.0 M⊙ considering three values for the rate of change of G, namely Ġ/G = −5 × 10-11 yr-1, Ġ/G = −1 × 10-11 yr-1, and Ġ/G = −1 × 10-12 yr-1. To the best of our knowledge these are the only self-consistent evolutionary sequences of cooling white dwarfs incorporating the effects of a varying G.
 |
Fig. 4 Surface luminosity versus age for several 1.0 M⊙ white dwarf sequences, adopting different values of Ġ/G. See text for details. |
Cooling times, in Gyr, at log (L/⊙) = −4.0 for different values of Ġ/G and two representative white dwarf masses.
We found that the mechanical structure and energy balance of cool white dwarfs are strongly modified when a slowly varying G is adopted, and that the white dwarf evolution is sensitive to the initial value of G at the beginning of the cooling phase. Because of the compact nature of massive white dwarfs, the impact of a decreasing G on the cooling time increases markedly with the stellar mass. We found as well that for a rate of Ġ/G = −5 × 10-11 yr-1, the cooling ages of dim white dwarfs are much smaller than the cooling ages given by the standard evolution at constant G. The calculations presented here show that the white dwarf evolution is very sensitive to the exact value of Ġ/G and that a detailed fit to the white dwarf luminosity function of NGC 6791 may place tight constraints on a possible rate of change of G. Last but not least, we mention that calculations to study the evolution of the progenitors of white dwarfs, which may also affect the cooling times, are currently under way.
Acknowledgments
This research was supported by AGAUR, by MCINN grants AYA2008-04211-C02-01 and AYA08-1839/ESP, by the ESF EUROCORES Program EuroGENESIS (MICINN grant EUI2009-04170), by the European Union FEDER funds, by AGENCIA: Programa de Modernización Tecnológica BID 1728/OC-AR, and by PIP 2008-00940 from CONICET. L.G.A. also acknowledges a PIV grant of the AGAUR of the Generalitat de Catalunya.
References
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., García-Berro, E., Renedo, I., et al. 2010, ApJ, 719, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Assunção, M., et al. 2006, Phys. Rev. C, 73, 055801 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Biesiada, M., & Malec, B. 2004, MNRAS, 350, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., Althaus, L. G., & Torres, D. F. 1999, MNRAS, 305, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., García-Berro, E., & Jordi, I., 2004, Phys. Rev. D, 69, 082002 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Copi, C. J., Davis, A. N., & Krauss, L. M. 2004, Phys. Rev. Lett., 92, 171301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- degl’Innocenti, S., Fiorentini, G., Raffelt, G. G., Ricci, B., & Weiss, A. 1996, A&A, 312, 345 [NASA ADS] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1988, Nature, 333, 642 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1995, MNRAS, 277, 801 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Isern, J., & Kubyshin, Y. A., 2007, A&ARv, 14, 113 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Althaus, L. G., Córsico, A. H., & Isern, J. 2008, ApJ, 677, 473 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gaztañaga, E., García-Berro, E., Isern, J., Bravo, E., & Domínguez, I. 2002, Phys. Rev. D, 65, 023506 [NASA ADS] [CrossRef] [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Schneider, A. S., & Berry, D. K. 2010, Phys. Rev. Lett., 104, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Mochkovitch, R., García-Berro, E., & Hernanz, M. 1997, ApJ, 485, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Hernanz, M., & Chabrier, G. 2000, ApJ, 528, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Lorén-Aguilar, P., García-Berro, E., Isern, J., & Kubyshin, Y. A. 2003, Class. & Quantum Grav., 20, 3885 [NASA ADS] [CrossRef] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Marigo, P., & Aringer, B. 2009, A&A, 508, 1539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mestel, L. 1952, MNRAS, 112, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Mohr, P. J., Taylor, B. N., & Newell, D. B. 2008, Rev. Mod. Phys, 80, 633 [Google Scholar]
- Müller, J., & Biskupek, L. 2007, Class. & Quantum Grav., 24, 4533 [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rohrmann, R. D., Althaus, L. G., & Kepler, S. O. 2010, MNRAS, in press [arXiv:1009:3254] [Google Scholar]
- Segretain, L., & Chabrier, G. 1993, A&A, 271, L13 [NASA ADS] [Google Scholar]
- Segretain, L., Chabrier, G., Hernanz, M., García-Berro, E., & Isern, J. 1994, ApJ, 434, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Uzan, J.-P. 2003, Rev. Mod. Phys., 75, 403 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Cooling times, in Gyr, at log (L/⊙) = −4.0 for different values of Ġ/G and two representative white dwarf masses.
All Figures
 |
Fig. 1 Surface luminosity versus age for a 0.609 M⊙ white dwarf assuming Ġ/G = −5 × 10-11 yr-1 and different initial values of G at the start of the cooling track. We also show with square symbols the luminosity and age at which the present value of G is reached in the cooling track. |
| In the text | |
 |
Fig. 2 Surface luminosity versus age for a 1.0 M⊙ white dwarf assuming Ġ/G = −5 × 10-11 yr-1 and different initial values of G at the start of the cooling track. We also show with square symbols the luminosity and age at which the present value of G is reached in the cooling track. |
| In the text | |
 |
Fig. 3 Surface luminosity versus age for several 0.609 M⊙ white dwarf sequences, adopting different values of Ġ/G. See text for details. |
| In the text | |
 |
Fig. 4 Surface luminosity versus age for several 1.0 M⊙ white dwarf sequences, adopting different values of Ġ/G. See text for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.