| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201015626 | |
| Published online | 24 January 2011 | |
Iron lines in model disk spectra of Galactic black hole binaries
1
N. Copernicus Astronomical Center, Bartycka 18,
00-716
Warsaw,
Poland
e-mail: agata@camk.edu.pl
2
Warsaw University Observatory, Al. Ujazdowskie 4, 00-478
Warsaw,
Poland
e-mail: jm@astrouw.edu.pl
3
Toruń Centre for Astronomy, N. Copernicus University,
Gagarina 11,
87-100
Torun,
Poland
Received: 22 August 2010
Accepted: 1 November 2010
Context. We present angle-dependent, broad-band intensity spectra from accretion disks around black holes of 10 M⊙. In our computations disks are assumed to be slim, which means that the radial advection is taken into account while computing the effective temperature of the disk.
Aims. We attempt to reconstruct continuum and line spectra of X-ray binaries in soft state, i.e. dominated by the disk component of multitemperature shape. We follow how the iron-line complex depends on the external irradiation, an accretion rate, and a black hole spin.
Methods. Full radiative transfer is solved including effects of Compton scattering, free-free and all important bound-free transitions of 10 main elements. We assume the LTE equation of state. Moreover, we include here the fundamental series of iron lines from helium-like and hydrogen-like ions, and fluorescent Kα and Kβ lines from low ionized iron. We consider two cases: nonrotating black hole, and black hole rotating with almost maximum spin a = 0.98, and obtain spectra for five accretion disks from hard X-rays to the infrared.
Results. In nonirradiated disks, resonance lines from He-like and H-like iron appear mostly in absorption. Such disk spectra exhibit limb darkening in the whole energy range. External irradiation causes that iron resonance lines appear in emission. Furthermore, depending on disk effective temperature, fluorescent iron Kα and Kβ lines are present in disk emitting spectra. All models with irradiation exhibit limb brightening in their X-ray reflected continua.
Conclusions. We show that the disk around stellar black hole itself is hot enough to produce strong-absorption resonance lines of iron. Emission lines can only be observed if heating by external X-rays dominates thermal processess in a hot disk atmosphere. Irradiated disks are usually brighter in X-ray continuum when seen edge on, and fainter when seen face on.
Key words: accretion, accretion disks / radiative transfer / X-rays: binaries
© ESO, 2011
1. Introduction
The newest X-ray satellite spectra of Galactic black hole binaries (GBHBs) clearly show a UV/X-ray bump peaking at about 1 keV in their high/soft states (Davis et al. 2006). It is widely believed that this emission originates in an accretion disk circulating around the central black hole of stellar-like mass (Mitsuda et al. 1984; Dotani et al. 1997). Since individual rings of the accretion disk exhibit various effective temperatures, the radiation spectrum integrated over radii is responsible for the multiblackbody shape of the observed spectrum. Similar optical/UV bumps were observed in the spectra of active galactic nuclei (AGN) (Shields 1978; Malkan 1983). However, accretion disks in AGN exhibit relatively low effective temperatures, since the mass of the central black hole is on the order of 108 M⊙, and the disk temperature is inversely proportional to the mass with the power of 0.25. A multicolor disk model (MCD) still does not explain some spectral details (Merloni et al. 2000; Kubota et al. 2010), but up to now there is no better explanation for the observed continuum.
In addition, in both cases of GBHBs and AGN, a substantial fraction of the bolometric luminosity is emitted by a hard X-ray tail extending up to several tens or even hundreds of keV (Gierlinski et al. 1997; Nandra & Pounds 1994). The shape of many X-ray tails shows evidence of interaction between radiation emitted near the central object and the nearby accreting gas (Pounds et al. 1990). The most prominent evidence of this interaction is the detection of fluorescent iron Kα line at 6.4 keV in different types of accreting sources (Tanaka et al. 1995; Iwasawa et al. 1999; Miniutti et al. 2004; Miller et al. 2004; Di Salvo et al. 2005).
The shape of an iron line profile carries important information about the physics of the material around the compact object. Close to the black hole, the emission line profile is relativistically broadened and skewed, which together with a circular gas movement in the disk, makes the final profile asymmetric with a strong red wing (Fabian et al. 1989; Reynolds & Begelman 1997; Fabian et al. 2002). But there is a one example of broad line profile detected in cataclysmic variable, GK Per (Titarchuk et al. 2009), where relativistic effects cannot work at all, suggesting that different mechanisms can be responsible for the line broadening. Also in some cases, the detected iron line profile has a narrow component (Watanabe et al. 2003; Reeves et al. 2004; Yaqoob et al. 2007), indicating that interaction between hard X-rays and accreting gas occurs farther away from the black hole.
In all models used to fit X-ray data, iron line profile is assumed to be Gaussian with eventual kinematic broadening. In this paper we present detailed computations of iron line profiles in the case of GBHBs, taking thermal, natural, pressure, and Compton broadening of lines into account when radiation passes through the atmosphere. These calculations were already done for the disk in AGN (Różańska & Madej 2008, hereafter RM08), showing profiles of fluorescent Kα, Kβ lines, and their Compton shoulders. But accretion disks in GBHBs are hot enough to create of resonance iron lines due to thermal processes in the atmosphere. The main goal of this paper is to show how strong full iron-line complex (6.3−7.1 keV) will be from hot illuminated disk atmospheres in GBHBs.
Numerous theoretical models of the accretion disk spectra have been developed recently, still a lot of effort is needed to achieve an undisputable solution. One of the obvious reasons for such a situation is that each mechanism responsible for the accretion makes disk matter very turbulent (Ohsuga 2007), and no code can at present compute radiative transfer through moving gas, regardless of whether this mechanism is driven by viscosity (Shakura & Sunyaev 1973) or by magnetorotational instability (Hawley et al. 2001).
A second serious problem is that, depending on geometrical and physical assumptions, we have several available global models of accretion disks. The earliest was the standard Shakura & Sunyaev (1973), SS disk, which is geometrically thin and optically thick, with all dissipated energy converted into radiation. Relativistic corrections for a such disk was derived by Novikov & Thorne (1973, hereafter NT disk). But in other models some thermal energy or mass in the disk can be carried into a black hole by radial advection. Such a process generates two branches of disk solutions: optically thin ADAFs (advection-dominated accretion flows) (Narayan & Yi 1995), and optically thick, slim disks developed by Abramowicz et al. (1988). Models of disk spectra presented recently by Davis et al. (2006) and stored in xspec library as fits templates, have been computed for an NT disk.
We present, for the first time, sample spectra of optically thick, slim accretion disks (Abramowicz et al. 1988). The global slim disk model (Sa¸dowski et al. 2011) was computed for several values of the accretion rate and for two values of the black hole spin: 0 and 0.98. In this paper we present precise calculations of the radiative transfer through the atmosphere of a disk around a stellar mass black hole.
We use here the code developed by Madej (1991) for hot stellar atmospheres and then adopted to atmospheres illuminated by an external hard X-ray source (Madej & Różańska 2000), and to accretion disk geometry (Różańska & Madej 2001). Adopting atmospheric computations for an accretion disk, we solve the vertical structure and outgoing spectra for several neighboring rings in hydrostatic and radiative equilibrium. The final spectrum presented in a specific intensity scale for different aspect angles is integrated over radii and presented at the source frame. No kinematic special relativity effects are included in our model.
Our radiative transfer equation includes the effects of multiple Compton scattering of radiation on free electrons in relativistic thermal motion and a rich set of bound-free and free-free opacities. Ionization populations are computed by assuming the LTE equation of state for ideal gas. External irradiation is taken into account as a non-LTE contribution to the equation of transfer and the equation of radiative equilibrium. The method allows for a large relative photon-electron energy exchange at the time of Compton scattering and, si is able to reconstruct Compton scattering of photons with energy approaching or even exceeding the electron rest mass (Madej & Różańska 2004).
We compute profiles of thermal and fluorescent iron lines coming from the accretion disk atmosphere irradiated by hard X-rays with a power-law spectral distribution. By taking emissivity of fluorescent Kα and Kβ lines of low ionized iron in full NLTE into account, we are able to estimate the relative importance of thermal and nonthermal (fluorescent) iron lines as the function of distance from the black hole, accretion rate, and aspect angle.
In the next section we overview modeling of theoretical disk specra. Section 3 contains global structure of a slim accretion disk model and the main equations used in our radiative transfer computations. Results are presented in Sect. 4, and main conclusions are given in the summary section.
2. Modeling theoretical disk spectra
Theoretical disk spectra can be obtained on various levels of sophistication, from the simple black body emission to the detailed numerical simulation of the radiation field. In both cases, a locally emitted spectrum has to be integrated over the disk surface. The first approach is quite simple as soon as we know the radial distribution of effective temperatures in the disk (Shakura & Sunyaev 1973). The second approach depends on the assumptions made in calculations of vertical structure and radiative transfer in the disk atmosphere. The most important aspects to take into account are treatment of energy-dependent opacities of elements, free-free processes including Compton scattering, vertical stratification of temperature, density and degrees of gas ionization, illumination by an external X-ray source and eventual fluorescent emission, vertical energy dissipation by accretion, The eventual influence of vertical height-dependent gravity, which operates in the disk. Close to the black hole relativistic corrections on the vertical disk structure and emitted spectrum should be taken into account.
In the pioneering work done by Laor & Netzer (1989) radiative transfer was solved in the Eddington approximation, neglecting Compton scattering. On the other hand, Shimura & Takahara (1993) considered fully ionized hydrogen-helium disks and assumed only bremstrahlung and Compton scattering. Doerrer et al. (1996) has taken some absorption into account but only that of pure hydrogen. None of those papers have treated external illumination.
On the other hand, there were studies of reprocessing of the external hard X-rays by cold matter, neglecting or simplifying the treatment of hydrostatic equillibrium or detailed source function calculations. Reprocessed radiation, created mostly by Compton scattering process, could be succesfully reconstructed by Monte Carlo simulations (George & Fabian 1991; Magdziarz & Zdziarski 1995), with true absorption considered in a very schematic way.
Reprocessing of radiation by Compton scattering could be described by Kompaneets equation (Ross & Fabian 1993; Merloni et al. 2000). For many years it was the most advanced approach to computing the iron line models in the reflected X-ray spectrum. But those authors assume that reflection occurs on a constant density slab with optical depth on the order of 3, while thermalization of hard X-rays may occur deeper in an atmosphere. Hydrostatic equilibrium was a serious complication of the problem (as discussed by Różańska et al. 2002, and references therein). With the constraint of hydrostatic equillibrium, we can precisely calculate the strong density and ionization gradient in the atmosphere (Madej & Różańska 2004). Even if resulting X-ray spectra from constant density slab do not differ significantly in the spectral domain where the iron line appears (Ross & Fabian 2007), we point out here that they do not properly reproduce thermal optical UV bump and the strength of soft X-ray lines, the latter depending on ionization vertical profiles.
Very sophisticated calculations of unilluminated accretion disk spectra were done with tlusty code developed by Hubeny (1990). They assume the disk atmosphere is in hydrostatic and radiative equilibrium and solve the radiative transfer equation with a non-LTE equation of state (Hubeny & Hubeny 1997), heavy element abundances, and Compton scattering treated with the Kompaneets equation (Hubeny et al. 2001). However, those authors do not consider the effects of the external X-ray illumination, so they cannot precisely compute iron line profiles, Nevertheless, the level of sophistication of our radiative transfer calculations is comparable to those presented by Hubeny et al. (2001).
3. Method and model assumptions
All our models are calculated assuming black hole of the mass 10 M⊙. Throughout this paper we express radial distances, R, in units of the Schwarzsild radius defined as rSchw = 2GM/c2. In the first stage of calculations we solve the global two-dimensional, hydrodynamical, relativistic slim disk model presented in Sa¸dowski et al. (2011). In contrast to the classical SS and NT disk models it does not assume radiative equilibrium, i.e. an exact balance between the dissipated energy and the cooling rate at a given radius. The slim disks allow for advection of heat with inflowing matter which becomes important for moderate and high accretion rates (ṁ > 0.3 ṀEdd1) and which affects the disk appearence e.g., its effective temperature and photosphere profiles. The model adopted here (Sa¸dowski et al. 2011) solves the slim disk equations in two dimensions (i.e. assuming only the axial symmetry). The vertical structure is not assumed ad hoc, but is solved consistently.
We assume that the dissipation rate is proportional to the local pressure (i.e., we adopt the α prescription with α = 0.01). The energy transport in the vertical direction is treated under the diffusive approximation with convection described by the mixing-length theory. The fraction of the dissipated heat that is advected is independent of the vertical coordinate by assumption. Also, we are unable to calculate how advected flux depends on the external X-ray illumination.
We computed 3+2 models of accretion disks for the accretion rates ṁ = 0.01, 0.1, and 1 in units of the Eddington accretion rate. For all values of the accretion rate, we consider nonrotating black hole a = 0, while models with a = 0.98 were also computed for the two lowest values of ṁ.
 |
Fig. 1 Radial dependence of vertical gravity (upper panel) and effective temperature (lower panel) in our slim disk models for three accretion rates: ṁ = 0.01, 0.1, and 1, denoted as black, blue, and red respectiverly. Two dashed lines (blue and black) represent models for which we assume that the spin of a black hole equals 0.98. Thin horizontal lines mark the position of horizon and ISCO for rotating (dashed line) and nonrotating black holes (solid line). Points mark annuli for which detailed radiative transfer computations were performed. |
Global models considered in this paper are presented in Fig. 1. The upper panel represents the radial distribution of vertical gravity on the disk surface, and the lower panel the radial distribution of the disk’s effective temperature. Both quantities are input parameters in our radiative transfer calculations. Detailed radiative calculations were performed for the distances marked in Fig. 1. As the black hole rotates the innermost stable circular orbit (ISCO) and event horizont moves closer to the black hole. Therefore, for a rotating black hole we can also receive radiation from below R = 3. This value defines the location of ISCO in nonrotating case.
In all cases, the disk matter is assumed to have a solar-like chemical composition. Number abundances of elements relative to hydrogen (Nelem/NH) equal to 1.00 (for H), 9.54 × 10-2 (He), 4.72 × 10-4 (C), 9.65 × 10-5 (N), 8.55 × 10-4 (O), 3.84 × 10-5 (Ne), 4.17 × 10-5 (Mg), 4.94 × 10-5 (Si), 1.64 × 10-5 (S), and 6.58 × 10-5 (Fe).
3.1. Radiative transfer calculations
A detailed description of the present code and the corresponding equations were given in paper RM08, and here we call only a few of them. The equation of transfer for the specific intensity Iν at frequency ν is solved in plane-parallel geometry on the monochromatic optical depth τν:  (1)where Sν is the frequency-dependent source function. In this paper we use the LTE (local thermodynamic equilibrium) absorption κν, whereas coefficients of emission jν and scattering σν include non-LTE terms. Emission coefficient jν is the sum of three terms,
(1)where Sν is the frequency-dependent source function. In this paper we use the LTE (local thermodynamic equilibrium) absorption κν, whereas coefficients of emission jν and scattering σν include non-LTE terms. Emission coefficient jν is the sum of three terms,  , which represent thermal emission, Compton scattering emission, and the emission in iron fluorescent lines, respectively.
, which represent thermal emission, Compton scattering emission, and the emission in iron fluorescent lines, respectively.
The coefficient of thermal emission jν in LTE is proportional to the Planck function  . The coefficient of true absorption κν is the sum of bound-free absorption from numerous levels of atoms and ions for all elements, plus free-free absorption from all ions. We also included absorption of the 4 lowest lines of fundamental series of helium-like iron and of similar 4 lowest lines of hydrogen like iron, all formed in LTE by the assumption.
. The coefficient of true absorption κν is the sum of bound-free absorption from numerous levels of atoms and ions for all elements, plus free-free absorption from all ions. We also included absorption of the 4 lowest lines of fundamental series of helium-like iron and of similar 4 lowest lines of hydrogen like iron, all formed in LTE by the assumption.
The external intensity from the point-like lamp is emitted in the form of power law with spectral index αX and exponential cut-off limits νmin and νmax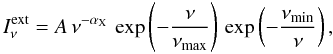 (2)and normalized to the luminosity of the source, LX:
(2)and normalized to the luminosity of the source, LX: ![\begin{equation} A = \frac{ L_{\rm X}}{4 \pi r_l^2 \left[ \int_{\nu_{\rm min}}^{\nu_{\rm max}} \nu^{- \alpha_{\rm X}} \, \exp\left(- \frac{\nu}{\nu_{\rm max}}\right) \, \exp\left(- \frac{\nu_{\rm min}}{\nu} \right) {\rm d}\nu \right]}\cdot \end{equation}](/articles/aa/full_html/2011/03/aa15626-10/aa15626-10-eq48.png) (3)The distance from an X-ray source depends on the ring radius r, and the lamp height hl, in the casual relation
(3)The distance from an X-ray source depends on the ring radius r, and the lamp height hl, in the casual relation  . The luminosity, spectral index, and cut-off limits of irradiating spectrum are free parameters of our model, all of them described in Sect. 4.
. The luminosity, spectral index, and cut-off limits of irradiating spectrum are free parameters of our model, all of them described in Sect. 4.
Expressions for the Compton scattering terms and emission coefficient in an irradiated atmosphere were derived in Madej & Różańska (2004) and are valid in a disk atmosphere without any changes  (4)In the above equation variable Uν denotes the angle-averaged intensity of the external irradiation (RM08).
(4)In the above equation variable Uν denotes the angle-averaged intensity of the external irradiation (RM08).
Compton scattering cross sections were computed following the paper by Guilbert (1981). Functions Φ1 and Φ2 are properly weighted, angle-averaged Compton redistribution functions for photons both incoming or outgoing of frequency ν after scattering in thermal electron gas (Madej & Różańska 2004).
 |
Fig. 2 Vertical temperature structure for various rings in three unilluminated disk models. Models differ by accretion rate ṁ and dimensionless spin of the black hole a. Curves are labeled by the distance from the black hole, R. In all cases we observe temperature rise in the outermost layers of atmosphere due to Compton scattering (see text for details). |
Fluorescence of low-ionized iron gas was approximated by two emission lines, Kα and Kβ, therefore,  (5)where
(5)where  and
and  denote the integrated intensity of Kα and Kβ emission lines, respectively. Frequency-dependent variables
denote the integrated intensity of Kα and Kβ emission lines, respectively. Frequency-dependent variables  and
and  define profiles of fluorescent lines, both normalized to unity.
define profiles of fluorescent lines, both normalized to unity.
Energy emitted in Kα and Kβ lines was derived by absorption of hard continuum X-rays from the radiation field penetrating the disk atmosphere. A hard X-ray photon interacting with neutral or low-ionized iron most probably ionize and remove the electron from the innermost K shell, and then the remaining hole is filled by another electron falling from L shell (Kα) or M shell (Kβ transition). The integrated emissivity for Fe Kα fluorescent line is given by 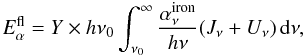 (6)where we set Y = 0.34 (Krause & Oliver 1979). Variable
(6)where we set Y = 0.34 (Krause & Oliver 1979). Variable  is the bound-free absorption coefficient for ionization from the K shell of iron counted for 1 atom. A similar expression holds for the integrated intensity
is the bound-free absorption coefficient for ionization from the K shell of iron counted for 1 atom. A similar expression holds for the integrated intensity  .
.
The fluorescence yield, Y, defines the fraction of the energy of hard X-rays absorbed by iron atoms, which was reemitted as photons in the Kα line. The remaining energy of absorbed X-rays, 1 − Y, was spent for releasing Auger electrons.
Iron Kα fluorescent line is a doublet line, and such a structure was reproduced by our code. The doublet structure is caused by the L shell having three subshells depending on the value of the spin and orbital angular momentum, and only two transitions are allowed by the selection rules. We set the central energies for Kα1 and Kα2 lines to 6.404 keV and 6.391 keV, respectively. Natural widths (FWHM) of both lines, 2.7 eV (Kα1) and 3.3 eV (Kα2) were taken from Krause & Oliver (1979). The Kβ line was approximated by a singlet line at the energy 7.057 keV. We set the natural width of the line to 2.5 eV arbitrarily.
Integrated emissivity  was divided in the proportion 2:1 between Kα1 and Kα2 components of the doublet, since the number of electrons on L shell with total spin equal to 1 is twice higher than the number of electrons with total spin equal 0. Following Basko (1978) we quite arbitrarily assumed that the integrated intensity
was divided in the proportion 2:1 between Kα1 and Kα2 components of the doublet, since the number of electrons on L shell with total spin equal to 1 is twice higher than the number of electrons with total spin equal 0. Following Basko (1978) we quite arbitrarily assumed that the integrated intensity  . Opacity profiles of all three lines were set to Voigt functions with depth-dependent parameters describing natural and thermal broadening.
. Opacity profiles of all three lines were set to Voigt functions with depth-dependent parameters describing natural and thermal broadening.
On each discrete ring we performed radiative transfer calculations assuming that the disk atmosphere remains in hydrostatic and radiative equillibrium (Eqs. (11) and (12) in RM08). Neither turbulences nor convection were taken into account. The full set of model atmosphere equations is solved by the method of partial linearization (Madej & Różańska 2004). Equation of hydrostatic equillibrium was excluded from the linearization scheme. The equation of transfer, Eq. (1) is solved by the Feautrier method and the variable Eddington factor method (Mihalas 1978).
 |
Fig. 3 Comparison of the temperature structure in three disk models before (black line) and after (red line) illumination by external radiation in the form of a power law. Results are shown for various distances from the black hole. |
4. Results
Our code allowed us to compute the structure of disk atmospheres over a very wide range of electron scattering optical depth starting from τes = 10-8 up to τes = 105. Furthermore, we have been able to reproduce the overall continuum spectrum from deep infrared of 0.4 eV up to hard X-rays of 400 keV. We solved the radiative transfer problem on the grid of 175 optical depth and 2200 photon energies simultaniously.
All spectra are presented as energy-dependent outgoing specific intensities, IE, which are suitable for disk geometry. We reject presenting monochromatic fluxes since they are only relevant to the geometry of a spherical star. Our intensities are shown for eight cosines of viewing angles, which represent angles of the Legendre quadrature. Exact values of those angles, their cosines, and the type of lines used in all figures presenting disk spectra are given in Table 1. In later discussion we draw the attention of the reader to the extreme angles: solid black line represents almost vertical direction (face-on aspect), whereas the solid red line represents an almost horizontal direction (edge-on aspect).
We only consider one choice of an irradiating power law with αX = 0.7 and luminosity LX = 1035 erg s-1, ranging from hνmin = 0.1 up to hνmax = 100 keV. The position of the X-ray lamp is fixed arbitrarily at the height hl = 5 rSchw above the disk at the radius R = 2 from the black hole.
4.1. Temperature structure
The radial distribution of effective temperatures in all global models has a characteristic shape (see Fig. 1). For nonrotating black holes, the maximum value of the effective temperature occurs at R ≈ 5. Closer to the black hole, there is a slight temperature drop, which is stronger for the lower accretion rate. For ṁ = 0.01, the effective temperature at R = 3 has the same value at R of about 60, while the surface gravity is slightly higher. This matters for irradiated atmospheres, where the fluorescent line can be created by illumination of the innermost ring with the effective temperature on the order of 7 × 105 K (see Sect. 4.2). Moving farther from the black hole temperature decreases and, at R = 100, is a half order of magnitude lower than its maximum value. When the black hole rotates, the temperature of innermost rings increases reaching 107 K, and we can expect a high ionization degree of iron in such conditions.
 |
Fig. 4 Outgoing intensity spectra from individual rings in four unilluminated disk models at different accretion rates and black hole spins. Spectra are shown in the energy range corresponding to the resonanse lines from hydrogen and helium-like iron. Spectra are shifted along the vertical axis in order to demonstrate the evolution of lines with distance from the black hole (marked on the right vertical axis). The limb darkening effect, where intensity from “face-on” disk (black solid line) is higher than intensity from “edge-on” disk (red solid line), is observed in all cases, except in some line cores. |
Vertical temperature profiles computed for individual rings are presented for various global models and distances at Figs. 2 and 3. All profiles of the disk atmospheres exhibit an inverse temperature rise in the uppermost atmospheric layers. In the case of unilluminated disks, presented in Fig. 2, the inverse temperature rise is comes from Compton heating by hot X-ray photons from below the photosphere. This result agrees with the models of hot neutron star atmospheres computed by Majczyna et al. (2005) and Suleimanov & Werner (2007), and with the atmosphere of accretion disks presented by Hubeny et al. (2001). In Fig. 2, we present the three hottest models where the surface temperature reaches 2.2 × 107 K. In such conditions, iron is almost fully ionized due to heating by radiation generated already via the accretion process.
In disks with external illumination, the heating effect is enhanced (see red lines in Fig. 3) due to Compton scattering of hot external X-ray photons. The amount of this heating depends on the disk effective temperature determined by the accretion rate and the black hole spin. For the lowest accretion rate and the nonrotating black hole (left panel) the effect of irradiation is seen in all rings, since effective temperatures for this model are the lowest. When the black hole rotates (middle panel) X-rays mostly heat up the outer rings. The same is observed for a higher accretion rate and a nonrotating black hole (Fig. 3 right panel). We do not show the temperature run for the two hottest disks, since then the external irradiation does not create any significant heating effect.
Our results include the influence of both Compton heating sources: by hot photons from the photosphere and from the external X-ray source. Because of that, the surface temperature structure depends on the shape and the normalization of the external irradiation. In cases where the atmosphere is hot by itself, additional soft X-ray photons can cool down the hottest layers thanks to Compton down-scattering. This happens for rings located close to the black hole, for the model with ṁ = 1 and a = 0, where the temperature of the uppermost irradiated surface layers is lower than for nonirradiated atmospheres (Fig. 3 right panel). Compton down-scattering is mostly caused by photons with energies lower than gas temperature, so we can expect that hot disk atmospheres in Galactic black hole binaries can cool down due to irradiation by soft X-rays. We plan to study this effect in a forthcoming paper.
4.2. Spectra from individual annuli
Intensity spectra emitted by individual rings of nonirradiated accretion disks are presented in Fig. 4. Each panel shows the evolution of resonance lines from He-like (6.7 keV) and H-like (6.9 keV) iron for four models with the lowest effective temperatures. Line profiles change with distance from the black hole, which is marked on the right vertical axis. In some rings the line at 6.7 keV exhibits reverse emission in the line core, which (for LTE) is the signature of the temperature inversion.
 |
Fig. 5 Outgoing intensity X-ray spectra for the sample of irradiated accretion disks. Spectra are shifted along vertical axis to demonstrate the evolution of iron-line complex with distance from the black hole (marked on the right vertical axis). |
For the disk with the lowest accretion rate and zero spin, only an absorption line from the He-like iron is present, originating in rings of the maximum effective temperature. Spectra from two rings located near the black hole and from all rings above R = 20 are featureless, since temperature is low and there are not enought He-like and iron ions. The situation changes for the same accretion rate when the black hole rotates. Iron line at 6.7 keV is stronger and the line at 6.9 keV becomes visible. For ṁ = 1 and a = 0 both lines are clearly seen for most of radii R. Energy-dependent limb darkening exists in all nonirradiated models. At some rings, differences between intensities emitted at various angles are strong, while sometimes they are not seen at all.
Spectra of irradiated disks are presented in Fig. 5 for the energy range 6.3−7.1 keV. For most rings both resonance lines of iron appear in emission. This effect, caused by external illumination, is only visible for those rings, when there is temperature change due to irradiation (see also Fig. 3). For the model presented in the middle panel for R < 6, both resonant lines appear in absorption.
Rings with relatively lower effective temperature, usually located farther from the black hole show cold fluorescent iron lines, Kα at 6.4 keV and Kβ at 7.05 keV. We point out here that those lines can be visible in the whole iron-line complex, when integrated over the disk surface (see the following section).
External irradiation causes limb brightening in intensity spectra emitted from numerous rings. In the energy domain of Fig. 5 continuum limb brightening is apparently correlated with the reverse emission in both resonance lines of iron. For the model presented in the middle panel, lines emitted from innermost rings are in absorption, and we simultaneously observe the usual limb darkening.
 |
Fig. 6 Broad-band intensity spectra integrated over the disk surface for all unilluminated disk models for eight viewing angles. The shape of continuum is affected by several spectral edges and iron-line complex around 6.9 keV. Depending on the accretion rate and spin of the black hole, we can follow how limb darkening changes with energy. |
 |
Fig. 7 Profiles of resonance lines from helium-like and hydrogen-like iron, integrated over the disk surface for all unilluminated disk models. Neither kinematic nor general relativity effects were taken into account. |
4.3. Disk-integrated spectra
At the last step of computations we integrate spectra emitted from individual rings over the disk surface according to the usual formula:  (7)where n is a ring number, μ the cosine of viewing angle, and ΔRn the width of the nth ring.
(7)where n is a ring number, μ the cosine of viewing angle, and ΔRn the width of the nth ring.
Figure 6 presents continuum spectra integrated over the disk surface for all nonirradiated models. The lefthand part of each panel displays the featureless UV, optical, and near infrared spectrum of disk, whereas the righthand part reaches hard X-rays and the iron line region. All spectra show limb darkening over the full range of energies. This is clearly seen in Fig. 7: intensity edge on (solid red line) is much lower than face on intensity (solid black line).
Resonance iron lines always appear in absorption for nonirradiated models (Fig. 7). They are very deep; i.e., the central intensity in the line can drop almost three orders of magnitude (panel a) as compared to the continuum level. Our code takes pressure broadening into account of all resonance lines, and particulary Lyα line of He-like iron can be very wide, as seen in panels c and e. Such prominent lines can certainly be detected in current X-ray observations (Kubota et al. 2007). Accretion disks with the highest effective temperature do not show strong iron lines in absorption, and iron is fully ionized for the hottest model (see Panel d).
 |
Fig. 8 Broad-band intensity spectra integrated over the disk surface for all irradiated disk models for eight viewing angles. The shape of continuum is extended toward hard X-rays due to both thermal emission of hot atmospheric zone and the radiation from the external source reflected by Compton scattering. |
 |
Fig. 9 Iron-line complex in the energy range 6.3−7.2 keV, integrated over the disk surface for all illuminated disk models. In three upper panels, Lyman alfa lines of helium-like iron (6.7 keV) and of hydrogen-like iron (6.9 keV) are in emission, which is caused by the layer of temperature invertion in the uppermost atmosphere. |
Continuum spectra of the same disk models with external irradiation are displayed in Fig. 8. All spectra exhibit Compton reflection bump in hard X-rays. The relative position of Compton reflection with the UV/X-ray disk bump depends on the accretion rate and black hole spin. External irradiation causes shift to limb brightening in the whole region of the Compton reflection bump. For low accretion rate and nonrotating black hole, limb brightening appears also in the visible and near infrared spectral regions (panels a and c in Fig. 8).
The iron-line complex for illuminated accretion disk models is presented in Fig. 9. Its structure is rather complicated, and its properties, i.e. line absorption/emission and limb darkening/brightening, do not depend on the accretion rate and the black hole spin in a straightforward way.
Lines from hellium-like hydrogen-like iron appear in emission only for low accretion rates. For the accretion rate ṁ = 1, those lines are in absorption. The higher level of irradiation may change this into emission, but this depends on the shape of the illuminating radiation. Increasing the soft X-ray photon number leads to efficient Compton down-scattering, which effectively cools down an already hot atmosphere in Galactic black hole binaries (see Sect. 4.1).
Resonance lines in emission presented in panel b are very wide and do not show any limb brightening. We suppose that this wide profile is caused by Compton scattering in hot atmosphere. As expected, model presented in panel d is featureless.
The important result of our paper is that in models with lower effective temperature, cold fluorescent Kα and Kβ lines are emitted. These lines are strong enough to contribute to the final iron-line complex. In our code we assume that the cold fluorescent Kα line has fixed energy 6.4 keV. But this energy depends on detailed ionization structure of iron atoms, and we shall discuss this problem in a forthcoming paper.
5. Summary
In this paper we have presented model atmospheres and intensity spectra for a set of accretion slim disks around black holes in Galactic black hole binaries. Model atmospheres were computed for various accretion rates and the spin of the black hole. Our computations include the effects of Compton scattering and external irradiation by an X-ray lamp. Spectra were obtained for a large number of individual rings, depending on the particular model, and the average number is 14. Outgoing intensity spectra were computed for a wide energy range from infrared to hard X-rays, up to 400 keV. The results presented in our previous paper (RM08) were calculated for SS disk global models, whereas the present paper dealt with slim disks with advection.
We demonstrated that the external irradiation develops a huge temperature rise in the outermost layers of disk atmospheres. The effect is most prominent in cases where the atmosphere has a lower effective temperature (in the outer and the innermost rings of our slim disk models). In those colder rings, strong Kα and Kβ fluorescent lines of iron are emitted. Results of the paper also demonstrate that the external irradiation causes a change of limb darkening of a nonirradiated disk to limb brightening particularly in the hard X-ray region. This implies that accretion disks seen edge on are brighter in X-rays than disks seen face on.
Our models clearly show that it is rather difficult to obtain strong hot iron resonance lines in emission for high accretion rates. This is because the disk atmospheres in Galactic black hole binaries are generally very hot. In such a situation, iron can be fully ionized and produces no line features. For low accretion rates, resonance iron lines appear in emission, when the heating by Comptonization of external photons causes a huge temperature rise.
Our results differ from previously computed spectra from constant density slabs of 10 Thomson optical depths (Ross & Fabian 2007; García & Kallman 2010). These papers did not take the possibility of the resonance iron lines formation into account in hot atmospheres of the accretion disk around a stellar black hole. In both cases iron lines only appear in emission.
Results of this paper show that both resonance iron X-ray lines can be formed in absorption for hot accretion disk atmospheres in GBHc. This is another possibility for explaining observations of those absorption lines in some black hole transients (Kubota et al. 2007, and references therein).
Moreover, iron line profiles computed at the source must always be pressure-broadened, and their profiles deviate from the Gaussian shape. Most of emission and absorption line profiles are not Gaussian (Figs. 7 and 9). For the same accretion rate, iron line profiles differ for the two values of spin considered in our paper (panels a − c, c in Fig. 9). This should be taken into account when fitting black hole spin to observe iron lines.
Acknowledgments
This research was supported by the Polish Ministry of Science and Higher Education grant No. N N203 511638.
References
- Abramowicz, M. A., Czerny, B., Lasota, J. P., & Szuszkiewicz, E. 1988, ApJ, 332, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Basko, M. M. 1978, ApJ, 223, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., Done, C., & Blaes, O. M. 2006, ApJ, 647, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Iaria, R., Méndez, M., et al. 2005, ApJ, 623, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Doerrer, T., Riffert, H., Staubert, R., & Ruder, H. 1996, A&A, 311, 69 [NASA ADS] [Google Scholar]
- Dotani, T., Inoue, H., Mitsuda, K., et al. 1997, ApJ, 485, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Vaughan, S., Nandra, K., et al. 2002, MNRAS, 335, L1 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., & Kallman, T. R. 2010, ApJ, 718, 695 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Gierlinski, M., Zdziarski, A. A., Done, C., et al. 1997, MNRAS, 288, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Guilbert, P. W. 1981, MNRAS, 197, 451 [NASA ADS] [Google Scholar]
- Hawley, J. F., Balbus, S. A., & Stone, J. M. 2001, ApJ, 554, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Hubeny, V. 1997, ApJ, 484, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., Blaes, O., Krolik, J. H., & Agol, E. 2001, ApJ, 559, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, K., Fabian, A. C., Young, A. J., Inoue, H., & Matsumoto, C. 1999, MNRAS, 306, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M. O., & Oliver, J. H. 1979, J. Phys. Chem. Ref. Data, 8, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., Dotani, T., Cottam, J., et al. 2007, PASJ, 59, 185 [NASA ADS] [Google Scholar]
- Kubota, A., Done, C., Davis, S. W., et al. 2010, ApJ, 714, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., & Netzer, H. 1989, MNRAS, 238, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Madej, J. 1991, ApJ, 376, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Madej, J., & Różańska, A. 2000, A&A, 363, 1055 [NASA ADS] [Google Scholar]
- Madej, J., & Różańska, A. 2004, MNRAS, 347, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Majczyna, A., Madej, J., Joss, P. C., & Różańska, A. 2005, A&A, 430, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malkan, M. A. 1983, ApJ, 268, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Fabian, A. C., & Ross, R. R. 2000, MNRAS, 313, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar atmospheres, 2nd Ed. (San Francisco: W. H. Freeman and Co.), 650 [Google Scholar]
- Miller, J. M., Fabian, A. C., Reynolds, C. S., et al. 2004, ApJ, 606, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Miniutti, G., Fabian, A. C., & Miller, J. M. 2004, MNRAS, 351, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Nandra, K., & Pounds, K. A. 1994, MNRAS, 268, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 444, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, in Black Holes, Les Astres Occlus, ed. C. Dewitt, & B. S. Dewitt, 343 [Google Scholar]
- Ohsuga, K. 2007, ApJ, 659, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Nandra, K., Stewart, G. C., George, I. M., & Fabian, A. C. 1990, Nature, 344, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Nandra, K., George, I. M., et al. 2004, ApJ, 602, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., & Begelman, M. C. 1997, ApJ, 488, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 1993, MNRAS, 261, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2007, MNRAS, 381, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A., & Madej, J. 2001, Adv. Space Res., 28, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A., & Madej, J. 2008, MNRAS, 386, 1872 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A., Dumont, A.-M., Czerny, B., & Collin, S. 2002, MNRAS, 332, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Sa¸dowski, A.,Abramowicz, M., Bursa, M., et al. 2011, A&A, 527, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shields, G. A. 1978, Nature, 272, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Shimura, T., & Takahara, F. 1993, ApJ, 419, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V., & Werner, K. 2007, A&A, 466, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Laurent, P., & Shaposhnikov, N. 2009, ApJ, 700, 1831 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, S., Sako, M., Ishida, M., et al. 2003, ApJ, 597, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Yaqoob, T., Murphy, K. D., Griffiths, R. E., et al. 2007, PASJ, 59, 283 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Radial dependence of vertical gravity (upper panel) and effective temperature (lower panel) in our slim disk models for three accretion rates: ṁ = 0.01, 0.1, and 1, denoted as black, blue, and red respectiverly. Two dashed lines (blue and black) represent models for which we assume that the spin of a black hole equals 0.98. Thin horizontal lines mark the position of horizon and ISCO for rotating (dashed line) and nonrotating black holes (solid line). Points mark annuli for which detailed radiative transfer computations were performed. |
| In the text | |
 |
Fig. 2 Vertical temperature structure for various rings in three unilluminated disk models. Models differ by accretion rate ṁ and dimensionless spin of the black hole a. Curves are labeled by the distance from the black hole, R. In all cases we observe temperature rise in the outermost layers of atmosphere due to Compton scattering (see text for details). |
| In the text | |
 |
Fig. 3 Comparison of the temperature structure in three disk models before (black line) and after (red line) illumination by external radiation in the form of a power law. Results are shown for various distances from the black hole. |
| In the text | |
 |
Fig. 4 Outgoing intensity spectra from individual rings in four unilluminated disk models at different accretion rates and black hole spins. Spectra are shown in the energy range corresponding to the resonanse lines from hydrogen and helium-like iron. Spectra are shifted along the vertical axis in order to demonstrate the evolution of lines with distance from the black hole (marked on the right vertical axis). The limb darkening effect, where intensity from “face-on” disk (black solid line) is higher than intensity from “edge-on” disk (red solid line), is observed in all cases, except in some line cores. |
| In the text | |
 |
Fig. 5 Outgoing intensity X-ray spectra for the sample of irradiated accretion disks. Spectra are shifted along vertical axis to demonstrate the evolution of iron-line complex with distance from the black hole (marked on the right vertical axis). |
| In the text | |
 |
Fig. 6 Broad-band intensity spectra integrated over the disk surface for all unilluminated disk models for eight viewing angles. The shape of continuum is affected by several spectral edges and iron-line complex around 6.9 keV. Depending on the accretion rate and spin of the black hole, we can follow how limb darkening changes with energy. |
| In the text | |
 |
Fig. 7 Profiles of resonance lines from helium-like and hydrogen-like iron, integrated over the disk surface for all unilluminated disk models. Neither kinematic nor general relativity effects were taken into account. |
| In the text | |
 |
Fig. 8 Broad-band intensity spectra integrated over the disk surface for all irradiated disk models for eight viewing angles. The shape of continuum is extended toward hard X-rays due to both thermal emission of hot atmospheric zone and the radiation from the external source reflected by Compton scattering. |
| In the text | |
 |
Fig. 9 Iron-line complex in the energy range 6.3−7.2 keV, integrated over the disk surface for all illuminated disk models. In three upper panels, Lyman alfa lines of helium-like iron (6.7 keV) and of hydrogen-like iron (6.9 keV) are in emission, which is caused by the layer of temperature invertion in the uppermost atmosphere. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


