| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014833 | |
| Published online | 10 February 2011 | |
Research Note
The progenitor of binary millisecond radio pulsar PSR J1713+0747
1
Department of PhysicsShangqiu Normal University,
476000
Shangqiu, PR China
e-mail: chenwc@nju.edu.cn
2
School of Physics and State Key Laboratory of Nuclear Physics and
Technology, Peking University, 100871
Beijing, PR
China
3
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing
University), Ministry of Education, 210093
Nanjing, PR
China
4
Facultad de Ciencias Astronómicas y Geofísicas,
UNLP, Paseo del Bosque S/N, La Plata
B1900 FWA,
Argentina
e-mail: panei@fcaglp.unlp.edu.ar
5
Instituto de Astrofísica de La Plata (CCT La Plata),
CONICET-UNLP,
Argentina
Received:
21
April
2010
Accepted:
10
January
2011
Context. PSR J1713+0747 is a binary system comprising millisecond radio pulsar with a spin period of 4.57 ms, and a low-mass white dwarf (WD) companion orbiting the pulsar with a period of 67.8 days. Using the general relativistic Shapiro delay, the masses of the WD and pulsar components were previously found to be 0.28 ± 0.03 M⊙ and 1.3 ± 0.2 M⊙ (68% confidence), respectively.
Aims. Standard binary evolution theory suggests that PSR J1713+0747 evolved from a low-mass X-ray binary (LMXB). Here, we test this hypothesis.
Methods. We used a binary evolution code and a WD evolution code to calculate evolutionary sequences of LMXBs that could result in binary millisecond radio pulsars such as PSR J1713+0747.
Results. During the mass exchange, the mass transfer is nonconservative. Because of the thermal and viscous instabilities developing in the accretion disk, the neutron star accretes only a small part of the incoming material. We find that the progenitor of PSR J1713+0747 can be modelled as an LMXB including a donor star with mass 1.3 − 1.6 M⊙ and an initial orbital period ranging from 2.40 to 4.15 days. If the cooling timescale of the WD is 8 Gyr, its present effective temperature is between 3870 and 4120 K, slightly higher than the observed value. We estimate a surface gravity of Log(g) ≈ 7.38 − 7.40.
Key words: stars: low-mass / pulsars: general / white dwarfs
© ESO, 2011
1. Introduction
Since the first X-ray source Sco X-1 was discovered (Giacconi et al. 1962), it was proposed that the strong Galactic X-ray sources were accreting neutron stars or black holes in binary systems (Zeldovich & Guseynov 1966; Novikov & Zel’Dovitch 1966; Shklovskii 1967). These sources have significant higher flux in X-ray than other wavelengths. Over 90% of strong Galactic X-ray sources can be classified in two kinds as follows: high-mass X-ray binaries and low-mass X-ray binaries (LMXBs). The latter consists of a neutron star or a black hole and a low-mass donor star (≲1−2 M⊙).
The mechanisms that drive mass transfer in LMXBs depend on the initial separations of the binary components (Bhattacharya & van den Heuvel 1991). In narrow systems with an orbital period (Porb) less than two days, mass transfer is driven by angular momentum loss due to gravitational radiation and magnetic braking. However, mass transfer is driven by the evolution of the secondary in relatively wide LMXBs (Porb ≳ 2 d). In LMXBs, mass accretion onto neutron star causes a magnetic field decay and spins it up to a short spin period ( ≲ 20 ms). It is believed that circular binaries including millisecond radio pulsar and He or CO white dwarfs (WDs) are formed as a result of long-term mass accretion (Alpar et al. 1982; Stairs 2004). The discovery of the first millisecond X-ray pulsar in LMXB SAX 1808.4-3658 strongly supports this scenario (Wijnards & van der Klis 1998).
Through a survey for millisecond pulsars with the 305 m Arecibo radio telescope, 9 have discovered PSR J1713+0747. This pulsar has a spin period of 4.57 ms. It is in a circular orbit of 67.8 days and has a low-mass WD as companion. It has a weak magnetic field of 1.9 × 108 G and a spin-down age of 8.9 ± 1.0 Gyr, so is an older neutron star. By detecting the general relativistic Shapiro delay, the neutron star and WD were set up as the low limits for the masses of 1.2 M⊙ and 0.27 M⊙, respectively (Camilo et al. 1994).
Through observations for 12 years between April 1992 and May 2004, 343 pulse times of arrival for PSR J1713+0747 were recorded with uncertainties down 200 nanosecond. These timing data can result in the measurement of the Shapiro delay, which can constrain the mass of the WD M2 and the inclination of the orbit i. The observational data constrained the masses of the pulsar to 1.3 ± 0.2 M⊙ and the WD to 0.28 ± 0.03 M⊙ (68% confidence, Splaver et al. 2005).
It is clear that PSR J1713+0747 is a recycled pulsar, because it gained mass and angular
momentum from its donor star, the progenitor of the WD (Alpar
et al. 1982). Assuming the mass of the WD is equal to the helium core mass of its
progenitor, binary evolution theory has presented a peculiar relation between the orbital
period Porb and the mass of WD M2
(Rappaport et al. 1995; Tauris & Savonije 1999; Podsiadlowski
et al. 2002). According to this relation, Tauris & Savonije (1999) obtained the
range of the WD mass for PSR J1713+0747,
0.31 M⊙ < M2 < 0.34 M⊙.
Later on, M2 was constrained in the range of
0.30 − 0.35 M⊙ (Pfahl et al.
2002). After adopting the predicted value by the theoretical relation of
Porb − M2, the pulsar has a
somewhat higher mass, 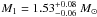 (68% confidence) (Splaver et al. 2005).
(68% confidence) (Splaver et al. 2005).
Assuming that the neutron star accretes 10 % of the material coming from the donor star, 3 have calculated the evolution of PSR J1713+0747 progenitor to fit its component masses and the orbital period. Their results show that the progenitor of PSR J1713+0747 may be an LMXB with initial masses of M1 = 1.4 M⊙ and M2 = 1.5 M⊙ and an initial orbital period of Pi = 3.10 d (Z = 0.02) or Pi = 3.05 d (Z = 0.01). Adopting a semi-analytic approach, Chen et al. (2006) have also performed binary evolution calculations to account for the component masses and the orbital period of PSR J1713+0747.
In this paper, where we employ a detailed stellar evolutionary code and a WD evolutionary code, we attempt to simulate the evolutionary history of the progenitor of binary millisecond radio pulsar PSR J1713+0747. The structure of this paper is organized as follows. In Sect. 2, we describe the stellar evolutionary codes, input physics in the binary evolution calculations, and the WD evolutionary code. Numerically calculated results for the evolutionary sequences of binary system resulting in the birth of PSR J1713+0747 are presented in Sect. 3. Finally, we discuss and summarize our results in Sect. 4.
2. Stellar evolutionary code and input physics
By employing an updated version of the stellar evolutionary code developed by 6; 7 (see Han et al. 1994; Pols
et al. 1995), we investigated the evolution of LMXBs. The LMXBs consist of a main
sequence donor star with a mass of M2 and a neutron star with a
mass of M1. Radiative opacities are those from 19 and at low-temperature molecular opacities from 1. For the secondary star, we take a mixing-length
parameter of α = 2.0 and an effective Roche lobe radius given by 8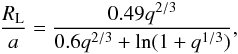 (1)where a and
q = M2/M1 are the
orbital separation and the mass ratio of the binary, respectively.
(1)where a and
q = M2/M1 are the
orbital separation and the mass ratio of the binary, respectively.
The mass transfer rate from the donor star via Roche lobe overflow can be written as
![\begin{equation} \dot{M}_{2}=-{\rm RMT}\cdot {\rm max}[0,(R_{2}/R_{\rm L}-1)^{3}]~\emph{M}_{\odot}\,\rm yr^{-1}, \end{equation}](/articles/aa/full_html/2011/03/aa14833-10/aa14833-10-eq33.png) (2)here we take RMT to be 1000 in the
calculations. We neglect the spin angular momentum of LMXBs because it is smaller compared
with the total orbital angular momentum of the system1.
In the calculations we consider two types of mechanisms for orbital angular momentum loss
from the binary system, they are described as follows.
(2)here we take RMT to be 1000 in the
calculations. We neglect the spin angular momentum of LMXBs because it is smaller compared
with the total orbital angular momentum of the system1.
In the calculations we consider two types of mechanisms for orbital angular momentum loss
from the binary system, they are described as follows.
2.1. Orbital angular momentum loss mechanisms
2.1.1. Magnetic braking
The low-mass main-sequence donor stars in LMXBs were braked by the coupling between the magnetic field and the stellar winds (Verbunt & Zwaan 1981). The loss of specific angular momentum in stellar winds is very large because the outflowing ionized particles are bound in the magnetic field lines to corotate with the stars out to the magnetospheric radius (see Weber & Davis 1967; Mestel & Spruit 1987; Kalogera 1999). In LMXBs, the spin angular momentum loss of the donor star by magnetic braking causes its spin-down, while the tidal interaction between two components would continuously act to spin the donor star back up into corotation with the orbital motion. Because the spin-up of the donor star consumes the orbital angular momentum, magnetic braking indirectly extracts the orbital angular momentum of LMXBs.
A standard magnetic braking model for the angular momentum loss is widely applied in
studying the evolution of cataclysmic variables, and the angular momentum loss rate can
be written as (Rappaport et al. 1983)
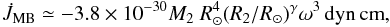 (3)where R2 is the
radius, ω the angular velocity of the donor star, and
γ is a dimensionless parameter in the range of zero to four.
(3)where R2 is the
radius, ω the angular velocity of the donor star, and
γ is a dimensionless parameter in the range of zero to four.
However, observations based on rapidly rotating stars with a spin period less than two
to five days in young open clusters, indicate that the standard magnetic braking
description should overestimate the angular momentum loss rate (Queloz 1998; Andronov et al.
2003). 21 propose the induced magnetic
braking model, and the angular momentum loss rate is given by
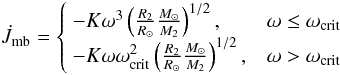 (4)where
K = 2.7 × 1047 g cm2 (Andronov et al. 2003). Observations show that there is a saturation
level in the angular momentum loss, and ωcrit is the
critical angular velocity at which the angular momentum loss rate reaches a saturated
state. 14 suggest that
ωcrit is inversely proportional to the convective
turbulent timescale in the star at 200 Myr age,
(4)where
K = 2.7 × 1047 g cm2 (Andronov et al. 2003). Observations show that there is a saturation
level in the angular momentum loss, and ωcrit is the
critical angular velocity at which the angular momentum loss rate reaches a saturated
state. 14 suggest that
ωcrit is inversely proportional to the convective
turbulent timescale in the star at 200 Myr age,
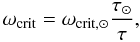 (5)where
ωcrit,⊙ = 2.9 × 10-5 Hz,
τ⊙, and τ are the convective turbulent
timescales of the Sun and donor star, respectively (Krishnamurthi et al. 1997).
(5)where
ωcrit,⊙ = 2.9 × 10-5 Hz,
τ⊙, and τ are the convective turbulent
timescales of the Sun and donor star, respectively (Krishnamurthi et al. 1997).
2.1.2. Accretion disk instability and mass loss
According to the mass of PSR J1713+0747 inferred by its Shapiro delay, there is a large
amount of transfer material that should be lost from this binary system during the mass
exchange. Either the accretion disk instabilities (Pringle 1981; van Paradijs 1996) or the
propeller effect (Illarionov & Sunyaev 1975)
may be responsible for the mass loss even for sub-Eddington accretion. During the mass
transfer via Roche Lobe overflow, the transferring material would form an accretion disk
around the neutron star. It is well known that disk accretion in LMXBs may suffer
thermal and viscous instability, if the effective temperature in the disk is below the
hydrogen ionization temperature about 6500 K (van
Paradijs 1996; King et al. 1997; Lasota 2001). This corresponds to a critical
mass-transfer rate under which the accretion disk is unstable. This critical
mass-transfer rate is (van Paradijs 1996; Dubus et al. 1999)
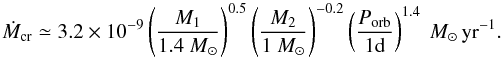 (6)When an accretion-disk instability occurs,
the accreting neutron star will become a transient X-ray source, experiencing
short-lived outbursts separated by long-term quiescence. When the mass transfer rate
− Ṁ2 is lower than Ṁcr, we
assume that the neutron star accretes only during outbursts, so the accretion rate is
(6)When an accretion-disk instability occurs,
the accreting neutron star will become a transient X-ray source, experiencing
short-lived outbursts separated by long-term quiescence. When the mass transfer rate
− Ṁ2 is lower than Ṁcr, we
assume that the neutron star accretes only during outbursts, so the accretion rate is
 , where
tout,tr are the outburst
timescale and the recurrence time, respectively. Introducing the duty cycle
f = tout/tr,
we have
Ṁac = −Ṁ2/f
[a typical duty cycle is in the range of 0.1–0.001 (King
et al. 2003)]. If
− Ṁ2 ≥ Ṁcr, the accretion
rate is Ṁac = −Ṁ2. In addition,
in both cases the mass growth rate of the neutron star Ṁ1 is
limited to the Eddington accretion rate ṀEdd, i.e.
, where
tout,tr are the outburst
timescale and the recurrence time, respectively. Introducing the duty cycle
f = tout/tr,
we have
Ṁac = −Ṁ2/f
[a typical duty cycle is in the range of 0.1–0.001 (King
et al. 2003)]. If
− Ṁ2 ≥ Ṁcr, the accretion
rate is Ṁac = −Ṁ2. In addition,
in both cases the mass growth rate of the neutron star Ṁ1 is
limited to the Eddington accretion rate ṀEdd, i.e.
![\begin{equation} \dot{M}_{1}=\min [\dot{M}_{\rm ac},\dot{M}_{\rm Edd}], \end{equation}](/articles/aa/full_html/2011/03/aa14833-10/aa14833-10-eq57.png) (7)where
ṀEdd ≈ 1.5 × 10-8 M⊙ yr-1
is the Eddington accretion rate of the neutron star.
(7)where
ṀEdd ≈ 1.5 × 10-8 M⊙ yr-1
is the Eddington accretion rate of the neutron star.
The transferred matter that exceeds the Eddington accretion rate is assumed to be
ejected in the vicinity of the neutron star. The matter forms an isotropic wind and
carries away the specific orbital angular momentum of the neutron star. Based on the
above assumptions, we can derive the angular momentum loss rate:
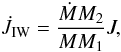 (8)where
J = a2μΩ is the total
orbital angular momentum of the LMXB with a circular orbit,
μ = M1M2/(M1 + M2),
M = M1 + M2,
and
Ṁ = Ṁ1 − Ṁac
are the reduced mass, the total mass, and the mass-loss rate of the binary system,
respectively.
(8)where
J = a2μΩ is the total
orbital angular momentum of the LMXB with a circular orbit,
μ = M1M2/(M1 + M2),
M = M1 + M2,
and
Ṁ = Ṁ1 − Ṁac
are the reduced mass, the total mass, and the mass-loss rate of the binary system,
respectively.
2.2. WD regime: the evolutionary code
When the LMXB becomes a detached system, the donor star evolves into an He-core WD. From this stage, during thermonuclear flashes scenario and in WD regime, we adopt the stellar evolutive code LPCODE (Althaus et al. 2005). The code is based on a detailed description of the main physical processes involved in the formation of WD. Radiative opacities are those from OPAL (including carbon- and oxygen-rich compositions) for arbitrary metallicity (Iglesias & Rogers 1996). These opacities are calculated for metallicities consistent with the diffusion predictions. During the WD cooling regime gravitational settling leads to metal-depleted outer layers. The equation of state is an updated version of that of 16. High-density conductive opacities and the various mechanisms of neutrino emission are taken from works of 13. Hydrogen burning is taken into account by considering a complete network of thermonuclear reaction rates corresponding to the proton-proton chain and CNO cycle. Nuclear reactions rates are taken from 5. We consider the evolution of the chemical abundance distribution caused by element diffusion during the WD regime. Our treatment of time-dependent diffusion is based on the multicomponent gas treatment presented by 4, for element diffusion scheme we considered the following nuclear species 1H, 3He, 4He, 12C, 14N, and 16O. Abundance changes are computed according to element diffusion and then to nuclear reactions and convective mixing.
In this work, we have computed the complete evolution of seven remnants arisen from binary systems as soon as the transfer of mass has ceased. The masses of these seven pre-WDs are listed in Table 1 (M2,f). The evolution of these WDs is continued until they arrive at a luminosity of Log(L/L⊙) ≈ −4.8.
3. Results
To study the characteristics of the progenitor of PSR J1713+0747, we calculated evolutionary sequences of many LMXBs. We consider both the angular momentum loss mechanisms described in Sect. 2.1, adopting the induced magnetic braking model (Eq. (4)) for the donor stars with mass less than 1.5 M⊙. Some initial input parameters were set as follows, the neutron star has a canonical mass of M1,i = 1.4 M⊙, the mass of the donor star M2,i is in the range of 1.0 − 2.0 M⊙ (with a solar metallicity of Z = 0.02), the duty cycle f = 0.01.
 |
Fig. 1 Evolution of the orbital period (solid curve) and the donor star mass (dashed curve) vs. evolutive timescale for LMXB. LMXB has a donor star with an initial mass of 1.5 M⊙ and an initial orbital period of 2.57 d. Horizontal dotted lines on the bottom of the figure correspond to the observed mass of WD with its error, and horizontal dotted line on the top of the figure represents the observed orbital period. |
The characteristic age of PSR J1713+0747 estimated by Splaver et al. (2005) is τPSR ≈ 8 Gyr. This implies that the WD has a cooling timescale τcool of approximately 8 Gyr since the end of the mass transfer episode. Based on different initial orbital period Porb,i, we stop the binary evolution calculation when the binary becomes a detached system and the donor star evolve into a WD. Subsequently, a WD evolutionary code (LPCODE) is applied to the donor star. If the final donor star mass is in the range of 0.25 to 0.31 M⊙, and the orbital period of the binary is approximately of 67.8 d, the corresponding binary was assumed to be the progenitor candidate of PSR J1713+0747.
Firstly, we calculated the evolutionary sequences of an LMXB with M2,i = 1.5 M⊙ and Porb,i = 2.57 d. In Figs. 1 and 2 we plot the evolution of orbital period and donor star mass, and the mass transfer rate and the neutron star mass, respectively. In the early phase, the orbital period decrease to be approximately 2.56 d due to magnetic braking even if there is no mass exchange. With nuclear evolution, the donor star fills its Roche lobe when its age is 2.54 Gyr. When M2 = 0.66 M⊙, and Porb = 9.66 d, the binary system detaches and mass transfer ceases about 4.9 Myr. This detached phase also is found in other studies for the evolution of LMXBs (Tauris & Savonije 1999; 10; Podsiadlowski et al. 2002). After the temporary shrinkage, the donor star fills its Roche lobe again and climbs the giant branch. When the age is 2.79 Gyr, the second Roche lobe overflow (RLOF) episode terminates. Hereafter, the donor star evolves to a helium WD and cools. The evolution end point is a binary pulsar with an orbital period of 68.3 d. The binary consists of an He-core WD of 0.3070 M⊙ and a neutron star of 1.5184 M⊙. Because the material is transferred from the more massive donor star to the less massive neutron star, the mass transfer proceeds initially on short thermal timescale about 10 Myr. In this phase, the mass transfer rate is in a range of 10-7 to 10-8 M⊙ yr-1, and the LMXB is a short-lived persistent X-ray source. Subsequently, the mass transfer occurs on a much longer nuclear timescale of 0.25 Gyr, with a rate of 10-9 or 10-8 M⊙ yr-1. This rate is always less than the critical mass transfer rate. Therefore, the progenitor of PSR J1713+0747 should be a transient X-ray source about 95% of all its life.
Calculated results for different initial input parameters.
In Fig. 3, we plot the evolutionary path of the donor star in the Hertzsprung-Russell diagram (HRD). After the donor star evolves into a pre-WD, a hydrogen thermonuclear flash occurs. During this stage the element diffusion is a key physical ingredient in obtaining a thin hydrogen envelope. We stress that thermonuclear flashes also occur in the absence of element diffusion, but in this case the residual hydrogen envelope is thick, according to 2 and 18. Figure 4 presents theoretical predicted relation between Porb,f and M2,f for binary radio pulsars. It is clear that our simulation result is consistent with the theoretical prediction.
 |
Fig. 2 Evolution of the mass transfer rate (solid curve) and the neutron star mass (dashed curve) with the evolutive timescale for the same LMXB of Fig. 1. The dotted curve represents the critical mass transfer rate, under which the disk accretion is unstable. The mass transfer rate has been slightly smoothed for clarity. |
 |
Fig. 3 Calculated evolutionary tracks in H – R diagram for the donor star with an initial mass of 1.5 M⊙. The open triangle, solid triangle, and open star indicate the beginning of RLOF, the end of the last episode of RLOF and the present situation of the donor star, respectively. |
 |
Fig. 4 Theoretical predicted relation between Porb,f and M2,f for binary radio pulsars. The solid curves and dashed curves correspond to the relations obtained by Rappaport et al. (1995) and Tauris & Savonije (1999). The open star sign represents our simulation result. |
To investigate the distribution of the initial donor star mass and orbital period for the progenitor system of PSR J1713+0747, we calculated the evolution of a large amount of LMXBs for different initial input parameters. Table 1 summarizes the calculated results. Assuming that the cooling timescale of the WD is τcool = 8 Gyr, as seen in Table 1 makes it clear that the donor star with an initial mass of M2,i = 1.0 − 1.2 M⊙ would require times in excess of the Hubble time in order to evolve into a dim WD like the one observed in PSR J1713+0747. Therefore, PSR J1713+0747 may originated from an LMXB with a donor star of M2,i = 1.3 − 1.6 M⊙ and an initial orbital period of Porb,i = 2.40 − 4.15 d. Thus with an age of τcool = 8 Gyr, we obtain WD effective temperatures in the range of ~ 3870 − 4120 K, approximately in agreement with the observational datum 3700 ± 100 K given by 15, 3 derived a value of 4320 ± 180 K and 4250 ± 250 K determined by 20. In addition, the luminosity of the WD was determined to be −4.171 ≤ Log(L/L⊙) ≤ − 4.047. Apparently, the final effective temperature of the WD in our calculations is sensitive to its cooling timescale, and a long cooling timescale can result in a low effective temperature. On the basis of these models with real history, we estimated the range of surface gravity for the WD in 7.386 ≤ Log(g) ≤ 7.401 (g in units of g cm-2). Detailed tabulations of our WD evolutionary sequences are available at http://www.fcaglp.unlp.edu.ar/~panei/papers.html.
Although the final mass of the neutron star (see Nos. 6 and 7 in Table 1) is slightly higher than the one derived by Splaver et al. 2005, it is still in the allowed mass
interval by theoretical orbital period - WD mass relation
(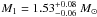 ). Though adopting various scenarios, our
results are approximately consistent with the ones derived by 3.
). Though adopting various scenarios, our
results are approximately consistent with the ones derived by 3.
4. Summary and discussion
In this paper, we attempt to carefully study the evolution history and the progenitor characteristics of PSR J1713+0747. Based on Eggleton’s stellar evolution code, we calculated the evolutionary sequences of a number of LMXBs to fit the observed data (M1,M2, and Porb) of PSR J1713+0747. For the WD regime we employed the stellar evolution code LPCODE (Althaus et al. 2005).
In calculations, angular momentum loss via magnetic braking is included if the mass of the donor star is less than 1.5 M⊙. The observations show that PSR J1713+0747 has only accreted less than 0.1 M⊙ from the donor star during evolution. Unstable mass transfer due to the thermal and viscous instability of the accretion disk may be responsible for the extensive mass loss2. Therefore, LMXBs may be transient X-ray sources for most of their life. If we adopt a duty cycle of 0.01, the progenitor of PSR J1713+0747 can be constrained to be an LMXB with an initial donor star of 1.3 − 1.6 M⊙ (Z = 0.02) and an initial orbital period of 2.40 − 4.15 d. Adopting a cooling timescale of 8 Gyr for the WD, our calculations show that at present its effective temperature is between 3870 and 4120 K. Compared with the results derived by 3, for Z = 0.02, the cooling timescale of the WD in our model is close to the spin-down age of the pulsar3. We obtained absolute magnitudes of MV ≈ 15.7 ± 0.4 and MI ≈ 13.8 ± 0.3 in the V and I bands, and inferred effective temperatures Teff ≈ 3301–4169 K and Teff ≈ 3946–4694 K. Detailed tabulations of our WD evolutionary sequences are available at http://www.fcaglp.unlp.edu.ar/~panei/papers.html.
Our accretion disk instability model successfully reproduces the orbital period and the mass of the WD. However, the effective temperature of the WD is slightly higher than observations, although we consider gravitational settling and chemical and thermal diffusion during the evolution of the WD (Panei et al. 2007). Employing Hubble Space Telescope (HST), 15 performed optical observations for the WD companion of PSR J1713+0747. Adopting the temperature calibration of (V − I) colour given by 17, they presented the effective temperature of the WD is Teff = 3700 ± 100 K. Assuming a blackbody spectrum, 11 fitted the HST data, and obtained Teff = 3430 ± 270 K. A long cooling timescale of the WD may be responsible for the discrepancy between our evolution results and the inferred value of observations. In this work we take τco = 8 Gyr (Splaver et al. 2005). However, it is very rough to estimate the spin-down age of the pulsar from τPSR = P/2Ṗ, where P and Ṗ are the spin period and the period derivative of the pulsar, respectively4. We expect that further spectroscopic and photometric observations can help us understand the evolutionary track of PSR J1713+0747.
As an alternative evolution channel, millisecond pulsars may also be formed by accretion-induced collapse (AIC) when the mass of the accreting ONe WD exceeds the Chandrasekhar mass of 1.4 M⊙ (Nomoto 1984; Nomoto 1986). Statistical analysis shows that the birthrate of LMXBs is 1–2 orders of magnitude lower than that of millisecond pulsars (Cote & Pylyser 1989; Lorimer 1995). The AIC channel was raised to interpret this birthrate discrepancy (Bailyn & Grindlay 1990). Based on a scenario including both the AIC of an accreting WD and unstable disk accretion, 22 propose that GRO J1744-28 may be evolved from a WD binary. Recently, the estimated birthrates of millisecond pulsars show that the often neglected AIC channel cannot be ignored (Hurley et al. 2010). Therefore, the formation possibility of PSR J1713+0747 via the AIC of a massive WD cannot be ruled out. We plan to explore the AIC channel for the formation and evolution of PSR J1713+0747.
Of course, there are many uncertainties in our input physics. Firstly, the orbital angular momentum loss plays a vital role in the evolution of LMXBs. Some mechanism of extracting angular momentum possibly exists besides magnetic braking and mass loss due to the accretion disk instability. For example, the propeller effect of the neutron star may carry away the specific orbital angular momentum at the magnetosphere of the neutron star (Illarionov & Sunyaev 1975). In addition, a circumbinary disk around LMXBs may also extract orbital angular momentum efficiently from the binary system (Spruit & Taam 2001; Taam & Spruit 2001). Secondly, our results strongly depend on duty cycles, which are poorly known. In this work, we take a constant duty cycle. However, duty cycles may change from one system to another (Lasota 2001), and change with the orbital period and the mass transfer rate. Finally, a gamma-ray flux caused by the interaction of the magnetic field of the neutron star with the accretion disk may drive a wind from the donor star by heating its outer layers; i.e., the donor star may be evaporated (van den Heuvel & van Paradijs 1988; Kluźiniak et al. 1988; Ruderman et al. 1989a; Ruderman et al. 1989b).
If we take typical parameters for the binary, such as
M1 = 1.4 M⊙,M2 = 1.0 M⊙,R1 = 106 cm,R2 = 1 R⊙,
the spin period of the NS is 1 ms, and the orbital period is
Porb = 3 d, the orbital angular momentum of the binary is
estimated to be
Jorb = 1.9 × 1052 g cm2s-1.
Assuming that the donor star corotates with the orbital rotation, we have
J1 = 7.0 × 1048 g cm2 s-1,
 (k2 ≈ 0.1 for
main-sequence stars, Dervişoǧlu et al. 2010), where
J1,J2 are the spin angular
momentum of the NS, and the donor star, respectively. It is clear that the orbital angular
momentum is three to four orders of magnitude greater than the spin angular momentum.
(k2 ≈ 0.1 for
main-sequence stars, Dervişoǧlu et al. 2010), where
J1,J2 are the spin angular
momentum of the NS, and the donor star, respectively. It is clear that the orbital angular
momentum is three to four orders of magnitude greater than the spin angular momentum.
Certainly, the propeller effect of the pulsar cannot be excluded (Illarionov & Sunyaev 1975).
3 propose that the WD needs 10.8 ± 2 Gyr to cool when Z = 0.02.
The standard spin-down age of the pulsar is ![\hbox{$\tau_{\rm PSR}=\frac{P}{(n-1)\dot{P}}[1-(P_{0}/P)^{n-1}]$}](/articles/aa/full_html/2011/03/aa14833-10/aa14833-10-eq149.png) , where P0 is
the initial period and n the braking index of the pulsar. When
P0 ≪ P and n = 3,
τPSR = P/2Ṗ. However, the
derived braking indice of several young radio pulsars are all less than 3 (Xu & Qiao 2001; Chen & Li 2006).
, where P0 is
the initial period and n the braking index of the pulsar. When
P0 ≪ P and n = 3,
τPSR = P/2Ṗ. However, the
derived braking indice of several young radio pulsars are all less than 3 (Xu & Qiao 2001; Chen & Li 2006).
Acknowledgments
We are grateful to the referee, Christopher A. Tout, for his constructive suggestions for improving this manuscript. We also thank Zhan-Wen Han and Xue-Fei Chen for their helpful discussions, and thank Stephen Justham for his help in improving the English of this manuscript. This work has been supported in part by the National Natural Science Foundation of China (Grant No 10873011), Program for Science & Technology Innovation Talents in Universities of Henan Province, and Innovation Scientists and Technicians Troop Construction Projects of Henan Province, China. We acknowledge the Facultad de Ciencias Astronómicas y Geofísicas (UNLP), Instituto de Astrofísica de La Plata (CCT La Plata, CONICET-UNLP) and Lic. H. Viturro for his technical support.
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andronov, N., Pinsonneault, M., & Sills, A. 2003, ApJ, 582, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Bailyn C. D., & Grindlay J. E. 1990, ApJ, 353, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., & De Vito, M. A. 2004, MNRAS, 352, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., Rohrmann, R. D., & De Vito, M. A. 2006, MNRAS, 366, 1520 [NASA ADS] [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Burgers, J. M. 1969, Flow Equations for Composite Gases (New York: Academic Press) [Google Scholar]
- Camilo, F., Foster, R. S., & Wolszczan, A. 1994, ApJ, 437, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 284 [Google Scholar]
- Chen, W.-C., & Li, X.-D. 2006, A&A, 450, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W.-C., Li, X.-D., & Wang, Z.-R. 2006, PASJ, 58, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Cote J., & Pylyser, E. H. P. 1989, A&A, 218, 131 [NASA ADS] [Google Scholar]
- Dervişoǧlu, A., Tout, C. A., & Ibanoǧlu, C. 2010, MNRAS, 406, 1071 [NASA ADS] [Google Scholar]
- Dubus, G., Lasota, J.-P., Hameury, J.-M., & Charles, P. 1999, MNRAS, 303, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, R. S., Wolszczan, A., & Camilo F. 1993, ApJ, 410, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Giacconi, R., Gursky, H., Paolini, F. R., & Rossi, B. B. 1962, Phys. Rev. Lett., 9, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, Ph., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Phinney, E. S. 1998, MNRAS, 294, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley J. R., Tout C. A., Wickramasinghe, D. T., Ferrario, L., & Kiel, P. D. 2010, MNRAS, 402, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Itoh, N., Mutoh, H., Hikita, A., & Kohyama, Y. 1992, ApJ, 395, 622 [NASA ADS] [CrossRef] [Google Scholar]
- ; Erratum: 1993, ApJ, 404, 418 [NASA ADS] [Google Scholar]
- Kalogera, V. 1999, ApJ, 521, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y.-C., & Demarque, P. 1996, ApJ, 457, 340 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Frank, J., Kolb, U., & Titter, H. 1997, ApJ, 484, 844 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Rolfe, D. J., & Schenker, K. 2003, MNRAS, 341, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźiniak, W., Ruderman, M., Shaham, J., & Tavani, M. 1988, Nature, 334, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997, ApJ, 480, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Lasota, J.-P. 2001, NewAR, 45, 449 [Google Scholar]
- Lundgren, S. C., Foster, R. S., & Camilo, F. 1996, in Pulsars: Problems and Progress (San Francisco), ASP Conf. Ser. 105, IAU Colloq., 160, 497 [NASA ADS] [Google Scholar]
- Lorimer, D. R. 1995, MNRAS, 274, 300 [NASA ADS] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Mestel, L., & Spruit, H. C. 1987, MNRAS, 226, 57 [Google Scholar]
- Monet, D. G., Dahn, C. C., Vrba, F. J., et al. 1992, AJ, 103, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1984, in Problems of Colalpse and Numerical Relativity, ed. D. Bancel, & M. Sifnore (Dordrecht: Reidel), 89 [Google Scholar]
- Nomoto K. 1986, in Accretion Processes in Astrophysics, ed. J. Audouze, J. Tran Thanh Van (Gif-sur-Yvette: Éditions Frontières), 137 [Google Scholar]
- Novikov, I. D., & Zel’Dovitch, Y. B. 1966, Nuova Cimento Sup., 4, 810 [Google Scholar]
- Panei, J. A., Althaus, L. G., Chen, X., & Han, Z. 2007, MNRAS, 382, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Pfahl, E., Rappaport, S., & Podsiadlowski, Ph. 2002, ApJ, 573, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, Ph., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Allain, S., Mermilliod, J. C., Bouvier, J., & Mayor, M. 1998, A&A, 335, 183 [NASA ADS] [Google Scholar]
- Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Podsiadlowski, Ph., Joss, P. C., Di Stefano, R., & Han, Z. 1995, MNRAS, 273, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M., Shaham, J., & Tavani, M. 1989a, ApJ, 336, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M., Shaham, J., Tavani, M., & Fichler, D. 1989b, ApJ, 343, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Schönberner, D., Driebe, T., & Blöcker, T. 2000, A&A, 356, 929 [NASA ADS] [Google Scholar]
- Shklovskii, I. 1967, ApJ, 148, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Sills, A., Pinsonneault, M. H., & Terndrup, D. M. 2000, ApJ, 534, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Splaver, E. M., Nice, D. J., Stairs, I. H., et al. 2005, ApJ, 620, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Taam, R. E. 2001, ApJ, 548, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Stairs, I. H. 2004, Science, 304, 547 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Taam, R. E., & Spruit, H. C. 2001, ApJ, 561, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., & Savonije, G. J. 1999, A&A, 350, 928 [NASA ADS] [Google Scholar]
- van den Heuvel, E. P. J., & van Paradijs, J. 1988, Nature, 334, 227 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J. 1996, ApJ, 464, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]
- Weber, E. J., & Davis, L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnards, R., & van der Klis, M. 1998, Nature, 394, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, R. X., & Qiao, G. J. 2001, ApJ, 561, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X.-J., & Li, X.-D. 2009, A&A, 495, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeldovich, Ya. B., & Guseynov, O. H. 1966, ApJ, 144, 840 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of the orbital period (solid curve) and the donor star mass (dashed curve) vs. evolutive timescale for LMXB. LMXB has a donor star with an initial mass of 1.5 M⊙ and an initial orbital period of 2.57 d. Horizontal dotted lines on the bottom of the figure correspond to the observed mass of WD with its error, and horizontal dotted line on the top of the figure represents the observed orbital period. |
| In the text | |
 |
Fig. 2 Evolution of the mass transfer rate (solid curve) and the neutron star mass (dashed curve) with the evolutive timescale for the same LMXB of Fig. 1. The dotted curve represents the critical mass transfer rate, under which the disk accretion is unstable. The mass transfer rate has been slightly smoothed for clarity. |
| In the text | |
 |
Fig. 3 Calculated evolutionary tracks in H – R diagram for the donor star with an initial mass of 1.5 M⊙. The open triangle, solid triangle, and open star indicate the beginning of RLOF, the end of the last episode of RLOF and the present situation of the donor star, respectively. |
| In the text | |
 |
Fig. 4 Theoretical predicted relation between Porb,f and M2,f for binary radio pulsars. The solid curves and dashed curves correspond to the relations obtained by Rappaport et al. (1995) and Tauris & Savonije (1999). The open star sign represents our simulation result. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


