EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 526 (February 2011) A&A, 526 (2011) A109 Full HTML
Free Access
Issue
A&A
Volume 526, February 2011
Article Number A109
Number of page(s) 4
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201016156
Published online 07 January 2011

© ESO, 2011

1. Introduction

Several observations can establish limits to the variation of different fundamental constants, such as the atomic clocks (Bize et al. 2003; Fischer et al. 2004; Peik et al. 2004; Prestage et al. 1995; Sortais et al. 2000; Marion et al. 2003), the Oklo natural fission reactor (Damour & Dyson 1996; Fujii et al. 2000) and the analysis of the spectra of quasar absorption systems. These astronomical observations suggest a possible variation of the fine structure constant and the electron-to-proton mass ratio (Webb et al. 1999, 2001; Murphy et al. 2001a,b, 2003; Ivanchik et al. 2005; Reinhold et al. 2006; Tzanavaris et al. 2007). However, another analysis of similar astronomical data gives null variation of the fine structure constant (Martínez Fiorenzano et al. 2003; Quast et al. 2004; Bahcall et al. 2004; Srianand et al. 2004; King et al. 2008; Thompson et al. 2009; Malec et al. 2010).

The Big Bang nucleosynthesis (BBN) is a useful tool to study the time variation of fundamental constants, such as the fine structure constant, α, the Higgs vacuum expectation value, v, and the Planck mass, among others. Several theories that attempt to unify the four fundamental interactions, such as super-strings (Wu & Wang 1986; Barr & Mohapatra 1988; Maeda 1988; Damour & Polyakov 1994; Damour et al. 2002a,b), brane world (Youm 2001a,b; Brax et al. 2003; Palma et al. 2003) and Kaluza-Klein theories (Kaluza 1921; Klein 1926; Weinberg 1983; Gleiser & Taylor 1985; Overduin & Wesson 1997), allow fundamental constants to vary within cosmological time scales. The time variation of several fundamental constants was studied by Campbell & Olive (1995), Bergström et al. (1999), Ichikawa & Kawasaki (2002), Nollett & Lopez (2002), Yoo & Scherrer (2003), Müller et al. (2004), Ichikawa & Kawasaki (2004), Cyburt et al. (2005), Landau et al. (2006), Coc et al. (2007), Chamoun et al. (2007), Mosquera et al. (2008), Landau et al. (2008), Landau & Scóccola (2010), Mosquera & Civitarese (2010), Civitarese et al. (2010), among others.

If the Higgs vacuum expectation value acquires a different value during BBN than the present one, the electron mass, the proton-neutron mass difference, the Fermi constant, and the deuterium binding energy, ϵD, will be different from the corresponding actual values. Several authors have studied the dependence of ϵD on v (Flambaum & Shuryak 2002, 2003; Dmitriev & Flambaum 2003; Beane & Savage 2003; Epelbaum et al. 2003; Yoo & Scherrer 2003; Dmitriev et al. 2004; Flambaum & Wiringa 2007; Berengut et al. 2010; Mosquera & Civitarese 2010; Civitarese et al. 2010).

In this work, we study the effects of a possible variation of the fine structure constant and of the Higgs vacuum expectation value, considering a fixed value of the strong-coupling constant ΛQCD. To perform the calculation of the primordial abundances, we use the linear dependence of ϵD with v discussed in Mosquera & Civitarese (2010); Civitarese et al. (2010). We use observational data of D, 4He, and 7Li to obtain constraints on the variation of the participant fundamental constants. We also perform an analysis of the sensibility of these constraints on the lithium abundance and the dependencies between ϵD and v.

This work is organized as follows. In Sect. 2 we calculate the primordial abundances and obtain constraints on the joint variation of α and v. The conclusions are presented in Sect. 3.

2. Bounds from BBN

In this section we study the effect of a possible variation of the fine structure constant, α, and of the Higgs vacuum expectation value, v, during primordial nucleosynthesis. If α acquires a value different from the actual one, the neutron-to-proton ratio, the neutron-proton mass difference, the weak decay rates, and the cross sections of several reactions involved during BBN would be different from current estimates (Landau et al. 2008), and consequently, the primordial abundances would be modified. The electron mass, the Fermi constant, the neutron-proton mass difference, the weak decay rates, the masses of light nuclei, the deuterium binding energy, ϵD, and the initial abundance of deuterium will be modified if the Higgs vacuum expectation value varies with time (Landau et al. 2008; Mosquera & Civitarese 2010).

The dependence of the deuterium-binding energy on the Higgs vacuum expectation value is model dependent (Flambaum & Wiringa 2007). In this work, we use the results obtained by Mosquera & Civitarese (2010); Civitarese et al. (2010). The authors had calculated the constant of proportionality, κ, which relates ϵD and v, for four different nucleon-nucleon potentials (Argonne v18 potential, Bonn potential, Nijmegen potential and Reid 93 potential), 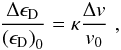(1)where 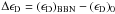, and Δv = vBBN − v0. The subindexes BBN and 0 indicate the value of the constant at primordial nucleosynthesis and at the present time, respectively. In Table 1 we present the values of κ obtained by Mosquera & Civitarese (2010); Civitarese et al. (2010).

Table 1

Values of the coefficient κ of Eq. (1).

The Argonne v18 potential includes an electromagnetic interaction (Wiringa et al. 1995), proportional to the fine structure constant. We modified this potential to include the variation of the fine structure constant and performed the calculation of ϵD. We obtained the relation .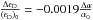

In order to calculate the primordial abundances, we modified the code developed by Kawano (Kawano 1988, 1992) for each nucleon-nucleon potential of Table 1 (Mosquera & Civitarese 2010; Civitarese et al. 2010). For details about the corrections introduced in the public version of Kawano’s code see Mosquera et al. (2008); Landau et al. (2008); Mosquera & Civitarese (2010).

The WMAP data are able to constraint the baryon density ΩBh2 (related to the baryon-to-photon ratio ηB) with great accuracy, but there is still some degeneracy between the model parameters, namely: one is dealing with a parametric hypersurface defined by the values of ΩBh2, ΩCDMh2 (dark matter density in units of the critical density), Θ (gives the ratio of the comoving sound horizon at decoupling to the angular diameter distance to the surface of last scattering), τ (reionization optical depth), ns (scalar spectral index), As (amplitude of the density fluctuations). For this reason we computed the light nuclei abundances for the following cases:

  • i)

    variation of α and v allowing ηB vary,

  • ii)

    variation of α and v keeping ηB fixed at WMAP value 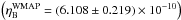(Spergel et al. 2003, 2007).

In order to obtain the best-fit values for the parameters, we performed a χ2-test to compare the theoretical abundances and the observational data.

The observational data for D were extracted from Burles & Tytler (1998a,b), O’Meara et al. (2001), Pettini & Bowen (2001), Levshakov et al. (2002), Kirkman et al. (2003), Crighton et al. (2004), O’Meara et al. (2006), Pettini et al. (2008), Ivanchik et al. (2010).

We used the data from Izotov et al. (2006), Peimbert et al. (2007), Izotov et al. (2007), Izotov & Thuan (2010) for 4He, and for 7Li we considered the data given by Bonifacio & Molaro (1997), Molaro et al. (1997), Ryan et al. (2000), Bonifacio et al. (2002), Boesgaard et al. (2005), Asplund et al. (2006), Bonifacio et al. (2007), Hosford et al. (2009). Regarding the consistency of the data, we followed the treatment of Yao et al. (2006) and increased the errors by a fixed factor: ΘD = 2.37, Θ4He = 2.69 and Θ7Li = 1.43 for D, 4He and 7Li, respectively.

2.1. Variation of α and v allowing ηB to vary

We calculated the BBN abundances for different values of the fine structure constant, the Higgs vacuum expectation value and ηB, for each potential considered (see Table 1). We performed a χ2-test to find the best-fit values of the parameters. In Table 2 we show the results of the parameters corresponding to the best fit, at 1σ, for the BBN constraints on ηB (in units of 10-10), 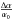(in units of 10-3) and 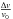(in units of 10-3). The values were obtained for the different values of κ given in Table 1. For all these cases, the value of 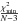is 1.00.

Table 2

Best-fit parameter values for the BBN constraints.

We found good agreement at the level of three standard deviations between our best-fit value of ηB and the one obtained using WMAP data (Spergel et al. 2007). We also found null variation of α within two standard deviations, and variation of the Higgs vacuum expectation value, even at the level of six standard deviations. In Fig. 1 we present the 3σ-likelihood contours for ηB, 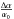and 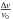, and the one-dimensional likelihood for all potentials.

thumbnail Fig. 1

3σ Likelihood contours for , and ηB and one-dimensional likelihood for all values of κ.

2.2. Variation of α and v keeping ηB fixed

Once again, we calculated the BBN abundances for different values of the fine structure constant and of the Higgs vacuum expectation value for each potential considered (see Table 1). This calculation was made keeping ηB fixed at WMAP value 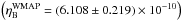(Spergel et al. 2007). We performed a χ2-test to find the best-fit value. In Table 3 we present the results for the best-fit parameter values within one standard deviation for the BBN constraints on 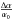(in units of 10-3) and 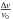(in units of 10-3), with ηB fixed at the WMAP estimate, for the different values of κ, as given in Table 1.

Table 3

Best-fit parameters with ηB fixed by WMAP.

In Fig. 2 we present the 3σ-likelihood contours for 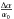and 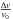and one-dimensional likelihood, for all potentials.

thumbnail Fig. 2

3σ Likelihood contours for vs. and one-dimensional likelihood for all values of κ.

We found null variation of α at 2σ level, but the variation of v is non-null even at 6σ. If the analysis does not include the lithium-data-set, we found null variation of both fundamental constants at the level of 2σ.

3. Conclusion

We obtained bounds on the joint variation of α and v using the observational abundances of D, 4He, and 7Li. We performed the analysis for different estimates of the dependence of the deuterium-binding energy on the Higgs vacuum expectation value. We found that the four dependencies considered, that is for the four values of κ of Table 1, give similar results. We found reasonable fits for the variation of α, v and ηB for the whole data set. However, and referring to the particular case of v, its variation is significant only when the data-set includes the 7Li abundance. If the present values of 7Li abundances are correct (Meléndez & Ramírez 2004; Richard et al. 2005; Prodanović & Fields 2007), then varying fundamental constants would be a possible explanation to solve the discrepancy between the light element abundances and the WMAP estimates.

Acknowledgments

Support for this work was provided by the PIP 0740 of the National Research Council (CONICET) of Argentina. The authors are members of the Scientific Research Career of the CONICET.

References

  1. Asplund, M., Lambert, D. L., Nissen, P. E., Primas, F., & Smith, V. V. 2006, ApJ, 644, 229 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bahcall, J. N., Steinhardt, C. L., & Schlegel, D. 2004, ApJ, 600, 520 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barr, S. M., & Mohapatra, P. K. 1988, Phys. Rev. D, 38, 3011 [NASA ADS] [CrossRef] [Google Scholar]
  4. Beane, S. R., & Savage, M. J. 2003, Nucl. Phys. A, 713, 148 [NASA ADS] [CrossRef] [Google Scholar]
  5. Berengut, J. C., Flambaum, V. V., & Dmitriev, V. F. 2010, Phys. Lett. B, 683, 114 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bergström, L., Iguri, S., & Rubinstein, H. 1999, Phys. Rev. D, 60, 45005 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bize, S., Diddams, S. A., Tanaka, U., et al. 2003, Phys. Rev. Lett., 90, 150802 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  8. Boesgaard, A. M., Novicki, M. C., & Stephens, A. 2005, in From Lithium to Uranium: Elemental Tracers of Early Cosmic Evolution, ed. V. Hill, P. François, & F. Primas, IAU Symp., 228, 29 [Google Scholar]
  9. Bonifacio, P., & Molaro, P. 1997, MNRAS, 285, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bonifacio, P., Pasquini, L., Spite, F., et al. 2002, ApJ, 390, 91 [Google Scholar]
  11. Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Brax, P., van de Bruck, C., Davis, A.-C., & Rhodes, C. S. 2003, Astro. Nucl. Space Sci., 283, 627 [NASA ADS] [CrossRef] [Google Scholar]
  13. Burles, S., & Tytler, D. 1998a, ApJ, 499, 699 [NASA ADS] [CrossRef] [Google Scholar]
  14. Burles, S., & Tytler, D. 1998b, ApJ, 507, 732 [NASA ADS] [CrossRef] [Google Scholar]
  15. Campbell, B. A., & Olive, K. A. 1995, Phys. Lett. B, 345, 429 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chamoun, N., Landau, S. J., Mosquera, M. E., & Vucetich, H. 2007, J. Phys. G Nucl. Phys., 34, 163 [NASA ADS] [CrossRef] [Google Scholar]
  17. Civitarese, O., Moliné, M. A., & Mosquera, M. E. 2010, Nucl. Phys., A, 846, 157 [Google Scholar]
  18. Coc, A., Nunes, N. J., Olive, K. A., Uzan, J.-P., & Vangioni, E. 2007, Phys. Rev. D, 76, 023511 [NASA ADS] [CrossRef] [Google Scholar]
  19. Crighton, N. H. M., Webb, J. K., Ortiz-Gil, A., & Fernández-Soto, A. 2004, MNRAS, 355, 1042 [NASA ADS] [CrossRef] [Google Scholar]
  20. Cyburt, R. H., Fields, B. D., Olive, K. A., & Skillman, E. 2005, Astropart. Phys., 23, 313 [NASA ADS] [CrossRef] [Google Scholar]
  21. Damour, T., & Dyson, F. 1996, Nucl. Phys. B, 480, 37 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  22. Damour, T., & Polyakov, A. M. 1994, Nucl. Phys. B, 95, 10347 [Google Scholar]
  23. Damour, T., Piazza, F., & Veneziano, G. 2002a, Phys. Rev. Lett., 89, 081601 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Damour, T., Piazza, F., & Veneziano, G. 2002b, Phys. Rev. D, 66, 046007 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  25. Dmitriev, V. F., & Flambaum, V. V. 2003, Phys. Rev. D, 67, 063513 [NASA ADS] [CrossRef] [Google Scholar]
  26. Dmitriev, V. F., Flambaum, V. V., & Webb, J. K. 2004, Phys. Rev. D, 69, 063506 [NASA ADS] [CrossRef] [Google Scholar]
  27. Epelbaum, E., Meißner, U., & Glöckle, W. 2003, Nucl. Phys. A, 714, 535 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fischer, M., Kolachevsky, N., Zimmermann, M., et al. 2004, Phys. Rev. Lett., 92, 230802 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Flambaum, V. V., & Shuryak, E. V. 2002, Phys. Rev. D, 65, 103503 [NASA ADS] [CrossRef] [Google Scholar]
  30. Flambaum, V. V., & Shuryak, E. V. 2003, Phys. Rev. D, 67, 083507 [NASA ADS] [CrossRef] [Google Scholar]
  31. Flambaum, V. V., & Wiringa, R. B. 2007, Phys. Rev. C, 76, 054002 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fujii, Y., Iwamoto, A., Fukahori, T., et al. 2000, Nucl. Phys. B, 573, 377 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gleiser, M., & Taylor, J. G. 1985, Phys. Rev. D, 31, 1904 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hosford, A., Ryan, S. G., García Pérez, A. E., Norris, J. E., & Olive, K. A. 2009, A&A, 493, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Ichikawa, K., & Kawasaki, M. 2002, Phys. Rev., D65, 123511 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ichikawa, K., & Kawasaki, M. 2004, Phys. Rev. D, 69, 123506 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ivanchik, A., Petitjean, P., Varshalovich, D., et al. 2005, A&A, 440, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Ivanchik, A. V., Petitjean, P., Balashev, S. A., et al. 2010, MNRAS, Soc., 297 [Google Scholar]
  39. Izotov, Y. I., & Thuan, T. X. 2010, ApJ, 710, L67 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  40. Izotov, Y. I., Schaerer, D., Blecha, A., et al. 2006, A&A, 459, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kaluza, T. 1921, Sitzungber. Preuss. Akad. Wiss. K, 1, 966 [Google Scholar]
  43. Kawano, L. 1988, fERMILAB-PUB-88-034-A [Google Scholar]
  44. Kawano, L. 1992, fERMILAB-PUB-92-004-A [Google Scholar]
  45. King, J. A., Webb, J. K., Murphy, M. T., & Carswell, R. F. 2008, Phys. Rev. Lett., 101, 251304 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  46. Kirkman, D., Tytler, D., Suzuki, N., O’Meara, J. M., & Lubin, D. 2003, ApJSS, 149, 1 [NASA ADS] [CrossRef] [Google Scholar]
  47. Klein, O. 1926, Z. Phys., 37, 895 [Google Scholar]
  48. Landau, S. J., & Scóccola, G. 2010, A&A, 517, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Landau, S. J., Mosquera, M. E., & Vucetich, H. 2006, ApJ, 637, 38 [NASA ADS] [CrossRef] [Google Scholar]
  50. Landau, S. J., Mosquera, M. E., Scóccola, C. G., & Vucetich, H. 2008, Phys. Rev. D, 78, 083527 [NASA ADS] [CrossRef] [Google Scholar]
  51. Levshakov, S. A., Dessauges-Zavadsky, M., D’Odorico, S., & Molaro, P. 2002, ApJ, 565, 696 [NASA ADS] [CrossRef] [Google Scholar]
  52. Müller, C. M., Schäfer, G., & Wetterich, C. 2004, Phys. Rev. D, 70, 083504 [NASA ADS] [CrossRef] [Google Scholar]
  53. Maeda, K. 1988, Modern Phys. Lett. A, 31, 243 [NASA ADS] [CrossRef] [Google Scholar]
  54. Malec, A. L., Buning, R., Murphy, M. T., et al. 2010, MNRAS, 403, 1541 [NASA ADS] [CrossRef] [Google Scholar]
  55. Marion, H., Pereira Dos Santos, F., Abgrall, M., et al. 2003, Phys. Rev. Lett., 90, 150801 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  56. Martínez Fiorenzano, A. F., Vladilo, G., & Bonifacio, P. 2003, Soc. Astron. Ital. Mem. Suppl., 3, 252 [NASA ADS] [Google Scholar]
  57. Meléndez, J., & Ramírez, I. 2004, ApJ, 615, L33 [NASA ADS] [CrossRef] [Google Scholar]
  58. Molaro, P., Bonifacio, P., & Pasquini, L. 1997, MNRAS, 292, L1 [NASA ADS] [CrossRef] [Google Scholar]
  59. Mosquera, M. E., & Civitarese, O. 2010, A&A, 520, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Mosquera, M. E., Scóccola, C., Landau, S., & Vucetich, H. 2008, A&A, 478, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Murphy, M. T., Webb, J. K., Flambaum, V. V., et al. 2001a, MNRAS, 327, 1208 [NASA ADS] [CrossRef] [Google Scholar]
  62. Murphy, M. T., Webb, J. K., Flambaum, V. V., Prochaska, J. X., & Wolfe, A. M. 2001b, MNRAS, 327, 1237 [NASA ADS] [CrossRef] [Google Scholar]
  63. Murphy, M. T., Webb, J. K., & Flambaum, V. V. 2003, MNRAS, 345, 609 [NASA ADS] [CrossRef] [Google Scholar]
  64. Nollett, K. M., & Lopez, R. E. 2002, Phys. Rev., D66, 063507 [NASA ADS] [CrossRef] [Google Scholar]
  65. O’Meara, J. M., Tytler, D., Kirkman, D., et al. 2001, ApJ, 552, 718 [NASA ADS] [CrossRef] [Google Scholar]
  66. O’Meara, J. M., Burles, S., Prochaska, J. X., et al. 2006, ApJ, 649, L61 [NASA ADS] [CrossRef] [Google Scholar]
  67. Overduin, J. M., & Wesson, P. S. 1997, Phys. Rep., 283, 303 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  68. Palma, G. A., Brax, P., Davis, A. C., & van de Bruck, C. 2003, Phys. Rev. D, 68, 123519 [NASA ADS] [CrossRef] [Google Scholar]
  69. Peik, E., Lipphardt, B., Schnatz, H., et al. 2004, Phys. Rev. Lett., 93, 170801 [NASA ADS] [CrossRef] [Google Scholar]
  70. Peimbert, M., Luridiana, V., & Peimbert, A. 2007, ApJ, 666, 636 [NASA ADS] [CrossRef] [Google Scholar]
  71. Pettini, M., & Bowen, D. V. 2001, ApJ, 560, 41 [NASA ADS] [CrossRef] [Google Scholar]
  72. Pettini, M., Zych, B. J., Murphy, M. T., Lewis, A., & Steidel, C. C. 2008, MNRAS, 391, 1499 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  73. Prestage, J. D., Tjoelker, R. L., & Maleki, L. 1995, Phys. Rev. Lett., 74, 3511 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  74. Prodanović, T., & Fields, B. D. 2007, Phys. Rev. D, 76, 083003 [NASA ADS] [CrossRef] [Google Scholar]
  75. Quast, R., Reimers, D., & Levshakov, S. A. 2004, A&A, 415, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Reinhold, E., Buning, R., Hollenstein, U., et al. 2006, Phys. Rev. Lett., 96, 151101 [NASA ADS] [CrossRef] [Google Scholar]
  77. Richard, O., Michaud, G., & Richer, J. 2005, ApJ, 619, 538 [NASA ADS] [CrossRef] [Google Scholar]
  78. Ryan, S. G., Beers, T. C., Olive, K. A., Fields, B. D., & Norris, J. E. 2000, ApJ, 530, L57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  79. Sortais, Y., Bize, S., Abgrall, M., et al. 2000, Phys. Scripta, T95, 50 [NASA ADS] [CrossRef] [Google Scholar]
  80. Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJSS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
  81. Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJSS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
  82. Srianand, R., Chand, H., Petitjean, P., & Aracil, B. 2004, Phys. Rev. Lett., 92, 121302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  83. Thompson, R. I., Bechtold, J., Black, J. H., et al. 2009, ApJ, 703, 1648 [NASA ADS] [CrossRef] [Google Scholar]
  84. Tzanavaris, P., Murphy, M. T., Webb, J. K., Flambaum, V. V., & Curran, S. J. 2007, MNRAS, 374, 634 [NASA ADS] [CrossRef] [Google Scholar]
  85. Webb, J. K., Flambaum, V. V., Churchill, C. W., Drinkwater, M. J., & Barrow, J. D. 1999, Phys. Rev. Lett., 82, 884 [NASA ADS] [CrossRef] [Google Scholar]
  86. Webb, J. K., Murphy, M. T., Flambaum, V. V., et al. 2001, Phys. Rev. Lett., 87, 091301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  87. Weinberg, S. 1983, Phys. Lett. B, 125, 265 [NASA ADS] [CrossRef] [Google Scholar]
  88. Wiringa, R. B., Stoks, V. G. J., & Schiavilla, R. 1995, Phys. Rev. C, 51, 38 [NASA ADS] [CrossRef] [Google Scholar]
  89. Wu, Y., & Wang, Z. 1986, Phys. Rev. Lett., 57, 1978 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  90. Yao, W.-M., Amsler, C., Asner, D., et al. 2006, J. Phys. G, 33, 1 [NASA ADS] [CrossRef] [Google Scholar]
  91. Yoo, J. J., & Scherrer, R. J. 2003, Phys. Rev. D, 67, 043517 [NASA ADS] [CrossRef] [Google Scholar]
  92. Youm, D. 2001a, Phys. Rev. D, 63, 125011 [NASA ADS] [CrossRef] [Google Scholar]
  93. Youm, D. 2001b, Phys. Rev. D, 64, 085011 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Values of the coefficient κ of Eq. (1).

In the text
Table 2

Best-fit parameter values for the BBN constraints.

In the text
Table 3

Best-fit parameters with ηB fixed by WMAP.

In the text

All Figures

thumbnail Fig. 1

3σ Likelihood contours for , and ηB and one-dimensional likelihood for all values of κ.
In the text
thumbnail Fig. 2

3σ Likelihood contours for vs. and one-dimensional likelihood for all values of κ.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.