| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201015974 | |
| Published online | 13 December 2010 | |
Letters to the Editor
The spin and orbit of the newly discovered pulsar IGR J17480-2446
1
Dipartimento di FisicaUniversità degli Studi di Cagliari,
SP Monserrato-Sestu, KM 0.7,
09042
Monserrato, Italy
e-mail: apapitto@oa-cagliari.inaf.ig
2
INAF – Osservatorio Astronomico di Cagliari, Poggio dei
Pini, Strada 54,
09012
Capoterra ( CA), Italy
3
Dipartimento di Scienze Fisiche ed Astronomiche, Università di
Palermo, via Archirafi
36, 90123
Palermo,
Italy
4
INAF – Osservatorio Astronomico di Brera,
via E. Bianchi 46, 23807
Merate,
Italy
Received:
21
October
2010
Accepted:
28
November
2010
We present an analysis of the spin and orbital properties of the newly discovered accreting pulsar IGR J17480-2446, located in the globular cluster Terzan 5. Considering the pulses detected by the Rossi X-ray Timing Explorer at a period of 90.539645(2) ms, we derive a solution for the 21.27454(8) hr binary system. The binary mass function is estimated to be 0.021275(5) M⊙, indicating a companion star with a mass larger than 0.4 M⊙. The X-ray pulsar spins up while accreting at a rate of between 1.2 and 1.7 × 10-12 Hz s-1, in agreement with the accretion of disc matter angular momentum given the observed luminosity.
We also report the detection of pulsations at the spin period of the source during a Swift observation performed ~2 d before the beginning of the RXTE coverage. Assuming that the inner disc radius lies in between the neutron star radius and the corotation radius while the source shows pulsations, we estimate the magnetic field of the neutron star to be within ~2 × 108 G and ~2.4 × 1010 G. From this estimate, the value of the spin period and of the observed spin-up rate, we associate this source with the still poorly sampled population of slow, mildly recycled, accreting pulsars.
Key words: stars: neutron / stars: rotation / X-rays: binaries / pulsars: individual: IGR J17480-2446
© ESO, 2010
1. Introduction
The dense environment of a globular cluster and the resulting frequent stellar encounters (Meylan & Heggie 1997) make the production of binary systems hosting a compact object very efficient. Terzan 5 is probably one of the densest and metal-richest cluster in our Galaxy (Cohn et al. 2002; Ortolani et al. 2007), as clearly indicated by the large number of rotation-powered millisecond pulsars discovered there (≳30, Ransom et al. 2005; Hessels et al. 2006). The cluster also contains at least 28 discrete X-ray sources, a substantial number of which can be identified as quiescent low-mass X-ray binaries (LMXB, Heinke et al. 2006). According to the recycling scenario (see, e.g. Bhattacharya & van den Heuvel 1991), the population of rotation-powered millisecond pulsars and low-mass X-ray binaries (LMXB) share an evolutionary link, because the former are thought to be spun up by the accretion of mass and angular momentum in an LMXB. Accreting pulsars in LMXB are usually found with periods clustering in two distinct groups. So far, 13 sources have been discovered with spin periods lower than 10 ms and were therefore termed accretion-powered millisecond pulsars (see, e.g., Wijnands & van der Klis 1998). However, a smaller number of sources are found with longer periods and correspondingly higher estimates of the neutron star (NS) magnetic field.
So far, the only bright transient LMXB known in the cluster Terzan 5 was the burster EXO 1745-248 (Makishima et al. 1981). The first detection of a new outburst of a source in this cluster was made on 2010 October 10.365 with INTEGRAL (Bordas et al. 2010) and was tentatively attributed to EXO 1745-248. Follow-up Swift observations refined the source position, and a comparison with the position of sources previously known thanks to Chandra observations of the cluster suggested instead a different association (Heinke et al. 2010; Kennea et al. 2010; Pooley et al. 2010). The X-ray transient is then considered a newly discovered source and named as IGR J17480-2446 (J17480 in the following). A coherent signal at a period of 90.6 ms was detected thanks to observations performed with the Rossi X-ray Timing Explorer (RXTE in the following, Strohmayer & Markwardt 2010). A signal at the same period is present also during the several bursts that the source shows (Altamirano et al. 2010b), while burst oscillations have never been observed from NS rotating at periods exceeding a few ms. A sudden decrease of the flux was tentatively attributed to an eclipse of the source by the companion (Strohmayer & Markwardt 2010). However, eclipses were not observed during subsequent observations, and the earlier flux decrease was identified with a lunar occultation (Strohmayer et al. 2010, S10 in the following).
Below we present the first analysis of the properties of the coherent signal emitted by this source, using RXTE and Swift observations performed between 2010 October 10 and November 6, and give a refined orbital and timing solution of the pulsar with respect to those first proposed (Papitto et al. 2010, P10 in the following; S10).
2. Observations and data analysis
 |
Fig. 1 J17480 in the time interval considered here as observed by the PCU2 of the PCA aboard RXTE. |
After the source discovery on 2010 October 10.365 (Bordas et al. 2010), RXTE started monitoring the source on MJD 55 482.010 (October 13.010; all the epochs reported in this paper are given with regard to the Barycentric Dynamical Time, TDB, system). We present an analysis of the observations performed until MJD 55 506.359 (ObsId 95437-01-12-01), for a total exposure of 206 ks. In this time interval, a large number (>300) of X-ray bursts are observed with a recurrence time decreasing from ≳26 to ~3 min as the X-ray flux increases. The analysis of the bursts shown by the source, as well as of its aperiodic timing properties, will appear in a companion paper. The 2.5–25 keV light curve recorded by PCU2 of the Proportional Counter Array (PCA) on-board RXTE, with the burst intervals removed and background subtracted, is plotted in Fig. 1. The count rate increases during the first days of the outburst, reaching a peak value of ~1700 s-1 at MJD 55 487.5, and then decreases to a value of ~800 s-1 with an exponential decay time scale of ~5 d. Quite complex dipping-like structures also appear especially between MJD 55 485 and 55 490 as the flux shows sudden variations up to 75% on timescales of ~10 min.
The combined X-ray spectrum observed by the top layer of the PCU2 of the PCA (2.5–25 keV), and by Cluster A of the High Energy X-ray Timing Experiment (HEXTE, 22–50 keV), can be well modelled by a sum of a blackbody and a Comptonized component, which we model with compps (Poutanen & Svensson 1996). Throughout the observations considered here, the spectrum softens significantly as the source evolves towards higher luminosities. The unabsorbed total flux, extrapolated in the 0.1–100 keV band, rises from 0.47(3) × 10-8 to a maximum level of 1.89(4) × 10-8 erg cm-2 s-1, observed during the observation of MJD 55 487.5. All the uncertainties on the fluxes given here are quoted at a 90% confidence level.
To analyse the spin and orbital properties of the source we consider data taken by the PCA
in Event (122 μs temporal resolution) and Good Xenon (1 μs
temporal resolution) packing modes. We discard 10 s prior, and 100 s after the onset of each
type-I X-ray burst. The time series were also preliminarly barycentred with respect to the
solar system barycentre using the available RXTE orbit files and assuming
the best Chandra estimate of the source position,
RA = 17h48m4.831s, Dec = –24°46′48.87′′, with an error
circle of 0.06′′ (1σ confidence level, Heinke et al. 2006; Pooley et al. 2010). A
coherent signal at a frequency of 11.045(1) Hz [equivalent to a period of 90.539(8) ms] is
clearly detected in the power spectrum at a Leahy-normalised power of
≃ 1.5 × 104. A first orbital solution is obtained modelling the observed
modulation caused by the orbital motion,
![\begin{equation} P(t)= P_0 \left\{1+\frac{2\pi x}{P_{\rm orb}} [\cos{m}+e\cos(2m-\omega)]\right\}. \end{equation}](/articles/aa/full_html/2011/02/aa15974-10/aa15974-10-eq24.png) (1)Here
\begin{formule}$P_0$\end{formule} is the barycentric spin period of the source,
x = asini/c the
semi-major axis of the NS orbit, Porb the orbital period,
m = 2π(t − T ∗ )/Porb
the mean anomaly, T∗ the epoch at which
m = 0, e the eccentricity and ω the
longitude of the periastron measured from the ascending node. The periods
P(t) are estimated by performing an epoch-folding search
on 1.5 ks long data segments (for a total of 127) around the periodicity indicated by the
power spectrum. The resulting variance profiles are fitted following Leahy (1987) and the uncertainties affecting the period estimates are
evaluated accordingly. The best-fitting orbital solution we obtain with this technique is
shown in the leftmost column of Table 1.
(1)Here
\begin{formule}$P_0$\end{formule} is the barycentric spin period of the source,
x = asini/c the
semi-major axis of the NS orbit, Porb the orbital period,
m = 2π(t − T ∗ )/Porb
the mean anomaly, T∗ the epoch at which
m = 0, e the eccentricity and ω the
longitude of the periastron measured from the ascending node. The periods
P(t) are estimated by performing an epoch-folding search
on 1.5 ks long data segments (for a total of 127) around the periodicity indicated by the
power spectrum. The resulting variance profiles are fitted following Leahy (1987) and the uncertainties affecting the period estimates are
evaluated accordingly. The best-fitting orbital solution we obtain with this technique is
shown in the leftmost column of Table 1.
Spin and orbital parameters of IGR J17480-2446.
 |
Fig. 2 Pulse profiles and best-fitting harmonic decomposition, obtained by folding observations performed by RXTE on MJD 55 482 (left scale, solid line) and MJD 55 483 (right scale, dashed lines) around PF = 90.539645 ms. Both profiles are evaluated after background subtraction and are normalised to the current average flux. |
The time series were then corrected for the orbital motion with these parameters and folded around the best estimate of the spin period over 300 s data segments (for a total of 717). The pulse profiles could generally be modelled using up to three harmonics. The pulsed fraction is observed to greatly vary in between the first (MJD 55 482.010 to 55482.043) and the other RXTE observations. During the former the pulse fractional amplitude of the first harmonic is very high [A1 ≃ 0.252(2)], while the second harmonic is detected at a much lower amplitude [A2 = 0.016(2)]. In subsequent observations the amplitude of the first harmonic drastically decreases to values between 0.02 and 0.04, whereas the second harmonic amplitude remains stable and a third harmonic is sometimes requested by the profile modelling. To show this, we plot in Fig. 2 the pulse profiles calculated over the observations performed during MJD 55 482 (solid line) and MJD 55 483 (dashed line), with the latter profile shown at a magnified scale. The pulsed fraction decrease is evident, as are the variation of the shape of the peak at rotational phase ~0.75.
To increase the accuracy of our timing solution we model the temporal evolution of the
phases evaluated on the first and second harmonic of the pulse profiles with the relation:
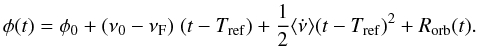 (2)Here
Tref is the reference epoch for the timing solution,
ν0 is the pulsar frequency at the reference epoch,
νF = 1/PF is the folding
frequency and
(2)Here
Tref is the reference epoch for the timing solution,
ν0 is the pulsar frequency at the reference epoch,
νF = 1/PF is the folding
frequency and 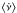 is the average spin frequency derivative. The term
Rorb(t) describes the phase residuals induced
by a difference between the actual orbital parameters, namely x,
Porb, T∗,
esinω and ecosω, and
those used to correct the time series (see e.g. Deeter
et al. 1981). Once a new set of orbital parameters is found, it is used to correct
the time series, and the resulting phases are modelled again with Eq. (2). This procedure is iterated until the phase
residuals are normally distributed around zero.
is the average spin frequency derivative. The term
Rorb(t) describes the phase residuals induced
by a difference between the actual orbital parameters, namely x,
Porb, T∗,
esinω and ecosω, and
those used to correct the time series (see e.g. Deeter
et al. 1981). Once a new set of orbital parameters is found, it is used to correct
the time series, and the resulting phases are modelled again with Eq. (2). This procedure is iterated until the phase
residuals are normally distributed around zero.
Although no residual modulation at the orbital period is observed, the phases of the first
harmonic are strongly affected by timing noise. The reduced χ2
we obtain modelling their evolution with Eq. (2) is extremely large (≃ 11.9 over 662 d.o.f.). Such a behaviour is most probably
caused by to pulse shape changes like the one shown in Fig. 2. The second harmonic phases appear to be less affected by timing noise,
resulting in a reduced 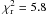 (566 d.o.f.). We argue that the second harmonic phases are better fitted with respect to the
first harmonic because of the greater stability of this component (as already observed in
some accreting millisecond pulsars, see, e.g., Burderi et al.
2006; Riggio et al. 2008). The best-fitting
parameters calculated over the phase evolution of the first and second harmonic are quoted
in the central and rightmost column of Table 1. In
Fig. 3 we show the phases of both harmonics, when the
observations corrected for the orbital motion of the source are folded around
PF = 90.539645 ms. The phase evolution is clearly driven by at
least a quadratic component. A consequence of timing noise is that the spin frequency and
its derivative, estimated over the two harmonic components, are significantly different. We
quote conservatively a value of ν0 = 11.0448854(2) Hz that
overlaps both frequency estimates, and use a spin frequency derivative between
1.2–1.7 × 10-12 Hz s-1 in the discussion below. However, it is
worthwhile to note that the orbital parameters are entirely consistent between the two
harmonic solutions, which supports the reliability of these estimates. The solution we
obtained is entirely compatible with, but more precise than, those proposed by P101 and S10. Given the accuracy of the source position
considered here (0.06′′), the systematic uncertainties introduced by the position
indetermination on the measured values of spin frequency and of its derivative (e.g. Burderi et al. 2007) are
σpos,ν ≲ 3 × 10-10 Hz and
(566 d.o.f.). We argue that the second harmonic phases are better fitted with respect to the
first harmonic because of the greater stability of this component (as already observed in
some accreting millisecond pulsars, see, e.g., Burderi et al.
2006; Riggio et al. 2008). The best-fitting
parameters calculated over the phase evolution of the first and second harmonic are quoted
in the central and rightmost column of Table 1. In
Fig. 3 we show the phases of both harmonics, when the
observations corrected for the orbital motion of the source are folded around
PF = 90.539645 ms. The phase evolution is clearly driven by at
least a quadratic component. A consequence of timing noise is that the spin frequency and
its derivative, estimated over the two harmonic components, are significantly different. We
quote conservatively a value of ν0 = 11.0448854(2) Hz that
overlaps both frequency estimates, and use a spin frequency derivative between
1.2–1.7 × 10-12 Hz s-1 in the discussion below. However, it is
worthwhile to note that the orbital parameters are entirely consistent between the two
harmonic solutions, which supports the reliability of these estimates. The solution we
obtained is entirely compatible with, but more precise than, those proposed by P101 and S10. Given the accuracy of the source position
considered here (0.06′′), the systematic uncertainties introduced by the position
indetermination on the measured values of spin frequency and of its derivative (e.g. Burderi et al. 2007) are
σpos,ν ≲ 3 × 10-10 Hz and
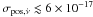 Hz s-1,
respectively. Finally, as the cluster moves towards the solar system at a velocity of
85 ± 10 km s-1 (Ferraro et al. 2009),
the measured value of the spin frequency is affected by a systematic offset of
~+3 × 10-3 Hz, though this is unimportant when making conclusions
about the source properties.
Hz s-1,
respectively. Finally, as the cluster moves towards the solar system at a velocity of
85 ± 10 km s-1 (Ferraro et al. 2009),
the measured value of the spin frequency is affected by a systematic offset of
~+3 × 10-3 Hz, though this is unimportant when making conclusions
about the source properties.
 |
Fig. 3 Evolution of the first (top) and second (bottom) harmonic phases obtained by folding the orbitally corrected time series around PF = 90.539645 ms (see text). The solid lines show the best-fit models from Eq. (2). |
In order to extend the range of fluxes at which the source was observed and pulsations were detected, we also analysed three Swift observations (Obs. 00031841002, 00031841003 and 00031841004) in which the XRT observed in Windowed Timing (WT) mode, with a temporal resolution of 1.7 ms. The Swift XRT started monitoring the source on MJD 55 479.737, more than two days before RXTE, with the first observation in WT mode starting at MJD 55 479.802 for 2 ks. After applying barycentric corrections for the satellite orbit, then correcting for the source orbital motion and selecting photons from a 50 pixel wide box around the source position, a pulsation is clearly detected at a period of PS = 90.5395(2) ms by means of an epoch-folding search. The XRT signal is particularly strong and consistent with that seen by RXTE during its first observation, with a pulse profile modelled by a sinusoid of amplitude 0.23(2). Pulsations were also searched for in the subsequent ~1 ks long XRT WT observations starting on MJD 55 484.767 and 55 485.357. Only a weak signal was detected in the latter at a fractional amplitude of 0.018(4), still compatible with that seen by RXTE at those later times.
3. Discussion and conclusions
We reported on the spin and orbital properties of the newly discovered accreting pulsar, IGR J17480-2446. Its 90.6 ms period makes it the first confirmed accreting pulsar in the range 10–100 ms. Pulsations were detected in all observations performed by RXTE, as well as in two out of the three Swift observations performed in WT mode presented here. The pulsed fraction is observed to drastically change on a timescale of ≲1 d, after the RXTE observation performed on MJD 55 482. While previously both Swift and RXTE observations revealed a strong signal dominated by a first harmonic component of fractional amplitude as large as 0.25, later observations at higher fluxes performed by both satellites never detected an amplitude ≳0.03. Simultaneously the pulse shape changes and becomes more complex. This behaviour is suggestive of a change of the geometrical properties of the flow in the accretion columns above the NS hot spots.
Because pulsations are detected throughout the observations shown here, an estimate of the
NS magnetic field strength can be made. For accretion to proceed and pulsations to appear in
the X-ray light curve, the inner disc radius, Rin, has to lie in
between the NS radius, RNS, and the corotation radius,
RC, defined as the distance from the NS at which the velocity
of the magnetosphere equals the Keplerian velocity of the matter in the disc. For a larger
accretion radius, accretion would be inhibited or severely reduced by the onset of a
centrifugal barrier. For a pulsar spinning at 90.6 ms,
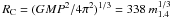 km,
where m1.4 is the NS mass in units of 1.4
M⊙. Defining the inner disc radius in terms of the pressure
equilibrium between the disc and the magnetosphere, one obtains
km,
where m1.4 is the NS mass in units of 1.4
M⊙. Defining the inner disc radius in terms of the pressure
equilibrium between the disc and the magnetosphere, one obtains
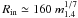
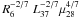 km
(Burderi et al. 2001), where
R6 is the NS radius in units of 10 km,
L37 the accretion luminosity in units of 1037 erg
s-1, and μ28 the magnetic dipole moment of the NS
in units of 1028 G cm3. Extrapolating the fluxes observed by
RXTE to the 0.1–100 keV band, and assuming a distance of
d = 5.5 ± 0.9 kpc to Terzan 5
(Ortolani et al. 2007), we estimate a maximum and
minimum bolometric luminosities of
km
(Burderi et al. 2001), where
R6 is the NS radius in units of 10 km,
L37 the accretion luminosity in units of 1037 erg
s-1, and μ28 the magnetic dipole moment of the NS
in units of 1028 G cm3. Extrapolating the fluxes observed by
RXTE to the 0.1–100 keV band, and assuming a distance of
d = 5.5 ± 0.9 kpc to Terzan 5
(Ortolani et al. 2007), we estimate a maximum and
minimum bolometric luminosities of 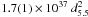 erg s-1
and
erg s-1
and 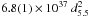 erg s-1,
during the time covered by the observations considered here. Assuming that the X-ray
luminosity is a good tracer of the accretion power and imposing
RNS < Rin ≲ RC,
we obtain
erg s-1,
during the time covered by the observations considered here. Assuming that the X-ray
luminosity is a good tracer of the accretion power and imposing
RNS < Rin ≲ RC,
we obtain 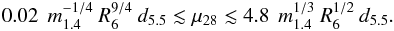 (3)The upper limit on the
magnetic dipole can be reduced considering that pulsations are detected also in a Swift
observation taking place ~2 d earlier than the first RXTE
observation. Bozzo et al. (2010) estimated
the source flux in that observation as
4.5(2) × 10-10 erg cm-2 s-1 (1–10 keV). This value is a
factor ~4 lower than the value obtained extrapolating the spectrum of the first
RXTE observation in the same energy band. Assuming that this ratio holds
also for the bolometric luminosity of the source, we get to an upper limit on the magnetic
dipole moment of ≃ 2.4 × 1028 G cm-3. The limits thus derived
translate to a magnetic surface flux density between ~2 × 108 and
~2.4 × 1010 G. The upper bound of this interval can be overestimated
because the exact flux at which the pulsations appeared is unknown at present. Monitoring
the presence of coherent pulsations as a function of the flux when the source fades will
probably allow us to derive a tighter constraint. Altamirano
et al. (2010a) have also reported the presence of a kHz QPO at ~815 Hz
(10–50 keV) during the RXTE observations performed on MJD 55 487. Under the
hypothesis that this feature originates in the innermost part of the accretion disc, it
indicates an inner disc radius
(3)The upper limit on the
magnetic dipole can be reduced considering that pulsations are detected also in a Swift
observation taking place ~2 d earlier than the first RXTE
observation. Bozzo et al. (2010) estimated
the source flux in that observation as
4.5(2) × 10-10 erg cm-2 s-1 (1–10 keV). This value is a
factor ~4 lower than the value obtained extrapolating the spectrum of the first
RXTE observation in the same energy band. Assuming that this ratio holds
also for the bolometric luminosity of the source, we get to an upper limit on the magnetic
dipole moment of ≃ 2.4 × 1028 G cm-3. The limits thus derived
translate to a magnetic surface flux density between ~2 × 108 and
~2.4 × 1010 G. The upper bound of this interval can be overestimated
because the exact flux at which the pulsations appeared is unknown at present. Monitoring
the presence of coherent pulsations as a function of the flux when the source fades will
probably allow us to derive a tighter constraint. Altamirano
et al. (2010a) have also reported the presence of a kHz QPO at ~815 Hz
(10–50 keV) during the RXTE observations performed on MJD 55 487. Under the
hypothesis that this feature originates in the innermost part of the accretion disc, it
indicates an inner disc radius 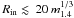 km. As
the luminosity we estimated during that day is
km. As
the luminosity we estimated during that day is 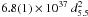 erg s-1,
this would imply a magnetic field ≲7 × 108 d5.5 G
if the disc is truncated at the magnetospheric radius.
erg s-1,
this would imply a magnetic field ≲7 × 108 d5.5 G
if the disc is truncated at the magnetospheric radius.
Despite the presence of timing noise, the analysis of the phase evolution over the
~24 d time interval presented here clearly indicates the need for a quadratic
component to model these phases. Interpreting this component as a tracer of the NS spin
evolution, we thus conclude that the source spins up while accreting. Values of the spin-up
rate between 1.2 and 1.7 × 10-12 Hz s-1 are found, depending on the
harmonic considered. This discrepancy is probably due to the effect of timing noise. These
values are compatible with those expected for a NS accreting the Keplerian disc matter
angular momentum given the observed luminosity, 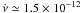 (L37/5)
(Rin/70 km)1/2
(L37/5)
(Rin/70 km)1/2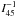 R6m1.4
Hz s-1. Here I45 is the NS moment of inertia in units
of 1045 g cm2. The observed spin period and the magnetic field we
estimated place this source between the population of “classical”
(B ≳ 1011 G, P ≳ 0.1 s) and millisecond
(B ≃ 108–109 G, P ≃ 1.5–10 ms)
rotation-powered pulsars. The observation of a significant spin-up at rates compatible with
those predicted by the recycling scenario further supports the identification of this source
as a slow, mildly recycled pulsar. We note that the only other two accreting pulsars with
similar, though significantly different parameters, are GRO
J1744-28 (PS = 467 ms,
B ≃ 2.4 × 1011 G, Cui
1997), and 2A 1822-371
(PS = 590 ms, B ≲ 1011 G, Jonker & van der Klis 2001).
R6m1.4
Hz s-1. Here I45 is the NS moment of inertia in units
of 1045 g cm2. The observed spin period and the magnetic field we
estimated place this source between the population of “classical”
(B ≳ 1011 G, P ≳ 0.1 s) and millisecond
(B ≃ 108–109 G, P ≃ 1.5–10 ms)
rotation-powered pulsars. The observation of a significant spin-up at rates compatible with
those predicted by the recycling scenario further supports the identification of this source
as a slow, mildly recycled pulsar. We note that the only other two accreting pulsars with
similar, though significantly different parameters, are GRO
J1744-28 (PS = 467 ms,
B ≃ 2.4 × 1011 G, Cui
1997), and 2A 1822-371
(PS = 590 ms, B ≲ 1011 G, Jonker & van der Klis 2001).
The orbital parameters we measured for the NS in J17480 allow us to derive constraints on the nature of its companion star. With a mass function of f(M2;M1,i) ≃ 0.02 M⊙, a minimum mass for the companion can be estimated to be as low as 0.41 M⊙ for an inclination of 90°, and an NS mass of 1.4 M⊙. Since the source shows no eclipses, the inclination is most probably ≲80°, and the lower limit increases to m2 = 0.16 + 0.26m1.4, where m2 is the mass of the companion star in solar units. An upper limit can be obtained if the companion star is assumed not to overfill its Roche lobe. Using the relation given by Eggleton (1983) and the third Kepler law to relate the Roche Lobe radius to the orbital period and to the companion mass, RL2 ≃ 0.55(GM⊙)1/3(Porb/2π)2/3m1.4q2/3(1 + q)1/3/[0.6q2/3 + log (1 + q1/3)], where q = M2/M1, and assuming the companion star follows a main sequence mass-radius relation, R2/R⊙ ≈ (M2/M⊙), yields a maximum mass of 2.75 M⊙ for the companion when m1.4 = 1. This upper limit is indeed higher than the maximum mass expected for a main sequence star belonging to one of the two stellar populations found by Ferraro et al. (2009) in Terzan 5. One has in fact m2 ≲ 0.95 if the companion of J17480 belongs to the older population (t = 10 Gyr, D’Antona et al. 2010), while m2 ≲ 1.2 and m2 ≲ 1.5 if it belongs to a younger population of 6 and 4 Gyr, respectively (D’Antona, priv. comm.). We conclude that a reasonable upper limit for the companion-star mass is 1.5 M⊙, possibly a main sequence or a slightly evolved star.
Acknowledgments
This work is supported by the Italian Space Agency, ASI-INAF I/088/06/0 contract for High Energy Astrophysics, as well as by the operating program of Regione Sardegna (European Social Fund 2007–2013), L.R.7/2007, “Promotion of scientific research and technological innovation in Sardinia”. We thank F. D’Antona for providing the mass estimates of main sequence stars in Terzan 5, and the referee for the prompt reply and useful comments.
References
- Altamirano, D., Homan, J., Linares, M., et al. 2010a, ATel, 2952, 1 [NASA ADS] [Google Scholar]
- Altamirano, D., Watts, A., Kalamkar, M., et al. 2010b, ATel, 2932, 1 [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bordas, P., Kuulkers, E., Alfondo Garzon, J., et al. 2010, ATel, 2919, 1 [NASA ADS] [Google Scholar]
- Bozzo, E., Ferrigno, C., & Bordas, P. 2010, ATel, 2922, 1 [NASA ADS] [Google Scholar]
- Burderi, L., Possenti, A., D’Antona, F., et al. 2001, ApJ, 560, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Burderi, L., Di Salvo, T., Menna, M. T., et al. 2006, ApJ, 653, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Burderi, L., Di Salvo, T., Lavagetto, G., et al. 2007, ApJ, 657, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Cohn, H. N., Lugger, P. M., Grindlay, J. E., et al. 2002, ApJ, 571, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, W. 1997, ApJ, 482, L163 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., Caloi, V., & Ventura, P. 2010, MNRAS, 405, 2295 [NASA ADS] [Google Scholar]
- Deeter, J. E., Boynton, P. E., & Pravdo, S. H. 1981, ApJ, 247, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Dalessandro, E., Mucciarelli, A., et al. 2009, Nature, 462, 483 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Heinke, C. O., Linares, M., & Gladstone, J. 2010, ATel, 2933, 1 [NASA ADS] [Google Scholar]
- Heinke, C. O., Wijnands, R., Cohn, H. N., et al. 2006, ApJ, 651, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jonker, P. G., & van der Klis, M. 2001, ApJ, 553, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Kennea, J. A., Evans, P. A., & Beardmore, A. P. 2010, ATel, 2937, 1 [NASA ADS] [Google Scholar]
- Leahy, D. A. 1987, A&A, 180, 275 [NASA ADS] [Google Scholar]
- Makishima, K., Ohashi, T., Inoue, H., et al. 1981, ApJ, 247, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, G., & Heggie, D. C. 1997, A&ARv, 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Barbuy, B., Bica, E., et al. 2007, A&A, 470, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papitto, A., Burderi, L., D’Aì, A., et al. 2010, ATel, 2939, 1 [NASA ADS] [Google Scholar]
- Pooley, D., Homan, J., Heinke, C., et al. 2010, ATel, 2974, 1 [NASA ADS] [Google Scholar]
- Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ransom, S. M., Hessels, J. W. T., Stairs, I. H., et al. 2005, Science, 307, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Riggio, A., Di Salvo, T., Burderi, L., et al. 2008, ApJ, 678, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., & Markwardt, C. B. 2010, ATel, 2929, 1 [Google Scholar]
- Strohmayer, T. E., Markwardt, C. B., Pereira, B., et al. 2010, ATel, 2946, 1 [Google Scholar]
- Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 J17480 in the time interval considered here as observed by the PCU2 of the PCA aboard RXTE. |
| In the text | |
 |
Fig. 2 Pulse profiles and best-fitting harmonic decomposition, obtained by folding observations performed by RXTE on MJD 55 482 (left scale, solid line) and MJD 55 483 (right scale, dashed lines) around PF = 90.539645 ms. Both profiles are evaluated after background subtraction and are normalised to the current average flux. |
| In the text | |
 |
Fig. 3 Evolution of the first (top) and second (bottom) harmonic phases obtained by folding the orbitally corrected time series around PF = 90.539645 ms (see text). The solid lines show the best-fit models from Eq. (2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


