| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201015942 | |
| Published online | 21 December 2010 | |
The giant planet orbiting the cataclysmic binary DP Leonis
1 Institut für Astrophysik,
Georg-August-Universität, Friedrich-Hund-Platz 1, 37077
Göttingen,
Germany
e-mail: beuermann@astro.physik.uni-goettingen.de
2 Max-Planck-Gymnasium, Theaterplatz
10, 37073
Göttingen,
Germany
3 Astrophysikalisches Institut Potsdam,
An der Sternwarte
16, 14482
Potsdam,
Germany
4 Dept. of Astronomy, University of
Texas at Austin, RLM
16.236, Austin,
TX
78712,
USA
Received: 17 October 2010
Accepted: 11 November 2010
Planets orbiting post-common envelope binaries provide fundamental information on planet formation and evolution, especially for the yet nearly unexplored class of circumbinary planets. We searched for such planets in DP Leo, an eclipsing short-period binary, which shows long-term eclipse-time variations. Using published, reanalysed, and new mid-eclipse times of the white dwarf in DP Leo, obtained between 1979 and 2010, we find agreement with the light-travel-time effect produced by a third body in an elliptical orbit. In particular, the measured binary period in 2009/2010 and the implied radial velocity coincide with the values predicted for the motion of the binary and the third body around the common center of mass. The orbital period, semi-major axis, and eccentricity of the third body are Pc = 28.0 ± 2.0 yrs, ac = 8.2 ± 0.4 AU, and ec = 0.39 ± 0.13. Its mass of sini c Mc = 6.1 ± 0.5 MJup qualifies it as a giant planet. It formed either as a first generation object in a protoplanetary disk around the original binary or as a second generation object in a disk formed in the common envelope shed by the progenitor of the white dwarf. Even a third generation origin in matter lost from the present accreting binary can not be entirely excluded. We searched for, but found no evidence for a fourth body.
Key words: planets and satellites: detection / planets and satellites: formation / planetary systems / novae, cataclysmic variables / stars: individual: DP Leonis / binaries: eclipsing
© ESO, 2010
1. Introduction
Many eclipsing post-common envelope (CE) binaries, including the cataclysmic variables, display long-term eclipse-time variations, which represent either true or apparent changes of the orbital period. True changes may result from the angular-momentum loss by gravitational radiation or magnetic braking or from spin-orbit exchange processes within the binary. Apparent changes may be effected by apsidal motion or the presence of a third body. Eclipse-time variations in cataclysmic variables (CVs) have often been attributed to Applegate’s (1992) mechanism of spin-orbit coupling, resulting from changes in the internal constitution of the secondary, but this process is generally too feeble to account for the observed amplitudes (Brinkworth et al. 2006; Chen 2009; Schwarz et al. 2009). Apsidal motion (Todoran 1972) is unlikely to be present in CVs, because tidal interaction is expected to circularize the orbits effectively. Furthermore, apsidal motion can not account for the observed non-sinusoidal shape of the eclipse-time variations (e.g. Beuermann et al. 2010). In recent years, interest has therefore shifted back to the third-body hypothesis, which explains a periodic variation of the eclipse times as the light-travel-time (LTT) effect caused by the motion of the binary and an unseen third object around the common center of gravity of the triple.
DP Leo1 belongs to the still small group of post-CE binaries known or suspected to possess planets, among them HW Vir (Lee et al. 2009), NN Ser (Beuermann et al. 2010), HU Aqr (Schwarz et al. 2009; Nasiroglu et al. 2010), and QS Vir (Parsons et al. 2010). DP Leo ab is an 18.5 mag short-period (Porb = 89.9 min) polar, in which a synchronously rotating magnetic white dwarf accretes matter from its Roche-lobe filling companion (Schwope et al. 2002; Pandel et al. 2002). The observed effective temperature of the white dwarf of 13 500 K (Schwope et al. 2002) is likely due to accretional heating (Townsley & Bildsten 2004), suggesting an age exceeding the cooling age of the white dwarf of 0.5 Gyr (Wood 1995).
Schwope et al. (2002) and Pandel et al. (2002) noted a decrease of the binary period that could be described by a quadratic term in the ephemeris. More recently, Qian et al. (2010) found that a reversal of the long-term trend had taken place and suggested that the data support a sinusoidal variation instead. They attributed this modulation to a giant planet, which moves around the close binary in a wide circular orbit with a period of 23.8 yrs.
The eclipsed light sources in DP Leo include the white dwarf, the accretion spot on the white dwarf, and the magnetically controlled accretion stream, which suffers only a grazing eclipse at the inclination of i = 79.5° (Schwope et al. 2002). The part of the stream closest to the white dwarf forms the accretion column, which emits X-ray bremsstrahlung and optical cyclotron radiation, heating the wider surrounding of the accretion spot by irradiation. An accurate measurement of the period change in an accreting binary requires that the contributions of these light sources to the observed flux can be identified and the measured eclipse time can be reduced to the mid-eclipse or superior conjunction of the white dwarf (Schwope et al. 2002). In early 2009, we started a long-term program to measure accurate mid-eclipse times of the white dwarf in DP Leo. This work is part of the ongoing effort of the University of Göttingen to conduct research projects with high-school students.
2. Observations and data analysis
 |
Fig. 1 Coadded light curve of 18 eclipses of DP Leo. The model curves represent the accretion stream (dashed), the sum of the stream component and the photospheric emission of the white dwarf (dot-dashed), and the sum of the latter and the spot component (solid). |
Between 24 March 2009 and 19 February 2010, we measured 53 optical eclipse light curves of DP Leo, using the remotely controlled MONET/North 1.2-m telescope at McDonald Observatory via the MONET internet remote-observing interface, either in white light or with a Sloan r′ filter. The exposure times were mostly 10 s, separated by a 3 s read-out interval. Part of the observations were taken by two groups of 10th and 11th grade high-school students at the Max-Planck-Gymnasium Göttingen during normal school hours. One additional eclipse was observed on 12 July 2010 with the McDonald 2.1-m telescope using a BG40 filter. We performed relative photometry with respect to comparison star C1 (SDSS 111722.63+175848.2), which is located 31′′ E and 65′′ N of DP Leo and has Sloan r′ = 14.47 mag.
Throughout the observations, DP Leo showed the usual orbital variation, reaching r′ ≃ 18 in the two cyclotron maxima and dimming to r′ = 18.5 − 18.7 before eclipse and to r′ > 21 in eclipse. In the first half of 2009, a noticeable flux from the accretion stream was present, which almost vanished later in the year and stayed low in 2010. The white-dwarf eclipse in DP Leo is clearly discernible in light curves measured with high sensitivity and time resolution. For the MONET/North data, we obtained a sufficient S/N ratio by coadding 18 light curves taken in good atmospheric conditions in winter 2009/2010. Figure 1 shows the resulting mean observed light curve collected into phase bins of Δφ = 0.001. The eclipse of the white dwarf and the accretion spot on the white dwarf are clearly discernible at egress as the moderately and steeply rising sections, respectively. The spot is seen near the trailing edge of the white dwarf at egress and more centrally on the white dwarf at ingress. The weak stream component contributes noticeably only around φ ≃ − 0.012. Employing information from our spring 2009 observations, when the stream was brighter, we modeled the stream contribution in the individual eclipse light curves by a series of concatenated straight lines. The average stream contribution is shown by the dashed curve in Fig. 1. Our eclipse model represents the white dwarf by a uniform disk and the excess emission of the spot over the photospheric emission of the white dwarf by a second smaller uniform disk. The latter is taken to include the optical emission of the accretion column and of the heated polar cap of the white dwarf. The assumed geometry of the spot is not relevant for the present study. The combined fit of these contributions is shown by the solid green curve in Fig. 1; the dot-dashed black curve denotes the sum of the stream and the white dwarf. Before least-squares fitting the model light curve, it was folded with the 10 s exposure times. We find that the ingress and or egress of the white dwarf takes 56.0 ± 1.5 s, that of the spot last 10.5 ± 1.4 s. The eclipse of the accretion spot takes place Δt = 7.6 ± 1.5 s after superior conjunction of the white dwarf. All quoted uncertainties refer to the unbiased 1-σ errors obtained by stepping through the parameter in question with all other parameters free.
Reanalysed and new white-dwarf mid-eclipse times of DP Leo.
Mid-eclipse times of the white dwarf were determined by least-squares fitting the composite model to the individual light curves, using Δt = 7.6 s and a relative flux of the white dwarf fixed at the level shown in Fig. 1. The fluxes of the spot at ingress and egress and the linear functions that describe the time-dependent flux of the stream were considered free parameters of the fit. We determined the mid-eclipse time of the white dwarf and its error by stepping the eclipse center in time and fitting a parabola to the resulting χ2 variation. The derived white-dwarf mid-eclipse times with their 1-σ statistical errors are listed in Table 1. All times were shifted to the solar system barycenter, corrected for leap seconds, and are quoted as barycentric Julian days in the terrestrial time system. The 1.5-s uncertainty in Δt represents an additional systematic error common to all eclipse times.
The 10th grade students used a simplified method of determining the mid-eclipse times by visually cross-correlating the known eclipse profile with the individual measured eclipse light curves. This method, employed for didactic reasons, yielded internal errors for individual eclipses of 3 s, not much larger than those from the formal fits used in this paper.
Schwope et al. (2002) measured two optical eclipses in white light using the Optima high speed photometer on the Calar Alto 3.5-m telescope in January 2002. Of these, only the first was published. We reanalysed the original data, which allowed us to discern the eclipses of the white dwarf and the spot, employing the same model as for the mean MONET light curve in Fig. 1. The derived mid-eclipse times of the white dwarf are given as the first two entries in Table 1. The 1-σ formal errors of our fits are significantly reduced over the conservative estimate of Schwope et al. (2002) for E = 56 307.
Qian et al. (2010) reported five eclipse times with a mean error of 6.9 s. We did not include them in our analysis, because their relation to the mid-eclipse of the white dwarf is uncertain and our data cover the same time period with smaller errors.
Schwope et al. (2002) summarized all eclipse-time measurements of DP Leo available by 2002. Their list includes results from X-ray, ultraviolet, and optical wavelengths, which they corrected to represent the mid-eclipse time of the white dwarf, utilizing the known slow secular drift of the accretion spot in azimuth. We adopt the 32 timings from Schwope et al. (2002, their Table 2) in addition to the 56 timings from Table 1. Our entire data set consists of 18 subsets loosely grouped in time, nine for the 1979-2002 data and nine for our 2009/2010 measurements. Within each subset, statistics dominate the scatter in the O − C eclipse-time variations.
 |
Fig. 2 Observed-calculated time differences for the mid-eclipse of the white dwarf in DP Leo relative to the linear ephemeris of Eq. (1). |
3. Results
Our 54 mid-eclipse times of the white dwarf in DP Leo taken in 2009/2010 (E = 98 482 − 106 096) define the linear ephemeris 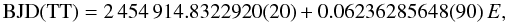 (1)where the statistical errors are quoted in brackets and refer to the last digits. The fit has a reduced
(1)where the statistical errors are quoted in brackets and refer to the last digits. The fit has a reduced 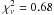 ( χ2 = 35.18 for 52 d.o.f.). The residuals with respect to the linear fit of Eq. (1) are given in Col. 5 of Table 1 and displayed in Fig. 2. The rms deviation from the fit is 1.1 s. With 79% of the values deviating from the linear ephemeris by less than 1σ, the observed spread is consistent with a purely statistical origin. The 1.5-s error in Δt represents an additional systematic error of the first term of Eq. (1).
( χ2 = 35.18 for 52 d.o.f.). The residuals with respect to the linear fit of Eq. (1) are given in Col. 5 of Table 1 and displayed in Fig. 2. The rms deviation from the fit is 1.1 s. With 79% of the values deviating from the linear ephemeris by less than 1σ, the observed spread is consistent with a purely statistical origin. The 1.5-s error in Δt represents an additional systematic error of the first term of Eq. (1).
Including the pre-2002 white-dwarf mid-eclipse times of Schwope et al. (2002) yields an entirely different picture. While the data available up to 2002 indicated a continuous period decrease (Schwope et al. 2002; Pandel et al. 2002), Qian et al. (2010) first noted that a reversal had taken place some time after 2002 and suggested that DP Leo exhibits a sinusoidal eclipse-time variation caused by a third body in a circular orbit with a period of 23.8 yrs. Our larger data set supports the third-body hypothesis by the detection of a finite eccentricity of the orbit.
We fit the entire data set of 88 white-dwarf mid-eclipse times with the sum of a linear ephemeris and the LTT effect produced by a third body DP Leo (ab)c, orbiting the binary DP Leo ab, 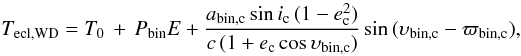 (2)where E is the cycle number. Note that we have not included the quadratic term considered by Schwope et al. (2002) and Pandel et al. (2002). The seven free parameters in the fit are the epoch T0, the binary period Pbin, the amplitude of the LTT effect Kbin,c = sin ic abin,c/c, the orbital eccentricity ec, the longitude ϖbin,c of the periastron from the ascending node in the plane of the sky, the orbital period Pc, and the time Tc of periastron passage. The quantities ic, υbin,c, abin,c, and c are the orbital inclination, the true anomaly, the semi-major axis of the orbit of the center of mass of the binary around the common center of mass of the triple, and the speed of light. The latter orbit is point-symmetric with respect to that of body c and offset by π in longitude. Quantities referring to the binary orbit carry the index “bin”. The motion of the center of gravity of the binary caused by the third body is indicated by the index “bin, c”, and that of the third body itself by “c”. If the latter two quantities are identical we use index “c”.
(2)where E is the cycle number. Note that we have not included the quadratic term considered by Schwope et al. (2002) and Pandel et al. (2002). The seven free parameters in the fit are the epoch T0, the binary period Pbin, the amplitude of the LTT effect Kbin,c = sin ic abin,c/c, the orbital eccentricity ec, the longitude ϖbin,c of the periastron from the ascending node in the plane of the sky, the orbital period Pc, and the time Tc of periastron passage. The quantities ic, υbin,c, abin,c, and c are the orbital inclination, the true anomaly, the semi-major axis of the orbit of the center of mass of the binary around the common center of mass of the triple, and the speed of light. The latter orbit is point-symmetric with respect to that of body c and offset by π in longitude. Quantities referring to the binary orbit carry the index “bin”. The motion of the center of gravity of the binary caused by the third body is indicated by the index “bin, c”, and that of the third body itself by “c”. If the latter two quantities are identical we use index “c”.
The best fit to the 88 eclipse times yields an amplitude of the LTT effect Kbin,c = 33.7 s and a period Pc = 28.0 yrs, with a reduced 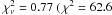 for 81 d.o.f.). The orbit has an eccentricity ec = 0.39 ± 0.13, with ec = 0 excluded at the 3.0σ level. With ϖbin,c = −78°, periastron occurs 12° from the line of sight and was last passed near 2004.0. Figure 3 shows the O − C eclipse-time variations relative to the linear part of Eq. (2) in the upper panel and the residuals from the fit including the third term of Eq. (2) in the lower panel. While the curve represents the fit to all data points, we avoid excessive clutter of the data points by displaying only the weighted mean O − C values for each of the 18 subsets of the data, with the symbols placed at the weighted mean eclipse times. The underlying time dependence of the O − C variation becomes much clearer this way. The parameters of DP Leo (ab)c are summarized in Table 2, which gives also the unbiased 1-σ errors determined by systematically varying the parameter in question with all other parameters free. The substantial correlated uncertainties in ϖbin,c and Tc affect also the magnitude of the errors in the other parameters and obliterate the small effect caused by the uncertainty of the offset Δt between the eclipses of white dwarf and spot. For the first two entries in Table 2, the errors are quoted in brackets, referring to the last digit.
for 81 d.o.f.). The orbit has an eccentricity ec = 0.39 ± 0.13, with ec = 0 excluded at the 3.0σ level. With ϖbin,c = −78°, periastron occurs 12° from the line of sight and was last passed near 2004.0. Figure 3 shows the O − C eclipse-time variations relative to the linear part of Eq. (2) in the upper panel and the residuals from the fit including the third term of Eq. (2) in the lower panel. While the curve represents the fit to all data points, we avoid excessive clutter of the data points by displaying only the weighted mean O − C values for each of the 18 subsets of the data, with the symbols placed at the weighted mean eclipse times. The underlying time dependence of the O − C variation becomes much clearer this way. The parameters of DP Leo (ab)c are summarized in Table 2, which gives also the unbiased 1-σ errors determined by systematically varying the parameter in question with all other parameters free. The substantial correlated uncertainties in ϖbin,c and Tc affect also the magnitude of the errors in the other parameters and obliterate the small effect caused by the uncertainty of the offset Δt between the eclipses of white dwarf and spot. For the first two entries in Table 2, the errors are quoted in brackets, referring to the last digit.
Assuming a central binary that consists of a white dwarf of 0.6 M⊙ (Schwope et al. 2002) and a secondary of 0.1 M⊙, the semi-major axis of the orbit of the third body becomes ac = 8.2 AU. The amplitude Kbin,c of the LTT effect implies an inclination-dependent mass sinic Mc = 6.1 MJup, qualifying the object as a giant planet for any inclination ic > 28°. The inclination ic may be close to the binary inclination of 79.5°, but can not be determined by present means. The amplitude and the period of the eclipse-time variations quoted by Qian et al. (2010) are roughly consistent with the results presented here, while the sinusoidal form of the eclipse-time variations assumed by them is not confirmed.
Parameters derived from the eccentric orbit fit.
The χ2-minimization ensures that the eccentric-orbit fit meets the centroid of our 2009/2010 data points. That the fit also reproduces the observed derivative of the O − C curve to a high degree of accuracy is not self-evident and provides additional support for the third-body hypothesis. The eccentric-orbit fit to all data points yields P = 0.0623628561 days for the JD = 2 454 919 − 2 455 389 time interval, in agreement with the observed period of Eq. (1), P = 0.0623628565(9) days. Both numbers refer to the mean period in 2009/2010. Their agreement is illustrated in the inset to Fig. 3 and documented by the nearly identical residuals for the linear and eccentric-orbit fits in Table 1. The difference ΔP = P(t) − Pbin between the period P(t) at time t and the intrinsic binary period Pbin (Table 2) varies between − 1.29 ms and + 1.52 ms over the 28-year period. This range of ΔP corresponds to radial velocities of the center of gravity of the binary on its path around the center of gravity of the triple, vrad = c ΔP/Pbin, between − 72 and + 85 m s-1. The observed period difference in 2009/2010, ΔP = 1.20 ± 0.08 ms, corresponds to vrad = 66.8 ± 4.5 m s-1 in agreement with the velocity of 65 m s-1 expected from the fit.
The present data provide a perfect fit without the quadratic term 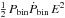 that Schwope et al. (2002) and Pandel et al. (2002) included in the ephemeris. This term measures the secular variation Ṗbin of the binary period. Its inclusion distorts the run of the O − C values displayed in Fig. 3 by adding a parabolic variation, which can be compensated for to some extent by adjusting the fit parameters, notably Pc and Kbin,c. The fit deteriorates with increasing positive and negative values of Ṗbin and at the 1-σ level, we find
that Schwope et al. (2002) and Pandel et al. (2002) included in the ephemeris. This term measures the secular variation Ṗbin of the binary period. Its inclusion distorts the run of the O − C values displayed in Fig. 3 by adding a parabolic variation, which can be compensated for to some extent by adjusting the fit parameters, notably Pc and Kbin,c. The fit deteriorates with increasing positive and negative values of Ṗbin and at the 1-σ level, we find 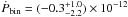 s s-1, about an order of magnitude lower than the negative value suggested by Schwope et al. (2002) and Pandel et al. (2002) and consistent with zero. Obviously, a much longer time basis is needed to discern a secular change of the binary period against the LTT effect produced by the third body. The interpretation of the O − C variation as the LTT effect caused by a third body turns out to be robust. However, a finite Ṗbin, if it exists, would change some of the fit parameters. For a negative Ṗbin at the 1-σ level in χ2, the planetary period, mass, and eccentricity rise to Pc ≃ 40 yrs, sin ic Mc ≃ 10 MJup, and ec = 0.45.
s s-1, about an order of magnitude lower than the negative value suggested by Schwope et al. (2002) and Pandel et al. (2002) and consistent with zero. Obviously, a much longer time basis is needed to discern a secular change of the binary period against the LTT effect produced by the third body. The interpretation of the O − C variation as the LTT effect caused by a third body turns out to be robust. However, a finite Ṗbin, if it exists, would change some of the fit parameters. For a negative Ṗbin at the 1-σ level in χ2, the planetary period, mass, and eccentricity rise to Pc ≃ 40 yrs, sin ic Mc ≃ 10 MJup, and ec = 0.45.
 |
Fig. 3 Light-travel-time (LTT) effect produced by a third body in an elliptical orbit about DP Leo. Upper panel: O − C time differences relative to a linear ephemeris. The curve shows the eccentric orbit fit, the data points represent the weighted means for 18 independent subsets of data taken between 1979 and 2010, as explained in the text. The inset is an enlargement of the section containing the new MONET/North data. Lower panel: residuals relative to the eccentric-orbit fit. |
Detecting planets by the LTT effect is limited by the statistical and systematic errors that affect the measurements of the mid-eclipse times. Kepler’s third law yields an LTT amplitude Kbin,c = 0.47 M sini (P/Mbin)2/3 s, where Mbin is the binary mass in M⊙, M is the mass of the planet in units of MJup, P its orbital period in years, and i the inclination. The statistical and remaining systematic errors of our 2009/2010 observations of DP Leo (Fig. 2) may still hide a modulation with an amplitude ≲ 0.5 s for a period of about 1 year, allowing us to set an approximate upper limit to the mass of an additional body with such a period of Msin i ≲ 0.8 MJup. Since the fits yield 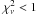 , the present data provide no evidence for a fourth body in DP Leo.
, the present data provide no evidence for a fourth body in DP Leo.
Systematic errors of the white-dwarf mid-eclipse times in polars arise from the non-uniform brightness distribution of the white dwarf caused by the accretion spot, its extended and variable structure, and the formation of a heated pole cap by irradiation of the surrounding photosphere. In DP Leo, the main accretion region forms a ribbon that extends over about 30° or 4 × 108 cm on the surface of the white dwarf (Schwope et al. 2002, and references therein), accounting for the 10-s ingress and egress times of the spot component. Weak emission has been detected from a second pole. That the mid-eclipse of the white dwarf in DP Leo can nevertheless be measured to better than 1 s is due to favorable circumstances: (i) the accretion rate is sufficiently low to allow the identification of the white-dwarf component in individual light curves; (ii) the uneclipsed stream emission is faint, at least at times; and (iii) the accretion geometry has remained unchanged since its discovery 1979. In other polars, the accretion spot outshines the white dwarf, impeding an easy reduction of the measured eclipse time to the mid-eclipse of the white dwarf. The problem may be further aggravated if the white dwarf is not synchronized, but rotates freely as in intermediate polars. As a consequence, the 0.1 s accuracy for the eclipse times of the detached system NN Ser (Beuermann et al. 2010) is probably not attainable for such systems.
4. Discussion
The quality of our eccentric-orbit fit to the observed eclipse time variations of DP Leo suggests that the detection of a third body is a robust result. It can be tested by measuring the period (radial velocity) evolution in the years to come, but the decisive next periastron passage is expected to occur only in 2032. Of the alternative explanations, apsidal motion can easily produce the observed amplitude for an eccentricity as small as ebin = 0.01 (Todoran 1972), but predicts an O − C variation that is sinusoidal to a high degree of accuracy, and can therefore be excluded by the finite eccentricity found by us. Applegate’s (1992) mechanism, on the other hand, often discussed in attempts to explain the observed eclipse-time variations in CVs, can not produce the observed amplitude (e.g. Brinkworth et al. 2006; Chen 2009; Schwarz et al. 2009). The detection of planets in HW Vir (Lee et al. 2009) and NN Ser (Beuermann et al. 2010), as well as the likely detection in HU Aqr (Schwarz et al. 2009; Nasiroglu et al. 2010) and QS Vir (Parsons et al. 2010), suggests that the occurrence of planets or planetary systems in post-CE binaries may not be a rare incidence.
The progenitors of CVs are normal binaries with a primary of a couple of solar masses and a low-mass secondary (e.g. Willems et al. 2005). The mass of the primary is set by the requirement that its core has reached the present white dwarf mass when the star fills its Roche lobe, catastrophic mass transfer sets in, and a CE is formed. Rapid spiral-in of the secondary leads to the ejection of the envelope and the emergence of the newly born white dwarf (e.g. Sandquist et al. 1998). The system may become a CV if angular momentum loss by gravitational radiation and magnetic braking causes the secondary to reach its Roche lobe and mass transfer resumes. In such systems, two principal paths of planet formation exist: first generation planets that formed in a circumbinary protoplanetary disk; and second generation planets that originated from a disk formed in the ejected envelope (Perets 2010). In the CE phase, a pre-existing
planet undergoes an outward motion caused by the diminishing central mass and a less well understood inward motion caused by the drag, which it experiences in the dense slowly expanding envelope. This drag is usually ascribed to a supersonic Bondi-Hoyle type momentum transfer (Alexander et al. 1976). A preliminary study suggests that the drag-induced inward drift may compensate for the mass-related outward motion (Beuermann et al. 2010, and in prep.). This is particularly true if the inclination of the planet is near that of the binary, ensuring that the planet moves in the densest parts of the CE. The uncertainties concerning the fate of a first generation planet are large, however, and the origin of the planet in DP Leo must presently be considered uncertain. Finally, there may be a third channel of planet formation in matter lost from the secondary that was not accreted by the white dwarf but left the binary and accumulated in a circumbinary disk. Although such a disk may not contain enough mass for planet formation (Taam & Spruit 2001), the impact of a nova shell on the stagnant matter could lead to the formation of planetesimals. Even without such complications, planet formation around post-CE binaries presents a variety of theoretical challenges.
Acknowledgments
This work is based on data obtained with the MONET telescopes funded by the “Astronomie & Internet” program of the Alfried Krupp von Bohlen und Halbach-Foundation, Essen, and operated by the Georg-August-Universität Göttingen, the McDonald Observatory of the University of Texas at Austin, and the South African Astronomical Observatory, on data obtained with the 2.1-m telescope at McDonald Observatory, and on data obtained with the 3.5-m telescope of the German-Spanish Astronomical Centre, Calar Alto. We acknowledge helpful comments by the anonymous referee. We also thank Andreas Seifahrt and Ulf Seemann for taking part of the light curves with the MONET/North telescope. We gratefully acknowledge the support from the Robert-Bosch-Foundation by awarding the Robert-Bosch-Prize 2010 “Schule trifft Wissenschaft” to our collaborative project.
References
- Alexander, M. E., Chau, W. Y., & Henriksen, R. N. 1976, ApJ, 204, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Hessman, F. V., Dreizler, S., et al. 2010, A&A, 521, L60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinkworth, C. S., Marsh, T., Dhillon, V. S., & Knigge, C. 2006, MNRAS, 365, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W.-C. 2009, A&A, 499, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J. W., Kim, S.-L., Kim, C.-H., et al. 2009, AJ, 137, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Nasiroglu, I., Słowiokowska, A., Kanbach, G., Schwarz, R., & Schwope, A. D. 2010, High Time Resolution Astrophysics IV, The Era of Extremely Large Telescopes, Cret, Greece, in press [Google Scholar]
- Pandel, D., Cordova, F. A., Shirey, R. E., et al. 2002, MNRAS, 332, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Parsons, S. G., Marsh, T. R., Copperwheat, C. M., et al. 2010b, MNRAS, 407, 2362 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B. 2010, ApJ, submitted [arXiv:1001.0581] [Google Scholar]
- Qian, S.-B., Dai, Z.-B., Liao, W.-P., et al. 2010, ApJ, 708, L66 [Google Scholar]
- Sandquist, E. L., Taam, R. E., Chen, X., Bodenheimer, P., & Burkert, A. 1998, ApJ, 500, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, R., Schwope, A. D., Vogel, J., et al. 2009, A&A, 496, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwope, A. D., Hambaryan, V., Schwarz, R., Kanbach, G., & Gänsicke, B. T. 2002, A&A, 392, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taam, R. E., & Spruit, H. C. 2001, ApJ, 561, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Todoran, I. 1972, Ap&SS, 15, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Townsley, D. M., & Bildsten, L. 2004, ApJ, 600, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Willems, B., Kolb, U., Sandquist, E. L., Taam, R. E., & Dubus, G. 2005, ApJ, 635, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, M. A. 1995, in White Dwarfs, ed. D. Koester, & K. Werner (Heidelberg: Springer), LNP 443, 41 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Coadded light curve of 18 eclipses of DP Leo. The model curves represent the accretion stream (dashed), the sum of the stream component and the photospheric emission of the white dwarf (dot-dashed), and the sum of the latter and the spot component (solid). |
| In the text | |
 |
Fig. 2 Observed-calculated time differences for the mid-eclipse of the white dwarf in DP Leo relative to the linear ephemeris of Eq. (1). |
| In the text | |
 |
Fig. 3 Light-travel-time (LTT) effect produced by a third body in an elliptical orbit about DP Leo. Upper panel: O − C time differences relative to a linear ephemeris. The curve shows the eccentric orbit fit, the data points represent the weighted means for 18 independent subsets of data taken between 1979 and 2010, as explained in the text. The inset is an enlargement of the section containing the new MONET/North data. Lower panel: residuals relative to the eccentric-orbit fit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


