EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 526 (February 2011) A&A, 526 (2011) A91 Full HTML
Free Access
Issue
A&A
Volume 526, February 2011
Article Number A91
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201015250
Published online 04 January 2011

© ESO, 2011

1. Introduction

An outstanding problem in stellar astrophysics concerns the identification of physical processes responsible for the heating of outer stellar atmospheres and the acceleration of stellar winds (see reviews by Narain & Ulmschneider 1990, 1996; and Güdel 2007). For the Sun and other types of stars with surface convection zones, acoustic heating has been identified as most likely responsible for balancing the “basal” flux emission (e.g., Buchholz et al. 1998; Cuntz et al. 2007). On the other hand, it is well known that most, if not all stars also exhibit a large amount of magnetic activity. Thus, the chromospheres of main-sequence stars, including the Sun, are expected to be shaped significantly by magnetically heated structure (e.g., Saar 1994; Schrijver 1996).

There is a large body of literature devoted to the description of the two-component structure of stellar chromospheres, which are the acoustically and magnetically heated components, associated with magnetic and non-magnetic surface structure, or more precisely, surface structure shaped by strong and weak magnetic fields (e.g., Schrijver & Zwaan 2000). The magnetic chromospheric component is typically assumed to be dominantly heated by longitudinal flux tube waves. Cuntz et al. (1999) computed two-component theoretical chromosphere models for K2 V stars with different levels of magnetic activity where the filling factor for the magnetic component was determined from an observational relationship between the measured magnetic area coverage and the stellar rotation period. For stars with very slow rotation, they were able to reproduce the basal flux limit of chromospheric emission previously identified with non-magnetic regions. Most notably, however, Cuntz et al. (1999) deduced a relationship between the Ca II H+K emission and the stellar rotation rate that is consistent with the relationship previously obtained by observations; see also Cuntz et al. (1998) for earlier results.

Further studies for a large spectral range of stars were performed by Fawzy et al. (2002) based on specified values for the magnetic filling factor. They concluded that heating by acoustic and longitudinal flux tube waves is able to explain most of the observed range of chromospheric activity as gauged by the Ca II and Mg II lines. On the other hand, indirect evidence of non-wave (i.e., reconnective) heating was also obtained noting that this type of heating was needed to explain the structure of the highest layers of stellar chromospheres.

Anticipated future models of chromospheric heating and emission that are partially motivated by the quest to investigate the effects of UV and EUV emission on planetary atmosphere and (potentially) the evolution of life (e.g., Guinan et al. 2003; Lammer et al. 2003; Güdel 2007; Cuntz et al. 2010), require the continuation of detailed simulations of magnetic wave energy generation, including studies of longitudinal tube waves in different types of stars, particularly main-sequence stars. This latter goal is the focus of the present paper.

Previous work on the calculation of longitudinal tube waves was based on progress made by Musielak et al. (1994). These authors corrected the Lighthill-Stein theory by incorporating an improved description of the spatial and temporal spectrum of the turbulent convection and utilized the corrected theory to calculate revised stellar acoustic wave energy fluxes (Ulmschneider et al. 1996, 1999). This type of work focused on the generation of acoustic waves but did not consider stellar magnetic fields. Owing to the fundamental importance of magnetic heating in most, if not all stars, a set of papers focusing on the study of longitudinal and transverse tube wave generation was pursued (e.g. Musielak et al. 1989, 1995; Ulmschneider & Musielak 1998). In subsequent work, Ulmschneider et al. (2001) used the approach developed by Ulmschneider & Musielak (1998) to compute the wave energy fluxes carried by longitudinal tube waves propagating along thin and vertically oriented magnetic flux tubes that are embedded in atmospheres of late-type stars. This numerical approach supplemented previous work by Musielak et al. (2000), who analytically calculated the longitudinal wave energy fluxes generated in stellar convective zones.

In the numerical approach by Ulmschneider & Musielak (1998), longitudinal tube waves are generated as a result of the squeezing of a thin, vertically oriented magnetic flux tube by external pressure fluctuations (or associated velocity fluctuations) produced by the turbulent motions in a stellar photosphere and convection zone (e.g., reviews by Narain & Ulmschneider 1990, 1996). Hence, to compute the pressure fluctuations imposed on the tube, it is required to know the external turbulent motions. The motions are modeled by specifying the rms velocity amplitude and using an extended Kolmogorov turbulent energy spectrum with a modified Gaussian frequency factor (Musielak et al. 1994).

The main advantage of this approach is that it is not restricted to linear waves and that it allows for occasionally large-amplitude waves observed on the Sun at the photospheric level (e.g., Muller 1985; Komm et al. 1991; Nesis et al. 1993; Muller et al. 1994) and also seen in detailed time-dependent simulations of solar and stellar convection (e.g., Nordlund & Dravins 1990; Nordlund & Stein 1991; Cattaneo et al. 1991; Steffen 1993; Nordlund et al. 1997). Horizontal flow patterns are a notable candidate process for the initiation of wave modes with respect to flux tubes (see Fig. 1); see Stein et al. (2009a,b) for recent models of convective flows for the Sun based on up-to-date simulations extending toward the scale of supergranules.

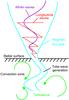thumbnail Fig. 1

Diagram of a flux tube embedded into a stellar convective zone. The squeezing point of the tube is assumed to be located at optical depth τ5000 = 1, coinciding with the “stellar surface”. Credit: P. Ulmschneider.

The code used by Ulmschneider & Musielak (1998) was originally developed by Herbold et al. (1985) who treated magnetic flux tubes in the so-called thin flux tube approximation and described them mathematically by using a set of one-dimensional, time-dependent and nonlinear MHD equations. It allows to compute the instantaneous and time-averaged longitudinal tube wave energy fluxes as well as the corresponding wave energy spectra. It requires specifying the strength of the magnetic field inside the flux tube and the height in the stellar atmosphere where the squeezing is assumed to take place. The code has previously been used to calculate wave energy fluxes and spectra for longitudinal tube waves propagating in the solar atmosphere (see Fawzy et al. 1998, for models of different spreading factors), and to investigate the dependence of these fluxes on the magnetic field strength, the rms velocity amplitude of turbulent motions, and the location of the squeezing in the atmosphere; for models of stars with non-solar metallicities, we refer to Fawzy (2010).

The reason for reinvestigating the generation of longitudinal flux tube waves in main-sequence stars is three-fold. First, we would like to use realistic combinations of (Teff, log g) where Teff denotes the stellar effective temperature and log g the surface gravity, for main-sequence stars guided by up-to-date studies of Kurucz and Gray. Note that log g is typically close to 4.5 (see Table 1). Previous models developed by Ulmschneider et al. (2001) and others have adopted either log g = 4 or 5, thus resulting in unnecessary interpolation errors. Secondly, we would like to investigate the amount of upwardly propagating longitudinal wave energy flux for a wider range of stellar convective and magnetic parameters, notably the mixing length α in the light of the progress made by the models of Stein et al. (2009a,b) and others. Thirdly, we would like to deduce a fitting formula for the wave energy flux that provides insight into the role of the relevant parameters concerning that flux and, furthermore, can be applied more universally.

Our paper is structured as follows. In Sect. 2, we comment on the parameters of theoretical main-sequence stars. In addition, we describe the methods that we use to compute longitudinal tube waves as well as construct stellar flux tube models. Our results are given in Sect. 3. Finally, in Sect. 4 we present the summary and conclusions.

Table 1

Theoretical main-sequence stars.

2. Methods

2.1. Comments on the theoretical main-sequence stars

Stellar parameters for theoretical main-sequence stars were evaluated by Gray (2005) (see his Table B.1). His values, notably of Teff and log g, serve as a basis for the present study. We also improved the accuracy of the log g values if more accurate values for the stellar masses and stellar radii were given. For stellar spectral types for which no data were given, we calculated the data using biparabolic interpolation. The stellar data are summarized in Table 1.

Another set of spectral models has been constructed by Kurucz and collaborators. They take into account millions or hundreds of millions of lines for a large array of atoms and molecules; see Castelli & Kurucz (2004) and Kurucz (2005) for technical details. These models consider effective temperatures very similar to the models of Gray (2005) for most types of stars. However, for stellar spectral types of K5 V and below, the effective temperatures provided by Kurucz are consistently lower noting that the difference amounts to nearly 300 K for spectral type M0 V. Therefore, we assume in the following average values between the models by Gray and Kurucz for stars of spectral type K5 V and M0 V.

2.2. Convective zone models and turbulent velocities

The method for calculating wave energy fluxes carried by longitudinal tube waves adopted in the present paper has been described in detail by Ulmschneider et al. (2001). Thus, it is not necessary to enter a detailed discussion here. In the solar application, it is possible to select many model parameters and characteristic values directly from observations. However, for stars other than the Sun these data are mostly unavailable. Therefore, we need to discuss in some detail the physical reasoning behind our choice of relevant parameters used in our calculations.

In the current approach, the magnetic flux tubes are embedded in nonmagnetized photospheric convection zones (see Fig. 1). Given that the interaction between the flux tubes and the convective turbulence is the driving mechanism behind the generation of longitudinal tube waves, among other waves, models of the stellar convection zones are required. Guided by previous studies, it is assumed that the squeezing of the tube is symmetric with respect to the tube axis. The computed pressure fluctuations are subsequently translated into gas pressure and magnetic field fluctuations inside the tube assuming horizontal pressure balance. Finally, the internal velocity perturbation resulting from the internal pressure fluctuation is calculated. This internal velocity serves as a boundary condition in the numerical simulation of the generation of the longitudinal tube waves.

Numerical simulations of stellar convection as well as mixing length models show that the maximum convective velocities occur at optical depths of τ5000 ≈ 10 to 100. For example, Steffen (1993) found in his time-dependent numerical solar convection calculations that maximum convective velocities vCMax ≃ 2.8 km s-1 are reached at τ5000 ≈ 50 and that these values can be reproduced by mixing length theory based on a mixing length parameter of α ≃ 2. The value α = 2 is furthermore indicated by time-dependent hydrodynamic simulations of stellar convection for stars other than the Sun (Trampedach et al. 1997), as well as by a careful fitting of evolutionary tracks to the Sun for its present luminosity, effective temperature, and age (Schröder & Eggleton 1996).

Nevertheless, there is still some debate about the most appropriate value of α. Nordlund & Dravins (1990) originally pursued detailed numerical simulations based on 3-D hydrodynamics coupled with 3-D non-grey radiative transfer for stars akin to Procyon (F5 IV-V), α Cen A (G2 V), β Hyi (G2 IV), and α Cen B (K1 V). They inferred a mixing-length parameter of α = 1.5 (or slightly higher), although the mixing length concept appeared to be problematic at photospheric heights. A mixing length of 1.5 was also used by Cuntz et al. (1999) in their two-component theoretical chromosphere models for K2 V stars with different levels of magnetic activity. Even though the deduced relationship between the Ca II H+K emission and the stellar rotation rate was found to be largely consistent with the observed relationship, the agreement could probably be improved if a somewhat higher longitudinal wave energy flux, corresponding to a slightly larger mixing length parameter, was adopted. Stein et al. (2009a,b) pursued updated state-of-the-art simulations of solar convection zone extending toward the scale of supergranules, which indicated a mixing length parameter of α ≃ 1.8. For these reasons, we calculate a set of models concerning wave energy generation of longitudinal tube wave for a set of α values, which are α = 1.5, 1.8, and 2.0.

thumbnail Fig. 2

Root mean square turbulent velocities at the squeezing point (τ5000 = 1) for the set of theoretical main-sequence stars for different values of the mixing-length parameter α.

2.3. Computation of stellar magnetic flux tube models

Our treatment of stellar convection associated with the facilitation of stellar flux tube models is akin to that described by Ulmschneider et al. (1996). In their approach, information is needed about the velocities of turbulent motions in the overshooting layer near the stellar surface, where the squeezing of the magnetic flux tube is assumed to occur. Steffen’s numerical calculations show that the rms velocities decrease toward the solar surface and reach a plateau in the overshooting layer. Between τ5000 = 1 and 10-4, he finds values of vrms = 1.4 km s-1, which are essentially independent of height. For the Sun, Ulmschneider & Musielak (1998) adopted a variety of observed rms velocity amplitudes ut in the range 0.9 < ut < 1.9 km s-1, and illustrated the dependence of the computed fluxes on this velocity. For stars, these velocities cannot be determined from observations; thus, we follow Ulmschneider et al. (2001) by assuming that the rms velocity fluctuations at the squeezing points are given by ut = vCMax/2. The values of vt and vCMax (see Fig. 2) are evaluated from stellar convection zone models based on the adopted mixing length parameter. The numerical factor of two used in our calculations ensures that in our approach the considered convective velocities are always lower than the local speed of sound.

After specifying the rms velocities that are responsible for the wave generation, we also determine the height in the stellar atmospheres, where the most efficient squeezing of magnetic flux tubes takes place. We build on earlier studies performed by Ulmschneider & Musielak (1998), who pointed out that shifting the height of the excitation point did not significantly alter the resulting wave energy fluxes for the Sun. On the basis of these results, we take the squeezing point to be located at optical depth τ5000 = 1 for all considered stars. This depth is commonly taken as the zero height level in stellar atmosphere computations.

For the computation of stellar magnetic flux tubes, we consider the “thin flux tube approximation” (e.g., Spruit 1981). Two dimensional modeling of magnetic flux tubes by Hasan et al. (2003) indicates that this approach renders reasonable results if the models do not extend beyond a small number of scale heights above the stellar surface; note that this approximation is fully compatible with our study. In the following, we augment the commonly used concept of solar magnetic flux tubes (e.g., Stenflo 1978; Solanki 1993) to stellar flux tubes; we refer to Solanki (1996) for further discussion. Stellar magnetic flux tubes at the stellar surface are assumed to have diameters roughly equal to the local pressure scale height as in case of the Sun.

For the Sun, the magnetic flux tubes within the solar photosphere have field strengths on the order B0 = 1500 G (e.g., Solanki 1993). If we assume that pe = 1.17 × 105  dyn  cm-2 as in model C of Vernazza et al. (1981) at the height z = 0 where τ5000 = 1, then the equipartition field strength (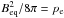) is given as Beq = 1716 G. This corresponds to a ratio B/Beq = 0.875, which may or may not be typical of stellar flux tubes. Since this ratio is likely to vary even on the Sun (e.g., Schrijver & Zwaan 2000), it is appropriate to consider a range of values of this ratio for the sake of completeness. Therefore, we consider B/Beq = 0.75, 0.85, and 0.95 for our stellar flux tube models, motivated by the range of B/Beq values considered by existing theoretical models (see Sect. 1). This allows us to deduce an appropriate set of energy fluxes for upwardly propagating longitudinal tube waves for specified values of α, given as 1.5, 1.8, and 2.0, resulting in a total of nine models per theoretical target star.

thumbnail Fig. 3

Power spectra of the instantaneous wave energy flux in flux tubes with B/Beq = 0.85 for F5 V, G5 V, K5 V, and M0 V stars (from top to bottom) as a function of the circular frequency ω. The mixing-length parameter is assumed as α = 2.

thumbnail Fig. 4

Different types of energy fluxes (see text) for the set of theoretical main-sequence stars for α = 2. Results are given for B/Beq = 0.75 (top), 0.85 (middle), and 0.95 (bottom).

3. Results and discussion

3.1. Computation of wave energy fluxes

The instantaneous and time-averaged tube wave energy fluxes are computed by employing a modified time-dependent wave code based on an earlier version by Herbold et al. (1985). The external turbulent motion is translated into internal pressure and velocity fluctuations. The time-averaged wave energy fluxes at the squeezing point are computed for each combination of effective temperature Teff, surface gravity log g, η = B/Beq, and mixing-length parameter α for flux tubes embedded in the atmospheres of the main-sequence stars as considered.

To evaluate reliable time-averaged wave energy fluxes and because of the spiky nature of the instantaneous wave energy fluxes, the wave propagation code has to be run over a time of about 35PD where PD is the wave period of the Defouw cut-off frequency (Defouw 1976). The generated waves include both propagating and non-propagating wave energy fluxes. We apply a high pass filter at the Defouw cut-off frequency, ωD, to the velocity and pressure fluctuations inside the flux tubes to separate the propagating waves and compute the time-averaged upwardly propagating wave components. The position of the filter is indicated by the low frequency cut-off depicted in Fig. 3, which compares the power spectra of different types of stars. We note that the power spectra reach their maxima at roughly 2ωD and decrease toward higher frequencies.

thumbnail Fig. 5

Upwardly propagating energy fluxes, also referred to as FLTW, for the set of theoretical main-sequence stars for α = 2 and different values of η = B/Beq.

Table 2

Wave energy fluxa for different parameters α and η.

Figures 4 and 5 as well as Tables 2 and 3 show the computed wave energy of the magnetic flux tube. For α = 2, Table 3 also distinguishes between the total energy flux, propagating energy flux, and the upwardly propagating energy flux; we refer to Ulmschneider et al. (2001) for detailed definitions. The wave energy flux FLTW identified as upwardly propagating energy flux shows a characteristic behaviour as function of the model parameters, notably the stellar spectral type (or Teff). It is found that the value of FLTW decreases by about a factor of 1.7 between G0 V and K0 V stars, and drops by almost two orders of magnitude between K0 V and M0 V stars. This is a direct consequence of the action of stellar convection, noting that in relatively hot main-sequence stars there is an enhanced efficiency in the creation of turbulence, which is reflected by the higher values of the rms velocity ut (see Fig. 2).

Table 3

Wave energy fluxa for different values of η based on α = 2.

We also found that the wave energy flux FLTW depends significantly on the magnetic field strengths inside the tubes, given as η = B/Beq, and depends relatively weakly on the mixing-length parameter α. Furthermore, the wave energy fluxes are found to increase with decreasing magnetic field strength inside the flux tube, a phenomenon that can be explained by the decreasing stiffness of the magnetic tube; see Fig. 5 for details. This behaviour was also pointed out by Ulmschneider et al. (2001).

Moreover, we find that the wave energy flux for upwardly propagating waves is also somewhat sensitive to the choice of α for the stellar convective zone. Note that an increase in the mixing length from α = 1.5 to 2.0 amplifies the simulated longitudinal wave energy fluxes by a factor of approximately 1.45, which is most notable for relatively hot main-sequence stars. This can be explained by, for higher values of α, the convective zones being more efficient in generating turbulence, thus resulting in higher values of the rms velocity ut (see Fig. 2).

3.2. Derivation of the fitting formula

The amount of information about FLTW for stars of different spectral types and the various choices for η and the mixing-length parameter α are a strong motivation for the derivation of a fitting formula. Our main focus are stars of temperatures between Teff = 6000 K (i.e., spectral type F9.5 V) and Teff = 4500 K (i.e., spectral type K5 V). Stars cooler than mid K-type are increasingly dominated by flare activity or other processes such as, e.g., magnetic reconnection (e.g., Narain & Ulmschneider 1996), which ensures that an accurate fitting formula is less essential. Nevertheless, we extended our fitting formula to stars of spectral type M0 V (with Teff = 3850 K) while reproducing the wave energy flux of M0 V stars with a precision of 10-3.

However, no attempt has been made to accurately reproduce the knee in the wave energy flux function near K8 V as this would have led to a significant complication in our fitting formula without obvious merits. This approach is motivated by the finding that energy dissipation by longitudinal tube waves appears to be less important in dwarfs stars of spectal type from mid-K to M than, e.g., flare heating as pointed out by Fawzy et al. (2002) in their comparison between empirical and theoretical radiative chromospheric emission losses.

Our formula is given by 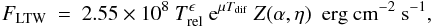(1)where Trel = Teff/Teff, ⊙  and Teff, ⊙  = 5777 K. Furthermore, Z(α,η) is given as 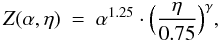(2)where η = B/Beq and γ = −4.5−30·|η − 0.85|. Moreover, Tdif is defined as Min(0,Teff − 4500 K), which means that Tdif is zero for Teff ≥ 4500   K and is otherwise negative. Note that the parameters ϵ and μ of Eq. (1) depend weakly on α and η; see Tables 4 and 5 for detailed information. If a reduced level of accuracy is permitted, it might be appropriate to use average values for α and μ, given as α = 5.21 and μ = 4.66 × 10-3, respectively.

Our formula for the upwardly propagating longitudinal wave energy flux has been subjected to thorough testing for stars of spectral type F9.5 V, G2 V, G5 V, G8 V, K0 V, K2 V, and K5 V. The simulated data for the F9.5 V star were obtained via logarithmic interpolation between the data for the F8 V and G0 V stars. Detailed information on the tests is given in Appendix A.

Table 4

Data for the parameter ϵ.

Table 5

Data for the parameter μ.

4. Summary and conclusions

We have studied the generation of longitudinal waves in stellar magnetic flux tubes of theoretical main-sequence stars. Our results are commensurate with those obtained from previous studies, especially the work of Ulmschneider et al. (2001). Our investigations show that by means of nonlinear time-dependent responses of stellar magnetic flux tubes to continuous and impulsive external turbulent pressure fluctuations, longitudinal tube waves were effectively produced via dipole emission. Furthermore, the shapes of the computed power spectra were found to be similar for stars of different effective temperature. Moreover, the longitudinal wave energy fluxes are found to increase with higher effective temperature, i.e., stars of earlier spectral types.

As part of our study, we have investigated the role of the magnetic field strength inside the tube B as well as that of the adopted convective model characterized by the mixing-length parameter α concerning the generated wave energy flux. We have found that the computed wave energy flux strongly depends on the strength of the magnetic field as already discussed in previous studies (e.g., Ulmschneider & Musielak 1998; Ulmschneider et al. 2001). For a given spectral type, the flux is considerably higher in tubes with a field strength of B/Beq = 0.75 compared to B/Beq = 0.95, although the difference as a function of spectral type is not as large as previously pointed out by Ulmschneider et al. (2001) owing to the differences in stellar surface gravity for the different types of stars. We note that the difference in the magnetic field strength of B/Beq = 0.75 and 0.95 is found to be a factor of 7.6, 6.1, 5.3, and 4.4 (for α = 2) for stars of spectral type F5 V, G0 V, K0 V, and M0 V, respectively. This difference exhibits a noticeable, albeit little dependence on the mixing-length parameter α for stars hotter than G2 V, related to the behaviour of the adopted root mean square velocity at the squeezing point of the tube.

Another aspect of our study was to consider a limited range of the mixing-length parameter α, which are 1.5, 1.8, and 2.0. It was found that an increase in the mixing length from α = 1.5 to 2.0 enhances the computed energy fluxes by a factor of about 1.45, corresponding to a proportionality of α1.25. This relationship can be compared with previous findings for acoustic energy generation, which show a dependence such as α2.8 (Bohn 1984) or α3.8 in updated models by Musielak et al. (1994). The relatively weak influence of α on the amount of upwardly propagating wave energy flux FLTW is apparently due to the latter being largely controlled by magnetic processes, as also indicated by the strong influence of η up to η-7.5, rather than being controlled by convective processes, which are, however, essential for the excitement of the tubes subsequently resulting in magnetic wave generation.

We note that the strong dependence of the generated wave energy fluxes on the stellar and magnetic parameters is in general agreement with the findings of previous studies, although some noticeable differences can be discerned. The wave energy flux FLTW decreases by about a factor of 1.7 between the G0 V and K0 V stars, and drops by almost two orders of magnitude between the K0 V and M0 V stars. For α = 2 at a fixed value of Teff = 5000 K, Ulmschneider et al. (2001) deduced a fitting formula for the behaviour of FLTW as a function of B/Beq, which is found to be commensurate with the results obtained in our current study. On the other hand, the fitting formula for the wave energy flux given in our paper is more general than any of the previously deduced formulae because it is applicable to a large range of stellar effective temperatures and furthermore allows insight into the role of the governing magnetic and convective parameters related to the amount of generated upwardly propagating wave energy flux. Therefore, it is of interest to future solar and stellar physics studies as it allows flexibility both concerning the mixing-length parameter α and the magnetic parameter η = B/Beq. Note that even for the Sun, η is expected to exhibit considerable spatial and temporal fluctuations across the surface as implied by previous solar physics research (see, e.g., Schrijver & Zwaan 2000, for background information).

Acknowledgments

This work has been supported by the Faculty of Engineering and Computer Sciences, Izmir University of Economics (D.E.F.) and the Department of Physics, University of Texas at Arlington (M.C.). The authors also appreciate previous comments by P. Ulmschneider and Z. E. Musielak.

References

  1. Bohn, H. U. 1984, A&A, 136, 338 [NASA ADS] [Google Scholar]
  2. Buchholz, B., Ulmschneider, P., & Cuntz, M. 1998, ApJ, 494, 700 [NASA ADS] [CrossRef] [Google Scholar]
  3. Castelli, F., & Kurucz, R. L. 2004, in Modelling of Stellar Atmospheres ed. N. E. Piskunov, W. W. Weiss, & D. F. Gray (San Francisco: ASP), IAU Symp., 210, CD-ROM, Poster 20 [Google Scholar]
  4. Cattaneo, F., Brummell, N. H., Toomre, J., Malagoli, A., & Hulburt, N. E. 1991, ApJ, 370, 282 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cuntz, M., Ulmschneider, P., & Musielak, Z. E. 1998, ApJ, 493, L117 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cuntz, M., Rammacher, W., Ulmschneider, P., Musielak, Z. E., & Saar, S. H. 1999, ApJ, 522, 1053 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cuntz, M., Rammacher, W., & Musielak, Z. E. 2007, ApJ, 657, L57 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cuntz, M., Guinan, E. F., & Kurucz, R. L. 2010, in Solar and Stellar Variability: Impact on Earth and Planets, ed. A. G. Kosovichev, A. H. Andrei, & J.-P. Rozelot (Cambridge: Cambridge Univ. Press), IAU Symp., 264, 419 [Google Scholar]
  9. Defouw, R. J. 1976, ApJ, 209, 266 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fawzy, D. E. 2010, MNRAS, 408, 293 [NASA ADS] [CrossRef] [Google Scholar]
  11. Fawzy, D. E., Ulmschneider, P., & Cuntz, M. 1998, A&A, 336, 1029 [NASA ADS] [Google Scholar]
  12. Fawzy, D., Ulmschneider, P., Stȩpień, K., Musielak, Z. E., & Rammacher, W. 2002, A&A, 386, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres, 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
  14. Güdel, M. 2007, Liv. Rev. Sol. Phys., 4, 3 [Google Scholar]
  15. Guinan, E. F., Ribas, I., & Harper, G. M. 2003, ApJ, 594, 561 [NASA ADS] [CrossRef] [Google Scholar]
  16. Hasan, S. S., Kalkofen, W., van Ballegooijen, A. A., & Ulmschneider, P. 2003, ApJ, 585, 1138 [NASA ADS] [CrossRef] [Google Scholar]
  17. Herbold, G., Ulmschneider, P., Spruit, H. C., & Rosner, R. 1985, A&A, 145, 157 [NASA ADS] [Google Scholar]
  18. Komm, R., Mattig, W., & Nesis, A. 1991, A&A, 243, 251 [NASA ADS] [Google Scholar]
  19. Kurucz, R. L. 2005, Mem. S. A. It., 8, 14 [Google Scholar]
  20. Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
  21. Muller, R. 1985, Sol. Phys., 100, 237 [NASA ADS] [CrossRef] [Google Scholar]
  22. Muller, R., Roudier, Th., Vigneau, J., & Auffret, H. 1994, A&A, 283, 232 [NASA ADS] [Google Scholar]
  23. Musielak, Z. E., Rosner, R., & Ulmschneider, P. 1989, ApJ, 337, 470 [NASA ADS] [CrossRef] [Google Scholar]
  24. Musielak, Z. E., Rosner, R., Stein, R. F., & Ulmschneider, P. 1994, ApJ, 423, 474 [Google Scholar]
  25. Musielak, Z. E., Rosner, R., Gail, H. P., & Ulmschneider, P. 1995, ApJ, 448, 865 [NASA ADS] [CrossRef] [Google Scholar]
  26. Musielak, Z. E., Rosner, R., & Ulmschneider, P. 2000, ApJ, 541, 410 [NASA ADS] [CrossRef] [Google Scholar]
  27. Narain, U., & Ulmschneider, P. 1990, Space Sci. Rev., 54, 377 [NASA ADS] [CrossRef] [Google Scholar]
  28. Narain, U., & Ulmschneider, P. 1996, Space Sci. Rev., 75, 453 [NASA ADS] [CrossRef] [Google Scholar]
  29. Nesis, A., Hanslmeier, A., Hammer, R., et al. 1993, A&A, 279, 599 [NASA ADS] [Google Scholar]
  30. Nordlund, Å., & Dravins, D. 1990, A&A, 228, 155 [NASA ADS] [Google Scholar]
  31. Nordlund, Å., & Stein, R. F. 1991, in Stellar Atmospheres: Beyond Classical Models, ed. L. Crivellari, & I. Hubeny (Dordrecht: Kluwer), 263 [Google Scholar]
  32. Nordlund, Å., Spruit, H. C., Ludwig, H.-G., & Trampedach, R. 1997, A&A, 328, 229 [NASA ADS] [Google Scholar]
  33. Saar, S. H. 1994, in Cool Stars, Stellar Systems, and the Sun 8, ed. J.-P. Caillault, San Francisco, ASP Conf. Ser., 64, 319 [Google Scholar]
  34. Schrijver, C. J. 1996, in Stellar Surface Structure, ed. K. G. Strassmeier, & J. L. Linsky (Dordrecht: Kluwer), IAU Symp., 176, 1 [Google Scholar]
  35. Schrijver, C. J., & Zwaan, C. 2000, Solar and Stellar Magnetic Activity (Cambridge: Cambridge Univ. Press) [Google Scholar]
  36. Schröder, K.-P., & Eggleton, P. P. 1996, Rev. Mod. Astr., 9, 221 [NASA ADS] [Google Scholar]
  37. Solanki, S. K. 1993, Space Sci. Rev., 63, 1 [NASA ADS] [CrossRef] [Google Scholar]
  38. Solanki, S. K. 1996, Stellar Surface Structure, ed. K. G. Strassmeier & J. L. Linsky (Dordrecht: Kluwer), IAU Symp., 176, 201 [Google Scholar]
  39. Spruit, H. C. 1981, A&A, 98, 155 [NASA ADS] [Google Scholar]
  40. Steffen, M. 1993, Habilitation Thesis, Univ. Kiel, Germany [Google Scholar]
  41. Stein, R. F., Nordlund, Å., Georgobiani, D., Benson, D., & Schaffenberger, W. 2009a, in Solar Stellar Dynamos as Revealed by Helio- and Asteroseismology, ed. M. Dikpati, T. Arentoft, I. González Hernández, C. Lindsey, & F. Hill (San Francisco: ASP), 416, 421 [Google Scholar]
  42. Stein, R. F., Georgobiani, D., Schaffenberger, W., Nordlund, Å., & Benson, D. 2009b, in Cool Stars, Stellar Systems, and the Sun 15, ed. E. Stempels, Melville, AIP Conf. Proc., 1094, 764 [NASA ADS] [CrossRef] [Google Scholar]
  43. Stenflo, J. O. 1978, Rep. Progr. Phys., 75, 3 [Google Scholar]
  44. Trampedach, R., Christensen-Dalsgaard, J., Nordlund, Å., & Stein, R. F. 1997, in Solar Convection and Oscillations and their Relationship, ed. F. P. Pijpers, J. Christensen-Dalsgaard, & C. S. Rosenthal (Dordrecht: Kluwer), 73 [Google Scholar]
  45. Ulmschneider, P., & Musielak, Z. E. 1998, A&A, 338, 311 [NASA ADS] [Google Scholar]
  46. Ulmschneider, P., Theurer, J., & Musielak, Z. E. 1996, A&A, 315, 212 [NASA ADS] [Google Scholar]
  47. Ulmschneider, P., Theurer, J., Musielak, Z. E., & Kurucz, R. 1999, A&A, 347, 243 [NASA ADS] [Google Scholar]
  48. Ulmschneider, P., Musielak, Z. E., & Fawzy, D. E. 2001, A&A, 374, 662 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: tests for the fitting formula

To test our fitting formula (see Eq. (1)), we considered two different metrices, i.e., the linear and the quadratic metric, which allow us to assess the accuracy of the formula. The linear metric is given by 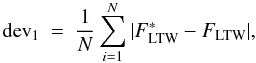(A.1)whereas the quadratic metric (also referred to as the rms metric) is given by 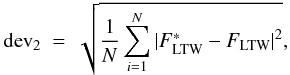(A.2)where FLTW refers to the wave energy flux of the detailed models, 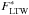refers to the wave energy flux obtained by the fitting formula (or vice versa), and N denotes the number of stars per test series.

The test results were derived for the different values of η and α (see Table A.1 for details). It is found that the average deviation, regardless of the selected metric, is typically considerably better than 10%, and for some of the test series, the average deviation is found to be better than 5%. We also checked the maximal deviation for individual stars, denoted as Δmax, for a given test series. Our results indicate that the maximal deviation almost never exceeds 15%. Finally, we also calculated the mean deviation between the model data and the data given by the formula for the entire set of considered theoretical main-sequence stars, comprising 63 models. We found that for the entire set of model stars, the linear metric yields a mean deviation of 5.5%, whereas the quadratic metric yields a mean deviation of 6.5%, a strong testimony of the quality of our fitting formula for the overall range of solar-type stars.

Table A.1

Accuracy of the fitting formula.

All Tables

Table 1

Theoretical main-sequence stars.

In the text
Table 2

Wave energy fluxa for different parameters α and η.

In the text
Table 3

Wave energy fluxa for different values of η based on α = 2.

In the text
Table 4

Data for the parameter ϵ.

In the text
Table 5

Data for the parameter μ.

In the text
Table A.1

Accuracy of the fitting formula.

In the text

All Figures

thumbnail Fig. 1

Diagram of a flux tube embedded into a stellar convective zone. The squeezing point of the tube is assumed to be located at optical depth τ5000 = 1, coinciding with the “stellar surface”. Credit: P. Ulmschneider.

In the text
thumbnail Fig. 2

Root mean square turbulent velocities at the squeezing point (τ5000 = 1) for the set of theoretical main-sequence stars for different values of the mixing-length parameter α.
In the text
thumbnail Fig. 3

Power spectra of the instantaneous wave energy flux in flux tubes with B/Beq = 0.85 for F5 V, G5 V, K5 V, and M0 V stars (from top to bottom) as a function of the circular frequency ω. The mixing-length parameter is assumed as α = 2.

In the text
thumbnail Fig. 4

Different types of energy fluxes (see text) for the set of theoretical main-sequence stars for α = 2. Results are given for B/Beq = 0.75 (top), 0.85 (middle), and 0.95 (bottom).

In the text
thumbnail Fig. 5

Upwardly propagating energy fluxes, also referred to as FLTW, for the set of theoretical main-sequence stars for α = 2 and different values of η = B/Beq.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.