| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201015686 | |
| Published online | 29 November 2010 | |
Letter to the Editor
Implementation of the Nambu Jona-Lasinio model in hybrid stars
1
INFN, Sezione di Roma. Piazzale Aldo Moro 2,
00185
Roma,
Italy
e-mail: omar.benhar@roma1.infn.it
2
Dipartimento di Fisica, “Sapienza” Università di Roma. Piazzale
Aldo Moro 2, 00185
Roma,
Italy
e-mail: andrea.cipollone@roma1.infn.it
Received:
3
September
2010
Accepted:
6
November
2010
The model of Nambu and Jona-Lasinio has been extensively used to model the possible occurrence of quark matter in the core of compact stars. While based entirely on similar physical assumptions, previous studies have been performed using a variety of model versions, differing in both the number of active quark flavors and the structure of the quark-quark interaction. We discuss the results of our systematic analysis, designed to clarify the role of the vector and instanton-induced interactions in determining the properties of hybrid stars. The results of our calculations, carried out using a state-of-the-art description of the hadronic phase, show that the instanton-induced interaction does not affect the stiffness of the quark matter equation of state, whereas the effect of the repulsive vector interaction is sizable. However, no values of the corresponding coupling constants allow for the formation of a stable core of quark matter.
Key words: dense matter / equation of state / stars: neutrons / stars: interiors
© ESO, 2010
1. Introduction
The Nambu Jona-Lasinio (NJL) model (for a thorough review see, e.g., Buballa 2005) has been extensively used to study the possible occurrence of deconfined quark matter in the inner core of compact stars, where the density is believed to exceed several times the central density of atomic nuclei, ρ0 ≈ 2.7 × 1014 g/cm3 (Schertler et al. 1999; Baldo et al. 2003, 2007; Coehlo et al. 2010).
While not including a mechanism leading to quark confinement, the NJL model explains the spontaneous breakdown of chiral symmetry and provides a quantitative account of the spectrum of pseudoscalar mesons. However, its applications in studies of hybrid stars are based on a variety of implementations of the underlying physics, featuring differences in the number of active quark flavors as well as in the structure of the interactions. Schertler et al. (1999) and Baldo et al. (2003) consider u, d, and s quarks, whose dynamics are described by a Lagrangian including scalar and pseudoscalar four-quark interactions, supplemented by an instanton induced six-quark interaction (‘t Hooft 1976). On the other hand, Baldo et al. (2007) restrict their analysis to the light flavor sector, in which the six-quark interaction term vanishes, and allow for a density-dependent momentum cutoff. Finally, in the two flavor model of Coehlo et al. (2010) the Lagrangian includes an additional vector interaction term.
Besides the differences associated with the description of deconfined quark matter, hybrid star modeling also involves a degree of ambiguity arising from the description of the hadronic phase at supranuclear densities. At ρ ≳ ρ0, the relevant degrees of freedom are neutrons and protons, and most calculations of the equation of state (EOS) are carried out using either non-relativistic nuclear many body theory (NMBT) and phenomenological nuclear hamiltonians (Akmal et al. 1998; Gandolfi et al. 2010; Baldo 1999), or the relativistic mean field (RMF) approach, in which nucleons are described as Dirac particles interacting by means of meson exchange (Walecka 1974). The NMBT and RMF formalisms can both be generalized to take into account the appearance of strange baryons (hyperons), which may become energetically favored at higher density. However, the available models of the hyperon-nucleon interaction are only loosely constrained by a small amount data, while no empirical information is available on the hyperon-hyperon interaction.
This work is designed to analyze the impact of the differences in the implementation of the NJL model on the static properties of hybrid stars. To clearly identify the role of quark interactions, the systematic uncertainty associated with the description of the hadronic phase must be minimized. Hence, we assume that the hadronic phase consist of neutrons and protons only, whose dynamics is described by a non-relativistic Hamiltonian strongly constrained by phenomenology. Thanks to developments in nuclear many-body theory, this Hamiltonian can be used to carry out highly accurate calculations of the properties of neutron-star matter within quantum Monte Carlo approaches (Gandolfi et al. 2010). The deconfined phase is described within the three-flavor NJL model, taking into account both the vector and the instanton-induced interactions. The vector term is known to play an important role in the treatment of interacting systems within the mean field approximation, whereas the inclusion of the six-quark interaction has been shown to provide a remarkably good description of light scalar meson decays (‘t Hooft et al. 2008). To focus on the effects of the vector and instanton interactions, we do not take into account in our analysis non-standard features included in the NJL model, such as the chemical potential-dependence of the cutoff (Baldo et al. 2007; Lenzi et al. 2010).
The approach employed to obtain the hadronic EOS is outlined in Sect. 2, while Sect. 3 is devoted to a description of the SU(3) NJL model of the deconfined phase. In Sect. 4, we discuss our numerical results and present our conclusions.
2. Hadronic phase
All models of EOS based on hadronic degrees of freedom predict that in the density range ρ0 ≲ ρ ≲ 2ρ0 the matter in compact stars consists mainly of neutrons, with the admixture of a small number of protons, electrons, and muons.
This picture may change significantly at higher density with the appearance of hyperons (Λ0,Σ − ,...) produced in weak interaction processes. However, in view of the large uncertainties involved in describing hyperon dynamics, the possible occurrence of strange hadrons is not taken into account in this work.
Accurate calculations of the EOS of both isospin symmetric nuclear matter (SNM) and pure
neutron matter (PNM) have been carried out using the auxiliary field diffusion monte carlo
(AFDMC) approach (Gandolfi et al. 2010), using a
phenomenological Hamiltonian including the Argonne 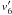 nucleon-nucleon (NN) potential (Wiringa & Pieper
2002). The effects of many-body interactions, which are known to become significant
at ρ ≳ ρ0, have also been taken into account,
following the scheme originally proposed by Lagaris
& Pandharipande (1981). The EOS of Gandolfi
et al. (2010) reproduces the empirical equilibrium properties of SNM (binding
energy per nucleon, equilibrium density ,and compressibility) and is compatible with the
constraints extracted from the analysis of nuclear collisions (Danielewicz et al. 2002).
nucleon-nucleon (NN) potential (Wiringa & Pieper
2002). The effects of many-body interactions, which are known to become significant
at ρ ≳ ρ0, have also been taken into account,
following the scheme originally proposed by Lagaris
& Pandharipande (1981). The EOS of Gandolfi
et al. (2010) reproduces the empirical equilibrium properties of SNM (binding
energy per nucleon, equilibrium density ,and compressibility) and is compatible with the
constraints extracted from the analysis of nuclear collisions (Danielewicz et al. 2002).
The SNM and PNM results can been used to obtain the EOS of nuclear matter at arbitrary
proton fraction
x = np/nB,
where np and nB are the proton and
baryon number density, respectively. For any given value of nB,
x is determined by the conditions of β-equilibrium and
charge neutrality given by  In
the above equations, ℓ denotes the lepton flavor (electron or muon), while
μα is the chemical potential of the particles
of species α.
In
the above equations, ℓ denotes the lepton flavor (electron or muon), while
μα is the chemical potential of the particles
of species α.
For the densities of 107 g/cm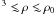 , corresponding to the
outer and inner crust of the star, we use the EOS of Baym
et al. (1971) and Pethick et al. (1995),
respectively. However, our results are largely unaffected by the details of the EOS at
subnuclear density.
, corresponding to the
outer and inner crust of the star, we use the EOS of Baym
et al. (1971) and Pethick et al. (1995),
respectively. However, our results are largely unaffected by the details of the EOS at
subnuclear density.
3. Deconfined phase
The main assumption underlying the NJL model is that, at low energy and momentum, gluon
degrees of freedom are frozen and quark dynamics can be described by a local effective
interaction. Within this picture, and including the contributions of three active flavors,
the Lagrangian of the fundamental theory of strong interactions (quantum chromo dynamics, or
QCD) can be replaced by ![\begin{eqnarray} \label{lag} \mathcal{L}&=&\sum_{i=1}^3\bar{q}_i({\rm i}\gamma_{\mu}\partial^{\mu}-m_{0i})q_i \nonumber\\ &\quad+&g_S\sum_{a=0}^{8}[ (\bar{q}\,\lambda^a\,q)^2+(\bar{q}\,{\rm i} \gamma_5\lambda^a\,q)^2] \\ &\quad-&g_V\sum_{a=0}^8[(\bar{q}\,\gamma_{\mu}\lambda^a\,q)^2 +(\bar{q}\,\gamma_5\gamma_{\mu}\lambda^a\,q)^2)]\nonumber\\ &\quad +&g_T\{\det[\bar{\psi}(1+\gamma_5)\psi]+\det[\bar{\psi}(1-\gamma_5)\psi]\} \nonumber \ , \end{eqnarray}](/articles/aa/full_html/2011/01/aa15686-10/aa15686-10-eq23.png) (3)where
qi denotes the quark field, the index
i specifies the flavor, the
λa with
a = 1,2,...8 are
Gell-Mann matrices acting in flavor space,
(3)where
qi denotes the quark field, the index
i specifies the flavor, the
λa with
a = 1,2,...8 are
Gell-Mann matrices acting in flavor space, 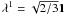 , and the
determinant is to be performed in flavor space.
, and the
determinant is to be performed in flavor space.
In the chiral limit, corresponding to m0i = 0,
the Lagrangian of Eq. (3) is invariant under
the same chiral group as QCD, i.e.,
SU(3)L ⊗ SU(3)R ⊗ U(1)V,
whose spontaneous breakdown is signaled by non-vanishing quark condensates
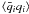 (i = 1,2,3). The
U(1)A symmetry is explicitly broken by the
instanton-induced determinant interaction, leading to
η − η′ mixing. In the case of two flavors,
with u and d quarks only, the breaking of
U(1)A can be taken into account using an
SU(2)L ⊗ SU(2)R ⊗ U(1)V
symmetric four-point interaction.
(i = 1,2,3). The
U(1)A symmetry is explicitly broken by the
instanton-induced determinant interaction, leading to
η − η′ mixing. In the case of two flavors,
with u and d quarks only, the breaking of
U(1)A can be taken into account using an
SU(2)L ⊗ SU(2)R ⊗ U(1)V
symmetric four-point interaction.
The model parameters are the quark bare masses, the coupling constants gS, gV, and gT and a cutoff Λ, needed to regularize divergent loop integrations. The values of m0i, gS, gT, and Λ are determined assuming isospin symmetry, i.e. setting m0u = m0d, and reproducing the masses of the pseudoscalar mesons, π, K, and η′, as well as the pion decay constant fπ. In our work, we assume that m0u = m0d = 5.5 MeV, m0s = 140.7MeV, gS = 20.23 GeV-2 and Λ = 0.6023 GeV (Rehberg et al. 1996). To explore the sensitivity of our results to the strength of the instanton induced interaction, we carried out calculations for several values of gT, ranging from 0 to 0.08 fm5 (for comparison, the value resulting from the fit of Rehberg et al. (1996) is gT = 155.9GeV-5 = 0.047 fm5).
The value of the vector coupling constant cannot be obtained using the procedure employed to determine gS, as the masses of the vector mesons are not dictated by chiral symmetry. To carry out a systematic analysis of the effects of the vector interaction term on the properties of hybrid stars, we allowed the ratio ξ = gV/gS to vary in the range 0 ≤ ξ ≤ 1.
The properties of quark matter at zero temperature are obtained from the Lagrangian of
Eq. (3) within the mean field
approximation, i.e. neglecting quantum fluctuations. This procedure leads to the gap
equations for the dynamically generated quark masses and chemical potentials,
mi and
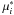
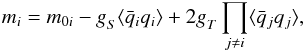 (4)and
(4)and 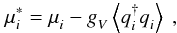 (5)where
(5)where
 ,
pFi being the Fermi momentum of the quark of
flavor i. Equation (5)
clearly shows that the vector interaction plays a critical role in determining the value of
the chemical potential. Within the mean field approximation, this is the only interaction
term that survives in the non-relativistic limit, and is the same in all theories featuring
a four-particle interaction (e.g. the Hubbard model and BCS theory). The correction to the
chemical potential describes the interaction between a quasi-particle and the mean field
generated by all particles in the Fermi sea. Setting
gV = 0, which amounts to neglecting this
interaction altogether, significantly affects the determination of quark Fermi momenta by
means the β-equilibrium conditions.
,
pFi being the Fermi momentum of the quark of
flavor i. Equation (5)
clearly shows that the vector interaction plays a critical role in determining the value of
the chemical potential. Within the mean field approximation, this is the only interaction
term that survives in the non-relativistic limit, and is the same in all theories featuring
a four-particle interaction (e.g. the Hubbard model and BCS theory). The correction to the
chemical potential describes the interaction between a quasi-particle and the mean field
generated by all particles in the Fermi sea. Setting
gV = 0, which amounts to neglecting this
interaction altogether, significantly affects the determination of quark Fermi momenta by
means the β-equilibrium conditions.
 |
Fig. 1 Left panel: quark matter EOS obtained setting ξ = gV/gS = 0 and using different values of gT. Right panel: same as the left panel but with gT = 0 and different values of ξ. The inset of the left panel shows the function (ϵ − ϵ0)ρ/ρ0, with ϵ0 = 220 MeV. |
As pointed out in Sect. 2, the composition of matter
in the star interior is dictated by the requirements of charge neutrality and equilibrium
with respect to weak interaction processes. In the case of three-flavor quark matter at
fixed baryon density nB, the corresponding equations can be
written in the form (compare to Eqs. (1)
and (2))
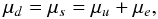 (6)
(6)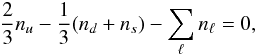 (7)with
(7)with
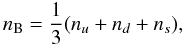 (8)where
(8)where
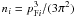 is the number density of quarks
of flavor i.
is the number density of quarks
of flavor i.
We note that Eqs. (1) and (6) do not include the contributions of neutrinos
produced in the weak interaction processes. This is a consequence of the assumption that
neutrinos can freely escape, so that their chemical potential vanishes. Using the quark
densities resulting from the solution of Eqs. (6) and (7) with the lepton chemical
potentials given by 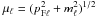 , one
obtains the EOS at zero temperature, i.e. the relation linking pressure to energy density.
, one
obtains the EOS at zero temperature, i.e. the relation linking pressure to energy density.
Figure 1 illustrates the effects of the vector and instanton-induced interactions on the quark matter EOS. The left panel displays the curves P(ϵ) corresponding to different values of gT and ξ = 0, while the right panel shows the results obtained using different values of ξ and setting gT = 0. It clearly appears that when ξ increases the EOS gets stiffer, i.e. matter becomes more incompressible, since the vector interaction is repulsive. On the other hand, for large values of gT we observe a change in concavity, reflecting a similar pattern in ϵ(ρ), shown in the inset of the left panel (since the variations in ϵ are very small, the function displayed is (ϵ − ϵ0)ρ/ρ0 with ϵ0 = 220 MeV, the additional linear term does not affect the concavity). In general, that the free energy is not a convex function of density implies that a separation into two phases is favored. However, in this context the two different phases have no clear physical interpretation, and the effect disappears as ξ increases.
Besides the knowledge of the hadronic and quark matter EOS, hybrid star modeling requires a quantitative understanding of the nature of the deconfinement phase transition. Early works on the possible occurrence of quark matter in compact stars (e.g. Baym & Chin 1976) were based on the assumption that nuclear and quark matter are both charge neutral, and separated by a sharp interface. As a consequence, the transition takes place at constant pressure, and can be described using the Maxwell double tangent construction (Huang 1963).
In the 1990s, Glendenning (1992) first pointed out that the requirement that the two phases be individually charge-neutral is in fact too restrictive. In a more general scenario, charged nuclear and quark matter may share a common lepton background, thus giving rise to a mixed phase extending in space over a sizable fraction of the star.
A transition at constant pressure necessarily leads to the appearance of a discontinuity in the star density profile, i.e. to a star consisting of an inner core of quark matter at energy density ϵQM surrounded by nuclear matter at energy density ϵNM. On the other hand, the mixed phase allows for a smooth variation in the energy density, leading in turn to a smooth variation in the star density profile.
Whether the transition can proceed at constant pressure or by forming of a mixed phase depends on the value of the Debye screening length, driving charge separation, and the amount of electrostatic and surface energy needed to form the structures of quark and nuclear matter in the mixed phase. If screening is too strong for a uniform lepton density to be possible, or if the energy loss due to Coulomb and surface effects exceeds the gain in bulk energy, the simpler scenario predicted by Maxwell construction turns out to be favorable. The results of numerical estimates show that the stability of the mixed phase is driven by the largely unknown surface tension of quark matter. According to the philosophy outlined in the Introduction, we avoid this additional uncertainty and assume that the phase transition takes place at constant pressure. This assumption is supported by the results of the studies of Alford et al. (2001) and Benhar & Rubino (2005), suggesting that the mixed phase is unlikely to be stable for a broad range of values of the surface tension.
 |
Fig. 2 Mass-central density relations corresponding to different values of the parameter ξ and gT. |
 |
Fig. 3 Mass-radius relations corresponding to different values of the parameter ξ and gT. |
4. Hybrid star structure
As pointed out above, within our picture hybrid stars consist of charge-neutral nuclear
matter at baryon number density 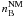 coexisting
with charge-neutral quark matter at densities
coexisting
with charge-neutral quark matter at densities 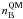 ,
,
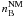 , and
, and
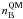 constrained by the
requirements
constrained by the
requirements 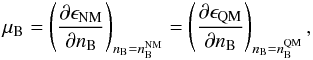 (9)where
μB is the chemical potential associated with the conservation
of baryon number. When
(9)where
μB is the chemical potential associated with the conservation
of baryon number. When 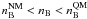 , the pressure
and chemical potential remain constant.
, the pressure
and chemical potential remain constant.
Given the EOS of matter in the star interior, the equilibrium configurations of a compact star are obtained by solving the Tolman Oppenheimer Volkoff (TOV) equations, combining Einstein’s equations for a static sphericallysymmetric perfect fluid with the classical equation of hydrostatic equilibrium. For any value of the energy density at the center of the star, ϵc, the numerical solution of the TOV equations provides the star radius (R), defined as the distance from the center at which the pressure vanishes, and its mass (M). Stable equilibrium configurations correspond to the region of ϵc in which ∂M/∂ϵc > 0.
The development of a stable core of quark matter is driven by the compressibility of the quark matter EOS at the onset of the deconfinement phase transition. If the EOS is too soft, the hybrid star exhibits an instability, signaled by the appearance of a cusp in the curve M(R).
Figures 2 and 3 show the mass-central density and mass-radius relations, respectively, obtained using the EOS described in Sects. 2 and 3, and assuming that the deconfinement transition takes place at constant pressure. The different curves correspond to different values of the couplings constants associated with the vector and instanton-induced interactions. For comparison, we also show the results corresponding to a neutron star, with no quark matter core. It is apparent that no values of ξ and gT allow a stable core of quark matter to form.
The instanton-induced interaction has almost no impact on the compressibility of quark matter, as illustrated by the slope of the curves of Fig. 1 becoming nearly independent of gT at large ϵ. As a consequence, the maximum mass of the hybrid star configurations corresponding to ξ = 0.5 and 0.01 ≤ gT ≤ 0.08 are very close to one another.
On the other hand, the inclusion of the repulsive vector interaction leads to significant changes in the compressibility. Larger ξ corresponds to stiffer EOS and a higher maximum mass, and for ξ = 1 the hybrid-star maximum mass turns out to be hardly distinguishable from the neutron star one. However, the instability of the quark matter core persists, as indicated by the cusps exhibited by the curves displayed in Fig. 3.
Our results, obtained by including both the vector and instanton interactions and exploring a broad region of parameter space, are in qualitative agreement with those of Baldo et al. (2003, 2007), which were obtained using a similar EOS for the hadronic phase but neglecting the vector interaction term. The generalization of the NJL model based on the use of a density-dependent cutoff does not appear to change the picture but leads to a softer EOS, thus enhancing the instability of the quark matter core (Baldo et al. 2007). The results obtained including the repulsive vector interaction also agree with those described by Coehlo et al. (2010). A somewhat different picture is suggested by the results of Lenzi et al. (2010). However, they neglect the vector interaction term and, to obtain a stable hybrid star, introduce a rather “ad hoc” dependence of the cutoff on the chemical potential.
We finally note that our conclusions do not appear to be affected significantly by the assumption that the hadronic phase consists of nucleons only and by the procedure adopted to describe the deconfinement transition. The analysis of Schertler et al. (1999) suggests that even in the presence of strange hadrons the stability of hybrid stars with a quark core described within the NJL model is very unlikely. As for the phase transition, although the formation of a mixed phase would lead to a different scenario, the presence of a stable quark matter core would still be excluded.
References
- Akmal, A., Pandharipande, V., & Ravenhall, D. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Rajagopal, K., Reddy, S., & Wilczek, F. 2001, Phys. Rev. D, 64, 074017 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M. 1999, in Nuclear Methods and the Nuclear Equation of State, ed. M. Baldo (Singapore: World Scientific), 1 [Google Scholar]
- Baldo, M., Buballa, M., Burgio, G., et al. 2003, Phys. Lett. B, 562, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Burgio, G., Castorina, P., Plumari, S., & Zappalà, D. 2007, Phys. Rev. C, 75, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., & Chin, S. 1976, Phys. Lett. B, 62, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Pethick, C., & Sutherland, J. 1971, ApJ, 170, 299 [Google Scholar]
- Benhar, O., & Rubino, R. 2005, A & A, 434, 247 [NASA ADS] [Google Scholar]
- Buballa, M. 2005, Phys. Rep., 407, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Coehlo, J., Lenzi, C., Malheiro, M., Marinho, R., & Fiolhais, M. 2010, Int. J. Mod. Phys. D, 19, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Danielewicz, P., Lacey, R., & Lynch, W. 2002, Science, 298, 1592 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gandolfi, S., Illarionov, A., Fantoni, S., et al. 2010, Mon. Not. R. Astron. Soc., 404, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. 1992, Phys. Rev. D, 46, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, K. 1963, Statistical Mechanics (New York: Wiley Interscience) [Google Scholar]
- Lagaris, I., & Pandharipande, V. 1981, Nucl. Phys. A, 359, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzi, C., Schneider, A., Providencia, C., & Marinho, R. 2010, Phys. Rev. C, 82, 015809 [NASA ADS] [CrossRef] [Google Scholar]
- Pethick, C., Ravenhall, D., & Lorenz, C. 1995, Nucl. Phys. A, 369, 470 [Google Scholar]
- Rehberg, P., Klevansky, S., & Hüfner, J. 1996, Phys. Rev. C, 53, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Schertler, K., Leupold, S., & Schaffner-Bielich, J. 1999, Phys. Rev. C, 60, 025801 [NASA ADS] [CrossRef] [Google Scholar]
- ‘tHooft, G. 1976, Phys. Rev. Lett., 37, 8 [NASA ADS] [CrossRef] [Google Scholar]
- ‘tHooft, G., Isidori, G., Maiani, L., Polosa, A., & Riquer, V. 2008, Phys. Lett. B, 662, 424 [Google Scholar]
- Walecka, J. 1974, Ann. Phys., 83, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Wiringa, R., & Pieper, S. 2002, Phys. Rev. Lett, 89, 182501 [Google Scholar]
All Figures
 |
Fig. 1 Left panel: quark matter EOS obtained setting ξ = gV/gS = 0 and using different values of gT. Right panel: same as the left panel but with gT = 0 and different values of ξ. The inset of the left panel shows the function (ϵ − ϵ0)ρ/ρ0, with ϵ0 = 220 MeV. |
| In the text | |
 |
Fig. 2 Mass-central density relations corresponding to different values of the parameter ξ and gT. |
| In the text | |
 |
Fig. 3 Mass-radius relations corresponding to different values of the parameter ξ and gT. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


