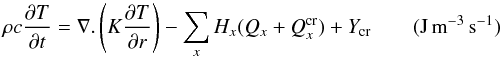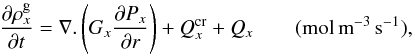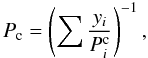EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 525 (January 2011) A&A, 525 (2011) A144 Full HTML
Free Access
Issue
A&A
Volume 525, January 2011
Article Number A144
Number of page(s) 4
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201015438
Published online 09 December 2010

© ESO, 2010

1. Introduction

For several years, Jupiter-family comets (hereafter JFCs) have been the targets of spacecraft missions whose aims are to determine the comets’ composition, structure, and physical properties. The Stardust mission has collected dust originating from Comet 81P/Wild 2 in January 2004 (Tsou et al. 2004), and the Rosetta mission is currently flying towards Comet 67P/Churyumov Gerasimenko for a rendezvous in August 2014 (Schulz et al. 2004). Moreover, Comet 46P/Wirtanen, which was the initial target of the Rosetta mission (Schulz & Schwehm 1996), is again considered for a rendezvous in 2021 with the PriME (Primitive Material Explorer) mission, which is currently proposed to NASA as a Discovery mission (Cochran et al. 2010).

Marboeuf et al. (2010) recently proposed that CO and CO2 clathrate hydrates (hereafter clathrates) could exist within short period comets1 (hereafter SPCs). Clathrates are non-stoichiometric crystalline compounds, with hydrogen-bonded H2O molecules forming cages in which gas molecules are trapped individually by van der Waals interactions. At a given temperature, the stability of these cages is ensured as long as the gas phase pressure equals or exceeds the dissociation pressure of the considered clathrate. Using a thermodynamic model of JFCs including a mixture of H2O, CO, and CO2 ices, Marboeuf et al. (2010) showed that the stability zone of clathrates in these comets is restricted to a small part of the nucleus. They also found that the stability zone of clathrates could almost disappear at perihelion in Halley-type comets.

Using a mixture of gases, Mousis & Schmitt (2008) showed that the resulting clathrate is also a mixture of volatiles whose equilibrium pressure is somewhere between that of the individual gases. In the present work, we consider a larger and more representative set of volatiles (CO, CO2, CH4, and H2S) that might exist in the nuclei compared to the one (CO and CO2) initially adopted by Marboeuf et al. (2010). We then investigate the formation conditions of clathrates within the two JFCs 67P/Churyumov-Gerasimenko (hereafter 67PCG) and 46P/Wirtanen (hereafter 46PW) and show that irrespective of the latitude of the considered area, a permanent layer of multiple guest clathrates is likely to form in the subsurfaces of the two comets, and in a broader manner, in the subsurfaces of all SPCs. This suggests new directions of investigation for comet nucleus modelling which will be addressed in a forthcoming paper.

2. Nucleus model

The nucleus model employed in this work is based on the one-dimensional model developed by Marboeuf (2008) and Marboeuf et al. (2009). The model considers an initially homogeneous sphere composed of a predefined porous mixture of ices and dust in specified proportions. It describes heat transmission, gas diffusion, sublimation/recondensation of volatiles within the nucleus, water ice phase transition, dust release, and mantle formation. Water ice can be initially amorphous or crystalline, depending on the formation location of the body in the primitive nebula. When the ice is initially amorphous, a fraction of the volatiles is trapped in the water ice matrix and the remaining fraction forms pure condensates in the pores. When heated, the fraction of volatiles condensed in the pores sublimates first, and then the other fraction trapped within the matrix is released during the transition from amorphous to crystalline water ice. The released gas diffuses throughout the porous matrix by tortuous capillary tubes and eventually escapes from the object. The crystallization occurs on a temperature-dependant timescale 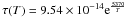, where T is the temperature (K) (Schmitt et al. 1989). Hence crystallization becomes efficient and effectively occurs at temperatures ~110 K.

These physical processes are described by the equation of diffusion of heat and mass. The heat diffusion throughout the nucleus is described by the energy conservation equation:

(1)

with 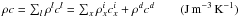. Here t is the time (s), K the heat conduction coefficient (J s-1 m-1 K-1) of the porous matrix, whose formula is based on geometric assumptions (Espinasse et al. 1993; Orosei et al. 1999), r the distance (m) from the centre of the nucleus, ρl the density (kg m-3) and cl the specific heat capacity (J kg-1 K-1) of the solid component l in the comet nucleus (l =  d for dust or i for pure ices of elements x). Hx is the molar latent heat of sublimation of ice x (J mol-1) and 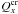(mol m-3 s-1) and Ycr are the rate of moles of gas x and the power per unit volume released during the crystallization process of amorphous water ice respectively (Espinasse et al. 1991; Orosei et al. 1999). Qx is the rate of volatile molecule x (mol m-3 s-1) that sublimates/condenses in the pores of the matrix, and is given by the gas diffusion equation that describes the diffusion of gas through the porous matrix for each molecule x:

(2)

where 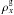is the molar density of gas x (mol m-3), Px its partial pressure (Pa) and Gx its diffusion coefficient (mol m-1 s-1 Pa-1). The flux of gas diffusing through the porous matrix can be either a free molecular flow or a viscous flow, because the mechanism governing the diffusion of volatiles is selected according to the mean free path of molecules (Prialnik et al. 2004).

At the surface, the local temperature is given by a thermal balance between the adsorbed solar energy, the thermal emission, the heat diffusion towards the interior and the energy of sublimation of the existing ices (Orosei et al. 1999). Note that at each time step the porosity and the radius of pores are recomputed for each layer, taking into account the density variations of the solid phase.

3. Thermodynamic parameters and initial composition

At the beginning of the computation, the initial water ice of our nucleus is assumed to be amorphous (Taylor 1992; Kouchi et al. 1994). The JFCs come probably from the Kuiper Belt (Lowry et al. 2008), which is populated by objects likely made from amorphous ice. Kouchi et al. (1994) showed that temperatures lower than ~110 K, corresponding to heliocentric distances greater than ~12 AU in the solar nebula would preserve the amorphous ice initially formed in the ISM. Below ~12 AU, the disk temperature exceeded ~110 K, resulting in the crystallization of the amorphous grains embedded in that part of the nebula. In addition to water ice, the model takes into account the solid phases of CO, CO2, CH4, and H2S. These molecules are among the most abundant volatile species (production rates relative to water greater than 1%) observed in cometary nuclei (Bockelée-Morvan et al. 2004) and are susceptible to form clathrates at low-pressure conditions (Lunine & Stevenson 1985). Other molecules such as H2CO, CH3OH, and NH3, which are also abundant in comets, have not been considered in this study because there are no experimental data concerning the equilibrium of H2CO and CH3OH clathrates (Fray & Schmitt 2009; Marboeuf et al. 2008; Mousis et al. 2009), while NH3 does not form clathrates (Lunine & Stevenson 1985). Table 1 gives the X/H2O (JX) mole fractions relative to water (with X = CO, CO2, CH4 or H2S) of the volatiles initially present in the nucleus, either condensed in the porous network (first number), or trapped in the amorphous matrix (second number, in parenthesis). The latter depends on the environment temperature, the molecule (equilibrium pressure, size, polarizability) and its initial abundance in the molecular cloud (Kouchi et al. 1994; Bar-Nun et al. 2007), which leads to very large differences among the trapping efficiencies of various gases (Bar-Nun et al. 2007). Schmitt et al. (1989) showed that amorphous ice can trap other volatiles only up to 8% in mole of water. Unfortunately, there are currently no experimental data that give the relative proportions of volatiles trapped in amorphous ice and in porous network. We therefore choose plausible arbitrary initial concentrations, considering the initial abundances and equilibrium pressure of volatiles. Changing the concentrations by a factor of a few only speeds up or delays the progression of the crystalization and sublimation fronts, but not the actual temperature of the sublimation interface and the vapor pressure in the pores. In other words, this does not change the overall effects described here. The values of JX are consistent with the observations in cometary comae of molecular species that are directly released from the nucleus (Bockelée-Morvan et al. 2004).

Table 1

Physical parameters of the nuclei at the beginning of the computation.

The vapour pressures of the pure condensates are obtained from Fray & Schmitt (2009) and the amorphous to crystalline ice phase transition is postulated exothermic2 and irreversible. Thermodynamic quantities characterizing other materials derive from Marboeuf et al. (2010). Table 1 summarizes the orbital parameters adopted in our study for comets 67PCG and 46PW.

The presence of several volatile compounds in the gas phase of the porous network can generate the formation of a multiple guest clathrate (hereafter MG clathrate) whose equilibrium pressure varies as a function of the gas phase composition and the temperature. The equilibrium pressure of the MG clathrate Pc is given by (Lipenkov and Istomin 2001; Hand et al. 2006)

(3)

where yi is the mole fraction of the volatile i in the gas phase and 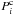the equilibrium pressure of the corresponding clathrate. Here we assume that the clathrate hydrate behaves as an ideally diluted solution and that the ratio of occupancies for cages is constant and the same for all guest molecules. The equilibrium pressures of the different single guest clathrates are modelled by 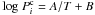, where A and B are constants (Miller 1961) whose values are given in Table 2 (with 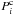in bars and T in K). When the gas pressure is higher than the equilibrium pressure of the MG clathrate, the ice and gas phases can combine to form the clathrate cages in the pores. Below the dissociation pressure, the cages become unstable, which leads to their dissociation, and only the ice and gas phase remain.

Table 2

Parameters of the equilibrium curves of the considered single guest clathrates.

4. Results

We computed the thermodynamic evolution of comets 67PCG and 46PW as a function of time and for two angles of insolation. We find that the stability conditions of MG clathrates are permanently met in the subsurface, irrespective of the adopted angles of insolation and dust conductivities. Only the thickness of the clathrate layer is affected by these latter quantities. Figures 1 and 2 represent the evolution of the stratigraphies of comets 67PCG and 46PW over 70 yr and 80 yr timespans, respectively, for a latitude θ of 0° (i.e., the maximum insolation angle) and a dust conductivity of 4 W m-1 K-1. The two figures show that the stability zone of the MG clathrate extends from the base of the amorphous-to-crystalline water ice phase transition layer up to the surface of the nuclei. This region grows slowly with time and also always contains the sublimation interfaces of H2S and CO2 pure ices. In both comets, the gas phase, from which the MG clathrate can be formed, is dominated by CO (~95%) and CH4 (~5%) and contains small fractions of H2S (~0.1%) and CO2 (~0.05%). When the comet approaches perihelion for the first time, the amorphous layers start to crystallize and CO, CO2, CH4, and H2S released in the pores can be enclathrated by the crystalline water ice available on their surface because the gas pressure (a few hundreds of Pa) is greater than the clathrate equilibrium pressure (order of 1 Pa).

thumbnail Fig. 1

Stratigraphy of the nucleus 67PCG as a function of time and for θ = 0°. The lines represent the surface and the minimum depths at which solid CO2 and CH4 (dashed lines), H2S and CO (bold solid lines) exist. The dotted area corresponds to the zone where the amorphous-to-crystalline water ice phase transition occurs and the dashed area to the zone of the MG clathrate stability.

thumbnail Fig. 2

Same as in Fig. 1, but for 46PW.

As shown in Figs. 1 and 2, the thickness of the stability zone of the MG clathrate slightly oscillates with time as a function of the heliocentric distance, but never vanishes. In particular, when approaching the Sun, about the top 10 m of the clathrate layer destabilize and, inversely, become stable again as the nucleus cools. The destabilization of these top layers is caused by an increase of the local temperature at perihelion, which makes the MG clathrate equilibrium pressure rises above the gas pressure in the pores. When the comet moves away from perihelion, the layer cooling decreases the equilibrium pressure of the MG clathrate below the gas pressure in the pores, favouring again the possible formation of MG clathrate layers close to the surface, provided that there is enough available crystalline water ice. Note that at each perihelion passage, at least 1 to 2 m of new clathrate layer would be destabilized for the first time in subsurface, i.e. the gas pressure becomes lower than the clathrate equilibrium pressure. As an example, a region located in the middle of this oscillation zone has a gas pressure above that of clathrate equilibrium during more than three years for each orbit of Comet 67P/Churyumov-Gerasimenko.

It is interesting to note that the top clathrate layers, which are closer to the nucleus surface, are heated and destabilized when the comets approaches perihelion before the amorphous ice will be transformed into crystalline ice. We also performed tests with lower abundances of CH4 (4 times lower) and H2S (20 times lower) to the lowest values in Bockelée-Morvan et al. (2004), and our results show that the stability area of clathrates varies only by a few percent.

5. Discussion

Our calculations show that assuming a plausible set of volatile abundances and irrespective of the adopted thermodynamic parameters of the nuclei, JFCs possess a region where clathrates would be stable, extending from the amorphous-to-crystalline water ice phase transition interface up to the surface. Additional calculations lead to the same results for Halley-type comets and then for all SPCs. The main improvement over Marboeuf et al. (2010) is the use of two additional volatiles (CH4 and H2S), which increases the stability of MG clathrates. This allows the trapping of CO and CO2 at higher temperatures than if they were alone. Thus, clathrates containing CO and CO2 are permanently stable in much larger regions than shown in Marboeuf et al. (2010).

The permanent stability of clathrates in the subsurface of JFCs and SPCs raises two important questions. The first concerns the kinetics of clathrate formation. Do the various gases spend enough time inside the pores before they are outgassed at the surface to actually be trapped in clathrate cages? A rough estimate of this possibility for SPCs can be given with the following argument. The rate of formation/dissociation of clathrates in their stable/instable regions is mainly the function of the kinetics constant λcl, the ice surface to volume ratio As, and the difference between the gas pressure and the clathrate equilibrium pressure ΔP, and can be writen as λclAsΔP (Kim et al. 1987; Englezos et al. 1987; Schmitt 1986; Sun & Mohanty 2006). On average, one has λcl ~ 5 × 10-12 mol m-2 Pa-1 s-1 (Englezos et al. 1987), As ~ 2 × 104 in our model and ΔP ≃ 10−100 Pa in most of the region of stability of clathrates. Integrating the formation rate over the thickness of the clathrate stability layer (~40 m as seen in Figs. 1 and 2) we get a formation rate per unit surface of 4−40 × 10-5 mol m-2 s-1. This is to be compared to the typical gas production rate at the surface of the nucleus of 0.8−4 × 10-4 mol m-2 s-1. Hence the clathrate formation rate is similar to the classical degasing. At the same time, the amount of volatiles present in gas form per unit area of nucleus surface is ~4 mol m-2. Hence the gaseous reservoir is only capable of supplying material for clathration for a few hours before there is a strong competition between clathration and degasing. Unfortunately, a precise evaluation of this effect can only be done with a fully self-consistent model.

This leads to the second question concerning the thermodynamics of the reactions. The present work is based on a comparison between the equilibrium pressure of clathrates and that of the gaseous phase in the porous network. In our model of a comet nucleus no clathrate forms (and thus decomposes) within the porous network. The influence of clathrate formation/dissociation on the internal temperature of the nucleus, pressure of the gaseous phase and gas production of SPCs is therefore not accounted for. We expect the temperature and gas pressure to be different in a self-consistent model, but we reckon this should not modify our main conclusions on the stability regions because the gas pressure is much higher than the clathrate equilibrium pressure. As for gas production, again only a fully self-consistent model can answer this question. Developping such a model accounting for the kinetics and thermodynamics of the formation/dissociation of clathrates is the subject of a forthcoming paper.

1

SPCs are divided into two categories: Halley type comets (periods between 20 and 200 years) and JFCs (period less than 20 years).

2

It has been shown by Kouchi Sirono (2001) that crystallization of amorphous mixtures made of water and some other volatiles can become endothermic.

References

  1. Bar-Nun, A., Herman, G., Laufer, D., & Rappaport, M. L. 1985, Icarus, 63, 317 [Google Scholar]
  2. Bar-Nun, A., Notesco, G., & Owen, T. 2007, Icarus, 190, 655 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bockelée-Morvan, D., Crovisier, J., Mumma, M. J., & Weaver, H. A. 2004, Comets II, 391 [Google Scholar]
  4. Cochran, A. L., et al. 2010, BAAS, submitted [Google Scholar]
  5. Delsemme, A. H., & Miller, D. C. 1971, Planet. Space Sci., 19, 1229 [NASA ADS] [CrossRef] [Google Scholar]
  6. Englezos, P., Kalogerakis, N., Dholabhai, P. D., & Bishnoi, P. R. 1987, Chem. Eng. Sci., 42, 2647 [Google Scholar]
  7. Espinasse, S., Klinger, J., Ritz, C., & Schmitt, B. 1991, Icarus, 92, 350 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Espinasse, S., Coradini, A., Capria, M. T., et al. 1993, Planet. Space Sci., 41, 409 [Google Scholar]
  9. Fray, N., & Schmitt, B. 2009, Planet. Space Sci., 57, 2053 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hand, D. P., Chyba, C. F., Carlson, R. W., & Cooper, J. F. 2006, AstroBiology, 6, 463 [NASA ADS] [CrossRef] [Google Scholar]
  11. Hersant, F., Gautier, D., & Lunine, J. I. 2004, Planet. Space Sci., 52, 623 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hudson, R. L., & Donn, B. 1991, Icarus, 94, 326 [NASA ADS] [CrossRef] [Google Scholar]
  13. Kidger, M. R. 2003, A&A, 408, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Kim, H. C., Bishnoi, P. R., Heidemann, R. A., & Rizvi, S. S. H. 1987, Chem. Eng. Sci., 42, 1645 [CrossRef] [Google Scholar]
  15. Kossacki, K. J., & Szutowicz, S. 2006, Planet. Space Sci., 54, 15 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kouchi, A., & Sirono, S.-i. 2001, Geophys. Res. Lett., 28, 827 [Google Scholar]
  17. Kouchi, A., Yamamoto, T., Kozasa, T., Kuroda, T., & Greenberg, J. M. 1994, A&A, 290, 1009 [NASA ADS] [Google Scholar]
  18. Lipenkov, V. Y., & Istomin, V. A., 2001, Mater. Glyatsiol. Issled, 91, 1 [Google Scholar]
  19. Lowry, S., Fitzsimmons, A., Lamy, P., & Weissman, P. 2008, The Solar System Beyond Neptune, 397 [Google Scholar]
  20. Lunine, J. I., & Stevenson, D. J. 1985, ApJS, 58, 493 [NASA ADS] [CrossRef] [Google Scholar]
  21. Marboeuf U., 2008, Ph.D. Thesis, Univ. de Franche-Comté [Google Scholar]
  22. Marboeuf, U., Mousis, O., Ehrenreich, D., et al. 2008, ApJ, 681, 1624 [NASA ADS] [CrossRef] [Google Scholar]
  23. Marboeuf, U., Petit, J.-M., & Mousis, O. 2009, MNRAS, 397, L74 [NASA ADS] [Google Scholar]
  24. Marboeuf, U., Mousis, O., Petit, J.-M., & Schmitt, B. 2010, ApJ, 708, 812 [NASA ADS] [CrossRef] [Google Scholar]
  25. Miller, S. L. 1961, Proceedings of the National Academy of Science, 47, 1798 [Google Scholar]
  26. Mousis, O., & Schmitt, B. 2008, ApJ, 677, L67 [NASA ADS] [CrossRef] [Google Scholar]
  27. Mousis, O., Lumine, J. I., Thomas, C., et al. 2009, ApJ, 691, 1780 [NASA ADS] [CrossRef] [Google Scholar]
  28. Orosei, R., Capaccioni, F., Capria, M. T., et al. 1999, Planet. Space Sci., 47, 839 [NASA ADS] [CrossRef] [Google Scholar]
  29. Prialnik, D., Benkhoff, J., & Podolak, M. 2004, Comets II, 359 [Google Scholar]
  30. Schmitt B., 1986, Ph.D. Thesis, Univ. Joseph Fourier [Google Scholar]
  31. Schulz, R., & Schwehm, G. 1996, P&SS, 44, 619 [NASA ADS] [Google Scholar]
  32. Schulz, R., Stüwe, J. A., & Boehnhardt, H. 2004, A&A, 422, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Schmitt, B., Espinasse, S., Grim, R. J. A., Greenberg, J. M., & Klinger, J. 1989, Phys. Mech. Comet. Mat., 302, 65 [Google Scholar]
  34. Sun, X., & Mohanty, K. K. 2006, Chem. Eng. Sci., 61, 3476 [CrossRef] [Google Scholar]
  35. Taylor, S. R. 1992, Solar system evolution: a new perspective. An inquiry into the chemical composition, origin, and evolution of the solar system (Cambridge, New York: Cambridge University Press) [Google Scholar]
  36. Tsou, P., Brownlee, D. E., Anderson, J. D., et al. 2004, JGRE, 109, 12 [Google Scholar]

All Tables

Table 1

Physical parameters of the nuclei at the beginning of the computation.

In the text
Table 2

Parameters of the equilibrium curves of the considered single guest clathrates.

In the text

All Figures

thumbnail Fig. 1

Stratigraphy of the nucleus 67PCG as a function of time and for θ = 0°. The lines represent the surface and the minimum depths at which solid CO2 and CH4 (dashed lines), H2S and CO (bold solid lines) exist. The dotted area corresponds to the zone where the amorphous-to-crystalline water ice phase transition occurs and the dashed area to the zone of the MG clathrate stability.
In the text
thumbnail Fig. 2

Same as in Fig. 1, but for 46PW.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.