| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201015179 | |
| Published online | 02 December 2010 | |
Ceres’ sunlight atlas⋆
INAF Osservatorio Astronomico di Trieste, via G. B. Tiepolo
11,
34143
Trieste,
Italy
e-mail: molaro@oats.inaf.it
Received:
8
June
2010
Accepted:
27
September
2010
Context. Astronomical research dealing with accurate radial velocity measurements need reliable astronomical standards to calibrate the spectrographs and to assess possible systematics. Stellar radial velocity standards offer a reference at the level of a few hundred m s-1 and are not adequate for most present needs.
Aims. We aim to show that sunlight reflected by asteroids is a fairly accessible way to record a high-resolution solar spectrum from the whole disk, which can therefore be used as a radial velocity standard and can improve the uncertainties of solar line positions.
Methods. We used solar light reflected by the asteroid Ceres observed with HARPS to measure solar lines’ wavelengths.
Results. We provide a new solar atlas with 491 line wavelengths in the range 540−690 nm and 222 lines in the range 400−410 nm obtained from reflected solar spectrum of Ceres. These measurements are consistent with those of Allende Prieto & Garcia Lopez (1998b) based on FTS solar atlases but with a factor 3 higher precision.
Conclusions. This atlas provides a benchmark for wavelength calibration to check radial velocity accuracy down to 44 m s-1 locally and a few m s-1 globally. The asteroid-based technique could provide a new way to track radial velocity shifts with solar activity cycle, as well as to derive convective shifts suitable for comparison with theoretical atmospheric models. It could also be used to study radial velocity deviations in spectrographs such as those recently detected in HIRES and UVES. Dedicated HARPS observations of other asteroids could improve present results substantially and these investigations have been solicited.
Key words: atlases / reference systems / Sun: photosphere / Sun: activity / stars: atmospheres / planets and satellites: individual: Ceres
Full Table 2 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/525/A74
© ESO, 2010
1. Introduction
In the past years there has been increasing interest in better radial velocity measurements of astronomical sources. The reasons are manifold and range from the intensive search for extra solar planets of lower and lower mass to astronomical checks of changes in the coupling fundamental constants, to projects aimed at measuring the change in the expansion velocity of the Universe (Mayor et al. 2009; Levshakov et al. 2007; Liske et al. 2008).
Currently, the most precise optical measurements in differential radial velocities reach precision of m s-1 or even better, obtained by averaging over thousands of stellar photospheric lines. When the positions of a limited number of lines are needed, as in the case of absorption lines in the QSO spectra used to probe fine-structure constant variability, the precision goes down to ≈50 m s-1 (Levshakov et al. 2007; Molaro et al. 2008b). Strictly speaking, in both of these observations there is no need to determine the zero point. However, absolute measurements become important when observations taken in different spectral regions at different epochs or spectrographs have to be combined or compared.
A practical way to move from relative to absolute radial velocities is to use standard radial velocity sources. Best-studied stars provide radial velocities with accuracy in the range of 100−300 m s-1 (Nidever et al. 2002; Nordström et al. 2004; Famaey et al. 2005). Limitation arises from several factors that produce line shifts, such as the presence of convective motions, stellar activity and spots, stellar cycles and photospheric granulation, line asymmetries, as well as gravitational perturbations due to the presence of a system of exoplanets (Livingston et al. 1999). The amplitude of the radial velocity difference in granules is 1−2 km s-1, so the approximate 5 million granules on the solar surface will leave a noise at the level of 1 m s-1. The number of granules is lower in supergiants and also related to the coverage of magnetic regions. Thus a stellar activity cycle would lead to cyclic changes in line position.
Asteroids were suggested as good radial velocity standards since they reflect almost unaltered sunlight, and their radial velocity is known very precisely (Zwitter et al. 2007; Molaro et al. 2008a). They have no intrinsic emission spectrum apart from a minor olivine infrared emission, and at least large asteroids have almost spherical shapes and are slow rotators. In fact asteroids will also complement radial velocity standards for the Gaia mission, providing calibration standards at the level of 10 m s-1 (Crifo et al. 2007).
The major limitation arises here, rather surprisingly, from very poor knowledge of the position of lines in the solar spectrum. Even though we have at our disposal solar flux atlases obtained on the McMath Solar Telescope at Kitt Peak National Observatory with the Fourier transform spectrometer (FTS) with extremely high resolution and S/N (Kurucz 1984; Brault & Neckel 1987), the precision of the almost 5000 observed wavelengths produced by Allende Prieto & Garcia Lopez (1998b) is ≈150 m s-1 or lower.
In general determination of reliable radial velocities also has to deal with the measurement apparatus and with the laboratory sources used for spectrometer calibration. So far, hollow cathode thorium lamps and iodine absorption cells have been used to generate a large set of calibration lines. There are several factors affecting the quality of the wavelength scale. Laboratory wavelengths are known with limited precision, which varies from about 15 m s-1 of the stronger lines to more than 100 m s-1 for the weaker lines. Moreover, irregularities in line spacings and intensities, blending, and lamps aging limit their repeatability (Murphy et al. 2007; Lovis & Pepe 2007).
The paths for ThAr light and quasar light through the spectrograph are not identical, so that small distortions between ThAr and quasar wavelength scales should be expected. In addition sometimes ThAr lamps are not even taken close to the astronomical observations. For instance at UVES they are taken during daytime to save precious dark time, which means several hours before the science exposures and different thermal and pressure conditions are theoretically compensated.
Differences in the slit illuminations are not traced by the calibration lamp. Since source centring into the slit is varying from one exposure to another, an offset at the zero point on the scales of different frames is induced, which could be up a few hundred m s-1. This effect was measured at UVES by cross-correlating 15 different exposures of the same object showing a peak to peak offset up to 800 m s-1 and a mean value of ≈180 m s-1 (Wendt & Molaro 2010).
Stability is limited even in the best spectrographs due to the calibration light source, but the precise value remains to be precisely determined. Griest et al. (2010) on HIRES spectra and Whitmore et al. (2010) on UVES spectra by comparing the ThAr wavelength scale with one established from very precise I2-cell observations of a bright quasar found absolute wavelength offsets up to 500−1000 m s-1 for the Th-Ar scale in addition to an order modulation with an amplitude of about 300 m s-1. Systematic errors at the level of a few hundred m s-1 are revealed also in UVES data by detecting unexpected shifts of FeII absorption lines with comparable response to changes of the fine structure constant (Centurión et al. 2010).
Several of these problems have been solved in the HARPS spectrograph, specifically designed to measure the most accurate stellar radial velocities to detect small exoplanets through the radial velocity technique. HARPS is a fiber-fed instrument placed under a vacuum vessel and thermally stabilized and has been able to deliver a sequence of observations with a dispersion along the exoplanet orbit of 64 cm s-1 over a 500-day baseline. However, Wilken et al. (2010) found that CCD defects could be responsible for adaptation of the dispersion curves in the wavelength calibration analysis at the level of ≈50 m s-1 at a specific wavelength. While awaiting a new generation of laser-comb-frequency calibrations, today’s efforts to improve radial velocity accuracy requires understanding these systematics.
In the present paper we analyse HARPS observations of the asteroid Ceres to show how to use asteroid observations to improve both accuracy and precision of the solar atlas and how this could be used as benchmark to calibrate ground or space spectrographs to the limit of the present atlas. Asteroids are an easy and economical way to record the integrated solar spectrum over the whole disk. This technique also offers a new way to monitor radial velocity line shifts with solar activity cycle and to provide convective shifts for theories of line formation in the solar photosphere.
2. Data and data reduction
The observations were performed with the spectrograph HARPS at the European Southern Observatorys 3.6-m telescope at La Silla, Chile, on 16 July, 2006 and downloaded from the ESO HARPS public archive. The High Accuracy Radial velocity Planet Searcher at the ESO La Silla 3.6 m telescope is a spectrograph dedicated to the discovery of extrasolar planets through radial velocity oscillations and was especially designed for optimal opto-mechanical stability (e.g. Mayor et al. 2003). The spectrograph consists of a white pupil design with a grism crossdispersed R4 echelle housed in a temperature-controlled vacuum vessel. With a 1 arcsec aperture on the sky it has a resolving power of R = λ / δλ = 115 000 and provides a sampling of the FWHM with 4.1 pixels each 15 μ wide. HARPS covers simultaneously the 380−690 nm range, with a small gap at 530−539 nm, distributing the light over 72 dispersed echelle orders onto a mosaic of two 2 K × 4 K CCD detectors with pixels of 15 μ wide. To avoid spectral drift due to temperature and air pressure variations HARPS is contained in a vacuum thermalized vessel. A second fibre is used to record simultaneously a Th-Ar reference spectrum to monitor the spectrograph’s residual drifts. Both fibers are equipped with an image scrambler to provide a uniform spectrograph pupil illumination. This is an important difference to slit spectrographs like UVES at VLT or HIRES at Keck, where non uniformity of slit illuminations induces radial velocity difference between different exposures. Thanks to its excellent performance, a large number of Neptunian exo-planets and super-Earths are currently been discovered with HARPS (Bouchy et al. 2009). Ceres was about V = 8 at the epoch of the observation. The exposure was of 1800 s producing a reflected solar spectrum with a signal-to-noise varying from about 75 up to 200 (see Table 1). In the course of the exposure, the radial velocity of the asteroid changes by ≈50 m s-1. The various components of the expected velocities are reported in Table 1 and refer to the mid-exposure times.
Journal of the observations.
3. Asteroids as radial velocity standards
Asteroids are very accessible and potentially precise radial velocity standard sources. They reflect integrated sunlight without substantial modification of the solar spectrum, and their velocity component with respect to the observer can be predicted with very high accuracy reaching the m s-1 level (Zwitter et al. 2007; Molaro et al. 2008a). Thus they provide a standard of radial velocity provided we can measure the solar lines with comparable precision.
For comparison, slightly more than one hundred stars were followed for a time baseline of 20 years with the two CORAVEL spectrometers showing that they are a reference system of radial velocities with a precision of several hundred m s-1 (Udry et al. 1999).
Ceres has a radius of 476.2 km and a spherical shape that produces a constant reflectance of the sunlight. Ceres is rotationally symmetric to the limit of measurement accuracy and can be described by an oblate spheroid of axes a = 487.3 ± 1.6 and b = 454.7 ± 1.6 km (Thomas et al. 2005). The rotational period of Ceres is 9.075 h which provides a rotational velocity of ≈91 m s-1. This is much lower than the solar one and will not cause further extra broadening to the lines. On 16 July, Ceres showed an illuminated fraction of 99% and an angular size of 0.63 arcsec so that the reflected and the direct solar spectra are probably identical. Variation in reflectance with wavelength or the presence of regolith caused by meteoroid impact on the asteroid does not affect the high-resolution spectrum.
Table 1 reports the motion components and the resulting expected radial velocity shifts ΔRV. Ephemeris for Ceres was computed by means of the JPL’s Horizons system1, which provides accurate ephemeris for the minor bodies of the solar system. The sunlight reflected by the asteroid is shifted by the heliocentric radial velocity of the asteroid with respect to the Sun at the time t1 when the photons left the asteroid and were shifted by the component of the Earth rotation towards the asteroid at time t2, when the photons reach the Earth. The latter is the projection along the line-of-sight of the asteroid motion with respect to the observer at the La Silla site adjusted for aberration, and comprises both the radial velocity of the asteroid and the component from the earth’s rotation towards the line of sight. At La Silla the observed Ceres radial velocity is 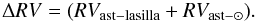 (1)Thus our solar spectrum reflected by Ceres was corrected for the corresponding quantity. The rate of the change in radial velocity is ≈2 m s-1 every minute, which produces a spectral smearing of about 50 m s-1 along the whole exposure. The values reported in Table 1 refer to mid-exposure values, and since the spectral smearing is symmetrical, it does not produce net shifts in radial velocities.
(1)Thus our solar spectrum reflected by Ceres was corrected for the corresponding quantity. The rate of the change in radial velocity is ≈2 m s-1 every minute, which produces a spectral smearing of about 50 m s-1 along the whole exposure. The values reported in Table 1 refer to mid-exposure values, and since the spectral smearing is symmetrical, it does not produce net shifts in radial velocities.
3.1. Solar reference
Any photospheric line is built up of many contributions from a variety of temporally variable inhomogeneities across the stellar surface. In particular, the solar lines should reveal a variation connected to solar activity, which effectively suppresses the granulation cells. Deming & Plymate (1994) measured these displacements in a peak-to-peak modulation of 30 m s-1 over the 11-year solar activity period with the positions redshifted in correspondence of the maximum of activity. However, by contrast, McMillan et al. (1993) did not reveal any drift within 4 m s-1 in the solar line position from a long data series spanning from 1987 to 1992. These two investigations differ in the lines they followed and in the technique, but overlap in the period. Thus that they obtain an entirely different result suggests that the solar shifts depend on the spectral feature monitored and on the analysis method.
The highest quality solar spectra in the optical domain are the solar flux and disk-center atlas obtained on the McMath Solar Telescope at Kitt Peak National Observatory with the Fourier transform spectrometer (FTS) by Kurucz et al. (1984) and Brault & Neckel (1987). These atlases comprise a set of 8 wavelength scans each made of several observations to produce an integrated solar disk flux performed in the period from November 1980 and June 1981. The whole spectrum covers the spectral region from 296 and 1300 nm and achieves a signal-to-noise ratio of ≈2500 with a resolving power of R ≈ 400 000. However, even neighbouring scans were taken through different atmospheric conditions with different amounts of water vapour and ozone.
Allende Prieto & Garcia Lopez (1998a,b) used these atlases to measure the central wavelength for a considerable number of lines and produced the most precise atlas of solar lines presently available. Allende Prieto & Garcia Lopez (1998a,b) line positions have a precision of ≈150 m s-1.
The frequency scale for each FTS scan was determined by observing the O2 688.38335 nm line through a gas absorption cell. As this line only appears in scan 1, it cannot be used for other scans that were calibrated by using either terrestrial lines or by aligning clean solar lines in overlapping regions. Thus actually the wavelengths are aligned with the observations taken on 24 March 1981. After all the shifting and fitting, Kurucz et al. (1984) estimate the error on the zero scale of about 100 m s-1.
Allende Prieto & Garcia Lopez (1998a,b) used strong lines, which are fairly insensitive to convective shifts, to find the zero point of the FTS observations. The stronger lines show a plateau at 612 ± 58 m s-1, which when compared with the solar Gravitational redshift of 636.5 m s-1, provides the uncertainty associated with the zero point of the solar FTS atlas.
More specifically, the data we compare in this paper belong to three different FTS scans: N. 7 for the region between 401.9−473.8 nm, scan N. 9 for the region between 473.8−576.5 nm and scan N. 11 for the region 576.5−753.9 nm, and they were taken with a resolving power of R = 340 500, 521 360, and 522 900, respectively. Scan N. 7 was taken on 23 November 1980 while the other two on 24 and 25 March 1981. The first scan had an exposure of 5925 s, the second of 7770 s while the third was of 6987 s and the maximum signal-to-noise in these scans reaches about 3000. The Earth motion induces a change in radial velocity of 156 m s-1, 212 m s-1, and 193 m s-1 during scans 7, 9, and 11, respectively, thus resulting in ≈200 m s-1 broadening of the solar lines.
4. Analysis of the Ceres’ sunlight
The selection of suitable features for the final analysis is somewhat subjective. The line list from Allende Prieto & Garcia Lopez (1998b), including 4000 unblended solar lines, was chosen as a guide for selecting the features to be measured. The lines were treated as Gaussian profiles and measured by means of the NGAUSS2 routine available in STSDAS. Only lines providing a 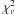 between 0.5 and 1.6 were retained, and 491 lines were measured in the red CCD range from 5400−6915 where the lines are rarefied enough to allow accurate measurements. The observed wavelengths and the errors are provided in Table 2.
between 0.5 and 1.6 were retained, and 491 lines were measured in the red CCD range from 5400−6915 where the lines are rarefied enough to allow accurate measurements. The observed wavelengths and the errors are provided in Table 2.
Line list sample.
 |
Fig. 1 Velocity difference between the position lines provided here and those of the solar flux by Allende Prieto & Garcia Lopez (1998b). |
In Fig. 1 our measurements are compared with the measurements by Allende Prieto & Garcia Lopez (1998b). The differences between our measurements and those of Allende Prieto and Garcia Lopez are expressed in velocities, as are the errors of the difference. However, as discussed below, the total error budget is largely dominated by the Allende Prieto & Garcia Lopez (1998b) error.
The weighted mean of the velocity difference is 10.19 ± 5.9 m s-1, showing good agreement within errors between the global solar radial velocity measured in Ceres’ reflected sunlight and in the direct integrated solar flux spectrum of Kurucz et al. (1984) measured by Allende Prieto & Garcia Lopez (1998b). We note that observations refer to two different epochs, 1981 and 2006, showing that the integrated solar spectrum is a fairly stable reference for absolute accuracies at the level of few m s-1. However, since the time interval between the solar atlas and the Ceres observations is slightly more than twice the solar cycle, these measurements do not allow variations in the mean radial velocity of the solar cycle to be checked. It also doesn’t verify that global solar cycle variations are like those measured by Deming & Plymate (1994). In particular, as discussed in the previous section, the uncertainty of the zero point of the solar spectrum is at the level of ±100 m s-1, according to the original observers, and as good as ±48 m s-1, according to the line positions that are not sensitive to convective motions. These uncertainties prevent drawing strong conclusions on changes of solar line radial velocities connected to the solar cycle.
The second column of Table 2 provides the errors returned by model fitting of lines of the Ceres’s HARPS spectrum. The mean error involved in our measurements is 44 ± 45 m s-1, while the measurement errors quoted by Allende Prieto & Garcia Lopez (1998b) for the same set of lines have a mean value of 140.6 ± 47 m s-1. The two error distributions are compared in Fig. 2, where it is possible to see that the errors in the old solar atlas are more than 3 times larger. Despite the higher resolution and the signal-to-noise of the FTS solar atlas, the asteroid spectrum provides more precise results. This is largely because the FTS spectrum needed significantly longer integrations with large Earth motions.
The solar line list provided in Table 2 thus improves the precision of the line positions of the solar line atlas of Allende Prieto & Garcia Lopez (1998a,b) by a factor 3. Overall they provide a zero point accuracy of the order of 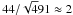 m s-1 provided there is no unknown larger systematic in HARPS. We emphasize here that the ultimate precision that can be reached with this asteroid technique largely depends on the signal-to-noise, which is of about 150−200 in the red, and on the total number of available lines. Obtaining reflected sunlight from brighter asteroids or from multiple observations would result in a higher signal-to-noise and correspondingly smaller errors in the wavelength position. The present atlas already offers the possibility to monitor global radial velocity solar changes at the level of few m s-1, but an improved atlas could be even more precise.
m s-1 provided there is no unknown larger systematic in HARPS. We emphasize here that the ultimate precision that can be reached with this asteroid technique largely depends on the signal-to-noise, which is of about 150−200 in the red, and on the total number of available lines. Obtaining reflected sunlight from brighter asteroids or from multiple observations would result in a higher signal-to-noise and correspondingly smaller errors in the wavelength position. The present atlas already offers the possibility to monitor global radial velocity solar changes at the level of few m s-1, but an improved atlas could be even more precise.
 |
Fig. 2 Line positional error histogram for the lines measured here and the one of Allende Prieto & Garcia Lopez (1998b) for the same lines. The continuous red line indicates our errors, the dotted blue line shows the errors reported in Allende Prieto & Garcia Lopez (1998b). |
A considerable number of the measured lines, namely 275, are identified with neutral iron, thus forming a large clean and homogeneous subsample. This sample can be compared with the laboratory measurements for FeI provided by Nave et al. (1994), which have an accuracy of ≥20 m s-1 in the optical. The comparison shows that the lines are generally highly shifted with shifts that exceed several hundred m s-1 and, moreover, with large scatter. Gravitational shift and convective motions are responsible for the observed line to line displacements shown in Fig. 3. The solar gravitational redshift of 636.5 m s-1, or 633.5 m s-1 as measured at Earth’s distance, produces a corresponding shift to the red, while the convective motions produce a shift to the blue that can be low or even exceed the gravitational redshift. The lines formed at the top of the photosphere show shifts close to the gravitational redshift, while the other lines reveal convective motions with variable blue shifts.
 |
Fig. 3 Line shifts of FeI lines compared to laboratory wavelengths by Nave et al. (1994) given in velocity. |
A known correlation exists between the equivalent width and the line shift, which reaches a plateau for lines stronger than 150−200 mÅ. The stronger lines are rather insensitive to convective shifts and were used by Allende Prieto & Garcia Lopez (1998a,b) to estimate the absolute zero of the solar spectrum. Out of our sample 10 lines have EW greater than 150 mA and show values of ≈500 m s-1, which is somewhat less than the theoretical gravitational shift. In the solar atlas of Kurucz et al. (1984), Allende Prieto and Garcia Lopez measured 612 ± 58 m s-1. We note that these line positions could be very useful for comparison with theoretical models and could be easily monitored with an asteroid observation campaign to follow small radial velocity shifts of solar lines forming in solar convective zone in relation to the solar activity cycle.
The blue range has a higher number of solar lines per spectral unit and unblended lines to be measured are comparably more difficult to find. Moreover, in this portion of the spectrum the signal-to-noise is ≈75 or about half of the red part. In correspondence with the start of Allende Prieto’s range of measurements, we measured 222 lines in the narrow range of 394−410 nm, but a non-negligible number (68) with somewhat worse χ2. The comparison with the Allende Prieto & Garcia Lopez (1998a,b) measures returns a weighted mean difference of 45.0 m s-1 and an error of the mean of ±16.6 m s-1 showing consistency in the two spectra and with the red CCD. The average error in position measurement is 89 ± 69 m s-1 resulting mainly from the degradation in the signal-to-noise of the blue part of the spectrum. Allende Prieto & Garcia Lopez (1998b) also reported considerably larger errors with a mean value of 289 ± 114 m s-1. However, the error distribution is highly skewed as reported in Fig. 6 and this is probably due to the crowding of absorption features. However, a considerable fraction shows small errors. There are 77 lines with an error smaller than 50 m s-1 providing a mean value of 37 ± 7 m s-1. As it is possible to see in Fig. 6, where the distribution of errors of Allende Prieto & Garcia Lopez (1998b) are also shown, a substantial fraction of lines provide an improvement of about one order of magnitude in the precision of the positions of solar lines.
4.1. Comparison with theoretical models
The 3D radiative-hydrodynamical convection models for FeI and FeII solar lines were computed by Asplund et al. (2000). These models provide an absolute line shift that can be compared directly with the observed line positions. The comparison reveals excellent agreement for weak lines (Wλ ≤ 60 mÅ). For FeI lines it is 0 ± 53 m s-1 and 51 ± 81 m s-1 when including intermediate strong lines (Wλ ≤ 100 mÅ), and becomes slightly worse for the FeII lines with a mean difference of −64 ± 85 m s-1. However, in this comparison the error in the observed line positions taken from Allende Prieto & Garcia Lopez (1998b) is not considered, and it could be a substantial component of the differences quoted by Asplund et al. (2000). The 3D radiation-hydrodynamical models, computed with the CO5BOLD code, provided a convective shift of −371 m s-1 for the FeI 5525.544 line (Caffau 2010, private communication). Details of the models can be found in Caffau & Ludwig (2007). As reported in Table 2, the observed line position for this line results redshifted by +211 m s-1 with respect to the laboratory wavelength and, therefore, blue-shifted by −422 m s-1 when a gravitational redshift of +633 m s-1 is adopted. The difference between the observed and the predicted one is 51 m s-1 and is consistent with the errors in the line position of the present atlas. This match strongly supports the realism of 3D modelling of solar atmosphere and shows how an improved solar line position could be useful in constraining theoretical models. A more precise observational position for the lines that we provide here could be a more valuable tool challenging predictions of theoretical models of the solar photosphere.
 |
Fig. 4 Line shifts of FeI lines of the red portion of the spectrum plotted as a function of their equivalent widths. |
5. Summary and future prospects
From the analysis of a single 30 min solar spectrum reflected by Ceres, we have provided a new atlas of 491 solar lines in the range 540−69 nm and of 220 lines in the range of 394−410 nm. The atlas should be fairly accurate within 2 m s-1, although this cannot be verified with an independent measurement and must ultimately rely on HARPS performances. Internal precision of individual line position is ≈45 m s-1 in the red and ≈89 m s-1 in the blue. These improve by a factor 3 the precision of the existing solar atlas of Allende Prieto & Garcia Lopez (1998a,b).
The atlas can be used to calibrate existing spectrographs at any wavelength in the covered range down to a precision of ≈45 m s-1 and by using the whole range to provide an absolute reference at the level of 2 m s-1. For instance it can be used to check the systematic deviations observed in HIRES spectra by Griest et al. (2009) and in UVES spectra by Whitmore et al. (2010). By comparing spectra of the same source calibrated by adopting either the I2 cell or the ThAr calibration lamp, they observed offsets up to 1 km s-1 between different observations and a modulation of about 300 m s-1 or about 200 m s-1 within a single spectral order in HIRES and UVES.
The technique of exploiting the sunlight reflected by asteroids moving by known radial velocity could be be usefully applied to monitoring the behaviour of convective solar lines along the cycle of magnetic activity through sequences of observations along the solar cycle. However, since these movements are expected at the level of few m s-1, they call for a further refinement of precision. The present atlas offers a significant advancement but can be easily expanded and improved both in terms of spectral range and of line position precision. New asteroid observations with HARPS are solicited along the direction outlined here.
Available at http://ssd.jpl.nasa.gov/horizons.cgi.
Acknowledgments
We are thankful to the HARPS group for providing CERES observations from their archive, to Carlos Allende Prieto for providing the EWs of their analysis, to Elisabetta Caffau and Piercarlo Bonifacio for providing results from the CO5BOLD code, to Sergio Monai for an early treatment of the Ceres spectrum and to Gabriella Schiulaz for improving the english. An anonymous referee is warmly acknowledged.
References
- Allende Prieto, C., & Garcia Lopez, R. J. 1998a, A&AS, 129, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allende Prieto, C., & Garcia Lopez, R. J. 1998b, A&AS, 131, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Nordlund, A., Trampedach, R., Allen de Prieto, C., & Stein, R. F. 2000, A&A, 359, 729 [NASA ADS] [Google Scholar]
- Bouchy, F., Mayor, M., Lovis, C., et al. 2009, A&A, 496, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Bedding, T. R., Kjeldsen, H., et al. 2004, ApJ, 600, 75 [Google Scholar]
- Caffau, E., & Ludwig, H. G. 2007, A&A, 467, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centurión, M., Molaro, P., & Levshakov, S. 2010, Mem. SAIt, 80, 929 [Google Scholar]
- Crifo, F., Jasniewicz, G., Soubiran, C., et al. 2007, SF2A-2007: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics held in Grenoble, France, July 2−6, 2007, ed. J. Bouvier, A. Chalabaev, & C. Charbonnel, 459 [Google Scholar]
- de Cuyper, J.-P., & Hensberge, H. 1988, A&AS, 129, 409 [Google Scholar]
- Deming, D., & Plymate, C. 1994, ApJ, 426, 382 [Google Scholar]
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F., Tycner, C., & Brown, K. 2000, PASP, 112, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Griest, K., Whitmore, J. B., Wolfe, A. M., et al. 2010, ApJ, 708, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufer, A., D’Odorico, S., & Kaper, L. 2004, UV-Visual Echelle Spectrograph. User Manual (http://www.eso.org/instruments/uves/userman/), 40 [Google Scholar]
- Kurucz, R. L., Furenlid, I. J., & Testerman, L. 1984, NOAO Atlas No. 1, The Solar Flux Atlas from 296 to 1300 nm. Sunspot (NM: National Solar Observatory) [Google Scholar]
- Levshakov, S. A., Molaro, P., Lopez, S., et al. 2007, A&A, 466, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liske, J., Grazian, A., Vanzella, E., et al. 2008, MNRAS, 386, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W., Wallace, L., Huang, Y., & Moise, E. 1999, ASPC, 183, 494 [NASA ADS] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, Msngr, 114, 20 [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMillan, R. S., Moore, T. L., Perry, M. L., & Smith, P. H. 1993, ApJ, 403, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Levshakov, S. A., Monai, S., et al. 2008a, A&A, 481, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molaro, P., Reimers, D., Agafonova, I. I., & Levshakov, S. A. 2008b, EPJST, 163, 173 [Google Scholar]
- Murphy, M. T., Tzanavaris, P., Webb, J. K., & Lovis, C. 2007, MNRAS, 378, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Marcy, G. W., Butler, R. P., et al. 2002, ApJS, 141, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Queloz, D., et al. 2005, The Messenger, 120, 22 [NASA ADS] [Google Scholar]
- Thomas, P. C., Parker, J. Wm., McFadden, L. A., et al. 2005, Nature, 437, 224 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Udry, S., Mayor, M., & Queloz, D. 1999, in Precise Radial Velocities, ed. J. B. Hearnshaw, & C. D. Scarfe, ASP Conf. Ser., 185, 367 [Google Scholar]
- Wendt, M., & Molaro, P. 2010, A&A, submitted [Google Scholar]
- Wilken, T., Lovis, C., Manescau, A., et al. 2010, MNRAS, 405, 16 [Google Scholar]
- Whitmore, J. B., Murphy, M. T., & Griest, K. 2010, ApJ, 723, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Mignard, F., & Crifo, F. 2007, A&A, 462, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Velocity difference between the position lines provided here and those of the solar flux by Allende Prieto & Garcia Lopez (1998b). |
| In the text | |
 |
Fig. 2 Line positional error histogram for the lines measured here and the one of Allende Prieto & Garcia Lopez (1998b) for the same lines. The continuous red line indicates our errors, the dotted blue line shows the errors reported in Allende Prieto & Garcia Lopez (1998b). |
| In the text | |
 |
Fig. 3 Line shifts of FeI lines compared to laboratory wavelengths by Nave et al. (1994) given in velocity. |
| In the text | |
 |
Fig. 4 Line shifts of FeI lines of the red portion of the spectrum plotted as a function of their equivalent widths. |
| In the text | |
 |
Fig. 5 As Fig. 1, but for the lines in the blue region. |
| In the text | |
 |
Fig. 6 As Fig. 2, but for the lines in the blue. |
| In the text | |
 |
Fig. 7 As Fig. 4, but for the lines in the blue. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


