| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201015028 | |
| Published online | 02 December 2010 | |
A microquasar classification from a disk instability perspective
1
AstroParticule & Cosmologie (APC), UMR 7164, Université Paris
Diderot,
10 rue Alice Domon et Leonie Duquet,
75205
Paris Cedex 13,
France
e-mail: varniere@apc.univ-paris7.fr
2
Laboratoire de Physique et Chimie de l’Environnement et de
l’Espace, Université d’Orléans/CNRS, France
3
Laboratoire AIM, CEA/IRFU-CNRS/INSU-Université Paris Diderot, CEA
DSM/IRFU/SAp, Centre de Saclay, 91191
Gif-sur-Yvette,
France
Received: 21 May 2010
Accepted: 12 September 2010
Aims. The spectacular variability of microquasars has led to many efforts to classify their observed behaviors in a few states. The progress made in the understanding of the quasi-periodic oscillations observed in these objects now makes it possible to develop a new way of identifying order in their behavior, based on the theorized physical processes associated with these oscillations. This development will also help us to reunite microquasars in a single classification based on the physical processes at work and therefore independent of their specific properties (mass, variation timescale, outburst history, etc.). This classification is intended to be a tool to improve our understanding of microquasar behavior and not to replace phenomenological states.
Methods. We start by considering three instabilities that can cause accretion in the disk. We compare the conditions for their development, and the quasi-periodic oscillations they can be expected to produce, with the spectral states in which these quasi-periodic oscillations are observed and sometimes coexist.
Results. From the three instabilities that we proposed to explain the three states of GRS 1915+105 we actually found the theoretical existence of four states. We compared those four states with observations and also how those four states can be seen in a model-independent fashion. Those four state can be used to find an order in microquasar observations, based on the properties of the quasi-periodic oscillations and the physics of the associated instabilities.
Key words: accretion, accretion disks / black hole physics / magnetohydrodynamics / X-rays: binaries
© ESO, 2010
1. Introduction
Since the first observations of microquasars, their strong variability has led to successive attempts to classify them in universal spectral states, defined by observables such as the luminosity, the energy spectrum of the emission, and also the presence of quasi-periodic oscillations (QPOs). Historically, the classification has involved five different states, based on the shape of the energy spectrum and the flux level in the 1–10 keV band (see for example Van der Klis 1994; Nowak 1995). The first classification attempts started with the observation of Cyg X-1 and GX 339-4, and interpretations were based on the mass accretion rate of the black hole. As Ṁ increased, the source was assumed to go from quiescent to low/hard, intermediate, high/soft, and very high state.
These states can be described as follows:
-
Low/hard state.
The spectrum is a power-law with aphoton index on the order of 1.5 to 1.9 and an exponential cutoff around 100 keV. The X-ray luminosity is estimated to be below 10% of the Eddington luminosity (Nowak 1995).
-
High/soft state.
In this state, the total luminosity is higher; the spectrum is dominated by a soft, blackbody-like component with a characteristic temperature of the order of 1 keV. A power-law tail is also present but much less luminous than in the hard state, and its photon index is close to 2.5.
-
Intermediate state.
This state is seen during transitions between the low/hard and high/soft states, with spectral characteristics ranging “in-between” those of these states.
-
Very high state.
In some systems, a state with very high luminosities is observed. In this state, the nonthermal tail and blackbody components become comparable in flux. The power-law component has a photon index of 2.5 and does not show evidence of a cutoff even out to a few hundred keV.
-
Quiescent/off state.
In the last state, the object appears to be “off”, with a flux level much lower than in the other states and a photon index softer than in the low/hard state.
Remillard et al. (2002), and again Remillard & McClintock (2006) took another approach. They defined a set of three “fundamental” states (using more descriptive names, not based on the X-ray luminosity) and the transitions between them. These three states are the low-hard, steep power law (very high), and thermal (high-soft) states, hereafter respectively LHS, SPL and thermal states. Other states are simply transitions between these three. XTE J1550-564 is a good example of this classification.
Given the strong differences between the behaviors of the known microquasars, the differences between these classifications can arise simply from the sources that receive more attention in each work. However, we note the strong link between these three classes and the temporal behavior of the sources: the thermal state does not exhibit QPOs and the SPL has both low-frequency and high-frequency QPOs (hereafter LFQPO and HFQPO). For the low-hard state, the association is not as straightforward. This state often exhibits a LFQPO whose frequency has been shown to be correlated with various properties of the accretion disk, and therefore ultimately to the accretion rate itself. One must note, however, that there are sources for which the LFQPO is not detected in the LHS. There are several possibilities for this absence. Either the QPO is truly absent, or the amplitude of the QPO is too weak to be detected. The latter possibility can again have various origin. The low luminosity of the source may not permit us to detect it, or the QPO frequency may simply fall out of the frequency range. Another explanation is that the underlying instability mechanism giving rise to it is itself weak or fails to generate a strong observable modulation of the X-ray emission. This may be the case if, e.g., the physical properties of the disk and its corona, or its inclination (one must remember for instance that a simple rotating hot spot would not cause a QPO, even in a strongly inclined source) make the detection difficult, or the QPO falls out of the frequency range analyzed, or the QPO is truly absent. In a weak source such as XTE J1752-322, the LFQPO seems absent from the LHS, but appears weakly when observations are summed (Munoz-Daria et al. 2010). In a stronger source such as XTE J1550-564 (Rodriguez et al. 2003), LFQPOs appear early in the initial low-hard state and immediately after the transition back to the low-hard state. Given the very frequent observation of LFQPOs in the LHS in other sources (H1743-322, e.g. Prat et al. 2009; XTE J1118+480, Revnivtsev et al. 2000; XTE J1908+094, Gogus et al. 2004; 4U 1630-474, Dieters et al. 2000), we consider it as a property, which may or not grow to be observable, of that state.
The original three state description has been refined further using from the start X-ray timing properties, especially the type of low-frequency quasi-periodic oscillation, and observations at other wavelengths such as the presence of a jet seen in radio, to separate the different states. Homan & Belloni (2005) introduced a 4-state classification in the continuity of the previous ones, but with a stronger link to the QPOs observed, and in particular to the identification of three different flavors (A, B, and C) of the LFQPO (Remillard et al. 2002). The high-soft state is a direct extrapolation of the previous classification, while the low-hard state is defined similarly exceptwhen a type C LFQPO is observed. It mainly corresponds to the early part of outbursts. The two other states of their classification are the Hard Intermediate State, in which a C-type LFQPO is detected, while the Soft Intermediate state is characterized by either a B- or A-type LFQPO (Homan & Belloni 2005). The differences between those LFQPOs include the evolution of both frequency and amplitude, the harmonic content and the noise components such as the band limited noise (BLN). This classification is coherent with an evolution from the low/hard to hard intermediate, soft intermediate, high soft, hard intermediate, and back to the quiescent/low-hard state. However, even this more refined classification does not encompass all the observed behavior; for example, the case of HFQPOs without LFQPOs (as seen in GRS 1915+105 in the B state) does not fit into any class.
A different classification was defined by Belloni et al. (2000) for the special case of the most spectacular and active microquasar, GRS 1915+105. They defined 3 fundamental spectral states, labeled A, B, and C (not related to the A, B, and C LFQPO types), which combine into 12 reproducible classes of variability (α,β, ...). The three states, defined in a color-color diagram, are again characterized by different contributions from the disk (thermal component of the X-ray) and its corona (non-thermal component at higher energy). Each of the 12 variability classes is composed of either only one state A (class φ), C (χ), or repetitive cycles of various length of BAB (δ,γ), CAC (θ), or CAB (α,ν,ρ,κ,λ,β,μ). This classification has proven useful, but is limited to that particular object. The main difference between GRS 1915+105 and the other microquasars, besides that it has remained active since it was first observed, is the occurrence of these cycles on short (up to a few tens of minutes) timescales, and their repeatability over the years.
There is no one-to-one connection between this spectral classification and the previous ones, partly because GRS 1915+105 tends to stay at a much higher flux level than other objects (see e.g. Fender & Belloni 2004). However, considering the short-term temporal behavior of the three basic spectral states, a one-to-one association does seem to exist: the A state of Belloni et al. (2000) does not display any quasi-periodic oscillation, while C always exhibits the low-frequency one. The B state seems always to be present when HFQPO are detected alone (i.e. without a LFQPO), though no extensive study has yet been published (see for example Morgan et al., 1997).
These classifications are based on observations and their differences reflect the differences between the sources used as references. The SPL, which may be defined by the joint observation of LF and HFQPOs, was often seen in XTE J1550-564 but was not, until recently, observed in GRS 1915+105 and therefore was absent from the classification of Belloni et al. (2000). As we have already mentioned, the same can be said about the B state of Belloni et al. (2000), during which GRS 1915+105 seems to exhibit a HFQPO alone. This has not yet been observed in XTE J1550-564 and is therefore absent from the classification of Remillard et al. (2002) and Remillard & McClintock (2006).
Here we take another approach. We decided to look at the different behaviors of microquasars from the perspective of the disk instabilities happening inside them. We focus here on instabilities that have clear observational signatures, namely the ones that could explain the QPOs (HF and LF). We assume that the mechanisms (instabilities) causing the QPOs become, when they occur, the dominant effect in the disk. These instabilities may also affect the disk even before the observable “QPO” can be detected with our present capabilities (see for example the numerical work of Caunt & Tagger 2001, for the evolution of a disk affected by the accretion-ejection instability). In all existing classifications, that the different states may always be linked with to change in the QPO-content tend to agree with that assumption. Our goal is to base our classification of the behavior on what occurs in the disk. We therefore consider the different instabilities understood to be active in the accretion disk and infer the different observables they would lead to. This approach allows us to overcome the limitation caused by “not yet observed” properties because it is not based on observations but on more general principles.
The first step in this direction was made with the magnetic flood scenario (MFS: Tagger et al. 2004), which was proposed as a possible explanation of the 30 min cycle (class β) of GRS 1915+105. This scenario is based on the tentative association of the LFQPO with the accretion-ejection instability (AEI: Tagger & Pellat 1999; Varniere et al. 2002; Rodriguez et al. 2002), and compares the observed properties of the source in the various states defined by Belloni et al. (2000) and the physical requirements for and expected consequences of the development of the AEI. The second step (Tagger & Varniere 2006) was to propose the Rossby-wave instability (RWI) as a possible mechanism for the high-frequency QPO in microquasars. In these works, the properties of the disk expected to result from these instabilities were part of the argument for their identification with the QPOs.
In the present work, we continue this effort by undertaking a classification that starts from the physics of the different instabilities that can exist in disks. Throughout this paper we consider one instability for the LFQPOs, without entering into their different types which will be treated in more detail in a forthcoming publication (Varniere et al. 2010, in prep.), and one instability for the HFQPOs. By comparing the conditions required for them to appear, and their expected consequences on the disk, we then turn to the observations and attempt to find any correspondence that can exist. Since this step is based on the instabilities at the origin of the QPOs, we focus first on them and do not seek any one-to-one association with observation-based classifications.
In Sect. 2, we briefly review the three states of Belloni et al. (2000), and the three MHD instabilities that have been predicted in magnetized disks. We then discuss how these instabilities can be accommodated within the magnetic flood scenario and the three spectral states it involves. In the following section, we then show that the occurrence of the three instabilities can lead to four instability-defined states. In Sect. 4, we thus concentrate on the fourth state: we first demonstrate that it occurs in MHD disk simulations, and confirm in observations of several sources and not just GRS 1915+105 from which we started. In Sect. 5, we consider this tentative classification based on the instabilities occurring in the disk and see how it can be seen as a model independent classification based only on physical processes without naming the instabilities. This allows us to focus on what this type of physics-based classification can give us compared with the phenomenological one.
2. Magnetic flood: a three instability scenario
2.1. The three states of Belloni et al. (2000)
Belloni et al. (2000) classified the behavior of the microquasar GRS 1915+105 in terms of three fundamental spectral states labeled A, B, and C, based on their position in a color-color diagram (see Fig. 1). The hardness ratio was defined to be HR1 = B/A and HR2 = C/A, where A corresponds to the channel 0–13 (2–5 keV), B to 14–35 (5–13 keV), and C to 36–255 (13–60 keV).
 |
Fig. 1 Three states of Belloni shown on the color-color diagram of the class β of GRS 1915+105. |
Their definitions of the three states, using color ratios HR1 and HR2, are as follows:
-
State A: This state has a low count rate, low HR1 and HR2 ratios, and corresponds to the lower left corner of the color-color diagram. In this state, the disk flux represents a substantial contribution to the total flux. There is no quasi-periodic variability and the X-ray emission is mostly from the thermal disk emission. In comparison with other classifications, this is closest to the High/Soft or Thermal state since there is a dominant disk and no quasi-periodic variability.
-
State C: State C has a low count rate, low HR1, and variable HR2 depending on the length of the event. The power-law flux dominates, there being little or no visible disk flux contribution. This state is known to exhibit a LF-QPO and band-limited noise (BLN). In comparison with other classifications, this is closest to the low/hard state.
-
State B: This state is located above state A in the CC with a high HR1. This state also has a high count rate. Substantial red-noise variability is visible on timescales longer than 1 s. The disk is visible and hotter than in state A, and spectral fits indicate that it is close to the last stable orbit. High-frequency QPOs alone are observed in this state. There seems to be no equivalent to this state in the other classifications schemes.
2.2. The three instabilities at the origin of the three states
Three instabilities have been proposed to exist in magnetized accretion disks. They differ in terms of their physics, in the conditions for their existence and their expected consequences.
Magneto-rotationnal instability (MRI). The MRI is a local instability that develops in a weakly magnetized disk (below equipartition with gas pressure, i.e. a plasma β = 8πp / B2 > 1), when 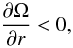 (1)which is always true for (pseudo-)Keplerian disks. Numerical simulations have confirmed that it results in small-scale turbulence, and it is assumed to be responsible for accretion in general. However, no simulation of the MRI has yet displayed a QPO of any kind. We thus assume that the corresponding variability, lacking any strong feature, is the one most well adapted to correspond to a power-law temporal spectrum (Balbus & Hawley 2002).
(1)which is always true for (pseudo-)Keplerian disks. Numerical simulations have confirmed that it results in small-scale turbulence, and it is assumed to be responsible for accretion in general. However, no simulation of the MRI has yet displayed a QPO of any kind. We thus assume that the corresponding variability, lacking any strong feature, is the one most well adapted to correspond to a power-law temporal spectrum (Balbus & Hawley 2002).
Accretion-ejection instability (AEI). The AEI (Tagger & Pellat 1999) is a global instability occurring in disks threaded by a poloidal magnetic field close to the equipartition, namely when the plasma β ~ 1. These conditions are the ones found to be necessary in MHD models of jets (see e.g.Casse & Ferreira 2000).
The AEI belongs to the same family as the spiral instability of self-gravitating disk galaxies, and the Papaloizou-Pringle instability. In the language of diskoseismology (Wagoner 1999; Kato 2001), these could be described as unstable p-modes, while the RWI discussed below would correspond to the g-mode. The AEI is characterized by a spiral structure that develops in the inner region of the disk. At the corotation radius where the gas and the spiral wave rotate at the same angular velocity, the spiral excites a Rossby vortex to which it transfers the energy and angular momentum that it extracts from the disk.
Furthermore, in a low density corona, the Rossby vortex twists the footpoints of the magnetic field lines, generating an Alfvén wave propagating to the corona where it might provide the source for a wind or a jet (Varniere & Tagger 2002). This instability is stronger when the plasma β is on the order of one and requires that 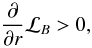 (2)where
(2)where 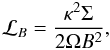 (3)Ω and κ are the rotation and epicyclic frequencies (in a Keplerian disk Ω = κ), Σ is the surface density, and B is the equilibrium magnetic field. This criterion is obeyed in disks with “reasonable” density and magnetic field profiles, whereas for the Papaloizou-Pringle instability in an unmagnetized disk the criterion becomes
(3)Ω and κ are the rotation and epicyclic frequencies (in a Keplerian disk Ω = κ), Σ is the surface density, and B is the equilibrium magnetic field. This criterion is obeyed in disks with “reasonable” density and magnetic field profiles, whereas for the Papaloizou-Pringle instability in an unmagnetized disk the criterion becomes 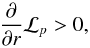 (4)where
(4)where 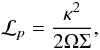 (5)which would require a very steep density gradient to be destabilizing.
(5)which would require a very steep density gradient to be destabilizing.
We have previously presented the AEI as a good candidate for the low-frequency quasi-periodic oscillation (Rodriguez et al. 2002; Varniere et al. 2002; Mikles et al. 2009) and discussed (Varniere & Tagger 2002) how the correlation observed between this QPO and coronal activity could be explained in terms of the emission of Alfvén waves. In a forthcoming publication (Varniere et al. 2010, in prep.), we will also show how the three types of LFQPOs can be explained by the AEI within the framework presented here.
Rossby wave instability (RWI). The RWI can develop in unmagnetized as well as magnetized disks, requiring an extremum of ℒP or ℒB respectively. This extremum can correspond to an extremum of density (Lovelace et al. 1999; Tagger & Melia 2006) or to relativistic effects near the last stable orbit (LSO) in the accretion disk of a microquasar (Tagger & Varniere 2006): the LSO is defined by a vanishing epicyclic frequency κ, whereas further out in the disk κ is close to Ω. Thus κ2 / 2Ω, and consequently both ℒP and ℒB have extrema near the LSO. This extremum of κ occurs at r ≃ 1.3 rLSO, so that the RWI can occur whenever the inner radius of the disk is within that radius.
As with the AEI, the RWI excites Alfvén waves and can be expected to energize the corona if the disk is threaded by a poloidal magnetic field, though the field is not necessary for the instability. We proposed the RWI as a possible explanation of the observed HFQPOs in microquasars (Tagger & Varniere 2006).
2.3. Magnetic flood scenario
The magnetic flood scenario (Tagger et al. 2004) was first introduced to explain the β class of the classification of Belloni et al. (2000) (also known as the 30-min cycle). The MFS explains the repetitive X-ray behavior as a limit cycle determined by the advection of poloidal magnetic flux to the inner disk and its destruction via magnetic reconnection (which can lead to relativistic ejection) with the magnetic flux trapped close to the source.
The MFS starts with the identification of the low frequency quasi-periodic oscillation with the AEI. It then proceeds by assuming that the onset of the state C of the Belloni et al. (2000) classification (possibly identifiable with the low-hard state in other classifications or the hard intermediate state in the classification by Homan & Belloni 2005), which also corresponds to the onset of the QPO, is triggered when the disk magnetization becomes large enough (of the order of equipartition with the gas pressure, so that we might call this a “fully magnetized” disk) for the AEI to become unstable.
We also noted that state A was the one closest to that expected from an α-disk dominated by viscous-like transport of angular momentum due to small-scale turbulence. We thus proposed to associate state A with the presence of the magneto-rotational instability (MRI). Finally, we proposed recently the Rossby-wave instability (RWI) as a possible explanation of the HFQPO observed in microquasars (Tagger & Varniere 2006). An interpretation of the B state of Belloni et al. (2000) was thus called for, in which this state would be dominated by the RWI when the disk inner radius is close to the last stable orbit.
As a consequence, we associated the three fundamental states of Belloni et al. (2000) with three distinct instabilities, based on their properties and variabilities.
3. Three instabilities but four states
We now discuss the instability criteria for the three instabilities presented in Sect. 2.2, in terms of two parameters of the inner disk region: the location of its inner radius, measured by a parameter ξ = rint / rLSO, and the magnetization of its inner region, measured by β = 8πp / B2:
-
the MRI requires a weakly magnetized disk,i.e. β > 1. It does not depend on ξ, and it is not believed to cause QPOs;
-
the RWI requires an inner edge close to the LSO, i.e. ξ < ξext where ξext, is the position of the extremum of either ℒB or ℒP. It is stronger if β is of the order of unity, but can exist even in an unmagnetized disk. It has been proposed to explain the HFQPO;
-
the AEI requires a positive gradient of the quantity ℒB, which as discussed in Sect. 2.2 is obtained with “reasonable” assumptions about the radial profiles of Σ and B. It also requires a magnetic field of the order of equipartition, i.e. β ~ 1. Its existence does not depend on ξ, but its frequency is a fraction of the Keplerian rotation frequency at rint, thus a function of ξ. It has been proposed to explain the LFQPO.
These criteria are not mutually exclusive. In particular, if the inner disk edge is close enough to the last stable orbit (so that the RWI exists) and the magnetic field is sufficient, the AEI can exist further out in the disk, with a lower frequency.
Thus with the two parameters β and ξ we can map four cases, defining four states of variability:
-
β > 1, ξint > ξext:
The disk is weakly magnetized and is not at the last stable orbiteven if it is really close to it. The MRI must dominate, leading to aturbulent disk with no QPO. This state is similar to the high/soft,thermal or A state in previous classificationsas it does not displayany QPOs.
-
β > 1, ξint < ξext:
The disk is weakly magnetized and its inner edge is close to the last stable orbit. The RWI is present at the inner edge, while the MRI acts further out. Observationally this should appear as a warm disk with a HFQPO and no LFQPO.
-
β ~ 1, ξint > ξext:
The disk is “fully magnetized”, i.e. the field is of the order of equipartition with the gas pressure, and the inner edge does not approach the last stable orbit. The AEI causes a LFQPO, so that the inner region of the disk cools down while the corona becomes active.
-
β ~ 1, ξint < ξext:
The disk is fully magnetized and the inner edge is close to the last stable orbit. Both the AEI and the magnetized version of the RWI are present, producing both a LF- and HF-QPO. The frequency of the LFQPO varies little since it is a fraction of the rotation frequency at the inner disk edge, which cannot change much. The interaction between these two modes can be presumed to affect their characteristics and their effect on the disk (see Varniere et al. 2010, in prep., for a comparison of those effects with the different types of LFQPO).
Thus from the two parameters β and ξ, we defined four regions of parameter space, leading to four types of behavior. The three states that were discussed in the magnetic flood scenario can be easily associated with the states A, B, and C of Belloni et al. (2000) . We reached the conclusion that a fourth state is required to describe all possible behaviors. In this state, the AEI and the RWI are active, thus there are both LF- and HF-QPO.
We note that, while this separation into four states started from the QPOs alone, the presence of the band-limited noise seems to correlate with only one state, namely the AEI/LFQPO-only state.
4. The state {AEI + MRI}: β ~ 1, rint / rLSO ~ 1
The fourth state is defined in the parameter space by the co-existence of two instabilities, which lead to the observable that are the HFQPO and LFQPO. To validate this, we need to show that a state with these observables is actually observed and that these two instabilities can co-exist.
4.1. Observations of a state with both HF and LF QPOs
On the basis of observations of GRS 1915+105, the MFS is at the origin of the association of the three instabilities with the three A, B, and C states. That the fourth state (the one with both LF and HF QPO) was observed in this source by Belloni et al. (2006) is important as it gives support to and confidence in our tentative classification.
On the other hand, while this fourth prescription had already been observed in other sources such as XTE J1550-564 (so this state is already part of the standard three/five-state description), the HFQPO-only state has so far never been seen in any of those other objects. There are a couple of reasons why this state has not yet been observed: 1) the HFQPO is too weak to be detected or 2) those sources are able to meet the criteria for the RWI only when they also meet the criteria for the AEI. In either case, it would be interesting to see what is singling out GRS 1915+105 to either have its HFQPO alone strong enough to be detected or being able to meet the criteria for one of the HFQPO and not for the LFQPO at the same time. This would require a more extensive study of the observation and is beyond the scope of this paper.
4.2. Numerical evidence of the {AEI + RWI} state
Since we have discussed the importance of observing the LF- and HF-QPO together, we now proceed to show that this can also occur in numerical simulations. This is numerically demanding since it requires coping with different timescales and different instability criteria, and we thus stick to a proof-of-principle simulation, choosing parameters that make it easier rather than claiming realism.
4.2.1. Numerical setup
As in Tagger & Varniere (2006), we use the 2.5D MHD code first introduced by Caunt & Tagger (2001) to study the non-linear evolution of the AEI. The code, based on a Zeus-type scheme, is similar to those used for simulations of galactic spiral structures before full 3D simulations were possible; it describes an infinitely thin disk in vacuum. The magnetic field can be described by a magnetic potential outside the disk, related to the field in the disk by a Poisson equation similar to that for self-gravity. The code uses cylindrical coordinates with a logarithmic radial grid. This allows high precision in the inner region of the disk where the instabilities develop, and a large dynamic range in r (typically 50 inner radii) to avoid boundary condition issues. The code also implements the FARGO scheme (Masset, 2000), which enhances execution speed by eliminating the Keplerian speed from the Courant condition. Finally the code mimics the relativistic rotation curve (needed for the RWI) with a pseudo-Newtonian potential (Paczyńsky & Wiita 1980) 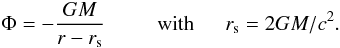 This gives us
This gives us  , which has a maximun close to the last stable orbit.
, which has a maximun close to the last stable orbit.
The conditions to obtain both instabilities are:
-
a disk near equipartition between the gaspressure and the magnetic field, namelyβ = 8πp / B2 ~ 1;
-
with its inner edge near the last stable orbit, ξint ≈ 1;
-
an extremum of ℒB = κ2 / (2Ω)Σ / B2 for the RWI;
-
and a positive derivative for ℒB for the AEI.
By using a pseudo-Newtonian potential, we already have an extremum of ℒB close to the last stable orbit. We need to ensure that it also has a positive derivative further away in the disk so that the AEI can develop.
We thus seek (κ2 / (2Ω))Σ / B2 to have a positive gradient away from the last stable orbit. For this, we can use the Keplerian form of 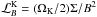 . Away from the last stable orbit,
. Away from the last stable orbit, 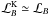 . We impose
. We impose 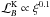 and we use it to fix the radial profile of B for a given density profile. This ensure that the AEI develops in the disk.
and we use it to fix the radial profile of B for a given density profile. This ensure that the AEI develops in the disk.
We then need to define the density Σ. Since we wish to derive a profile that is not too steep at the inner edge of the simulation, we consider 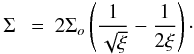 Finally we use the definition of
Finally we use the definition of 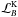 to define the magnetic field
to define the magnetic field 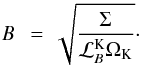 This setup ensures that we have both the RWI and the AEI appearing in the inner region of the disk.
This setup ensures that we have both the RWI and the AEI appearing in the inner region of the disk.
4.2.2. Results
Figure 2 shows a contour plot of the amplitude of m = 1 and m = 2 perturbations in radial velocity, as a function of radius and time. These plots are a convenient way to study waves as they allow us to identify their propagation, i.e. oblique features corresponding to a traveling wave while horizontal ones indicate a standing pattern. The AEI appears as a standing pattern within its corotation radius, emitting a wave traveling outward beyond it. The RWI is a standing pattern trapped in the extremum of ℒB and a traveling wave elsewhere.
 |
Fig. 2 Contour plot of modes m = 1 a) and m = 2 b) of the radial velocity as a function of radius and time. |
In Fig. 2, we see the m = 1 and m = 2 modes1 of the RWI close to the relativistic maximum of ℒℬ (which occurs in our simulation to around 1.3 rLSO). Further away, we can also see the m = 1 and m = 2 modes of the AEI.
When both instabilities are present, the spectrum appears to be noisier than when they are separate, as they are not fully radially separated. In a companion paper (Varniere et al. 2010, in prep.), we will focus on how the instabilities are modified in that case and how this result could explain some of the characteristics of the different types of LFQPOs. We insist that, given the crudeness of the model, this numerical simulation can only be considered as a proof-of-principle. In particular, the value of m that is most unstable, and thus dominant, depends on the profiles we have used, but also on the quality of the model. In a separate study of unmagnetized disks (Meheut et al. 2010), we find that 3D simulations can give a result differing from the 2D one.
5. An instability-based classification
5.1. A model independent look at the classification
Although we have discussed our proposed classification in the context of definite QPO models, it is based only on the predicted presence or absence of LF and HF QPOs. As such, it is model-independent and can be compared with other classifications based on the spectral properties. This means that we consider the QPOs to be the cause of the spectral properties, which are assumed to depend on the transport and deposition in either the disk or the corona, of the accretion energy. Spectral-based classifications, on the other hand, simply describe the QPOs as properties of the spectral states. We find that these spectral properties agree well with what we expect from our QPO models, but this may not be unique to these models and therefore any model agreeing with the spectral properties and having the possibilities of both HF and LF QPOs would give the same four-state classification.
This leads us to four states, defined by the presence or the absence of HF and/or LF QPOs. We represent these four states as a tree diagram, shown in Fig. 3.
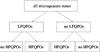 |
Fig. 3 Model independant view of our classification in a tree form. |
This classification resembles those of both Belloni et al. (2000) and Remillard et al. (2006); Remillard & McClintock (2006). The main difference from the classification of Belloni et al. (2000), based on GRS 1915+105, is that we separate their C state into two (AEI-dominated state and AEI-RWI-dominated state), depending on the high frequency variability. Since this classification was first proposed, we have learned that HFQPOs occur in the C state as defined by Belloni et al. (2000) (see Belloni et al. 2006), so the AEI-MRI-dominated state has been observed in GRS 1915+105.
With respect to the classification, mostly based on XTE J1550-564, given in Remillard et al. (2006) and Remillard & McClintock (2006), the main difference is in the state with only HFQPOs, which has not yet been observed and was not part of their classification. It will be interesting to look understand why that state is observed in the case of GRS 1915+105 and not for other objects. The major differences between our classification and the one of Homan & Belloni is that they do not have the HFQPO-alone state and that they separate the low-hard state and the hard intermediate state based on multi-wavelength properties (nevertheless, they clearly state that their components are clearly related).
5.2. A method to find more HFQPOs?
As one can see this instability-based classification is coherent with the other classifications, which are based on a combination of spectral and timing behavior. This strengthens our hypothesis of a strong causal link between timing and spectral changes. This classification attempts to develop a framework to more clearly understand what drives the source behavior and is not to be used instead of a spectral classification, which is easier to use when dealing with observations. A classification based on the detection/non-detection of HF-LF QPOs is limited interest when one is searching purely to classify a state for reference not only because HFQPOs are more difficult to detect but also they require some processing of the data.
On the other hand, we can turn around that difficulty and use the classification means of studying HFQPOs. One can focus our search on the states that are clearly not-MRI or AEI-dominated. This is similar to the method that Remillard et al. (2006) used to detect HFQPO in H1743-322 following the discovery of HFQPO by Homan et al. (2005).
In a second paper (Varniere et al. 2010, in prep.), we will focus on the state where both the AEI and the RWI are present in the disk. In particular, we will study the impact of having both instabilities, more precisely the link between HFQPO and LFQPO, and if the effect on the LFQPO can be used to infer the presence of a weaker HFQPO.
5.3. When the instability criteria are met or not
As we have shown in Sect. 5.1, this model-independant classification into four states is only based on the presence or absence of the LF and HF QPO and not on the actual instabilities at their origin. We note that most objects do not seem to exhibit a particular one of the four states, namely the one with the HFQPO-only. Until now, GRS 1915+105 is the only source known to exhibit all of the four states with some regularity. Since this source has always been singled out as being unusual. It is not a surprise to find in it behavior that other sources do not exhibit, but with this classification we have a way oftackling the problem. There are only 2 reasons why those HFQPOs are not detected in other sources:
-
1)
the HFQPOs are present but are not detected because they aretoo weak;
-
2)
the instability criteria for the instability at the origin of the HFQPO alone (whichever instability is the “right” one) is not fulfilled without the criteria for the LFQO being also fulfilled.
In either case, we need to understand whyGRS 1915+105 either has its HFQPO strong enough to be detected , or is able to meet the criteria for a HFQPO without meeting that for the LFQPO.To achieve this we would need to complete an extensive study of observations to decide the state in which case the other sources are, which is beyond the scope of this paper.
6. Conclusion
We have discussed several disk instabilities that may occur in microquasars. From their instability criteria, we can divide the observed parameter space into four states characterized by their QPO content. This forms a classification of all microquasar observations as shown in the tree diagram 3. We find that this new classification re-unites previous ones, which were based on the spectral properties of the sources but, as a consequence, did not apply uniformly to all microquasars.
We have discussed primarily the instabilities that may be the cause of the variability. Following previous works, we have assumed the accretion-ejection instability is at the origin of the LFQPO, and the Rossby wave instability to be at the origin of the HFQPO, while the turbulent, thermal, disk state is assumed to be dominated by the magneto-rotationnal instability.
For these instabilities to develop, we have found, and confirmed by numerical simulations as well as in observations, that four states can be defined rather than the usual two, three, or five state classifications used up to now, which can now be included in the one we present here. The four states are defined by no QPO, only the LFQPO, only the HFQPO, and both LF- and HF-QPO, thus covering in a simple manner all the possible observations of QPOs. Furthermore, this
classification can be used as a guide in searching for occurrences of the HF-QPO, which is often difficult to detect.
Acknowledgments
The author thanks the anonymous referee that helped clarify the paper to this final form. This work has been financially supported by the GdR PCHE in France. J.R. acknowlegdes partial funding from the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement number ITN 215212 “Black Hole Universe”.
References
- Balbus, S. A., & Hawley, J. F. 2002, in Turbulence and Magnetic Fields in Astrophysics, ed. E. Falgarone, & T. Passot, Lecture Notes in Physics, 614, 329 [Google Scholar]
- Belloni, T., Klein-Wolt, M., Méndez, M., van der Klis, M., & van Paradijs, J. 2000, A&A, 355, 271 [NASA ADS] [Google Scholar]
- Belloni, T., Soleri, P., Casella, P., Mendez, M., & Migliari, S. 2006, MNRAS, 369, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Casella, P., Belloni, T., Homan, J., & Stella, L. 2004, A&A, 426, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casse, F., & Ferreira, J. 2000, A&A, 353, 1115 [NASA ADS] [Google Scholar]
- Caunt, S., & Tagger, M. 2001, A& A, 376, 1095 [Google Scholar]
- Eikenberry, S. S., Matthews, K., Muno, M. et al. 2000, ApJ, 532, 33-36 [Google Scholar]
- Dieters, S. W., Belloni, T., Kuulkers, E. et al. 2000, ApJ, 38, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R., & Belloni, T. 2004, ARA&A, 42, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Gogus, E., Finger, M H., Kouveliotou, C. et al. 2004, ApJ, 609, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., & Belloni, T. 2005, Ap&SS, 300, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., Miller, J.M., Wijnands, R. et al. 2005, ApJ, 623, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, S. 2001, PASJ, 53, L37 [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Meheut, H., Casse, F., Varniere, P., & Tagger, M. 2010, A&A, 516, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mikles, V. J., Varniere, P., Eikenberry, S.S., Rodriguez, J., & Rothstein, D. 2009, ApJ, 694, 132 [Google Scholar]
- Mirabel, I. F., Dhawan, V., Chaty, S. et al. 1998 A&A, 330, 9 [Google Scholar]
- Morgan, E. H., Remillard, R. A., & Greiner, J. 1997, ApJ, 482, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Munoz-Darias, T., Motta, S., Pawar, D. et al. 2010, MNRAS, 404, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Nowak, M. 1995, ASP, 107, 1207 [Google Scholar]
- Prat, L., Rodriguez, J., Cadolle Bel, M. et al. 2009, A&A, 494, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., Sobczak, G. J., Muno, M. P., & McClintock, J. E. 2002, ApJ, 564, 962 [Google Scholar]
- Remillard, R. A., McClintock, J. E., Orosz, J. A., & Levine, A. M. 2006, ApJ, 637, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., Sunyaev, R., & Borozdin, K. 2000, A&A, 361, L37 [NASA ADS] [Google Scholar]
- Rodriguez, J., Varniere, P., Tagger, M., & Durouchoux, P. 2002, A&A, 387, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez, J., Corbel, S., & Tomsick, J. A. 2003, ApJ, 595, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Hannikainen, D. C., Shaw, S. E. et al. 2008a, ApJ, 675, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Shaw, S. E., Hannikainen, D. C. et al. 2008b, ApJ, 675, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Sobczak, G., McClintock, J. E., Remillard, R. A. et al. 2000, ApJ, 531, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Soleri, P., Belloni, T., & Casella, P. 2007, MNRAS, 383, 1089 [Google Scholar]
- Paczyńsky, B., & Wiita, P. J. 1980, A&A, 88, 23 [NASA ADS] [Google Scholar]
- Tagger, M., & Melia, F. 2006, ApJ, 636, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Tagger, M., & Pellat, R. 1999, A&A, 349, 1003 [NASA ADS] [Google Scholar]
- Tagger, M., & Varniere, P. 2006, ApJ, 652, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Tagger, M., Varniere, P., Rodriguez, J., & Pellat, R. 2004, ApJ, 607, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Klis, M. 1994, ApJS, 92, 511 [Google Scholar]
- Varniere, P., & Tagger, M. 2002, A&A, 394, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varniere, P., Rodriguez, J., & Tagger, M. 2002, A&A, 387, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagoner, R. V. 1999, Phys. Rep., 311, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Homan, J., & van der Klis, M. 1999, ApJ, 526, 33 [Google Scholar]
All Figures
 |
Fig. 1 Three states of Belloni shown on the color-color diagram of the class β of GRS 1915+105. |
| In the text | |
 |
Fig. 2 Contour plot of modes m = 1 a) and m = 2 b) of the radial velocity as a function of radius and time. |
| In the text | |
 |
Fig. 3 Model independant view of our classification in a tree form. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


