| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 4 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014860 | |
| Published online | 06 December 2010 | |
Research Note
Possible manifestation of large-scale transverse oscillations of coronal loops in solar microwave emission
1
Space Research Institute, Austrian Academy of Sciences,
Graz, Austria
e-mail: maxim.khodachenko@oeaw.ac.at
2
Lobachevsky State University, Nizhny Novgorod,
Russia
e-mail: kiag2@uic.nnov.ru
3
Institute of Applied Physics, Russian Academy of
Sciences, Nizhny
Novgorod, Russia
e-mail: za130@appl.sci-nnov.ru
4
Institute of Radio Astronomy, National Academy of Sciences of
Ukraine, 61002
Kharkov,
Ukraine
e-mail: alexeyarkhipov@rambler.ru
5
Abastumani Astrophysical Observatory at Chavchavadze State
University, Kazbegi ave.
2a, Tbilisi,
Georgia
Received:
24
April
2010
Accepted:
1
October
2010
Aims. We interpret long-periodic (minutes) modulations detected in solar microwave emission during flaring events as signatures of large-scale transverse oscillations of coronal loops.
Methods. Our data analysis method is based methodologically on a sliding-window Fourier transform combined with the Vigner-Wille technique. We analyze three different events where TRACE detected post-flare oscillating loops (on Mar. 23, 2000; Sep. 15, 2001; Sep. 07, 2001)
Results. For the transverse large-scale oscillatory motion of a loop, a properly located observer, in addition to the modulation caused by the emission diagram pattern motion at the main frequency of the loop oscillation, may detect a modulation at twice the frequency, produced by the varying magnetic field during each inclination of the loop. Our main result consists in identification of these “modulation pairs” in the dynamic spectra of solar microwave emission and their association with the observed oscillating coronal loops.
Key words: Sun: corona / Sun: flares / Sun: magnetic topology / Sun: oscillations / Sun: radio radiation
© ESO, 2010
1. Introduction
Energetic phenomena associated with the processes of solar flaring activity are naturally accompanied by different kinds of electromagnetic emission, covering a wide frequency band from radio waves to gamma-rays. The radiation produced within a given plasma environment carries information about physical and dynamic conditions in a radiating source. Therefore, the electromagnetic radiation emitted by the Sun comprises an important diagnostic tool for understanding the nature and physics of its dynamic phenomena. In this context, as a relatively novel technique in solar microwave radio astronomy appears to be the analysis of long-periodic (e.g., >1 s) fluctuations in the radiation intensity (Zaitsev et al. 2003; Khodachenko et al. 2005).
Microwave radiation (hereafter mm-radiation) from magnetic loops in solar active regions (e.g., during solar flares) is usually interpreted as gyro-synchrotron radiation produced by fast electrons on harmonics of the gyro-frequency νB in the magnetic field B of the loop. For a power-law distribution of electrons in energy f(ℰ) ∝ ℰ − δ, the intensity of gyro-synchrotron radiation Iν from an optically thin loop (Dulk 1985) is 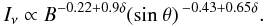 (1)For the observed typical values of electron energy spectrum index 2 ≤ δ ≤ 7, this implies that the intensity depends on a certain power of the background magnetic field, as well as the essential anisotropy of the radiation: Iν ∝ B1.58 ÷ 6.08(sinθ)0.87 ÷ 4.12.
(1)For the observed typical values of electron energy spectrum index 2 ≤ δ ≤ 7, this implies that the intensity depends on a certain power of the background magnetic field, as well as the essential anisotropy of the radiation: Iν ∝ B1.58 ÷ 6.08(sinθ)0.87 ÷ 4.12.
It follows from Eq. (1) that variations in the loop magnetic field, associated with disturbances of the electric current in a radiating source, should modulate the intensity of the mm-radiation of the loop (Zaitsev et al. 2003; Khodachenko et al. 2005). Another possible origin of the intensity modulation of the observed mm-radiation, which follows from Eq. (1), is due to the quasi-periodic motion (oscillation) of a coronal magnetic loop containing the radiation source. This mechanism is connected to the anisotropy of the gyro-synchrotron emission, as well as the variation in the magnetic field value during the oscillatory motion of the loop, which may both, according to Eq. (1) result in a quasi-periodic modulation of the received signal. Therefore, the analysis of long-periodic modulations of solar mm-radiation may be used to identify oscillating electric currents in the coronal loops, as well as to study the large-scale motion of the loops (including loop oscillations). In addition to this, it is natural to expect that the structural complexity of solar active regions will be reflected by peculiarities in the emitted radiation.
In several cases, long-periodic modulations of solar mm-radiation (with multi-track spectra and certain modulation frequency drift) have been interpreted as signatures of oscillating electric currents, running within the circuits of inductively connected coronal magnetic loops moving relative to each other (Khodachenko et al. 2009). The dynamics of these electric currents has been described by the equivalent electric circuit (LCR-circuit) models of the coronal loops (Zaitsev et al. 1998; Khodachenko et al. 2009). Khodachenko et al. (2009) pointed that the frequency of long-periodic LCR-oscillations of the electric current, which depends on specific parameters of a coronal loop, usually remains within the interval νLCR ≈ (0.03−1) Hz. At the same time, modulations caused by the oscillatory motions of loops that contain the radiation sources, because of their direct connection with the large-scale dynamics of loops, have to have typical frequencies of < 0.01 Hz and exhibit no drift. Thus, it has been proposed in Khodachenko et al. (2009) that one should distinguish, when speaking about different kinds of long-periodic modulations of the solar mm-radiation, between the low-frequency (LF) (≈0.03 ÷ 1 Hz) and very-low-frequency (VLF) (<0.01 Hz) modulations, assuming the first to be connected with the LCR-oscillations of electric currents in the coronal loops and the second to be caused by large-scale motions of the radiation sources confined within the oscillating loops. LF modulations (e.g., 0.03–1 Hz) have been studied and interpreted in terms of the equivalent electric circuit models of coronal loops in Zaitsev et al. (1998, 2003) and Khodachenko et al. (2005, 2009). Therefore, they are not considered here. The present paper addresses the VLF modulations (<0.01 Hz) of solar mm-radiation and their possible relation to the large-scale dynamics of coronal loops in solar active regions.
2. Diagnostics of large-scale oscillations of coronal loops by VLF modulations of mm-radiation
Large-scale transverse oscillatory motion of a coronal loop is accompanied by the periodic stress of a magnetic field created in the loop during each inclination, i.e. two times per oscillation cycle. This means that the magnetic field strength fluctuates during the oscillatory motion of the loop with a half-period Posc/2 of the loop oscillation. Therefore, according to Eq. (1), for a transverse oscillating loop, a properly located observer, in addition to the modulation caused by the emission diagram motion at the main oscillation frequency ν0 = 1/Posc, may see in some cases the modulation at the double frequency of the loop oscillation 2ν0, as well as weak higher order harmonics caused by the non-linearity of Eq. (1). The domination of the main and double-frequency harmonics in the spectrum is caused by these frequencies, according to the above-mentioned character of the intensity modulating factors, being implicitly present in the signal. In the real observed signals, usually only these first two harmonics can be detected. For the same reason, it is difficult to expect the appearance of significant (clearly detectable) harmonics at higher than the main frequency, caused only by the nonlinearity of Eq. (1), when the modulation of mm-radiation is connected only with the varying magnetic field, as it takes place in the case of LCR-oscillations of electric current in the loop (Zaitsev et al. 1998, 2003; Khodachenko et al. 2005), or for any internal wave process (e.g., sausage mode). Therefore, “modulation pairs” in the spectra, i.e., lines that can be associated with both the main and double frequencies of a loop oscillation (ν0 and 2ν0), may provide information about the transverse oscillatory dynamics of the loop.
We analyze the VLF modulations of solar microwave bursts recorded in Metsähovi Radio Observatory (Finland) with the 14-m and 1.8 m radio telescope antenna at 37 GHz and 11.7 GHz, respectively. The key selection criterion for the analyzed microwave data was their synchronism with the oscillating loops observed in EUV by TRACE (Aschwanden et al. 2002). At 37 GHz, the Metsähovi radio telescope is able to resolve spatially an active region with oscillating loops. This enables us to analyze the mm-radiation emitted directly from the region, imaged in EUV (e.g., as observed by TRACE). At 11.7 GHz, the analyzed radio signal is collected from the whole solar disk. However, by comparing with observations at other wavelengths and taking into account the timing of the events, it is also possible to identify modulation features related to energy release and dynamic phenomena in particular active regions.
A combination of the sliding-window Fourier (SWF) transform and the nonlinear Wigner-Ville (WV) method (Wigner 1932; Ville 1948; Cohen 1989) has been applied to detect VLF quasi-periodic features in the records of the solar mm-radiation intensity. Both methods (WV and SWF), combined in a proper way, were implemented in a common algorithm (Shkelev et al. 2004), along with different types of signal processing and filtration. Among the advantages of the combined SWF-WV data analysis algorithm are its high sensitivity, high spectral and temporal resolution, and its ability to detect complex multi-signal modulations. The outcome of the SWF-WV algorithm appears in the form of dynamic spectra of the VLF signals, modulating the radiation. To visualize all the detected modulations, averaged spectral density plots are also produced. These plots are obtained by averaging multiple instantaneous cuts of the dynamic spectrum, so that the short-living modulation features also become visible among the longer-lasting modulation lines. The SWF-WV data analysis algorithm is available to the scientific community via the on-line catalogue of models and data analysis tools1, developed within the JRA3-EMDAF (European modelling and data analysis facilities) activity2 of the research infrastructure project Europlanet-RI.
Among the available Metsähovi solar mm-radiation records, three events coincide in time with the large-scale transverse oscillations of coronal loops observed by TRACE. These events are considered below.
 |
Fig. 1 Dynamic spectra (left) and average spectral density plots (right) of very-low-frequency modulations of solar microwave bursts on a) Mar. 23, 2000 (11:20–12:20 UT); b) Sep. 07, 2001 (15:20–15:50 UT); c) Sep. 15, 2001 (10:00–14:00 UT). |
Figure 1a shows the dynamic spectrum and average spectral density plot of VLF modulations in the mm-radiation from the active region AR8910, where a group of oscillating loops was observed after M2.0 flare on Mar. 23, 2000, at 11:30–12:00 UT (Aschwanden et al. 2002). These observations were performed at 37 GHz, and the analyzed radiating source in the active region AR8910 was clearly resolved by the Metsähovi radio telescope. A remarkable feature of the VLF modulation spectrum in Fig. 1a consists of several “modulation pairs”, i.e., modulations at both a given and double frequency: (a) at 1.7 mHz (~10 min) and 3.4 mHz (~4.9 min); (b) at 6.0 mHz (~2.8 min) and 12.0 mHz (~1.4 min); as well as (c) at 7.8 mHz (~2.1 min) and 15.6 mHz (~64 s). These “modulation pairs” may reflect the transverse oscillating loops whose periods correspond to the main frequencies of pairs, i.e. ~10 min; ~2.8 min, and ~2.1 min for the cases (a), (b), and (c), respectively. By this, the first “modulation pair” (case (a)) as a signature of the loop transverse oscillation with a period ~10, closely fits the results of TRACE observations, which found the oscillating loop to have approximately the same period (~615 s) (Aschwanden et al. 2002; Schrijver et al. 2002). As can be seen from the dynamical spectrum in Fig. 1a, the spectral resolution of the analysis performed in this particular case was ~0.3 mHz. The frequency 1.62 mHz corresponding to the detected TRACE period of 615 s is definitely within the frequency interval 1.7 ± 0.3 mHz of the modulation feature revealed by the analysis of mm-radiation. It makes no sense to search in TRACE data for signatures of other oscillating loops (cases (b) and (c)) indicated by the VLF modulations of mm-radiation during the Mar. 23, 2000 event, since with the usual 40 s image sampling cadence of TRACE and the 4-point resolution limit of the instrument (Aschwanden et al. 2002) the fastest detectable by TRACE period is about 3 min. The remaining short-periodic “non-paired” modulation feature at 8.4 mHz (~1.9 min) may be a signature of another oscillatory process, which is unrelated to the large-scale transverse motion of loops, e.g., a sausage-type MHD wave excited in a loop. Detailed analysis of this special case remains however beyond the scope of this paper.
VLF modulations of mm-radiation during the burst on Sep. 07, 2001 are another indication of transverse oscillating coronal loops in microwaves. The burst was produced during M-flare activity at 15:30 UT in the active region AR9601, where TRACE has also registered a group of oscillating loops, observed immediately after the flare (Aschwanden et al. 2002). The corresponding mm-radiation record was made at 11.7 GHz. Thus, the emission from the whole solar disk contributed to the analyzed microwave intensity profile. At the same time, as can be seen in the VLF modulation dynamic spectrum in Fig. 1b, most of the modulation lines begin simultaneously with the impulsive phase of the flare in the active region AR9601 at 15:30 UT and can therefore be associated with this event. Three “modulation pairs” can be identified in the dynamic and averaged spectra in Fig. 1b: (a) 1.8 mHz (~9.2 min) and 3.6 mHz (~4.6 min); (b) 2.7 mHz (~6.2 min) and 5.4 mHz (~3.1 min); as well as (c) 4.3 mHz (~3.8 min) and 8.6 mHz (~1.9 min), which may be the signatures of transverse oscillating loops of periods ~9.2 min, ~6.2 min, and ~3.8 min, respectively. We note that the loop periods in the cases (a) and (b) are again consistent with the 6–10 min oscillating loops detected by TRACE (Aschwanden et al. 2002), whereas the shorter period oscillation (case (c)) cannot be resolved by TRACE because of the relatively long image sampling cadence. The modulation at 5.4 mHz (~3.1 min) may also be a weak third harmonic produced by the 9.2 min oscillating loop. If this is true, then the line at 2.7 mHz (~6.2 min) will not have a pair-companion, and one should exclude the possibility of the ~6.2 min transverse oscillating loop. A “non-paired” weak modulation feature at 6.4 mHz (~2.6 min) may represent an oscillating loop with no resolved second harmonic. At the same time, as for the Mar. 23, 2000 event, weak short-period harmonics may be the signatures of oscillatory processes that are unrelated to the transverse motion of a loop, but caused only by a changing magnetic field. The strong modulation line at 0.6 mHz (~27.7 min) in the spectra of the Sep. 07, 2001 event has to be considered independently of all other modulations mentioned above. The dynamical spectrum in Fig. 1b, and a separate study of VLF modulations of the mm-radiation recorded before the faring burst at 15:30 UT in the active region AR9601, reveal the presence of the ~27.7 min component also before the flare. Since the analyzed microwave emission was received from the whole solar disk, the ~27.7 min modulation feature very likely originates in another active region. It may also be connected with a kind of global solar seismology process.
The last available case of microwave observations of transverse oscillating coronal loops is associated with the event on Sep. 15, 2001, connected with M flare at 11:23 UT in the active region AR9608. The microwave burst on Sep. 15, 2001 was observed at 11.7 GHz, and the mm-radiation source in AR9608 was not resolved by the Metsähovi antenna. However, as for the burst on Sep. 07, 2001 all the spectral features related to the flaring active region AR9608 can be identified by event timing. In particular, most of the detected modulation lines begin simultaneously with the impulsive phase of the flare at 11:23 UT (see Fig. 1c). At least one “modulation pair”, 1.3 mHz (~12.8 min) and 2.6 mHz (~6.4 min), can be identified in the modulation spectra in Fig. 1c. It may be connected with a ~12.8 min transverse oscillating loop. This result agrees with the reported TRACE observations of oscillating loops in the active region AR9608 of period ~12–15 min (Aschwanden et al. 2002). Additional shorter period modulations at 3.8 mHz (~4.4 min) and 5.2 mHz (~3.2 min) could be higher-order harmonics produced by the 12.8 min oscillating loop, or the modulations associated with oscillatory processes not connected with the transverse motion of loops. We note that the ultra-low-frequency (ULF) modulation at 0.3 mHz (~56 min) in the Sep. 15, 2001 spectra visible in Figs. 1c, appears before the flaring burst (at 11:23 UT) and lasts much longer than all other modulation lines in the spectrum. Therefore it cannot be related to the flare in the active region AR9608. This modulation is probably connected with the solar seismology processes, or the slow dynamics of another active region Kislyakova et al. (2010).
3. Conclusions
We demonstrated in several (available) cases that VLF modulations of solar mm-radiation have similar temporal behaviour and coincide in time with the decaying large-scale transverse oscillatory motions of the coronal loops triggered by flares. This coincidence implies that there is possibly a physical link between the oscillatory motion of the loops and the temporal variations of the recorded radio emission. To take this possible link into account, we have considered a loop with propagating beams of non-thermal particles, generating microwave emission by electron gyro-synchrotron mechanism. As pointed out by Schrijver et al. (2002), who studied several cases of transverse oscillations in coronal loops observed with TRACE, including the event on
Mar. 23, 2000 addressed in the present paper, in almost all cases the oscillating loops lie at or near large-scale separatrices or near sites involved in reconnection. These regions may be sources of non-thermal particles injected into the loops.
The joint action of two radiation-modulating factors: (i) the quasi-periodic fluctuation of magnetic field and (ii) the motion of the radio emission diagram, for a transverse oscillating coronal loop causes the essentially non-sinusoidal (non-harmonic) character of the signal received by a remote observer, with strongly pronounced two first harmonics (at the main and double frequency of the oscillation), called in the present paper “modulation pairs”. This feature of the VLF spectrum has been used to identify oscillating loops triggered by flares. By superimposing the “modulation pairs” with the simultaneous TRACE observations in EUV, we have been able to associate some of the paired VLF modulation features, especially those with the main period of 6 ÷ 15 min, with the large-scale transverse oscillations of coronal loops. The shorter-period “modulation pairs” with the main period < 3 min may also be connected with transverse oscillating post-flare loops, although these loops could not be resolved by the TRACE instrument. The “non-paired” features in the VLF modulation dynamic spectra that are occasionally detected, may be either parts of “modulation pairs”, in which the second harmonic cannot be resolved because of the strong contamination of the analyzed signal, or be the features of other oscillatory processes (MHD modes) in the loops, unrelated to their large-scale transverse motion, e.g., sausage-type MHD waves. Investigation of this possibility would require a dedicated study that is beyond the scope of the present paper.
The exact detection of the transverse motion of coronal loops by means of the dynamical spectra of microwave emission (excluding other mechanisms that may also generate higher spectral harmonics) would require a quantitative study of the measured radio signal and the precise simulation of the radiation propagation from an oscillating loop, taking into account the position of the loop relative observer. This would involve dedicated numerical modeling, opening a special direction to additional development of the ideas expressed in the paper.
Acknowledgments
This work was supported by the Austrian Fond zur Förderung der wissenschaftlichen Forschung (project P21197-N16) and Georgian National Science Foundation grant GNSF/ST06/4-098.
References
- Aschwanden, M. J., DePontieu, B., Schrijver, C. J., & Title, A. 2002, Sol. Phys., 206, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, L. 1989, IEEE Proc., 77, 941 [Google Scholar]
- Dulk, G. A. 1985, ARA&A, 23, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Khodachenko, M. L., Zaitsev, V. V., Kislaykov, A. G., Rucker, H. O., & Urpo, S. 2005, A&A, 433, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khodachenko, M. L., Zaitsev, V. V., Kislyakov, A. G., & Stepanov, A. V. 2009, Space Sci. Rev., 149, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kislyakova, K. G., Zaitsev, V. V., Urpo, S., & Riehokainen, A. 2010, Longperiodical Oscillations Of Microwave Solar Radioemission, Astronomicheskii Zhurnal, in press [Google Scholar]
- Schrijver, C. J., & Brown, D. S. 2000, ApJ, 537, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Aschwanden, M. J., & Title, A. M. 2002, Sol. Phys., 206, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Shkelev, E. I., Kislyakov, A. G., & Lupov, S. Y. 2004, Izv. Vyss. Uchebn. Zaved., Ser. Radiofiz. (transl. as Radiophys. Quantum Electron.), 45, 396 [CrossRef] [Google Scholar]
- Ville, J. 1948, Câbles et Transm., 2A, 61 [Google Scholar]
- Wigner, E. 1932, Phys. Rev., 40, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitsev, V. V., Stepanov, A. V., Urpo, S., & Pohjolainen, S. 1998, A&A, 337, 887 [NASA ADS] [Google Scholar]
- Zaitsev, V. V., Kislyakov, A. G., Urpo, S., Stepanov, A. V., & Shkelev E. I. 2003, Astron. Z., 47, 873 [Google Scholar]
All Figures
 |
Fig. 1 Dynamic spectra (left) and average spectral density plots (right) of very-low-frequency modulations of solar microwave bursts on a) Mar. 23, 2000 (11:20–12:20 UT); b) Sep. 07, 2001 (15:20–15:50 UT); c) Sep. 15, 2001 (10:00–14:00 UT). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


