| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014808 | |
| Published online | 03 December 2010 | |
On the stability of the thermal Comptonization index in neutron star low-mass X-ray binaries in their different spectral states
1
Dipartimento di FisicaUniversità di Ferrara,
via Saragat 1,
44100
Ferrara,
Italy
e-mail: farinelli@fe.infn.it
2
NASA Goddard Space Flight Center, Greenbelt, MD, USA
3
George Mason University, Fairfax, VA, USA
4
US Naval Research Laboratory, Washington, DC, USA
Received:
16
April
2010
Accepted:
2
September
2010
Context. Most of the spectra of neutron star low-mass X-ray binaries (NS LMXBs), whether they are persistent or transient, are characterized by the presence of a strong thermal Comptonization bump, which is thought to originate in the transition layer (TL) between the accretion disk and the NS surface. The observable quantities that characterize this component, which is dominating the emission below 30 keV, are the spectral index α and the rollover energy, both related to the electron temperature and optical depth of the plasma.
Aims. Starting from observational results on a sample of NS LMXBs in different spectral states, we formulate the problem of X-ray spectral formation in the TL of these sources. We predict a stability of the thermal Comptonization spectral index in different spectral states if the energy release in the TL is much higher than the intercepted flux coming from the accretion disk.
Methods. We use an equation for the energy balance and the radiative transfer diffusion equation for a slab geometry in the TL to derive a formula for the thermal Comptonization index α. We show that in this approximation the TL electron temperature kTe and optical depth τ0 can be written as a function of the energy flux from the disk intercepted by the corona (TL) and that in the corona itself, Qdisk/Qcor. Because the spectral index α depends on kTe and τ0, this in turn leads to a relation α = f(Qdisk/Qcor), with α ~1 when Qdisk/Qcor ≪ 1.
Results. We show that the observed spectral index α for the sample of sources here considered lies in a belt around 1 ± 0.2 apart for the case of GX 354–0. Comparing our theoretical predictions with observations, we claim that this result, which is consistent with the condition Qdisk/Qcor ≪ 1, can give us constraints on the accretion geometry of these systems, an issue that seems difficult to be solved with only the spectral analysis method.
Key words: stars: neutron / X-rays: binaries / accretion, accretion disks / radiative transfer
© ESO, 2010
1. Introduction
It is well known since the 1980s that the spectra of low-mass X-ray binaries (LMXBs) hosting a neutron star (NS) can be described up to about 30 keV by a two-component model representing the contribution from different emitting regions of the system. However, the interpretation of the spectra is not unique as demonstrated by the variety of different models used over the years. Before the BeppoSAX and RXTE era, two concurring models were the standard to describe X-ray emission in LMXBs. In the so-called “eastern model” (Mitsuda et al. 1984, 1989) the spectra were fitted by the sum of a soft blackbody (BB) emission (actually modeled by a multi-color disk BB spectrum) attributed to the accretion disk, plus a hotter simple or Comptonized BB claimed to originate close to the NS surface. On the other hand, in the “western model” interpretation (White et al. 1986, 1988), the direct BB component was attributed to the NS surface, while an unsaturated Comptonization spectrum was thought to originate from a hot corona above the inner accretion disk, which supplies most of the soft seed photons for Comptonization. Indeed, even after the advent of BeppoSAX and RXTE, the persistent emission of NS LMXBs was described by the sum of a BB component plus a thermal Comptonization (TC) spectrum, usually described by the XSPEC Comptt model (Titarchuk 1994, hereafter T94). Despite the significant improvement in our knowledge of the source spectral properties by means of the broadband observations, the BB+TC model was subjected to a dichotomy. Indeed, both cases provide generally equally acceptable good fits, no matter whether the temperature of the direct BB spectrum (kTbb) is lower (e.g., Di Salvo et al. 2000a,b, 2001; Oosterbroek et al. 2001; Gierliński & Done 2002; Lavagetto et al. 2004; Paizis et al. 2005) or higher (e.g., Paizis et al. 2005; Farinelli et al. 2007; Farinelli et al. 2008, hereafter F08) than that of the thermally Comptonized seed photons (kTs).
The consequences of these results were the interpretation of the BB emission as owing either to the accretion disk (kTbb < kTs) or to the NS surface (kTbb > kTs). Moreover, in addition to the persistent X-ray emission, BeppoSAX (e.g., Di Salvo et al. 2000a, 2002) RXTE (D’Amico et al. 2001; Di Salvo et al. 2006) and later also INTEGRAL (Paizis et al. 2006, hereafter P06) allowed the possibility to discover a transient powerlaw (PL) X-ray emission above 30 keV in bright NS LMXBs.
Motivated by the need to put some order and give an unified scenario of the different NS system spectral states, Paizis et al. (2006, hereafter P06) performed a systematic observational campaign with the ISGRI (20–200 keV) monitor onborad INTEGRAL. Using long-term average spectra and including former INTEGRAL results on GX 354–0 (Falanga et al. 2006), P06 classified NS LMXBs into four main states: the hard/PL, low/hard, intermediate and soft. The high-energy (>20 keV) spectra in different sources were interpreted by P06 as the result of the interplay between thermal and bulk Comptonization processes, whose relative efficiency is ultimately dictated by the mass-accretion rate. At high energies (where the direct BB component is negligible), the hard/PL state spectra can be fitted with a simple PL component; the low/hard spectra by a TC spectrum of soft (≲1 keV) BB-like photons off an electron population with kTe ~20−30 keV and τ0 ≲ 3; the intermediate state spectra by a TC spectrum with kTe ~3−5 keV and τ0 ≳ 5 plus a PL component with photon index Γ ~2−3; the soft state spectra by a TC component similar to the intermediate state, but without the high-energy X-ray tail.
From the observational point of view, the quantities directly measurable in the data are the cut-off energy Ec of the dominating TC bump and the spectral slope, parameterized through the energy index α (= Γ−1). For pure TC spectra, α is tightly correlated with the plasma temperature kTe and optical depth τ0 (Sunyaev & Titarchuk 1980; Titarchuk & Lyubarskij 1995, hereafter TL95), while in the presence of a converging flow (bulk motion), the shape of the velocity field also determines the emerging spectral slope (Titarchuk et al. 1997; Laurent & Titarchuk 1999, F08). In mathematical terms, α represents the index of the system Green’s function (GF), namely as it responds to monochromatic line injection. The resulting emerging spectrum is then obtained as a convolution of the GF with the input seed photon spectrum. We also emphasize that the hard/PL, hard and soft states spectra of NS LMXBs are characterized by only one Comptonization index (see Fig. 4 in P06). In the first case, its value is interpreted as a result of a mixed thermal plus bulk Comptonization effect, while in the latter two cases α is derived from pure TC. On the other hand, the intermediate state spectra show two Comptonization indexes, one is related to the persistent TC component and the other one characterizes the transient PL-like hard X-ray emission.
In Sect. 2 we give an overview of the theoretical and observational issues related to spectral evolution in X-ray binary systems hosting a NS or a black hole (BH) and outline the differences among the two classes of sources. We subsequently report on results related to the observed TC index α for a sample of NS sources. In Sect. 3 we propose a theoretical model based on diffusion formalism for radiative transfer in order to explain the observational results. In Sect. 4 we discuss the comparison between theory and data, while in Sect. 5 we draw our conclusions and give future observational perspects.
2. Spectral index evolution in neutron star systems
Starting from the considerations of the previous section, it is important to make a comparison between the index evolution in accreting BH and NS sources. The spectral state of BH sources may be generally divided into low/hard state (LHS), where the spectrum is dominated by a TC component with electron temperature kTe ~60–100 keV, intermediate state (IS), with a BB bump (presumably coming from the accretion disk) and a superposed PL high-energy component, and high/soft state (HSS) where the BB component is even stronger and the PL emission is steeper.
Actually, in BH systems generally one high energy photon index Γ is
observed (see e.g. recent results on GRS 1915+015 by Titarchuk & Seifina 2009; and
Shaposhnikov & Titarchuk 2009) and its
value evolves with the source mass-accretion rate. The latter, which is not a direct
observable quantity, may be inferred in an indirect way by means of the the normalization of
the disk flux Ndisk. In a Γ vs.
Ndisk/Quasi Periodic Oscillation (QPO) frequency diagram, it
was found (Shaposhnikov & Titarchuk 2009;
Titarchuk & Seifina 2009; Montanari et al. 2009) that the photon index
progressively increases from Γ ~1.6–1.8 as the source moves from the LHS to the HSS, until
it reaches saturation around Γ ~2.2−2.4 (depending on the source). This interpretation of
the observed BH spectra was performed using the BMC model (Titarchuk et al. 1997), whose emerging spectral shape is ![\begin{equation} F(E)=\frac{C_N}{A+1} [BB(E)+ A \times G(E,E_0) \ast BB(E_0)]. \label{bmc} \end{equation}](/articles/aa/full_html/2011/01/aa14808-10/aa14808-10-eq27.png) (1)In Eq. (1), the first term on the right-hand side
represents the direct seed photon BB-like spectrum, while the second one gives its
modification due to Comptonization (convolution with GF). The hardness of the spectrum is
dictated by the energy index α of the GF which, in BMC, is a broken-PL with
G(E,E0) ∝ Eα + 3
for E < E0 and
G(E,E0) ∝ E−α
for E > E0, where
E0 is the monochromatic input energy. It is important to keep
in mind that the GF in BMC does not contain the exponential spectral rollover, so when the
latter is observed in the X-ray spectrum of a source, it can be taken into account by
multiplying the model with an exponential e-folding factor
∝ e−E/Ec.
(1)In Eq. (1), the first term on the right-hand side
represents the direct seed photon BB-like spectrum, while the second one gives its
modification due to Comptonization (convolution with GF). The hardness of the spectrum is
dictated by the energy index α of the GF which, in BMC, is a broken-PL with
G(E,E0) ∝ Eα + 3
for E < E0 and
G(E,E0) ∝ E−α
for E > E0, where
E0 is the monochromatic input energy. It is important to keep
in mind that the GF in BMC does not contain the exponential spectral rollover, so when the
latter is observed in the X-ray spectrum of a source, it can be taken into account by
multiplying the model with an exponential e-folding factor
∝ e−E/Ec.
The index saturation observed in BH sources as they move to the HSS finds a natural explanation in the framework of a bulk-dominated scenario (see mathematical proof of this statement in e.g. Titarchuk & Seifina 2009). Moreover, when the sources are in the LHS the points in the Γ vs. Ndisk/QPO diagram form a plateau around Γ ~1.5 before the rising phase. This clear mapping of the energy (or photon) index evolution is possible in BH sources because they are generally strongly variable and their X-ray spectrum allows for a one-to-one correspondence between the spectral state and the energy index α (or Γ) using spectral modeling according to Eq. (1). One of the advantages of BMC model is that it is a generic Comptonization model, because it allows to map the spectral evolution of sources through the Comptonization index α, which is a direct measurable quantity, no matter what the underlying physical conditions. The theoretical interpretation of the source spectral formation is postponed at another time.
For NS sources however, the situation is less straightforward. Most variable sources do exhibit pure TC spectra, with the electron temperature kTe progressively decreasing and the optical depth τ0 increasing, respectively, when they move from the hard to the soft state. Examples for this are GX 354–0 (Falanga et al. 2006) or 4U 1608–52 (Gierliński & Done 2002). On the other hand, bright LMXBs of the GX class such as the classical six known Z sources (Sco X–1, GX 17+2, Cyg X–2, GX 340+0, GX 5–1 and GX 349+2) and, more recently, GX 13+1, show only a small evolution of their persistent X-ray continuum (dominated by the strong TC bump with kTe ~3–5 keV and τ0 ≫ 1). They are additionally characterized by a transient hard X-ray PL-like component (intermediate state).
Other persistently bright sources such as GX 3+1, GX 9+1, and GX 9+9 have only been observed in the soft state without evidence of hard X-ray tails. Indeed, a mapping of the evolution of the transient hard X-ray tail of NS sources in the intermediate state has not been yet possible because of the insufficient statistics available at high energies. Some attempts (Di Salvo et al. 2000a, 2002, 2006) were actually undertaken to establish changes in the intensity of the transient hard X-ray tail by fitting it with a simple PL and, when statistics was poor, fixing the index by allowing to vary only its flux. But nothing could be concluded about the index evolution.
Thus, as of today, serious investigations can be performed only on the evolution of the spectral index related to the persistent TC component. This was done for the first time by Titarchuk & Shaposhnikov (2005, hereafter TS05), who performed a systematic analysis of the variable NS X-ray binary GX 354–0 (4U 1728-34) from the hard to the soft state with observations from the Proportional Counter Array (PCA, 3–30 keV) onboard RXTE. The source spectra were fitted with a two-BMC model, with A ≫ 1 (see Eq. (1)) and with the GF spectral index fixed equal for both components. Thus, the model used by TS05 actually was
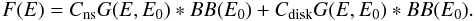 The main result found by
TS05 was that as the source moved from the hard to the soft state, the index Γ
(= α + 1) progressively increased without evidence of saturation, unlike
the BH case. Actually, the final soft state of GX 354–0 was represented by the sum of two BB
components, because for α ≫ 1,
G(E,E0) ∗ BB(E0) ≈ BB(E).
This result needs however a revision. Fitting the NS LMXBs soft state spectrum with a two-BB
model can be yet possible because of the lack of data below 3 keV, which is of key
importance, but the limited broadband resolution allows to have different models with the
same good fitting results. For example, recent results of the analysis of
PCA/RXTE data for 4U 1608–52 by Ding et al. (in prep.) show that the soft
state spectrum of the source can be fitted either by a two-BB model or by a single TC model
(Comptb, F08) with α ~1. Note also that Falanga et al. (2006)
fitted the soft state spectrum of GX 354–0 with a multi-color disk BB (DBB, Mitsuda et al. 1984) plus Comptt model, from
which the inferred value is again α ~1. Actually, when looking at the
BeppoSAX results obtained over years of observations of NS LMXB sources,
it is evident that the soft state spectra of these systems, rather than two BBs, need to be
described by the sum of a BB component plus an unsaturated TC spectrum with cut-off energy
below 10 keV.
The main result found by
TS05 was that as the source moved from the hard to the soft state, the index Γ
(= α + 1) progressively increased without evidence of saturation, unlike
the BH case. Actually, the final soft state of GX 354–0 was represented by the sum of two BB
components, because for α ≫ 1,
G(E,E0) ∗ BB(E0) ≈ BB(E).
This result needs however a revision. Fitting the NS LMXBs soft state spectrum with a two-BB
model can be yet possible because of the lack of data below 3 keV, which is of key
importance, but the limited broadband resolution allows to have different models with the
same good fitting results. For example, recent results of the analysis of
PCA/RXTE data for 4U 1608–52 by Ding et al. (in prep.) show that the soft
state spectrum of the source can be fitted either by a two-BB model or by a single TC model
(Comptb, F08) with α ~1. Note also that Falanga et al. (2006)
fitted the soft state spectrum of GX 354–0 with a multi-color disk BB (DBB, Mitsuda et al. 1984) plus Comptt model, from
which the inferred value is again α ~1. Actually, when looking at the
BeppoSAX results obtained over years of observations of NS LMXB sources,
it is evident that the soft state spectra of these systems, rather than two BBs, need to be
described by the sum of a BB component plus an unsaturated TC spectrum with cut-off energy
below 10 keV.
2.1. Observational results
We considered a sample of sources taken from the literature for which we can make a fiducial measurement of α. In our choice of the sources, we adopted the criterion to consider those in which α was determined either directly from the fit, as can be done with the Comptb model (where α is a free parameter), or can be derived from the temperature and optical depth obtained by the Comptt model.
The sources belonging to the first case are Sco X–1, GX 17+2, Cyg X–2, GX 340+0, GX 3+1
(Table 2 in F08), and GS 1826–238 (Table 2 in Cocchi et al.
2010). For GX 349+2 (Di Salvo et al. 2000a)
and GX 354–0 (Di Salvo et al. 2000b) we derived the
value of the spectral index α with the equation for the non-relativistic
regime (see Eq. (22) in TL95): 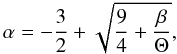 (2)where
Θ ≡ kTe/mec2
and β-parameter defined in Eq. (17) of TL95 for spherical geometry, as it
was assumed by the authors. In the case of X 1658–298, Oosterbroek et al. (2001) assumed a slab geometry, thus α was
obtained from Eqs. (2) and (17) of TL95 for
a slab geometry. For 1E 1724–3045, Barret et al.
(2000) report the best-fit value of the optical depth
τ0 of the Comptonization region for both cases of spherical
and slab geometry. We checked that the two derived values of α are
perfectly consistent. The errors on α for sources for which
kTe and τ0 were
reported, have been computed considering that the function
α [kTe,β(τ0)]
gets its absolute minimum and maximum values at the boundary of the box of its domain
delimited by the minimum and maximum value [
(2)where
Θ ≡ kTe/mec2
and β-parameter defined in Eq. (17) of TL95 for spherical geometry, as it
was assumed by the authors. In the case of X 1658–298, Oosterbroek et al. (2001) assumed a slab geometry, thus α was
obtained from Eqs. (2) and (17) of TL95 for
a slab geometry. For 1E 1724–3045, Barret et al.
(2000) report the best-fit value of the optical depth
τ0 of the Comptonization region for both cases of spherical
and slab geometry. We checked that the two derived values of α are
perfectly consistent. The errors on α for sources for which
kTe and τ0 were
reported, have been computed considering that the function
α [kTe,β(τ0)]
gets its absolute minimum and maximum values at the boundary of the box of its domain
delimited by the minimum and maximum value [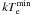 ,
,
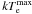 ] and
[
] and
[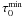 ,
,
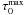 ] obtained in
computing the errors at 90% confidence level for the electron temperature and optical
depth by XSPEC.
] obtained in
computing the errors at 90% confidence level for the electron temperature and optical
depth by XSPEC.
 |
Fig. 1 Thermal Comptonization index α for sources in different spectral states as a function of the electron temperature kTe. Reference papers: Cyg X–2, Farinelli et al. (2009); Sco X–1, GX 17+2, GX 340+0 and GX 3+1, Farinelli et al. (2008); GX 354–0, Di Salvo et al. (2000b); GX 349+2, Di Salvo et al. (2001), X 1658–298, Oosterbroek et al. (2001); GS 1826–238, Cocchi et al. (2010); 1E 1724–3045, Barret et al. (2000). |
In Fig. 1 we report the measured values
of α for this sample of sources as a function of the electron
temperature kTe. This parameter can indeed
considered to be a good tracer of the source spectral state because
kTe decreases when sources move from the
hard to soft state as a result of a more efficient electron cooling by the enhanced seed
photon supply. Moreover, the electron temperature
kTe is a directly measurable quantity
because it is related to the cut-off energy of the spectrum, and it has the advantage of
being distance-independent. On the other hand, the instrumental energy-band coverage and
accumulation time can play some role in biasing the measured index value. For instance,
Falanga et al. (2006) performed a systematic
analysis of GX 354–0 as a function of its position on the hardness-intensity diagram when
the source moved from the hard to soft state. The authors fitted the 3–100 keV spectrum
with a DBB+Comptt model using the slab geometry. We computed the derived
α-values from their best-fit parameters, but the trend was not
monotonic, covering the range α ~1–3 and reflecting a behaviour of the
kTe − τ0
parameters (decreasing of kTe was not
followed by increasing of τ0, as expected). It is not clear
whether this was because of the lack of data below 3 keV, which is necessary to constrain
the seed photon temperature, or because of the accumulation time. Thus we prefer to skip
these measurements. Note also that Oosterbroek et al.
(2001) performed a BeppoSAX analysis of GX 3+1 and Ser X–1, both
sources characterized by typical soft state spectra, fitting them with a
DBB+Comptt model, but they did not specify which geometry (sphere or slab) was
assumed. We found 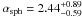 and
and 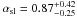 for GX 3+1,
for GX 3+1, 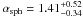 and
and 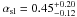 for Ser X–1, respectively. Looking at Fig. 1 we note
that for all analyzed sources the spectral index α lies in a belt around
1 ± 0.2, apart for the case of GX 354–0 where α ~1.6. We give a possible
interpretation of these observational results in the discussion.
for Ser X–1, respectively. Looking at Fig. 1 we note
that for all analyzed sources the spectral index α lies in a belt around
1 ± 0.2, apart for the case of GX 354–0 where α ~1.6. We give a possible
interpretation of these observational results in the discussion.
3. A model of the Comptonization region for a neutron star
The determination of the spectral index α obtained from Comptonization of seed photons in a bounded medium has been faced for a long time. The emerging radiation spectrum depends on several parameters such as the geometry of the plasma (e.g., slab or sphere), the electron temperature and optical depth, and the space distribution of the seed photons inside the medium. Sunyaev & Titarchuk (1980) report the value α obtained from the solution of the stationary radiative transfer equation in the non-relativistic case (Fokker-Planck approximation) obtained as a convolution of the time-dependent equation with the time-escape probability distribution for seed photons distributed according to the first eigenfunction of the space operator. Later T94, Hua & Titarchuk (1995), and TL95 extended the results to the sub-relativistic case considering both slab and spherical geometry.
In order to understand what happens in NS LMXBs sources, one has to consider the hydrodynamical conditions in the region between the accretion disk and the NS surface. We will refer to this region as the transition layer (TL), often also called boundary layer or corona. Actually, the production of a strong TC bump in the persistent X-ray spectra of NS LMXBs is thought to originate in this TL, namely the region where matter deviates from its Keplerian angular velocity in order to match that of the slowly spinning NS. The radiative and hydrodynamical configuration of the TL is mostly dictated by the Reynolds number γ (Titarchuk et al. 1998; Titarchuk & Osherovich 1999), which is proportional to the mass-accretion rate and is eventually the inverse of the viscosity parameter of the Shakura-Sunyaev disk. In particular, γ determines the radial extension of the TL and in turn, from the mass-accretion rate, its optical depth. We point out that the determination of the vertical height-scale of the TL is a very complicated problem, because it requires a complete 3D magneto-hydrodynamical treatment. Using the slim disk (thus vertical-averaged) equations for determining the radial hydrodynamical structure of the TL may indeed be an issue (e.g., Popham & Sunyaev 2001).
The enhanced radiation and thermal pressure because of higher electron temperature are expected to increase the vertical height-scale of the TL with Htl ≈ Rns. Moreover, the solution of the angular momentum for Reynolds number γ ≲ 5–10 gives a TL radial extension ΔRtl ≲ 0.5 Rns. With these characteristic length-scales, it seems more plausible to approximate the TL geometry to a slab whose normal is directed along the disk plane. We emphasize that Haardt & Maraschi (1993, hereafter HM93) determined the theoretical Comptonization index α considering a two-phase model for accretion disks in AGN, in which a hot corona is surrounding and enclosing the underlying cold accretion disk. The model can in principle be applied also to the case of solar-mass BH sources. The authors assume that the corona and the disk are two slabs at significantly different temperatures and are put in contact with each other. They concentrated on the case of high temperature (kTe ≳ 50 keV) and low optical depth (τ0 < 1) for the corona, so that the diffusion approximation cannot hold, which is different from what we are considering. One of the consequences of the high-temperature treatment is that electron scattering is anisotropic with a significant fraction of the power back-irradiating the disk. In the HM93 model, the inner boundary condition of the hot corona is the disk cool surface (with kTbb < 5 eV) with energy-dependent albedo. Note also that in their geometry, 100% of the disk flux is intercepted and reprocessed by the top plasma. In the geometry considered here on the other hand, it is possible that part of the disk emission directly escapes the system, while a fraction of its flux is intercepted by the TL. We are actually interested here on this portion of the intercepted disk flux (see next section).
Because of these differences between the two models, a direct comparison of the derived theoretical results is not straightforward. The reader can refer to the paper of HM93 for further details in order to better understand the differences of our respective approaches.
3.1. Energy release in the neutron star transition layer
The energy balance in the TL is dictated by Coulomb collisions with protons
(gravitational energy release), while inverse Compton and free-free emission are the main
cooling channels (see a formulation of this problem in the pioneer work by Zel’dovich
& Shakura 1969). However, for the characteristic electron temperature
(3 keV ≲ kTe ≲ 30 keV) and density values
(≲10-5 g cm-3) of these regions for NS LMXBs, Compton cooling
dominates over free-free emission, and the relation between the energy flux per unit
surface area of the corona Qcor, the radiation energy density
ε(τ), and electron temperature
Te is given by (see also Titarchuk et al. 1998) 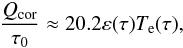 (3)where
τ0 is the characteristic optical depth of the TL.
(3)where
τ0 is the characteristic optical depth of the TL.
The distribution ε(τ) is obtained as a solution of the
diffusion equation 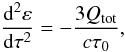 (4)where now
Qtot = Qcor + Qdisk
is the sum of the corona (TL) and intercepted disk fluxes, respectively. The two boundary
conditions for Eq. (4) are written as
(4)where now
Qtot = Qcor + Qdisk
is the sum of the corona (TL) and intercepted disk fluxes, respectively. The two boundary
conditions for Eq. (4) are written as
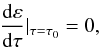 (5)
(5)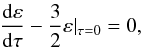 (6)which represent
the case of albedo A = 1 at the NS surface
(τ = τ0) and no diffusion emission falling
from outside onto the outer corona boundary (τ = 0). The condition for
A = 1 arises from the well-established observational result of NS
temperature kTbb ~1 keV, which implies a
ionized NS atmosphere. This is different from the case considered by HM93, where the cool
disk temperature (<5 eV) gives rise to an energy-dependent
albedo with photoelectric absorption for impinging photons with energy ≲10 keV. Another
important consideration to keep in mind is that Eq. (4) is to be considered frequency-integrated. This means that we are not
dealing with the specific (energy-dependent) shape of the reflected spectrum from the NS
surface, but we are considering the total energy density. The solution for
ε(τ) is then given by
(6)which represent
the case of albedo A = 1 at the NS surface
(τ = τ0) and no diffusion emission falling
from outside onto the outer corona boundary (τ = 0). The condition for
A = 1 arises from the well-established observational result of NS
temperature kTbb ~1 keV, which implies a
ionized NS atmosphere. This is different from the case considered by HM93, where the cool
disk temperature (<5 eV) gives rise to an energy-dependent
albedo with photoelectric absorption for impinging photons with energy ≲10 keV. Another
important consideration to keep in mind is that Eq. (4) is to be considered frequency-integrated. This means that we are not
dealing with the specific (energy-dependent) shape of the reflected spectrum from the NS
surface, but we are considering the total energy density. The solution for
ε(τ) is then given by ![\begin{equation} \varepsilon(\tau)=\frac{2\qtot}{c} \left[1+ \frac{3}{2}\tau_0\left(\frac{\tau}{\tau_0} - \frac{\tau^2}{2\tau_0^2}\right)\right]\cdot \label{ene_vs_tau} \end{equation}](/articles/aa/full_html/2011/01/aa14808-10/aa14808-10-eq82.png) (7)Note that
dε/dτ > 0
for τ < τ0, and as
Frad ∝ dε/dτ
for NS sources the radiative force always plays against gravity, unlike for BH sources.
(7)Note that
dε/dτ > 0
for τ < τ0, and as
Frad ∝ dε/dτ
for NS sources the radiative force always plays against gravity, unlike for BH sources.
Moreover the spectra of NS sources both in the soft and hard state can be adequately fitted by single-temperature Comptonization models (e.g., Falanga et al. 2006; Paizis et al. 2006; Farinelli et al. 2007; Cocchi et al. 2010). This observational fact demonstrates that an assumption of isothermal plasma in the TL can be applicable to X-ray data analysis from NS binaries. The question is how one can estimate this average temperature of the TL which is actually established by photon scattering and cooling processes.
In order to determine this average plasma temperature Te one
should estimate the mean energy density in the TL as 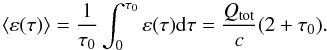 (8)Note the similarity
between Eqs. (3) and (8) in our paper and Eq. (13) in Bisnovatyi-Kogan et al. (1980), who studied the
radiation emission due to gas accretion onto a NS. If we now substitute the result of
Eq. (8) into Eq. (3), after a bit of straightforward algebra we
obtain
(8)Note the similarity
between Eqs. (3) and (8) in our paper and Eq. (13) in Bisnovatyi-Kogan et al. (1980), who studied the
radiation emission due to gas accretion onto a NS. If we now substitute the result of
Eq. (8) into Eq. (3), after a bit of straightforward algebra we
obtain 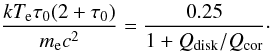 (9)Keeping in mind the
definition of the Comptonization parameter
Y ≈ ANsc (Rybicki
& Ligthman 1989), where
A ~ 4kTe/mec2
and
(9)Keeping in mind the
definition of the Comptonization parameter
Y ≈ ANsc (Rybicki
& Ligthman 1989), where
A ~ 4kTe/mec2
and 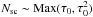 are the average photon energy
gain per scattering and average number of scatterings, respectively, we can rewrite
Eq. (9) as
are the average photon energy
gain per scattering and average number of scatterings, respectively, we can rewrite
Eq. (9) as 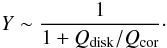 (10)Equation (10) is one of the main points of our
theoretical model and shows that in the diffusion approximation the Comptonization
parameter, which determines the spectral index, is just a function of the corona and
disk-cooling fluxes.
(10)Equation (10) is one of the main points of our
theoretical model and shows that in the diffusion approximation the Comptonization
parameter, which determines the spectral index, is just a function of the corona and
disk-cooling fluxes.
3.2. Radiative transfer formalism for spectral index determination
As we have shown in Sect. 2.1, the observed spectral index α of most NS LMXBs undergoes small variation around 1, namely α = 1 ± 0.2 when the electron temperature of the Compton cloud varies from about 2.5 to 25 keV (see Fig. 1). Thus we propose here a model for the spectral formation in the TL (corona) that can explain the stability of α if the flux from the disk intercepted by the corona is much less than that released in the corona itself. Namely we show that α ≈ 1 + O(Qdisk/Qcor).
As already pointed out in standard works (Sunyaev & Titarchuk 1980, 1985,
hereafter ST85, T94), spectral formation in plasma clouds of finite dimensions (bounded
medium) is related to the distribution law of the number of scatterings that seed photons
experience before escaping. If uav denotes the average number
of photon scatterings and the dimensionless scattering number is
u = NeσTct,
then the distribution law for u ≫ uav is
given by (see ST85) 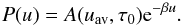 (11)For a diffusion
regime when τ0 ≳ 1.5, we get
(11)For a diffusion
regime when τ0 ≳ 1.5, we get
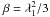 ,
where λ1 is the first eigenvalue of the diffusion space
operator. As reported in ST85, the eigenvalue problem for photon diffusion in a slab with
total optical depth 2τ0 is derived from solution of the
differential equation for the zero-moment intensity
,
where λ1 is the first eigenvalue of the diffusion space
operator. As reported in ST85, the eigenvalue problem for photon diffusion in a slab with
total optical depth 2τ0 is derived from solution of the
differential equation for the zero-moment intensity 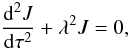 (12)with absorption
boundary conditions
dJ/dτ−(3/2)J = 0
and
dJ/dτ + (3/2)J = 0,
for τ = 0 and τ = 2τ0,
respectively. This leads to the trascendental equation for the eigenvalue
λn,
n = 1,2,3...
(12)with absorption
boundary conditions
dJ/dτ−(3/2)J = 0
and
dJ/dτ + (3/2)J = 0,
for τ = 0 and τ = 2τ0,
respectively. This leads to the trascendental equation for the eigenvalue
λn,
n = 1,2,3...
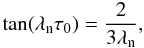 (13)which has the solution
for τ0 ≫ 1 and n = 1
(13)which has the solution
for τ0 ≫ 1 and n = 1
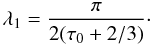 (14)The same result
for λ1 is obtained by solving Eq. (12) for a slab with total optical depth
τ0 but with reflection condition
dJ/dτ = 0 at
τ = τ0. This is not surprising because this
condition is actually met at the center of a symmetric slab with total optical depth
2τ0 and
0 ≤ τ ≤ 2τ0. Thus, the same mathematical
result is obtained for two different geometrical configurations. In the first case
(symmetric slab with total optical depth 2τ0) it represents,
e.g., an accretion disk (ST85 treatment), in our present case we are dealing with a
boundary layer with total optical depth τ0, whose asymmetry is
due to the presence of a reflector (NS surface) at one of the two boundaries. In both
cases one obtains
(14)The same result
for λ1 is obtained by solving Eq. (12) for a slab with total optical depth
τ0 but with reflection condition
dJ/dτ = 0 at
τ = τ0. This is not surprising because this
condition is actually met at the center of a symmetric slab with total optical depth
2τ0 and
0 ≤ τ ≤ 2τ0. Thus, the same mathematical
result is obtained for two different geometrical configurations. In the first case
(symmetric slab with total optical depth 2τ0) it represents,
e.g., an accretion disk (ST85 treatment), in our present case we are dealing with a
boundary layer with total optical depth τ0, whose asymmetry is
due to the presence of a reflector (NS surface) at one of the two boundaries. In both
cases one obtains 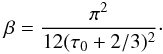 (15)Generalizing to the case
of arbitrary optical depth τ0, the diffusion operator
Ldiff = (1/3)d2J/dτ2
is replaced by the radiative transfer
operator Lτ applied to
J(τ) (see ST85 and TL95), which for disk geometry is
(15)Generalizing to the case
of arbitrary optical depth τ0, the diffusion operator
Ldiff = (1/3)d2J/dτ2
is replaced by the radiative transfer
operator Lτ applied to
J(τ) (see ST85 and TL95), which for disk geometry is
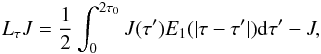 (16)where
E1(z) is the exponential integral of the
first order. In this case, the derived value for β is (T94, TL95)
(16)where
E1(z) is the exponential integral of the
first order. In this case, the derived value for β is (T94, TL95)
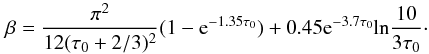 (17)Now having in mind Eq.
(9), we introduce the parameter
(17)Now having in mind Eq.
(9), we introduce the parameter
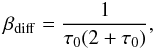 (18)and in Fig. 2 we show the values of β for the cases
reported in Eqs. (15), (17), and (18) as a function of optical depth τ0. It
is possible to see that actually for τ0 ≳ 1.5 all values
of β are practically close each other, but they deviate for
τ0 ≲ 1. For example their difference is about 30% for
τ0 = 1.
(18)and in Fig. 2 we show the values of β for the cases
reported in Eqs. (15), (17), and (18) as a function of optical depth τ0. It
is possible to see that actually for τ0 ≳ 1.5 all values
of β are practically close each other, but they deviate for
τ0 ≲ 1. For example their difference is about 30% for
τ0 = 1.
Using the definition of α (see Eq. (2)), where β is replaced by
βdiff (Eq. (18)), and Eq. (9), we obtain the
diffusion spectral index as 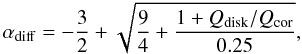 (19)or
αdiff ≈ 1 + 0.8 Qdisk/Qcor
for
Qdisk/Qcor ≪ 1.
(19)or
αdiff ≈ 1 + 0.8 Qdisk/Qcor
for
Qdisk/Qcor ≪ 1.
Thus, as it follows from Eq. (19), in the diffusion regime the TC spectral index can be expressed in terms of Qdisk/Qcor (the intercepted disk over corona fluxes), instead of TL electron temperature kTe and optical depth τ0 (see Eqs. (2) and (15)). In Fig. 3 we present a plot of αdiff as a function of Qdisk/Qcor, which shows that it ranges from 1 to 1.6 as Qdisk/Qcor increases from 0 to 1. One can see that the observable value of α ~ 1 takes place if the energy release in the disk is much less than in TL, namely if Qdisk/Qcor ≪ 1.
 |
Fig. 2 Values of the β-parameter as a function of the optical depth τ0. The solid, dashed, and dotted lines correspond to definition of β given in Eqs. (15), (17), and (18), respectively. |
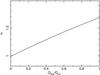 |
Fig. 3 Theoretical thermal Comptonization index α as a function of the ratio Qdisk/Qcor according to Eq. (19). |
4. Results and discussion
We compared observational data of a sample of NS LMXB sources (Fig. 1) with the theoretical results that follow from the radiative transfer model in the diffusion approximation. The data show that independently of the source spectral state, which we have parametrized through the measured TL electron temperature kTe, the spectral index α = 1 ± 0.2. We derived an estimate of the energy index α for TC spectra in NS LMXBs using an equation for the diffusion approximation in a slab geometry with reflection boundary condition at the NS surface, which is valid for optical depth τ0 ≳ 1.5. In particular, we find that in this approximation it is possible to express the value of α as a function of the ratio of the flux from the accretion disk intercepted by the corona (TL) and the energy release in the corona itself (see Eq. (19)). The agreement of the model with the data is reached when the condition Qdisk/Qcor ≪ 1 holds (see Fig. 3).
This behavior of the spectral index α actually has important consequences on putting constraints in the accretion geometry of NS LMXBs. Indeed, as already pointed-out in the introduction, the broadband persistent X-ray spectra of these sources are usually fitted by a two-component model consisting of BB-like emission plus a strong TC bump. Both the cases for which the BB temperature (kTbb) is lower or higher than that of the seed photons of the TC bump (kTs) provide equally acceptable fits. In the first case (kTbb < kTs), the origin of the direct BB component is attributed to the accretion disk, in the second case (kTbb > kTs) to the NS surface. This dichotomy in the spectral analysis has not been overcome for a long time. Some help in this direction has come with the discovery of the transient X-ray tails in some of the brightest sources (see references in the introduction): if the origin of the hard PL-like X-ray emission is attributed to a combined thermal plus bulk (converging flow) effect in the innermost part of the TL close to the NS surface, it becomes natural to suggest that the observed direct BB photon spectrum mostly originates in the TL/NS surface region, providing the seed photons for bulk Comptonization (see Fig. 1 in Farinelli et al. 2007).
The theoretical results derived here strengthen this scenario. When computing the total energetic spectral budget of the sources in the 0.1–40 keV (where most of the emission is produced), the dominating TC bump carries out more than 70% of the source luminosity, and the remaining part is due to the direct BB component. If this BB originates close to the NS surface, it is evident that the disk contribution to the X-ray luminosity is very small. Given that Qdisk in Eq. (19) represents the flux from the accretion disk intercepted by the corona and thus is smaller or at most equal to the directly emitted part, this eventually leads to α ~ 1. In this framework, we can make some considerations about the higher value of α (~1.6) measured for GX 354–0 (see Fig. 1). Di Salvo et al. (2000b) fitted the broadband spectrum of the source with a BB+Comptt model with kTbb < kTs, a modelization corresponding to the case where a significantly higher fraction of the X-ray luminosity comes from the accretion disk. This would turn of course into an enhanced value of Qdisk, and looking at Fig. 3 it is evident that increasing Qdisk/Qcor corresponds to increasing α. Actually, it would be interesting to see what does happen by fitting the BeppoSAX spectra of GX 354–0 with the same model, but with kTbb > kTs. Note also in Fig. 1 that for 1E 1724–3045 and two spectral states of GS 1826–238, α ~ 1 with electron temperature kTe ≳ 20 keV. With Eq. (9) and the best-fit values of kTe reported for the two sources, with Qdisk/Qcor ~ 0, we obtain τ0 ~ 1.3 for 1E 1724–3045 and τ0 ~ 1.6–1.7 for GS 1826–238, respectively. These values of the optical depth allow us to actually deal with the diffusion approximation within a degree of accuracy that is still satisfactory, as can be seen from Fig. 2. Moreover, for a slab with optical depth τ0 and inner reflection boundary condition, photons that are back-scattered from the reflecting surface before escaping experience an optical depth ~2τ0, which further enhances the diffusion approximation validity.
The other issue to point out is that the lower limit on α (for the extreme case Qdisk/Qcor = 0) derived by our model is 1, while there is a handful of sources for which 0.8 < α < 1. Different reasons can lead to this result. First of all, it is well known that multi-component modeling of X-ray spectra may have some influence in the determination of the best-fit parameters. In particular, in the energy band where TC dominates (≲ 30 keV), Gaussian emission lines around 6.4–6.7 keV are often observed, and the inclusion of narrow-feature component in the model can affect the continuum parameters. Additional biases can come from the energy-band coverage (in particular when using RXTE data, which start from about 3 keV) and uncertainties in the calibration of the instrumental effective area, which may play some role in particular for spectra that are far away from being powerlaw-like.
In terms of theoretical predictions, our analytical model is intended to provide a description of the observed stability of the spectral index but may of course have some limitations, in particular the energy-independent treatment of the radiation field and the simple slab approximation for the TL geometry. Yet, if it is possible that the vertical height-scale Htl of the TL is higher than its radial extension, it is also likely that there is some dependence of Htl on the radial distance from the NS surface. Moreover, in the pure plane-parallel geometry photons are allowed to escape only through the surface of the slab, while here the slab has limited extension and photons presumably can escape also from its lateral walls.
5. Conclusions
We reported results on the value of the thermal Comptonization spectral index α for a sample of NS LMXB sources in different spectral cases and found that apart from GX 354–0 it lies in a belt around 1 ± 0.2. We proposed a simple theoretical model using the diffusion approximation where α is found to be a function only of the ratio of the disk and corona fluxes. In particular, the condition Qdisk/Qcor ≪ 1 leads to α ~1, which is consistent with observations. We are hopeful that our work will encourage to significantly extend the sample of observed sources using archival data and observations from present and future missions, in particular using as broad as possible energy band, especially below 3 keV in order to avoid biases in the spectral results. We also claim that our model can be helpful in solving the dichotomy related to the fact that equally good fits are obtained for the cases where the observed direct BB component has a temperature higher or lower than that of the seed photons subjected to thermal Comptonization.
Acknowledgments
The authors are grateful to the referee whose suggestions greatly improved the quality of the paper with respect to the first version. This
work was supported by grant from Italian PRIN-INAF 2007, “Bulk motion Comptonization models in X-ray Binaries: from phenomenology to physics”, PI M. Cocchi.
References
- Barret, D., Olive, J. F., Boirin, L., et al. 2000, ApJ, 533, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Bisnovatyi-Kogan, G. S., Khlopov, M. Y., Chechetkin, V. M., & Eramzhyan, R. A. 1980, SvA, 24, 716 [Google Scholar]
- Cocchi, M., Farinelli, R., Paizis, A., & Titarchuk, L. 2010, A&A, 509, 2 [Google Scholar]
- D’Amico, F., Heindl, W. A., Rothschild, R. E., et al. 2001, ApJ, 547, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Stella, L., Robba, N. R., et al. 2000a, 554, L119 [Google Scholar]
- Di Salvo, T., Iaria, R., Burderi, L., & Robba, N. R. 2000b, ApJ, 542, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Robba, N. R., Iaria, R., et al. 2001, ApJ, 554, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Farinelli, R., Burderi, L., et al. 2002, A&A, 386, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Salvo, T., Goldoni, P., Stella, L., et al. 2006, ApJ, 649, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Falanga, M., Godtz, D., Goldoni, P., et al. 2006, A&A, 458, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinelli, R., Titarchuk, L., & Frontera, F. 2007, ApJ, 662, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Farinelli, R., Titarchuk, L., Paizis, A., & Frontera, F. 2008, ApJ, 680, 602 (F08) [NASA ADS] [CrossRef] [Google Scholar]
- Farinelli, R., Paizis, A., Landi, R., & Titarchuk, L. 2009, A&A, 498, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gierliński, M., & Done, C. 2002, MNRAS, 337, 1373 [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 50 (HM93) [Google Scholar]
- Hua, X.-M., & Titarchuk, L. 1995, ApJ, 449, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., & Titarchuk, L. 1999, ApJ, 511, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Lavagetto, G., Iaria, R., di Salvo, T., et al. 2004, Nucl. Phys. B, Proc. Suppl., 132, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Mitsuda, K., Inoue, H., Nakamura, N., & Tanaka, Y. 1989, PASJ, 41, 97 [NASA ADS] [Google Scholar]
- Montanari, E., Titarchuk, L., & Frontera, F. 2009, ApJ, 692, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterbroek, T., Parmar, A. N., Sidoli, L., in’t Zand, J. J. M., & Heise, J. 2001, A&A, 370, 532 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paizis, A., Ebisawa, K., Tikkanen, T., et al. 2005, A&A, 435, 599 [CrossRef] [EDP Sciences] [Google Scholar]
- Paizis, A., Farinelli, R., Titarchuk, L., et al. 2006, A&A, 459, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popham, R., & Sunyaev, R. A. 2001, ApJ, 547, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiat. Processes Astrophys. (New York: Wiley) [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. 1980, A&A, 86, 121 [NASA ADS] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. 1985, A&A, 143, 374 [NASA ADS] [Google Scholar]
- Shaposhnikov, N., & Titarchuk, L. 2009, ApJ, 699, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 (T94) [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Lyubarskij, Y. 1995, ApJ, 450, 876 (TL95) [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Osherovich, V. 1999, ApJ, 518, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Fiorito, R. 2004, ApJ, 612, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Shaposhnikov, N. 2005, ApJ, 626, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Seifina, E. 2009, ApJ, 706, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1997, ApJ, 487, 831 [NASA ADS] [Google Scholar]
- Titarchuk, L., Lapidus, J., & Muslimov, A. 1998, ApJ, 499, 315 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Peacock, A., Hasinger, G., et al. 1986, MNRAS, 218, 129 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Stella, L., & Parmar, A. 1988, ApJ, 324, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Zel’dovich, Ya. B., & Shakura, N. I. 1969, Sov. Astron., 13, 175 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Thermal Comptonization index α for sources in different spectral states as a function of the electron temperature kTe. Reference papers: Cyg X–2, Farinelli et al. (2009); Sco X–1, GX 17+2, GX 340+0 and GX 3+1, Farinelli et al. (2008); GX 354–0, Di Salvo et al. (2000b); GX 349+2, Di Salvo et al. (2001), X 1658–298, Oosterbroek et al. (2001); GS 1826–238, Cocchi et al. (2010); 1E 1724–3045, Barret et al. (2000). |
| In the text | |
 |
Fig. 2 Values of the β-parameter as a function of the optical depth τ0. The solid, dashed, and dotted lines correspond to definition of β given in Eqs. (15), (17), and (18), respectively. |
| In the text | |
 |
Fig. 3 Theoretical thermal Comptonization index α as a function of the ratio Qdisk/Qcor according to Eq. (19). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


