| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201014239 | |
| Published online | 29 November 2010 | |
Research Note
An educated search for transiting habitable planets:
Targetting M dwarfs with known transiting planets
1
Institut d’Astrophysique et de Géophysique, Université de
Liège,
Allée du 6 Août 17, Bat. B5C,
4000
Liège,
Belgium
e-mail: michael.gillon@ulg.ac.be
2
Observatoire de Genève, Université de Genève,
51 Chemin des
Maillettes, 1290
Sauverny,
Switzerland
3
Université Joseph Fourier Grenoble 1, Centre national de la
recherche scientifique, Laboratoire d’Astrophysique de Grenoble (LAOG), UMR 5571,
38041
Grenoble Cedex 09,
France
4
Department of Earth, Atmospheric and Planetary Sciences,
Department of Physics, Massachusetts Institute of Technology,
77 Massachusetts Avenue,
Cambridge, MA
02139,
USA
5
Planetary Systems Branch, Code 693, NASA/Goddard Space Flight Center Greenbelt,
MD
20771,
USA
Received: 11 February 2010
Accepted: 21 October 2010
Because the planets of a system form in a flattened disk, they are expected to share similar orbital inclinations at the end of their formation. The high-precision photometric monitoring of stars known to host a transiting planet could thus reveal the transits of one or more other planets. We investigate here the potential of this approach for the M dwarf GJ 1214 that hosts a transiting super-Earth. For this system, we infer the transit probabilities as a function of orbital periods. Using Monte-Carlo simulations we address both the cases for fully coplanar and for non-coplanar orbits, with three different choices of inclinations distribution for the non-coplanar case. GJ 1214 reveals to be a very promising target for the considered approach. Because of its small size, a ground-based photometric monitoring of this star could detect the transit of a habitable planet as small as the Earth, while a space-based monitoring could detect any transiting habitable planet down to the size of Mars. The mass measurement of such a small planet would be out of reach for current facilities, but we emphasize that a planet mass would not be needed to confirm the planetary nature of the transiting object. Furthermore, the radius measurement combined with theoretical arguments would help us to constrain the structure of the planet.
Key words: astrobiology / binaries: eclipsing / planetary systems / stars: individual: GJ 1214 / techniques: photometric
© ESO, 2010
1. Introduction
One of the most significant goals of modern astronomy is the detection and characterization of planets similar to our Earth: a terrestrial planet lying in the habitable zone (HZ; e.g., Kasting et al. 1993) of its host star. That will place our Earth into context, as just the closest member of the habitable telluric planet class, and will possibly establish whether life exists elsewhere in the Universe. While direct detection of habitable terrestrial planets around solar-type stars are envisioned with future ambitious missions like Terrestrial Planet Finder (e.g., Traub et al. 2007) and Darwin (e.g., Cockell et al. 2008), technological developments are still needed to make these missions successful, and none of them is fully funded. In this context, the indirect detection of terrestrial planets transiting nearby M dwarfs represent a promising shortcut (e.g., Charbonneau 2009). Indeed, the planet-to-star contrast for an Earth-size planet orbiting in the HZ of an M dwarf is much more favorable than for the Earth-Sun system, permitting the detection of atmospheric biosignatures by eclipse spectroscopy with the planned James Webb Space Telescope (JWST, e.g., Seager et al. 2009; Kaltenegger & Traub 2009) without the challenging need to separate the light of the planet from that of its host star.
Two different approaches are presently used to detect low-mass planets transiting nearby M dwarfs.
-
1.
Doppler surveys targeting nearby M dwarfshave detected several low-mass planets, including a few “hotNeptunes” and “super-Earths”1. The subsequent search for the transits of these plan-ets revealed the transiting nature of GJ 436b(Gillon et al. 2007b), the first transitingplanet significantly smaller than Jupiter. A growing num-ber of habitable super-Earths are expected in the near fu-ture and, clearly, this effort should be pursued and intensi-fied, because only a substantial increase of these detections (~ × 50−100) will reveal transiting habitable super-Earths.
-
2.
Most of the known transiting planets have been detected by dedicated photometric surveys monitoring thousands of stars in fairly large fields of view. Nevertheless, nearby M dwarfs are spread all over the sky, so most transit surveys do not probe enough of them to make a transit detection likely. An alternative approach is used by the MEarth Project (Nutzman & Charbonneau 2008). This survey individually monitors nearby M dwarfs with eight 40 cm telescopes located at Mt. Hopkins, Arizona. Thanks to the small size of its targets, MEarth is sensitive to transiting planets down to a few R⊕, as demonstrated by its recent detection of a 2.68 R⊕ super-Earth transiting GJ 1214 (Charbonneau et al. 2009; hereafter C09). After CoRoT-7b (Léger et al. 2009; Queloz et al. 2009), GJ 1214b is the second super-Earth caught in transit. Unlike CoRoT-7b, GJ 1214b is a good target for an atmospheric characterization with, e.g., the future JWST, thanks to the small size and infrared brightness of its host star. Nevertheless, the approach used by MEarth is young and its effectiveness to detect habitable planets is difficult to assess.
We outline here the potential of a third approach to discover habitable planets transiting nearby M dwarfs. Its main principle is simple: planets form within disks, therefore a planet orbiting in the HZ of a given star should have a higher a priori transit probability if its star harbors a known transiting planet. This assumption is supported by the small scatter of the orbital inclinations of the eight planets of the solar system (rms = 2.2 deg) and of the regular satellites of Jupiter (rms = 0.35 deg) and Saturn (rms = 2.8 deg). For dynamical stability reasons, the fact that low-mass planets systems (e.g., GJ 581, HD 40307) detected by Doppler surveys tend to be “packed” also favors a small scatter of the orbital inclinations. Recent Kepler results also support this assumption (Steffen et al. 2010; Holman et al. 2010). Depending on the orbital inclination of the known transiting planet, on the assumed distribution of the orbital inclinations of the planetary system, on the size of the star, and on its physical distance to its HZ, significantly enhanced transit probabilities can be expected for habitable planets. A dedicated high-precision photometric monitoring of M dwarfs known to harbor close-in transiting planets could thus be an efficient way to detect transiting habitable planets in the near future. The aim of this Research Note is to assess the potential of this approach for the only M dwarf presently known to host a transiting super-Earth, GJ 1214. Section 2 presents our computational method. Our results are given in Sect. 3 and are discussed in Sect. 4.
2. Transit probabilities for additional planets
To account for the uncertainty of the measured orbital inclination for the known planet and to include the possibility that the searched planet does not share the exact same inclinations, we compute the transit probability with Monte-Carlo simulations.
We define a “terrestrial” region extending from twice the period of the transiting planet to the ice line defined as (Ogihara & Ida 2009) 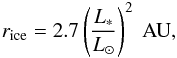 (1)where L∗ and L⊙ are the luminosity of the star and the Sun. For GJ 1214, we take L∗ = 0.00328 L⊙ for GJ 1214 (C09). This luminosity translates into rice = 0.155 AU. Using M∗ = 0.157 M⊙ for GJ 1214 (C09), the corresponding orbital period is only 56 days.
(1)where L∗ and L⊙ are the luminosity of the star and the Sun. For GJ 1214, we take L∗ = 0.00328 L⊙ for GJ 1214 (C09). This luminosity translates into rice = 0.155 AU. Using M∗ = 0.157 M⊙ for GJ 1214 (C09), the corresponding orbital period is only 56 days.
We assume circular orbits for all planets. We divide the deduced terrestrial region into 1000 equal steps in semi-major axis. For each semi-major axis ai (i = 1:1000), 10 000 orbital inclinations ik (k = 1:10000) are drawn via 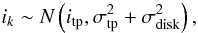 (2)where N(m,n2) represents the normal distribution of mean m and variance n2, itp and σtp are the orbital inclination of the known transiting planet and its 1-σ error, and σdisk is the assumed standard deviation of the orbital inclinations in the planetary systems. We adopt itp = 88.62 ± 0.35 deg (C09), and σdisk = 2.2 deg, the corresponding value for the eight planets of the solar system (Murray & Dermott 2000). We also test values twice smaller and larger for σdisk, i.e. 1.1 and 4.4 deg, and the unrealistic value σdisk = 0 deg to illustrate the influence of the inclination scatter in the planetary systems.
(2)where N(m,n2) represents the normal distribution of mean m and variance n2, itp and σtp are the orbital inclination of the known transiting planet and its 1-σ error, and σdisk is the assumed standard deviation of the orbital inclinations in the planetary systems. We adopt itp = 88.62 ± 0.35 deg (C09), and σdisk = 2.2 deg, the corresponding value for the eight planets of the solar system (Murray & Dermott 2000). We also test values twice smaller and larger for σdisk, i.e. 1.1 and 4.4 deg, and the unrealistic value σdisk = 0 deg to illustrate the influence of the inclination scatter in the planetary systems.
For each orbital inclination ik drawn via Eq. (2), a transit impact parameter bk is computed via 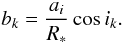 (3)We use R∗ = 0.211 R⊙ (C09). If the absolute value of bk is lower than 1, a transit is recognized. If so, the transit duration Dk is computed via
(3)We use R∗ = 0.211 R⊙ (C09). If the absolute value of bk is lower than 1, a transit is recognized. If so, the transit duration Dk is computed via  (4)where Pi is the orbital period. Equation (4) assumes that the planet has a negligible size compared to the star (e.g., Seager & Mallén-Ornelas 2003).
(4)where Pi is the orbital period. Equation (4) assumes that the planet has a negligible size compared to the star (e.g., Seager & Mallén-Ornelas 2003).
 |
Fig. 1 Top: transit probability for a planet in a circular orbit around GJ 1214 as a function of the orbital period, assuming σdisk = 0 (black), 1.1 (green), 2.2 (red) and 4.4 deg (blue), and neglecting the transiting nature of the known planet (dashed line). Middle: transit depth of a planet orbiting around GJ 1214 as a function of the planetary radius. Bottom: RV semi-amplitude above which a planet could be detected in the HARPS data. See text for details. |
For each step in semi-major axis, the transit probability is computed as the fraction of the 10 000 drawn inclinations leading to a transit. We also compute for each step the geometric transit probability Ptr, neglecting the transiting nature of the known planet, using 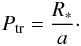 (5)Following Kasting et al. (1993), we define the inner edge HZin and outer edge HZout of the habitable zone as
(5)Following Kasting et al. (1993), we define the inner edge HZin and outer edge HZout of the habitable zone as  From these formula, the HZ of GJ 1214 extends from 0.054 to 0.078 AU. These edges correspond to orbital periods of 11.6 and 20.1 days. We finally average the transit probabilities and durations for the whole HZ to obtain a representative value for GJ 1214.
From these formula, the HZ of GJ 1214 extends from 0.054 to 0.078 AU. These edges correspond to orbital periods of 11.6 and 20.1 days. We finally average the transit probabilities and durations for the whole HZ to obtain a representative value for GJ 1214.
3. Application
Neglecting the transiting nature of GJ 1214b, a planet in the HZ of GJ 1214 would have a mean transit probability of only 1.5%. Taking into account the transits of GJ 1214b and assuming σdisk = 2.2 deg leads to a much higher transit probability of 25.1% (Fig. 1), the mean expected duration of a transit being 1.4 h. A scatter twice larger for the orbital inclinations in the GJ 1214 planetary system would lead to a reduced transit probability of 14.8%, which is still ten times higher than the probability expected if we do not consider that GJ 1214b does transit. For σdisk = 1.1 deg, the probability goes up to 30.1%, while it goes down to 7.7% for fully coplanar orbits. The difference between these latter two values well illustrates the advantage given by the fact that planets of the same system are probably not perfectly coplanar.
Assuming σdisk = 2.2 deg and that a terrestrial planet orbits in the HZ of GJ 1214, a constant photometric monitoring of the star during 20.1 days would therefore have a ~25% probability to catch at least one of its transits, if a sufficiently high photometric precision is reached. Two main options can be considered to perform this photometric search: a multi-site ground-based survey using several telescopes spread in longitude or a space-based monitoring using an instrument able to stare at GJ 1214 for three weeks.
Ground-based photometric time series reaching the sub-mmag precision level for a time sampling better than one minute have been obtained in the optical for several transiting planets (e.g., Gillon et al. 2009; Johnson et al. 2009; Winn et al. 2009). Our own analysis of most of these data makes us conclude that a transit with a depth as low as one mmag could be firmly detected with a such a photometric precision. Shallower occultations of short period transiting planets could be detected from the ground (e.g., Sing & López-Morales 2009), but only because the expected timing and shape of the occultations are known via the analysis of the transits and radial velocities (RV). For a transit that could happen anytime during a run of two months, a detection limit better than one mmag seems unrealistic with current instruments and techniques. Furthermore, the most precise ground-based differential light curves were obtained during nights with excellent atmospheric conditions and at low airmass, far from the average observation conditions of a multi-site survey observing the same star during three weeks. For these reasons, the actual detection limit for such a program would probably be closer to two than one mmag.
Figure 1 (middle panel) shows that with this photometric precision, a ground-based monitoring campaign of GJ 1214 would be sensitive to very small planets. Planets as small as the Earth or even smaller could be detected. It is worth noticing here that the detection limit achievable from the ground is mostly limited by the atmosphere and the photometric correlated noises that it creates.
The detection limit could be much better for a space-based telescope. For instance, the Spitzer telescope has produced several high-precision photometric time-series for another M-dwarf, GJ 436 (e.g., Gillon et al. 2007a; Deming et al. 2007). Spitzer’s cryogen is now depleted, but the telescope is still active (under the name “Warm Spitzer”) and keeps its full potential in the two bluest channels (3.6 and 4.5 μm) of its IRAC camera (Stauffer et al. 2007). Our analysis of the occultation photometry obtained for GJ 436b at 3.6 μm (Lanotte et al., in prep.) allows us to conclude that an eclipse of 200 ppm would be firmly detected for GJ 436 within the 3.6 μm channel of Spitzer. At 3.6 μm, GJ 1214 is 2.7 mag fainter than GJ 436. Considering a complete noise model and Spitzer instrumental throughput corrections2, we obtain a SNR of ~990 for a 12 s exposure at 3.6 μm. This translates into a theoretical error of 450 ppm per minute, and 59 ppm per hour. Considering only white noise, we would therefore conclude that a transit of 240 ppm and lasting one hour could consequently be detected at 4-σ. Still, fluxes measured with the InSb detectors of IRAC show a strong correlation with the changing position of the star on the array (e.g., Knutson et al. 2008). This purely spatial “pixel-phase” effect is due to the combination of the undersampling of the stellar image, the intra-pixel sensitivity, and the jitter of the telescope. It can be well modeled by an analytic function of the x and y coordinates of the stellar image center, but the inaccuracy of this model and the finite precision on the measured stellar positions result in a residual photometric correlated noise with a timescale similar to that of a typical transit. From our experience with GJ 436 (Lanotte et al., in prep.) and CoRoT-2 (Gillon et al. 2010), the impact of the “pixel-phase” effect on the final photometric precision is SNR-dependent, at least in the high SNR regime. Basically, it leads to errors on the fitted parameters (including the eclipse depth) ~twice larger than expected when considering only white noise. In the case of GJ 1214, a transit lasting one hour would thus need a depth of ~450 ppm to be detected at 4-σ. This limit is shown in Fig. 2. It corresponds to a planet size of 0.49 R⊕, i.e. smaller than Mars (0.53 R⊕).
 |
Fig. 2 Mass-radius curves for exoplanets. The horizontal lines show planets of a fixed radius. An upper mass limit comes from the pure iron planet case. A lower mass limit comes from theoretical arguments, namely the inability of a small and low-mass planet to retain H and He. Further arguments about water loss may be used to argue that a planet cannot have a significant interior water fraction. The solid lines are homogeneous planets. From top to bottom the homogeneous planets are made of water ice (blue solid line); silicate (MgSiO3 perovskite; red solid line); and iron (Fe ϵ; green solid line). The non-solid lines are differentiated planets. The red dashed line is for silicate planets with 32.5% by mass iron cores and 67.5% silicate mantles (similar to Earth) and the red dotted line is for silicate planets with 70% by mass iron core and 30% silicate mantles (similar to Mercury). The blue dashed line is for water planets with 75% water ice, a 22% silicate shell and a 3% iron core; the blue dot-dashed line is for water planets with 45% water ice, a 48.5% silicate shell and a 6.5% iron core (similar to Ganymede); the blue dotted line is for water planets with 25% water ice, a 52.5% silicate shell and a 22.5% iron core. Curves taken from Seager et al. (2007). |
Alternatively, one may await the RV detection of any additional planet before undertaking the photometric search for its transit. Not only would the presence of the planet be known with certainty, but the observational window would also be narrowed with an a priori ephemeris. To estimate the observational effort required for a RV detection for GJ 1214 (V = 15), we compute the detection limit (Zechmeister & Kürster 2009) imposed by the 28 HARPS RVs reported in the detection paper (C09). Figure 1 (bottom panel) shows the semi-amplitude above which a planet would have been detected, with a 99% confidence level (for all of our 12 trial phases). The plot shows fluctuations because we have too few data points for a clean sampling, but more data will smooth the curve and it will eventually be independent of the period. More data will scale down the detection limit and, anticipating a better sampling from these additional points, a K ~ 10 m.s-1 limit (indicated by a dashed line) seems a better estimate for the velocity amplitude we aim to scale. To detect an Earth-mass planet orbiting at 0.066 AU – or K ~ 0.88 m.s-1 – we will need 130 times more data points (>2000 h). A true Earth-mass planet (or lower mass) requires therefore unrealistic observing time with current velocimeters.
4. Discussion
GJ 1214 appears to be a promising target for the approach described here. Because of its small size and luminosity, the transit probability in its HZ is fairly large, and very small planets could be detected transiting this star. Another major advantage of GJ 1214 is the proximity of its HZ. To probe its HZ, a constant monitoring of the star during only three weeks would be needed. For planets orbiting in the inner part of the HZ, two transits could be observed during such a run of three weeks, leading to an improved sensitivity to very small planets.
For the area interior to the HZ, the transit probability goes up to a mean value of 44% for GJ 1214 (asssuming σdisk = 2.2 deg). Because of the larger number of transits observed for shorter periods, the sensitivity to smaller planets would be better than for the HZ. For instance, Warm Spitzer could then detect a planet as small as Mercury (0.38 R⊕).
Discovery of a transiting habitable-zone planet as small as Mars would create a very challenging mass measurement for the RV method. Mars is nearly ten times less massive that the Earth, and the mean semi-amplitude of the RV wobble due to a Mars-mass planet orbiting in the HZ of GJ 1214 would be only 9.4 cm s-1, while we have seen in Sect. 3 that an Earth-mass planet producing a RV signal ten times larger would be out of reach for current spectrographs. Of course, with the a priori knowledge of the phase and period, one would need to sample the RV orbit at its extrema only, facilitating the mass measurement of an Earth-mass planet. Still, the measure seems difficult and for sure, measuring the mass for a Mars-mass planet would remain out of reach for current instruments. To measure the mass of Earth and sub-Earth mass planets, one would have to rely on future facilities such as Espresso/VLT (Pasquini et al. 2009) or Codex/ELT (Liske et al. 2009).
We argue, however, that if the main goal is to find target planets for follow-up atmosphere observations for habitability, a planet mass is not completely necessary. This statement holds as long as the planet radius detection has a high SNR and as long as the planet is small enough. A high SNR transit detection for a small planet is sufficient to confirm planet candidacy for a transiting planet discovered from a targeted search. In contrast, a planet mass has traditionally been required for exoplanets discovered by planet transit surveys. Because transit surveys that simultaneously monitor tens of thousands of stars are fraught with false positives, a planet mass is the surest way to confirm the planetary nature of a transit signature. The argument here is that false positives are not a problem for transit signatures detected around a star with another known transiting planet, as long as the radius measurement is very robust.
For planets with small radii in the habitable zones of their host stars, we can derive an upper mass limit, assuming that the most massive a planet can be is one of pure iron (Fig. 2). We can argue for a lower mass limit, using theory and models, that a small planet in the stars HZ will not have an H/He envelope. Note that an H/He envelope is usually considered bad for habitability because it traps heat making the planet surface too hot for complex molecules to form. Arguments about the loss of a planets interior water reservoir (Kuchner et al. 2003; Léger et al. 2004) due to either stellar irradiation or from energy from tidal friction (e.g. Io) could be used to further theoretically constrain the planet mass.
If biosignatures or habitability features are detected, then mass estimates using future facilities are warranted, despite the huge amounts of telescope time needed.
Our results for GJ 1214 outline the scientific interest of the approach used by the MEarth Project. Not only has the MEarth survey demonstrated its capacity to detect super-Earths transiting nearby M dwarfs, but it also traces the shortest path to the detection of habitable planets as small, or even smaller, than the Earth and for which the detection of biosignatures could be possible in the near future. In this context, we advocate the development of the approach used by MEarth (other facilites spread in longitude, a similar survey observing from Southern hemisphere, larger telescopes and IR cameras to monitor cooler M dwarfs), but also an intense and high-precision photometric monitoring of GJ 1214 and of the other transiting systems that MEarth (or similar projects) will detect. This two-step approach targeting nearby M dwarfs permits the detection in the near-future of transiting habitable planets much smaller than our Earth, which would be out of reach for existing Doppler and transit surveys.
Acknowledgments
M. Gillon is a FNRS Research Associate, and acknowledges support from the Belgian Science Policy Office in the form of a Return Grant. A.H.M.J. Triaud researches are funded by the Swiss Fond National de la Recherche Scientifique. The authors thank Justin Crepp for having spotted an error in an equation in the first version of this manuscript. The anonymous referee is acknowledged for his valuable report. Last but not least, we sincerely thank NASA for believing in the idea proposed here and for having accepted our Spitzer GO-7 program of 485 h of continuous observation of GJ 1214.
References
- Charbonneau, D. 2009, Transiting Planets, Proceedings of the International Astronomical Union, IAU Symp., 253, 1 [NASA ADS] [Google Scholar]
- Charbonneau, D., Berta, Z., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cockell, C. S., Léger, A., Fridlund, M., et al. 2009, AsBio, 9, 1 [Google Scholar]
- Deming, D., Harrington, J., Laughlin, G., et al. 2007, ApJ, 667, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Demory, B.-O., Barman, T., et al. 2007a, A&A, 471, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Pont, F., Demory, B.-O., et al. 2007b, A&A, 472, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Smalley, B., Hebb, L., et al. 2009, A&A, 496, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Lanotte, A. A., Barman, T., et al. 2010, A&A, 511, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johnson, J. A., Winn, J. N., Cabrera, N. E., & Carter, J. A. 2009, ApJ, 692, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchner, M. 2003, ApJ, 596, 105 [Google Scholar]
- Léger, A., Selsis, F., Sotin, C., et al. 2004, Icarus, 169, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Liske, J., Pasquini, L., Bonifacio, P., et al. 2009, Science with the VLT in the ELT Era, Astrophysics and Space Science Proceedings, ISBN 978-1-4020-9189-6 (The Netherlands: Springer), 243 [Google Scholar]
- Murray, C. D., & Dermott, S. F. 2000, Solar Sytem Dynamics (Cambridge University Press) [Google Scholar]
- Nutzman, P., & Charbonneau, D. 2008, PASP, 120, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Ida, S. 2009, ApJ, 699, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Manescau, A., Avila, G., et al. 2009, Science with the VLT in the ELT Era, Astrophysics and Space Science Proceedings, ISBN 978-1-4020-9189-6 (The Netherlands: Springer), 395 [Google Scholar]
- Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2002, ApJ, 585, 1038 [Google Scholar]
- Seager, S., Kuchner, M., Hier-Majumde, C. A., & Militzer, B. 2007, ApJ, 669, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., Deming D., & Valenti J. A. 2009, Astrophys. Space Sci. Proc., ISBN 978-1-4020-9456-9 (The Netherlands: Springer), 123 [Google Scholar]
- Sing, D. K., & López-Morales, M. 2009, A&A, 493, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stauffer, J. R., Manning, V., Levine, D., et al. 2007, The Science Opportunities of the Warm Spitzer Mission Workshop, AIP Conf. Proc., 943, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, J. H., Batalha, N. M., Borucki, W. J., et al. 2010, ApJ, accepted [arXiv:1006.2763] [Google Scholar]
- Traub, W, Shaklan, S., & Lawnson, P. 2007, In the Spirit of Bernard Lyot: The Direct Detection of Planets and Circumstellar Disks in the 21st Century, University of California, Berkeley [Google Scholar]
- Winn, J. N., Holman, M. J., Carter, J. A., et al. 2009, AJ, 137, 3826 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Top: transit probability for a planet in a circular orbit around GJ 1214 as a function of the orbital period, assuming σdisk = 0 (black), 1.1 (green), 2.2 (red) and 4.4 deg (blue), and neglecting the transiting nature of the known planet (dashed line). Middle: transit depth of a planet orbiting around GJ 1214 as a function of the planetary radius. Bottom: RV semi-amplitude above which a planet could be detected in the HARPS data. See text for details. |
| In the text | |
 |
Fig. 2 Mass-radius curves for exoplanets. The horizontal lines show planets of a fixed radius. An upper mass limit comes from the pure iron planet case. A lower mass limit comes from theoretical arguments, namely the inability of a small and low-mass planet to retain H and He. Further arguments about water loss may be used to argue that a planet cannot have a significant interior water fraction. The solid lines are homogeneous planets. From top to bottom the homogeneous planets are made of water ice (blue solid line); silicate (MgSiO3 perovskite; red solid line); and iron (Fe ϵ; green solid line). The non-solid lines are differentiated planets. The red dashed line is for silicate planets with 32.5% by mass iron cores and 67.5% silicate mantles (similar to Earth) and the red dotted line is for silicate planets with 70% by mass iron core and 30% silicate mantles (similar to Mercury). The blue dashed line is for water planets with 75% water ice, a 22% silicate shell and a 3% iron core; the blue dot-dashed line is for water planets with 45% water ice, a 48.5% silicate shell and a 6.5% iron core (similar to Ganymede); the blue dotted line is for water planets with 25% water ice, a 52.5% silicate shell and a 22.5% iron core. Curves taken from Seager et al. (2007). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


