| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200913836 | |
| Published online | 03 December 2010 | |
The magnetohydrodynamic instability of current-carrying jets
1
INAF, Osservatorio Astrofisico di Catania,
via S. Sofia 78,
95123
Catania,
Italy
e-mail: abo@oact.inaf.it
2
INFN, Sezione di Catania,
via S. Sofia 72,
95123
Catania,
Italy
3
A. F. Ioffe Institute of Physics and Technology and Isaac Newton
Institute of Chile, Branch in St.
Petersburg, 194021
St. Petersburg,
Russia
Received:
9
December
2009
Accepted:
3
October
2010
Context. Magnetohydrodynamic instabilities can be responsible for the formation of structures with various scales in astrophysical jets.
Aims. We consider the stability properties of jets containing both the azimuthal and axial field of subthermal strength. A magnetic field with complex topology in jets is suggested by theoretical models and is consistent with recent observations.
Methods. Stability is discussed by means of a linear analysis of the ideal magnetohydrodynamic equations.
Results. We argue that in azimuthal and axial magnetic fields the jet is always unstable to non-axisymmetric perturbations. Stabilization does not occur even if the strengths of these field components are comparable. If the axial field is weaker than the azimuthal one, instability occurs for perturbations with any azimuthal wave number m, and the growth rate reaches a saturation value for low values of m. If the axial field is stronger than the toroidal one, the instability shows for perturbations with relatively high m.
Key words: magnetohydrodynamics (MHD) / instabilities / stars: pre-main sequence / ISM: jets and outflows / galaxies: jets
© ESO, 2010
1. Introduction
The magnetic field plays a key role in the formation and propagation of astrophysical jets. Polarization measurements provide important information about the orientation and the strength of the magnetic field, which seems to be highly organized on a large scale in many jets (see, e.g., Cawthorne et al. 1993; Leppänen et al. 1995; Gabuzda 1999; Gabuzda et al. 2004; Kharb et al. 2008). To explain the observational data, simplified models of the three-dimensional magnetic field distribution have been proposed (see, for example, Laing 1981, 1993; Pushkarev et al. 2005; Laing et al. 2006). In particular the polarization data suggest that the magnetic field has a significant transverse component in the main fration of the jet volume. In accordance with the “traditional” interpretation (see, e.g., Laing 1993), this magnetic structure can be associated with a series of shocks along the jet, which enhances the local transverse field. However, Very Long Baseline Interferometry (VLBI) observations of BL Lac 1803+784 (Hirabayashi et al. 1998) revealed that the transverse magnetic structure can be formed by a large-scale toroidal magnetic field, and indeed recent observations of a radio jet in the galaxy CGCG 049-033 also reveal a predominantly toroidal magnetic field (Bagchi et al. 2007; Laing et al. 2006).
Magnetic structures with a significant toroidal field-component are predicted by several theoretical models for jet formation (Blandford & Payne 1982; Romanova & Lovelace 1992; Koide et al. 1998). In particular some models of the jet propagation (see, e.g., Begelman et al. 1984) propose that the toroidal field decays more slowly than the poloidal one as a function of the distance from the central object, therefore the toroidal field should eventually become dominant. Other generation mechanisms based either on the combined influence of turbulence and large-scale shear (see, e.g. Urpin 2006) or on dynamo action along with magneto-centrifugal and reconnection processes (de Gouveia Dal Pino 2005) also predict the occurence of a significant toroidal component. A situation where loops of the toroidal magnetic field dominate the field distribution would produce important dynamical consequences for the jet structure, for instance, providing pressure confinement through magnetic tension forces (Chan & Henriksen 1980; Eichler 1993). However, it is well known from plasma physics (see, e.g., Kadomtzev 1966) that the toroidal magnetic field may cause various magnetohydrodynamic (MHD) instabilities even in simple cylindrical configurations.
In general, different types of instabilities can occur in astrophysical jets. They can be caused by boundary effects, shear, stratification and magnetic fields and are also likely to be responsible for the observed morphological complexity of jets. For this reason several analytical (see, e.g., Ferrari et al. 1980; Bodo et al. 1989, 1996; Hanasz et al. 1999; see also Birkinshaw 1997, for a review) and numerical (Hardee et al. 1992; Appl 1996; Lucek & Bell 1996; Min 1997; Kudoh et al. 1999) works have been devoted to the study of the stability properties of jets. A systematic study of the Kelvin-Helmholtz instability in non-relativistic jets with the longitudinal magnetic field has been performed by Bodo et al. (1989, 1996) including also the effect of rotation. In particular several unstable modes including a slow mode associated with the magnetic field and an inertial mode caused by rotation have been found. Shear-driven instabilities can also be very important in jets (Urpin 2002). Numerical simulations (Aloy et al. 1999a,b) indicate that the radial structure of jets may be more complex with a transition shear layer surrounding the jet core. The thickness of the shear layer depends on the distance being around 20% of the jet radius near the nozzle but broadening near the head where it is of the order of the jet radius. This shear layer may have an important consequence for various properties of jets including their stability (see, e.g., Hanasz & Sol 1996, 1998; Aloy & Mimica 2008).
In this paper, we consider the instability associated with the topology of the magnetic field in jets. Magnetic fields generated by hydrodynamic motions can be topologically non-trivial and thus prone to pressure-driven or current-driven instabilities (see, e.g., Longaretti 2008, for review). This problem is well studied in the context of experiments on controlled thermonuclear fusion (see, e.g., Bateman 1978) and has been discussed in relation to jets by a number of authors (see, e.g., Eichler 1993; Appl 1996; Appl et al. 2000; Lery et al. 2000). A linear stability analysis of supermagnetosonic jets has been performed by Appl et al. (2000) for different magnetic configurations including a force-free field. It has been shown that the current-driven instabilities can occur in the axial field for various profiles of the azimuthal field even if these components are comparable. The non-linear development of the current-driven instability has been analysed by Lery et al. (2000), who found that this instability can modify the magnetic structure of a jet redistributing the current density in the inner part. The current-driven instability of relativistic jets and plerions in toroidal magnetic fields has been considered by Begelman (1998), who obtained that the dominant instability in this case are the kink (m = 1) and pinch (m = 0) modes. The kink mode generally dominates, thus destroying the concentric field structure. Apart from the current-driven instabilities, the pressure-driven ones caused by the thermal pressure gradient can also occur in jets. The modes, corresponding to these instabilities, are radially localized and characterized by high wavenumbers. Likely, these modes are responsible for generating MHD turbulence in the jet core (Kersale et al. 2000). The pressure-driven instabilities are well studied in laboratory pinch configurations as well. Robinson (1971) considers the stability of the pinch with a large ratio of the gas and magnetic pressure using the energy principle and finds that stability is possible if currents are located outside the main plasma column. The criterion of pressure-driven instabilities in cylindrical geometry has been derived by Longaretti (2003). This criterion is related to the Alfvénic modes, which usually require less restricting conditions for instability and can even be unstable if Suydam’s criterion of stability is satisfied. If both destabilizing factors, current and pressure gradient are present, then modes of mixed nature can generally show in a jet. An example of these unstable modes has been studied by Baty & Keppens (2002), who considered the jet to have equal density with the surrounding medium, separated by a shear layer. The magnetic field in the basic state was assumed to be supersonic and helical with a vanishing radial component. The linear stability analysis mainly addresses the behaviour of kink modes with m = ±1 where m is the azimuthal wavenumber. In this basic state, the thermal pressure gradient in combination with the component of the current parallel to the magnetic field produces the energy of the perturbations that feed the instability. The authors calculated the spectrum of these modes and have found that they can be unstable. The unstable modes are usually oscillatory and their growth rate exhibits a rather peculiar double peak dependence on the axial wavevector.
Note that numerical simulations often support the idea that magnetic jets should be unstable and can generate turbulent motions caused by instabilities. For instance, Lery & Frank (2000) found that the instabilities seen in their jet simulations develop with a wavelength and growth time that are well matched by a linear stability analysis. Relativistic simulations of extragalactic jets by Leismann et al. (2005) and Roca-Sogorb et al. (2008) also clearly show that the various irregularities that develop in the jet flow can be interpreted as MHD instabilities.
Our study focuses on the stability of jets with a subthermal magnetic field where the magnetic energy is lower than the thermal energy of particles. This kind of magnetic field can be generated, for instance, by the turbulent dynamo action or by hydrodynamic motions (stretching) in the process of jet propagation. We show that stability properties of jets with a subthermal field can be essentially different from those with a highly superthermal force-free magnetic field as was considered, for example, by Appl et al. (2000). In particular, higher azimuthal modes with m ≫ 1 can have the highest growth rate at variance with the superthermal case. In our jet model, both destabilizing factors – the pressure gradient and electric current – are presented simultaneously, and the instability occurs under the combined influence of both these factors. Therefore, the instability considered has a mixed pressure- and current-driven nature.
The paper is organized as follows. Section 2 contains the derivation of the relevant equations, and Sect. 3 shows the numerical results. Conclusions are presented in Sect. 4.
2. Basic equations
We consider a very simplified model assuming that the jet is an infinitely long stationary cylindrical outflow and its propagation through the ambient medium is modelled by a sequence of quasi-equilibrium states. For the sake of simplicity, it is often assumed that the velocity of plasma within a jet, V, does not depend on coordinates (see, e.g., Appl 1996; Appl et al. 2000; Lery et al. 2000), and we will adopt the same assumption in our study. Instabilities of the magnetic configurations associated to the electric current are basically absolute instabilities, i.e. they grow, but do not propagate. We suppose that this is the case also in the rest frame of the jet, and unstable perturbations are therefore simply advected with the flow at the jet velocity (see, e.g., Appl et al. 2000). Therefore, we treat the stability properties in the rest frame of the jet.
We explore the cylindrical coordinates (s, ϕ, z) with the unit vectors (es, eϕ, ez). The magnetic field is assumed to be axisymmetric with a non-vanishing z- and ϕ-component. The azimuthal field depends on the cylindrical radius alone, Bϕ = Bϕ(s), but the axial magnetic field Bz is constant in our model.
We study the behaviour of MHD modes in the incompressible limit. This approximation is well
justified for modes with the characteristic time-scale longer than the period of sound waves
and for subsonic motions (see, e.g., Landau & Lifshitz 1981). Perturbations of the density caused by these motions are small and
can be neglected in MHD equations. By making use of the incompressible limit in a magnetised
gas, one can consider slow modes with the growth rate (or frequency) lower than the
frequency of fast magnetosonic waves. Since the typical time scale of modes under study is
of the order of the inverse Alfvén frequency, our consideration applies if the Alfvén
velocity is lower than the sound speed or, in terms of the plasma
β-parameter, if β ≫ 1 (β is the ratio of
the gas and magnetic pressures). Note that the velocity of jet V can be
much higher than the Alfvén and sound speed. In the incompressible limit, the MHD equations
read 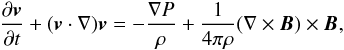 (1)
(1)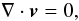 (2)
(2)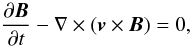 (3)
(3)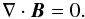 (4)In the basic state, the
gas is assumed to be in hydrostatic equilibrium in the radial direction, then
(4)In the basic state, the
gas is assumed to be in hydrostatic equilibrium in the radial direction, then
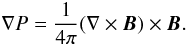 (5)Stability will be
studied by making use of a linear perturbative analysis. Because the basic state is
stationary and axisymmetric, the dependence of perturbations on t,
ϕ, and z can be taken in the form
exp(σt − ikzz − imϕ)
where kz is the wavevector in the axial
direction and m is the azimuthal wavenumber. Small perturbations will be
indicated by subscript 1, while unperturbed quantities will have no subscript. Then, the
linearized Eqs. (1)–(4) read
(5)Stability will be
studied by making use of a linear perturbative analysis. Because the basic state is
stationary and axisymmetric, the dependence of perturbations on t,
ϕ, and z can be taken in the form
exp(σt − ikzz − imϕ)
where kz is the wavevector in the axial
direction and m is the azimuthal wavenumber. Small perturbations will be
indicated by subscript 1, while unperturbed quantities will have no subscript. Then, the
linearized Eqs. (1)–(4) read ![\begin{equation} \sigma \vec{v}_{1} = - \frac{\nabla P_{1}}{\rho} + \frac{1}{4 \pi \rho}\left[ (\nabla \times \vec{B}_{1}) \times \vec{B} + (\nabla \times \vec{B}) \times \vec{B}_{1}\right], \end{equation}](/articles/aa/full_html/2011/01/aa13836-09/aa13836-09-eq25.png) (6)
(6)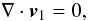 (7)
(7)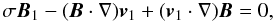 (8)
(8)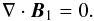 (9)Eliminating all
variables in favour of the radial velocity perturbation
v1s, we obtain
(9)Eliminating all
variables in favour of the radial velocity perturbation
v1s, we obtain
![\begin{eqnarray} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\frac{\textrm{d}}{\textrm{d}\textit{s}}\!\!\!\!\!\!&\!\!\!\! \!\!\!\!\left[ \frac{1}{\lambda} (\sigma^2 + \omega_{\rm A}^2) \left( \frac{{\rm d} v_{1s}}{{\rm d}s} + \frac{v_{1s}}{s} \right) \right] - k_z^2 (\sigma^2 + \omega_{\rm A}^2) v_{1s} \nonumber \\ &\quad -& 2 \omega_{{\rm B}} \left[ k_z^2 \omega_{{\rm B}} (1 \! - \! \alpha) \! - \! \frac{m (1 \! + \! \lambda)}{s^2 \lambda^2} \left( 1 \! - \! \frac{\alpha \lambda}{1 \! + \! \lambda} \right) (\omega_{{\rm A}z} \! + \! 2 m \omega_{{\rm B}} ) \right. \nonumber \\ &\quad -& \left.\frac{m \omega_{{\rm A}z}}{s^2 \lambda^2} \right] v_{1s} + \frac{4 k_z^2 \omega_{{\rm A}}^2 \omega_{{\rm B}}^2}{\lambda (\sigma^2 + \omega_{{\rm A}}^2)} v_{1s} =0, \end{eqnarray}](/articles/aa/full_html/2011/01/aa13836-09/aa13836-09-eq30.png) (10)where
(10)where
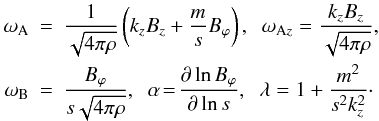 This
equation was first derived by Bonanno & Urpin (2008b) in their analysis of the non-axisymmetric stability of stellar magnetic
configurations. For axisymmetric perturbations (m = 0), Eq. (10) recovers
Eq. (11) of the paper by Bonanno & Urpin (2008a).
This
equation was first derived by Bonanno & Urpin (2008b) in their analysis of the non-axisymmetric stability of stellar magnetic
configurations. For axisymmetric perturbations (m = 0), Eq. (10) recovers
Eq. (11) of the paper by Bonanno & Urpin (2008a).
Instabilities of the magnetic configurations associated to the electric current are basically absolute instabilities, i.e. they grow but do not propagate. We suppose that this is the case also in the rest frame of the jet, and unstable perturbations are therefore simply advected with the flow at the jet velocity. Equation (10) represents a non-linear eigenvalue problem for σ, which can be solved once the boundary conditions are given. We assume that v1s should be finite at the jet axis. As far as the outer boundary is concerned, it is somewhat difficult to formulate a plausible boundary condition because actually there is no boundary between the jet and the ambient medium. Likely, the jet is separated from the ambient plasma by the shear layer that has a finite thickness. The effect of this thickness on the growth rate of instabilities has been studied by Baty (2005) who found that the results are only slightly affected by a change of the thickness. For the sake of simplicity, therefore, we assume that the shear layer is infinitely thin (see also Appl et al. 2000). In a supermagnetosonic jet, no signal can propagate from the jet interior to its surroundings, and we can expect that the instabilities behave as if the jet is bounded by a rigid conducting wall. Therefore, we can mimic the outer boundary by supposing v1s = 0 at the jet radius s = s1. Note that we also tried other outer boundary conditions (for example, with v1s ≠ 0), but this does not change the results qualitatively.
We can represent the azimuthal magnetic field as
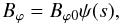 (11)where
Bϕ0 is the characteristic field strength and
ψ ~ 1. To calculate the growth rate of the instability, it is convenient
to introduce dimensionless quantities
(11)where
Bϕ0 is the characteristic field strength and
ψ ~ 1. To calculate the growth rate of the instability, it is convenient
to introduce dimensionless quantities
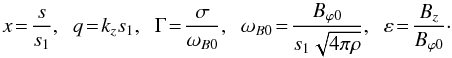 (12)Then, Eq. (10) reads
(12)Then, Eq. (10) reads
![\begin{eqnarray} \label{pert} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\frac{\textrm{d}}{\textrm{d}\textit{x}} \!\!\!\!\!\!\!&\!\!\!\!\!\!\! \left( \! \frac{{\rm d} v_{1s}}{{\rm d}x} \! + \! \frac{v_{1s}}{x} \! \right) \! + \! \left( \! \frac{{\rm d} v_{1s}}{{\rm d}x} \! + \! \frac{v_{1s}}{x} \! \right) \frac{{\rm d} \ln \Delta}{{\rm d} x} \! - \! q^2 \! \left( \! 1 \! + \! \frac{m^2}{q^2 x^2} \! \right) v_{1s} \nonumber \\&\quad-& \frac{2 q^2 \psi(x)}{x (\Gamma^2 \! \! + \! \! f^2)} \left\{ \left[ \left( \! 1 \! - \! \frac{m^2}{q^2 x^2} \! \right) \! \frac{\psi(x)}{x} \!-\! \frac{m \varepsilon}{q x^2} \! \right] (1 \! - \! \alpha) \! - \! \frac{2 m f}{m^2 \! \! + \! \! q^2 x^2} \! \right\} v_{1s} \nonumber \\ &\quad+& \frac{4 q^2 f^2 \psi^2(x)}{x^2 (\Gamma^2 + f^2)^2} v_{1s} = 0, \;\;\;\;\;\; \end{eqnarray}](/articles/aa/full_html/2011/01/aa13836-09/aa13836-09-eq40.png) (13)where
(13)where
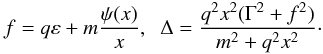 (14)We thus solve Eq. (13) for
a wide range of the parameters and different functional dependence
ψ(x).
(14)We thus solve Eq. (13) for
a wide range of the parameters and different functional dependence
ψ(x).
3. Numerical results
We assume that the function ψ(s), determining the
dependence of the azimuthal magnetic field on the radial coordinate, is given by
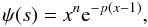 (15)where
n and p are the parameters. The function
ψ goes to 0 at the jet axis and is equal to 1 at the surface
x = 1 for any n and p. For the purpose
of illustration,we plot ψ(x) for several values of
p and n in Fig. 1.
Field profile (15) with n = 1 corresponds to the magnetic configurations
with non-vanishing current at the jet axis, whereas this current goes to 0 for
n = 2. The total axial current, integrated over the jet section, is the
same for both cases. Therefore, the distributions with n = 1 and
n = 2 can be the representatives of the jet models with the current
density being relatively smoothed and concentrated to the outer boundary, respectively. The
function (15) has the maximum at
xm = n/p
and therefore Bϕ reaches the maximum at the jet
boundary if n ≥ p or inside the jet if
p > n. Therefore, the cases
p = 1,n = 1 and 2 represent the jet models with the
maximum toroidal field at the outer boundary, whereas the field has its maximum within the
jet for p = 2,n = 1. Because the real distribution of the
magnetic field is unknown in jets, we will use Eq. (15) to mimic different possible
dependences of Bϕ on x. As far
as the axial field is concerned, we assume that
Bz is constant. In real jets, however,
Bz can depend on x as well.
Generally, this dependence does not qualitatively change the stability properties (see
Bonanno & Urpin 2008a), but it can provide an
additional destabilizing effect if Bz changes
the sign inside the jets (Robinson 1971).
(15)where
n and p are the parameters. The function
ψ goes to 0 at the jet axis and is equal to 1 at the surface
x = 1 for any n and p. For the purpose
of illustration,we plot ψ(x) for several values of
p and n in Fig. 1.
Field profile (15) with n = 1 corresponds to the magnetic configurations
with non-vanishing current at the jet axis, whereas this current goes to 0 for
n = 2. The total axial current, integrated over the jet section, is the
same for both cases. Therefore, the distributions with n = 1 and
n = 2 can be the representatives of the jet models with the current
density being relatively smoothed and concentrated to the outer boundary, respectively. The
function (15) has the maximum at
xm = n/p
and therefore Bϕ reaches the maximum at the jet
boundary if n ≥ p or inside the jet if
p > n. Therefore, the cases
p = 1,n = 1 and 2 represent the jet models with the
maximum toroidal field at the outer boundary, whereas the field has its maximum within the
jet for p = 2,n = 1. Because the real distribution of the
magnetic field is unknown in jets, we will use Eq. (15) to mimic different possible
dependences of Bϕ on x. As far
as the axial field is concerned, we assume that
Bz is constant. In real jets, however,
Bz can depend on x as well.
Generally, this dependence does not qualitatively change the stability properties (see
Bonanno & Urpin 2008a), but it can provide an
additional destabilizing effect if Bz changes
the sign inside the jets (Robinson 1971).
 |
Fig. 1 Dependence of ψ on x for p = 1,n = 1 (solid line), p = 1,n = 2 (dashed line), and p = 2,n = 1. |
 |
Fig. 2 Ratio of perpendicular and parallel to the magnetic field components of the electic current on x for ε = 0.1, p = 1,n = 1 (solid curve), ε = 0.5, p = 1,n = 2 (dashed), ε = 1, p = 1,n = 2 (dot-dashed), and ε = 2, p = 1,n = 2 (dot-dot-dashed). |
In our jet model, the electric current, j = (c/4π)∇ × B, only has a z-component, whereas B has both z- and ϕ-components. Therefore, the current j can be represented as a sum of components parallel and perpendicular to the magnetic field, j ∥ and j ⊥ , respectively. The parallel component does not contribute to the Lorentz force. However, even if j ⊥ = 0 and the magnetic field is force-free, this component alone can produce an unstable magnetic configuration. This type of instability is usually called current-driven. On the contrary, j ⊥ contributes to the Lorentz force, which should then be balanced by a pressure force in the basic state. The magnetic configurations with j ⊥ ≠ 0 and j ∥ = 0 can be unstable as well, and this type of instability is called pressure-driven. In our model, both destabilizing factors are presented and, most likely, the instability is of the mixed nature. To some extent, the relative importance of pressure- and current-driven effects can be characterized by the ratio j ⊥ /j ∥ in the basic state. This ratio is high if Bz ≪ Bϕ0 (ε ≪ 1) and the pressure-driven effects determine stability properties. On the contrary, the current-driven effects are more important if Bz ≫ Bϕ0 (ε ≫ 1). In Fig. 2 we plot the ratio j ⊥ /j ∥ as a function of the radius for different values of parameters determining the magnetic configuration. Evidently the pressure- and current-driven effects generally are comparable if ε is of the order of 1.
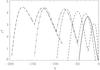 |
Fig. 3 Dependence of the normalized growth rate of instability on the wavevector q for ε = 0.1, p = 1 and n = 1. Different types of lines correspond to different azimuthal wavenumbers: m = 0 (solid), m = 1 (dashed), m = 2 (dot-and-dashed), m = 4 (dot-dot-dashed), and m = 6 (long-dashed). |
Equation (13) together with the given boundary conditions is a two-point boundary value problem, which can be solved by using the “shooting” method (Press et al. 1992). In order to solve Eq. (13), we used a fifth-order Runge-Kutta integrator embedded in a globally convergent Newton-Rawson iterator. We checked that the eigenvalue was always the fundamental mode because the corresponding eigenfunction had no zero except for that at the boundaries.
In Fig. 3 we plot the dependence of the growth rate on the axial wavevector for the magnetic configuration with non-vanishing current at the axis and a relatively weak axial magnetic field, ε = Bz/Bϕ0 = 0.1. As was noted by Bonanno & Urpin (2008), an axial field breaks the symmetry between positive and negative values of the axial wavevector q in Eq. (13) even if Bz is small compared to Bϕ. However, Eq. (13) still contains some degeneracy because it is invariant under (m,q) → (− m, − q) or (m,ε) → (− m, − ε) transformation. The instability occurs only for perturbations with q within a narrow range that depends on the azimuthal wavenumber m. For example, perturbations with m = 1 and m = 6 are unstable if 0 > q > −70 and −60 > q > −200, respectively. Note that the unstable perturbations with positive m should have negative q and, on the contrary, if m is negative, instability occurs only for perturbations with positive q.
The growth rate has two clear maxima with the highest maximum corresponding to
q ~ − m/ε. By the
order of magnitude, the axial wave-vector of the most rapidly growing perturbation can be
estimated from the condition of magnetic resonance
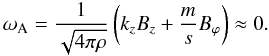 (16)Indeed, this equation
implies
ωA ∝ qε + mψ(x) ≈ 0.
Since ψ(x) ~ 1 in our model, the condition
ωA = 0 corresponds to
(16)Indeed, this equation
implies
ωA ∝ qε + mψ(x) ≈ 0.
Since ψ(x) ~ 1 in our model, the condition
ωA = 0 corresponds to
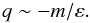 (17)The most rapidly
growing modes turn out to be highly anisotropic if the axial field is weak compared to the
toroidal one: their axial wavelength
λz = 2π/kz ~ 2πεs
is much shorter than the radial and azimuthal lengthscale. The growth rate is fairly high
and is of the order of the inverse Alfven time scale. The growth rate slowly increases with
m and perturbations with a shorter azimuthal scale grow faster. The
axisymmetric mode (m = 0) turns out to be the most slowly growing.
(17)The most rapidly
growing modes turn out to be highly anisotropic if the axial field is weak compared to the
toroidal one: their axial wavelength
λz = 2π/kz ~ 2πεs
is much shorter than the radial and azimuthal lengthscale. The growth rate is fairly high
and is of the order of the inverse Alfven time scale. The growth rate slowly increases with
m and perturbations with a shorter azimuthal scale grow faster. The
axisymmetric mode (m = 0) turns out to be the most slowly growing.
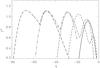 |
Fig. 4 Dependence of the normalized growth rate of instability on the wavevector q for ε = 0.1, p = 1 and n = 2. Different types of lines correspond to the same azimuthal wavenumbers as in Fig. 2. |
The model with p = 1,n = 2 exhibits a similar behaviour of perturbations (see Fig. 4). As mentioned, electric currents are more concentrated near the outer boundary in this model. The values of q that allow the instability are smaller in this case and therefore the corresponding vertical wavelengths are longer, but the range of unstable q is narrower. For the considered values of m, the growth rate is lower approximately by a factor 2. The general impression is that the configuration with currents concentrated closer to the outer boundary is more stable than that with more uniformly distributed currents. This conclusion qualitatively agrees with the result obtained by Robinson (1971) from the hydromagnetic energy principle. The author considers a pinch configuration with large β and finds that the configuration is more stable if large axial currents flow outside the main plasma column.
Note that the equilibrium state of both the configurations considered in Figs. 3 and 4 is
characterized by the negative pressure gradient that is required for the development of
instability (Longaretti 2008). Indeed, using Eq. (5)
and expression (15) for the toroidal field, we obtain
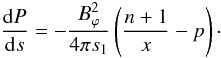 (18)Evidently
dP/ds < 0
everywhere within the range
1 > x > 0 if
p = 1 and n = 1,2. The sign of the
pressure gradient is important because it determines the destabilizing effect in the so
called Suydam’s criterion. This criterion represents a necessary condition for stability
(see, e.g., Longaretti 2003) and reads in our
notations
(18)Evidently
dP/ds < 0
everywhere within the range
1 > x > 0 if
p = 1 and n = 1,2. The sign of the
pressure gradient is important because it determines the destabilizing effect in the so
called Suydam’s criterion. This criterion represents a necessary condition for stability
(see, e.g., Longaretti 2003) and reads in our
notations 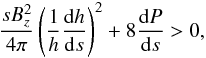 (19)where
h = sBz/Bϕ
is the magnetic shear. For the equilibrium configuration with the toroidal field given by
Eq. (15), this criterion can be rewritten as
(19)where
h = sBz/Bϕ
is the magnetic shear. For the equilibrium configuration with the toroidal field given by
Eq. (15), this criterion can be rewritten as
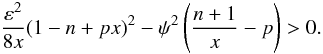 (20)For the chosen
parameters (p = 1,n = 1,2), the necessary
condition for stability is not satisfied in some fraction of the jet volume (for example,
near the outer boundary), and the corresponding configurations can generally be unstable.
(20)For the chosen
parameters (p = 1,n = 1,2), the necessary
condition for stability is not satisfied in some fraction of the jet volume (for example,
near the outer boundary), and the corresponding configurations can generally be unstable.
Figure 5 shows the dependence of the growth rate on q for the model with p = 2,n = 1. In this case, the maximum of the azimuthal field is located within the jet volume, at x = 0.5. The maximum value is approximately 1.3 times higher than the boundary one. It appears that the instability grows slightly faster in this type of magnetic configurations, but all the main qualitative features of the instability are unchanged. Because Bϕ is stronger in this model, the instability occurs for larger q as follows from Eq. (16). Note that we calculate Γ only for m ≤ 3 because of computational problems at larger m.
 |
Fig. 5 Dependence of the normalized growth rate of instability on the wavevector q for ε = 0.1, p = 2 and n = 1. Different types of lines correspond to different m: m = 0 (solid), m = 1 (dashed), m = 2 (dot-and-dashed), and m = 3 (dot-dot-dashed). |
 |
Fig. 6 Growth rate as a function of q for ε = 0.01 and distribution of the toroidal field (15) with p = 1 and n = 2. |
In Fig. 6 we plot the growth rate of instability for the configuration with the axial field much weaker than the toroidal one, ε = 0.01. The distribution of the toroidal field is given by Eq. (15) with p = 1 and n = 2. The instability can occur in this case as well, but only perturbations with very large q can be unstable. Even for the mode m = 1, the growth rate reaches its maximum at q ≈ 200. For modes with larger m, the maximum growth rate corresponds to substantially higher values of q (very short axial wavelengths). Unfortunately, our numerical code does not allow us to resolve the modes with a very short axial wavelength, and we were able to extend our calculations only to q ≈ 300. Note that that even perturbations with a q this high still grow rapidly and the growth rate is of the order of the inverse Alfven time.
Figure 7 shows the growth rate versus q for a higher ratio of the axial and toroidal fields (ε = 0.5) and for the model with p = 1 and n = 2. In this case, the instability occurs at substantially lower values of q and, correspondingly, at longer axial wavelength. The modes with small m grow relatively slowly, but the growth rate increases with increasing m. The mode with m = 8 has the growth rate comparable to the inverse Alfven time, but the modes with larger m are growing even faster. In that sense, the dependence of modes on m in the cases ε ~ 1 and ε < 1 seems to be qualitatively similar.
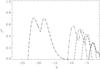 |
Fig. 7 Growth rate as a function of q for ε = 0.5, p = 1 and n = 2. The curves correspond to m = 1 (solid), m = 2 (short-dashed), m = 3 (dot-and-dashed), m = 4 (dot-dot-dashed) and m = 8 (long-dashed). |
Figure 8 compares the growth rates for the cases ε = 1 and 2. We considered the model with p = 1 and n = 2, but the behaviour is qualitatively the same as for the other models. The growth rates are generally lower than in the previous cases (ε < 1), but the instability is still present. A suppression of the growth rate is certainly more pronounced if ε = 2. However, even in this case, Γ increases relatively rapidly with increasing m and it is likely to reach a saturation value ~1 at sufficiently large m. The values of q that correspond to unstable perturbations are lower than in Figs. 3–6. Figure 8 illustrates very well that the instability cannot be completely suppressed even if the axial field is sufficiently strong and ε > 1. At large ε, the instability is not very efficient (Γ2 > 0 but very small) for perturbations with not very large m but those with large m can still reach a saturation value of Γ2 ~ 0.1. Indeed in the specific case of ε = 2 we could not find significant growth rate for modes with m ≤ 5, but we found that the growth rate is of the order of the inverse Alfven crossing time for sufficiently high azimuthal wavenumbers.
 |
Fig. 8 Comparison of the growth rate for the cases ε = 1 (solid) and 2 (dashed). The parameters determining the distribution of the toroidal field are p = 1 and n = 2. |
To illustrate how velocity perturbations depend on the cylindrical radius, in Fig. 9 the eigenfunctions for one of the models shown in Fig. 8 (ε = 1) are plotted. The eigenfunctions correspond to the azimuthal wavenumbers m = 1 (solid), 5 (dashed), and 10 (dot-and-dashed). The m = 1 mode is the only mode that does not go to zero at the jet axis. Typically, the modes reach their maximum closer to the outer boundary, and an increase of m results in the eigenfunctions that are more and more localized. For large m, motions in the core region of the jet are substantially suppressed. This sharpness of the eigenfunctions is the main reason of the problems in numerical calculations for high m.
 |
Fig. 9 The eigenfunctions for the model with ε = 1, p = 1, and n = 2. The curves correspomd to m = 1 (solid), m = 5 (dashed), and m = 10 (dot-and-dashed). |
4. Discussion
We considered the instability that can occur in jets if the magnetic field has a relatively complex structure with non-vanishing azimuthal and axial components. A magnetic field with complex topology is suggested by both the theoretical models for jet formation and the mechanisms of generation of the magnetic field. Our study considers only jets with subthermal magnetic fields because the the stability properties of jets with superthermal fields can be essentially different (Appl et al. 2000).
The considered model is very simplified and does not take into account many physical factors that can be important in the evolution of real jets. For instance, we model the transition from the jet to the external medium in terms of the infinitely thin boundary layer. In fact, the boundary can be somewhat extended and the velocity can change smoothly within the transition layer. Shear has a destabilising influence on jets (Urpin 2002), and the shear-driven instability can often be faster than instabilities associated to electric currents. An interplay of the shear-driven effects with the magnetic instabilities will be considered elsewhere. Another important assumption concerns the topology of the background magnetic field. Generally, the magnetic geometry of jets can be much more complicated than that considered in our paper and can include magnetic structures of various scales. Likely, the influence of these structures on the stability of jets can be studied only by using 3D numerical modelling. One more essential assumption of our model concerns the lack of hydrodynamical motions in the basic state of the jet in a co-moving frame. The presence of motions with the velocity comparable to the sound speed (for example, rotation) can drastically change the stability properties.
It turns out that the magnetic jet is always unstable if the azimuthal field increases to the outer boundary. This does not depend on the ratio of the axial and azimuthal fields. However, the character of the instability can be essentially different for different ε. If the axial field is weaker than the azimuthal one and ε < 1, the growth rate tends to a saturation value of the order of the inverse of a few Alfven crossing times for m > 1. Our code does not allow us to calculate eigenfunctions and eigenvalues for very large m in this case, but Figs. 3 and 4 indicate that the growth rate shows a saturation trend for m ≫ 1. Then the fastest growing mode has the axial wavevector kz ~ − m/εs, which is determined by the condition of magnetic resonance. This wavevector corresponds to the axial wavelength λz = 2π/ | kz | ~ (2πε)(s/m). At small ε, the axial wavelength of the most rapidly growing perturbations should be very small. Therefore, if the longitudinal magnetic field is weaker than the azimuthal one, we expect that the instability generates structures in jets with a very short length scale in the z-direction. Note that this behaviour can cause problems in numerical modelling of the instability because a very high resolution in the axial direction is required.
When the ratio of the axial and azimuthal fields becomes comparable to or greater than 1, the behaviour of the instability as a function of m is qualitatively similar, although the growth rate is significantly smaller. In this case perturbations with relatively small m are substantially suppressed, but we still find a numerical evidence for a saturation trend as we increase m, although it is reached for much higher values of m than in the ε < 1 case. It is important to stress that even m ~ 100 in the azimuthal direction is still a macroscopic scale, and dissipative effects are negligible in this case.
The conlusion that the instability can arise even if ε ≥ 1 with a characteristic azimuthal wavenumber m ≫ 1 is at variance with the widely accepted opinion that magnetic configurations should be stabilised at Bz ~ Bϕ. Note that the similar conclusion has been obtained by Goedbloed & Hagebruk (1972) for the magnetic configuration with the constant pitch, Bϕ/sBz = const.
The dependence of the growth rate on q has generally a very particular
shape with two maxima. The origin of these maxima in Γ2 is caused by the resonant
nature of unstable modes. The resonance is associated with the last term on the l.h.s. of
Eq. (13) (or Eq. (10)) which is proportional to
f2/(Γ2 + f2)2.
For the sake of simplicity, we can consider the case p = 0,
n = 1. Then, ψ/x = 1
and the function f (Eq. (14)) characterizes a departure of
q from the resonant value given by Eq. (17). This resonant dependence
reaches its maximum value (equal to 1/2Γ2) at
f2 = Γ2. At given Γ, this condition can be
fulfilled for two values of q,
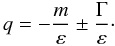 (21)These two values of
q correspond to two maxima in Γ2(q). Note
that the gap between the maxima ≈2Γ/ε increases with
decreasing ε and does not depend on m, which agrees
qualitatively and quantitatively well with the results of our numerical calculations.
(21)These two values of
q correspond to two maxima in Γ2(q). Note
that the gap between the maxima ≈2Γ/ε increases with
decreasing ε and does not depend on m, which agrees
qualitatively and quantitatively well with the results of our numerical calculations.
Note that the detailed physical nature and many properties of the instability investigated in our paper are not well understood yet. Our study also does not allow us to answer the question what type of the magnetic configuration is formed because of the development of instability. To answer this question, one needs 3D numerical simulations. However, it is possible that the much better understanding of the nature of the magnetic field in jets is required to answer this question. For example, the resulting large scale magnetic field can be formed by balancing the rate of field decay caused by instability and the rate of generation owing to some mechanism (e.g., dynamo). It would be important to investigate the consequences of our findings for jets by performing more realistic numerical simulations, and we hope to address this question in the near future.
Acknowledgments
V.U. thanks the INAF-Osservatorio Astrofisico di Catania for hospitality and financial support.
References
- Aloy, M., & Mimica, P. 2008, ApJ, 681, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Aloy, M. A., Ibánez, J. M., Marti, J. M., & Müller, E. 1999a, ApJS, 122, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Aloy, M. A., Ibánez, J. M., Marti, J. M., & Müller, E. 1999b, ApJ, 523, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Appl, S. 1996, A&A, 314, 995 [NASA ADS] [Google Scholar]
- Appl, S., Lery, T., & Baty, H. 2000, A&A, 355, 818 [Google Scholar]
- Bagchi, J., Gopal-Krishna, K. M., & Joshi, S. 2007, ApJ, 670, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Bateman, G. 1978, MHD Instabilities (Cambridge: MIT Press) [Google Scholar]
- Baty, H. 2005, A&A, 430, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baty, H., & Keppens, R. 2002, ApJ, 580, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. 1998, ApJ, 493, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M., Blandford, R., & Rees, M. 1984, Rev. Mod. Phys., 56, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Birkinshaw, M. 1997, in Advanved Topics on Astrophysical and Space Plasmas, ed. E. Gouveia Dal Pino, A. Peratt, G. Medina Tanco, & A. Chian (Dordrecht: Kluwer) [Google Scholar]
- Blandford, R., & Payne, D. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Rosner, R., Ferrari, A., & Knobloch, E. 1989, ApJ, 341, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Rosner, R., Ferrari, A., & Knobloch, E. 1996, ApJ, 470, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, A., & Urpin, V. 2008a, A&A, 477, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanno, A., & Urpin, V. 2008b, A&A, 488, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cawthorne, T., Wardle, J., Roberts, D., Gabuzda, D., & Brown, L. 1993, ApJ, 416, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, K. L., & Henriksen, R. N. 1980, ApJ, 241, 534 [NASA ADS] [CrossRef] [Google Scholar]
- de Gouveia Dal Pino, E. M., AdSpR, 35, 908 [Google Scholar]
- Eichler, D. 1993, ApJ, 419, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, A., Trussoni, E., & Zaninetti, L. 1980, MNRAS, 193, 469 [NASA ADS] [Google Scholar]
- Hanasz, M., & Sol, H. 1996, A&A, 315, 355 [NASA ADS] [Google Scholar]
- Hanasz, M., & Sol, H. 1998, A&A, 339, 629 [NASA ADS] [Google Scholar]
- Hanasz, M., Sol, H., & Sauty, C. 1999, in Plasma Turbulence and Energetic Particles in Astrophysics, ed. M. Ostrowski, R. Schlickeiser, Krakow: Obserwatorium Astronomiczne, Universytet Jagiellonski [Google Scholar]
- Hardee, P., Cooper, M., Norman, M., & Stone, J. 1992, ApJ, 399, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Hirabayashi, H., Hirosawa, H., Kobayashi, H., et al. 1998, Science, 281, 1825 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gabuzda, D. 1999, in Plasma Turbulence and Energetic Particles in Astrophysics, ed. M. Ostrowski, & R. Schlickeiser, Krakow: Obserwatorium Astronomiczne, Universytet Jagiellonski [Google Scholar]
- Gabuzda, D., Murray, E., & Cronin, P. 2004, MNRAS, 351, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Goedbloed, J., & Hagebruk, H. 1972, Phys. Fluid, 15, 1090 [Google Scholar]
- Kadomtzev, B. 1966, in Rev. Plasma Phys., ed. M. Leontovich (New York: Consultants Bureau) [Google Scholar]
- Kersale, E., Longaretti, P.-Y., & Pelletier, G. 2000, A&A, 363, 1166 [NASA ADS] [Google Scholar]
- Kharb, P., Gabuzda, D., & Shasti, P. 2008, MNRAS, 384, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Koide, S., Shibata, K., & Kudoh, T. 1998, ApJ, 495, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Kudoh, T., Matsumoto, R., & Shibata, K. 1999, AdSpR, 23, 1101 [NASA ADS] [Google Scholar]
- Laing, R. A. 1981, ApJ, 248, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A. 1993, in Astrophysical Jets, ed. D. Burgarella, M. Livio, & C. O’Dea (Cambridge: Cambridge University Press) [Google Scholar]
- Laing, R., Canvin, J., & Bridle, A. 2006, AN, 327, 523 [NASA ADS] [Google Scholar]
- Landau, L., & Lifshitz, E. 1981, Fluid Mechanics (London: Pergamon Press) [Google Scholar]
- Leismann, T., Anton, L., Aloy, M., et al. 2005, A&A, 436, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leppänen, K., Zensus, A., & Diamond, P. 1995, AJ, 110, 2479 [NASA ADS] [CrossRef] [Google Scholar]
- Lery, H., & Frank, A. 2000, ApJ, 533, 877 [Google Scholar]
- Lery, T., Baty, H., & Appl, S. 2000, A&A, 355, 1201 [NASA ADS] [Google Scholar]
- Longaretti, P.-Y. 2003, PhLA, 320, 215 [Google Scholar]
- Longaretti, P.-Y. 2008, in Numerical MHD and Instabilities, Lecture Notes in Physics (Berlin: Springer), 754, 131 [Google Scholar]
- Lucek, S. G., & Bell, A. R. 1996, MNRAS, 281, 245 [NASA ADS] [Google Scholar]
- Min, K. W. 1997, ApJ, 482, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipies in FORTRAN, The art of scientific computing (Cambridge: UP) [Google Scholar]
- Pushkarev, A., Gabuzda, D., Vetikhovskaya, Yu., & Yakimov, V. 2005, MNRAS, 356, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, D. C. 1971, Plasma Physics, 13, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Roca-Sogorb, M., Perucho, M., Gomez, J. L., et al. 2008, in Extragalactic Jets: Theory and Observations from Radio to Gamma Ray, ed. T. A. Rector, & D. S. De Young (San Francisco: ASP), ASP Conf. Ser., 386, 488 [Google Scholar]
- Romanova, M., & Lovelace, R. 1992, A&A, 262, 26 [NASA ADS] [Google Scholar]
- Urpin, V. 2002, A&A, 385, 14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urpin, V. 2006, A&A, 455, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Dependence of ψ on x for p = 1,n = 1 (solid line), p = 1,n = 2 (dashed line), and p = 2,n = 1. |
| In the text | |
 |
Fig. 2 Ratio of perpendicular and parallel to the magnetic field components of the electic current on x for ε = 0.1, p = 1,n = 1 (solid curve), ε = 0.5, p = 1,n = 2 (dashed), ε = 1, p = 1,n = 2 (dot-dashed), and ε = 2, p = 1,n = 2 (dot-dot-dashed). |
| In the text | |
 |
Fig. 3 Dependence of the normalized growth rate of instability on the wavevector q for ε = 0.1, p = 1 and n = 1. Different types of lines correspond to different azimuthal wavenumbers: m = 0 (solid), m = 1 (dashed), m = 2 (dot-and-dashed), m = 4 (dot-dot-dashed), and m = 6 (long-dashed). |
| In the text | |
 |
Fig. 4 Dependence of the normalized growth rate of instability on the wavevector q for ε = 0.1, p = 1 and n = 2. Different types of lines correspond to the same azimuthal wavenumbers as in Fig. 2. |
| In the text | |
 |
Fig. 5 Dependence of the normalized growth rate of instability on the wavevector q for ε = 0.1, p = 2 and n = 1. Different types of lines correspond to different m: m = 0 (solid), m = 1 (dashed), m = 2 (dot-and-dashed), and m = 3 (dot-dot-dashed). |
| In the text | |
 |
Fig. 6 Growth rate as a function of q for ε = 0.01 and distribution of the toroidal field (15) with p = 1 and n = 2. |
| In the text | |
 |
Fig. 7 Growth rate as a function of q for ε = 0.5, p = 1 and n = 2. The curves correspond to m = 1 (solid), m = 2 (short-dashed), m = 3 (dot-and-dashed), m = 4 (dot-dot-dashed) and m = 8 (long-dashed). |
| In the text | |
 |
Fig. 8 Comparison of the growth rate for the cases ε = 1 (solid) and 2 (dashed). The parameters determining the distribution of the toroidal field are p = 1 and n = 2. |
| In the text | |
 |
Fig. 9 The eigenfunctions for the model with ε = 1, p = 1, and n = 2. The curves correspomd to m = 1 (solid), m = 5 (dashed), and m = 10 (dot-and-dashed). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


