| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 6 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201015516 | |
| Published online | 25 November 2010 | |
An analysis of the temperature structure of galaxy clusters by means of the thermal Sunyaev-Zel’dovich effect
1
Korea Astronomy and Space Science Institute,
Hwaam-dong, Yuseong-gu,
Daejeon
305-348,
Republic of Korea
e-mail: prokhoro@iap.fr
2
Yukawa Institute for Theoretical Physics, Kyoto University,
Kitashirakawa Oiwake-cho,
Sakyo-ku, Kyoto,
606-8502,
Japan
3
Astrophysics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford,
OX13 RH,
UK
Received: 3 August 2010
Accepted: 15 September 2010
Context. Measurements of the Sunyaev-Zel’dovich (hereafter SZ) effect distortion of the cosmic microwave background provide us with an independent method to derive the gas temperature of galaxy clusters. In merging galaxy clusters the gas distribution is inhomogeneous and, therefore, the method of temperature measuring based on the SZ effect should be more relevant than that based on an X-ray emission analysis.
Aims. We study a method for measuring the gas temperature in merging clusters by means of the SZ effect.
Methods. Our calculations of intensity maps of the SZ effect include relativistic corrections considered within the framework of the Wright formalism and utilize a cosmological numerical simulation of a merging galaxy cluster evolved with its baryon physics.
Results. We found that the gas temperature in merging clusters can be inferred from the ratio of the SZ intensity at a low frequency (128 GHz) to that at a high frequency (369 GHz). This SZ intensity ratio permits us to reveal prominent features of the temperature structure caused by violent merger shock waves. Therefore, measurements of the ratio of the SZ intensities are a promising tool for measuring the gas temperature in merging galaxy clusters.
Key words: galaxies: clusters: intracluster medium / relativistic processes / cosmic background radiation
© ESO, 2010
1. Introduction
Galaxy clusters are large structures in the Universe, with radii of the order of a megaparsec. The space between galaxies in the clusters is filled with low-density (10-1–10-3 cm-3) high temperature (kBT ~ 1−10 keV) electron-proton plasma (for a review, see e.g., Sarazin 1986). Inverse Compton scattering of hot free electrons in clusters of galaxies by the cosmic microwave background (CMB) radiation field causes a change in the intensity of the CMB radiation towards clusters of galaxies (the Sunyaev-Zel’dovich effect, hereinafter the SZ effect; for a review, see Sunyaev & Zel’dovich 1980).
The SZ effect is important for cosmology and the study of clusters of galaxies (for a review, see Birkinshaw 1999). It measures the pressure of the electron population integrated along the line of sight as long as the free electrons are non-relativistic. Relativistic effects are significant for high temperature plasmas in galaxy clusters (see, e.g., Rephaeli 1995). A relativistically correct formalism for the SZ effect based on the probability distribution of the photon frequency shift after scattering was given by Wright (1979) to describe the Comptonization process of soft photons by mildly relativistic plasma.
The relativistic treatment of the SZ effect permits us to measure the temperature of intracluster plasma (see Pointecouteau et al. 1998; Hansen et al. 2002). This method is more promising for measuring the temperature of merging and/or distant clusters of galaxies than those based on studies of an X-ray spectrum analysis (see Pointecouteau et al. 1998). This is because the X-ray emission traces the denser component (the X-ray emission is proportional to 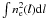 where ne is the electron number density and dl is the integrated line of sight, while the SZ effect is proportional to
where ne is the electron number density and dl is the integrated line of sight, while the SZ effect is proportional to 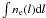 ); in addition the cluster’s X-ray surface brightness strongly decreases with redshift, while the SZ brightness is independent of redshift.
); in addition the cluster’s X-ray surface brightness strongly decreases with redshift, while the SZ brightness is independent of redshift.
Using hydrodynamic simulations of galaxy clusters, Kay et al. (2008) compare the temperatures derived from the X-ray spectroscopy and the SZ effect. Their method for measuring the SZ temperature is based on an equation (see Eq. (6) from Kay et al. 2008) that is only valid in the Rayleigh-Jeans limit. As known relativistic effects on the CMB intensity distortion are more significant at higher frequencies, Colafrancesco & Marchegiani (2010) conclude that to obtain detailed information about the cluster temperature distribution one must use high-frequency spectral observations of the SZ effect in the range 300–400 GHz and show that the SZ temperature can be extracted even for cool non-merging galaxy clusters, such as the Perseus and Abell 2199 clusters.
In this paper, using the relativistically correct Wright formalism and results of a cosmological numerical simulation of a cool distant merging cluster, we show how the SZ temperature can be derived by means of multi-frequency observations of the SZ effect. We calculate intensity maps of the SZ effect at different frequencies and propose to use the ratio of the SZ intensities at two frequencies to derive the SZ temperature of galaxy clusters.
The layout of the paper is as follows. We describe the cosmological numerical simulation of the cool distant merging cluster in Sect. 2. We calculate the SZ intensity maps at different frequencies in the framework of the Wright formalism in Sect. 3. We consider the ratio of the SZ intensities at two frequencies to find a convenient method for measuring the SZ temperature of galaxy clusters in Sect. 4 and present our discussions and conclusions in Sects. 5 and 6.
2. Numerical simulations
The galaxy cluster simulations of Dubois et al. (2010), which we use in this paper are run with the adaptive mesh refinement (AMR) code RAMSES (Teyssier 2002). The evolution of the gas is followed using a second-order unsplit Godunov scheme for the Euler equations. The Riemann solver used to compute the flux at a cell interface is the acoustic solver using a first-order MinMod total variation diminishing scheme to reconstruct the interpolated variables from their cell-centered values. Collisionless particles (dark matter, stars, and black hole particles) are evolved using a particle-mesh solver with cloud-in-cell interpolation.
The simulations are performed using a re-simulation (zoom) technique: the coarse region is a 1283 grid with MDM = 2.9 × 1010 M⊙ DM resolution in a 80 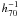 Mpc simulation box, where h70 is the Hubble constant in units of 70 km s-1 Mpc-1. This region contains a smaller 2563 equivalent grid in a sphere of radius 20
Mpc simulation box, where h70 is the Hubble constant in units of 70 km s-1 Mpc-1. This region contains a smaller 2563 equivalent grid in a sphere of radius 20 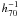 Mpc with MDM = 3.6 × 109 M⊙ DM resolution, which in turn encloses the final high resolution sphere with radius 6
Mpc with MDM = 3.6 × 109 M⊙ DM resolution, which in turn encloses the final high resolution sphere with radius 6 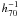 Mpc, 5123 equivalent grid, and MDM = 4.5 × 108 M⊙ DM resolution. The maximum level of refinement reached in this simulation allows us to resolve a minimum spatial scale of
Mpc, 5123 equivalent grid, and MDM = 4.5 × 108 M⊙ DM resolution. The maximum level of refinement reached in this simulation allows us to resolve a minimum spatial scale of 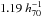 kpc.
kpc.
A flat ΛCDM cosmology was assumed with total matter density Ωm = 0.3, baryon density Ωb = 0.045, dark energy density ΩΛ = 0.7, fluctuation amplitude at 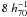 Mpc σ8 = 0.90, and Hubble constant H0 = 70 km s-1 Mpc-1 that corresponds to the Wilkinson microwave anisotropies probe 1 year best-fit cosmology (Spergel et al. 2003).
Mpc σ8 = 0.90, and Hubble constant H0 = 70 km s-1 Mpc-1 that corresponds to the Wilkinson microwave anisotropies probe 1 year best-fit cosmology (Spergel et al. 2003).
The resimulated region tracks the formation of a galaxy cluster with a 1:1 major merger occurring at z = 0.8. This z = 0.8 major galaxy merger drives the cluster gas to temperatures twice the virial temperature thanks to violent shock waves. The projected mass-weighted temperature map is shown in Fig. 1, where the x-direction is orthogonal to the merger plane.
Standard recipes for atomic cooling, heating from UV background, and star formation in high density regions are included. This simulation also includes a novel recipe for AGN feedback based on a kinetic-jet energy input that prevents the cooling catastrophe occurring, the formation of unrealistic massive cooling flows, and regulates the star formation in the central galaxy (see Dubois et al. 2010, for further details of the simulation).
 |
Fig. 1 The mass-weighted temperature map (in keV) of the simulated cluster along the x-direction at z = 0.74. |
3. The SZ effect from the simulated cluster
We calculate the SZ intensity maps in the framework of the relativistic Wright formalism for the simulated galaxy cluster.
The CMB intensity change produced by the SZ effect of non-relativistic electrons in the framework of the Kompaneets approximation is (for a review, see Birkinshaw 1999) 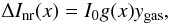 (1)where x = hν/kbTcmb, I0 = 2(kbTcmb)3/(hc)2, and the spectral function g(x) is given by
(1)where x = hν/kbTcmb, I0 = 2(kbTcmb)3/(hc)2, and the spectral function g(x) is given by 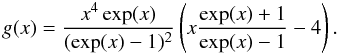 (2)The subscript “nr” denotes that Eq. (1) was obtained in the non-relativistic limit. The Comptonization parameter ygas is given by
(2)The subscript “nr” denotes that Eq. (1) was obtained in the non-relativistic limit. The Comptonization parameter ygas is given by 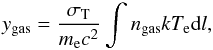 (3)where the line-of-sight integral extends from the last scattering surface of the CMB radiation to the observer at redshift z = 0, Te is the electron temperature, ngas is the number density of the gas, σT is the Thomson cross-section, me the electron mass, c the speed of light, kb the Boltzmann constant, and h the Planck constant.
(3)where the line-of-sight integral extends from the last scattering surface of the CMB radiation to the observer at redshift z = 0, Te is the electron temperature, ngas is the number density of the gas, σT is the Thomson cross-section, me the electron mass, c the speed of light, kb the Boltzmann constant, and h the Planck constant.
The CMB intensity change in the Wright formalism can be written in the form proposed by Prokhorov et al. (2010) given by 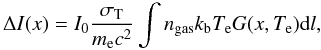 (4)where the spectral function g(x) is changed to the generalized spectral function G(x,Te), which depends explicitly on the electron temperature.
(4)where the spectral function g(x) is changed to the generalized spectral function G(x,Te), which depends explicitly on the electron temperature.
The relativistic spectral function G(x,Te) derived in the framework of the Wright formalism is given by 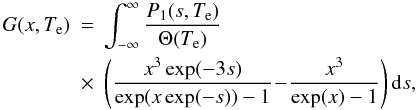 (5)where Θ(Te) = kbTe/mec2, and P1(s,Te) is the distribution of frequency shifts for single scattering (Wright 1979; Birkinshaw 1999).
(5)where Θ(Te) = kbTe/mec2, and P1(s,Te) is the distribution of frequency shifts for single scattering (Wright 1979; Birkinshaw 1999).
There are three basic spectral features that characterize the thermal, non-relativistic SZ effect signal: a minimum of its intensity is located at a dimensionless frequency x1 = 2.26 (ν = 128 GHz), the crossover frequency is x0 = 3.83 (ν = 217 GHz), and a maximum of its intensity is located at a dimensionless frequency x2 = 6.51 (ν = 369 GHz).
Observations of the SZ effect close to the crossover frequency are biased by the kinematical SZ effect (for a review, see Birkinshaw 1999), which is associated with the peculiar velocity of the galaxy cluster. The unknown value of the peculiar velocity limits our ability to measure the cluster temperature directly from the displacement of the crossover frequency of the SZ effect in the correct relativistic treatment (Colafrancesco et al. 2009).
Prokhorov et al. (2010) show that the choice of frequencies x1 = 2.26 and x2 = 6.51 corresponding to minimum and maximum values of the SZ intensity in the Kompaneets approximation is suitable to analyze mildly relativistic electron populations. Since the frequency of its maximum is located at 369 GHz, observations at this high frequency should be promising to derive the temperature by means of the SZ effect (Colafrancesco et al. 2010).
To produce the SZ intensity maps at frequencies x1 = 2.26 and x2 = 6.51, we use the 3D density and temperature maps for the simulated galaxy cluster considered in Sect. 2. We calculated the SZ effect using the Wright formalism. The intensity maps of the SZ effect at these frequencies derived from the simulation maps of the gas density and temperature are plotted in Figs. 2 and 3, respectively.
 |
Fig. 2 The intensity map I/I0 of the SZ effect at a frequency 128 GHz derived from the numerical simulation in the framework of the Wright formalism. |
 |
Fig. 3 The intensity map I/I0 of the SZ effect at a frequency 369 GHz derived from the numerical simulation in the framework of the Wright formalism. |
The morphologies of the SZ intensity simulated maps at frequencies x1 = 2.26 and x2 = 6.51 are similar. This is because the SZ effect from cool galaxy clusters can be described approximately in the framework of the Kompaneets approximation. We note that the spectral function g(x) does not depend on gas temperature. However, we now show that the gas temperature structure of a cool galaxy cluster can be derived by means of a more accurate analysis.
4. The ratio of the SZ intensity at frequency 128 GHz to that at frequency 369 GHz
We demonstrate that the ratio of the SZ intensities at frequencies 128 GHz to 369 GHz provides us with a convenient method for measuring the SZ temperature of galaxy clusters.
Multi-frequency analysis of the SZ effect permits us to derive temperature maps for galaxy clusters. Colafrancesco & Marchegiani (2010) fitted the six-frequency SZ effect data (ν = 300, 320, 340, 360, 380, and 400 GHz) with a relativistic model of the thermal SZ effect assuming, for each experimental data point, an uncertainty of 0.1%. They present results of the fitting procedure used to extract the cluster temperature from a set of simulated spatially resolved spectroscopic SZ effect observations in different bands of the spectrum. The Perseus and Abell 2199 clusters studied in Colafrancesco & Marchegiani (2010) are relaxed galaxy clusters. We present here our results of an analysis of the temperature structure of the simulated merging galaxy cluster.
Using the relativistic Wright formalism for the SZ effect, we found that the ratio of the relativistic spectral function G(x1,Te) at frequency 128 GHz to that of function G(x2,Te) at frequency 369 GHz is a monotonic function of temperature. For an isothermal galaxy cluster, the ratio of the SZ intensities is given by ΔI(x1)/ΔI(x2) = G(x1,Te)/G(x2,Te). We note that the ratio of the SZ intensities does not depend on temperature in the framework of the Kompaneets formalism.
We checked that the obtained monotonical dependence using the generalized Kompaneets equation derived by Challinor & Lasenby (1998) including relativistic effects. Using their Eq. (28), which is valid for kBTe < 10 keV, we find that the ratio of the SZ intensity at frequency 128 GHz to that at frequency 369 GHz equals 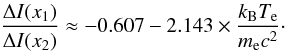 (6)Comparing Eq. (4) from this paper and Eq. (6) from Kay et al. (2008), we find that the temperature derived from the ratio of the SZ intensities at frequency 128 GHz to that at frequency 369 GHz within the framework of the Wright formalism is equivalent to the Compton-averaged electron temperature for cool galaxy clusters for which Eq. (28) from Challinor & Lasenby (1998) is valid.
(6)Comparing Eq. (4) from this paper and Eq. (6) from Kay et al. (2008), we find that the temperature derived from the ratio of the SZ intensities at frequency 128 GHz to that at frequency 369 GHz within the framework of the Wright formalism is equivalent to the Compton-averaged electron temperature for cool galaxy clusters for which Eq. (28) from Challinor & Lasenby (1998) is valid.
The ratio of the SZ intensity maps at frequencies 128 GHz to 369 GHz derived within the framework of the Wright formalism (see Figs. 2 and 3) is shown in Fig. 4. We note that regions of high temperature on the mass-weighted temperature map (see Fig. 1) corresponds to regions with low values of the SZ intensity ratio as expected from Eq. (6).
 |
Fig. 4 The ratio of the SZ intensity at frequency 128 GHz to that at frequency 369 GHz for the simulated cluster. |
Using the monotonical dependence of the SZ intensity ratio on temperature derived within the framework of the Wright formalism, we derive the SZ temperature map from the map of the ratio of the SZ intensities at frequencies 128 GHz to 369 GHz. The SZ temperature map is shown in Fig. 5.
 |
Fig. 5 Temperature (in keV) of the simulated cluster along the x direction at z = 0.74 derived from the ratio of the SZ intensities. |
The temperature maps in Figs. 1 and 5 contain high temperature “arc-like” structures. The origin of these “arc-like” structures is the major merger of two galaxy clusters occurring at z = 0.8. The evolution of the mass-weighted temperature along the x-direction during its merging phase is shown in Fig. 5 from Dubois et al. (2010) at different redshifts z = 0.88, z = 0.74, and z = 0.58. As shown by Dubois et al. (2010), this major merger drives the cluster gas to temperatures twice the virial temperature thanks to violent merger shock waves.
Figure 5 shows that the SZ temperature is higher than the mass-weighted temperature (see Fig. 1). This is consistent with the results of Kay et al. (2008). We find, from Eq. (6), that a sensitivity of the order of ~ 0.3% of the predicted SZ effect is necessary to measure the SZ temperature in cool galaxy clusters with a precision of 1 keV by means of the SZ intensity ratio. Our analysis shows that the ratio of the SZ intensities is a promising approach for measuring the temperature structure in merging galaxy clusters.
5. Discussions
A source of bias in the observations of the SZ effect could be provided by a possibly relevant kinematic SZ effect. The kinematic SZ effect arises from the bulk motion of the medium relative to the CMB rest frame. In this section, we propose a method to extract the kinematical SZ effect from SZ observations and also discuss various constraints on our ability to measure the gas temperature in distant merging galaxy clusters by means of X-ray observations.
5.1. The kinematic SZ effect
To study the kinematical SZ effect from SZ observations, Rephaeli & Lafav (1991) proposed to measure the SZ effect at the crossover frequency. The contribution of the kinematical SZ effect is maximal at the crossover, where the thermal SZ effect in the Kompaneets approximation equals zero. Using Eq. (28) from Challinor & Lasenby (1998), we calculate the ratio of the intensities of the relativistic SZ effect to the kinematic SZ effect at the crossover frequency. This ratio is given by 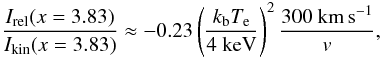 (7)where v is the peculiar velocity of a galaxy cluster and 300 km s-1 is the rms value of the peculiar velocity distribution of galaxy clusters (see Giovanelli et al. 1998).
(7)where v is the peculiar velocity of a galaxy cluster and 300 km s-1 is the rms value of the peculiar velocity distribution of galaxy clusters (see Giovanelli et al. 1998).
Equation (7) shows that the relativistic corrections to the thermal SZ effect in galaxy clusters at the crossover frequency can be significant and biases measurements of peculiar velocity by the Rephaeli & Lafav method, particulary in hot clusters with temperature ~10 keV. Therefore, below we propose another method to measure peculiar velocities. We note that the approximate function describing the SZ relativistic corrections taken from Challinor & Lasenby (1998) for kBTe < 10 keV has two frequencies at which relativistic corrections equal zero. The values of these frequencies are xa = 3.33 and xb = 8.02. Measurements of SZ intensities at these frequencies provide us with a method to derive the peculiar velocity. Using Eq. (28) from Challinor & Lasenby (1998), we find 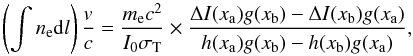 (8)where the spectral function h(x) describing the kinematic SZ effect is
(8)where the spectral function h(x) describing the kinematic SZ effect is 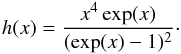 (9)The optical depth of the gas to Compton scattering can be obtained from spectral and spatial X-ray observations, and can be determined accurately in relaxed galaxy clusters. The proposed method to derive the peculiar velocity of a galaxy cluster based on Eq. (8) is not affected by biases caused by the relativistic corrections of the thermal SZ effect.
(9)The optical depth of the gas to Compton scattering can be obtained from spectral and spatial X-ray observations, and can be determined accurately in relaxed galaxy clusters. The proposed method to derive the peculiar velocity of a galaxy cluster based on Eq. (8) is not affected by biases caused by the relativistic corrections of the thermal SZ effect.
It is important that measurements of the value of (∫nedl)v/c permit us to extract contributions of the kinematical SZ effect from SZ observations at frequencies of 128 GHz and 369 GHz, since the contribution of the kinematical SZ effect is proportional to (∫nedl)v/c.
5.2. Constraints on our ability to measure the gas temperature via X-ray observations
To compare methods for measuring the gas temperature in merging clusters based on the SZ effect with that based on X-ray emission, we produce the X-ray surface brightness map of thermal bremsstrahlung emission for the simulated cluster. For the sake of illustration, the normalized X-ray surface brightness map of the simulated cluster in the [2.0–10.0 keV] band in logarithmic scale is shown in Fig. 6, which can be obtained by modern X-ray satellites, such as XMM-Newton, Chandra, and Suzaku. The region corresponding to the highest temperature in Fig. 5 is shown by a black circle in Fig. 6. The X-ray surface brightness of this region is two orders of magnitude lower than the maximal surface brightness value in Fig. 6, while the SZ intensity (see contours of the SZ intensity superimposed on the X-ray surface brightness map, the inner contour representing 10% of the maximum of the SZ intensity and the outer contour representing 1% of the maximum of the SZ intensity) of this region is one order of magnitude lower than the maximal SZ intensity value in Figs. 2 and 3. Therefore the X-ray emission traces the denser component, while the SZ effect provides us with a method to study more rarified gas regions.
 |
Fig. 6 The normalized X-ray surface brightness map of the simulated cluster in the [2.0–10.0 keV] band in logarithmic scale. The region corresponding to the highest temperature in Fig. 5 is shown by a black circle. |
The Abell 3376 cluster at redshift z = 0.046 is a cool nearby cluster and provides us with an example of galaxy clusters where a shock has not been revealed by X-ray observations with the XMM-Newton X-ray satellite, but has been detected instead by radio observations with the Very Large Array telescope (Bagchi et al. 2006). This is because the X-ray surface brightness in the region of the east ringlike structure is very weak and does not permit us to detect this shock.
Since the X-ray surface brightness decreases with redshift as 1/(1 + z)4, the X-ray surface brightness for the simulated cluster at z = 0.74 is lower by a factor by ~9 than that of the same cluster at z = 0. The decrease in the X-ray surface brightness with redshift constrains our ability to measure the gas temperature in distant galaxy clusters by means of X-ray observations.
6. Conclusions
Merging galaxy clusters are an interesting astrophysical laboratory for studying gasdynamic processes. Mergers of galaxy clusters are very energetic astrophysical events in which huge gravitational energy is released. In the course of a merger, a significant portion of this energy, which is carried by the gas, is dissipated by merger shock waves. This leads to a heating of the gas to higher temperatures. Studying the temperature structure of merging galaxy clusters is important to reveal heated gas regions associated with merger shock waves.
Studying X-ray spectra provides us with two independent approaches to determining the gas temperature in galaxy clusters, because the bremsstrahlung continuum spectrum depends on the gas temperature and the ratios of emission-line fluxes are functions of the gas temperature (e.g., the ratio of the He-like to H-like iron line fluxes, see e.g. Prokhorov et al. 2009). An analysis of the SZ effect permits us to determine the gas temperature by studying deviations of the SZ intensity spectrum from that derived within the framework of the Kompaneets approximation. Colafrancesco & Marchegiani (2010) show that the method based on the SZ intensity deviations can be interesting for measuring the gas temperature even in cool clusters, such as the Perseus and Abell 2199 clusters, if uncertainties in the observational data are 0.1–1%. In this paper, using the relativistically correct Wright formalism and results of 3-D hydrodynamic numerical simulations of a cool distant merging cluster, we have demonstrated how the SZ temperature can be derived by means of multi-frequency observations of the SZ effect.
To produce a realistic cool distant merging cluster, we have used a zoomed cosmological simulation from Dubois et al. (2010). We have found that the simulated cluster undergoes a violent merger at z = 0.8, which drives the cluster gas to higher temperatures. The temperature map of the simulated cluster becomes very inhomogeneous because of the merger activity (see Fig. 1). We have considered a method for measuring the temperature structure in this merging simulated cluster by means of distortions of the SZ intensity map caused by relativistic effects.
We have incorporated the relativistic Wright formalism for modeling the SZ effect in the numerical simulation using the algorithm proposed by Prokhorov et al. (2010). We calculated the SZ intensity maps at low (128 GHz) and high (369 GHz) frequencies and found that these SZ intensity maps are similar as expected for a cool galaxy cluster. To provide a method for measuring the temperature structure in cool merging galaxy clusters we have proposed using the ratio of the SZ intensities at two frequencies.
We calculated the ratio of the SZ intensity at a low frequency (128 GHz) to that at a high frequency (369 GHz) for the simulated merging cluster and showed that this ratio is a promising method for measuring the SZ temperature in galaxy clusters. The calculated map of the SZ temperature illustrates how the main features (such as “arc-like” structures) of the temperature structures of merging clusters can be revealed using this method.
The next generation SZ effect experiments discussed in Colafrancesco & Marchegiani (2010) are needed to reach the required high sensitivity to establish an independent means of measuring gas temperature in galaxy clusters. Experimental configurations, which are basically the same as those of the Millimetron project1, will have the power to measure the gas temperature via the SZ effect in any cluster, including cool ones.
Acknowledgments
We are grateful to Florence Durret for valuable discussions of X-ray emission of the Abell 3376 cluster and to Sergio Colafrancesco for valuable discussions of experimental configurations for Millimetron.
References
- Bagchi, J., Durret, F., Lima Neto, G. B., & Paul, S. 2006, Science, 314, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Birkinshaw, M. 1999, Phys. Rep., 310, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Challinor, A., & Lasenby, A. 1998, ApJ, 499, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Colafrancesco, S., & Marchegiani, P. 2010, A&A, 520, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colafrancesco, S., Prokhorov, D., & Dogiel, V. 2009, A&A, 494, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubois, Y., Devriendt, J., Slyz, A., & Teyssier, R. 2010, MNRAS, in press, [arXiv:1004.1851] [Google Scholar]
- Giovanelli, R., Hayness, M. P., Salzer, J. J., et al. 1998, AJ, 116, 2632 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, S. H., Pastor, S., & Semikoz, D. V. 2002, ApJ, 573, L69 [Google Scholar]
- Kay, S. T., Powell, L. C., Liddle A. R., & Thomas, P. A. 2008, MNRAS, 386, 2110 [NASA ADS] [CrossRef] [Google Scholar]
- Pointecouteau, E., Giard, M., & Barret, D. 1998, A&A, 336, 44 [NASA ADS] [Google Scholar]
- Prokhorov, D. A., Durret, F., Dogiel, V. A., & Colafrancesco, S. 2009, A&A, 496, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prokhorov, D. A., Antonuccio-Delogu, V., & Silk, J. 2010, A&A, 520, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rephaeli, Y. 1995, ApJ, 445, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., & Lahav, O. 1991, ApJ, 372, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Ya. B. 1980, ARA&A, 18, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, E. L. 1979, ApJ, 232, 348 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 The mass-weighted temperature map (in keV) of the simulated cluster along the x-direction at z = 0.74. |
| In the text | |
 |
Fig. 2 The intensity map I/I0 of the SZ effect at a frequency 128 GHz derived from the numerical simulation in the framework of the Wright formalism. |
| In the text | |
 |
Fig. 3 The intensity map I/I0 of the SZ effect at a frequency 369 GHz derived from the numerical simulation in the framework of the Wright formalism. |
| In the text | |
 |
Fig. 4 The ratio of the SZ intensity at frequency 128 GHz to that at frequency 369 GHz for the simulated cluster. |
| In the text | |
 |
Fig. 5 Temperature (in keV) of the simulated cluster along the x direction at z = 0.74 derived from the ratio of the SZ intensities. |
| In the text | |
 |
Fig. 6 The normalized X-ray surface brightness map of the simulated cluster in the [2.0–10.0 keV] band in logarithmic scale. The region corresponding to the highest temperature in Fig. 5 is shown by a black circle. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


